欢迎访问《哈尔滨工业大学学报》编辑部网站！

考虑构件震害影响的城市桥梁震后通行功能损失评估方法

doi: 10.11918/202405059

李天翊^1,2 ，张东昱^1,2 ，张晓宇³

1. 哈尔滨工业大学土木工程学院,哈尔滨 150090

2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090

3. 中交公路长大桥建设国家工程研究中心有限公司,北京 100120

基金项目: 国家自然科学基金(U2239253) ；中交集团院士专项项目(YSZX-01-2022-01-B)

详细信息

作者简介

李天翊(2000—),男,博士研究生;

张东昱(1974—),男,教授,博士生导师

通讯作者

张东昱,dongyu.zhang@hit.edu.cn

中图分类号: TU375

文献标识码: A

文章编号: 0367-6234(2025)01-0035-11

Post-earthquake urban bridge traffic capacity loss assessment considering effects of structural component damage

LI Tianyi^1,2 ， ZHANG Dongyu^1,2 ， ZHANG Xiaoyu³

1. School of Civil Engineering, Harbin Institute of Technology, Harbin 150090 , China

2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters(Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090 , China

3. National Engineering Research Centre for the Construction of Long Highway Bridges of CCCC, Beijing 100120 , China

摘要

桥梁作为城市交通网络重要节点,其车辆通行能力在震后救灾和重建过程中起着至关重要的作用。但现有城市桥梁震后损失研究多集中于结构损伤维修成本方面,对桥梁震后车辆通行功能损失研究关注不足,难以为震后紧急救援和桥梁修复决策提供有效指导。因此,本文提出了综合考虑桥梁构件震害破坏及其对车辆通行影响的桥梁震后通行功能损失评估方法。首先,为了更准确地分析地震对桥梁结构整体系统的影响,采用 copula 函数,开展了考虑桥梁构件破坏相关性的桥梁系统地震易损性分析;其次,提出了地震导致桥梁车辆通行能力损失的评估方法。该方法综合考虑了桥梁结构损伤、承载力下降导致的开放车道减少以及桥梁伸缩缝损坏导致的车辆行驶速度降低等因素影响,因而可以更准确地反映震后桥梁车辆通行能力;最后,通过一个 4 跨连续梁桥算例发现相较于现有评估方法,本文提出的城市桥梁震后通行功能损失评估方法具有准确度更高、离散程度和不确定性更小的特点。与传统的定性和主观震后桥梁功能损失评估方法相比,本项研究提出的分析方法从物理层面考虑了桥梁构件震害对桥梁车辆通行能力的具体影响,为震后决策过程提供了一个数学模型。

关键词

桥梁易损性 / 构件破坏相关性 / 车辆通行能力 / 桥梁通行功能损失

Abstract

As key components in urban transportation network, bridges play crucial roles in post-earthquake relief and reconstruction efforts. However, existing studies on post-earthquake losses of urban bridges primarily concentrate on repair costs for structural damage, paying less attention to the loss of vehicular traffic capacity, which makes it difficult to provide effective guidance for post-earthquake emergency responses and bridge rehabilitation decisions. Therefore, in this paper a method was proposed to assess the loss of post-earthquake traffic capacity of a bridge by comprehensively considering the seismic damage to bridge components and its impact on vehicular traffic. Firstly, in order to accurately analyze the effect of the earthquake on the bridge structure system, a seismic fragility analysis of the bridge system was conducted using the copula function, considering the interdependence of damage to bridge components. Secondly, an evaluation method was proposed for estimating the loss of traffic capacity in bridges due to earthquakes. Finally, the proposed method for assessing post-earthquake vehicular traffic capacity loss of urban bridges was tested through an example of a 4-span continuous girder bridge, which proves that it is more accurate and has less dispersion and uncertainty compared to existing assessment methods. Compared to traditional qualitative and subjective postearthquake functionality assessment of the damaged bridge, the proposed analytical approach considers the specific impact of seismic damage to bridge components on the traffic capacity of the bridge from a physical perspective, and offers a mathematical model for the decision-making process.

Keywords

bridge seismic fragility analysis / correlation of structure components’ damage / vehicular traffic capacity / traffic capacity loss of bridge

1 桥梁地震易损性分析 1.1 桥梁构件易损性分析 1.2 考虑构件损伤相关性的桥梁系统易损性分析 1.3 Copula 函数确定方法 2 震后桥梁通行能力损失评估 2.1 桥梁通行能力 2.2 震后车辆行驶速度计算方法 2.2.1 车辆通过伸缩缝振动模拟 2.2.2 车辆舒适度评价 2.2.3 车辆过桥平均速度 2.3 震后开放车道数计算方法 2.4 功能损失的不确定性 3 算例分析 3.1 桥梁模型 3.2 桥梁易损性分析 3.3 桥梁通行能力损失评估 4 结论

城市桥梁作为城市交通网络的薄弱环节^[1]，在地震灾害中易发生较严重的结构损伤，导致桥梁车辆通行能力下降，严重影响震后救灾物资、人员和设备的运输。因此，准确评估桥梁震后车辆通行能力损失不仅可在桥梁修复过程中帮助决策者确定资源分配和受损桥梁修复工序的优先级^[2]，还可以在资源限制条件下优化既有桥梁的震前加固策略^[3]。

地震易损性分析建立了地震动强度与结构破坏概率间的关系，是桥梁震后功能损失评估的基础，现阶段易损性分析方法主要分为三类:经验易损性分析、理论易损性分析和混合易损性分析。 Li 等^[4] 基于汶川地震桥梁震害数据，使用改进的非线性高斯评估模型，提出了钢筋混凝土梁桥经验易损性评估方法; Rezaei 等^[5]使用进化系数和符号回归方法识别、推导出相关参数与地震响应之间的关系，进而建立桥梁的易损性曲线; 刘洋^[6] 使用云图法建立桥梁需求模型，并且基于试验识别的损伤极限状态对应的工程需求参数建立了桥梁能力模型，实现了桥梁混合易损性分析。

桥梁震后损失量化方法分为两类:一是通过震后修复成本、修复时间和人员伤亡等经济损失指标评估震后损失; 二是基于经验和历史震害数据自定义桥梁功能损失指标。针对第一类方法，Li 等^[7]建立了在建桥梁地震损伤状态与修复成本的对应关系，实现了不同施工阶段的桥梁功能损失评估; 吕大刚等^[8]基于改进的生活质量指数，建立了社会挽救生命成本和人员伤亡损失的货币价值评估框架; Liu 等^[9]拓展了桥梁震后功能评估指标的维度，建立了基于安全、社会、环境和经济等指标的多维功能损失评价体系。针对第二类方法，Dong 等^[10] 建立了桥墩震后竖向承载力的概率分布模型，并基于桥墩剩余承载力和桥梁可靠度指标计算出桥梁震后车辆通过能力; Ghasemi 等^[11] 使用可靠度反映桥梁的震后损伤状态，提出了一种基于可靠性指数的特定地震烈度下桥梁交通流量估计方法。在地震灾害应急期间，城市桥梁主要功能是受灾人员和救援人员转移以及救灾物资设备的运输^[12]，前述各类以经济指标为主的地震损失评估方法无法满足准确评估地震应急期内桥梁通行功能的需求，也难以为震后紧急救援和桥梁修复决策提供指导; 而基于经验或历史震害数据自定义功能指标虽然可以直观反映出桥梁震后通行功能损失，但是过于依赖经验且缺乏实际物理意义，难以对所有类型桥梁震后通行功能损失进行准确可靠的评估。

当前研究通常根据经验建立桥梁损伤状态与震后功能损失的对应关系，用于评估桥梁震后功能。Frangopol 等^[13]根据震后通行措施确定了不同损伤等级桥梁的功能损失，当桥梁超过中等损伤时，应禁止车辆通行，桥梁功能损失为 1，当桥梁介于轻微损伤和中等损伤之间时，应限制车辆通行，功能损失为 0.5; 王晓伟等^[14]基于专家经验，通过分析问卷调查数据得到了桥墩 4 种损伤状态对应的功能损失分别为 0.22、0.45、0.72、1; Liang 等^[15] 使用了三角形模糊函数表示桥梁功能损失，不同损伤状态对应的功能损失区间分别为 0~0.5、0.5~1、0.8~1、1。通过上述研究可以发现，不同学者根据经验给出的桥梁损伤状态与功能损失之间对应关系存在显著差异，因而得到的桥梁震后功能损失评估结果也不尽相同，存在较大的主观性。

为了更准确地评估桥梁震后通行功能损失，本文提出一种考虑桥梁构件震害损伤影响的城市桥梁震后通行功能损失评估方法。首先，开展了桥梁地震易损性分析，采用 copula 函数分析桥梁构件破坏相关性，得到桥梁整体损伤状态的地震易损性曲线; 其次，深入分析影响震后桥梁车辆通行能力的关键因素，提出综合考虑桥梁结构损伤、承载力下降导致的开放车道减少与桥梁伸缩缝损坏导致的车辆行驶速度降低影响的桥梁震后通行功能损失计算方法; 最后，以一个 4 跨连续梁桥为例，验证了本文提出的城市桥梁震后车辆通行功能损失评估方法的有效性。本项研究提出的桥梁震后通行功能损失评估方法，从物理层面充分考虑了桥梁构件震害对桥梁车辆通行能力的具体影响，具有实际可操作性，可推广用于各类桥梁的震后通行功能损失评估。

1 桥梁地震易损性分析

1.1 桥梁构件易损性分析

桥梁地震易损性分析是开展桥梁震后车辆通行功能损失研究的基础，本文采用增量动力分析方法^[16]（IDA），分析桥梁构件地震易损性。根据以往桥梁震害经验，以梁桥为主的城市桥梁在地震中主要震害大多发生在桥墩和支座位置，因此，本文仅评估桥墩和支座构件的地震易损性。地震易损性是指给定地震动强度 M 下结构或构件的地震需求 D 达到或超过其抗震能力 C 的概率，可表示为

P [D ⩾ C ∣ M] = Φ [\frac{l n (D / C)}{\sqrt{β_{d}^{2} + β_{c}^{2}}}]

(1)

式中:Φ（·）为标准正态分布函数，β_d为桥梁地震需求对数标准差，β_c为桥梁抗震能力对数标准差。当地震动强度参数为地震动峰值加速度 A_pg 时，

\sqrt{β_{d}^{2} + β_{c}^{2}}

取 0.5。

研究表明^[17]，结构地震需求 D 与地震动强度参数A_pg之间的关系服从式（2），式中 a、b 为回归系数，通过 IDA 方法计算提取的地震响应数据拟合得到。

l n D = a + b l n M

(2)

将式（2）代入式（1）可得

P [D ⩾ C ∣ M] = Φ [\frac{a + b l n M - l n C}{0.5}]

(3)

1.2 考虑构件损伤相关性的桥梁系统易损性分析

桥墩是桥梁系统最关键的构件，单个桥墩失效会导致整个桥梁系统失效，而支座子系统通常具有一定冗余性; 但对于城市桥梁，同一跨支座类型和支撑方向相似，支座的震后损伤状态也基本相同，可近似用单个支座失效表示支座系统失效。本文认为桥墩和支座以串联方式组成了桥梁主要荷载承担系统，因而桥梁系统整体的地震易损性，不仅取决于单个桥墩、支座的易损性，还与各个构件之间的地震破坏相关性有关。为此，本文使用 copula 函数^[18]来分析桥梁各子构件的地震响应相关性，建立各变量边缘概率密度与联合概率密度的联系，最终得到桥梁整体系统易损性模型，当系统由多个子系统串联构成时，其破坏概率为:

\begin{matrix} P [f_{1} (x_{1}) < 0, f_{2} (x_{2}) < 0] = \\ P [F_{1} (f_{1} (x_{1})) < F_{1} (0), F_{2} (f_{2} (x_{2})) < F_{2} (0)] = \\ P [U_{1} < F_{1} (0), U_{2} < F_{2} (0)] = \\ C [F_{1} (0), F_{2} (0)] = C [P_{1}, P_{2}] \end{matrix}

(4)

式中:f_i 为第 i 个串联子系统破坏模式功能函数，P_i为单个子系统的破坏概率，C[·]为多个子系统同时发生破坏的概率。

根据式（4）可得，由支座和桥墩串联构成的桥梁系统破坏概率为

\begin{matrix} P_{bridge} = \cup (P_{bearing}, P_{column}) = P_{bearing} + \\ P_{column} - C [P_{bearing}, P_{column}] \end{matrix}

(5)

式中:P_bearing和P_column为支座和桥墩构件单独破坏的概率，可通过 1.1 节的构件地震易损性确定; P_bridge 为桥梁的破坏概率。

1.3 Copula 函数确定方法

本文采用了 Gumbel、Clayton 和 Frank 3 种常见的阿基米德簇 copula 函数，计算桥梁系统各构件的相关性。阿基米德簇 copula 函数由生成元 φ 生成，其统一表达式见式（6）。阿基米德簇 copula 函数的参数 θ 由相关变量之间的 Kendall 秩相关系数计算。 3 种 copula 函数的生成元 φ 分别为:

C (μ_{1}, μ_{2}, \dots, μ_{N}; θ) = φ^{- 1} (φ (μ_{1}; θ) + \dots + φ (μ_{N}; θ))

(6)

φ_{Clayton} (t; θ) = \frac{1}{θ} (t^{- θ} - 1), φ_{Claylon}^{- 1} (t; θ) = (1 + θ t)^{- \frac{1}{θ}}

(7)

φ_{Gumbel} (t; θ) = (- l n (t))^{θ}, φ_{Gumbel}^{- 1} (t; θ) = e x p (- t^{\frac{1}{θ}})

(8)

\begin{matrix} φ_{Frank} (t; θ) = - l o g (\frac{e x p (- θ t) - 1}{e x p (- θ) - 1}), \\ φ_{Frank}^{- 1} (t; θ) = - \frac{1}{θ} l n [1 + e x p (- t) (e x p (- θ) - 1)] \end{matrix}

(9)

为了判定所选 copula 函数是否能够反映真实构件破坏之间的相关关系，使用非参数 Kolmogorov-Smirnov 统计检验方法对 3 种 copula 函数建立的相关性模型和实际数据统计量进行拟合检验，其数学表达式为

D = m a x |F_{n} (x) - F_{0} (x)|

(10)

式中:F_n（x）为待检验的理论分布函数; F₀（ x）为实验样本统计得到的分布函数; D 代表样本所属总体分布与给定分布之间距离的最值，当 D≤D_α时所选 copula 函数可接受。

根据 3 种拟合 copula 函数的均方根误差（S_RME）确定最优 copula 函数，建立桥梁系统易损性曲线。 S_RME计算公式:

S_{R M E} = \sqrt{\frac{1}{n} \overset{n}{\underset{i = 1}{Σ}} {(p_{i}^{e} - p_{i})}^{2}}

(11)

式中:n 是样本个数，p^e_i 表示经验频率，p_i 表示理论频率。

2 震后桥梁通行能力损失评估

2.1 桥梁通行能力

桥梁通行能力^[19]是指正常交通条件下，一定时间内桥梁设施通过交通流的能力，它反映了桥梁疏导交通的最大能力和承担车辆运行的极限值。实际条件下的桥梁通行能力 C 可表示为

C = n \times f \times C_{0}

(12)

式中:n 为车道数; f 为行驶条件修正系数; C₀ 为单车道基本通行能力，指理想条件下道路的通行能力，可按下式计算:

C_{0} = \frac{3600}{t_{0}} = \frac{1000 v}{l_{0}}

(13)

式中:t₀是车头最小时距; v 为行车速度; l₀是车头最小间隔，由车辆平均长度、制动距离、司机反应距离和车辆安全间距决定。

假定地震前后的交通条件和车头最小间隔不发生变化，则可采用功能损失比 k 来表示震后桥梁通行功能损失。

k = 1 - \frac{C_{post}}{C_{pre}} = 1 - \frac{n_{post}}{n_{pre}} \times \frac{v_{post}}{v_{pre}} = 1 - k_{n} \times k_{v}

(14)

式中:v_pre和v_post分别为地震前后通行速度，n_pre和n_post分别为地震前后车道开放数目，k_n为震后车道数折减系数，k_v为震后行驶速度折减系数。

2.2 震后车辆行驶速度计算方法

震后桥梁伸缩缝宽度增大和桥面板破坏是影响车辆行驶速度的主要因素。动力特性不同的相邻梁体在地震作用下可能会产生较大的相对位移，甚至可能发生梁体碰撞，导致桥梁伸缩缝宽度扩大，桥梁伸缩缝的地震破坏见图1，随着伸缩缝宽度变大，车辆通过伸缩缝时会出现跳车加剧现象^[20]，需要减小车辆行驶速度来控制车辆通过伸缩缝时的振动幅度; 此外，由于地震作用下桥面板破坏较小^[6]，因此本文仅考虑通过伸缩缝时车辆振动对行驶速度的影响。

图1桥梁伸缩缝地震破坏

Fig.1Seismic damage of bridge expansion joints

2.2.1 车辆通过伸缩缝振动模拟

车辆通过伸缩缝过程可分为 3 个阶段:下伸缩缝、跨伸缩缝和上伸缩缝，丁勇等^[21] 考虑了伸缩缝的宽度、轮载大小得到了图2所示的车轮运动轨迹。当轮胎在普通路面上行驶时，轮载 F 作用下车轮竖向压缩量 ΔR 和车轮与路面接触长度 a 分别为:

Δ R = \frac{F}{K}

(15)

a = 2 \sqrt{R^{2} - (R - Δ R)^{2}}

(16)

式中 K 为轮胎的刚度。当车轮位于伸缩缝中心处，车轮底部部分脱空，脱空部分不受路面支持，此时车轮竖向压缩量 ΔR′为:

Δ R^{'} = \frac{F}{K \frac{a^{'} - d}{a^{'}}} = Δ R \frac{a^{'} - d}{a^{'}}

(17)

a^{'} = 2 \sqrt{R^{2} - {(R - Δ R^{'})}^{2}}

(18)

式中:d 为伸缩缝的宽度; a′为通过伸缩缝时轮胎与路面的接触长度。轮胎在伸缩缝内和普通路面压缩量之差 ΔR′-ΔR 是车轮通过伸缩缝过程中的最大竖向位移 h。车轮通过伸缩缝前后，假设竖向位移为零，跨伸缩缝过程中车轮竖向位移始终为 h，上下伸缩缝运动轨迹为余弦函数。

图2通过伸缩缝时车轮运动轨迹

Fig.2Trajectory of vehicle wheel when across expansion joints

通过伸缩缝时车轮竖向位移会导致车辆悬挂系统产生振动，本文采用了 1 / 4 小型车模型的单自由度车辆动力学模型（图3），用于分析伸缩缝产生的车辆悬挂系统振动。式（19）给出了车辆悬挂系统的动力学方程。

M \ddot{x} + C (\dot{x} - \dot{y}) + k (x - y) = 0

(19)

式中:M = 500 kg，C = 2.50 × 10³ N·s/ m，k = 3.33 × 10⁴ N/ m，x 为车辆悬挂系统的竖向位移，y 为车轮经过伸缩缝时的竖向位移。

图3车辆单自由度动力学模型

Fig.3Single-degree-of-freedom dynamic model of vehicles

2.2.2 车辆舒适度评价

根据式（19）求解通过伸缩缝时车辆竖向加速度时程，并按照式（20）计算竖向加速度均方根值，表1列出了 ISO ^[22]提供的车辆均方加速度与车辆行驶舒适度之间的对应关系。

\bar{a} = \sqrt{\frac{1}{T} \int_{0}^{T} a^{2} (t) d t}

(20)

式中 T 为车辆整体通过伸缩缝的时间。

表1加权加速度均方根值与人体主观感受之间的关系

Tab.1 Relation between weighted root-mean-square acceleration and human subjective perception

本文取

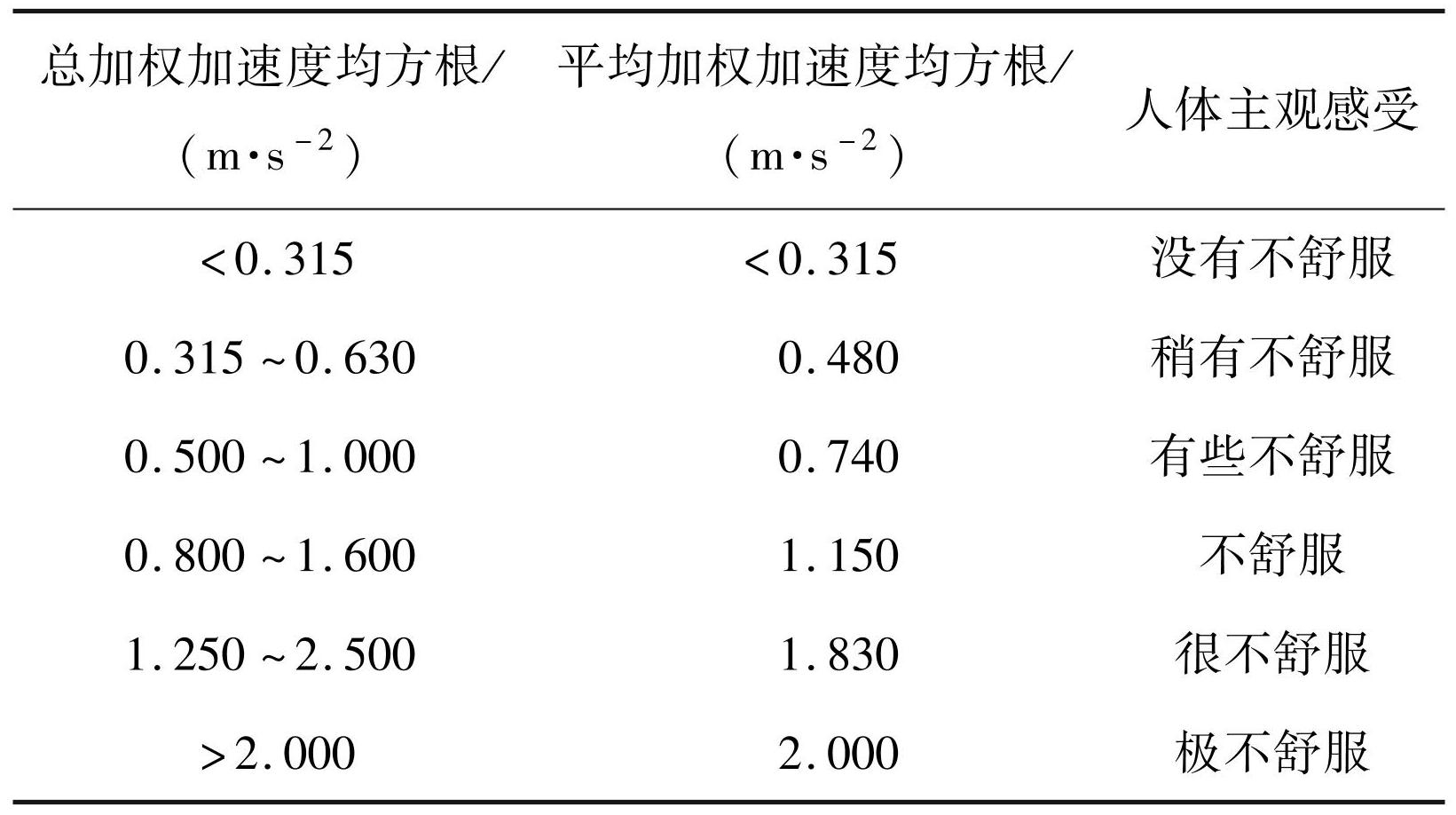
\bar{a}

= 1.15 m / s² ^[23] 作为震后可以正常行驶的均方加速度限值，并认为震后伸缩缝控制速度总是小于震前车辆通过伸缩缝的允许速度。图4给出了在伸缩缝初始宽度为 5 cm 条件下，震后车辆控制速度与伸缩缝宽度之间的关系。

图4震后车辆控制速度与桥梁伸缩缝宽度之间关系曲线

Fig.4Relation curve between vehicle control speed and bridge expansion joint width

2.2.3 车辆过桥平均速度

由于车辆通过伸缩缝时需要减速，从而降低了车辆过桥的平均行驶; 为了研究车辆过桥平均速度，本文将车辆行驶过程分为加速行驶过程、匀速行驶过程、制动过程三部分。

车辆制动过程^[24]包括感知反应阶段、动作控制阶段和车辆减速阶段。平均可预知的感知反应时间^[25] 约为 0.54 s，平均动作控制时间为 0.22 s，总反应时间 0.76 s，车辆平均加速度为 a = 1 m / s²。本文建立的震后车辆行驶速度模型基于以下 3 个假设:1）车辆到达伸缩缝时恰减速至控制速度; 2）车辆速度始终不超过最高限速 80 km / h; 3）车辆以最短时间通过桥梁。设车辆匀速行驶阶段速度为 v₀，车辆以 v₀ 速度在桥上的行驶时长为 t₁，桥总长度为 L，桥梁两端伸缩缝处控制速度分别为 v₁ 和 v₂，则车辆通过桥梁的时间 t 可表示为:

t = t_{1} + \frac{2 v_{0} - (v_{1} + v_{2})}{a}

(21)

\begin{matrix} v_{0} t_{1} + \frac{2 v_{0}^{2} - (v_{1}^{2} + v_{2}^{2})}{2 a} ⩾ L, \\ m a x (v_{1}, v_{2}) ⩽ v_{0} ⩽ 80 k m / h, t_{1} ⩾ 0.76 s \end{matrix}

(22)

式（22）给出了通行时间 t 的参数约束条件，联立式（21）和（22）可求得车辆过桥最小通行时间 t_min。

2.3 震后开放车道数计算方法

震后开放车道数是影响通行能力的另一关键因素，与桥梁地震损伤状态相关。地震可能造成桥墩墩底出现塑性铰损伤，导致桥梁竖向承载力下降^[26]，桥梁在日常运行中控制荷载主要为恒载（即桥梁自重）与车辆荷载的组合，由于桥梁震后所受恒载不会减少，为了保持桥梁安全性能（震后桥梁可靠度出现不显著下降），需要减小桥梁允许通过车辆荷载。当桥梁损伤程度较轻微时，仅关闭部分车道不仅能满足应急交通需求，还可以保护桥梁受损严重部分，研究人员一般根据桥梁损伤状态来确定震后桥梁通行措施，根据工程经验，表2^[27] 列出了不同损伤状态下桥梁建议通行措施。

表2震后桥梁损伤状态与通行措施对应关系^[27]

Tab.2 Relation between bridge post-earthquake damage states and traffic control measures ^[27]

由于地震动的不确定性以及桥梁损伤状态与震后通行措施之间映射存在的模糊性，本文使用了三角形隶属度函数（MF）^[28]量化桥梁损伤状态与震后开放车道数之间的模糊映射。三角形隶属度函数最可能发生点根据该损伤状态的建议通行措施计算，桥梁损伤状态与震后车道数折减系数k_n的三角形隶属度函数见图5，桥梁在所有可能损伤时的震后车道数折减系数k_n通过式（23）中模糊数计算。由于震后开放车道数为整数，因此 n = [（1-k_n）× n₀ ]。其中，[·]为四舍五入取整。

k (σ) = \cup_{i} [P (S_{D, i}) \times k_{i} (σ_{i})]

(23)

式中: k（ σ）为震后车道数折减系数的模糊数; P（S_D，_i）为桥梁损伤状态为S_D，_i 时的概率; k_i（σ_i）为 S_D，_i对应的震后车道数折减系数的模糊数。

图5震后车道折减系数隶属度函数

Fig.5Membership function of post-earthquake lane reduction coefficients

2.4 功能损失的不确定性

前文建立了综合考虑震后开放车道数和震后车辆通行速度的城市桥梁震后通行能力评估体系。但在评估过程中存在地震动、结构承载能力、车道数与损伤状态映射关系等多个不确定性变量，导致桥梁震后通行功能损失实际上是一个随机变量，本文使用蒙特卡洛模拟方法，考虑评估过程的不确定性因素影响，通过大量模拟分析结果计算，得到桥梁通行功能损失的均值 μ 与标准差 σ，图6给出了考虑不确定性的城市桥梁震后通行功能损失评估流程。

图6桥梁震后通行能力损失评估框架

Fig.6Evaluation framework of post-earthquake traffic capacity loss of bridges

3 算例分析

3.1 桥梁模型

本节针对某城市高架桥，开展震后通行能力损失评估。桥梁原型是一座钢筋混凝土连续梁桥，双向四车道路面，桥段跨径布置为 4 × 18 m，桥梁宽 19.6 m，见图7。桥梁主梁由 8 片 T 梁并排组成，支座为板式橡胶支座（PTEB）和铅芯橡胶支座（LRB），支座水平刚度 K₁ = 6.875 MN/ m，竖向刚度 K₂ = 660 MN/ m，铅芯橡胶支座屈服后水平刚度与初始刚度之比 α = 0.156，支座摩擦系数 μ = 0.2。下部结构由矩形盖梁和 2 个桥墩组成，桥墩直径为 1.5 m，保护层厚度为 5 cm，纵向钢筋为 32 根直径为 30 mm 的 HRB335 钢筋，箍筋直径为 10 mm，箍筋间距取 100 mm。

本文采用 OpenSees 软件建立桥梁有限元模型，通过质量-弹簧-阻尼模型^[29] 来模拟选取桥段相邻结构的影响。上部结构作为能力保护设计，在地震作用下保持弹性状态，采用弹性梁柱单元模拟。墩柱和支座作为地震中主要传力和受力构件，采用非线性单元模拟，伸缩缝使用 Impact Material 碰撞模型模拟。

3.2 桥梁易损性分析

本文从 Medina ^[30]建立的 4 个震级-震中距条带中各选取 5 条单向地震动，从 ATC-63 推荐的 22 组非近场地震动记录中选取任一方向地震动，共 42 条地震动。地震动记录反应谱见图8，从图8可以看出，本文选择地震动的反应谱与设计反应符合度较好，并且结构基本周期处选择的地震动反应谱与设计反应谱相对误差小于 15%。将选择的地震动记录的A_pg在 0.1g 到 1.2g 范围内以 0.1g 为步长调幅，调幅后的地震动记录输入到有限元模型中计算桥梁构件地震响应。本文主要将地震动沿纵桥向输入研究结构的纵向地震易损性。

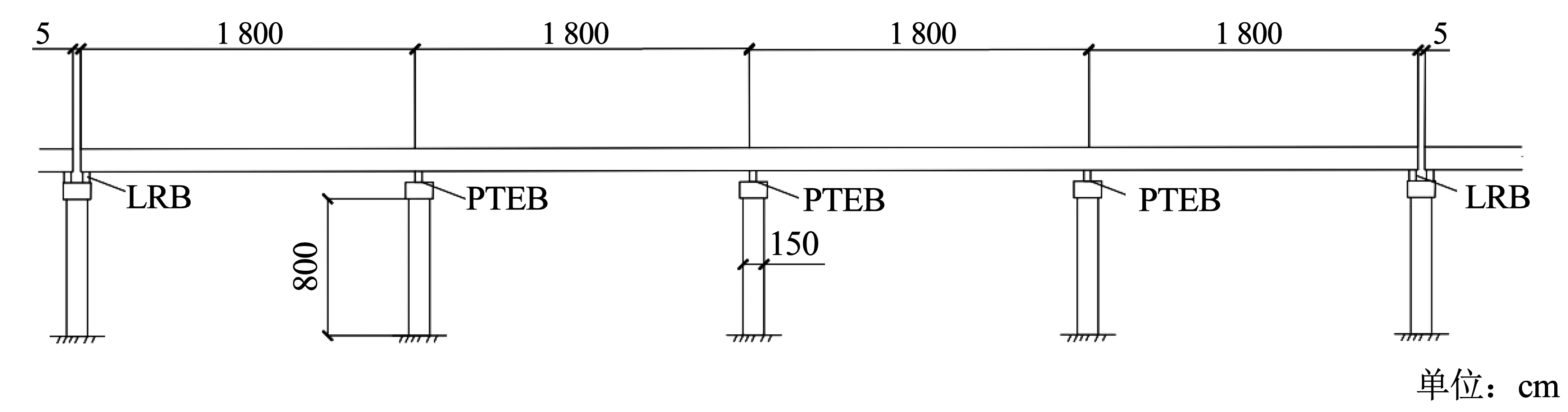
图7算例桥梁结构侧视图

Fig.7Side view of the bridge structure in numerical example

图8所选择地震动的反应谱

Fig.8Response spectral of selected ground motion records

图9（a）、（b）给出了由 IDA 方法建立的支座和桥墩构件易损性曲线。在 4 种破坏状态下支座完全损伤概率明显大于墩柱，这是因为墩柱对桥梁具有更为重要的支撑作用，在抗震设计中墩柱具有更高的安全储备; 在实际抗震设计中，常使用分离式减震榫^[31]来限制梁端位移，减小支座地震破坏，提高桥梁抗震性能。本文使用串联模型计算桥梁系统易损性，采用 copula 函数模拟桥梁系统构件相关性，桥梁系统易损性曲线见图9（c），可以看出，桥梁系统失效概率大于单一构件失效概率，且使用不同 copula 函数建立的桥梁系统易损性模型非常相近，不同 copula 函数的拟合优度评价指标计算结果见表3，3 种 copula 函数的 K-S 检验统计量 D 均小于临界值D_{0. 05}= 0.209 9，因此 3 种 copula 函数均可用于描述桥梁构件损伤相关性模型; 依据S_RME值越小，copula 函数拟合情况就越好的准则，本文选择 Gumbel copula 函数来建立桥梁系统易损性模型。图9（d）中圆柱和圆锥分别代表支座和桥墩联合概率分布的累积经验频率和理论频率，可以发现，不同概率区间内两者均无较大偏差，验证了 Gumbel copula 函数模拟桥梁各构件震害相关性的能力。

表3三种 copula 函数拟合优度评价指标计算结果

Tab.3 Assessment results of goodness of fit for three copula functions

3.3 桥梁通行能力损失评估

根据式（21）和（22）提供的方法，可求得不同地震动强度下车辆行驶速度折减系数和震后开放车道数的概率分布，分别见图10、11。桥梁的安全保证率是指通过蒙特卡洛方法得到的不同震后车道开放数对应的分布函数值，地震动强度增大会使桥梁伸缩缝间距增大，造成震后车辆通行速度降低; 当地震动强度相同时，随着震后开放车道数目增多，桥梁安全保证率会降低，因此可以得出地震动强度增大使桥梁损伤更严重，震后允许开放车道数减少。

图9桥梁系统易损性分析

Fig.9Fragility analysis of bridge system

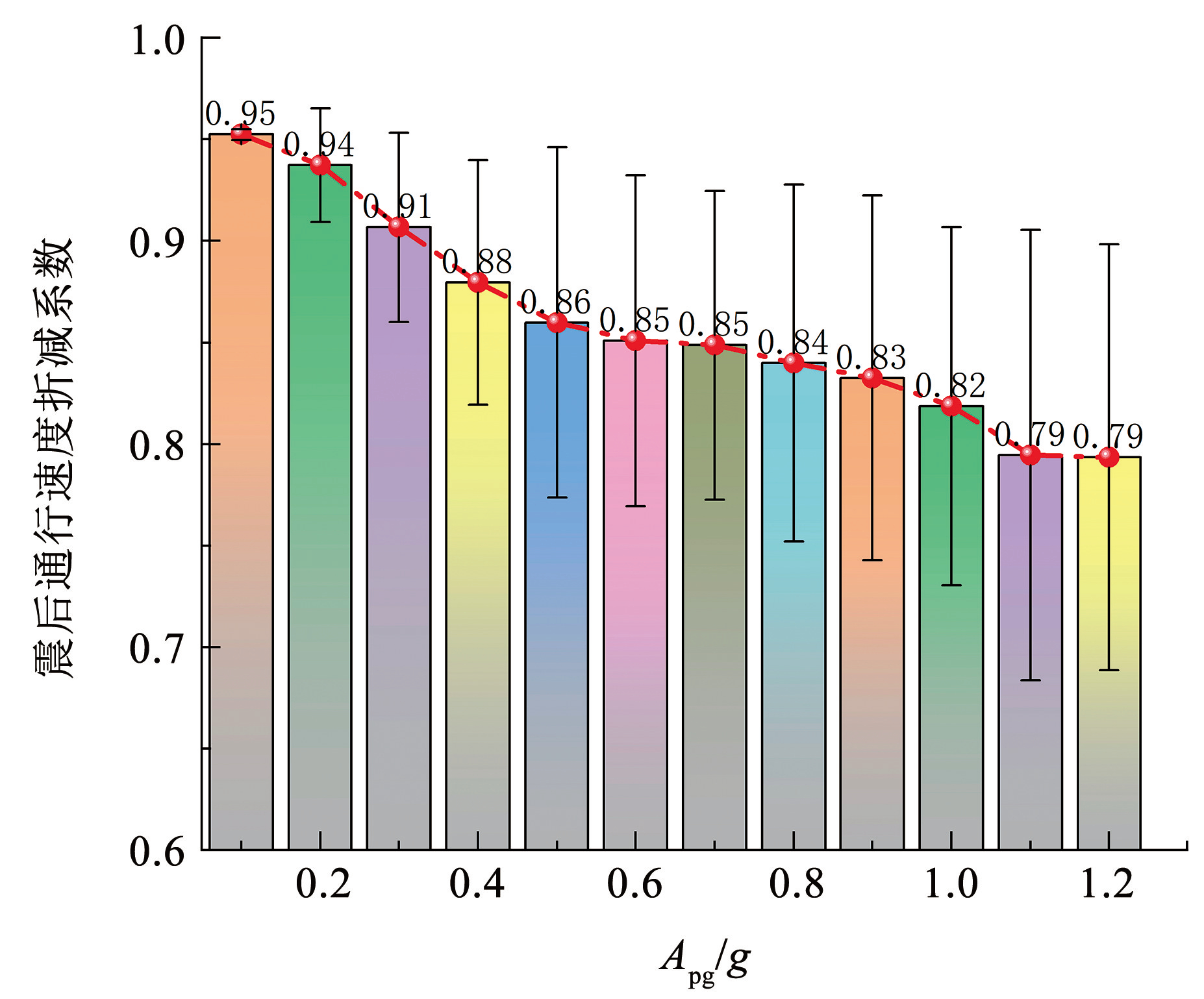
图10震后行驶速度折减系数均值与标准差

Fig.10Mean and Std values of post-earthquake speed reduction coefficients

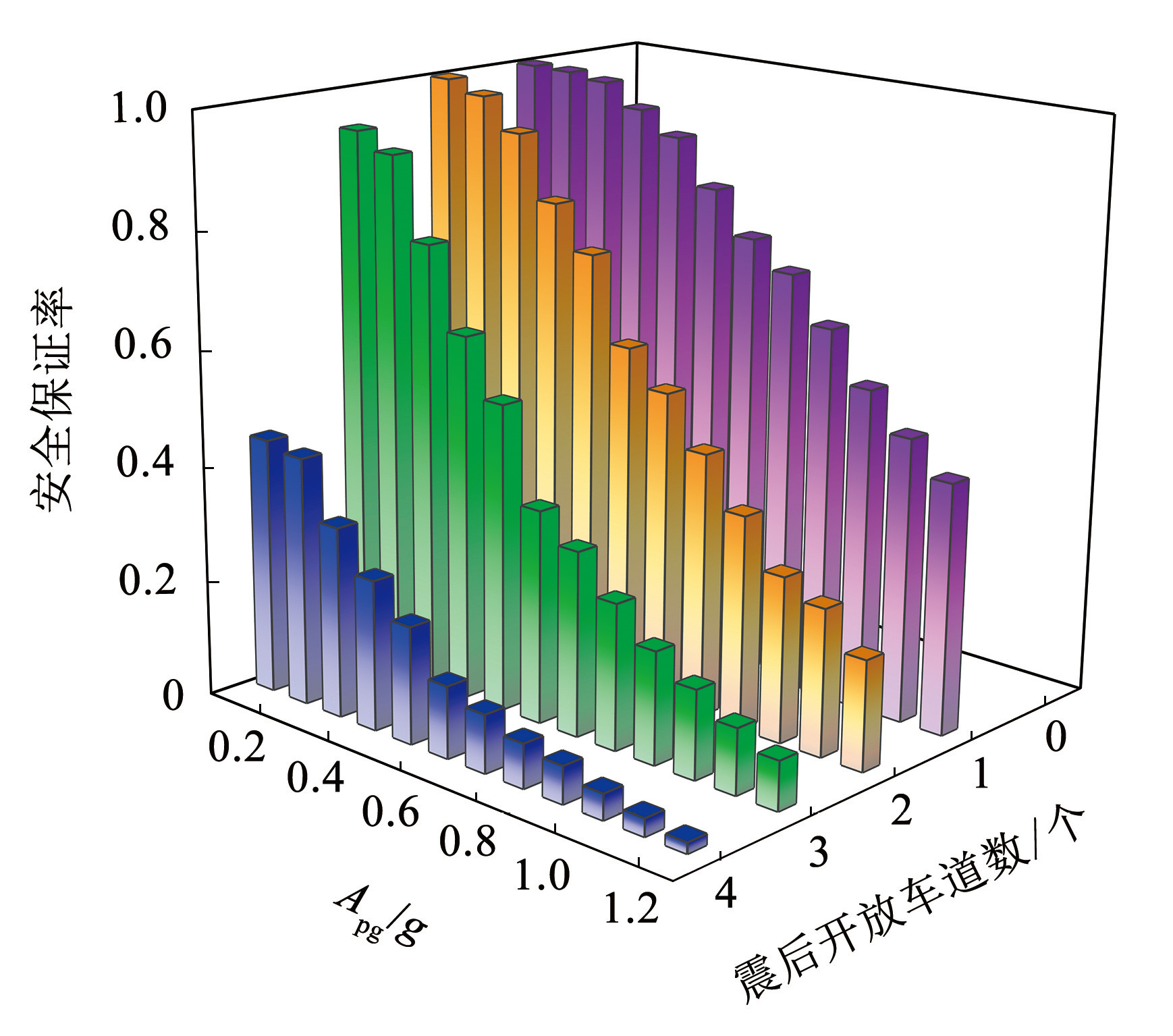
图11不同地震动作用下震后允许开放车道数与安全保证率的关系

Fig.11Relationship between allowable open lane numbers and safety assurance rate under different earthquake scenarios

假设车辆行驶速度与车道宽度相互独立，由前文中结论和式（14）可以计算桥梁通行能力损失比随机变量 k 的数学期望 μ 和标准差 σ，其结果见图12。可以看出，随着地震动强度增大，桥梁地震通行功能损失逐渐增大; 在抗震设防烈度 8 度地区的设防地震（A_pg = 0.2g）作用下，桥梁震后预期剩余通行功能为震前通行功能的 0.84，因此可认为桥梁在基本地震作用下能基本满足正常城市交通需求，桥梁具有较好的抗震性能; 随着地震动强度增大，车辆通行功能损失均值增大趋势逐渐减小，这是由于震后开放车道数目和行驶速度两个影响因素共同决定的，算例桥梁各损伤状态对应的震后开放车道数目的均值随损伤状态变化逐渐减小，且震后车辆通行速度与伸缩缝宽度呈负指数相关，随着伸缩缝破坏更严重，车辆行驶速度减小趋势逐渐变小。对比图10、11可以发现，桥梁震后通行功能主要是由震后允许开放车道数控制，由桥梁结构损伤、承载力下降决定。图13给出了本文提出的基于通行能力指标的桥梁震后功能损失计算结果与 Frangopol 等^[13]、王晓伟等^[14]、Liang 等^[15] 基于经验或历史震害数据自定义指标的计算结果的对比，可以看出，本文得到的桥梁震后功能损失显著大于以往研究计算结果，特别是在地震动强度较小时; 本文提出方法在不同地震动强度下计算的功能损失变异系数均值为 0.472，也明显小于其他 3 种自定义指标的变异系数均值（分别为 0.618、0.878、0.581）。因此，本文提出的基于通行能力指标评估桥梁震后功能损失可以提高评估结果的准确性，减小离散程度和不确定性，增大评估结果的可信度。

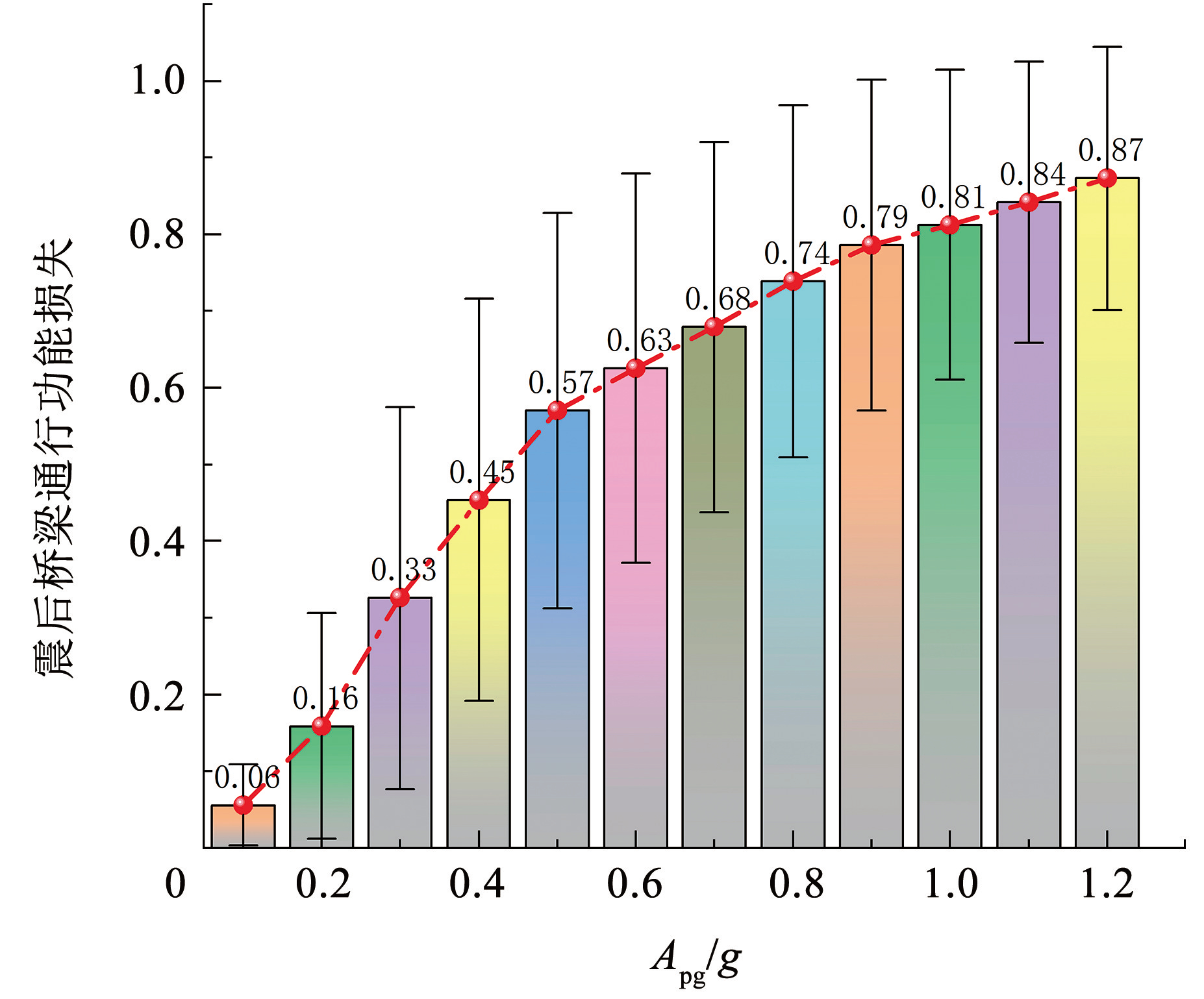
图12车辆通行能力损失比均值与标准差

Fig.12Mean and Std values of vehicle traffic capacity loss ratio

图13基于通行能力指标和基于经验自定义指标的桥梁功能损失计算结果比较

Fig.13Comparison of bridge function loss between traffic capacity based indicators and empirically customized indicators

4 结论

本文以常规城市钢筋混凝土连续梁桥为研究对象，引入通行能力作为桥梁震后损失评价指标。分别基于车辆振动模型和桥梁损伤状态推导了影响通行能力的两个重要因素:行驶速度和车道数，最终得到桥梁的震后通行功能损失，主要结论如下:

1）本文使用 copula 函数考虑了桥梁构件破坏的相关性以及空间组合关系进行桥梁系统易损性分析。基于 Gumbel copula 函数建立的各构件相关性模型与有限元模拟结果符合度最高。桥梁系统破坏概率大于任一构件破坏概率，使用系统易损性可以更加准确反映桥梁的破坏状态。

2）传统的桥梁功能损失评估侧重于桥墩、支座等构件破坏对桥梁安全功能和承载能力的影响，忽略了地震前后车辆行驶速度的变化。本文研究发现，随着地震动增大，车辆震后行驶速度不仅均值减小，而且离散性增大，对车辆通行能力有较大影响。

3）本文提出的通行能力是一个具有实际物理意义并能全面概括桥梁主要功能的指标，可以准确评估桥梁的抗震性能，为工程实际应用提供参考。相较于以往研究，基于通行能力指标计算的桥梁地震功能损失的均值较大，离散程度较小。

本研究尚存在以下几个不足之处:首先，本文仅考虑远场地震动对桥梁震后损伤状态的影响，不同地震区的动力特性不同，对桥梁破坏的影响也不同，后续研究中应综合考虑近场区地震动、远场区地震动和过渡区地震动进行易损性分析; 其次，本文仅考虑地震不确定性，但胡章亮等^[32] 发现结构的不确定性同样也对地震响应预测的准确度也存在一定影响，在未来研究中应全面考虑更多参数的不确定性; 最后，为了保证震后车辆应急通行，通常可以降低安全储备来提高桥梁的交通承载能力，但本文通过损伤状态评估桥梁震后通行功能，忽略了桥梁地震前后安全储备的变化，后续研究在评估桥梁震后通行功能时应考虑安全储备的降低。

图1桥梁伸缩缝地震破坏

Fig.1Seismic damage of bridge expansion joints

下载: 全尺寸图片

图2通过伸缩缝时车轮运动轨迹

Fig.2Trajectory of vehicle wheel when across expansion joints

下载: 全尺寸图片

图3车辆单自由度动力学模型

Fig.3Single-degree-of-freedom dynamic model of vehicles

下载: 全尺寸图片

图4震后车辆控制速度与桥梁伸缩缝宽度之间关系曲线

Fig.4Relation curve between vehicle control speed and bridge expansion joint width

下载: 全尺寸图片

图5震后车道折减系数隶属度函数

Fig.5Membership function of post-earthquake lane reduction coefficients

下载: 全尺寸图片

图6桥梁震后通行能力损失评估框架

Fig.6Evaluation framework of post-earthquake traffic capacity loss of bridges

下载: 全尺寸图片

图7算例桥梁结构侧视图

Fig.7Side view of the bridge structure in numerical example

下载: 全尺寸图片

图8所选择地震动的反应谱

Fig.8Response spectral of selected ground motion records

下载: 全尺寸图片

图9桥梁系统易损性分析

Fig.9Fragility analysis of bridge system

下载: 全尺寸图片

图10震后行驶速度折减系数均值与标准差

Fig.10Mean and Std values of post-earthquake speed reduction coefficients

下载: 全尺寸图片

图11不同地震动作用下震后允许开放车道数与安全保证率的关系

Fig.11Relationship between allowable open lane numbers and safety assurance rate under different earthquake scenarios

下载: 全尺寸图片

图12车辆通行能力损失比均值与标准差

Fig.12Mean and Std values of vehicle traffic capacity loss ratio

下载: 全尺寸图片

图13基于通行能力指标和基于经验自定义指标的桥梁功能损失计算结果比较

Fig.13Comparison of bridge function loss between traffic capacity based indicators and empirically customized indicators

下载: 全尺寸图片

表1加权加速度均方根值与人体主观感受之间的关系

下载: 全尺寸图片

表2震后桥梁损伤状态与通行措施对应关系^[27]

下载: 全尺寸图片

表3三种 copula 函数拟合优度评价指标计算结果

下载: 全尺寸图片

图1桥梁伸缩缝地震破坏

Fig.1Seismic damage of bridge expansion joints

图2通过伸缩缝时车轮运动轨迹

Fig.2Trajectory of vehicle wheel when across expansion joints

图3车辆单自由度动力学模型

Fig.3Single-degree-of-freedom dynamic model of vehicles

图4震后车辆控制速度与桥梁伸缩缝宽度之间关系曲线

Fig.4Relation curve between vehicle control speed and bridge expansion joint width

图5震后车道折减系数隶属度函数

Fig.5Membership function of post-earthquake lane reduction coefficients

图6桥梁震后通行能力损失评估框架

Fig.6Evaluation framework of post-earthquake traffic capacity loss of bridges

图7算例桥梁结构侧视图

Fig.7Side view of the bridge structure in numerical example

图8所选择地震动的反应谱

Fig.8Response spectral of selected ground motion records

图9桥梁系统易损性分析

Fig.9Fragility analysis of bridge system

图10震后行驶速度折减系数均值与标准差

Fig.10Mean and Std values of post-earthquake speed reduction coefficients

图11不同地震动作用下震后允许开放车道数与安全保证率的关系

Fig.11Relationship between allowable open lane numbers and safety assurance rate under different earthquake scenarios

图12车辆通行能力损失比均值与标准差

Fig.12Mean and Std values of vehicle traffic capacity loss ratio

图13基于通行能力指标和基于经验自定义指标的桥梁功能损失计算结果比较

Fig.13Comparison of bridge function loss between traffic capacity based indicators and empirically customized indicators

表1加权加速度均方根值与人体主观感受之间的关系

表2震后桥梁损伤状态与通行措施对应关系^[27]

表3三种 copula 函数拟合优度评价指标计算结果

图1桥梁伸缩缝地震破坏

Fig.1Seismic damage of bridge expansion joints

图2通过伸缩缝时车轮运动轨迹

Fig.2Trajectory of vehicle wheel when across expansion joints

图3车辆单自由度动力学模型

Fig.3Single-degree-of-freedom dynamic model of vehicles

图4震后车辆控制速度与桥梁伸缩缝宽度之间关系曲线

Fig.4Relation curve between vehicle control speed and bridge expansion joint width

图5震后车道折减系数隶属度函数

Fig.5Membership function of post-earthquake lane reduction coefficients

图6桥梁震后通行能力损失评估框架

Fig.6Evaluation framework of post-earthquake traffic capacity loss of bridges

图7算例桥梁结构侧视图

Fig.7Side view of the bridge structure in numerical example

图8所选择地震动的反应谱

Fig.8Response spectral of selected ground motion records

图9桥梁系统易损性分析

Fig.9Fragility analysis of bridge system

图10震后行驶速度折减系数均值与标准差

Fig.10Mean and Std values of post-earthquake speed reduction coefficients

图11不同地震动作用下震后允许开放车道数与安全保证率的关系

Fig.11Relationship between allowable open lane numbers and safety assurance rate under different earthquake scenarios

图12车辆通行能力损失比均值与标准差

Fig.12Mean and Std values of vehicle traffic capacity loss ratio

图13基于通行能力指标和基于经验自定义指标的桥梁功能损失计算结果比较

Fig.13Comparison of bridge function loss between traffic capacity based indicators and empirically customized indicators

表1加权加速度均方根值与人体主观感受之间的关系

表2震后桥梁损伤状态与通行措施对应关系^[27]

表3三种 copula 函数拟合优度评价指标计算结果

CHEN M, MANGALATHU S, JEON J S. Betweenness centralitybased seismic risk management for bridge transportation networks[J]. Engineering Structures,2023,289:116301. DOI:10.1016/j.engstruct.2023.116301

BOCCHINI P, FRANGOPOL D M. Restoration of bridge networks after an earthquake:multicriteria intervention optimization[J]. Earthquake Spectra,2012,28(2):427. DOI:10.1193/1.4000019

LIU T, MEIDANI H. Optimizing seismic retrofit of bridges:integrating efficient graph neural network surrogates and transportation equity[C]//2023 Cyber-Physical Systems and Internet-of-things Week, CPS-LOT Week Workshops. New York: Assoc Computing Machinery,2023:367. DOI:10.1145/3576914.3587503

LI S Q, LIU H B, FARASANGI E N,et al. Seismic fragility estimation considering field inspection of reinforced concrete girder bridges[J/OL].(2023-04-28)[2024-06-12].https://webofscience.clarivate.cn/api/gateway. DOI:10.1080/15732479.2023.2208565

REZAEI H, ZARFAM P, GOLAFSHANI E M,et al. Seismic fragility analysis of RC box-girder bridges based on symbolic regression method[J]. Structures,2022,38:306. DOI:10.1016/j.istruc.2021.12.058

刘洋. 基于混合易损性与功能损失的钢-混组合梁桥地震风险与韧性评估[D]. 哈尔滨: 哈尔滨工业大学,2018. LIU Yang. Seismic risk and resilience assessment of steel-concrete composite girder bridges based on hybrid fragility and functionality loss[D]. Harbin: Harbin Institute of Technology,2018.DOI: 10. 27061 / d. cnki. ghgdu. 2018. 000024

LI H, HUANG Y, GUO E. Construction stage seismic resilience evaluation of a continuous girder bridge with the cast-in-place cantilever construction method[J]. Tehnički Vjesnik,2023,30(4):1010. DOI:10.17559/TV-20210929102016

吕大刚, 董尧, 王闽雄, 等. 基于改进生活质量指数的社会挽救生命成本及在地震生命损失估计中的应用[J]. 自然灾害学报,2018,27(4):1.LYU Dagang, DONG Yao, WANG Minxiong,et al. Societal life saving cost based on improved LQI with applications to evaluation of earthquake fatality losses[J]. Journal of Natural Disasters,2018,27(4):1. DOI:10.13577/j.jnd.2018.0401

LIU Y, XIANG C. A comprehensive framework for evaluating bridge resilience:safety,social,environmental,and economic perspectives[J]. Sustainability,2024,16(3):1135. DOI:10.3390/su16031135

DONG H, MA R, HAN Q,et al. Quantitative assessment framework for the post-earthquake traffic flow capacity of bridges based on the loss model of vertical load-carrying capacity[J]. Journal of Bridge Engineering,2024,29(3):04023125. DOI:10.1061/JBENF2. BEENG-6418

GHASEMI S H, LEE J Y. Reliability-based indicator for postearthquake traffic flow capacity of a highway bridge[J]. Structural Safety,2021,89:102039. DOI:10.1016/j.strusafe.2020.102039

WU Y, HOU G, CHEN S. Post-earthquake resilience assessment and long-term restoration prioritization of transportation network[J]. Reliability Engineering System Safety,2021,211(9):107612. DOI:10.1016/j.ress.2021.107612

FRANGOPOL D M, BOCCHINI P. Resilience as optimization criterion for the rehabilitation of bridges belonging to a transportation network subject to earthquake[C]//Structures Congress 2011-Proceedings of the 2011 Structures Congress. Reston, Virginia: American Society of Civil Engineers(ASCE),2011:2044. DOI:10.1061/41171(401)178

王晓伟, 叶爱君, 吴学平, 等. 梁式桥抗震韧性评估方法: I. 基于专家意见的构件震后功能恢复模型[J/OL].(2023-12-12)[2024-03-13].https://doi.org/10.15951/j.tmgcxb.23080638. WANG Xiaowei, YE Aijun, WU Xueping,et al. Seismic resilience assessment method for girder bridges: I.expert opinion-based postearthquake functionality recovery models of bridge components[J/OL].(2023-12-12)[2024-03-13].https://doi.org/10.15951/j.tmgcxb.23080638

LIANG Y, WEI Y, LI P,et al. Time-varying seismic resilience analysis of coastal bridges by considering multiple durability damage factors[J]. International Journal of Structural Integrity,2023,14(4):521. DOI:10.1108/IJSI-12-2022-0147

HWANG H, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报,2004(6):47.HWANG H, LIU Jingbo. Seismic fragility analysis of reinforced concrete bridges[J]. Journal of Civil Engineering,2004(6):47. DOI:10.15951/j.tmgcxb.2004.06.009

白玉磊, 张玉峰, 梅世杰, 等. 大应变FRP加固连续梁桥地震易损性分析[J]. 哈尔滨工业大学学报,2023,55(9):84. BAI Yulei, ZHANG Yufeng, MEI Shijie,et al. Seismic fragility of continuous girder bridge reinforced with large rupture strain FRP[J]. Journal of Harbin Institute of Technology,2023,55(9):84. DOI:10.11918/202111054

CHEN L, HUANG C, CHEN H,et al. Seismic fragility models of a bridge system based on copula method[J]. Earthquake Spectra,2022,38(2):1417. DOI:10.1177/87552930211052573

LIU Z, LI S, ZHAO W,et al. Post-earthquake assessment model for highway bridge networks considering traffic congestion due to earthquake-induced bridge damage[J]. Engineering Structures,2022,260:114395. DOI:10.1016/j.engstruct.2022.1143

ZANARDO G, HAO H, MODENA C. Seismic response of multispan simply supported bridges to a spatially varying earthquake ground motion[J]. Earthquake Engineering & Structural Dynamics,2010,31(6):1325. DOI:10.1002/eqe.166

丁勇, 王佩, 游玖昂, 等. 桥梁伸缩缝跳车冲击荷载计算方法与模型实验[J]. 哈尔滨工业大学学报,2020,52(3):129. DING Yong, WANG Pei, YOU Jiuang,et al. Numerical methods and model experiment for impact load induced by vehicle bumping at bridge expansion joint[J]. Journal of Harbin Institute of Technology,2020,52(3):129. DOI:10.11918/201807201

International Organization for Standardization. Mechanical vibration and shock-evaluation of human exposure to whole-body vibrationpart1:general requirements: ISO 2631-1-1997[S]. Switzerland: Geneva,1997

邓露, 闫王晨, 朱全军. 路桥过渡段容许台阶高度的确定[J]. 湖南大学学报(自然科学版),2015,42(3):10. DENG Lu, YAN Wangchen, ZHU Quanjun. Determination of allowable differential settlement between the bridge and the approach embankment[J]. Journal of Hunan University(Natural Sciences),2015,42(3):100. DOI:10.16339/j.cnki.hdxbzkb.2015.03.016

RASCH A, MOLL S, LOPEZ G,et al. Drivers’and cyclists’safety perceptions in overtaking maneuvers[J]. Transportation Research Part F: Traffic Psychology and Behaviour,2022,84:165. DOI:10.1016/j.trf.2021.11.014

王武宏. 道路交通系统中驾驶行为理论与方法[M]. 北京: 科学出版社,2001:265. WANG Wuhong. Theory and methods of driving behavior in road traffic systems[M]. Beijing: Science Publishing House,2001:265

AKBARI S, KHANMOHAMMADI M. A probabilistic framework to make a decision on the post-earthquake functionality of bridges considering the damage,residual displacement,and aftershock[J]. Bulletin of Earthquake Engineering,2022,20(2):1193. DOI:10.1007/s10518-021-01269-9

MACKIE K R, STOJADINOVI B. Post-earthquake functionality of highway overpass bridges[J]. Earthquake Engineering & Structural Dynamics,2006,35(1):77. DOI:10.1002/eqe.534

ANDRIC J M, LU D G. Fuzzy methods for prediction of seismic resilience of bridges[J]. International Journal of Disaster Risk Reduction,2017,22:458. DOI:10.1016/j.ijdrr.2017.01.001

范立础, 李建中, 王君杰. 高架桥梁抗震设计[M]. 北京: 人民交通出版社,2001:37. FAN Lichu, LI Jianzhong, WANG Junjie. Seismic design of viaduct bridges[M]. Beijing: People’s Transportation Publishing House,2001:37

MEDINA R, KRAWINKLER H. Seismic demands for nondeteriorating frame structures and their dependence on ground motions[J]. Dissertation Abstracts International,2004,64(3):1381

魏标, 闵浩峥, 汪伟浩, 等. 分离式减震榫的阻尼力模型研究———基于 Ramberg-Osgood 模型[J]. 工程力学,2023,40(11):81. WEI Biao, MIN Haozheng, WANG Weihau,et al. Research on damping force model of separated shock absorber based on rambergosgood model[J]. Engineering Mechanics,2023,40(11):81

胡章亮, 魏标, 蒋丽忠, 等. 高速铁路梁桥建模参数敏感性分析[J]. 铁道科学与工程学报,2023,20(2):12. HU Zhangliang, WEI Biao, JIANG Lizhong,et al. Sensitivity analysis of modeling parameters of high-speed railway girder bridges[J]. Journal of Railway Science and Engineering,2023,20(2):12. DOI:10.19713/j.cnki.43-1423/u. T20220316

1 桥梁地震易损性分析

2 震后桥梁通行能力损失评估

3 算例分析

4 结论

友情链接LINKS