欢迎访问《哈尔滨工业大学学报》编辑部网站！

板柱节点考虑弯剪相关性的受冲切承载力计算方法

doi: 10.11918/202312033

郑文忠^1,2 ，吕盛先^1,2 ，郑博文^1,2 ，王英^1,2

1. 结构工程灾变与控制教育部重点实验室(哈尔滨工业大学),哈尔滨 150090

2. 土木工程智能防灾减灾工业和信息化部重点实验室(哈尔滨工业大学),哈尔滨 150090

基金项目: 国家自然科学基金(52078162)

详细信息

作者简介

郑文忠(1965—),男,教授,博士生导师

通讯作者

王英,wangying888@hit.edu.cn

中图分类号: TU375

文献标识码: A

文章编号: 0367-6234(2025)01-0065-12

Calculation method for punching capacity of slab-column connections considering bending shear correlation

ZHENG Wenzhong^1,2 ， LYU Shengxian^1,2 ， ZHENG Bowen^1,2 ， WANG Ying^1,2

1. Key Lab of Structures Dynamic Behavior and Control (Harbin Institute of Technology), Ministry of Education, Harbin 150090 , China

2. Key Lab of Smart Prevention and Mitigation of Civil Engineering Disasters (Harbin Institute of Technology), Ministry of Industry and Information Technology, Harbin 150090 , China

摘要

对于同时受到竖向荷载和不平衡弯矩作用的板柱节点,目前已有方法大多将不平衡弯矩等效为竖向荷载,从而给出其受冲切承载力计算方法。但该方法所涉及的不平衡弯矩比例系数的计算还存在较大争议,且没有考虑竖向荷载与不平衡弯矩耦合的影响。因此,本文首先通过推导给出仅有竖向荷载作用的板柱节点受冲切承载力计算公式和仅有不平衡弯矩作用的板柱节点受弯承载力计算公式,并与试验结果进行对比,验证了所提公式的合理性。然后基于板柱节点在竖向荷载和不平衡弯矩共同作用下的试验结果,拟合得到板柱节点考虑弯剪相关性的受冲切承载力计算公式。最后对所提计算方法与不同规范计算方法进行对比,结果表明本文计算方法能够更加准确地预测板柱节点受冲切承载力。

关键词

板柱节点 / 竖向荷载 / 不平衡弯矩 / 受冲切承载力 / 计算方法

Abstract

For slab-column connections subjected to vertical loads and unbalanced bending moments, the unbalanced bending moment is typically equated to vertical loads in most existing methods for calculating their punching capacity. However, there is significant controversy regarding the calculation of the unbalanced bending moment ratio coefficient in existing methods, and the coupling effect between vertical loads and unbalanced bending moments has not been adequately considered. Therefore, this paper first proposes a new equation for calculating the punching capacity of slab-column connections under vertical loads only and validates it through comparison with experimental results. Additionally, a novel equation for calculating the flexural capacity of slabs under unbalanced bending moments is proposed. Based on experimental results and considering the bending-shear correlation, an equation for calculating the punching capacity of slab-column connections under the combined action of vertical loads and unbalanced bending moments is then derived. Finally, the proposed method is compared with various design code methods. The results indicate that the proposed method can more accurately predict the punching capacity of slab-column connections.

Keywords

slab-column connections / vertical load / unbalanced bending moment / punching capacity / calculation method

1 竖向荷载作用下的板柱节点受冲切承载力计算 1.1 计算模型 1.2 板受压区混凝土的贡献 1.3 混凝土骨料咬合作用的贡献 1.4 板受拉纵筋销栓作用的贡献 1.5 建议公式的评价 2 不平衡弯矩作用下的板柱节点受弯承载力计算 3 竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算 3.1 考虑弯剪相关性的拟合公式 3.2 建议公式计算结果与试验结果的比较 4 结论

钢筋混凝土板柱结构是由楼板和柱组成承重体系的结构，具有可有效提高楼层净高，降低建造成本等优势。但板柱结构的板柱节点易发生脆性的冲切破坏。某处板柱节点发生破坏，会使得相邻的板柱节点所承担的荷载增大，随后更多处板柱节点可能相继破坏，最终整个板柱结构倒塌或坍塌。因此，开展竖向荷载和不平衡弯矩共同作用下的板柱节点受力机理和承载力计算方法研究，具有十分重要的意义。

多年来各国学者进行了大量的板柱节点冲切试验研究和受力机理分析，提出了板柱节点在竖向荷载和不平衡弯矩共同作用下的受冲切承载力计算模型。如:1960 年 Stasio 等^[1] 基于弹性应力叠加提出了偏心剪应力模型; 2001 年马云昌等^[2] 在塑性铰理论的基础上，通过极限分析得到了板柱节点受冲切承载力计算公式; 2007 年 Tian ^[3]提出以拟梁法为基础的计算模型; 2018 年易伟建等^[4] 提出了考虑板弯曲变形和剪切变形的受力机理模型，并给出了偏心荷载作用下的板柱节点受冲切承载力计算公式。以上国内外不同学者提出的竖向荷载和不平衡弯矩共同作用下的板柱节点计算模型有着较大差异，且目前尚未形成统一的计算方法。

这是因为仅竖向荷载作用下的板柱节点受冲切计算已较为复杂。在竖向荷载作用下，板与柱相交处既承受剪力作用又承受弯矩作用。因此，受压区混凝土对受冲切承载力的贡献受到混凝土剪应力和压应力的共同影响。此外，板柱节点冲切斜裂缝上的混凝土骨料咬合作用和板受拉纵筋销栓作用也对其受冲切承载力有一定的贡献。而板柱节点在竖向荷载和不平衡弯矩共同作用下，由于发生冲切破坏时已进入塑性阶段，因此不能分开考虑竖向荷载和不平衡弯矩，需考虑竖向荷载与不平衡弯矩的耦合对板柱节点受冲切承载力的影响。

本文首先通过推导给出了仅承受竖向荷载作用的板柱节点受冲切承载力计算公式和仅承受不平衡弯矩作用的板柱节点受弯承载力计算公式。然后基于竖向荷载和不平衡弯矩共同作用下的板柱节点试验结果，考虑竖向荷载与不平衡弯矩的相互影响，从而提出了竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式。

1 竖向荷载作用下的板柱节点受冲切承载力计算

1.1 计算模型

假设竖向荷载作用下的板柱节点达到受冲切承载力极限状态时，其承载力由板受压区混凝土的贡献、冲切斜裂缝上的混凝土骨料咬合作用的贡献和与冲切斜裂缝相交的板受拉纵筋销栓作用的贡献组成，即受冲切承载力为三部分贡献之和。因此，竖向荷载作用下的板柱节点受冲切承载力计算公式为

V_{u} = V_{1} + V_{2} + V_{3}

(1)

式中:V_u为竖向荷载作用下的板柱节点受冲切承载力，N; V₁为板受压区混凝土对受冲切承载力的贡献，N; V₂为冲切斜裂缝上的混凝土骨料咬合作用对受冲切承载力的贡献，N; V₃为与冲切斜裂缝相交的板受拉纵筋的销栓作用对受冲切承载力的贡献，N。

为计算竖向荷载作用下的板柱节点受冲切承载力，采用了图1所示的受力模型。图1中:c 为方形柱截面边长; V 为竖向荷载; x₀为板受压区高度; α 为冲切斜裂缝与竖直方向的夹角; h 为板厚; h₀为板有效高度，按板两个方向有效高度的平均值考虑; δ 为冲切锥体的虚位移; ψ 为板的转角。

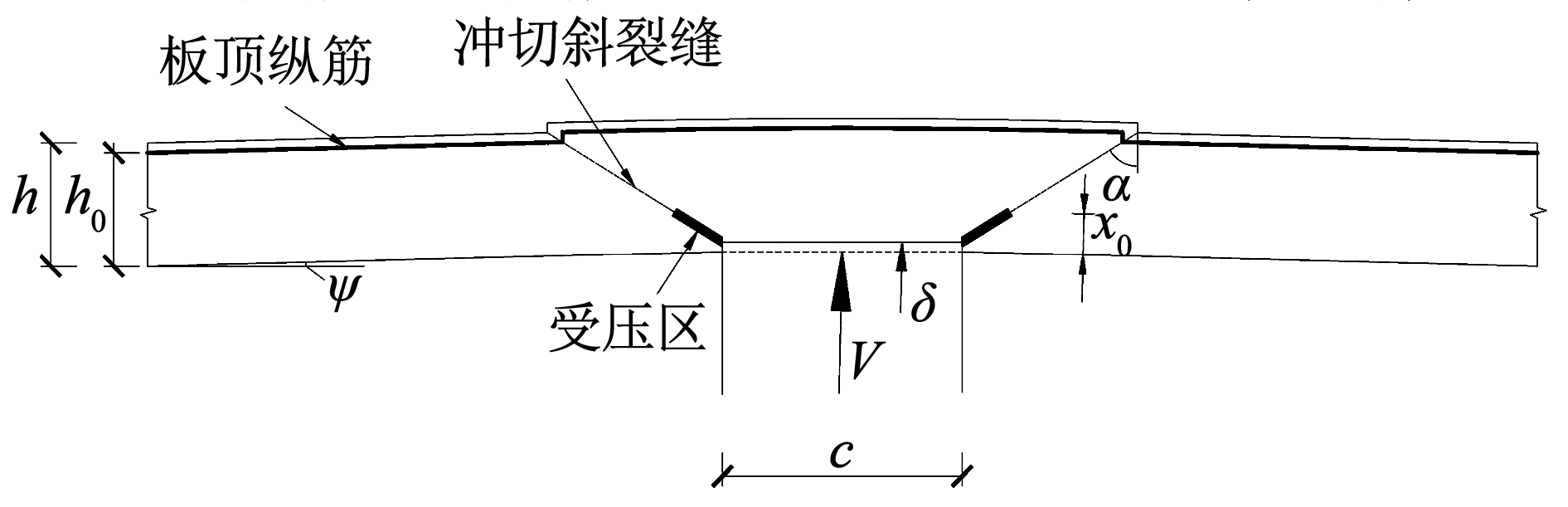
图1板柱节点冲切计算模型示意

Fig.1Schematic diagram of punching calculation model for slab-column connections

板柱节点达到受冲切承载力极限状态时，其冲切斜裂缝上的应力分布见图2。 σ_n和 τ_nt分别为板受压区混凝土受到的正应力和剪应力，τ₂ 为板柱节点冲切斜裂缝上的混凝土骨料咬合作用所产生的剪应力。

图2冲切锥体上的应力示意

Fig.2Schematic diagram of stresses on the punching cone

1.2 板受压区混凝土的贡献

本文认为当板受压区混凝土在压应力和剪应力共同作用下达到临界应力状态时，板柱节点达到受冲切承载力极限状态。假设板受压区混凝土在压应力和剪应力共同作用下的强度准则符合抛物线形的摩尔-库伦准则，该准则包络线见图3。抛物线形的摩尔-库伦准则:

\frac{σ_{n}}{f_{t}^{'}} + \frac{1}{K} {(\frac{τ_{n t}}{f_{c}^{'}})}^{2} = 1

(2)

K = m + 2 - 2 \sqrt{m + 1}

(3)

m = \frac{f_{c}^{'}}{f_{t}^{'}} = \frac{v_{c} f_{c}}{v_{t} f_{t}}

(4)

式中:σ_n和 τ_nt分别为混凝土所受到的正应力和剪应力，MPa; f_c和 f_t分别为混凝土轴心抗压强度和轴心抗拉强度，MPa; f′_c和f′_t 分别为混凝土进入塑性状态后的有效抗压强度和有效抗拉强度，MPa; v_c和 v_t分别为混凝土轴心抗压强度和轴心抗拉强度的强度折减系数，根据文献^[5]，v_c取为 0.35; 与板柱节点试验数据对比分析后，m 取为 f_c。

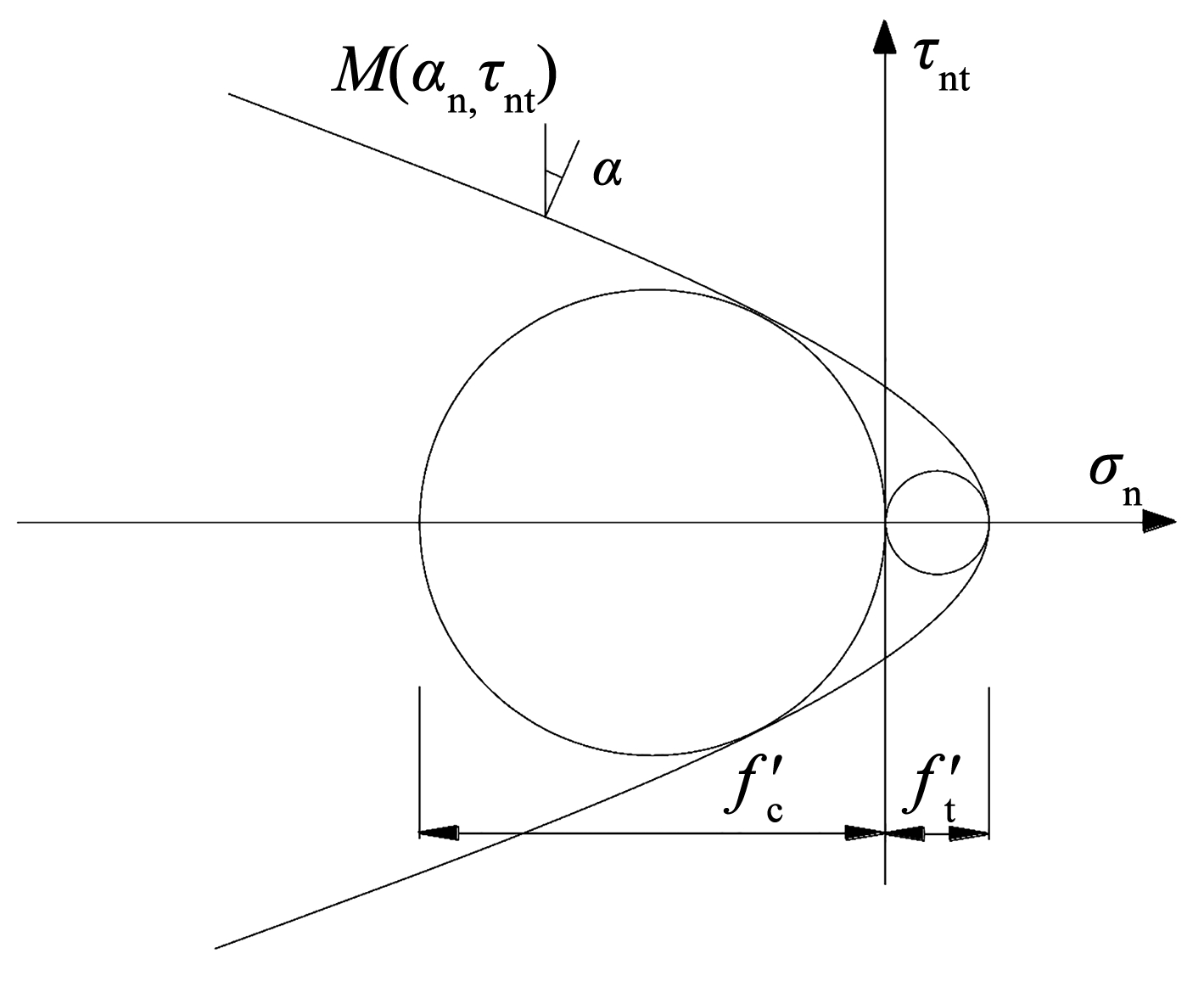
图3抛物线形的摩尔-库伦准则

Fig.3Parabolic Mohr-Coulomb criterion

抛物线形的摩尔-库伦准则抛物线的外法线方向和 τ_nt轴方向的夹角即为板柱节点冲切斜裂缝与竖直方向的夹角 α，从而对式（2）求导可以得到:

t a n α = - \frac{d τ_{n t}}{d σ_{n}} = \frac{K f_{t}^{'}}{2 τ_{n t}}

(5)

将式（5）代入式（2），得到板受压区混凝土的正应力和剪应力分别为:

σ_{n} = f_{t}^{'} (1 - \frac{K}{4} {c o t}^{2} α)

(6)

τ_{n t} = \frac{1}{2} K f_{t}^{'} c o t α

(7)

当板柱节点冲切锥体产生向上的虚位移 δ 时，根据虚功原理有

V_{1} δ = \int_{A} (σ_{n} δ s i n α + τ_{n t} δ c o s α) d A

(8)

式中 A 为板受压区的面积，mm²。

为计算板受压区高度，首先将板受拉纵筋面积等效换算成混凝土面积（图4）。然后利用换算后截面的受拉区对中性轴的面积矩等于受压区对中性轴的面积矩，求得板受压区高度。图4中，b 为板柱节点冲切锥体的上口边长，其计算公式为 b = c + 2h₀ tan α。

图4钢筋面积换算成混凝土面积

Fig.4Equivalent conversion of steel reinforcement area to concrete area

根据合力相等和应变相同，可以得到板受拉纵筋面积 A_s换算后的混凝土面积 A_c:

A_{c} = A_{s} \frac{E_{s}}{E_{c}}

(9)

将板受拉纵筋面积换算为混凝土面积后，截面中性轴通过换算后截面的重心，由此得到:

\frac{E_{s}}{E_{c}} A_{s} (h_{0} - x_{0}) = \frac{1}{2} b x_{0}^{2}

(10)

将板受拉纵筋配筋率 ρ = A_s /（ bh₀）代入上式，即可得到:

{(\frac{x_{0}}{h_{0}})}^{2} + 2 \frac{E_{s}}{E_{c}} ρ \frac{x_{0}}{h_{0}} - 2 \frac{E_{s}}{E_{c}} ρ = 0

(11)

从而得到板受压区高度为

x_{0} = \frac{E_{s}}{E_{c}} ρ h_{0} (\sqrt{1 + \frac{2 E_{c}}{ρ E_{s}}} - 1)

(12)

式中:x₀为板受压区高度，mm; E_s为板受拉纵筋弹性模量，MPa; E_c为混凝土弹性模量，MPa; h₀为板截面有效高度，mm。

混凝土弹性模量的计算采用中国 GB 50010— 2010《混凝土结构设计规范》 ^[6]（中国规范）中的建议公式:

E_{c} = \frac{10^{5}}{2.2 + 34.7 / f_{c u}}

(13)

式中 f_cu为混凝土标准立方体抗压强度，MPa。

根据文献^[7]，板柱节点冲切斜裂缝与竖直方向的夹角为 30°到 61.2°，且主要集中在 60°附近。为简化计算，本文取板柱节点冲切斜裂缝与竖向方向的夹角 α 为 60°，从而得到受压区的贡献为

\begin{matrix} V_{1} = (2.02 + 0.144 f_{c} - 0.289 \sqrt{f_{c} + 1}) \times \\ (4.64 c x_{0} + 8.04 x_{0}^{2}) = β (4.64 c x_{0} + 8.04 x_{0}^{2}) \end{matrix}

(14)

式中:c 为方形柱截面边长，mm; β 为计算系数。

1.3 混凝土骨料咬合作用的贡献

采用 Vecchio 等^[8]基于考察混凝土骨料咬合作用试件的试验数据拟合得到的公式，计算板柱节点冲切斜裂缝上的混凝土骨料咬合作用所产生的剪应力:

τ_{2} = \frac{0.18 \sqrt{f_{c}^{'}}}{0.31 + \frac{24 ω}{a_{g} + 16}}

(15)

式中:a_g为混凝土最大骨料的粒径，mm; ω 为冲切斜裂缝宽度，mm，按下式计算:

ω = ψ (h_{0} - x_{0})

(16)

板的转角 ψ 采用模式规范 MC 2010 ^[9]的近似计算方法:

ψ = \frac{1.5 r_{s}}{h_{0} E_{s}}

(17)

式中 r_s为柱边到板边的距离，mm。

由虚功原理，得到板柱节点冲切斜裂缝上的混凝土骨料咬合作用的贡献:

V_{2} δ = \int_{A} τ_{2} δ c o s α d A

(18)

由式（15）~（18）可得:

V_{2} = τ_{2} (h_{0} - x_{0}) [4 c + 4 \sqrt{3} (h_{0} + x_{0})]

(19)

1.4 板受拉纵筋销栓作用的贡献

板柱节点冲切斜裂缝发展到板受拉纵筋时，板受拉纵筋类似于插在混凝土中的销栓，从而对板柱节点受冲切承载力产生贡献。采用 Philippe ^[10] 基于考察纵筋销栓作用试件的试验数据得到的受拉纵筋销栓作用计算公式，来量化板受拉纵筋销栓作用的贡献:

V_{3} = \frac{1}{2} (\sum d^{2}) \sqrt{0.8 f_{c u} f_{y} (1 - η^{2})} c o s α

(20)

式中:d 为板受拉纵筋直径，mm; f_y为板受拉纵筋屈服强度，MPa; 系数 η 为板受拉纵筋的应力水平，按 0.8 考虑。

对式（20）进行变换，可以得到板受拉纵筋销栓作用的贡献为

V_{3} = 0.25 ρ (c + 2 \sqrt{3} h_{0}) h_{0} \sqrt{f_{c} f_{y}}

(21)

1.5 建议公式的评价

将板受压区混凝土的贡献、混凝土骨料咬合作用的贡献和板受拉纵筋销栓作用的贡献代入式（1），可得到竖向荷载作用下的板柱节点受冲切承载力计算公式:

\begin{matrix} V_{u} = β (4.64 c x_{0} + 8.04 x_{0}^{2}) + 4 τ_{2} (h_{0} - x_{0}) [c + \\ \sqrt{3} (h_{0} + x_{0})] + 0.25 ρ (c h_{0} + 2 \sqrt{3} h_{0}^{2}) \sqrt{f_{c} f_{y}} \end{matrix}

(22)

通过收集相关试验数据，建立了包含 157 组竖向荷载作用下的板柱节点试验数据库，见表1。

表1竖向荷载作用下的板柱节点试验数据库

Tab.1 Punching database of slab-column connections under vertical loads

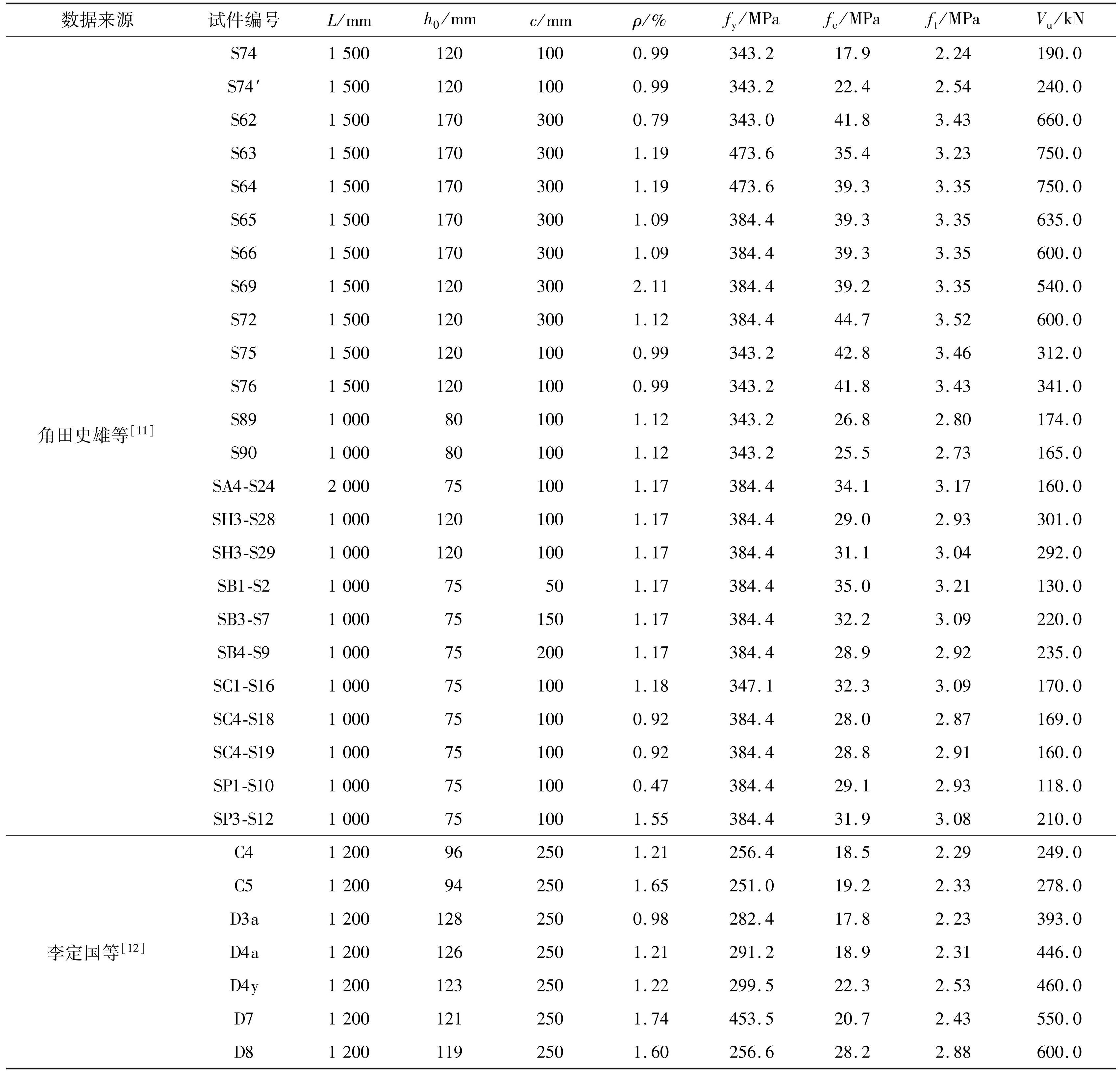
表1（续）

注:L 为方板的边长; h₀为板有效高度，取板两个方向有效高度的均值; c 为方形柱边长; ρ 为板受拉纵筋配筋率，

ρ = \sqrt{ρ_{x} ρ_{y}}

，ρ_x、ρ_y分别为 x、y 方向的板受拉纵筋配筋率; f_y为板受拉纵筋屈服强度; f_c为混凝土轴心抗压强度; f_t为混凝土轴心抗拉强度; V_u为破坏时的竖向荷载。

基于试验数据，对各规范的受冲切承载力公式和本文建议公式进行评价。表2给出了板柱节点受冲切承载力试验值与计算值的对比。中国规范^[6] 和美国 ACI 318-19《房屋建筑用结构混凝土规范要求及解释》 ^[43]（美国规范）的公式计算结果整体过于保守，且离散性相对较大。板柱节点受冲切承载力试验值与中国规范和美国规范的公式计算值之比的均值分别为 1.20 和 1.31，变异系数分别为 0.23 和 0.22。按本文建议公式计算得到的变异系数与 EN1992-1-1《欧盟混凝土结构设计规范》 ^[44]（欧盟规范）接近，分别为 0.18 和 0.16，而本文建议公式相较于欧盟规范更接近试验结果。综上，可以说明本文建议公式能够更加准确地预测竖向荷载作用下的板柱节点受冲切承载力。

表2竖向荷载作用下的板柱节点受冲切承载力试验结果与各计算方法预测结果的对比

Tab.2 Comparison between the test results of punching capacity and the predicted results of various calculation methods for slabcolumn connections under vertical loads

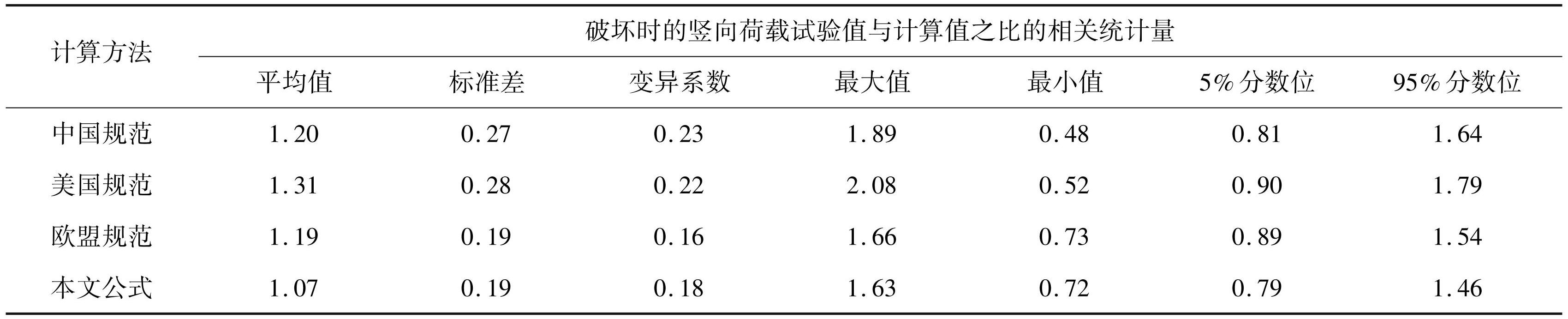
图5给出了板柱节点受冲切承载力试验值与各公式计算值之比随混凝土轴心抗压强度和板受拉纵筋配筋率的变化。可以看出:板柱节点受冲切承载力试验值与中国规范和美国规范公式计算值之比随板受拉纵筋配筋率的提高有上升趋势，致使中国规范和美国规范公式偏于保守。欧盟规范和本文公式合理地反映了混凝土轴心抗压强度和板受拉纵筋配筋率对板柱节点受冲切承载力的影响。

图5竖向荷载作用下的板柱节点受冲切承载力计算公式评价

Fig.5Evaluation of different formulas for predicting the punching capacity of slabs under vertical loads

2 不平衡弯矩作用下的板柱节点受弯承载力计算

板柱节点仅承受由水平荷载作用产生的单向不平衡弯矩作用时，其受力见图6。为推导不平衡弯矩作用下的板柱节点受弯承载力，考虑图6所示的计算截面（距柱边 0.5h₀ 处的截面）。计算截面由以下 4 个部分组成:水平荷载作用方向上的前截面和后截面，以及另一个方向（正交于水平荷载作用方向）上的两个侧面。前截面和后截面上存在弯矩和剪力，侧面上有扭矩。

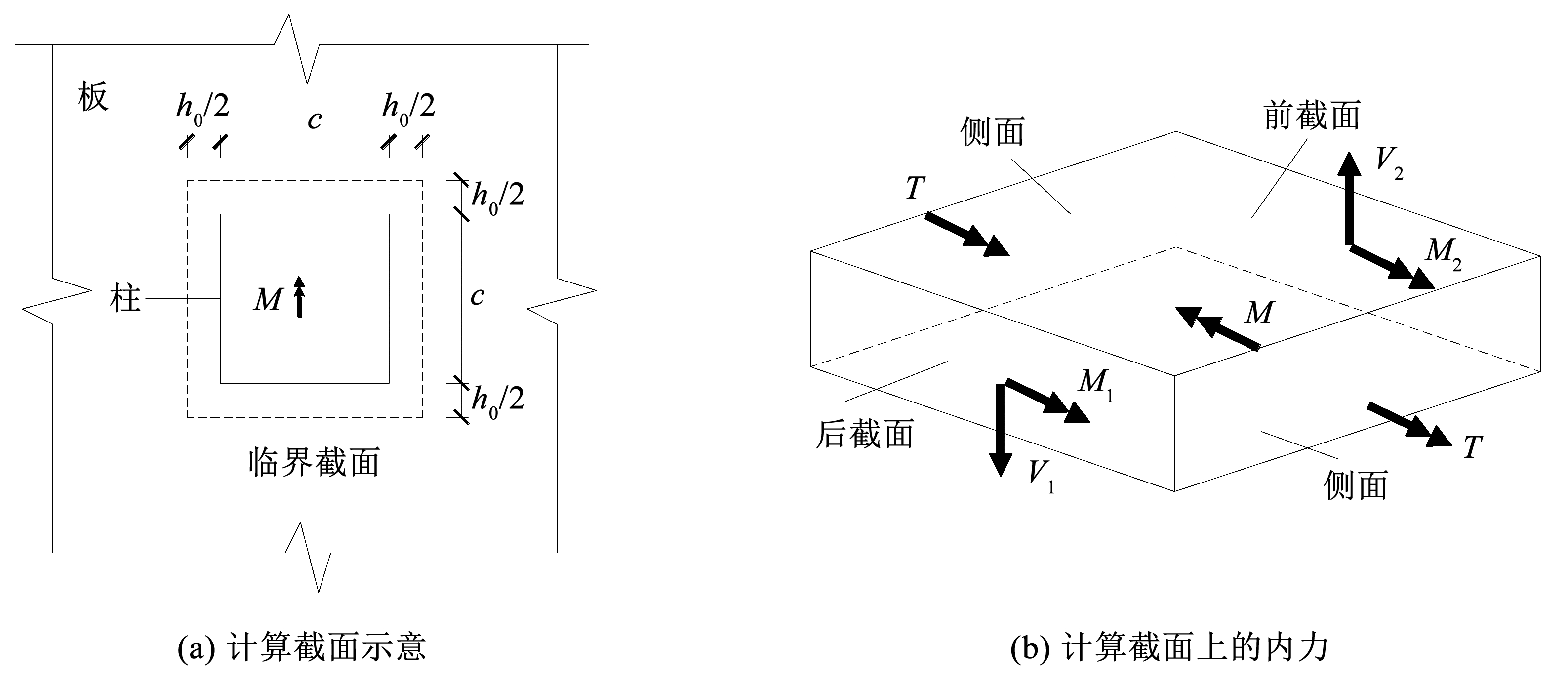
图6受单向不平衡弯矩作用的板柱节点计算模型

Fig.6Calculation model for slabs under unidirectional unbalanced bending moments

为简化计算，假设板柱节点破坏时计算截面上受弯、受剪和受扭同时达到其极限承载力。由此，不平衡弯矩作用下的板柱节点受弯承载力 M_u 可按下式计算:

M_{u} = M_{1} + M_{2} + M_{v 1} + M_{v 2} + 2 T

(23)

式中:M₁ 和 M₂ 分别为后截面和前截面所能提供的抵抗弯矩，N·mm; M_v1和 M_v2分别为后截面和前截面所能提供的剪力引起的弯矩，N·mm; T 为侧面所能提供的抵抗扭矩，N·mm。计算 M₁ 时考虑（ c + h₀）范围内的板顶纵筋，计算 M₂时考虑（ c + h₀）范围内的板底纵筋，其计算公式:

M_{1} = ρ f_{y} h_{0}^{2} (c + h_{0}) (1 - 0.5 \frac{ρ f_{y}}{f_{c}})

(24)

M_{2} = ρ^{'} f_{y} h_{0}^{2} (c + h_{0}) (1 - 0.5 \frac{ρ^{'} f_{y}}{f_{c}})

(25)

假设后截面和前截面所能抵抗的剪力 V₁和 V₂，可按竖向荷载作用下的板柱节点受冲切承载力计算:

V_{1} = V_{u} / 4

(26)

V_{2} = V_{u} / 4

(27)

从而可得剪力所引起的弯矩:

M_{v 1} = V_{u} (c + h_{0}) / 8

(28)

M_{v 2} = V_{u} (c + h_{0}) / 8

(29)

文献^[45] 表明:由于周围板的约束作用，按中国规范中的纯扭构件承载力公式计算侧面能够提供的抵抗扭矩时，会低估侧面能够提供的抵抗扭矩。因此，采用文献^[46]的公式来计算侧面能够提供的抵抗扭矩:

T = 2.28 W_{t} f_{t}

(30)

式中 W_t为截面的塑性抵抗矩，

将计算得到的各部分代入式（23），即可得到仅受不平衡弯矩作用的板柱节点受弯承载力 M_u :

\begin{matrix} M_{u} = ρ f_{y} h_{0}^{2} (c + h_{0}) (1 - 0.5 \frac{ρ f_{y}}{f_{c}}) + ρ^{'} f_{y} h_{0}^{2} (c + h_{0}) \times \\ (1 - 0.5 \frac{ρ^{'} f_{y}}{f_{c}}) + V_{u} \frac{c + h_{0}}{4} + 2.28 W_{t} f_{t} \end{matrix}

(31)

3 竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算

3.1 考虑弯剪相关性的拟合公式

对于竖向荷载和不平衡弯矩共同作用下的板柱节点，根据文献^[47-49]可知竖向荷载对其抵抗不平衡弯矩的能力有着显著影响。因此，参考文献^[50]，采用弯剪相关性的拟合公式的形式为

{(\frac{V}{V_{u}})}^{B} + C [1 - {(\frac{V}{V_{u}})}^{D}] {(\frac{M}{M_{u}})}^{E} = 1

(32)

式中:V 为板柱节点所受到的竖向荷载剪力，N; M 为板柱节点所受到的单向不平衡弯矩，N·mm; V_u为仅受竖向荷载作用时的板柱节点受冲切承载力，按式（22）计算; M_u为仅受单向不平衡弯矩作用时的板柱节点受弯承载力，按式（31）计算; B、C、D 和 E 为待拟合系数。经过多次尝试，发现 B = 1、C = 0.9、 D = 3 / 2 和 E =1 / 4 时，与试验结果吻和较好，见图7。

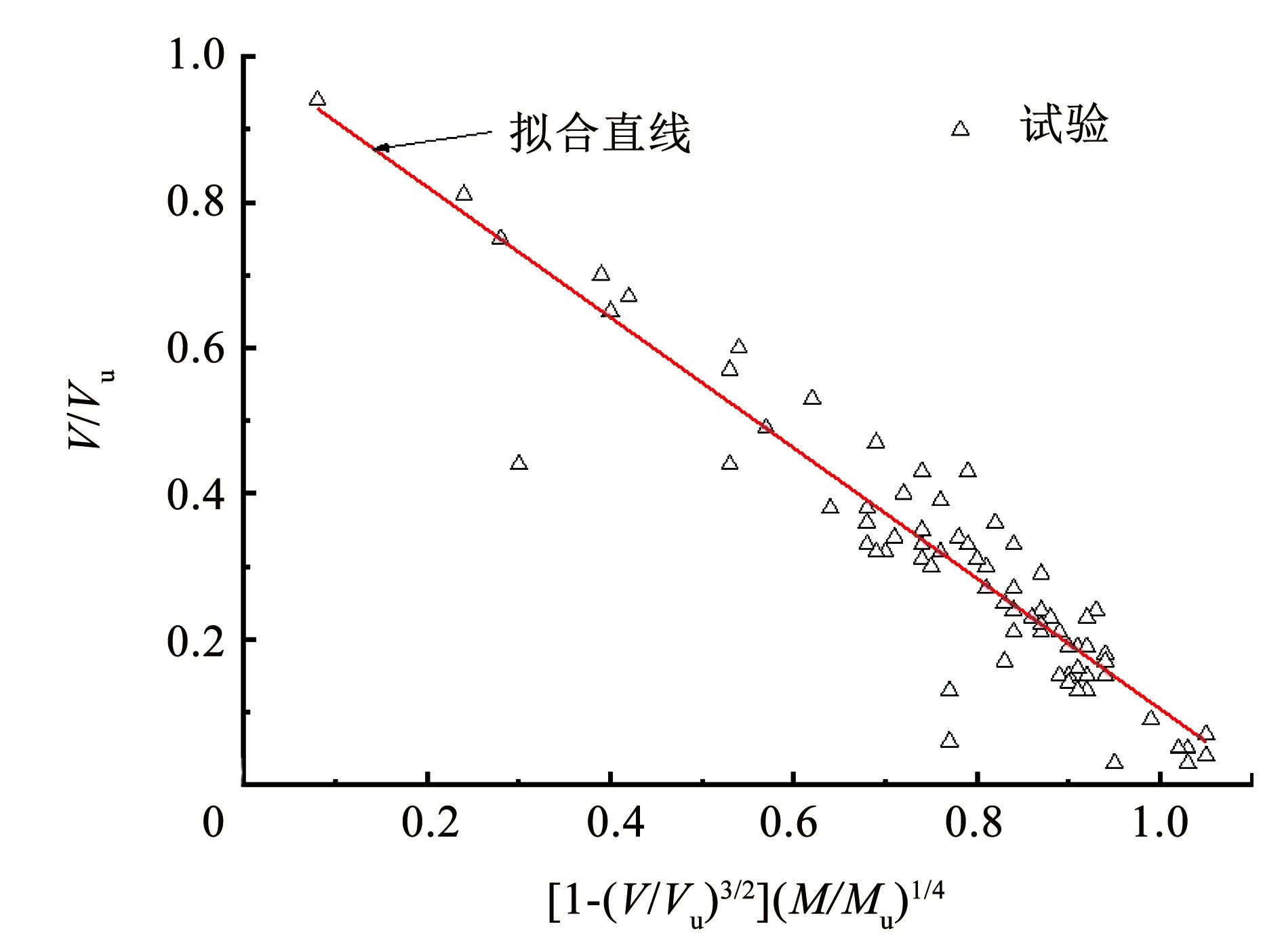
图7弯矩-剪力相关性公式的拟合

Fig.7Fitting of formulas related to bending moment and shear force

最终给出了考虑弯剪相关性的竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式:

\frac{V}{V_{u}} + 0.9 [1 - {(\frac{V}{V_{u}})}^{3 / 2}] {(\frac{M}{M_{u}})}^{1 / 4} = 1

(33)

3.2 建议公式计算结果与试验结果的比较

对于竖向荷载和不平衡弯矩共同作用下的板柱节点，各国规范均按竖向荷载作用下的板柱节点承载力公式计算其承载力，而冲切荷载采用等效集中反力。因此为便于比较各规范公式与本文建议公式的计算结果，将本文建议的弯矩相关性公式（33）乘以 V_u得到了基于建议公式的等效集中反力计算公式 F_l，eq :

F_{1, e q} = V + 0.9 V_{u} [1 - {(\frac{V}{V_{u}})}^{3 / 2}] {(\frac{M}{M_{u}})}^{1 / 4}

(34)

通过收集相关试验数据，建立了包含 76 组竖向荷载和不平衡弯矩共同作用下的板柱节点的试验数据库，该数据库见文献^[51]。根据不同公式，得到的竖向荷载与不平衡弯矩共同作用下的板柱节点等效集中反力试验结果和仅竖向荷载作用下的板柱节点受冲切承载力计算结果的比较，如表3和图8所示。可以看出:中国规范、美国规范和欧盟规范的离散程度均较大，且中国规范和美国规范计算公式较为保守; 本文建议公式优于其他公式，板柱节点等效集中反力试验值与受冲切承载力计算值的比值的平均值为 1. 02，变异系数为 0. 07。

表3不同计算方法等效集中反力试验值与受冲切承载力计算值的比较

Tab.3 Comparison of equivalent concentrated reaction test values and punching capacity calculation results using different methods

图8竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式评价

Fig.8Evaluation of different formulas for the punching capacity of slabs under vertical load and unbalanced moment

4 结论

1）考虑板受压区混凝土、冲切斜裂缝上的混凝土骨料咬合作用和板受拉纵筋销栓作用对板柱节点受冲切承载力的贡献，推导给出了仅竖向荷载作用下的板柱节点受冲切承载力计算公式。对比了仅竖向荷载作用下的板柱节点受冲切承载力试验结果与中国规范、美国规范、欧盟规范和本文建议公式计算结果。结果表明:中国规范和美国规范过于保守，本文建议公式与试验结果最为吻合。

2）对于仅受单向不平衡弯矩作用的板柱节点，通过合理假设，推导给出了计算截面上的弯矩、剪力和扭矩，从而给出了仅承受不平衡弯矩作用的板柱节点受弯承载力计算公式。

3）对于同时承受竖向荷载作用和不平衡弯矩作用的板柱节点，考虑弯剪相关性，拟合给出了其承载力计算公式。对根据不同公式得到的等效集中反力试验结果和受冲切承载力计算结果进行了比较，结果表明本文建议公式可以更加准确地预测竖向荷载和不平衡弯矩共同作用下的板柱节点极限荷载。

图1板柱节点冲切计算模型示意

Fig.1Schematic diagram of punching calculation model for slab-column connections

下载: 全尺寸图片

图2冲切锥体上的应力示意

Fig.2Schematic diagram of stresses on the punching cone

下载: 全尺寸图片

图3抛物线形的摩尔-库伦准则

Fig.3Parabolic Mohr-Coulomb criterion

下载: 全尺寸图片

图4钢筋面积换算成混凝土面积

Fig.4Equivalent conversion of steel reinforcement area to concrete area

下载: 全尺寸图片

图5竖向荷载作用下的板柱节点受冲切承载力计算公式评价

Fig.5Evaluation of different formulas for predicting the punching capacity of slabs under vertical loads

下载: 全尺寸图片

图6受单向不平衡弯矩作用的板柱节点计算模型

Fig.6Calculation model for slabs under unidirectional unbalanced bending moments

下载: 全尺寸图片

图7弯矩-剪力相关性公式的拟合

Fig.7Fitting of formulas related to bending moment and shear force

下载: 全尺寸图片

图8竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式评价

Fig.8Evaluation of different formulas for the punching capacity of slabs under vertical load and unbalanced moment

下载: 全尺寸图片

表1竖向荷载作用下的板柱节点试验数据库

下载: 全尺寸图片

表2竖向荷载作用下的板柱节点受冲切承载力试验结果与各计算方法预测结果的对比

下载: 全尺寸图片

表3不同计算方法等效集中反力试验值与受冲切承载力计算值的比较

下载: 全尺寸图片

图1板柱节点冲切计算模型示意

Fig.1Schematic diagram of punching calculation model for slab-column connections

图2冲切锥体上的应力示意

Fig.2Schematic diagram of stresses on the punching cone

图3抛物线形的摩尔-库伦准则

Fig.3Parabolic Mohr-Coulomb criterion

图4钢筋面积换算成混凝土面积

Fig.4Equivalent conversion of steel reinforcement area to concrete area

图5竖向荷载作用下的板柱节点受冲切承载力计算公式评价

Fig.5Evaluation of different formulas for predicting the punching capacity of slabs under vertical loads

图6受单向不平衡弯矩作用的板柱节点计算模型

Fig.6Calculation model for slabs under unidirectional unbalanced bending moments

图7弯矩-剪力相关性公式的拟合

Fig.7Fitting of formulas related to bending moment and shear force

图8竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式评价

Fig.8Evaluation of different formulas for the punching capacity of slabs under vertical load and unbalanced moment

表1竖向荷载作用下的板柱节点试验数据库

表2竖向荷载作用下的板柱节点受冲切承载力试验结果与各计算方法预测结果的对比

表3不同计算方法等效集中反力试验值与受冲切承载力计算值的比较

图1板柱节点冲切计算模型示意

Fig.1Schematic diagram of punching calculation model for slab-column connections

图2冲切锥体上的应力示意

Fig.2Schematic diagram of stresses on the punching cone

图3抛物线形的摩尔-库伦准则

Fig.3Parabolic Mohr-Coulomb criterion

图4钢筋面积换算成混凝土面积

Fig.4Equivalent conversion of steel reinforcement area to concrete area

图5竖向荷载作用下的板柱节点受冲切承载力计算公式评价

Fig.5Evaluation of different formulas for predicting the punching capacity of slabs under vertical loads

图6受单向不平衡弯矩作用的板柱节点计算模型

Fig.6Calculation model for slabs under unidirectional unbalanced bending moments

图7弯矩-剪力相关性公式的拟合

Fig.7Fitting of formulas related to bending moment and shear force

图8竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算公式评价

Fig.8Evaluation of different formulas for the punching capacity of slabs under vertical load and unbalanced moment

表1竖向荷载作用下的板柱节点试验数据库

表2竖向荷载作用下的板柱节点受冲切承载力试验结果与各计算方法预测结果的对比

表3不同计算方法等效集中反力试验值与受冲切承载力计算值的比较

STASIO D J, VAN BUREN M P. Transfer of bending moment between flat plate floor and column[J]. ACI Structural Journal,1960,57(9):299

马云昌, 吕西林. 钢筋混凝土板柱节点的抗震性能研究[J]. 建筑结构学报,2001,22(4):49. MA Yunchang, LYU Xilin. Seismic behavior of reinforced concrete slab-column system[J]. Journal of Building Structures,2001,22(4):49. DOI:10.14006/j.jzjgxb.2001.04.009

TIAN Y. Behavior and modeling of reinforced concrete slab-column connections[M]. Austin: The University of Texas at Austin,2007:146

易伟建, 刘彪. 混凝土板柱节点偏心冲切极限分析[J]. 西安建筑科技大学学报(自然科学版),2018,50(2):162.Yl Weijian, LIU Biao. Ultimate strength analysis of punching shear capacity under eccentrical load of concrete slab-column connections[J]. Journal of Xi’an University of Architechure & Technlolgy.(Natural Science Edition),2018,50(2):162. DOI:10.15986/j.1006-7930.2018.02.002

JIANG Dahua, SHEN Jinghua. Strength of concrete slabs in punching shear[J]. Journal of Structural Engineering,1986,112(12):2578

混凝土结构设计规范: GB 50010—2010[S]. 北京: 中国建筑工业出版社,2010.Code for design of concrete structures: GB 50010—2010[S]. Beijing: China Architecture & Building Press,2010

郑文忠, 王刚, 王英. 板柱节点承载力计算方法研究进展[J]. 哈尔滨工业大学学报,2022,54(10):1. ZHENG Wenzhong, WANG Gang, WANG Ying. Research progress in bearing capacity calculation methods of research progress in bearing capacity calculation methods of slab-column connections[J]. Journal of Harbin Institute of Technology,2022,54(10):1. DOI:10.11918/202112116

VECCHIO F J, COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. ACI Journal Proceedings,1986,83(2):219

Model Code for Concrete Structures: MC 2010[S]. Lausanne: International Federation for Structural Concrete,2013

PHILIPPE M. Analytical computation of the punching strength of reinforced concrete[J]. ACI Structural Journal,1996,93(5):503

角田史雄, 井藤昭夫, 藤田嘉夫. 鉄筋コンクリートスラブの押抜きせん断耐力に関する実験的研究[J]. 土木學會論文報告集,1974,229:105

李定国, 舒兆发, 余志武. 无抗冲切钢筋的钢筋混凝土板柱连接冲切强度的试验研究[J]. 湖南大学学报,1986,13(3):22. LI Dingguo, SHU Zhaofa, YU Zhiwu. Experimental investigation of punching strength of reinforced concrete slab-column connections without shear reinforcement[J]. Journal of Hunan University,1986,13(3):22

REGAN P E. Symmetric punching of reinforced concrete slabs[J]. Magazine of Concrete Research,1986,38(136):115

赵晋. 钢筋混凝土板柱节点冲切破坏后性能研究[D]. 长沙: 湖南大学,2016. ZHAO Jin. The Study on post-punching performance of RC slabcolumn connections[D]. Changsha: Hunan Institute of Science and Technology,2016

PARK H G, AHN K S, CHOI K K,et al. Lattice shear reinforcement for slab-column connections[J]. ACI Structural journal,2007,104(3):294

彭检. 钢筋混凝土板柱节点抗冲切试验研究[D]. 长沙: 湖南大学,2013. PENG Jian. Experimental study on punching shear failure of reinforced concrete slabs-column connections[D]. Changsha: Hunan Institute of Science and Technology,2013

GOSAV A V, KISS Z I, ONET T,et al. Failure assessment of flat slab-to-column members[J]. Magazine of Concrete Research,2016,68(17):887

易伟建, 洪枫, 彭检. 钢筋混凝土板柱节点抗冲切试验研究[J]. 建筑结构,2016,46(15):11. YI Weijian, Hong Feng, PENG Jian. Experimental investigation of punching shear failure of reinforced concrete slab-column connections[J]. Journal of Building Structures,2016,46(15):11. DOI:10.19701/j.jzjg.2016.15.003

郑建岚, 郑作樵. 钢筋混凝土板冲切强度的试验研究[J]. 福州大学学报(自然科学版),1992,20(2):65. ZHENG Jianlan, ZHENG Zuoqiao. Research on the test results of punching strength of reinforced concrete slabs[J]. Journal of Fuzhou University(Natural Science),1992,20(2):65

GUANDALINI S, BURDET O L, MUTTONI A. Punchingtests of slabs with low reinforcement ratios[J]. ACI Structural Journal,2009,106(1):87

HAWKINS N M, MITCHELL D, SHEU M S. Cyclicbehavior of six reinforced concrete slab-column specimens transferring moment and shear[D]. Seattle: University of Washington,1974

BIRKLE G, DILGER W H. Influence of slab thickness on punching shear strength[J]. ACI Structural Journal,2008,105(2):180

安玉杰, 赵国藩. 配筋钢纤维砼板抗冲切性能的试验研究(上)[J]. 建筑结构学报,1994,15(2):6. AN Yujie, ZHAO Guofan. Experimental study on punching shear resistance of SFRC slabs with steel bars[J]. Journal of Building Structures,1994,15(2):6

THEODORAKOPOULOS D D, SWAMY N. Contribution of steel fibers to the strength characteristics of lightweight concrete slab column connections failing in punching shear[J]. ACI Structural Journal,1993,90(4):342

毛明傑, 楊秋寧, 江上真介. 圧縮側補強による RC 床版のせん断強度への影響(スラブ)[J]. 工学年次論文集,2007,29(3):385

黄小坤, 刘立渠, 陶学康. 考虑纵筋率及加载面边长比影响的板受冲切承载力试验研究[J]. 土木工程学报,2008,41(7):21. HUANG Xiaokun, LIU Liqu, TAO Xuekang. Experimental study on the punching shear capacity of slabs considering the influences of tension reinforcement and column aspect ratios[J]. China Civil Engineering Journal,2008,41(7):21. DOI:10.15951/j.tmgcxb.2008.07.009

SISTONEN E, LYDAMN M, HUOVINEN S. The geometrical model of the calculation formula of the punching shear capacity of the reinforced concrete slab[D]. Helsinki: Helsinki University of Technology,1997

TALBOT A N. Reinforced concrete wall footings and column footings[D]. Urbana-Champaign: University of Illinois at Urbana Champaign,1925

EINPAUL J, BUJNAK J, RUIZ M F,et al. Study oninfluence of column size and slab slenderness on punching strength[J]. ACI Structural Journal,2016,113(1):135

张元伟. 钢筋混凝土板抗冲切试验研究[D]. 长沙: 湖南大学,2009. ZHANG Yuanwei. Punching shear research on reinforced concrete slabs[D]. Changsha: Hunan Institute of Science and Technology,2009

RIZK E, MARZOUK H. Experimentalvalidation of minimum flexural reinforcement for thick high-strength concrete plates[J]. ACI Structural Journal,2011,108(3):332

BIRKLE G, DILGER W H. Influence of slab thickness on punching shear strength[J]. ACI Structural Journal,2008,105(2):180

ALMEIDA A F O, INACIO M M G, LUCIO V J G,et al. Punching behaviour of RC flat slabs under reversed horizontal cyclic loading[J]. Engineering Structures,2016,117:204

CARLOS E, OSPINA SCOTT D B, ALEXANDER J J. Punching of two way concrete slabs with fiber reinforced polymer reinforcing bars or grids[J]. ACI Structural Journal,2001,100(61):589

CALDENTEY A P, LAVASELI P P, PEIRETTI H G,et al. Influence of stirrup detailing on punching shear strength of flat slabs[J]. Engineering Structures,2013,49(4):855

GHANNOUM C M. Effect of high-strength concrete on the performance of slab-column specimens[D]. Montreal: McGill University,1998

LIPS S. Punching of flat slabs with large amounts of shearreinforcement[D]. Lausanne:École Polytechnique Fédérale de Lausann,2012

DAM T X, WIGHT J K. Flexurally-triggered punching shear failure of reinforced concrete slab-column connections reinforced with headed shear studs arranged in orthogonal and radial layouts[J]. Engineering Structures,2016,110:258. DOI:10.1016/j.engstruct.2015.11.050

BARTOLAC M, DAMJANOVIC D, DUVNJAK I. Punching strength of flat slabs with and without shear reinforcement[J]. Gradevinar,2015,67(8):771. DOI:10.14256/JCE.1361.2015

MARZOUK H, HUSSEIN A. Punching shear analysis of reinforced high-strength concrete slabs[J]. Canadian Journal of Civil Engineering,1991,18(6):954

GUIDOTTI R. Poinçonnement des planchers-dalles avec colonnes superposées fortement sollicitées:[D]. Lausanne:École Polytechnique Fédérale de Lausann,2010

TOMASZEWICZ A. Reportpunching shear capacity of reinforced concrete slabs[J]. SINTEF Structures and Concrete,1993,42(3):55

Building code requirements for structural concrete andcommentary: ACI 318-19[S]. Farmington Hills: American Concrete Institute,2019

Design of concrete structures-Part 1-1:general rules and rules forbuildings: EN 1992-1-1[S]. Brussel: European Committee for Standardization,2004

周军, 吕西林. 混凝土平板结构中柱节点在剪力与不平衡弯矩共同作用下的分析研究[J]. 建筑结构学报,1997(5):32. ZHOU Jun, LYU Xilin. Analysis of interior slab-column connection RC flat slab structures under shear and unbalanced moment[J]. Journal of Building Structures,1997(5):32. DOI:10.14006/j.jzjgxb.1997.05.004

戴琨. 基于拟梁法的板柱节点承载力分析[D]. 南京: 南京航空航天大学,2012. DAI Kun. The strength analysis of slab-column connection[D]. Nanjing: Nanjing University of Aeronautics and Astronautics,2012

MORRISON D G, HIRASAWA I, SOZEN M A. Lateral-load tests of RC slab-column connections[J]. Journal of Structural Engineering,1983,109(11):2698

PAN A, MOEHLE J P. Lateral displacement ductility of reinforced concrete flat plates[J]. ACI Structural Journal,1989,86(3):250

唐明, 易伟建, 刘力维. 低周往复荷载下板柱中节点抗震性能研究[J]. 地震工程与工程振动,2019,39(3):109. TANG Ming, Yl Weijian, LIU Liwei. Investigation on seismic performance of interior slab-column connections subjected to reversed cyclic loading[J]. Earthquake Engineering and Engineering Dynamics,2019,39(3):109. DOI:10.13197/j.eeev.2019.03.109.tangm.011

唐明. 钢筋混凝土板柱节点抗震性能研究[D]. 长沙: 湖南大学,2021. TANG Ming. Study on seismic behavior of RC slab-column connections[D]. Changsha: Hunan Institute of Science and Technology,2021

郑文忠, 吕盛先, 郑博文, 等. 承受竖向荷载和不平衡弯矩的板柱节点受冲切计算方法[J/OL]. 哈尔滨工业大学学报.Zheng Wenzhong, LYU Shengxian, Zheng Bowen,et al. A calculation method for punching failure of slab-column connections subjected to vertical loads and unbalanced bending moments[J/OL]. Journal of Harbin Institute of Technology. DOI:10.11918/202312032

1 竖向荷载作用下的板柱节点受冲切承载力计算

2 不平衡弯矩作用下的板柱节点受弯承载力计算

3 竖向荷载和不平衡弯矩共同作用下的板柱节点受冲切承载力计算

4 结论

友情链接LINKS