摘要
为解决异形钢管混凝土柱阴角对其承载力的影响,提出了用 1 个冷弯薄壁方钢管和 2 个 U 形钢管焊接成 L 形钢管, 内填充混凝土形成 L 形冷弯薄壁型钢组合钢管混凝土柱形式。设计了 5 组共 10 根试件的轴压试验,并开展了有限元参数分析,研究了钢管厚度、U 形管外伸长度和钢材强度等参数对构件承载力和延性等力学性能的影响。结果表明:该类试件的主要破坏形态为中上部局部鼓曲破坏,适量增大 U 形管外伸长度可以提高承载力,但增大到一定程度之后易发生弯扭破坏;承载力和延性随着钢管厚度和钢材强度增大而增加;混凝土强度对构件的初始刚度和峰值荷载的影响都很小,但对曲线下降段的影响较大;试件端部和中部截面阴角处的混凝土应力值比各边中部更大,说明采用 U 形钢管与方钢管组合的方式改善了阴角处钢管对混凝土约束普遍较弱的问题。基于“统一理论”,给出了两种承载力建议计算公式,与试验结果吻合较好,两种计算方法在 0. 44 ~ 1. 94 的约束效应系数范围内具有良好的适用性。
Abstract
The study investigates the bearing capacity of specially shaped, concrete-filled steel tube columns, emphasizing the impact of reentrant corners. A novel design was proposed, involving the welding of one cold-formed, thin-walled square steel tube and two U-shaped steel tubes into an L-shaped configuration, which is then filled with concrete to form an L-shaped concrete-filled cold-formed thin-walled steel tubular columns. To explore this concept, a series of axial load tests were conducted on 10 specimens with total of 5 groups. These experiments were complemented by finite element analysis to assess the effects of various parameters, including steel tube thickness, protrusion length of the U-shaped tubes, and steel material strength, on the structural integrity and ductility of the columns. Results indicate that the predominant failure mechanism involved localized buckling in the upper-middle region. An increase in the U-shaped tubes’ protrusion length was found to enhance structural capacity up to a certain threshold, beyond which flexural-torsional failure becomes prevalent. Additionally, both the structural capacity and ductility of the columns were positively correlated with increases in steel tube thickness and material strength. The strength of the concrete was observed to have a minimal impact on the initial stiffness and peak load of the columns, yet significantly influenced the descending phase of the load-deflection curve. Moreover, concrete stresses were more pronounced at the reentrant corners of the specimen ends and mid-sections compared to the lateral mid-sections, suggesting an enhanced restraint by the combination of U-shaped and rectangular steel tubes in these regions. According to the“unified theory”, two sets of calculation formulas for load-bearing capacity were proposed. These formulas not only align closely with experimental results but also demonstrate robust applicability across a wide range of constraint effect coefficients, from 0. 44 to 1. 94.
钢管混凝土具有承载力高、塑性性能好、施工方便等特点,两者的组合能充分发挥混凝土和钢材的力学性能[1-2]。普通的钢管混凝土截面形状一般为圆形、矩形和方形,在住宅建筑中,这些形状规则的钢管混凝土柱往往会存在柱角外露的问题,既占用空间又不美观。为了满足平面设计需求,提升空间利用率,学者们提出了多种构造形式的异形钢管混凝土柱。
朱彦奇等[3]提出了加劲肋异形钢管混凝土柱,通过轴压试验,分析了 L 形钢管混凝土柱的屈曲形态和破坏形式等,指出纵向加劲可以明显提高延性和极限承载力,但在阴角处的加劲对受压性能无太大提升,给出了最优的加肋方式。孙刚等[4]、左志亮等[5-6]进行了拉杆约束的异形钢管混凝土短柱的轴压试验,分析了拉杆的直径和间距、钢管壁厚度等参数对构件轴压性能的影响,试验结果发现拉杆在很大程度上增加了异形钢管混凝土短柱的延性和承载力,起到了延缓局部屈曲的作用。屠永清等[7-9] 提出了一种通过焊接将 2 个或 3 个矩形钢管柱组合成 L 形、T 形或十字形截面的多室组合异形钢管混凝土柱,通过轴压试验对短柱和中长柱的轴压性能进行了研究,确定了当长细比小于等于 17 时为短柱,长细比在 17~90 时为中长柱,大于 90 时为长柱。徐礼华等[10] 提出了由两根矩形钢管焊接构成 T 形截面的钢管混凝土柱,通过轴压试验分析了含钢率、截面尺寸和剪跨比等参数对构件的影响,并提出了该截面柱的抗弯承载力计算公式。徐传国[11] 提出了一种十字形多腔钢管混凝土柱,其中部为方钢管,方钢管的 4 个面各焊 1 个槽钢,并对其进行了轴压和偏压研究,得到了其破坏过程,最后给出了两种受力情况下的简化承载力计算式。
目前所研究的异形钢管混凝土柱,有的对宽厚比较大的边的力学性能有所改善,但是阴角问题仍然没有解决,有的存在施工工艺要求高、含钢率高等问题。基于此,本文提出一种 L 形冷弯薄壁型钢组合钢管混凝土柱,由 1 个冷弯薄壁矩形钢管和 2 个冷弯薄壁 U 形钢管焊接成 L 形钢管,内部浇筑自密实混凝土而成。这种截面形式无阴角,消除了阴角的影响,增加了钢管对混凝土的约束。采用冷弯薄壁型钢,减轻构件自重,降低含钢率,更为经济。此外,这种钢管混凝土构造简单,焊接流程少,一根 L 形冷弯薄壁型钢组合钢管混凝土柱只需焊接三处,混凝土浇筑过程方便简单,适合在多层装配式建筑中使用。本文主要对 L 形冷弯薄壁型钢组合钢管混凝土柱进行了轴压试验,主要分析了钢管厚度、U 形管外伸长度、混凝土强度和钢材强度等参数对其破坏形态、承载力和延性等力学性能的影响。对比分析了现有规范和规程计算公式对 L 形冷弯薄壁型钢组合钢管混凝土柱承载力预测的适用性,并基于“统一理论”给出了两种 L 形冷弯薄壁型钢组合钢管混凝土柱的轴压承载力的简化计算公式。
1 试验概况
1.1 试件设计与制作
设计制作了 5 种共 10 根 L 形冷弯薄壁型钢组合钢管混凝土柱,主要变化了钢管厚度和冷弯薄壁 U 形钢管外伸长度等参数。柱上下端盖板尺寸为 340 mm ×340 mm ×10 mm; 方钢管的尺寸为 100 mm × 100 mm; 冷弯薄壁 U 形钢管的宽度为 100 mm,厚度与方钢管等厚,分别为 2、3、4 mm,长度 b 分别为 100、150、200 mm; 为了减少柱端部效应的影响,柱长 L 取 3 倍的截面最大宽度,即 200 mm ×3 =600 mm,最终试件见图1,截面形心 O 采用刚度换算截面法确定(O 为试件中心示意点)。试件中的方钢管选用无缝钢管,U 形钢管由薄壁钢板冷弯而成,将方钢管和 2 个冷弯薄壁 U 形钢管焊接成 L 形钢管,并将上、下端盖板分别焊接在柱上、下端,在柱端焊接多个钢板加劲肋,防止端部钢板局部屈曲,同时在上端盖板预留 3 个浇筑混凝土的圆孔,然后向钢管内部浇筑混凝土。试件设计具体参数见表1,钢板均采用 Q235 钢,混凝土设计标号为 C30,CFST 表示钢管混凝土柱,试件编号中字母“L”表示柱的截面形状,t 为钢管厚度,b 为 U 型管外伸长度,H 为柱的有效高度。
1.2 材料力学性能
按照 GB / T228.1—2021 《金属材料拉伸试验第 1 部分:室温试验方法》 [12]设计拉伸试样尺寸,由于取材相同,矩形钢管和 U 形钢管试样均从同一批钢板上裁取,每个厚度制作 3 个拉伸试样,一共制作了 9 个拉伸试件,钢材材性试验结果见表2。

图1试件详图
Fig.1Details of specimens
试件均采用同一强度自密实混凝土浇筑,在浇筑的同时,制作了 6 个标准混凝土试块,测定混凝土立方体平均抗压强度为 45.45 MPa,弹性模量为 3.17 × 10 4 MPa。
表1试件基本参数
Tab.1 Detailed parameters of test specimens
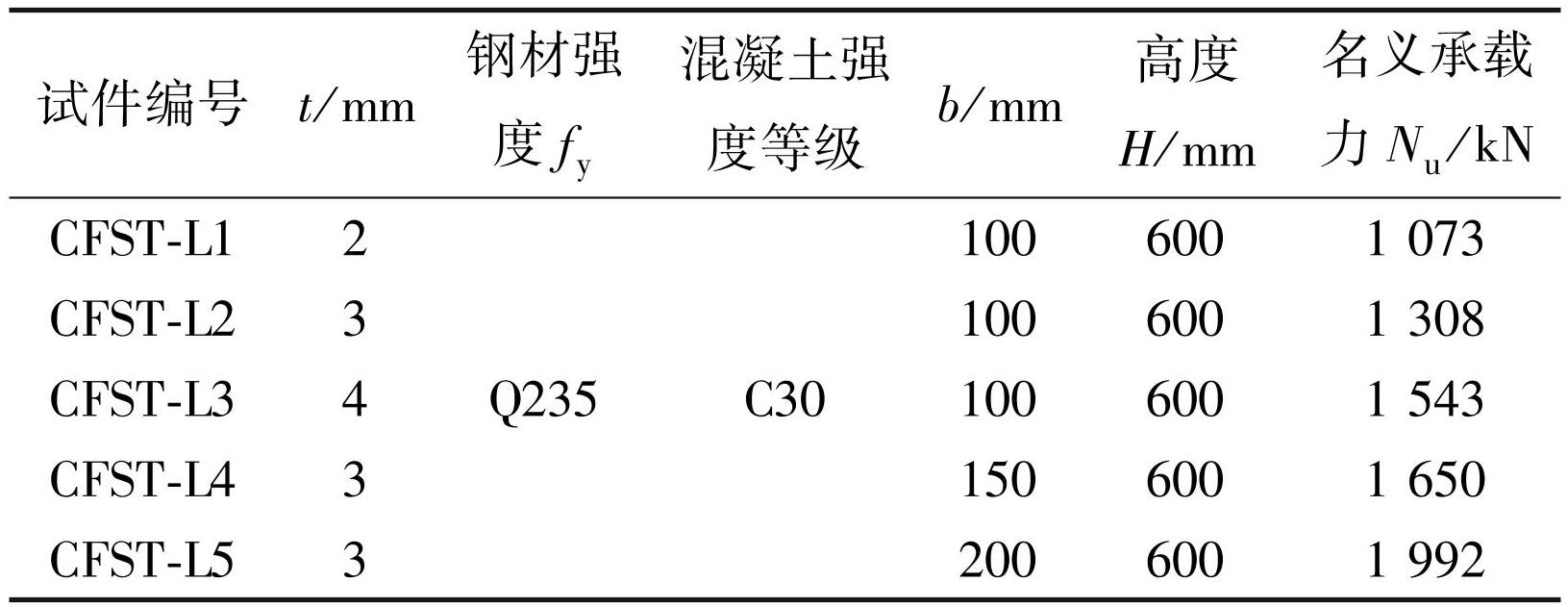
注:名义承载力 Nu = f yAs + f ckAc。其中 As 为钢管面积,Ac 为混凝土面积,f y 为钢材屈服强度,f ck 为棱柱体抗压强度,依据《混凝土结构设计规范》,本文的 f ck = 0.67f cu,f cu 为立方体抗压强度,计算时取立方体抗压强度平均值 f cu,m,本文统一采用实测值 f y 和 f ck计算。
表2钢材力学性能
Tab.2 Mechanical properties of steel
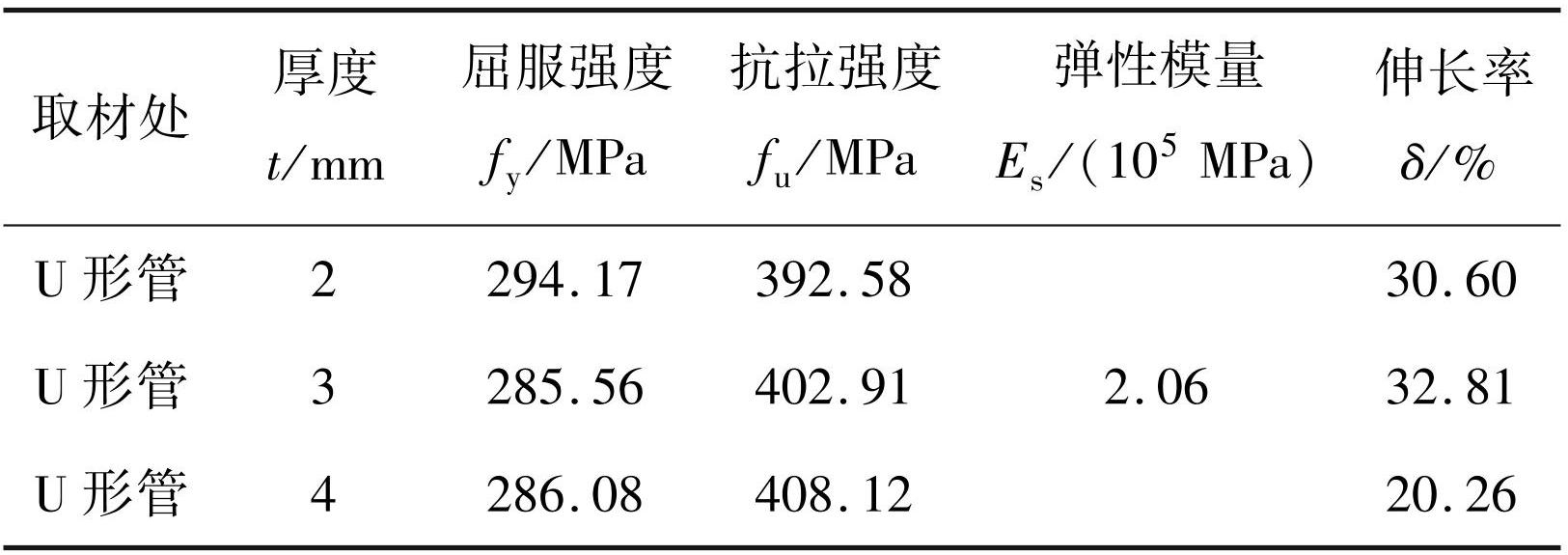
注:伸长率 δ =(Lu-L0)/ L0 × 100%,其中 L0 为原始标距,Lu 为断后标距。
1.3 加载装置与测量布置
试验在600 t 的压力试验机上进行,加载装置见图2。加载中心为点 O,加载过程分为预加载和正式加载,正式加载采用分级加载的方式,在达到极限荷载的 1 / 2 预先估计值之前,每级施加荷载为 1 / 10 预估值,达到极限荷载的 1 / 2 预先估计值之后,每级施加荷载为 1 / 20 预估值,每级荷载持续时间为 2 min,加载速度为 0.5 kN/ s。达到预估荷载后,改用位移加载,加载速度为 0.5 mm / min。当荷载下降到实测极限荷载的 85% 或变形过大时,则判定破坏,停止加载。

图2加载装置
Fig.2Test setup
试验采用电阻应变片和位移计,分别测量试件的横纵向应变和纵向位移。应变片布置见图3,其中 1~16 应变片布置在距离试件上端 100 mm 处; 17~32 应变片布置在试件中部; 33~36 应变片布置在中部的方钢管角部处; 37~40 应变片布置在中部的 U 形管角部处。位移计的布置见图4,在试件上下盖板处各布置 2 个位移计,用来测量 L 形冷弯薄壁型钢组合钢管混凝土柱在竖向荷载下的整体位移,在构件距离上下端 150 mm 处分别布置 1 个矩形框架,在下端框架的 4 个对角处分别放置 1 个量程为 1 000 mm 的拉绳位移计,用来测量构件腰部 300 mm 长度范围内在试验过程中的竖向变形。
2 试验结果分析
2.1 试验现象及破坏形态
从试验现象来看,L 形冷弯薄壁型钢组合钢管混凝土柱的破坏形式主要为中上部的局部鼓曲破坏。以 CFST-L1 为例,见图5、6。当施加的荷载值小于 0.8 Nu(试件的极限荷载值)时,采用力控制的加载方式,试件外形基本无变化,用铁棍敲击钢管可听出钢管的空鼓声,试件处于弹性工作阶段; 之后采用位移控制的加载方式,偶尔可听见混凝土被压碎的声音; 当荷载增加到 0.9 Nu 时,试件连续发出混凝土压碎以及钢管与混凝土发生剥离的响声; 试件中下部逐渐开始有向外鼓曲的趋势,当荷载到达 Nu 时,试件首先在离下端 20~200 mm 范围内出现较大鼓曲,承载力开始下降,试件向下迅速压缩变形,中下部整体向外鼓曲严重,判断试件已破坏并停止加载。
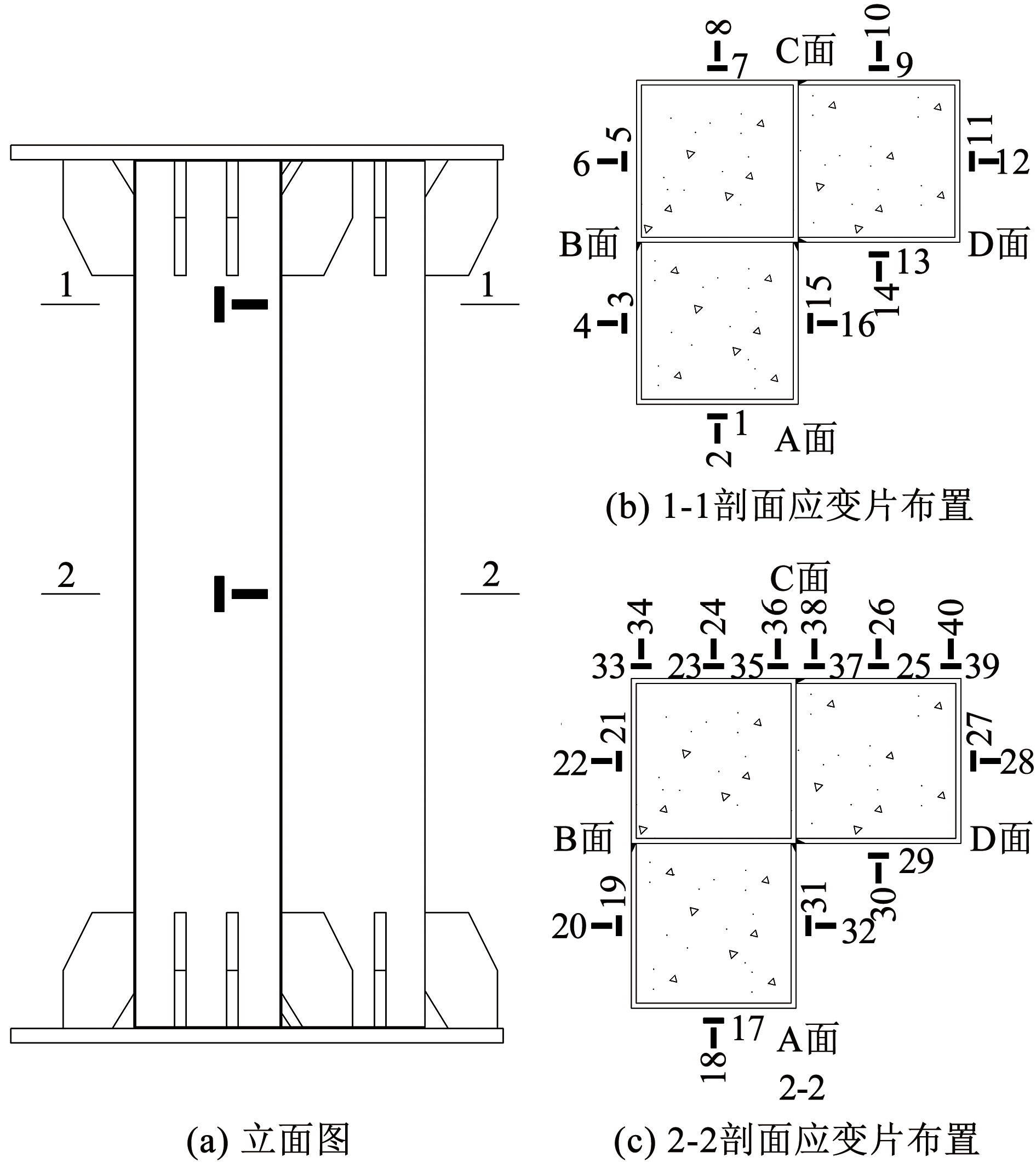
图3应变片布置
Fig.3Layout of strain gauge
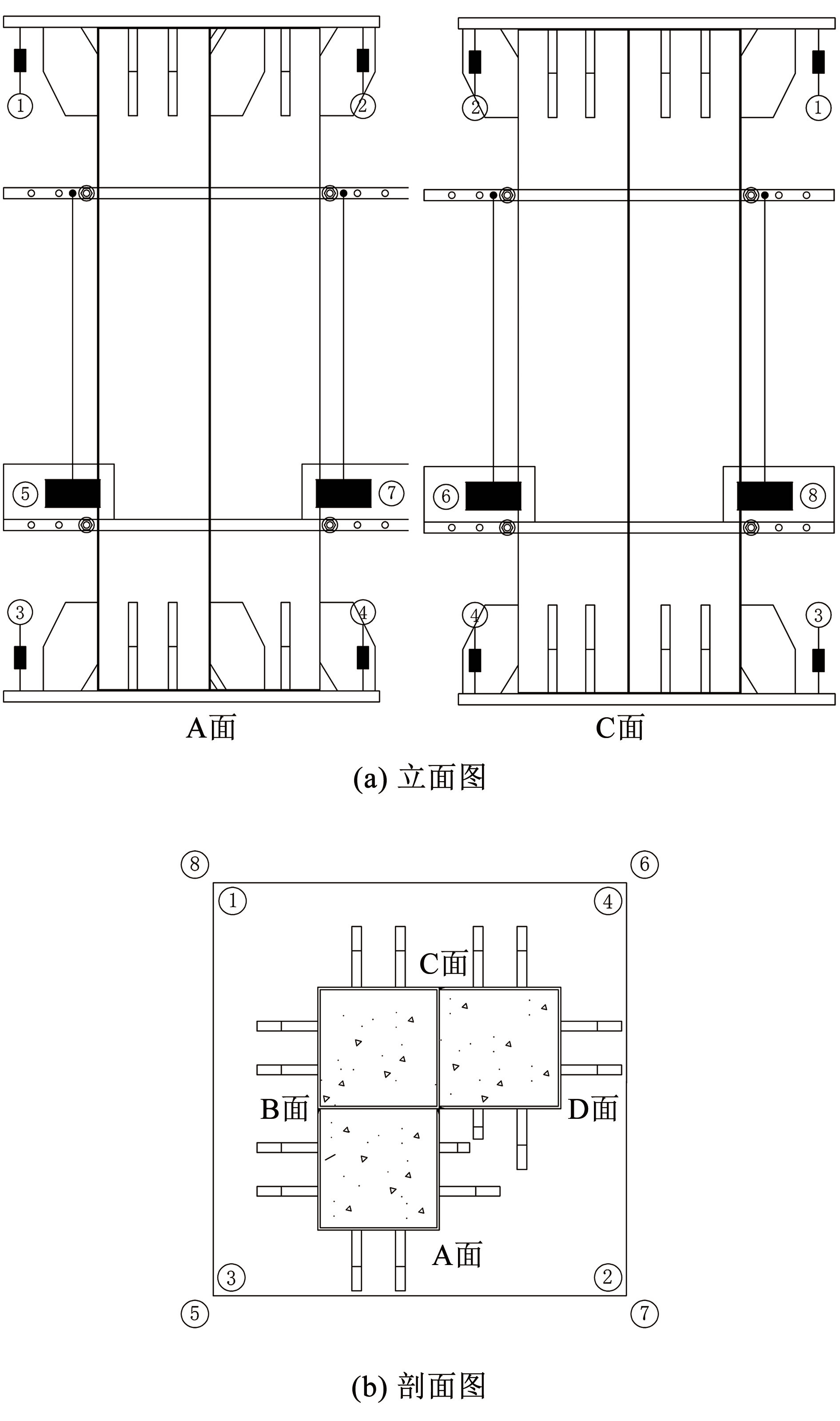
图4位移计布置
Fig.4Layout of displacement meter

图5CFST-L1a 整体破坏
Fig.5Failure mode of CFST-L1a

图6CFST-L1a 局部破坏
Fig.6Local failure of CFST-L1a
2.2 应变分析
L 形冷弯薄壁型钢组合钢管混凝土柱为单轴对称且为轴心受压,见图3( b),选取一半对称截面的中部应变片值作为代表值,选出 4 组应变片:4 个横向应变片和 4 个纵向应变片,整理后得到试件的荷载-应变曲线,见图7,“H”和“Z”分别代表横向和纵向。
图7荷载-应变曲线
Fig.7Load-strain curves
CFST-L1a 和 L1b、CFST-L2a 和 L2b、CFST-L3a 和 L3b、CFST-L4a 和 L4b 在试验过程中的破坏形态一致,且荷载-应变曲线差别很小,故每组试件选取一种进行分析,见图7( a)、( b)、( c)、( d)。由图7可知,L 形冷弯薄壁型钢组合钢管混凝土柱的钢管壁纵向始终受压,环向始终受拉; 同一个位置的横、纵应变片的荷载-应变曲线走势呈现出左右对称的情况,说明试件环向和纵向的受力状态很均匀,表明钢管对混凝土有着较好的约束效果。试件的荷载-应变曲线包含线性和非线性两个阶段,在达到极限荷载的 85% 之前,荷载与应变呈线性关系,此时试件钢管环向应变和纵向应变呈现出线弹性变化,纵向的应变值始终大于横向的应变值,说明在线性阶段主要由试件的纵向提供承载力; 达到极限荷载的 85% 之后,荷载-应变曲线主要呈现出非线性的变化趋势,表明试件进入了非线性变化阶段; 随着荷载的继续增大,此时的 L 形冷弯薄壁型钢组合钢管混凝土柱也进入了局部鼓曲破坏变形阶段,横、纵向应变片数值迅速增大,局部混凝土膨胀并压碎,混凝土对钢管的挤压导致了钢管向外鼓曲,钢管的环向应变同时迅速增大,上述两个阶段的过程和试验破坏过程表现一致。
图7(e)、(f)分别为 CFST-L5a、L5b 的荷载-应变曲线,可以发现,L5a 的纵向应变片 Z22、Z24 和 Z26 在加载开始时为正值,横向应变片 H23、H25 和 H27 为负值,随着荷载的增大又分别转变为负值和正值,这说明试件存在微小的初始偏心,而后随着荷载的增大,钢板鼓曲发生了变化,试验时 L5a 的最终破坏形式为局部弯扭破坏。在达到极限荷载的 60% 时,L5b 开始从线性向非线性阶段转变,在此荷载范围试件的 U 形管长边发生了局部鼓曲破坏; 在非线性变化阶段,U 形管处的应变片 H25、 Z26、 H27、Z28 数值相较方钢管处的应变片 H21、 Z22、 H23、Z24 数值小很多,说明 U 形管整体对混凝土的约束作用小于方钢管处钢管对混凝土的约束效果,U 形管处的变形和破坏先于方钢管,且在加载的后期,荷载主要由方钢管承担。
2.3 影响因素分析
通过各试件轴压荷载-平均纵向应变曲线对钢管厚度和 U 形管外伸长度等影响因素进行分析。平均纵向应变为位移计实测值的整体位移除以试件有效长度,其中整体位移是取 4 个拉绳位移计测量数据之和的平均值。
2.3.1 钢管厚度
CFST-L1、L2、L3 为不同钢管厚度(t = 2、3、4 mm)的L形冷弯薄壁型钢组合钢管混凝土柱,荷载-平均纵向应变曲线见图8,各曲线的总体趋势相同,在荷载达到极限承载力前,随着钢管厚度的增大,L 形冷弯薄壁型钢组合钢管混凝土柱的刚度和承载力稍有增大。不同钢管厚度试件的刚度、承载力和延性系数计算结果见表3,可知 L 形冷弯薄壁型钢组合钢管混凝土柱的理论压缩刚度和实际压缩刚度都随着钢管厚度的增加而增加。 L2 比 L1 的极限承载力提升约 22.54%,L3 比 L2 提升约 17.45%,前者的提高幅度更大,说明随着钢管厚度的增大,L 形冷弯薄壁型钢组合钢管混凝土柱的极限承载力随之增加,但是增幅会逐渐降低。在到达极限荷载后,进入塑性破坏阶段时,从 3 根试件的荷载-平均纵向应变曲线可以发现,L1a、L2b、L3a 的曲线分别下降至极限荷载的 85. 05%、91.74%、85.35% 后再趋于平缓。总体上,试件的理论刚度、实测刚度、极限承载力、承载力提高系数以及延性都随着钢管厚度的增大而增大。
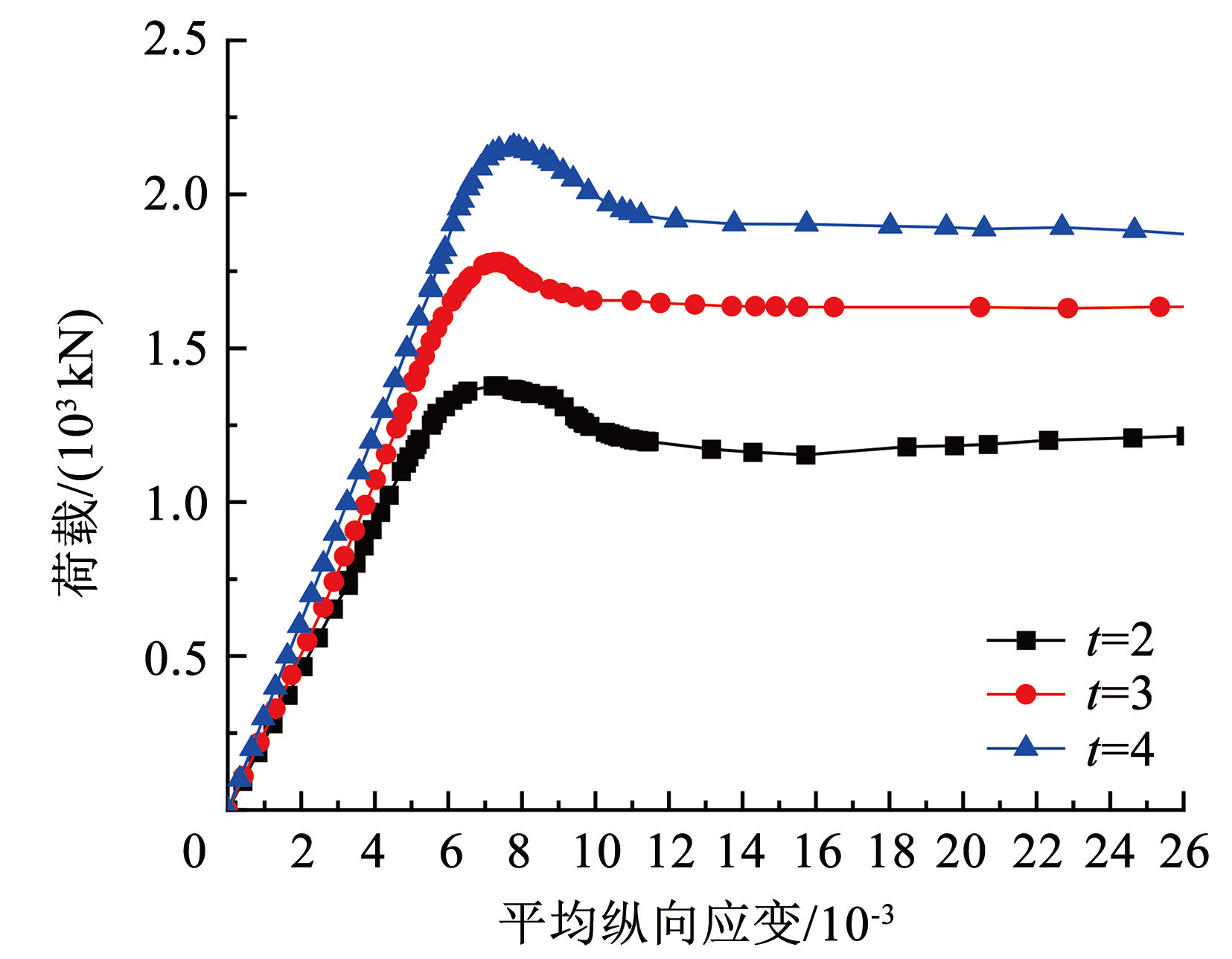
图8不同钢管厚度时的荷载-平均纵向应变曲线
Fig.8Load-longitudinal mean strain curves of different steel tube thicknesses
表3不同钢管厚度试件的刚度、承载力和延性系数计算结果
Tab.3 Stiffness, bearing capacity and ductility coefficient of steel tube with different thickness

注:EA 为理论压缩刚度,EA = EcAc + EsAs; EscAsc为实际压缩刚度,EscAsc = 0.4Nu / ; Nu为名义承载力,Nu = f yAs + f ckAc; Nue为实测承载力,承载力提高系数 δ =(Nue-Nu)/ Nu; μ 为延性系数,μ = ε0.85u / εy,其中 ε0.85u和 εy分别为试件荷载下降到极限荷载 85% 时的应变和屈服应变。
2.3.2 U 形管外伸长度
CFST-L2、L4、L5 为不同 U 形管外伸长度(b =100、 150、200 mm)的 L 形冷弯薄壁型钢组合钢管混凝土柱。结合图9和表4可知:达到极限承载力前 3 条曲线的趋势基本一致,且构件随着 U 形管外伸长度的增大,理论压缩刚度和实际压缩刚度都增大。 L4 极限承载力( 2 514.43 kN)比 L2 极限承载力(1 779.61 kN)增大了约 41.29%,L5 极限承载力(2 280.76 kN)比 L4 极限承载力(2 514.43 kN)反而减少了约 9.29%,这表明 L 形冷弯薄壁型钢组合钢管混凝土柱的极限承载力随着 U 形管外伸长度的增大而增大,但是增大到一定程度之后,其极限承载力反而会减少。三者的破坏形态除了偏压导致弯扭破坏的 L5a 以外几乎一样,都是中上部局部鼓曲破坏,表明偏压会导致试件的破坏形态发生从局部鼓曲破坏向弯扭破坏的转变,原因是 U 形管长度增加后,约束效果降低,U 形管部分先于中间的方钢管屈曲,且肢件屈曲后容易导致荷载偏压,进一步加剧破坏,最终导致构件的承载力反降不增进入塑性破坏阶段。 CFST-L2、L4、L5 曲线分别下降至极限荷载的 90.45%、76.61%、70.26% 后再趋于平缓,这表明随着 U 形管外伸长度的增大,钢管对混凝土总体的约束效果降低,L 形冷弯薄壁型钢组合钢管混凝土柱的延性也降低。

图9不同 U 形管外伸长度时的荷载-平均纵向应变曲线
Fig.9Load-longitudinal mean strain curves of different U-tube extension lengths
表4不同 U 形管外伸长度试件的刚度、承载力和延性系数计算结果
Tab.4 Stiffness, bearing capacity and ductility coefficient of specimens with different extended lengths of U-shaped pipes

3 有限元分析
3.1 钢材与混凝土的本构模型
1)钢材的本构模型
钢材的本构模型采用 ABAQUS 软件提供的塑性分析模型,其应力-应变关系使用二次塑流模型[13],数学表达式见式(1),钢材相关数据按钢材材性试验取值。
(1)
式中:f y为钢材屈服强度,Es为钢材弹性模量,εe为比例极限对应的应变值,εe1 为屈服强度对应的应变值,εe2为屈服段结束时对应的应变值,εe3为极限强度对应的应变值。
2)混凝土的本构模型
(2a)
(2b)
式中 f′c = 0.79f cu,k为混凝土圆柱体抗压强度,其他参数的具体含义及取值参照文献[13]。
3.2 有限元模型的建立
1)单元选取及网格划分
混凝土与盖板采用八节点减缩积分格式的三维实体单元(C3D8R)模拟,异形钢管采用壳体单元(S4R)模拟。混凝土和盖板的网格大小为 20 mm,钢管的网格大小为 25 mm。
2)边界条件及加载方式
钢管与混凝土之间的相互作用采用面-面接触,法向接触属性设置为“硬” 接触; 切向接触属性设置为“罚”接触,摩擦系数取 0.25。钢管与上、下端盖板对应面采用壳-实体耦合约束,混凝土与上、下端盖板对应面之间的约束类型均采用绑定( tie)约束。模型下端采用固端约束,上端仅释放 Z 轴方向的平动自由度,采用位移加载。
3.3 有限元模型验证
CFST-L2 的试验结果和对应有限元模型破坏对比见图10,两者的破坏形态非常相似,主要是中部和上部的局部鼓曲破坏,并呈现出上下对称的破坏形式。有限元计算的荷载-平均纵向应变曲线与部分试验实测的荷载-平均纵向应变曲线对比见图11,有限元计算曲线和试验曲线的吻合程度较好,说明数值模型可以较好地模拟 L 形冷弯薄壁型钢组合钢管混凝土柱的力学行为。
3.4 应力分析
3.4.1 核心混凝土截面应力
图12为有限元模拟的 L 形冷弯薄壁型钢组合钢管混凝土柱的核心混凝土端部截面和中部截面在极限荷载状态下的纵向应力云图。分析可知,除了 U 形管外伸长度为 200 mm 的 CFST-L5 以外,其余试件的核心混凝土端部截面和中部截面的纵向应力云图均沿截面对称轴对称分布,此分布形式和试件试验破坏形态大致沿截面对称分布一致; 端部的混凝土应力值总体上大于中部的混凝土应力值,这与试验过程中总是在端部先发生局部鼓曲破坏相吻合; 不管是在中部截面还是端部截面,U 形管和方钢管的角部处混凝土的应力值最大,且应力值超过了混凝土的立方体抗压强度 f cu ,表明此处钢管对混凝土的约束效应明显,钢管对混凝土约束效果的提升,提高了试件整体的承载能力。
观察试件端部和中部截面阴角处的混凝土应力值,可以发现此处的混凝土应力值比各边中部更大,尤其是方钢管内的混凝土应力值较其他区域更大,说明采用这种 L 形冷弯薄壁型钢组合钢管混凝土柱中的钢管对阴角处的核心混凝土具有较好的约束效果,改善了阴角处钢管对混凝土约束普遍较弱的问题。

图10试验破坏形态与模拟结果对比
Fig.10Comparison of failure modes between simulation and test results

图11试验荷载-平均纵向应变曲线与有限元模拟结果对比
Fig.11Comparison of load-longitudinal mean strain curve between FEM simulation and test
3.4.2 钢管应力
图13为极限荷载时 L 形冷弯薄壁型钢组合钢管混凝土柱钢管壁的 Von-Mises 应力云图。在达到极限荷载时,方钢管和 U 形管都已经达到了屈服荷载; CFST-L1、L2、L3 钢管上的应力主要集中在中部以及中部上下 200 mm 范围内,应力也是沿着对称轴对称分布,且 U 形管的侧面端部位置和方钢管的中部位置应力最大。此外,随着钢管厚度的增大,钢管上的应力分布逐渐从端部向中部转移,且应力分布更加均匀,这些结果和试件在试验过程中发生局部鼓曲的区域,以及呈现出的对称破坏的形式等试验结果是一致的。从图13( d)和( e)可以看出,在达到试件的极限荷载时,CFST-L4、L5 钢管上的应力主要集中在中上部,构件方钢管和 U 形管的上半部分已经达到了屈服荷载,但构件的下部并没有达到钢材的屈服荷载,并且当 U 形管外伸长度增大时,钢管上的应力逐渐从均匀分布向上端转移,且应力分布更加集中,这和试验过程中出现的 U 形管上端局部鼓曲破坏相对应; 当 U 形管外伸长度为200 mm 时,两个 U 形管上的应力并非是对称的,而是集中在一边的 U 形管上,这也和试验过程中出现的单个 U 形管先发生弯扭破坏的试验现象吻合。
3.5 承载力影响因素拓展分析
基于以上有限元模型,进一步分析钢材强度和混凝土强度变化对结构承载力的影响,将承载力计算值与名义承载力的比值作为纵坐标,作无量纲化处理,即 NFE / Nu,位移为横坐标。
1)钢材强度
图14为 L 形冷弯薄壁型钢组合钢管混凝土柱在钢板厚度、外伸长度及混凝土强度固定的情况下,不同钢材屈服强度下的 NFE / Nu-位移曲线,由图14可知,随着钢材强度的增加,曲线的初始刚度变化不大,承载力提高系数和曲线下降段的承载力均逐渐增大,但承载力提升的幅度逐渐减小。
2)混凝土强度
图15给出了钢板厚度、外伸长度及钢材强度固定情况下,3 种不同混凝土强度等级下的 NFE / Nu-位移曲线。由图15可知,混凝土强度对构件的初始刚度和极限承载力的影响都很小,但曲线下降段承载力的变化与混凝土的强度成反比。
图12核心混凝土截面纵向应力分布
Fig.12Longitudinal stress distribution of core concrete section
图13钢管应力分布
Fig.13Stress distribution of steel pipe

图14不同钢材屈服强度的影响
Fig.14Effect of different yield strength of steel
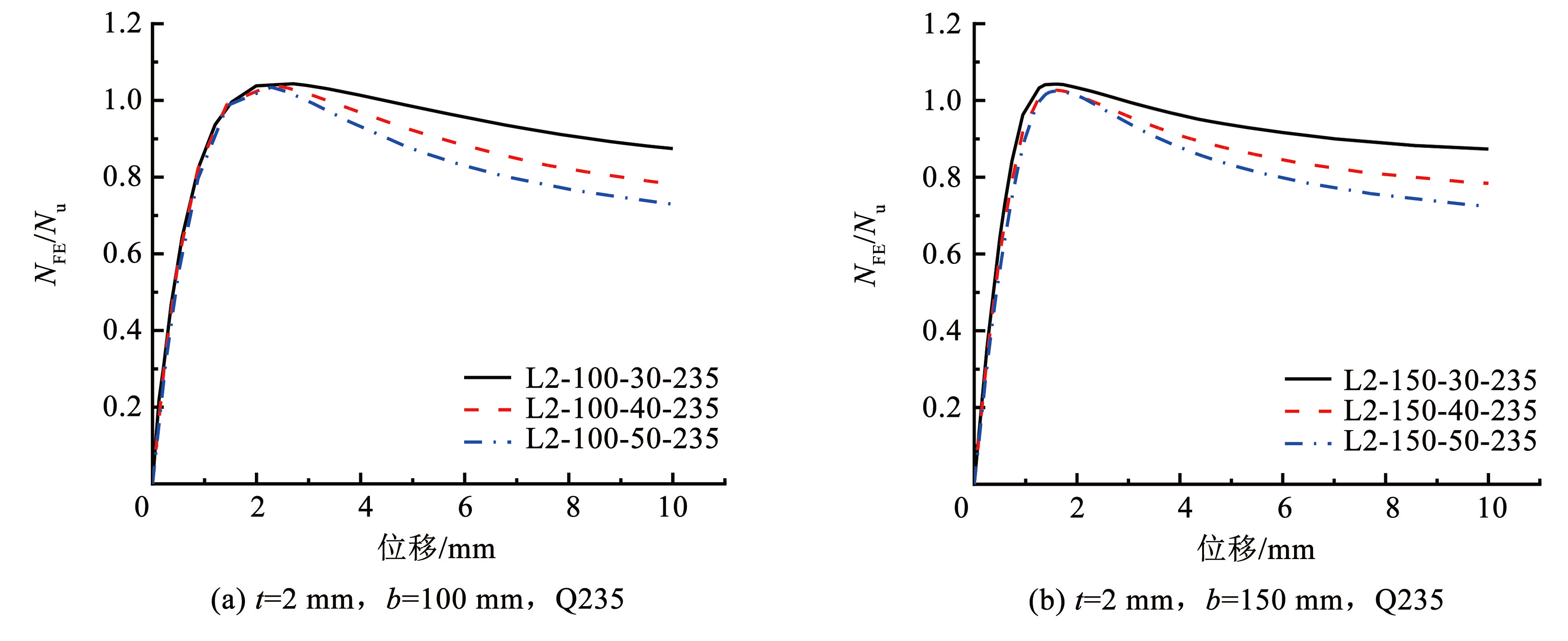
图15不同混凝土强度的影响
Fig.15Effect of different concrete strength
4 承载力计算方法
4.1 现有承载力计算方法对比
目前国内外关于钢管混凝土轴压承载力计算理论最常见的有拟混凝土理论、拟钢理论、叠加理论和统一理论等。针对这些理论对应规范标准不同:拟混凝土理论对应美国混凝土协会规范 ACI 318-19 [14] 和欧洲规范 EC 4 [15]; 拟钢理论对应美国钢结构协会规范 AISC-LRFD [16]和英国设计规程 BS 5400 [17]; 叠加理论对应日本规程 AIJ [18]和矩形钢管混凝土结构设计规范 CECS 159—2004 [19]; 统一理论对应钢管混凝土结构技术规范 GB 50936—2014 [20] 和实心与空心钢管混凝土结构技术规程 CECS 254— 2012 [21]。将第 2 节中 5 种截面形式的 10 个短柱试件的数据分别代入上述规范公式中计算,以实测承载力 Nue为横坐标,以各规范计算承载力与实测承载力之比为纵坐标,对结果进行对比,见图16。
如图16所示,与实际承载力最接近的为采用统一理论的规范 GB 50936—2014 和规程 CECS 254— 2012,两者的相对误差基本保持在 ± 6%; 其次是采用叠加理论的规范 AIJ 和 CECS 159—2004,与试验实测承载力的相对误差保持在-6%~-16% 之间; 与试验实测承载力差距最大的是采用拟混凝土理论的美国规范 ACI 318-19 和拟钢理论的英国规程 BS 5400,计算结果偏于保守。现行国内外规范中的钢管混凝土计算公式对于 L 形冷弯薄壁型钢组合钢管混凝土柱的轴压承载力计算结果普遍偏于保守,这是因为大部分承载力计算公式都有折减,其次除了统一理论考虑了钢管对混凝土的约束效应外,其他三种理论都没有考虑约束效应对钢管混凝土承载力的提高作用。
图16各规范计算承载力与实测承载力的对比
Fig.16Comparison of calculated bearing capacity of various specification and test results
4.2 基于“统一理论”的简化计算方法
从 4.1 节实测值与国内外钢管混凝土承载力计算公式计算结果对比可知,采用统一理论的计算方法结果与实测承载力较为接近,这是因为统一理论中考虑了约束效应。约束效应系数 ξ 可以综合反应钢材屈服强度、混凝土强度、钢管厚度和 U 形管外伸长度等因素的影响。统一理论的轴心受压组合强度指标就是通过约束效应系数 ξ 来体现钢管混凝土组合效应对轴压强度的提高,以下提出两种简化计算方法。
4.2.1 简化计算方法一
参考文献[22],将 L 形冷弯薄壁型钢组合钢管混凝土柱拆分为 3 个部分,其中 U 形钢管的开口侧添加上一个厚度与 U 形钢管一致的假想钢板,这样两个 U 形管就变成了两个截面大小为 a ×(b + t)的矩形钢管,见图17。
在推导 L 形冷弯薄壁型钢组合钢管混凝土柱的组合强度时,先采用统一理论分别计算方钢管和 2 个矩形钢管混凝土的承载力,将三部分承载力之和减去假想钢板部分的承载力后再除以总面积,就得到了 L 形冷弯薄壁型钢组合钢管混凝土柱的组合强度,具体计算推导过程如下:

图17截面拆分图
Fig.17Split view of section
(3)
(4)
(5)
(6)
将式(4)~(6)带入式(3)简化后得到
(7)
其中:
(8)
(9)
(10)
(11)
(12)
(13)
最终承载力计算公式同统一理论:
(14)
式中:f′sc为 L 形冷弯薄壁型钢组合钢管混凝土柱组合强度标准值,Asc为钢管混凝土横截面总面积,f sc,R 和 f sc,U分别为拆分的方钢管混凝土部分和加理想钢板后 U 形钢管混凝土部分的组合强度标准值,ξR和 ξU分别为拆分的方钢管混凝土部分和加理想钢板后 U 形钢管混凝土部分的约束效应系数,AR和 AU分别为拆分的方钢管混凝土部分和加理想钢板后 U 形钢管混凝土部分的面积,As,R和 Ac,R以及 As,U和 Ac,U 分别为拆分的方钢管混凝土部分和加理想钢板后 U 形钢管混凝土部分的钢管和混凝土面积,B 和 C 为方形截面形状对套箍效应的影响系数。
4.2.2 简化计算方法二
CFST-L5 由于 U 形管外伸长度(200 mm)过大,在试验过程中总是发生偏压破坏,导致其极限承载力相较破坏形式为轴压破坏的截面类型要降低 30% 左右,故单独采用规范 ACI 318-19 给出的公式计算:
(15)
式中:ϕ 为稳定系数,取 ϕ = 1; f′c 为混凝土圆柱体抗压强度,f′c = 0.79f cu; Ag 为钢管混凝土总截面面积,Ast为钢管截面面积。
规范 GB 50936—2014 和规程 CECS 254—2012 的钢管混凝土轴压承载力计算公式仅适用于截面形式为圆形、正方形和正八边形的钢管混凝土柱,故计算 L 形冷弯薄壁型钢组合钢管混凝土柱(L1~L4)的承载力时,需要先将 L 形截面拆分等效为正方形截面,然后再进行计算。综上,承载力计算公式:
(16)
(17)
(18)
(19)
式中:f sc为组合强度设计值,f 为钢材的抗压强度设计值,Asc为钢管混凝土横截面总面积,B、C 取值同式(12)和式(13)。
4.3 简化计算公式的验证和适用范围
4.3.1 简化公式验证
目前,国内外对异形钢管混凝土柱轴压承载力计算方法的研究尚不成熟,文献[23] 基于叠加理论,提出式(20)计算带缀材的 L 形方钢管混凝土组合异形短柱轴压承载力; 文献[24]提出式(21)计算内置钢骨的组合 L 形钢管混凝土柱轴压承载力; 文献[25]基于统一理论,提出式(22)计算普通 L 形钢管混凝土短柱轴压承载力; 文献[26] 基于统一理论,提出式(23)计算改进的焊接组合式 L 形钢管混凝土短柱轴压承载力。
(20)
式中:f s 和 f c 分别为钢材和混凝土的抗压强度设计值,As和 Ac为钢管和核心混凝土截面面积。
(21)
式中:k 为约束效应系数; θ 为套箍指标; ζ 为钢骨加劲系数,对于未配置钢骨的 L 形截面钢管混凝土柱,ζ = 0。
(22a)
(22b)
式中:f scy为混凝土等效轴压强度,ξ 为约束效应系数,f ck为混凝土抗压强度。
(23)
式中:α 为轴压承载力可靠度修正系数,取 α =0.99; αc 为混凝土脆性折减系数,C40 及以下取 αc = 1. 0,C50 取 αc = 0.9; αs 为钢管局部屈曲影响系数,5 mm 以下取 αs = 0.85,5 mm 及以上取 αs = 1. 0。
将本文试验设计的 4 种试件截面参数分别代入式(20)~(23)、(14)得到计算结果 Nui( i = 1~5),并与试验结果 Nue进行对比,见表5。由表5可知,采用式(20)~(23)计算的各构件承载力平均值与试验值之比分别为0.531、0.664、0.806 和0.475,这 4 个公式的计算结果与本文实测结果相差较大,主要由于文献[23-26]各自研究的 L 形钢管混凝土短柱截面形式与本文提出的 L 形冷弯薄壁型钢组合钢管混凝土短柱截面形式存在一定差别,而式(14)计算的结果 Nu5与 Nue之比为 0.954,两者吻合较好,表明式(14)更适合本文提出的 L 形冷弯薄壁型钢组合钢管混凝土短柱轴压承载力的计算。
表5轴压承载力公式计算结果
Tab.5 Calculation results of axial compression bearing capacity formula

4.3.2 公式的适用范围
图18给出了采用本文设计的 54 个有限元模型计算 L 形冷弯薄壁型钢组合钢管混凝土柱的约束效应系数分布范围(0.44~1.94)对式(14)、(16)的适用情况。结果表明,采用式(14)计算的 Nu / Nue的平均值为 0.969,标准差为 0. 037; 采用式(16)计算的 Nu / Nue的平均值为 1. 024,标准差为 0. 041。两式计算结果相对误差均位于-10%~10%,证明两者在 0.44~1.94 的约束效应系数范围内都有良好的适用性,且式(14)更适合。
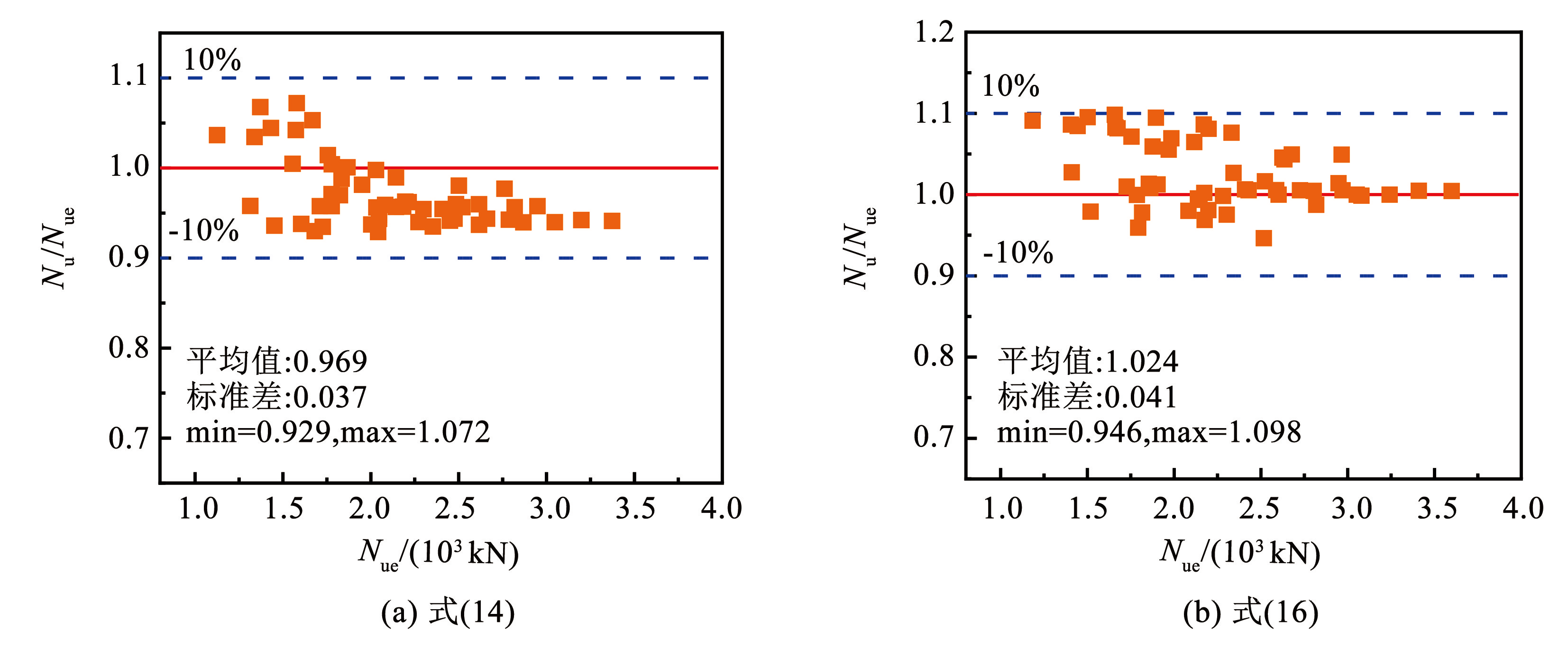
图18约束系数适用范围验证
Fig.18Verification of application of constraint coefficient
5 结论
1)试件的主要破坏形态为中上部局部鼓曲破坏,且沿截面的对称轴呈现出对称的局部鼓曲和变形; 当钢管厚度增大到 4 mm 时,易在 U 形管处发生钢材的拉裂破坏; 当 U 形管外伸长度增大到200 mm 时,易在 U 形管处发生局部弯扭破坏。
2)在试验过程中 L 形冷弯薄壁型钢组合柱的钢管壁始终处于纵向受压、横向受拉,且主要为纵向承压的状态; 同一位置的横、纵应变片的荷载-应变曲线走势呈现出对称趋势; 随着 U 形管外伸长度的增大,U 形管纵向应变会出现受拉向受压转变的偏压情况。
3)L 形冷弯薄壁型钢组合柱的理论刚度、实测刚度、极限承载力和延性等都随着钢管厚度的增大而增大,如钢管壁厚 3 mm 试件比 2 mm 试件的极限承载力提升约 22.54%,4 mm 试件比 3 mm 试件提高了约 17.45%,前者的提高幅度更大。试件的理论刚度和实测刚度随 U 形管外伸长度的增大而增大; 延性系数随着 U 形管外伸长度的增大而减小。试件的极限承载力随着 U 形管外伸长度的增大而增大,但增大到一定程度时由于弯扭破坏,其极限承载力反而会减少,如 L4 比 L2 的极限承载力增大了约41.29%,L5 比 L4 的承载力反而减少了约9.29%。
4)试件端部混凝土应力值总体上高于中部,且 U 形管和方钢管的角部混凝土应力值最大,超过了其抗压强度 f cu,钢管对混凝土的约束效应明显; 试件端部和中部截面阴角处的混凝土应力值比各边中部更大,这说明采用 U 形钢管与方钢管组合的方式改善了阴角处钢管对混凝土约束普遍较弱的问题。
5)数值分析结果表明,随着钢材强度的增加,峰值荷载和曲线下降段的承载力均逐渐增大,但提高幅度逐渐减小。混凝土强度对构件的初始刚度和极限承载力的影响都很小,但曲线下降段的承载力与混凝土的强度成反比。
6)本文基于“统一理论”给出两种 L 型冷弯薄壁型钢组合钢管混凝土柱轴压承载力的简化计算方法,计算结果与试验吻合较好,两种计算方法在 0.44~1.94的约束效应系数范围内有良好的适用性。




