摘要
为研究新型装配式剪力墙的抗震性能及其变形指标限值,基于课题组所做新型装配式剪力墙抗震性能试验,采用析因法,共设计 216 个不同剪跨比、轴压比、边缘构件纵筋配筋率等新型装配式剪力墙模型,完成相应的单推性能研究;基于有限元破坏形态识别,将构件破坏形态划分为弯曲破坏、弯剪破坏和剪切破坏 3 类,提出墙体破坏形态划分准则。参考GB 50011— 2010《建筑抗震设计规范》,对弯曲破坏和弯剪破坏划分 6 个性能状态,对剪切破坏划分两个性能状态,基于构件极限状态下混凝土、钢筋应变和承载力,确定墙体性能状态判定准则。通过线性回归分别得到弯曲破坏、弯剪破坏和剪切破坏形态下构件各塑性位移角限值的回归方程,并提出各破坏形态下具有 90% 保证率的构件变形指标限值标准,为基于性能的新型装配式剪力墙抗震设计提供参考。
Abstract
In order to study the seismic performance and deformation index limits of a new assembled shear wall, based on the seismic performance test of the new assembled shear wall made by the research group, a total of 216 wall models with different shear span ratio, axial compression ratios and longitudinal reinforcement ratios of edge members were designed using factor analysis method. The corresponding single push performance experiment was performed to investigate the structrual behavior. Based on the recognition of failure modes using finite element analysis, the failure modes were divided into three categories: bending failure, bending shear failure and shear failure. A criterion for classifying the failure modes of the shear wall was put forward. Referring to " Code for seismic design of buildings" ( GB 50011—2010), six performance states were defined for flexural failure and flexural-shear failure, while two performance states were defined for shear failure. Based on the strain and bearing capacity of concrete and steel bars under the limit state of the component, the criterion of the performance state of the wall was determined. Finally, regression equations were derived through linear regression to determine the limit values of plastic displacement angles for componments under bending failure, bending shear failure and shear failure modes. Furthermore, deformation index limites with 90% guarantee rate were proposed for each failure mode, providing a reference for performance-based seismic design of new assembled shear walls.
现阶段装配式结构获得了较大的发展,尤其是各类新型装配式结构层出不穷。 Wu 等[1] 设计了局部现浇的预制双肢剪力墙试件并开展了拟静力试验,预制墙体表现出更好的变形能力; Jiang 等[2] 提出了一种螺栓连接装配式剪力墙的新形式,以提高装配式剪力墙的施工效率和结构完整性; 陈彬彬等[3]设计了不同参数的 T 形 RC 剪力墙试件,研究了 T 形钢筋混凝土(RC)剪力墙的抗震性能及其变形指标限值。季静等[4] 以剪跨比和弯剪比为参数确定了构件破坏形态的判断标准。目前,针对新型装配式结构的研究更多地集中在节点连接技术上,而对于相应基于性能的设计方法有待深入和扩展。本文提出了一种新型装配式剪力墙结构,该结构采用箱型钢表面预焊锚固短筋,并将其与上部墙体内纵筋端部焊接连接,再整体浇筑混凝土,最后通过 U 型钢和螺栓连接装配; 剪力墙受到水平荷载时,内外型钢发生相对转动,实现荷载传递与摩擦耗能功能,构造设计见图1。基于其抗震性能试验及有限元模拟方法[5-7],共设计了 216 个不同剪跨比、轴压比、边缘构件纵筋配筋率等的墙体模型; 采用有限元破坏形态识别,划分构件破坏形态,提出相应的破坏形态划分准则。最后,通过线性回归分别得到弯曲破坏、弯剪破坏和剪切破坏形态下构件各塑性位移角限值的回归方程,并提出了各破坏形态下具有 90% 保证率的构件变形指标限值标准。
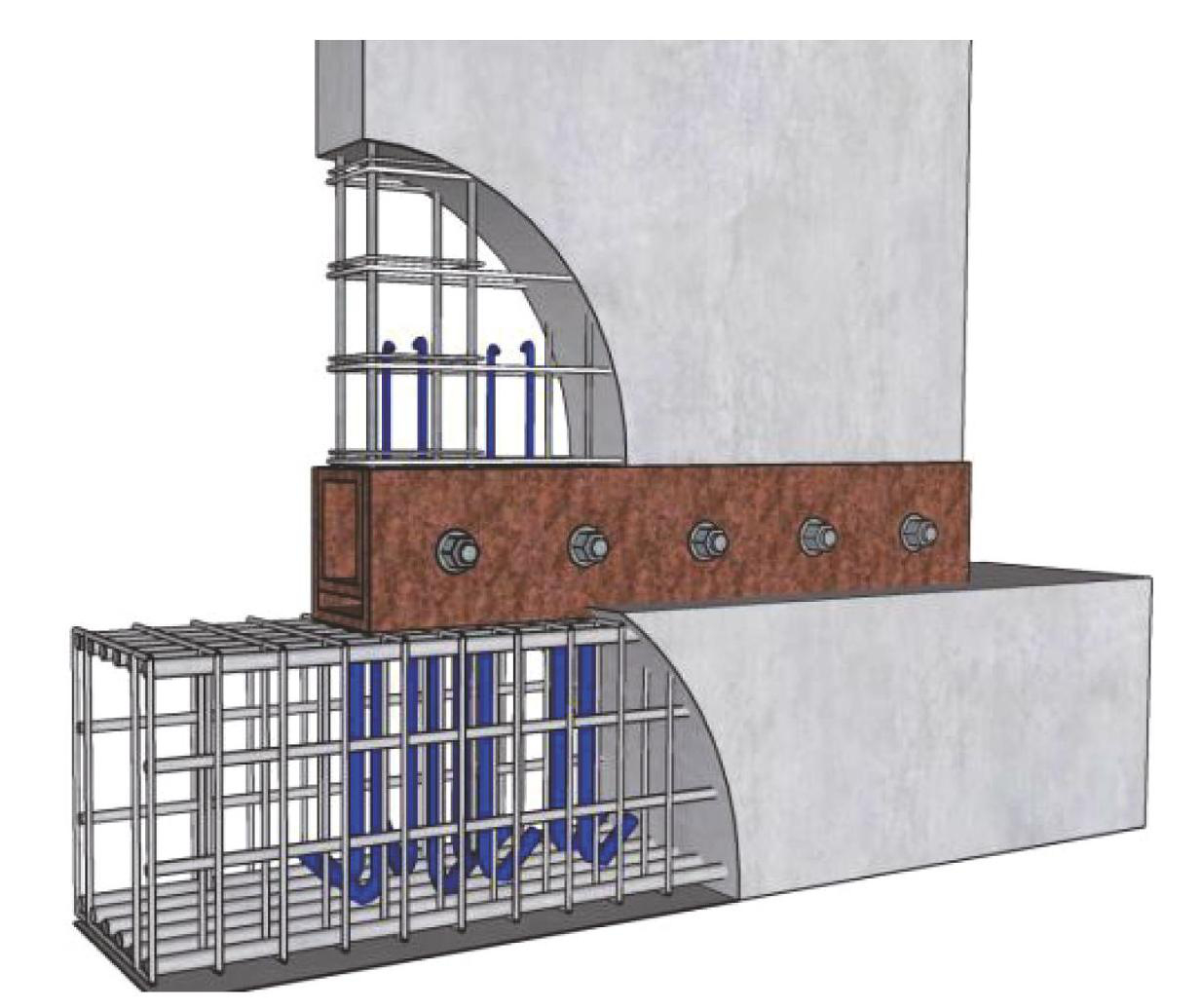
图1新型装配式剪力墙构造
Fig.1Structural design of new prefabricated shear wall
1 新型装配式剪力墙破坏形态划分
1.1 有限元模型及参数设置
基于课题组相关试验及有限元模拟分析[5-7],采用析因法,以剪力墙的剪跨比 λ、设计轴压比 ud、边缘构件纵筋配筋率 ρsv、边缘构件配箍特征值 λv、水平分布筋配筋率 ρsh和弯剪比 m 为参数,共设计了 216(4 × 3 × 3 × 3 × 2)个新型装配剪力墙结构模型,具体参数如表1所示。
表1模型设计参数
Tab.1 Model design parameters
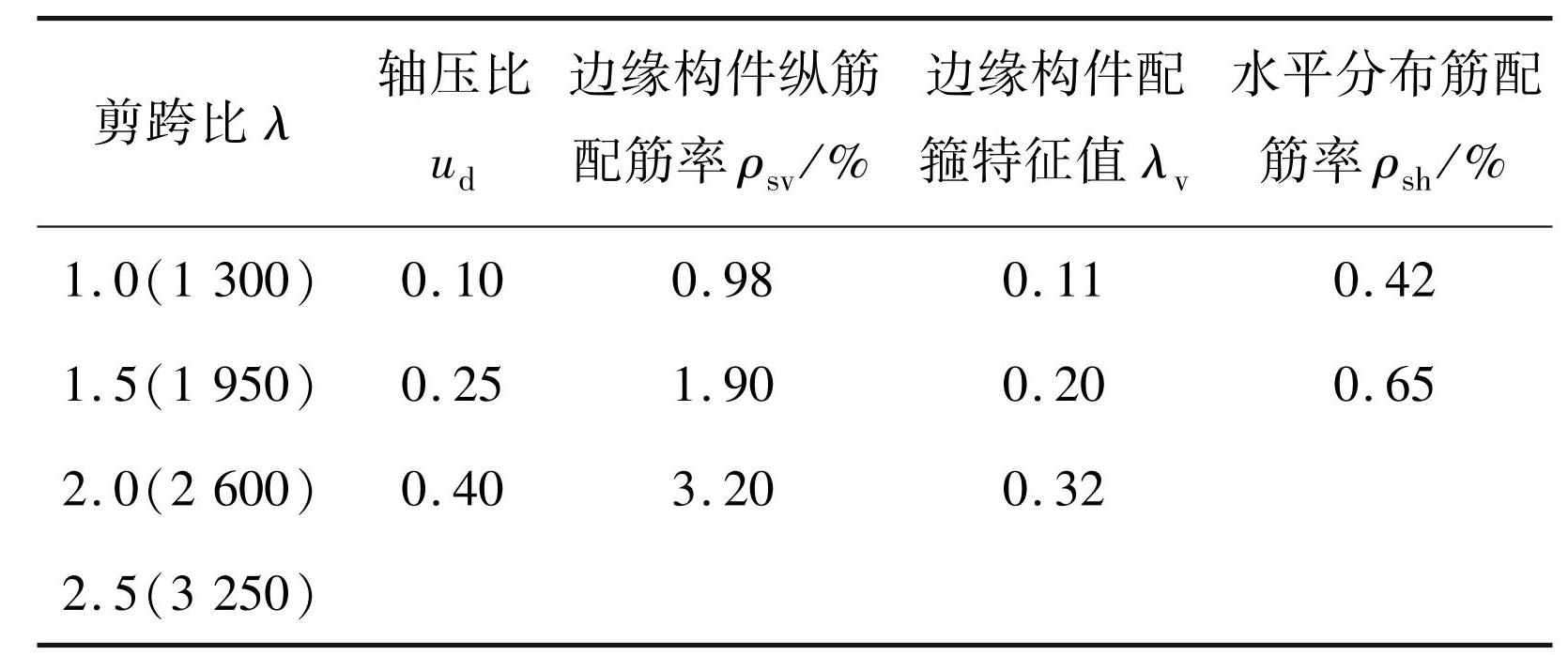
注:括号里是相应剪跨比下对应的墙高,单位 mm; 空白表示无此项。
采用 ABAQUS 建立新型装配式剪力墙实体模型。除墙体内部钢筋采用 T3D2 单元以外,其余实体部件均采用 C3D8R 单元。混凝土本构塑性损伤模型,根据试验实测数据输入参数:弹性模量取 30.8 GPa,泊松比取 0.2,膨胀角取 37°,黏性参数取 0. 000 5,偏心率取 0.1,双轴抗压强度与单轴抗压强度比值取 1.16,屈服形态影响参数取 0.666 7。剪力墙构件的墙体配筋、高强螺栓、钢垫片、箱型钢和 U 型槽钢均采用双折线模型,钢材屈服强度和抗拉强度依据试验实测确定。典型模型网格划分如图2所示。对其进行单调位移加载控制(见图3),所得的模拟曲线与试验荷载–位移曲线总体吻合良好,能够反映出新型装配式剪力墙的摩擦滑移特征和变形特点,如图4。将其试验破坏形态与有限元云图结果进行对比,如图5所示,建立的有限元模型可以有效地模拟新型装配式剪力墙的受力状态和破坏形态,从而验证了采用 ABAQUS 模拟的可靠性。

图2典型模型网格划分示意
Fig.2Typical model grid division diagram
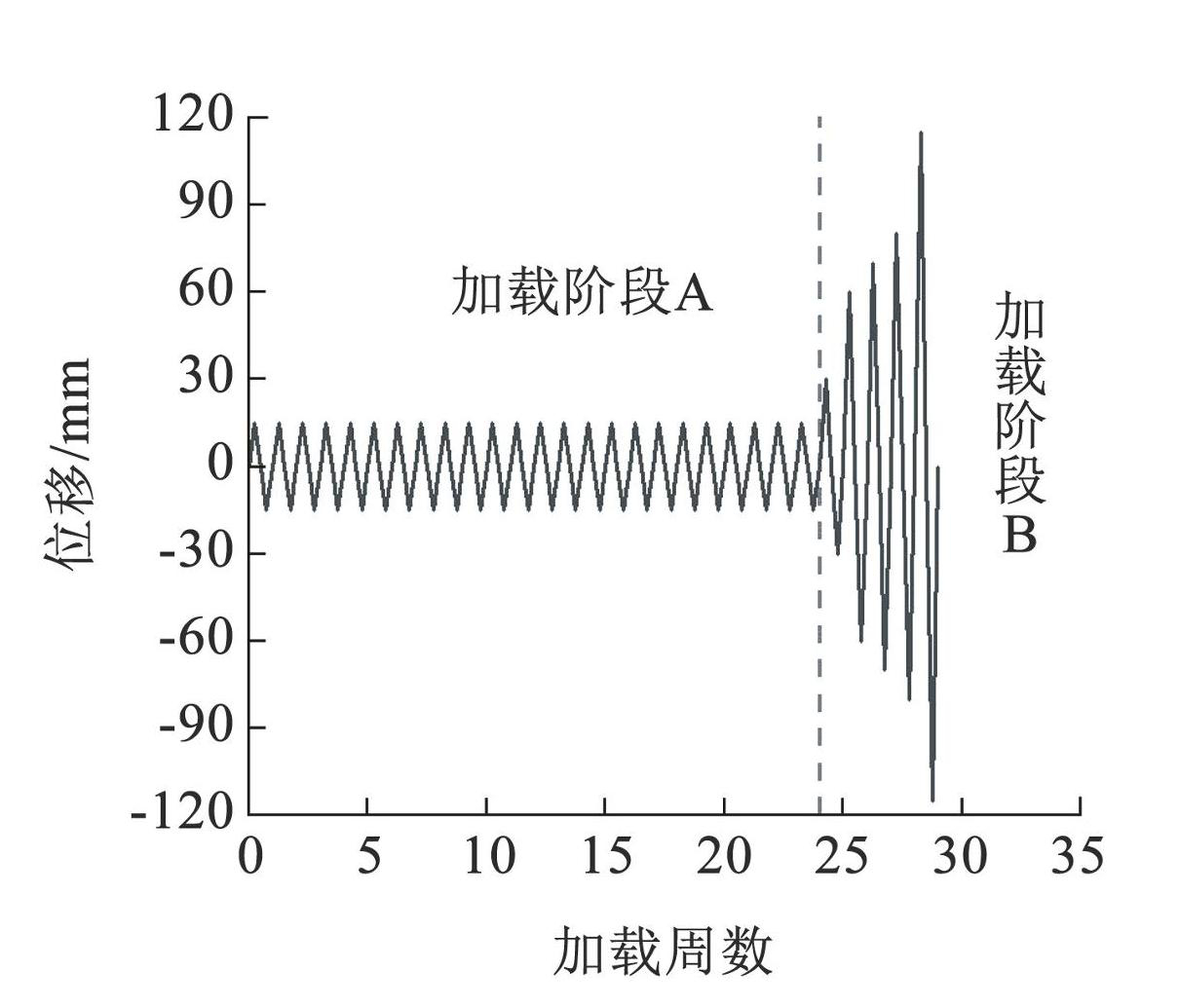
图3加载制度
Fig.3Loading history
1.2 破坏形态划分准则
轴压比、边缘构件纵筋配筋率、配箍特征值和水平分布筋配筋率对于剪力墙构件的破坏形态产生一定影响,但总体上遵循仅考虑剪跨比单一参数时的影响规律,且在某些特定剪跨比下,这 4 项参数对构件破坏形态的占比与仅考虑剪跨比单一参数时占比相差不大。此外,弯剪比对构件最终破坏形态的影响规律呈现一定独立性,也在一定程度上反映了构件的配筋形式。因此,选择剪跨比和弯剪比作为划分新型装配式剪力墙破坏形态的参数较为合理。
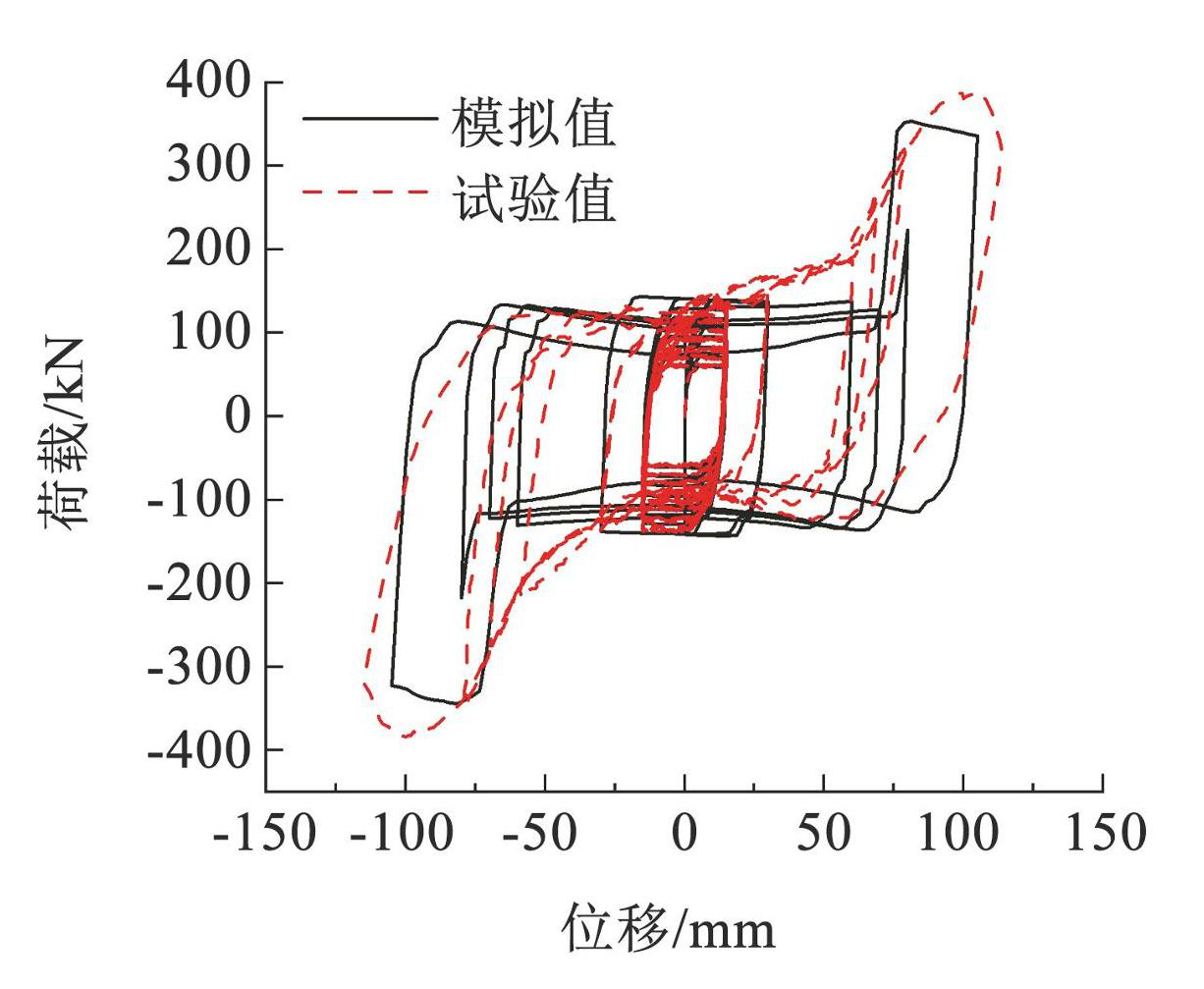
图4荷载-位移曲线对比
Fig.4Comparison of load-displacement curves

图5试验破坏形态与有限元云图对比
Fig.5Comparison of test failure mode and finite element cloud diagram
确定新型装配式剪力墙的弯剪比划分界限时,采用以破坏形态集中分布区间为基础,相邻破坏形态间以偏向构件受弯曲控制破坏为调整的划分方案。弯剪比 m 反映构件计算截面上抗弯承载力与抗剪承载力之间的相对关系,是判断构件破坏形态的重要指标[4],定义如下:
(1)
式中:Mu为根据实际配筋计算的截面抗弯承载力,Vu为根据实际配筋计算的截面抗剪承载力,L 为水平集中荷载至剪力墙底部的距离。
弯剪比数据均由式(1)计算得到,构件弯剪比参数分布情况如图6所示。
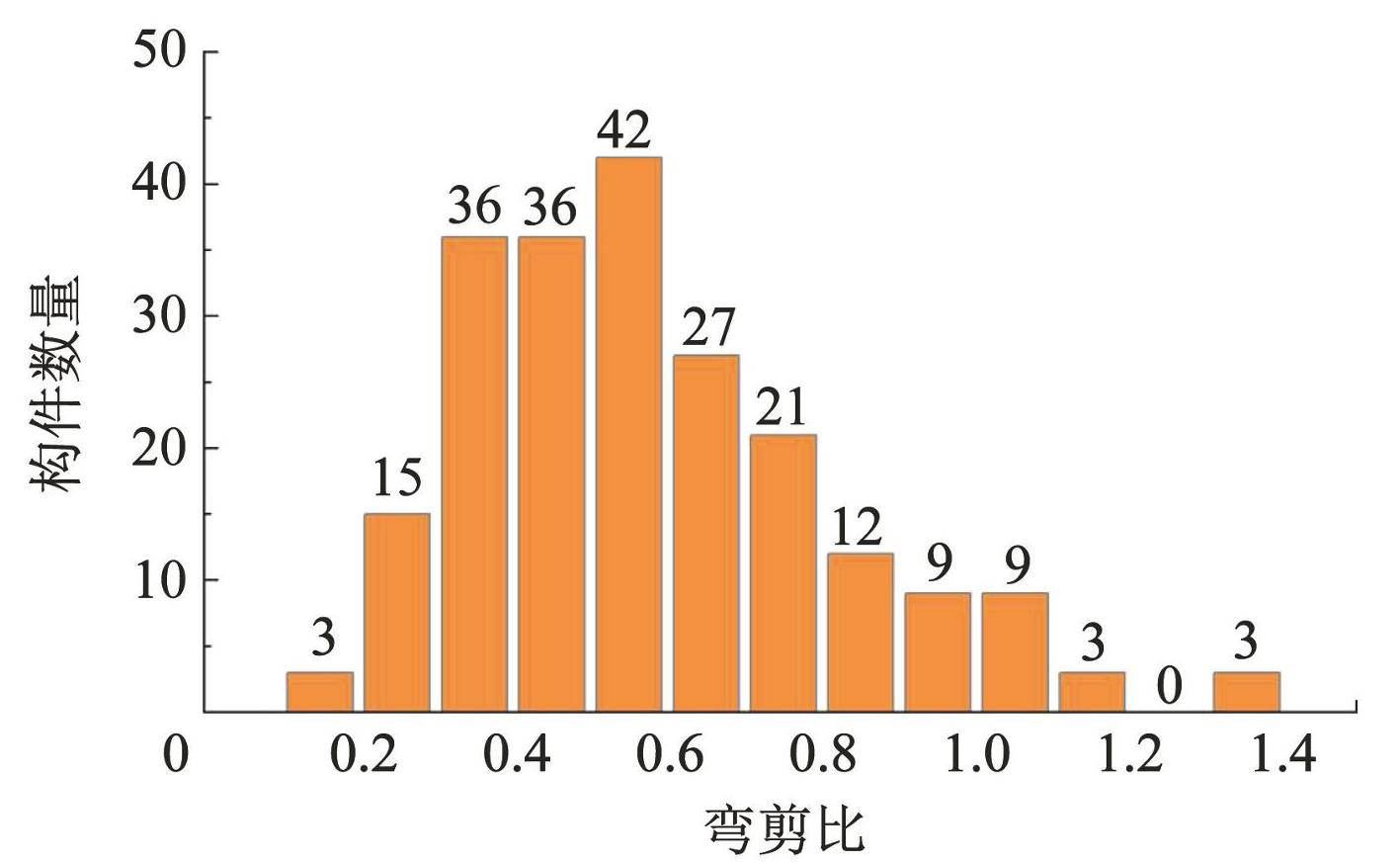
图6各弯剪比区间构件数量分布
Fig.6Quantity distribution of components in each flexural shear ratio interval
选取弯剪比限值的两个原则:1)当存在明确破坏形态界限时,弯剪比限值主要依据构件破坏形态的界限确定。 2)当不存在明确破坏形态界限时,从偏向结构或构件安全的角度确定弯剪比限值,将其偏向于受弯曲控制的破坏形态,即在弯曲破坏和弯剪破坏之间取值偏向于弯曲破坏,在弯剪破坏和剪切破坏之间的取值偏向于弯剪破坏。在不同剪跨比下,新型装配式剪力墙构件破坏形态累计数量随弯剪比变化曲线如图7所示,取 F(弯曲破坏)、FS(弯剪破坏)和 S(剪切破坏)。
如图7(a)所示,当剪跨比为 1. 0 时,构件基本只发生剪切破坏,从构件安全角度考虑,认为剪跨比为 1. 0 的剪力墙构件全部发生剪切破坏。
如图7(b)所示,当剪跨比为 1.5 时,弯剪破坏的集中分布区间为[0.35,0.55],剪切破坏的集中分布区间为[0.55,0.85],弯剪破坏和剪切破坏之间有明确界限,该弯剪比限值 m1.5,FS-S = 0.55。
如图7(c)所示,当剪跨比为 2. 0 时,弯曲破坏的集中分布区间为[0.25,0.50],弯剪破坏的集中分布区间为[0.45,0.60],剪切破坏和集中分布区间为[0.65,0.80]。根据两相邻破坏形态间的弯剪比限值取平均值的方法[8],式(2)、(3)分别为计算得到的弯曲破坏和弯剪破坏之间、弯剪破坏和剪切破坏之间的初始弯剪比限值:
(2)
(3)
分析发现,弯剪比在区间[0.45,m2.0,F-FS ]内发生弯曲破坏构件的累计数量不变,而发生弯剪破坏的构件累计数量呈增多趋势,偏向构件安全考虑,取 m2.0,F-FS = 0.45。弯剪比为[0.60,0.65] 区间内发生弯剪破坏和剪切破坏的累计数量均呈增多趋势,考虑到发生弯剪破坏构件的累计数量在弯剪比为 0.65 时达到峰值,且弯剪比为 0.60 时剪切破坏构件累计数量为 0,取 m2.0,FS-S = 0.65。
如图7(d)所示,当剪跨比为 2.5 时,构件仅发生弯曲破坏和弯剪破坏,两者的集中分布区间分别为[0.25,0.65]和[0.60,0.65]。划分弯剪破坏和弯曲破坏的初始弯剪比限值由式(4)计算得
(4)
弯剪比在区间[0.6,0.65] 内发生弯曲破坏和弯剪破坏构件的累计数量均有所增长,但该区间内发生弯曲破坏的构件数量少于弯剪破坏构件,偏向构件安全考虑,取 m2.5,F-FS = 0.60。此时,弯剪破坏构件和弯曲破坏构件的累计数量占比分别为 89.58% 和 10.42%,较为合理。
综上,以弯剪比和剪跨比参数为判别条件的新型装配式剪力墙破坏形态划分准则如表2所示。
表2新型装配式剪力墙破坏形态的划分准则
Tab.2 Division criteria of failure modes of new assembled shear wall

图7不同剪跨比下构件破坏形态随弯剪比累计数量曲线
Fig.7Cumulative quantity curves of component failure modes with varying shear-span ratios
2 新型装配式剪力墙变形指标限值研究
2.1 性能状态的确定
GB 50011—2010 《建筑抗震设计规范》 [9] 对地震作用下的结构构件划分了完好、基本完好、轻微损坏、轻中等损坏、中等损坏和不严重破坏共 6 个性能状态,并在相邻的性能状态之间区分了以承载力和弹塑性变形为主要判别依据的各性能限值。但根据众多试验研究发现,水平承载力的下降并不意味着构件失效或结构倒塌,试件达到极限状态以后仍具有可靠的承载力,大部分弯曲破坏构件也表现出较好的变形能力。对此,将 GB 50011—2010 《建筑抗震设计规范》 [9]中不严重破坏状态调整为较严重破坏状态和严重破坏状态,以此更为准确地判断构件是否失效。
2.1.1 弯曲破坏/ 弯剪破坏
1)完好。完好状态对应于构件未达到屈服之前的性能状态,构件仅发生弹性变形,试件表面可能存在微小裂缝,卸载后构件的变形和表面裂缝均可完全恢复。
2)轻微损坏。轻微损坏状态对应于部分承重构件产生轻微塑性变形,少数非承重构件发生明显破坏,表层混凝土没有脱落,受力纵筋屈服,残余裂缝的宽度相对较小。
①纵向钢筋应变小于 0. 030; ②混凝土压应变小于 0. 005。
4)中等破坏。中等破坏状态对应构件损伤加剧,伴有明显的塑性变形,多数构件出现轻微裂缝,部分非承重构件出现明显裂缝,构件需要加固修复。
①纵筋拉应变小于极限拉应变的 60% [14];
②混凝土压应变小于极限压应变[15]。
5)较严重破坏。较严重破坏对应结构主要承重构件产生明显塑性变形,混凝土保护层大量剥落,核心区混凝土损伤加剧,结构构件需大修才可恢复使用。
①纵筋拉应变同时不超过 0. 08 和钢筋极限拉应变的 90%; ②混凝土压应变小于极限压应变的 150%。
为偏向保守考虑,将构件承载力指标作为基于材料应变判定较严重破坏状态的补充判定依据,根据试验经验,认为:③构件承载力下降至峰值承载力的 85% 时,构件达到不严重状态阈值。
6)严重破坏。严重破坏状态是结构构件处于濒临失效或倒塌的前期状态,其中,大多数承重构件严重破坏,部分非承重构件出现倒塌,结构无修复必要,亟待拆除。
与较严重破坏状态类似,认为:③构件承载力下降至峰值承载力的 70% 时,构件达到严重状态阈值。
2.1.2 剪切破坏
1)完好。在完好状态下,认为构件始终处于弹性状态,其划分标准与前述弯曲/ 弯剪破坏状态下的标准一致。
2)较严重破坏。
将上述各性能状态下构件的材料应变限值及部分性能点的承载力限值汇总,得到新型装配式剪力墙性能状态划分标准,见表3。
表3新型装配式剪力墙性能状态划分标准
Tab.3 Performance state classification standards of new prefabricated shear wall
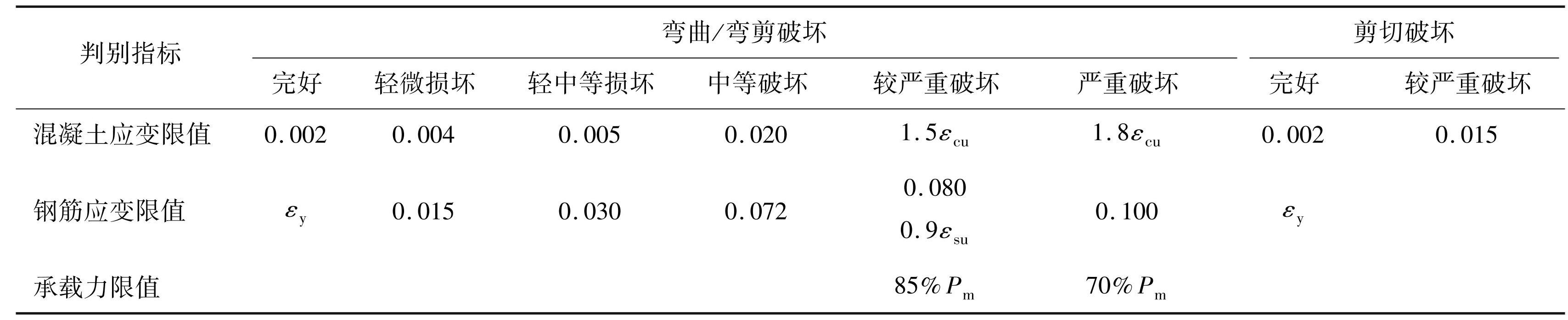
注:εcu ,εsu分别为混凝土极限压应变和钢筋极限拉应变,εy为钢筋屈服应变,Pm为剪力墙峰值承载力; 空白表示无此项。
2.2 性能指标的选取
从所建 216 个新型墙体有限元模型的破坏形态分布来看,弯曲破坏构件仅占比 30.56%,而弯剪破坏和剪切破坏构件共占比 69.44%。因此,选取结构塑性位移角表征构件不同性能状态下的变形较为合理。
3 塑性位移角限值计算公式的建立
3.1 自变量线性回归
选取剪跨比、轴压比、边缘构件纵筋配筋率、配箍特征值和水平分布筋配筋率作为自变量进行线性回归。通过线性回归分别得到弯曲破坏、弯剪破坏和剪切破坏形态下构件各塑性位移角限值的回归方程,见表4~6。
以相关系数 R、显著性 P、共线性指数 FVI和 F 统计量为判断指标,一般认为在 R >0.6,P <0. 05 和 FVI <7 时回归系数具有显著意义。由表4、5可知,对于发生弯曲破坏和弯剪破坏的构件,塑性位移角限值的回归模型整体较好,相关系数 R 普遍在 0.85左右; 由表6可知,发生剪切破坏的构件,塑性位移角限值回归模型的相关系数为 0.623,在可接受的范围内。
表4弯曲破坏构件塑性位移角限值线性回归结果
Tab.4 Linear regression results of plastic displacement angle limit value of bending failure member

注:δ2 ~δ6依次表示轻微损坏、轻中等损坏、中等破坏、较严重破坏和严重破坏状态下的塑性位移角限值,β0 为线性回归得到的常量非标准化系数,β1~β5依次为剪跨比、轴压比、边缘构件纵筋配筋率、配箍特征值和水平分布筋配筋率的线性回归非标准化系数,F 表示检验统计量,Pmax表示可接受的显著性水平最大值,R 表示线性相关系数。
由表4可知弯控 RC 剪力墙的位移角限值回归公式如下。
式中:λ为剪力墙的剪跨比,ud为设计轴压比,ρsv为边缘构件纵筋配筋率,λv 为边缘构件配箍特征值,ρsh为水平分布筋配筋率。
表5弯剪破坏构件塑性位移角限值线性回归结果
Tab.5 Linear regression results of plastic displacement angle limit of flexural-shear failure members
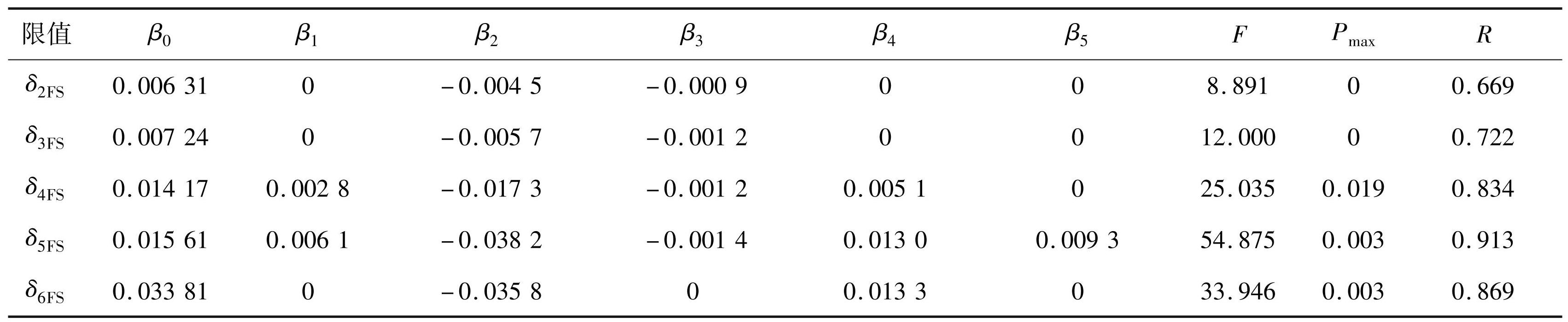
由表5可知弯剪控 RC 剪力墙的位移角限值回归公式如下。
表6剪切破坏构件塑性位移角限值线性回归结果
Tab.6 Linear regression results of plastic displacement angle limit of shear failure members

由表6可知剪控 RC 剪力墙的位移角限值回归公式如下。
3.2 变形指标限值标准的确定
通过选取轴压比和弯剪比这两项参数,对弯曲破坏和弯剪破坏下各性能指标限值进行统计区间划分。轴压比和弯剪比的上下限值由在不同轴压比和弯剪比下发生弯曲破坏和弯剪破坏构件的集中分布情况确定,最后,通过数理统计的方法确定各统计区间内的性能指标限值。对于受轴压比和弯剪比影响较弱的剪切破坏构件,则直接对发生该破坏的全体构件进行统计。
在各区间内统计服从标准正态分布下分位点取-0.100(保证率 90%)对应的性能指标限值标准,即
(5)
式中:P 表示概率,δ 表示性能指标,δ -0.100表示标准正态分布下分位点取-0.100 对应的性能指标限值分位点,σδ表示性能指标限值的标准差,uδ表示性能指标限值的均值。
表7分别为划分不同轴压比和弯剪比统计区间的弯曲破坏和弯剪破坏构件的各变形指标限值标准,表8为剪切破坏构件的各变形指标限值标准。
表7弯曲破坏构件变形指标限值标准(ud≤0.10,m≤0.30)
Tab.7 Limit value standards of deformation index of bending failure member (ud≤0.10, m≤0.30)

注:δ1e表示完好状态的位移角限值; 表中限值标准由式(5)计算得到,下同。
表8剪切破坏构件变形指标限值标准
Tab.8 Limit standards of deformation index of shear failure members

注:空白表示无此项。
对表7、8中构件变形指标限值标准进行汇总,得到新型装配式剪力墙变形指标限值标准,见表9。
由表9可知,新型装配式剪力墙在各性能状态下均表现出较好的变形性能,相比矩形截面 RC 剪力墙[16],其位移角限值标准有显著提升。从完好状态的位移角限值 δ1e来看,对于剪力墙的 3 种破坏形态,δ1e普遍可达到 0.035 左右,这是因为当输入的螺栓预紧作用较弱时,构件变形主要受到高强螺栓与U 型槽钢之间摩擦滑移的影响。从塑性位移角限值 δ2~δ6来看,发生弯曲破坏构件的变形能力对轴压比的敏感程度随弯剪比水平的提高而增强,对弯剪比的敏感程度同样随轴压比水平的提高而增强,而发生弯剪破坏构件的变形能力对轴压比的敏感程度总体随弯剪比水平的提高而减弱,对弯剪比的敏感程度则随轴压比水平的提高而增强。
表9新型装配式剪力墙变形指标限值标准
Tab.9 Limit value standards of deformation index of new assembled shear wall

注:完好状态的变形指标为位移角,其余性能状态下变形指标为塑性位移角; 对于表中划分范围以外的轴压比和弯剪比区间,允许采用线性差值法获取相应变形指标限值。
4 结论
1)通过变参设计了216 片新型装配式剪力墙模型,将构件破坏形态划分为弯曲破坏、弯剪破坏和剪切破坏 3 类,采用 ABAQUS 判定全体模型的破坏形态,并且提出了以弯剪比和剪跨比为判别指标的新型装配式剪力墙破坏形态划分准则。
2)根据新型装配式剪力墙的破坏机制,在现有规范基础上对弯剪破坏和弯曲破坏构件各划分了 6 个性能状态,对剪切破坏构件划分了两个性能状态。选取位移角作为性能指标进行量化,以材料应变限值和承载力为判别条件的全体模型变形指标限值。
3)在 3 种破坏形态下,以剪跨比、轴压比、边缘构件纵筋配筋率、配箍特征值和水平分布筋配筋率为自变量的各塑性位移角限值计算公式,较好地预测新型装配式剪力墙的变形。对 216 个模型的位移角数据进行分析,提出了各破坏形态下具有 90% 保证率的构件变形指标限值标准,为实现基于性能的新型装配式剪力墙抗震设计提供参考。
