欢迎访问《哈尔滨工业大学学报》编辑部网站！

氯盐侵蚀RC梁抗震性能试验与数值模拟方法

doi: 10.11918/202312027

胡卫兵^1,2 ，罗雨欣^1,2 ，白澄宇^1,2 ，郑山锁^1,2

1. 西安建筑科技大学土木工程学院,西安 710055

2. 结构工程与抗震教育部重点实验室(西安建筑科技大学),西安 710055

基金项目: 国家重点研发计划(2019YFC1509302) ；国家自然科学基金(52278530) ；陕西省重点研发计划(2021ZDLSF06-10)

详细信息

作者简介

胡卫兵(1966—),男,教授,博士生导师

通讯作者

罗雨欣,307363868@qq.com

中图分类号: TU375.4;TU317.1

文献标识码: A

文章编号: 0367-6234(2025)02-0143-10

Experimental and numerical simulation methods for seismic performance of RC beams affected by chloride salt erosion

HU Weibing^1,2 ， LUO Yuxin^1,2 ， BAI Chengyu^1,2 ， ZHENG Shansuo^1,2

1. School of Civil Engineering, Xi′an University of Architecture and Technology, Xi′an 710055 , China

2. Key Lab of Structural Engineering and Earthquake Resistance(Xi′an University of Architecture and Technology), Ministry of Education, Xi′an 710055 , China

摘要

为研究锈蚀钢筋混凝土(RC)梁抗震性能,对 8 根 RC 梁进行人工气候加速腐蚀试验和拟静力加载试验,分析了锈蚀程度和配箍率对 RC 梁破坏过程、承载能力、变形能力及耗能能力等的影响。在 OpenSees 中分别采用 SFI-MVLEM 单元和零长度截面单元模拟梁的弯剪变形和黏结滑移变形,并以承载力和耗能能力最优为原则对模型相关参数进行标定。结果表明:纵筋锈蚀率从 0 增加到 6. 8% ,试件剪切破坏特征愈加严重,承载力、延性及塑性转动能力分别降低 6. 7% 、5. 1% 、11. 5% ;随着配箍率的增加,试件的变形能力、延性和承载力逐渐提高;单位纵筋锈蚀率增量下,梁试件 DL-4 的峰值荷载、延性系数和塑性转角比相同配箍率试件 DL-3 分别降低 1. 48% 、1. 79% 和 3. 04% ;试件 DL-8 的峰值荷载、延性系数和塑性转角比相同配箍率试件 DL-7 分别降低 1. 77% 、3. 20% 和 6. 97% ,表明锈蚀率和配箍率参数存在耦合效应。模拟与试验的承载力误差均值为 8. 95% ,累积耗能能力误差均值为 9. 82% ,表明所提出的数值模型具有较好的准确性,可用于锈蚀 RC 梁抗震性能评估。

关键词

锈蚀 / 钢筋混凝土梁 / 销钉刚度系数 / 数值模型 / 抗震性能

Abstract

To investigate the seismic performance of reinforced concrete (RC) beams with corroded steel bars, artificial climate accelerated corrosion tests and quasi-static loading tests were conducted on eight RC beams. The influence of corrosion level and stirrup ratio on the failure process, load-carrying capacity, deformation capacity, and energy dissipation capacity of RC beams was analyzed. Additionally, SFI-MVLEM elements and zero length section elements were used in OpenSees to simulate the flexural-shear deformation and bond-slip deformation of the beams. Model parameters were calibrated based on the principles of optimal load-carrying capacity and energy dissipation capacity. The results show that as the corrosion rate of the longitudinal bars increase from 0 to 6.8% , the shear failure characteristics of the specimens become more severe, and the load-carrying capacity, ductility, and plastic rotational capacity decrease by 6.7% , 5.1% , and 11.5% respectively. As the stirrup ratio increases, the deformation capacity, ductility, and load-bearing capacity of the specimen gradually improve. For a unit increase in longitudinal bar corrosion rate, the peak load, ductility coefficient, and plastic rotation angle of specimen DL-4 decrease by 1.48% , 1.79% , and 3.04% respectively compared to specimen DL-3 with the same stirrup ratio. Similarly, for specimen DL-8, the peak load, ductility coefficient, and plastic rotation angle decrease by 1. 77% , 3.20% , and 6.97% respectively compared to specimen DL-7 with the same stirrup ratio, indicating a coupling effect between the corrosion rate and stirrup ratio parameters. The average errors in load-carrying capacity and cumulative energy dissipation capacity between simulation and testing are 8.95% and 9.82% respectively, indicating that the proposed numerical model has good accuracy and could be used for assessing the seismic performance of corroded RC beams.

Keywords

corrosion / RC beams / dowel action coefficient / numerical model / seismic performance

1 试验 1.1 试件设计 1.2 材料特性 1.3 腐蚀方案与锈蚀现象 1.4 加载方案 2 试验结果及分析 2.1 破坏形态 2.2 滞回曲线 2.3 骨架曲线与特征点 3 数值模型建立 3.1 建模思路 3.2 材料力学性能退化 3.2.1 锈蚀钢筋单轴材料模型 3.2.2 混凝土单轴材料模型 3.3 锈蚀钢筋与混凝土黏结滑移 3.4 销钉刚度系数标定 3.5 模型验证 4 结论

沿海环境中的 RC 结构在遭受氯盐侵蚀后钢筋会发生锈蚀，导致结构耐久性能和抗震性能发生劣化^[1-2]。钢筋锈蚀将引起保护层锈胀开裂、纵筋肋锈损与截面积减小、箍筋对混凝土约束能力降低等^[3]。 RC 梁通常被定义为抗弯构件，按照受弯破坏设计。但由于建筑形式、配筋情况等原因，跨高比较小的 RC 梁在建筑和土木工程领域中被广泛应用，如框架结构中的次梁、转换层、转换梁、剪力墙结构中连梁等，此类梁更容易发生剪切破坏。 RC 梁在纵筋和箍筋锈蚀的情况下，承载力和变形能力降低，将导致其在地震作用下有进一步发生剪切脆性破坏的风险。因此，有必要对氯盐环境中锈蚀 RC 梁的抗震性能进行评估，并提出可模拟其弯-剪变形的数值模拟方法。

目前，关于锈蚀 RC 梁的研究主要集中于单调荷载作用下力学性能研究与往复荷载下抗震性能研究。如 Cheng 等^[4] 采用恒电流法仅对箍筋进行锈蚀，通过拟静力试验研究了箍筋锈蚀对 RC 梁破坏模式和抗震性能指标的影响。 Ou 和 Chen 等^[5-7] 对 RC 梁内部不同位置钢筋进行了锈蚀，定量研究了钢筋锈蚀位置对弯曲破坏和剪切破坏梁抗震性能的影响。在数值模拟方面，通常采用塑性铰模型、考虑剪切的纤维模型和实体元模型模拟锈蚀 RC 梁的响应，如 Ou 等^[8]基于锈蚀 RC 梁拟静力试验数据标定了塑性铰长度计算公式，采用塑性铰模型模拟了锈蚀 RC 梁滞回响应。 Liu 等^[9] 采用实体元模型对锈蚀 RC 梁的抗震性能进行了数值分析。然而，塑性铰模型和纤维模型仅可模拟弯曲变形，并且等效塑性铰长度计算公式包含大量基本假定，导致其准确性欠缺，考虑剪切的纤维模型中的剪力-剪切变形关系需要大量试验数据标定，实体模型计算效率欠佳。

鉴于现有研究不足，设计制作了 8 根不同锈蚀程度和配箍率的 RC 梁试件，剪跨比为 2.6，对其进行人工气候加速腐蚀试验和拟静力加载试验，分析了锈蚀 RC 梁的锈蚀形态、破坏模式和抗震性能。此外，基于试验数据，修正了可模拟弯-剪变形的 SFI-MVLEM 单元中销钉刚度系数，通过 OpenSees 平台建立了锈蚀 RC 梁数值模型，并与试验数据对比验证了该建模方法准确性，成果可为锈蚀 RC 结构抗震性能评估提供理论基础。

1 试验

1.1 试件设计

RC 框架梁端部易发生地震损伤破坏，且其跨中存在反弯点，因此，可取框架节点至梁反弯点间的梁段为对象，研究 RC 框架梁的抗震性能，如图1所示。参照文献^[10-11]，以锈蚀程度和配箍率（箍筋间距）为变化参数，共设计了 8 根剪跨比为 2.6 的 RC 梁试件。各试件设计参数如表1所示，详细尺寸及配筋如图2所示。为避免底座锈蚀损伤影响梁失效模式，梁端与底座采用二次浇筑的方式进行连接。在浇筑梁试件前，对伸入底座钢筋刷涂环氧树脂进行防锈保护。随后，浇筑梁试件，并将其放入自然养护式养护 28 d，进行人工气候加速腐蚀试验，直至试件达到设计裂缝宽度，将其移出锈蚀实验室再浇筑底座。

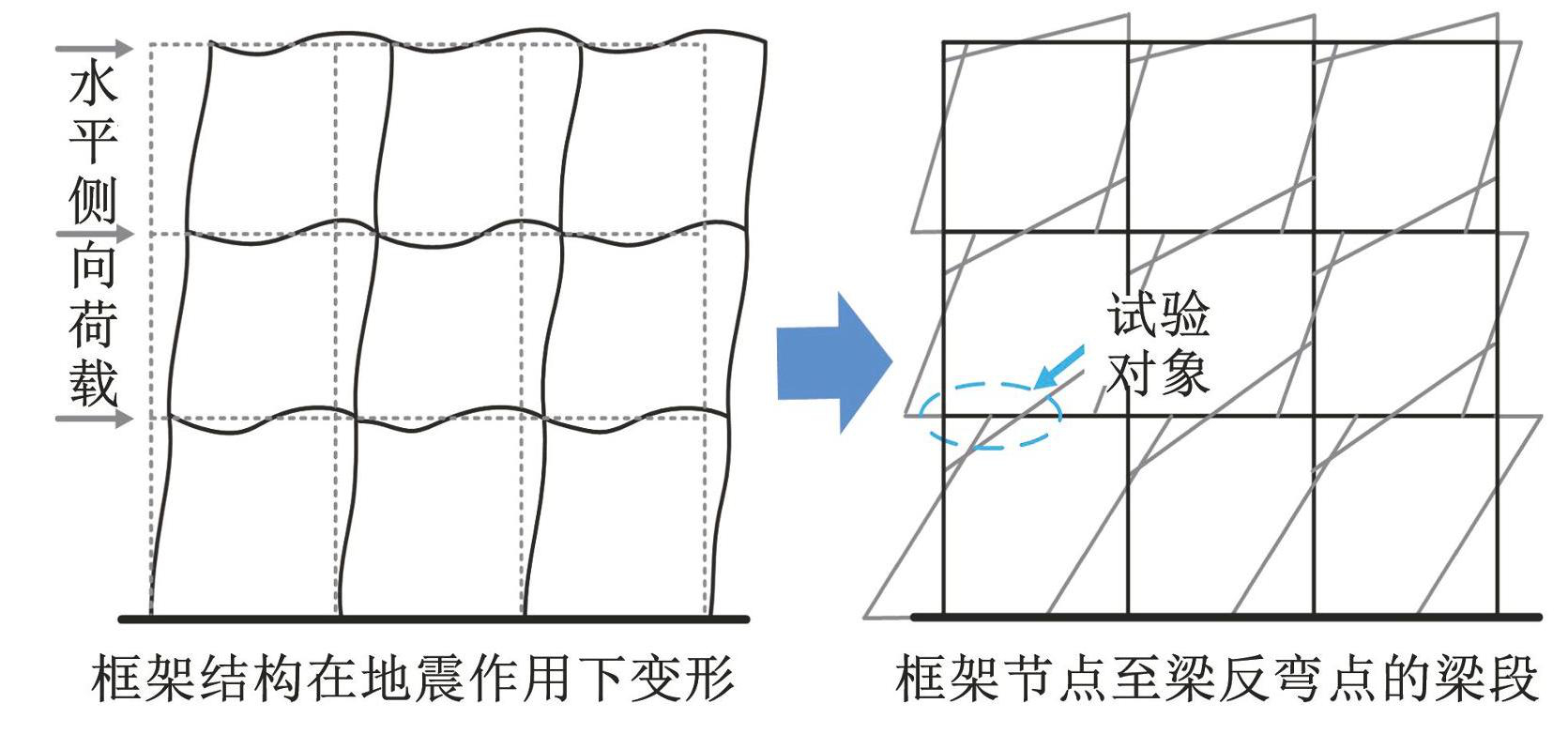
图1RC 梁设计原型

Fig.1Design prototype of RC frame beams

表1锈蚀 RC 梁试件设计参数

Tab.1 Design parameters of corroded RC beams

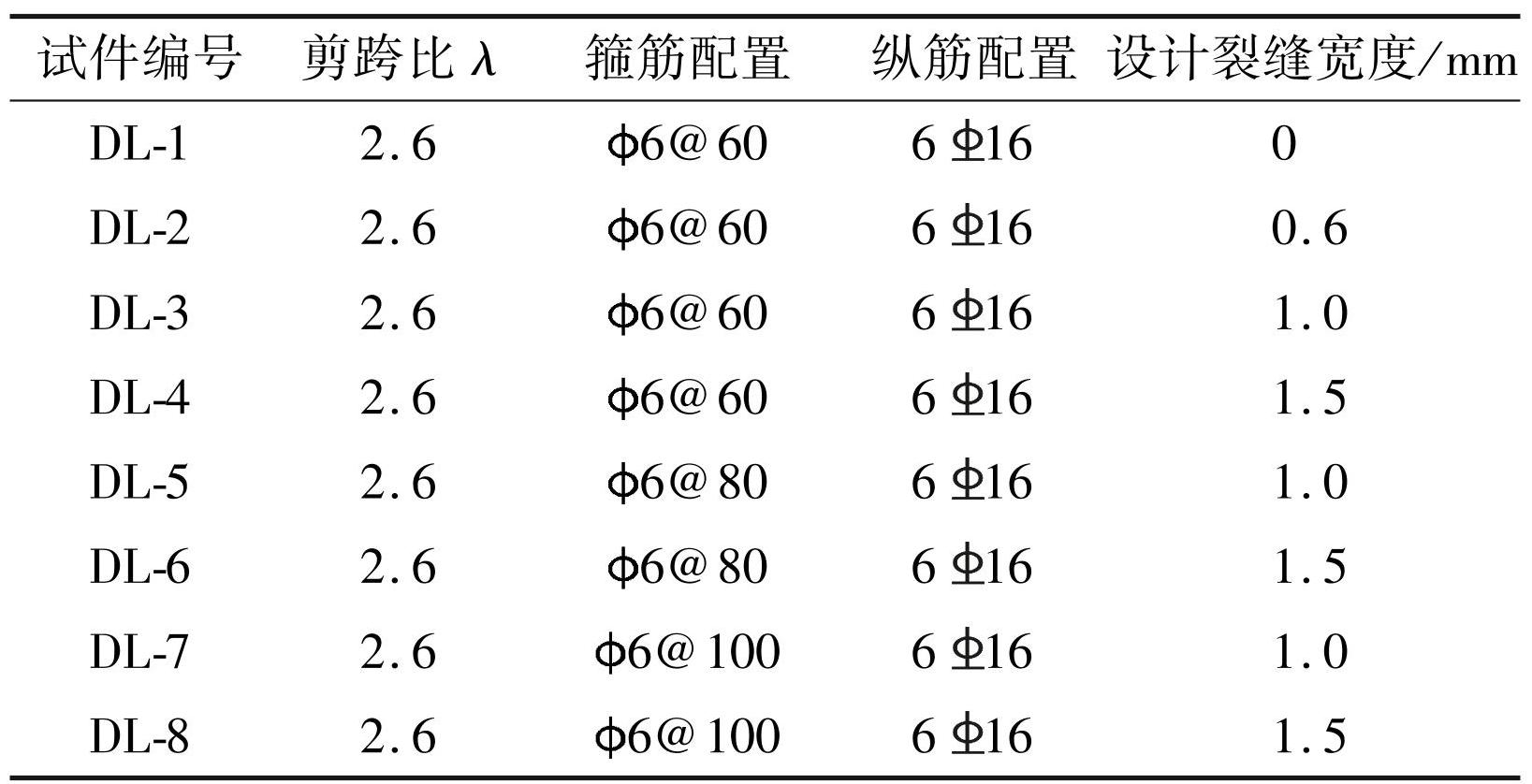
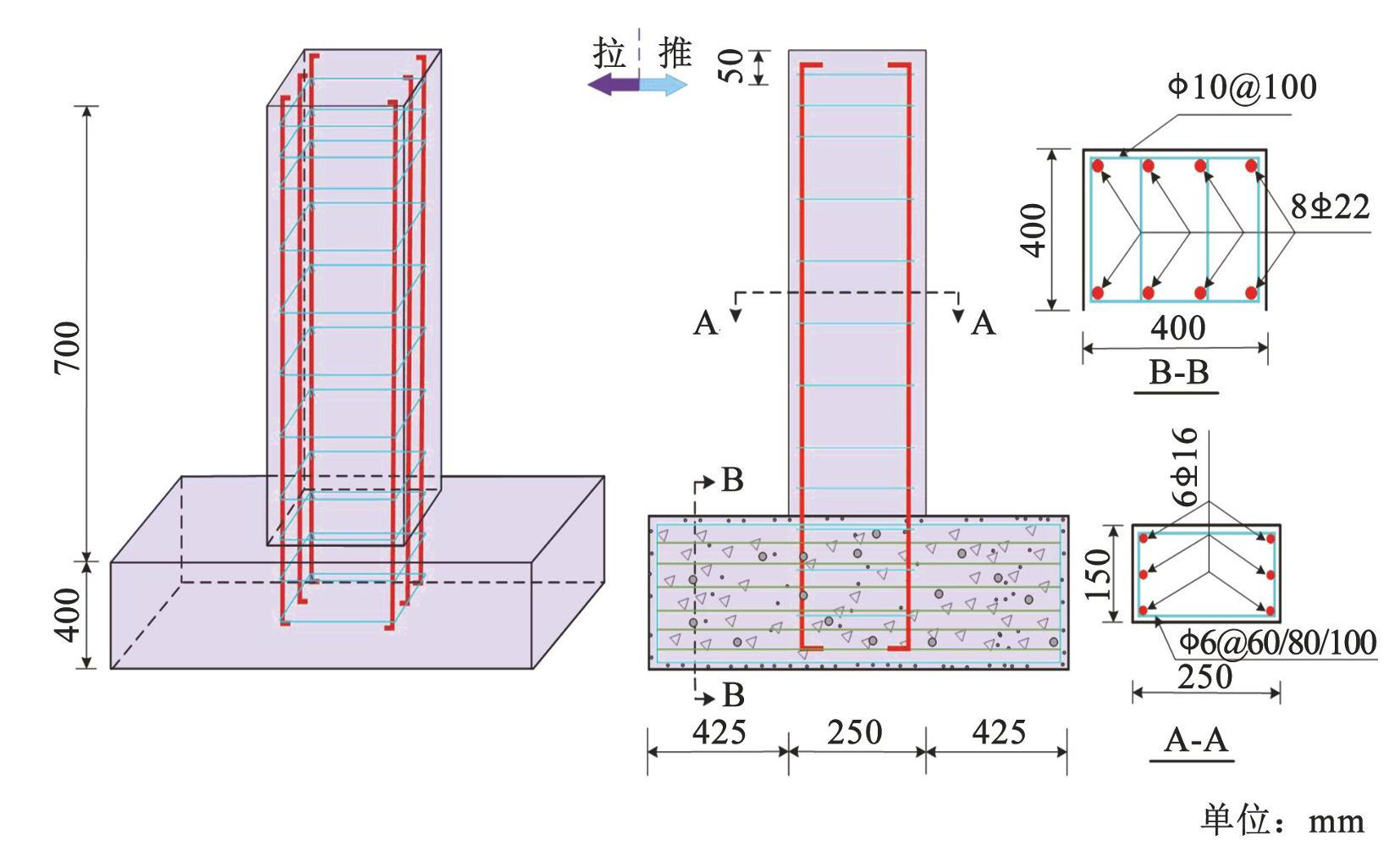
图2试件截面尺寸及配筋图

Fig.2Size and reinforcement of RC shear wall specimen

1.2 材料特性

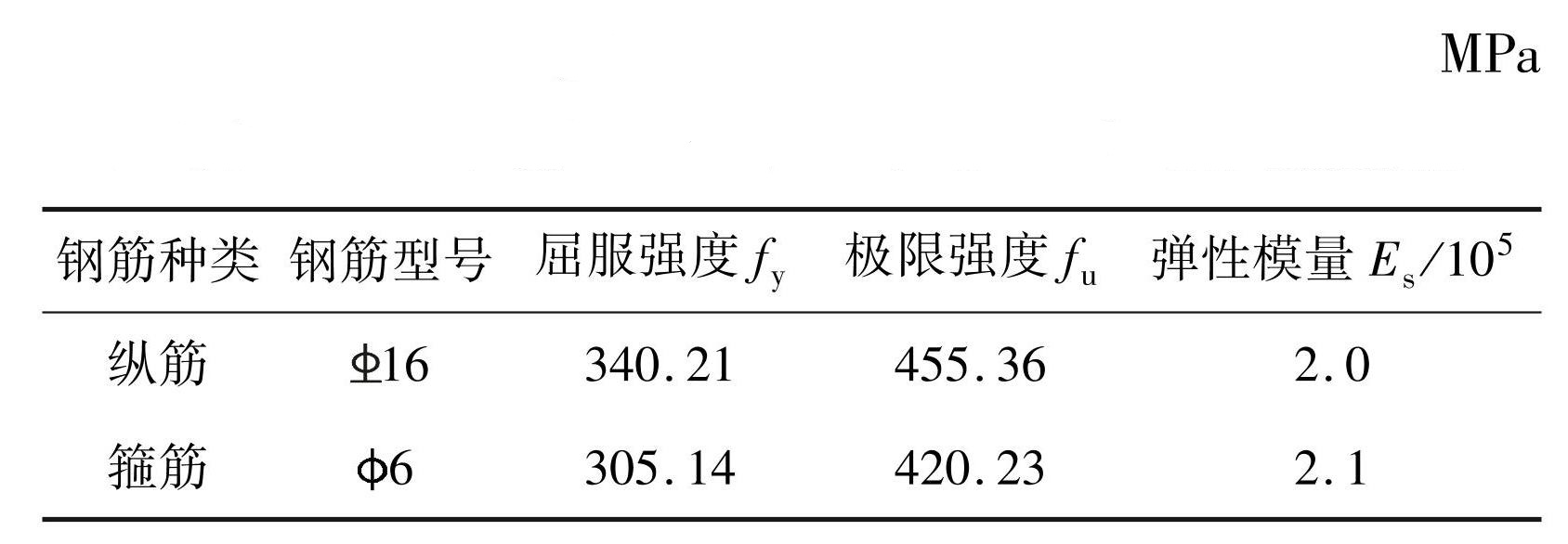
混凝土采用 C30，轴心抗压强度为 27. 05 MPa，弹性模量为30 GPa。试件采用普通硅酸盐 P. O 32.5R 水泥，河沙采用中砂，细石粒径为 5~15 mm，混凝土配合比如表2所示。纵筋采用 HRB335 钢筋，箍筋采用 HPB300 钢筋，钢筋材性参数如表3所示。

表2混凝土配合比

Tab.2 Proportions of concrete mix

表3钢筋材料的力学性能参数

Tab.3 Mechanical property parameters of rebar materials

1.3 腐蚀方案与锈蚀现象

加速锈蚀方案主要有浸泡加速锈蚀、通电加速锈蚀和人工气候环境加速锈蚀。浸泡加速锈蚀通过将试件浸泡在氯离子溶液中进行锈蚀，钢筋锈蚀形态和自然环境下相似，但试验周期较长。通电加速锈蚀将试件密封在保水薄膜中，对外露钢筋进行通电锈蚀和脱膜烘干交替整个过程循环进行，试件锈蚀速度较快但试验过程繁琐。人工气候环境加速锈蚀能够模拟自然环境下试件受气候作用发生锈蚀的过程，锈蚀速度较通电锈蚀慢，但试验过程相对简单，且构件锈蚀形态和自然环境下相似^[12]，可广泛用于加速锈蚀 RC 构件。因此，采用人工气候环境室（ ZHT / W2300）对各 RC 梁（DL-1 除外）进行锈蚀，如图3所示。

图3人工气候环境室

Fig.3Artificial climate environmental chamber

为加速钢筋表面钝化膜的破坏，在试件浇筑过程中于混凝土内掺入 5% 水泥质量的氯化钠，并采用间歇喷雾干燥法模拟氯化物侵蚀环境。其中，盐雾质量分数、喷雾持续时间、温度和湿度等参数设置详见文献^[13]。喷雾采用质量分数为 5% 氯化钠溶液。具体锈蚀过程如下:将环境室的温度控制在 45℃左右，湿度保持在 90% 相对湿度。采用间歇喷洒的方法保持环境室内盐雾质量分数恒定，即喷洒 20 min，中断 40 min，重复 3 个周期后，升高环境室温度至 60℃，干燥试样 2 h。最后，将温度降至 45℃，进行下一个循环盐雾试验。一次盐雾试验循环持续6 h，腐蚀方案如图4所示。参考文献^[14-15] 用控制锈胀裂缝宽度的方法控制试件锈蚀程度。定期进入人工气候实验室，量测各试件表面纵筋方向5 条锈胀裂缝宽度并取平均值，待平均值分别达到表1所示的预期宽度时，将试件从人工气候环境室中移出。

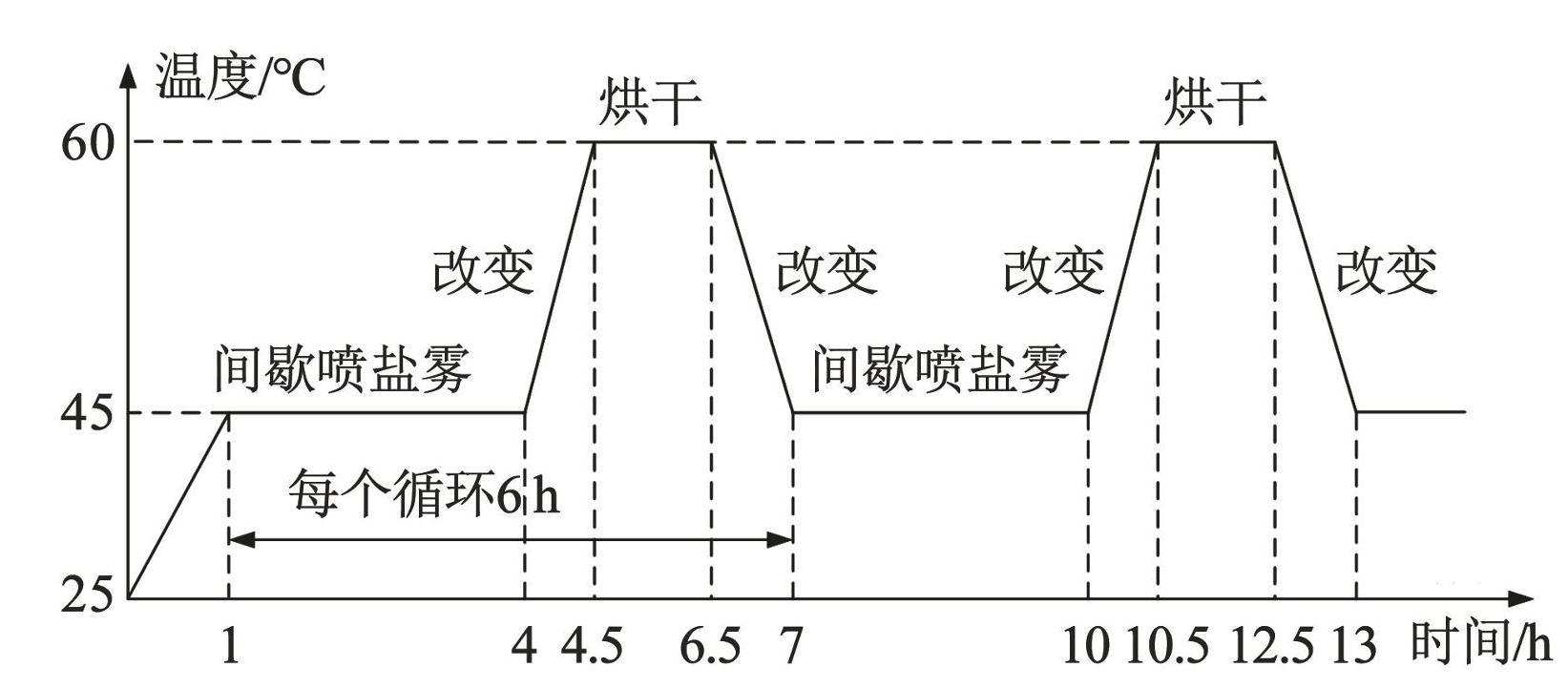
图4人工气候环境腐蚀方案

Fig.4Corrosion scheme of artificial climate environment

人工气候加速腐蚀试验完成后，观察试件锈蚀现象。试件混凝土保护层沿钢筋方向出现裂缝，拟静力加载完成后，将试件保护层破除，可以看出，红褐色锈蚀产物堆积在钢筋与混凝土界面，形成界面间隙，这将劣化钢筋与混凝土间的黏结性能。同时，锈蚀产物增多将引起钢筋锈蚀层不断膨胀，导致混凝土保护层锈胀开裂。试件内部锈蚀钢筋及表面锈胀裂缝如图5所示。

图5试件锈蚀现象

Fig.5Corrosion phenomenon of specimen

除锈前、后的钢筋和箍筋角部锈蚀情况如图6所示。可以看出，人工气候环境和自然环境下钢筋表面锈蚀特征相似^[17]，均形成了红褐色锈蚀产物，同时，钢筋表现出明显不均匀锈蚀。即纵筋近保护层侧较背离侧锈蚀更严重。由图6除锈后最右侧箍筋可以看出，箍筋直线部分横截面积显著减小，表面蚀坑更为明显。

图6锈蚀钢筋

Fig.6Corroded steel bar

1.4 加载方案

锈蚀试验完成后，采用悬臂梁式加载方式对锈蚀 RC 梁进行拟静力加载^[10，16]，通过 50 t 电液伺服作动器施加水平循环（推拉）荷载，见图7、8。加载制度如下:试件屈服前，位移增量采取有限元分析所得 0.1Δ_y（屈服位移），并循环 1 次，屈服前采用较小位移级差以便获取较准确的屈服点荷载和位移; 屈服后，位移增量取 0.5Δ_y，并循环 3 次，当水平荷载降至 0.85 倍峰值荷载或完全破坏时停止试验^[9]。

图7加载装置

Fig.7Loading equipment

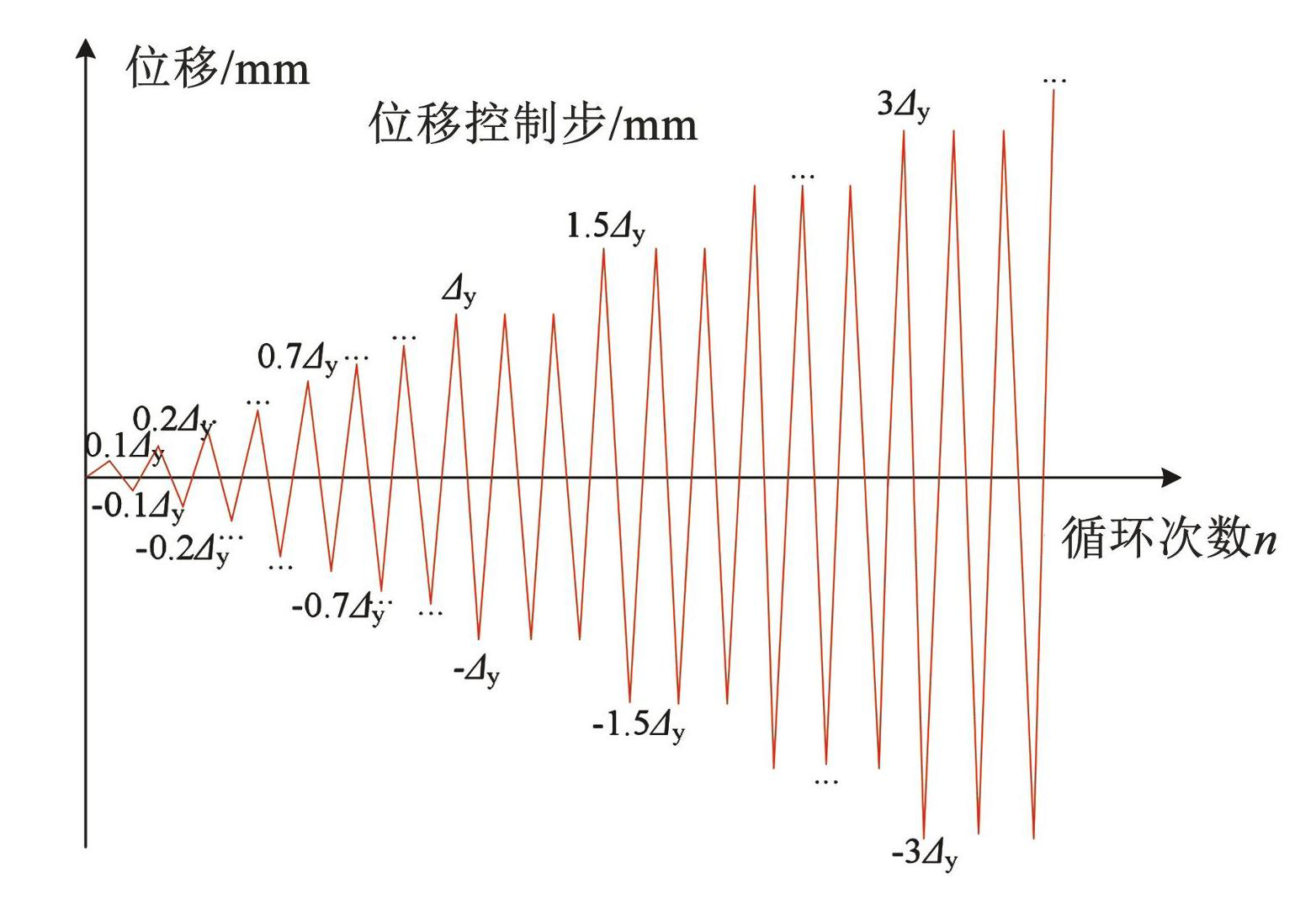
图8加载制度示意

Fig.8Schematic diagram of loading process

2 试验结果及分析

2.1 破坏形态

试验加载结束时，梁试件在往复荷载作用下均发生弯剪破坏，如图9所示，图中不同线型标记代表不同类型的裂缝，以 DL-1 为例进行详细叙述。加载初期，RC 梁试件底部受拉区首先出现初始水平裂缝，并随梁顶水平位移增大，其数量与长度均不断增加，但卸载后试件基本无残余变形，表明试件基本处于弹性状态。此后，随着梁顶水平位移的继续增大，试件底部水平裂缝不断伸长加宽，部分水平裂缝开始沿大致 45°方向斜向发展，并逐渐延伸至梁中心线附近，形成交叉斜裂缝。进一步加大梁顶水平位移，梁底纵向受拉钢筋逐步屈服，表明试件进入弹塑性阶段。此后，随着梁顶水平位移的继续增大，原有裂缝长度不断增长，宽度不断加宽，并在试件底部伴有纵向裂缝产生。当梁顶水平位移超过峰值位移后，与斜裂缝相交的部分箍筋逐渐受拉屈服，试件底部斜裂缝逐渐发展为主剪斜裂缝。最终，由于主剪斜裂缝持续扩展，以及底部剪压区混凝土外鼓并大面积压碎剥落，试件随即宣告破坏。

图9试件破坏形态

Fig.9Failure mode of specimens

试件梁满足强剪弱弯的设计目标，但由于其跨高比接近 5，受力特点更加接近短梁，在未锈蚀状态下发生了以弯曲破坏为主的弯剪破坏。对于锈蚀构件，钢筋有效截面积减少，钢筋表面生成锈蚀产物对包裹其的混凝土产生应力，导致混凝土保护层开裂甚至脱落，钢筋与混凝土黏结力和协同工作能力下降，进而导致构件承载力降低。由于箍筋相对于纵筋更靠近保护层外侧，箍筋的锈蚀情况比纵筋严重。试件梁角部受氯离子两边侵蚀作用下，箍筋角部腐蚀情况更为严重，导致箍筋横向约束力、控制裂缝和扩展、直接承担剪力的能力下降。不同锈蚀程度与配箍率 RC 梁的损伤破坏特征具有一定的差异性，即随着锈蚀加重以及配箍减少，试件底部弯剪斜裂缝的发展速率不断加快，宽度变宽，最终破坏时剪切破坏特征更加明显，表明随着钢筋锈蚀程度的增加以及配箍率的减小，RC 梁破坏模式逐渐由弯曲破坏为主的弯剪型破坏向剪切破坏特征更加明显的剪弯型破坏转变。

拟静力加载完成后，取出各锈蚀试件内部纵筋和箍筋，参考文献^[16] 的方法对锈蚀钢筋进行除锈，并量测锈蚀钢筋质量。采用式（1）计算钢筋质量损失率以衡量锈蚀程度。为消除锈蚀结果离散性，每种类型钢筋取 3 根，计算其平均锈蚀率，结果如表4所示。

η = (m_{0} - m_{1}) / m_{0} \times 100 %

(1)

式中:η 为质量损失率，m₀、m₁为未锈蚀及除锈后的钢筋质量。

表4钢筋平均锈蚀率

Tab.4 Average corrosion rate of reinforcements

2.2 滞回曲线

基于拟静力试验中量测的梁顶水平荷载与位移（P-Δ）数据，得到各试件滞回曲线，如图10所示。屈服前，试件均为弹性变形，滞回曲线近似直线，包围面积较小; 屈服后，由于加卸载刚度的减小，滞回曲线包围面积及残余变形增大，滞回环呈弓形出现捏缩; 峰值位移后，滞回曲线加卸载刚度退化速率逐渐加快，残余变形继续增大，滞回环呈反 S 形，捏拢现象更加严重。

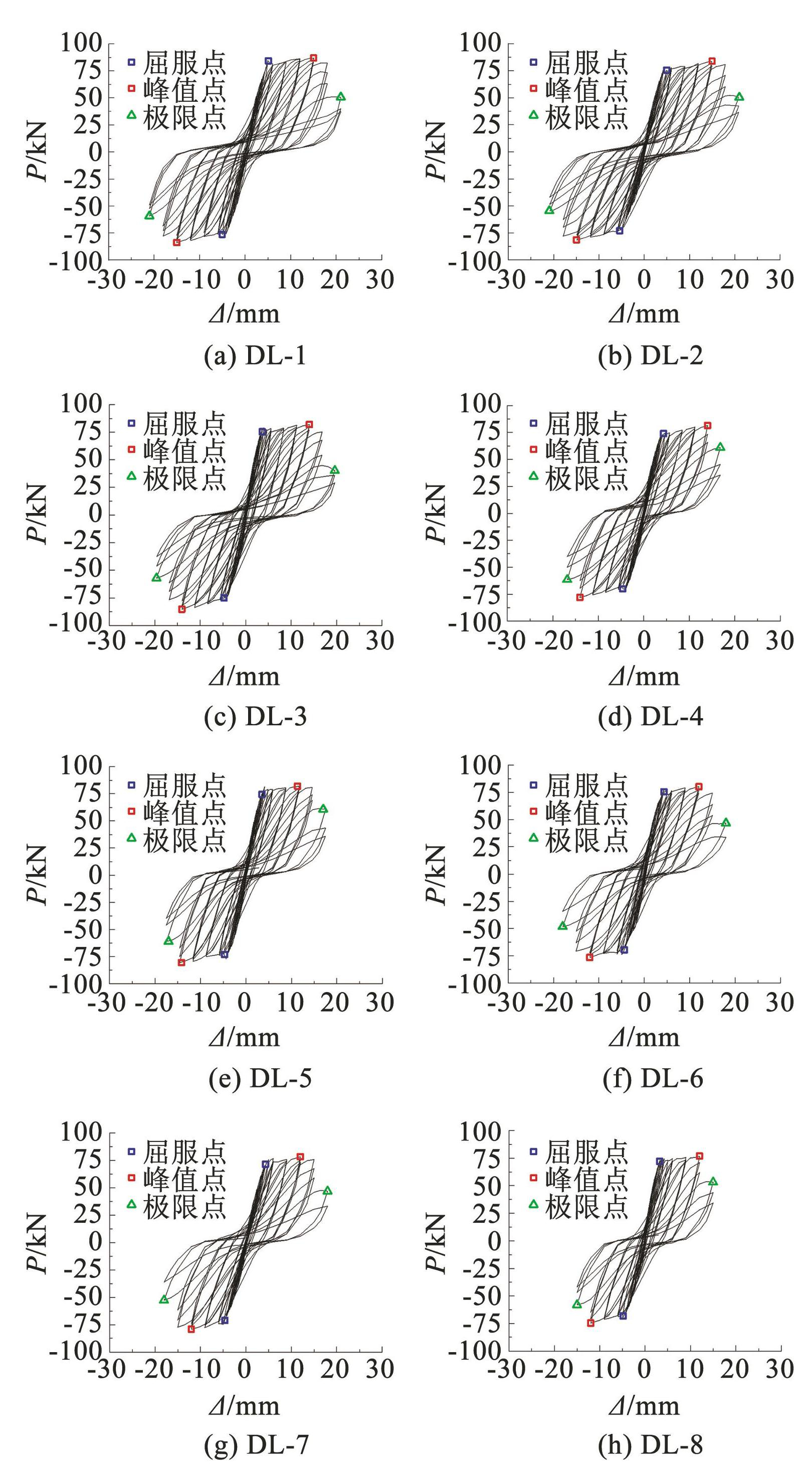
图10滞回曲线

Fig.10Hysteresis curves

此外，不同配箍率与锈蚀程度的试件，滞回性能具有一定的差异性。对比 DL-1、DL-2、DL-3、DL-4 可以看出，随锈蚀程度增加，滞回环捏缩现象愈加明显，包围面积逐渐减小，试件加卸载刚度逐渐降低，强度退化幅度增加。对比 DL-3、DL-5、DL-7 以及 DL-4、DL-6、DL-8 可知，随着配箍率减小，滞回曲线较为窄小，耗能能力和峰值荷载降低，塑性段的屈服平台缩短，延性变差。

2.3 骨架曲线与特征点

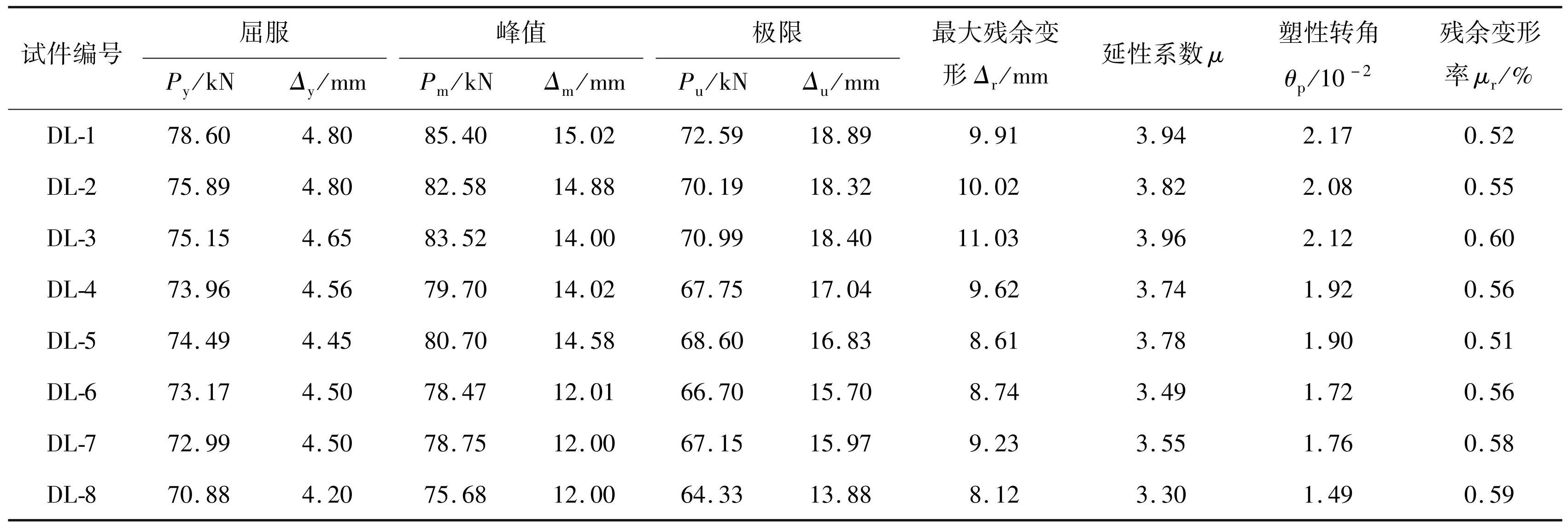
不同设计参数下试件的骨架曲线对比如图11所示。在往复荷载作用下，试件滞回曲线正负向是不对称的，因此，骨架曲线特征值为推拉方向的平均值，结果如表5所示。按照能量等值法^[16]定义屈服点，极限荷载取试件破坏点或者 0.85 倍峰值承载力点，极限位移取对应于极限荷载的位移值。

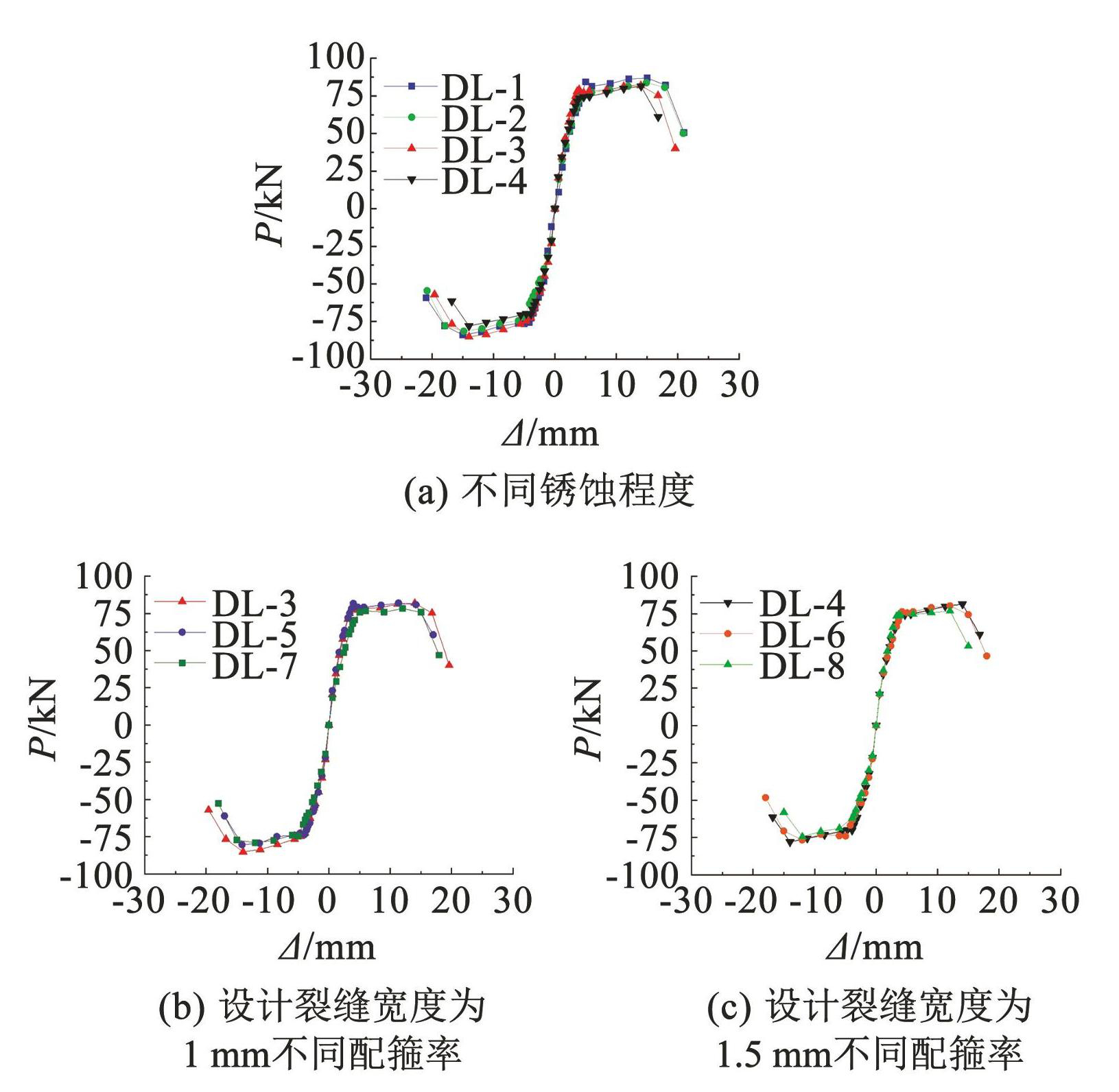
图11骨架曲线

Fig.11Skeleton curves

采用延性系数 μ 和塑性转角θ_p ^[18] 作为衡量锈蚀 RC 梁变形能力的指标。采用残余变形率μ_r ^[18]表示锈蚀 RC 梁的变形恢复能力。 μ、θ_p和 μ_r 采用下式计算，结果如表5所示。

μ = Δ_{u} / Δ_{y}

(2)

θ_{p} = (Δ_{u} - Δ_{y}) / L

(3)

μ_{r} = Δ_{r} / Δ_{u}

(4)

从图11和表5可以看出，随着锈蚀程度增加，试件初始刚度降低，刚度退化率增加，原因是锈胀裂缝导致混凝土强度和横截面有效面积减小。随着锈蚀程度增加，试件的特征荷载值与位移值、延性系数和塑性转角总体呈下降趋势，骨架曲线的下降段逐渐变陡，表明试件承载能力和延性降低。残余变形率随锈蚀程度增加逐渐增加（DL-2 较 DL-1 增加了 5.77%，DL-3 较 DL-2 增加了 9. 09%），说明锈蚀试件修复难度加大。随配箍率减小，试件各特征点的荷载和变形值均呈降低趋势，骨架曲线平直段变短，下降段变陡，表明试件的变形能力和延性均逐渐变差。此外，对比 DL-3 和 DL-4、DL-5 和 DL-6、DL-7 和 DL-8 数据可知，单位纵筋锈蚀率增量下，DL-6 的峰值荷载、延性系数和塑性转角比 DL-5 分别降低了 3.45%、9.59% 和 11.84%; DL-8 的峰值荷载、延性系数和塑性转角比 DL-7 分别降低了 1.77%、 3.20% 和 6.97%; DL-4 的峰值荷载、延性系数和塑性转角比 DL-3 分别降低了 1.48%、1.79% 和 3. 04%。从以上分析可以看出，随着锈蚀程度的增加，不同配箍率下锈蚀 RC 梁承载力和变形能力的劣化程度差异明显，这表明锈蚀率和配箍率两个参数间存在耦合效应。

表5骨架曲线特征参数

Tab.5 Skeleton curve characteristics parameters

3 数值模型建立

3.1 建模思路

根据第 2 节试验结果分析可知，往复荷载作用下，锈蚀 RC 梁发生弯剪破坏及纵筋黏结滑移破坏。因此，通过有限元分析软件 OpenSees，采用 SFIMVLEM 单元模拟构件弯剪变形，并在梁端串联零长度单元模拟黏结滑移变形，建立了锈蚀 RC 梁数值模型。其中，SFI-MVLEM ^[19-20]单元采用 FSAM 多轴材料，需给定混凝土和钢筋的单轴本构关系，同时通过混凝土摩擦因数和销钉刚度系数模拟抗剪机制。锈蚀 RC 梁数值建模方法示意如图12所示。

3.2 材料力学性能退化

3.2.1 锈蚀钢筋单轴材料模型

研究表明^[21-22]，钢筋的屈服强度、极限强度、屈服应变和极限应变均随锈蚀程度逐渐退化，而弹性模量基本不变。采用式（5）^[21] 计算 SteelMPF 本构模型中锈蚀钢筋的屈服强度。

f_{y c} = (1 - 1.435 η) f_{y}

(5)

式中:f_y、f_yc分别为未锈与锈蚀钢筋的屈服强度，η 为钢筋实际锈蚀率。参照文献^[19]，拉伸应变硬化率

$ b_{p}

、压缩应变硬化率

$ b_{n}

均取为 0. 02，曲率参数

$ R_{0}

、曲率退化参数

$ {c R}_{1} ， $ {c R}_{2}

分别取为 20，0.925，0.15。

图12锈蚀 RC 梁模型

Fig.12Corroded reinforced concrete beams model

3.2.2 混凝土单轴材料模型

混凝土采用 Concrete CM 本构模型模拟。考虑到梁保护层面积较小，核心区受箍筋包裹，将梁截面认为是约束混凝土材料。其中，约束混凝土的峰值应力考虑保护层混凝土的修正。计算公式如下:

\bar{f_{c c}^{'}} = \frac{f_{c c}^{'} A_{core} + f_{cerack}^{'} A_{cover}}{A_{core} + A_{cover}}

(6)

式中:

\bar{f_{c c}^{'}}

为修正后约束混凝土峰值应力，f′_cc为锈蚀约束混凝土抗压强度，f′_ccrack为锈胀开裂混凝土抗压强度，A_core和 A_cover分别为核心区和保护层的面积。

钢筋锈胀力将引起保护层开裂，降低抗压强度，因此，需考虑锈胀力方向的拉伸应变。本文基于 Belarbi and Hsu ^[23]提出的软化模型计算保护层混凝土抗压强度及相应应变值，即

f_{ccrack}^{'} = ζ f_{c 0}^{'}

(7)

ζ = \frac{0.9}{\sqrt{1 + 600 ε_{r}}}

(8)

ε_{r} = \frac{\sum W_{c r}}{p_{0}}

(9)

\sum W_{cr} = \frac{η_{1} - 0.0728}{0.177}

(10)

式中:f′_c0和 f′_ccrack为锈蚀导致混凝土保护层开裂前和开裂后的抗压强度; ζ 为修正系数; ε_r为混凝土保护层开裂后的抗压应变; ∑W_cr 为试件总的裂缝宽度，通过试验数据回归公式计算; p₀ 为试件周长; η_l为钢筋锈蚀率。

箍筋锈蚀将劣化其对核心区混凝土的约束作用，导致锈蚀箍筋约束混凝土峰值应力降低及其对应的峰值应变略有增加。参考文献^[24]，锈蚀箍筋约束混凝土抗压强度及相应应变值计算公式如下:

f_{c c}^{'} = (1 - 0.017 η_{s}) f_{c o}^{'} (- 1.254 + 2.254 \sqrt{1 + \frac{7.94 f_{1}^{'}}{f_{c 0}^{'}}} - \frac{2 f_{1}^{'}}{f_{c 0}^{'}})

(11)

f_{1}^{'} = k_{e} ρ_{s a} f_{y c s}

(12)

ρ_{s c} = (1 - 0.01 η_{s}) ρ_{s}

(13)

ε_{c c} = (1 + 0.01 η_{s}) ε_{c 0} (1 + λ_{t})

(14)

式中:f′_l为有效侧向围压; f_ycs为锈蚀箍筋屈服强度（如式（5）所示）; ρ_s 和 ρ_sc 分别为锈蚀前后的配箍率; η_s 为箍筋锈蚀率; k_e 为有效约束系数^[25]; ε_cc为锈蚀后约束混凝土峰值应变; λ_t 为配箍特征值; ε_c0 为素混凝土峰值应变，可取为 0.002。

3.3 锈蚀钢筋与混凝土黏结滑移

水平力作用下，随着梁端锚固区混凝土裂缝的开裂闭合，钢筋与混凝土间将发生黏结滑移变形，引起附加转角及试件顶部的非线性水平变形。锈蚀后保护层开裂，钢筋肋锈损，锈蚀产物在界面填充，这些都将劣化黏结性能。为准确模拟锈蚀 RC 梁变形特性，采用考虑应变渗透的钢筋应力-滑移（f_s-s）模型和零长度单元模拟黏结滑移变形^[26]，如图12所示。在模型底部串联零长度纤维截面单元，并将该单元中钢筋应变修改为滑移值。为保证二维板单元与零长度截面单元中材料应力和中和轴位置的协调，采用式（15）对零长度截面单元中混凝土应变进行修正，修正公式如下:

ε_{c s} = \frac{ε_{c} S_{y}}{ε_{y}}

(15)

式中:ε_c和 ε_y为混凝土峰值应变和钢筋屈服应变，S_y 为钢筋屈服滑移。

在零长度单元中采用 Hysteretic 材料模拟钢筋，并将钢筋本构关系替换为应力-滑移（ f_s-s）关系。该材料输入参数包括滞回规则参数和骨架参数。对于滞回规则参数，取变形捏缩参数 PinchX = 0.0，力捏缩参数 PinchY = 0.02，损伤参数 Damage1 = 0.0，Damage2 = 0.0; 骨架参数包括钢筋屈服强度 f_y、屈服滑移 S_y、极限强度 f_u、极限滑移 S_u。未锈蚀钢筋与混凝土间的 S_y0和 S_u0计算公式如下^[27] :

S_{y 0} = \frac{ε_{y} f_{y} d_{b}}{8 τ_{e}}

(16)

S_{u 0} = \frac{ε_{y} f_{y} d_{b}}{8 τ_{e}} + \frac{(ε_{u} + ε_{y}) (f_{u} - f_{y}) d_{b}}{8 τ_{p}}

(17)

τ_{e} = \sqrt{f_{c}}

(18)

τ_{p} = 0.27 \sqrt{f_{c}}

(19)

式中:S_y0 和 S_u0 分别为钢筋处于屈服和极限状态时的滑移量，d_b为钢筋直径，τ_e为钢筋弹性段的黏结强度，τ_p为钢筋弹性段的黏结强度。锈蚀钢筋与混凝土间的 S_yc和 S_uc计算公式如下^[28] :

S_{y c} = {[\frac{ε_{y} f_{y} d_{b} {(1 - 7.365 η_{l})}^{0.4}}{10 Φ_{u} \sqrt{f_{c}^{'}}}]}^{0.714}

(20)

S_{u c} = (1 - 7.365 η_{1}) S_{u 0}

(21)

Φ_{u} = 1 - (10.544 - 1.586 \frac{c}{d}) η_{1}

(22)

式中:S_yc和 S_uc分别为锈蚀钢筋处于屈服和极限状态时的滑移量，Φ_u为修正系数。

3.4 销钉刚度系数标定

FSAM 多轴材料考虑了两种相互独立的抗剪机制，即基于摩擦的骨料剪切互锁效应和钢筋销钉作用，分别由滑动摩擦因数 n_u 和销钉刚度参数 α 表示。 Kolozvari ^[19]指出，n_u取值对分析结果影响较小，可直接取为 0.6 ^[29]，而 α 在很大程度上影响构件滞回响应、剪切变形及滞回捏缩效应，需根据试验结果进行校准，一般可在 0~0.05 的范围内进行取值，销钉刚度系数示意如图13所示。因此，将 α 的取值定为 0.005、0.01、0.015、0.02、0.03、0.04 和 0.05，并采用承载力和耗能能力两个指标^[30] 评估模拟误差，进而选取最优 α 值，误差计算公式如式（23）、（24）所示。计算结果如表6所示。

E_{force} = \sqrt{\frac{\sum_{i = 1}^{n} {(F_{c}^{i} - F_{t}^{i})}^{2}}{n {(m a x (F_{t}))}^{2}}}

(23)

E_{energy} = |\frac{Ω_{c} - Ω_{t}}{Ω_{t}}|

(24)

式中:E_force和 E_energy分别为承载力和耗能误差，

F_{c}^{i}

和

F_{t}^{i}

为第 i 圈滞回曲线力的模拟值与试验值，n 为滞回曲线圈数，max（F_t）为峰值荷载试验值，Ω_c和 Ω_t分别为累积耗能模拟值与试验值。

绘制不同锈蚀程度和配箍率下 α 最优取值（α_top）的变化趋势，如图14所示。基于表6和图14可知，随着锈蚀程度的增加，α_top逐渐减小，这是由于钢筋锈蚀将导致构件抗剪能力下降。此外，随着锈蚀程度的增加，不同配箍率试件的 α_top降低程度不一致，这说明钢筋锈蚀与配箍率对锈蚀 RC 梁试件抗剪强度的影响存在耦合效应。基于上述分析，建立考虑纵向钢筋锈蚀率和配箍率影响的销钉刚度系数 α_top计算公式，即

α_{top} = (a - b η_{l}) ρ_{s}

(25)

α_{top} = (5.72 - 73.84 η_{1}) ρ_{s}, R^{2} = 0.88

(26)

式中:a、b 为拟合参数，η_l 和 ρ_s分别为纵筋锈蚀率和配箍率。

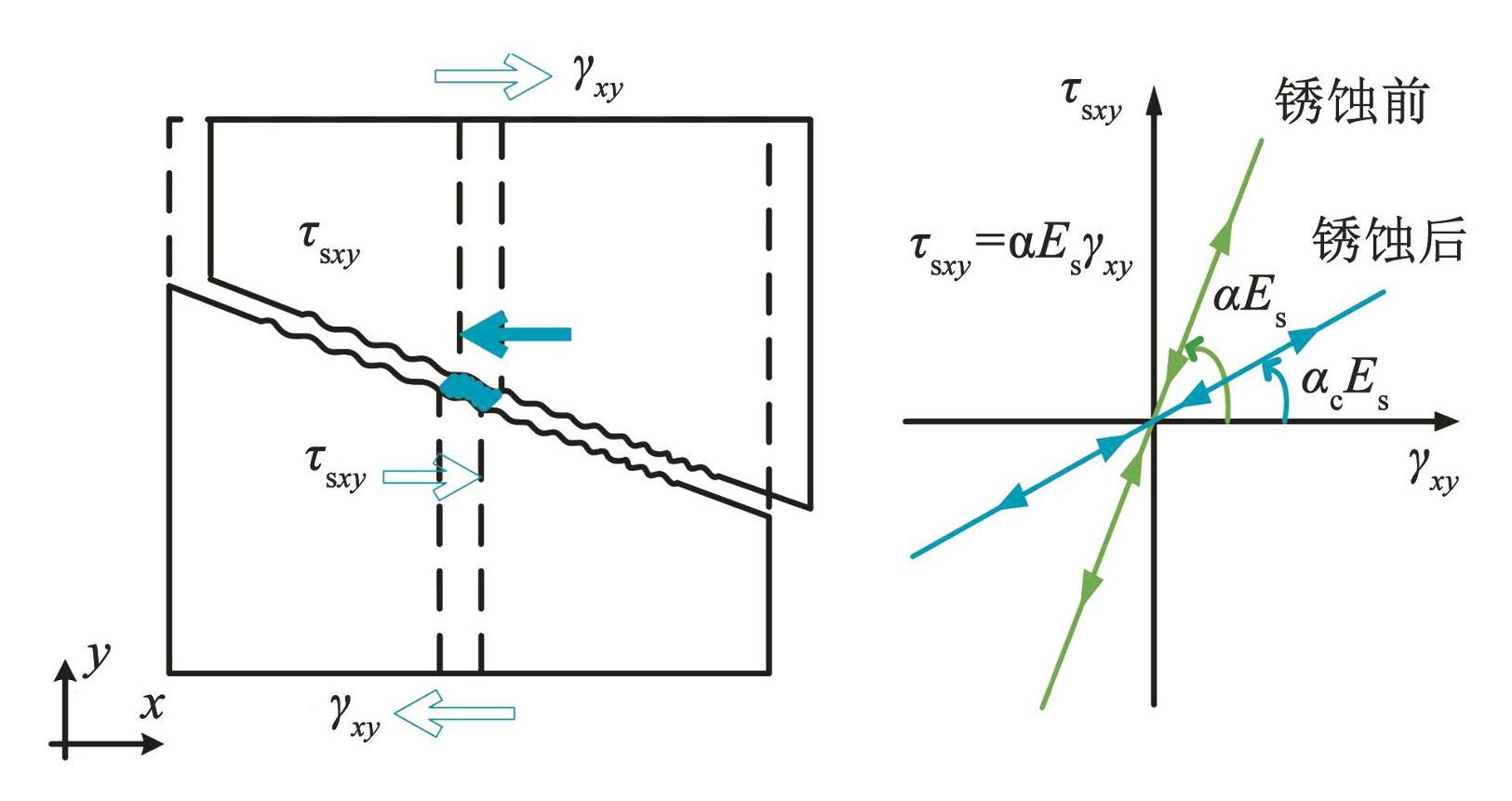
图13钢筋销钉作用

Fig.13Dowel action model

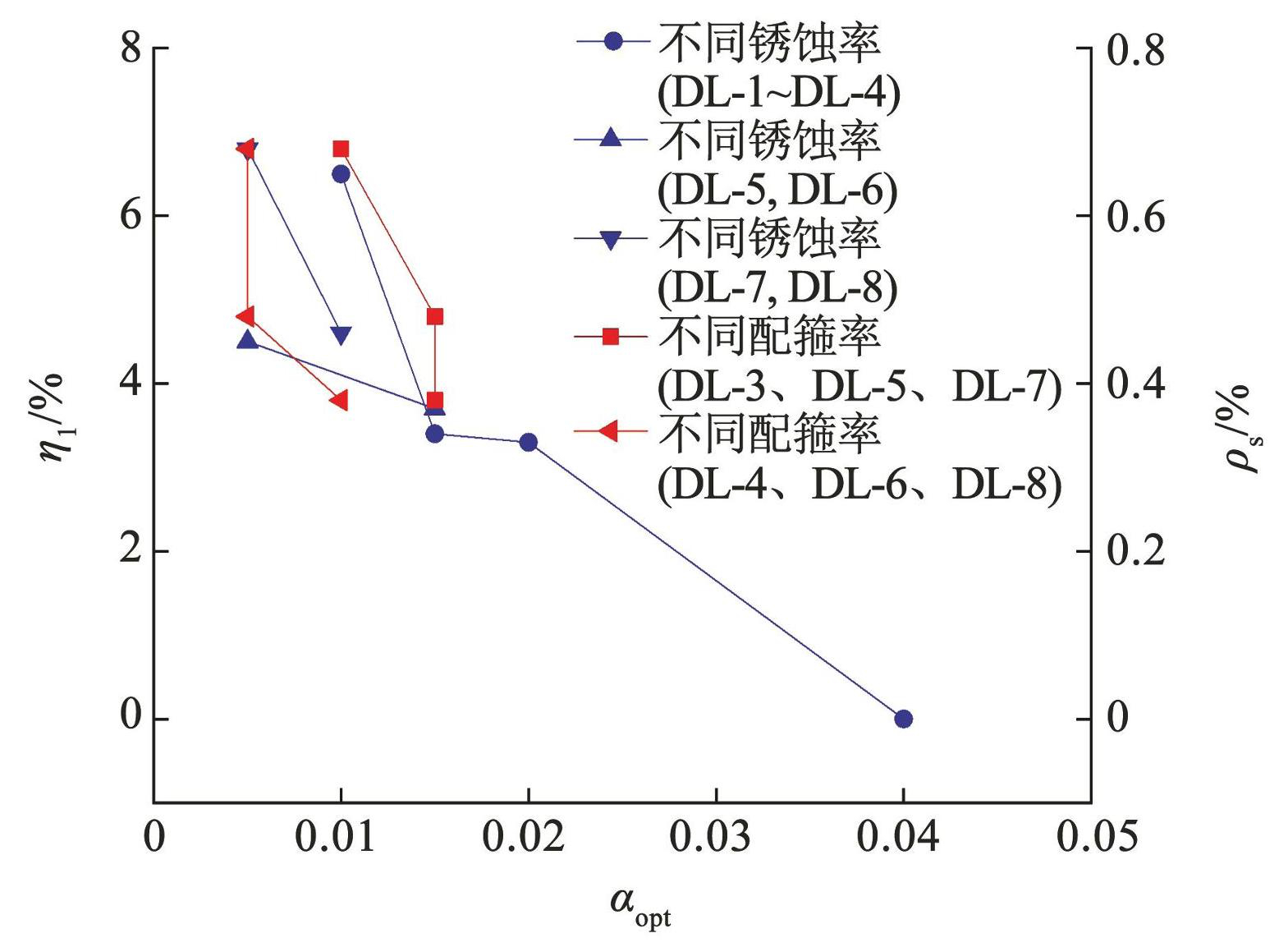
图14不同锈蚀程度及配箍率下销钉刚度参数

Fig.14Stiffness parameters of dowel action under different corrosion levels and stirrup ratios

表6不同 α 值下模型模拟误差

Tab.6 Modeling errors at different α values

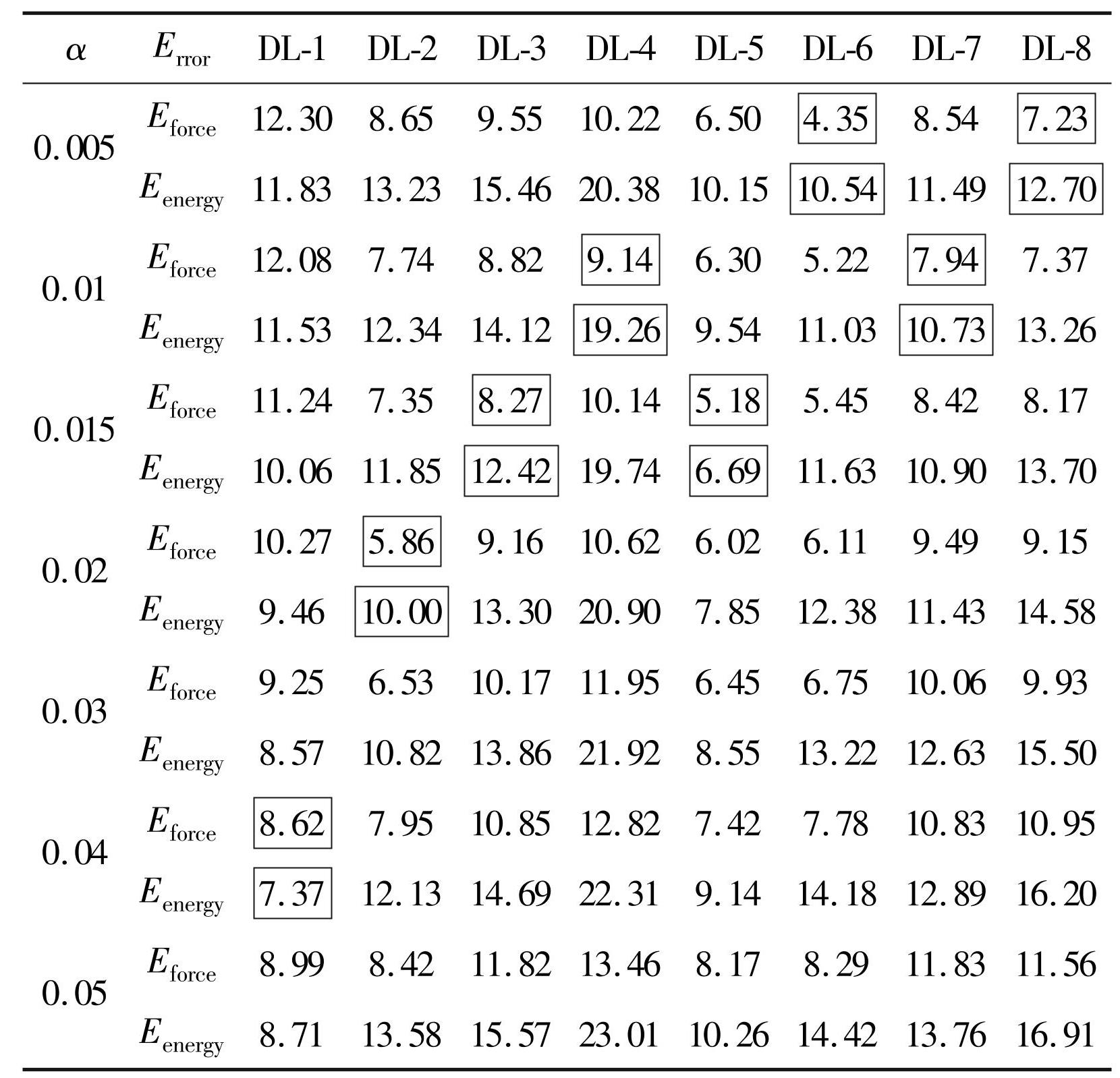
注:▭中为该试件在不同 α 值下的模拟误差最小值。

3.5 模型验证

基于上述建模方法，将 RC 梁试件按高度方向划分为 5 个 SFI-MVLEM 单元，按水平方向划分为 5 个RC 板单元（nDMaterial FSAM），分别对8 根不同参数下的 RC 试件进行数值建模。其中，SFIMVLEM 单元旋转中心参数 c 取为 0.4。模型中各锈蚀材料骨架曲线参数计算如前所述，滞回规则参数定义与未锈蚀材料相同。

采用式（23）、（24）计算试验曲线与模拟曲线的承载力误差（E_force）和累积耗能误差（E_energy），并将滞回曲线对比图绘于图15。可以看出，试验曲线与模拟曲线在初始刚度、承载力、捏缩特性、耗能特性等方面均吻合良好，所有试件的承载力和耗能能力误差均小于 20%，承载力误差的均值为8.95%，累积耗能能力误差的均值为 9.82%，表明该模型精度较高，可用于锈蚀 RC 梁抗震性能模拟。

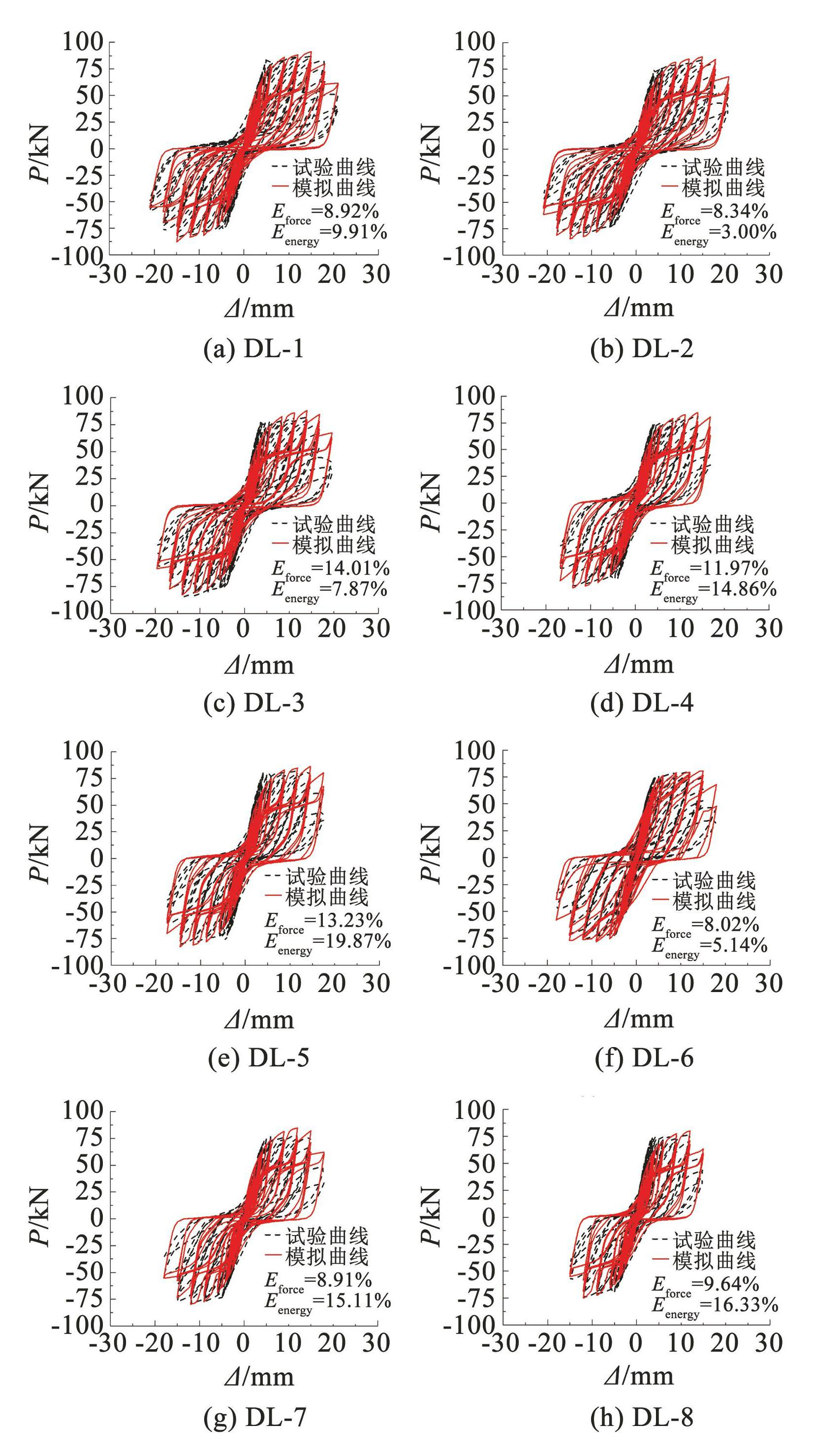
图15数值模拟与试验滞回曲线对比

Fig.15Comparison of numerical simulation and experimental hysteresis curves

4 结论

1）随锈蚀程度增加，试件的承载力、变形能力、耗能能力、延性等均降低，剪切破坏特征加重，不同配箍率下试件承载力和变形能力的劣化程度差异明显。配箍率的增加对锈蚀 RC 梁的承载力、变形能力和延性均有提高。

2）基于 SFI-MVLEM 单元和零长度单元，通过修正混凝土本构、钢筋本构模型和纵向钢筋的销钉作用本构模型，并考虑锈蚀钢筋混凝土黏结滑移效应，提出了锈蚀 RC 梁的数值建模方法。

3）根据所提数值模拟方法计算得到的滞回曲线与试验数据吻合较好，承载力误差与耗能误差均小于 20%，平均值分别为 8.95% 和 9.82%，表明该模拟方法能够较准确模拟锈蚀 RC 梁的滞回性能，可为氯盐侵蚀环境下 RC 结构抗震性能评估和新结构设计提供理论指导。

图1RC 梁设计原型

Fig.1Design prototype of RC frame beams

下载: 全尺寸图片

图2试件截面尺寸及配筋图

Fig.2Size and reinforcement of RC shear wall specimen

下载: 全尺寸图片

图3人工气候环境室

Fig.3Artificial climate environmental chamber

下载: 全尺寸图片

图4人工气候环境腐蚀方案

Fig.4Corrosion scheme of artificial climate environment

下载: 全尺寸图片

图5试件锈蚀现象

Fig.5Corrosion phenomenon of specimen

下载: 全尺寸图片

图6锈蚀钢筋

Fig.6Corroded steel bar

下载: 全尺寸图片

图7加载装置

Fig.7Loading equipment

下载: 全尺寸图片

图8加载制度示意

Fig.8Schematic diagram of loading process

下载: 全尺寸图片

图9试件破坏形态

Fig.9Failure mode of specimens

下载: 全尺寸图片

图10滞回曲线

Fig.10Hysteresis curves

下载: 全尺寸图片

图11骨架曲线

Fig.11Skeleton curves

下载: 全尺寸图片

图12锈蚀 RC 梁模型

Fig.12Corroded reinforced concrete beams model

下载: 全尺寸图片

图13钢筋销钉作用

Fig.13Dowel action model

下载: 全尺寸图片

图14不同锈蚀程度及配箍率下销钉刚度参数

Fig.14Stiffness parameters of dowel action under different corrosion levels and stirrup ratios

下载: 全尺寸图片

图15数值模拟与试验滞回曲线对比

Fig.15Comparison of numerical simulation and experimental hysteresis curves

下载: 全尺寸图片

表1锈蚀 RC 梁试件设计参数

下载: 全尺寸图片

表2混凝土配合比

下载: 全尺寸图片

表3钢筋材料的力学性能参数

下载: 全尺寸图片

表4钢筋平均锈蚀率

下载: 全尺寸图片

表5骨架曲线特征参数

下载: 全尺寸图片

表6不同 α 值下模型模拟误差

下载: 全尺寸图片

图1RC 梁设计原型

Fig.1Design prototype of RC frame beams

图2试件截面尺寸及配筋图

Fig.2Size and reinforcement of RC shear wall specimen

图3人工气候环境室

Fig.3Artificial climate environmental chamber

图4人工气候环境腐蚀方案

Fig.4Corrosion scheme of artificial climate environment

图5试件锈蚀现象

Fig.5Corrosion phenomenon of specimen

图6锈蚀钢筋

Fig.6Corroded steel bar

图7加载装置

Fig.7Loading equipment

图8加载制度示意

Fig.8Schematic diagram of loading process

图9试件破坏形态

Fig.9Failure mode of specimens

图10滞回曲线

Fig.10Hysteresis curves

图11骨架曲线

Fig.11Skeleton curves

图12锈蚀 RC 梁模型

Fig.12Corroded reinforced concrete beams model

图13钢筋销钉作用

Fig.13Dowel action model

图14不同锈蚀程度及配箍率下销钉刚度参数

Fig.14Stiffness parameters of dowel action under different corrosion levels and stirrup ratios

图15数值模拟与试验滞回曲线对比

Fig.15Comparison of numerical simulation and experimental hysteresis curves

表1锈蚀 RC 梁试件设计参数

表2混凝土配合比

表3钢筋材料的力学性能参数

表4钢筋平均锈蚀率

表5骨架曲线特征参数

表6不同 α 值下模型模拟误差

图1RC 梁设计原型

Fig.1Design prototype of RC frame beams

图2试件截面尺寸及配筋图

Fig.2Size and reinforcement of RC shear wall specimen

图3人工气候环境室

Fig.3Artificial climate environmental chamber

图4人工气候环境腐蚀方案

Fig.4Corrosion scheme of artificial climate environment

图5试件锈蚀现象

Fig.5Corrosion phenomenon of specimen

图6锈蚀钢筋

Fig.6Corroded steel bar

图7加载装置

Fig.7Loading equipment

图8加载制度示意

Fig.8Schematic diagram of loading process

图9试件破坏形态

Fig.9Failure mode of specimens

图10滞回曲线

Fig.10Hysteresis curves

图11骨架曲线

Fig.11Skeleton curves

图12锈蚀 RC 梁模型

Fig.12Corroded reinforced concrete beams model

图13钢筋销钉作用

Fig.13Dowel action model

图14不同锈蚀程度及配箍率下销钉刚度参数

Fig.14Stiffness parameters of dowel action under different corrosion levels and stirrup ratios

图15数值模拟与试验滞回曲线对比

Fig.15Comparison of numerical simulation and experimental hysteresis curves

表1锈蚀 RC 梁试件设计参数

表2混凝土配合比

表3钢筋材料的力学性能参数

表4钢筋平均锈蚀率

表5骨架曲线特征参数

表6不同 α 值下模型模拟误差

JUAN B, PONCE S, RUIZ S E,et al. Structural reliability of reinforced concrete buildings under earthquakes and corrosion effects[J]. Engineering Structures,2021,237(8):112161. DOI:10.1016/j.engstruct.2021.112161.

葛文杰, 张素康, 张志文, 等. 氯盐侵蚀作用后钢-BFRP 复合筋混凝土梁受弯性能[J]. 建筑结构学报,2023,44(8):170. GE Wenjie, ZHANG Sukang, ZHANG Zhiwen,et al. Flexural behavior of concrete beams reinforced with steel-BFRP composite bars subjected to chloride corrosion[J]. Journal of Building Structures,2023,44(8):170. DOI:10.14006/j.jzjgxb.2022. B037.

郑山锁, 郑跃, 刘华, 等. 氯盐侵蚀RC节点抗震性能与数值模拟方法[J]. 华中科技大学学报(自然科学版),2021,49(6):109. ZHENG Shansuo, ZHENG Yue, LIU Hua,et al. Seismic behavior and numerical modelling method of RC joints due to chloride erosion[J]. Journal of Huazhong University of Science and Technology(Natural Science Edition),2021,49(6):109. DOI:10.13245/j.hust.210620.

CHENG J F, LUO X Y, XIANG P. Experimental study on seismic behavior of RC beams with corroded stirrups at joints under cyclic loading[J]. Journal of Building Engineering,2020,32:101489. DOI:10.1016/j.jobe.2020.101489.

OU Y C, TASI L L, CHEN H H. Cyclic performance of large-scale corroded reinforced concrete beams[J]. Earthquake Engineering & Structural Dynamics,2012,41(4):593. DOI:10.1002/eqe.1145.

OU Y, CHEN H H. Cyclic behavior of reinforced concrete beams with corroded transverse steel reinforcement[J]. Journal of Structural Engineering,2014,140(9):04014050. DOI:10.1061/(ASCE)ST.1943-541X.0000932.

OU Y, NGUYEN N D. Influences of location of reinforcement corrosion on seismic performance of corroded reinforced concrete beams[J]. Engineering Structures,2016,126:210. DOI:10.1016/j.engstruct.2016.7.048.

OU Y, NGUYEN N D. Plastic hinge length of corroded reinforced concrete beams[J]. ACI Structural Journal,2014,111(5):1049. DOI:10.14359/51686872.

LIU X J, JIANG H J, YE Y. Deformation-based performance index of corroded reinforced concrete beams[J]. Journal of Building Engineering,2021,34:101940. DOI:10.1016/j.jobe.2020.101940.

中华人民共和国住房和城乡建设部. 建筑抗震试验规程: JGJ/T 101—2015[S]. 北京: 中国建筑工业出版社,2015.Ministry of Housing and Urban Rural Development of the People′s Republic of China. Specification for seismic test of buildings: JGJ/T 101—2015[S]. Beijing: China Architecture & Building Press,2015.

中华人民共和国住房和城乡建设部. 高层建筑混凝土结构技术规程: JGJ 3—2010[S]. 北京: 中国建筑工业出版社,2002.Ministry of Housing and Urban Rural Development of the People′s Republic of China. Technical specification for concrete structures of tall building: JGJ 3—2010[S]. Beijing: China Architecture & Building Press,2002.

ZHENG Yue, ZHENG Shansuo, YANG Lu,et al. Experimental study on the seismic behavior of corroded reinforced concrete walls in an artificial climate corrosion environment[J]. Engineering Structures,2022,252:113469. DOI:10.1016/j.engstruct.2021.113469.

中华人民共和国住房和城乡建设部. 普通混凝土长期性能和耐久性试验方法标准: GB/T 50082—2009[S]. 北京: 中国建筑工业出版社,2009.Ministry of Housing and Urban Rural Development of the People′s Republic of China. Standard for test methods of long-term performance and durability of ordinary concrete: GB/T 50082—2009[S]. Beijing: China Architecture & Building Press,2009.

袁迎曙, 章鑫森, 姬永生. 人工气候与恒电流通电法加速锈蚀钢筋混凝土梁的结构性能比较研究[J]. 土木工程学报,2006(3):42.YUAN Yingshu, ZHANG Xinsen, JI Yongsheng. A comparative study on structural behavior of deteriorated reinforced concrete beam under two different environments[J]. China Civil Engineering Journal,2006(3):42. DOI:10.3321/j.issn:1000-131X.2006.03.006.

蒋连接, 袁迎曙. 反复荷载下锈蚀钢筋混凝土柱力学性能的试验研究[J]. 工业建筑,2012,42(2):66.JIANG Lianjie, YUAN Yingshu. Experimental study on mechanical behavior of corroded reinforced concrete column under cyclic loading[J]. Industrial Construction,2012,42(2):66. DOI:10.13204/j.gyjz201202015.

ZHOU Y, ZHENG SS, CHEN L Z,et al. Experimental and analytical investigations into the seismic behavior and resistance of corroded reinforced concrete walls[J]. Engineering Structures,2021,238:112154. DOI:10.1016/j.engstruct.2021.112154.

YUAN Y S, JI Y S, SURENDRA P S. Comparison of two accelerated corrosion techniques for concrete structures[J]. ACI Structural Journal,2007,104:344. DOI:10.1002/tal.311.

薛伟辰, 程斌, 李杰. 预应力与非预应力高性能混凝土梁抗震性能试验研究与有限元分析[J]. 建筑结构学报,2004,25(1):1.XUE Weichen, CHENG Bing, LI Jie. Experimental studies and FEM analysis of seismic behavior of prestressed and non-prestressed high performance concrete beams[J]. Journal of Building Structure,2004,25(1):1. DOI:10.14006/j.jzjgxb.2004.01.001.

KOLOZVARI K. Analytical modeling of cyclic shear-flexure interaction in reinforced concrete structural walls[D]. Los Angeles: University of California,2013. DOI:10.1061/(ASCE)ST.1943-541X.0001083.

ULUGTEKIN D. Analytical modeling of reinforced concrete panel elements under reversed cyclic loadings[D]. Istanbul: Bogazici University,2010.

张伟平, 商登峰, 顾祥林. 锈蚀钢筋应力-应变关系研究[J]. 同济大学学报(自然科学版),2006(5):586.ZHANG Weiping, SHANG Dengfeng, GU Xianglin. Stress-strain relationship of corroded steel bars[J]. Journal of Tongji University(Natural Science),2006,34(5):586. DOI:10.3321/j.issn:0253-374X.2006.05.004.

HASKETT M, OEHLERS D, ALI M. Local and global bond characteristics of steel reinforcing bars[J]. Engineering Structures,2008,30:376. DOI:10.1016/j.engstruct.2007.04.007.

BELARBI A, HSU T. Constitutive laws of softened concrete in biaxial tension compression[J]. ACI Structural Journal,1995,92(5):562. DOI:10.14359/907.

郑山锁, 郑跃, 董立国, 等. 近海环境下锈蚀箍筋约束混凝土本构模型[J]. 浙江大学学报(工学版),2020,54(1):48.ZHENG Shansuo, ZHENG Yue, DONG Liguo,et al. Constitutive model of confined concrete by corroded stirrups in coastal environment[J]. Journal of Zhejiang University(Engineering Science),2020,54(1):48. DOI:10.3785/j.issn.1008-973X.2020.01.006.

MANDER J, PRIESTLEY M. Theoretical stress-strain model for confined concrete[J]. Journal of Structural Engineering,1988,114(8):1804. DOI:10.1061/(ASCE)0733-9445(1988)114:8(1804).

张艺欣, 郑山锁, 荣先亮, 等. 考虑粘结滑移的冻融损伤纤维梁柱模型研究[J]. 工程力学,2020,37(9):208.ZHANG Yixin, ZHENG Shansuo, RONG Xianliang,et al. Research on freeze-thaw damage model of fiber beam-column considering reinforcement slip effect[J]. Engineering Mechanics,2020,37(9):208. DOI:10.6052/j.issn.1000-4750.2019.11.0657.

GHANNOUM W M, MOEHLE J P. Dynamic collapse analysis of a concrete frame sustaining column axial failures[J]. ACI Structural Journal,2012,109(3):403.

潘志宏, 李爱群, 孙义刚. 反复荷载下锈蚀黏结退化的RC结构数值模拟[J]. 中国矿业大学学报,2010,39(3):362.PAN Zhihong, LI Aiqun, SUN Yigang. Numerical simulation of reinforced concrete structures under cyclic loads:the effects of bond deterioration due to reinforcement corrosion[J]. Journal of China University of Mining & Technology,2010,39(3):362.

CHORZEPA M, KIM Y J, YUN G J,et al. Cyclic shear-friction constitutive model for finite element analysis of reinforced concrete membrane elements[J]. ACI Structural Journal,2011,108(3):324. DOI:10.1128/MCB.20.21.7881-7892.2000.

LI L, LUO G, WANG Z,et al. Prediction of residual behaviour for post-earthquake damaged reinforced concrete column based on damage distribution model[J]. Engineering Structures,2021,234:111927. DOI:10.1016/j.engstruct.2021.111927.

1 试验

2 试验结果及分析

3 数值模型建立

4 结论

友情链接LINKS