欢迎访问《哈尔滨工业大学学报》编辑部网站！

型钢-钢纤维混凝土局部组合梁受力性能

doi: 10.11918/202310061

伍凯，杨毅恒，诸睿哲，张雁杰，梁庆庆，王世龙

河海大学土木与交通学院,南京 210024

基金项目: 国家自然科学基金(51208175) ；中央高校基本科研业务费专项(B200202067)

详细信息

作者简介

伍凯(1980—),男,博士,副教授

通讯作者

伍凯,wukai19811240@163.com

中图分类号: TU398

文献标识码: A

文章编号: 0367-6234(2025)02-0153-11

Structural behavior of locally composite steel and steel fiber reinforced concrete beams under monotonic loading

WU Kai ， YANG Yiheng ， ZHU Ruizhe ， ZHANG Yanjie ， LIANG Qingqing ， WANG Shilong

College of Civil and Transportation Engineering,Hohai University, Nanjing 210024 , China

摘要

为解决型钢混凝土结构的施工困难,充分发挥各部分材料的性能优势,将钢筋笼离散化为随机分布的钢纤维,并将钢纤维混凝土集中应用于受压区,形成型钢-钢纤维混凝土局部组合梁。对 18 根不同钢纤维体积率(ρ_sf)、剪跨比(λ)、型钢受压翼缘上下部混凝土保护层厚度(C_ss、C_sv)和型钢规格(I_s)的组合梁试件进行四点弯试验。分析试验参数对破坏模式、荷载-挠度曲线以及破坏对称性的影响。结果表明:增大 ρ_sf对小剪跨比试件(λ 为 1.5 或 1.7)的界面黏结性能具有积极改善作用,试件破坏模式由界面破坏转为弯扭破坏;混凝土保护层厚度须随 I_s 同步增大,确保混凝土保护层对型钢提供足够的“握裹效应”,避免或削弱弯扭变形的不利影响。通过高斯分布拟合,得到试件整体性能开始出现严重退化时的挠度退化系数,进而对构件整体性能开始出现严重退化时的挠度进行预测。

关键词

组合结构 / 型钢混凝土 / 钢纤维混凝土 / 破坏模式 / 荷载-挠度曲线 / 能量耗散

Abstract

To address the construction difficulties of steel reinforced concrete structures and fully leverage material performance, the rebar cage was discretized into randomly distributed steel fibers. Steel fiber reinforced concrete was concentrated in the compression zone to form the locally composite steel and steel fiber reinforced concrete structure. Four-point bending tests were carried out on 18 beam specimens with different steel fiber volume fractions (ρ_sf), shear span ratios (λ), concrete protective layer thicknesses for upper and lower parts of steel compression flange (C_ss and C_sv), and shaped steel specifications (I_s). The effects of these test parameters on failure modes, load-deflection curves, and failure symmetry of specimens were analyzed. The results show that increasing ρ_sfhad a positive effect on improving the interface bonding performance for specimens with smaller λ (1. 5 or 1. 7), and the failure mode changed from interface failure to bending-torsion failure. To ensure that the concrete protective layer provides sufficient " grip-wrap effect" on the shaped steel and avoid or weaken the adverse effects of bending and torsion deformation, C_ss and C_sv should increase simultaneously with I_s . The deflection degradation coefficient was obtained by Gaussian distribution fitting, and the deflection when the specimen′s overall performance began to seriously degrade was predicted.

Keywords

composite structure / steel reinforced concrete / steel fiber reinforced concrete / failure modes / loaddeflection curves / energy dissipation

1 试验 1.1 试验材料 1.1.1 钢纤维混凝土 1.1.2 型钢 1.2 试件设计 1.3 加载及测量方式 2 破坏模式及荷载-挠度曲线 2.1 破坏模式 2.1.1 λ 为 1.5 或 1.7 2.1.2 λ 为 2.5 或 2.8 2.2 荷载-挠度曲线 3 试件耗能分析 3.1 能量的定义与分类 3.2 挠度退化系数 4 结论

在传统的钢筋混凝土（ reinforced concrete，RC）结构中设置型钢形成型钢混凝土（ steel reinforced concrete，SRC）结构，已被广泛研究与应用^[1-3]。但 SRC 结构同时配置钢筋笼和型钢，容易出现钢材的空间冲突问题^[4-5]。此外，SRC 结构中钢材配置较为密集，混凝土浇筑、振捣空间受限，容易出现混凝土浇筑不密实的情况^[6-7]。外围钢筋笼的存在限制了结构所能配置型钢的规格，翼缘宽度以及腹板高度较小的型钢提供的受弯、受剪承载力有限，无法充分发挥 SRC 结构的优势。

在混凝土中掺入一定体积率的钢纤维形成钢纤维混凝土（ steel fiber reinforced concrete，SFRC），通过“桥接效应”，钢纤维可以改善混凝土的抗拉强度，抑制裂缝发展，进而提高构件的承载能力与延性^[8-10]。作为一种复合材料，SFRC 已经得到广泛的研究与工程应用^[11-13]，包括钢纤维代替箍筋甚至纵筋的可行性相关研究。 Yun 等^[14] 的研究结果表明，SFRC 梁的受剪承载力与钢纤维抗拉强度呈正相关，钢纤维可以起到箍筋的受剪加固作用。进一步，Sahoo 等^[15]基于无箍筋 SFRC 梁的单调加载试验，发现最小钢纤维体积率为 1% 时，无箍筋 SFRC 梁发生延性破坏。 Yoo 等^[16] 指出 0.75% 体积率的弯钩型钢纤维可以有效替代受剪箍筋。 Yakoub 和 Xu 等^[17-18]基于钢纤维对 SFRC 受剪承载力贡献的方程，进一步提出无箍筋 SFRC 梁受剪承载力计算公式。

在课题组已完成的试验研究中，为了解决 SRC 结构的工程应用难题，将 SRC 结构中的钢筋笼离散化为钢纤维，形成无钢筋笼的型钢钢纤维混凝土（steel and steel fiber-reinforced concrete，SSFRC）结构^[19-20]。相比 SRC 结构，无钢筋笼的 SSFRC 结构不再存在型钢与钢筋笼的空间位置冲突问题，避免了复杂的钢筋绑扎工序，保证了混凝土的浇筑质量。型钢翼缘可以更加远离中和轴，从而提供更大的受弯、受剪承载力，还可以避免受压区混凝土压碎后脱落伤人。结合钢-混凝土组合梁^[21]、 SRC 组合梁^[22]，在 SSFRC 结构的基础上，考虑钢纤维混凝土和型钢各自受拉、受压性能的特点。进一步提出型钢-钢纤维混凝土局部组合（ locally composite steel and steel fiber reinforced concrete，LCSSFRC）结构。 LCSSFRC 结构在继承 SSFRC 结构优点的同时，将抗拉能力弱的混凝土集中应用于组合梁受压区，型钢下翼缘直接承受拉力作用，充分发挥两种材料的性能优势。同时减轻构件自重，减小截面高度，增加了结构的可利用空间。

通过 18 根 LCSSFRC 试件的四点弯试验，得到试件的破坏发展过程与荷载-挠度曲线。在已有研究的基础上^[23]，进一步讨论了能量耗散与能量损伤之间的相对关系。由高斯分布拟合得到预估的挠度退化系数，用来预测 LCSSFRC 构件整体性能开始出现严重且迅速退化时的挠度，为结构加固工程提供参考。

1 试验

1.1 试验材料

1.1.1 钢纤维混凝土

共制备两种不同钢纤维体积率（ ρ_sf）的钢纤维混凝土，还包括不掺钢纤维的对照组。所选用水泥、骨料和钢纤维的性能参数详见文献^[23]的 2.1 节。根据 JGJ55—2011 ^[24] 进行混凝土配合比设计。在浇筑不同 ρ_sf的试件时，预留同批次钢纤维混凝土，制作标准立方体试块（150 mm × 150 mm × 150 mm）进行混凝土抗压强度试验。钢纤维混凝土详细配合比设计以及所测得的平均立方体抗压强度（ f_cu）见文献^[23]的表1。

1.1.2 型钢

采用符合 GB / T706—2016 ^[25] 的 I12 和 I14 热轧型钢，每种型钢分别从翼缘和腹板位置各取 3 个样本进行力学性能试验。型钢的详细尺寸及力学性能试验结果见表1。

表1型钢截面尺寸及力学性能

Tab.1 Section dimensions and mechanical properties of shaped steels

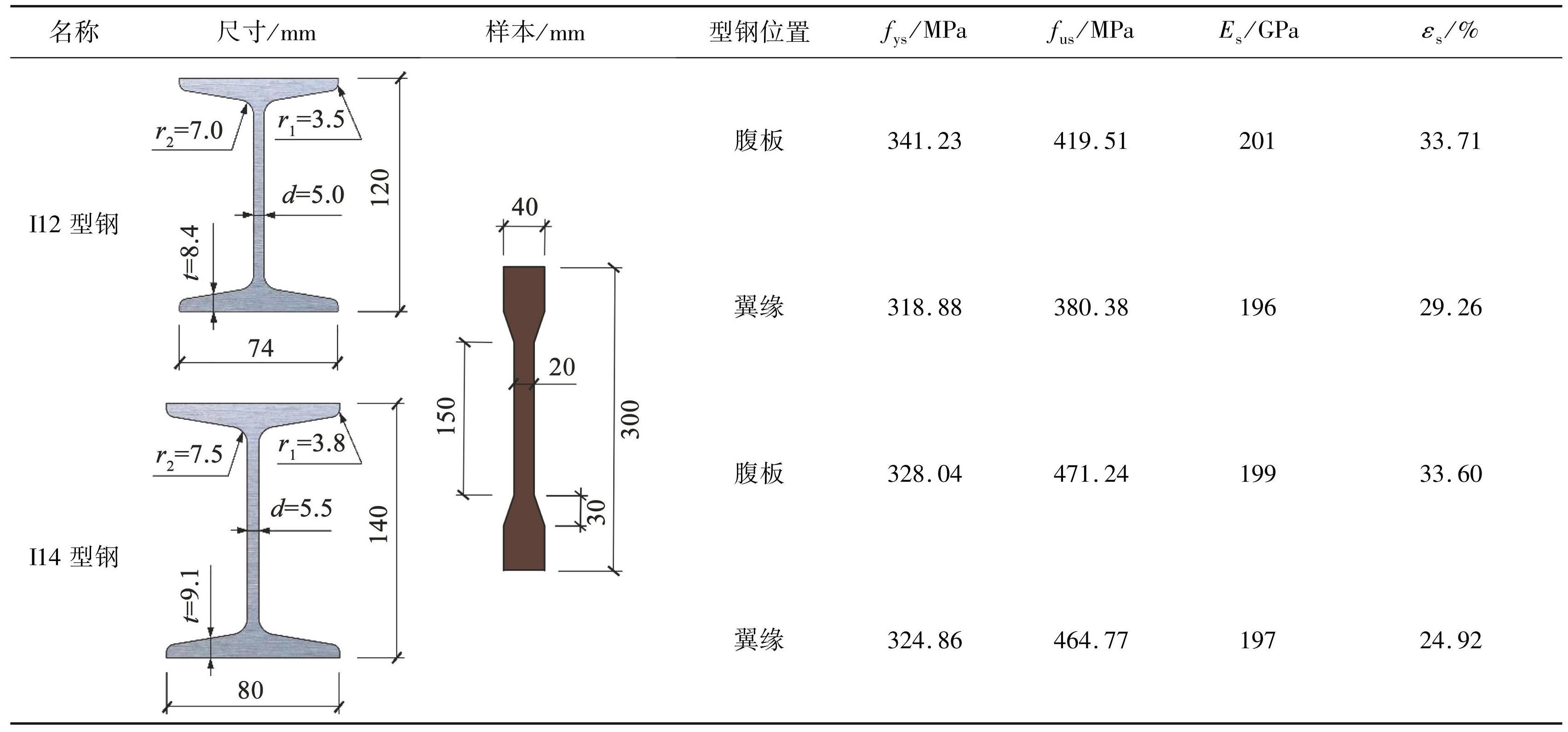
注:t 为翼缘平均厚度，d 为腹板厚度，r₁为翼缘弧半径，r₂为内弧半径，f_ys和 f_us分别为屈服强度和极限强度，E_s为弹性模量，ε_s为伸长率。

1.2 试件设计

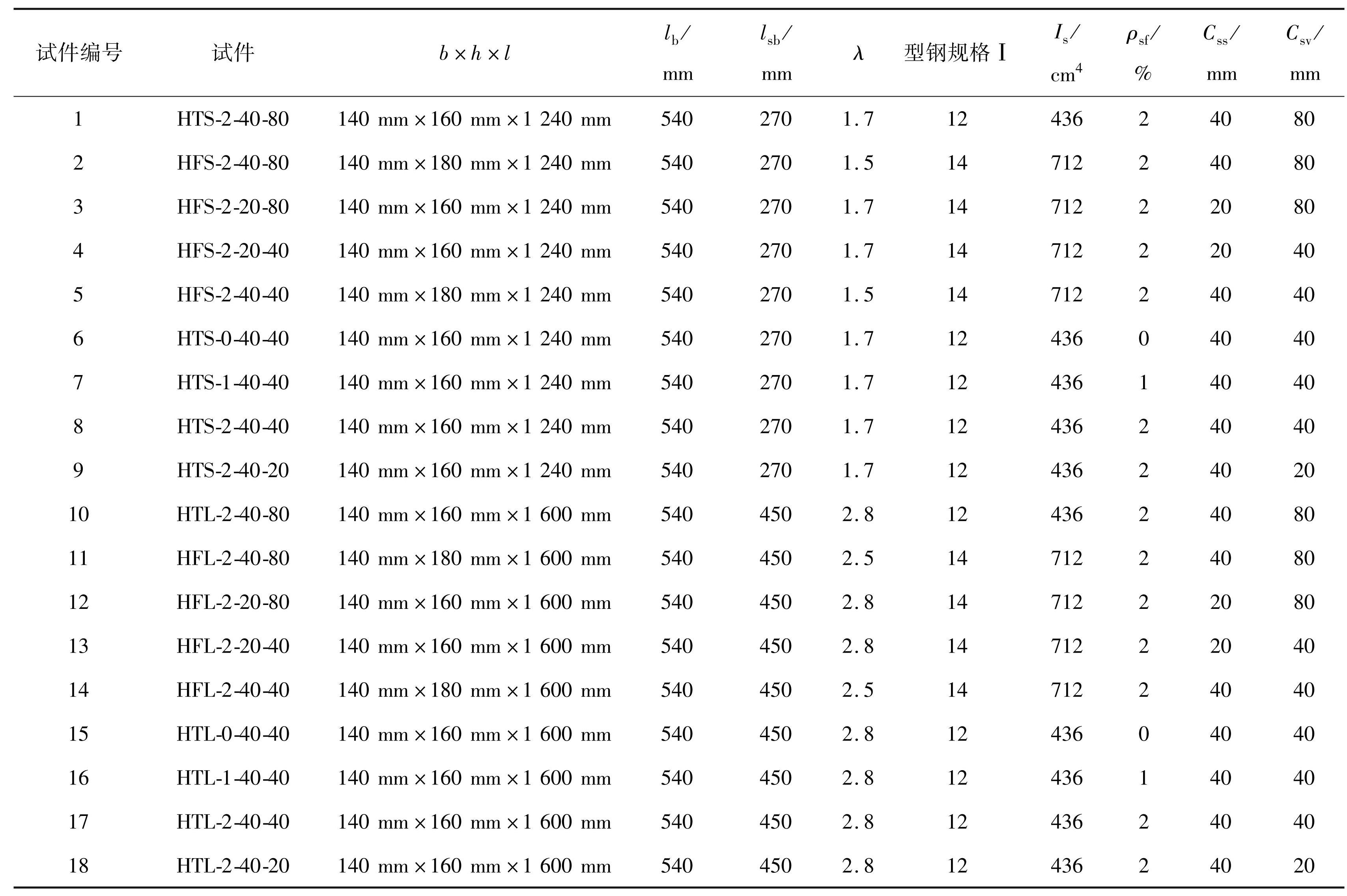
共设计 18 根 LCSSFRC 梁试件，所有试件的横截面宽度（ b）均为 140 mm，高度（ h）包括 160、 180 mm，横截面形式如图1所示。试件长度（ l）包括 1240、1600 mm。试件在两个分载点之间，仅承受弯矩部分的长度记为纯弯段长度（l_b）; 某一侧分载点到邻近支座之间，同时承受剪力和弯矩部分的长度记为剪弯段长度（ l_sb）。 LCSSFRC 梁的剪跨比（λ）分别为 1.5、1.7、2.5 和 2.8，这是因为 h 有两种取值，相同 l_sb的试件存在两种 λ。型钢规格包括 I12和 I14，两种型钢强轴方向惯性矩（ I_s）分别为 436、712 cm⁴。通过实际工程调查得 SRC 梁中纵筋与箍筋体积率之和介于 1%~3% ^[26-27]，平均值为 2%。由于钢纤维混凝土主要应用于梁受压区，并考虑钢纤维混凝土的流动性，本试验共设置 1% 和 2% 两种钢纤维体积率（ ρ_sf），并设置 ρ_sf 为 0 的对比试件（HTS-0-40-40 和 HTL-0-40-40）。如图1所示，型钢受压翼缘上、下部混凝土保护层厚度分别记为 C_ss、 C_sv，试件详细设计参数见表2。试件编号说明详见文献^[23]的 2.2 节。

图1试验加载方式以及试件截面

Fig.1Test setup and cross section of specimens

表2LCSSFRC 试件设计参数

Tab.2 Design parameters of LCSSFRC specimens

1.3 加载及测量方式

如图1所示，通过分载梁，液压伺服系统对试件施加对称的单调集中荷载（P）。所有试件采用位移控制加载方式，试件开裂前后的位移加载速率分别为 0.6、1 mm / min。直至试件荷载持续下降至 0.85 倍峰值荷载时停止加载。沿着梁的纵向布置多个位移传感器（ LVDT），测量试件跨中以及分载点位置的位移。由于监测系统故障，试件 HTS-2-40-20 与 HTL-2-40-40 仅测得试验机内部位移传感器数据，即两个分载点位移的平均值。

2 破坏模式及荷载-挠度曲线

2.1 破坏模式

根据主导破坏的裂缝类型，综合考虑各试件裂缝发展过程与最终的破坏形态，将 18 根试件的破坏模式分为界面破坏、弯扭破坏和弯曲破坏。

2.1.1 λ 为 1.5 或 1.7

λ 为 1.5 或 1.7 的 9 根小剪跨比试件中，HTS0-40-40、 HTS-1-40-40、 HTS-2-40-80、 HFS-2-20-40、HFS-2-20-80、HFS-2-40-40 和 HFS-2-40-80 发生界面破坏。加载过程中，变形不协调而产生的界面剪应力和拉应力是界面破坏的主要原因，界面破坏集中发生在剪切效应更加显著的小剪跨比试件中，破坏形态如图2（a）所示。

随着 ρ_sf增大或混凝土保护层厚度（C_ss和 C_sv）减小，小剪跨比试件的破坏由界面破坏转为弯扭破坏（HTS-2-40-20 和 HTS-2-40-40）。荷载作用下，部分试件的型钢除了产生竖向挠度，还会出现侧向弯曲与扭转变形。型钢翼缘的弯扭变形导致外裹混凝土由内而外被撕裂，试件顶部出现了不同程度的扭转斜裂缝，组合梁剪弯段存在翘起现象。在侧向弯曲与扭转的耦合作用下，试件发生弯扭破坏。试验结束后，将混凝土保护层剥离，可观察到型钢存在明显的弯扭变形，破坏形态如图2（b）所示。对比界面破坏试件（ HTS-0-40-40、HTS-1-40-40）与弯扭破坏试件（HTS-2-40-40）可知，增大 ρ_sf 可以改善试件界面黏结性能，更好地维持型钢与钢纤维混凝土的组合效应，避免出现界面破坏。

图2试件的破坏模式

Fig.2Failure modes of specimens

2.1.2 λ 为 2.5 或 2.8

随着剪跨比增大，试件所受弯曲效应更加显著，试件的破坏模式由界面破坏转为弯扭或者弯曲破坏。型钢规格（I_s）则对试件发生弯扭破坏还是弯曲破坏起着关键的控制作用。相比配置 I12 型钢的试件，配置 I14 型钢的 4 根试件（HFL-2-20-40、HFL-2-40-40、HFL-2-20-80 和 HFL-2-40-80）混凝土保护层的厚度相对较小，对型钢提供的握裹约束作用不足，弯扭变形的不利影响占主导作用，试件最终发生弯扭破坏。

相比 I14 型钢，I12 型钢所需握裹约束作用相对更小，在相同的混凝土保护层厚度下，侧向弯曲与扭转效应的影响被削弱，其余 5 根配置 I12 型钢的试件转而发生弯曲破坏。随着加载的进行，分载点下方钢纤维混凝土自下而上开始出现弯曲裂缝，并不断延伸和扩宽。当荷载增大至峰值荷载附近时，分载点下方可观察到长且宽的弯曲裂缝，称为主弯曲裂缝，同时纯弯区可观察到较多细小的弯曲裂缝，称为次弯曲裂缝。最终，试件的主、次弯曲裂缝发展充分，试件发生弯曲破坏，详见图2（c）。

2.2 荷载-挠度曲线

18 根试件的 P-

Δ

₁、P-

Δ

₂、P-

Δ

₃曲线及特征点位置如图3所示。其中，P 为分载点处荷载，

Δ

₁为梁的跨中挠度，

Δ

₂、

Δ

₃为梁两侧分载点挠度。（

Δ

₁-

Δ

₂）和（

Δ

₁-

Δ

₃）代表梁跨中与两侧分载点的挠度差，与组合梁弯曲效应强弱密切相关。特征点相关描述详见文献^[23]的 3.2 节，基于 P-

Δ

₁曲线的各特征点性能指标详见文献^[23]的表4。

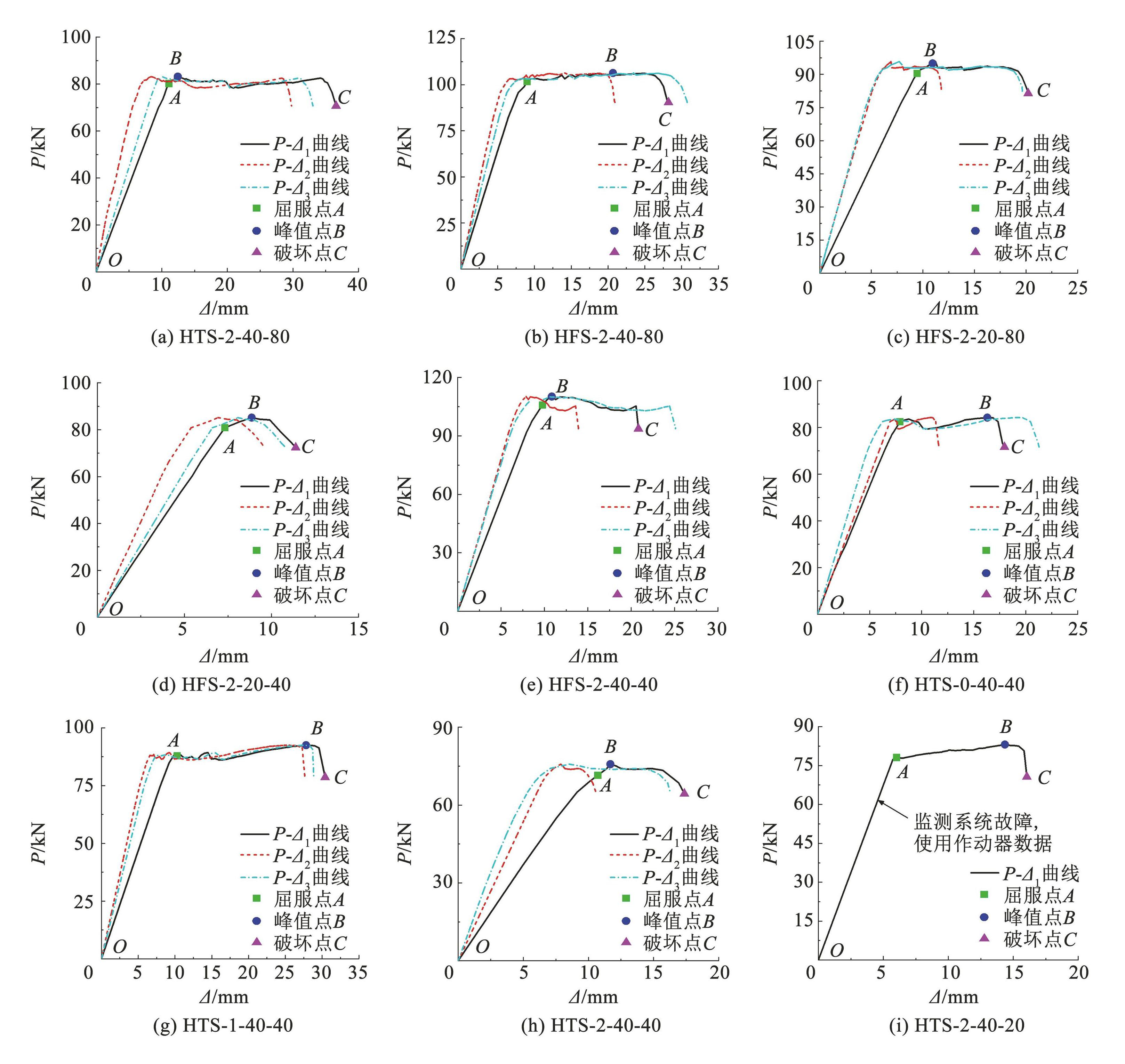
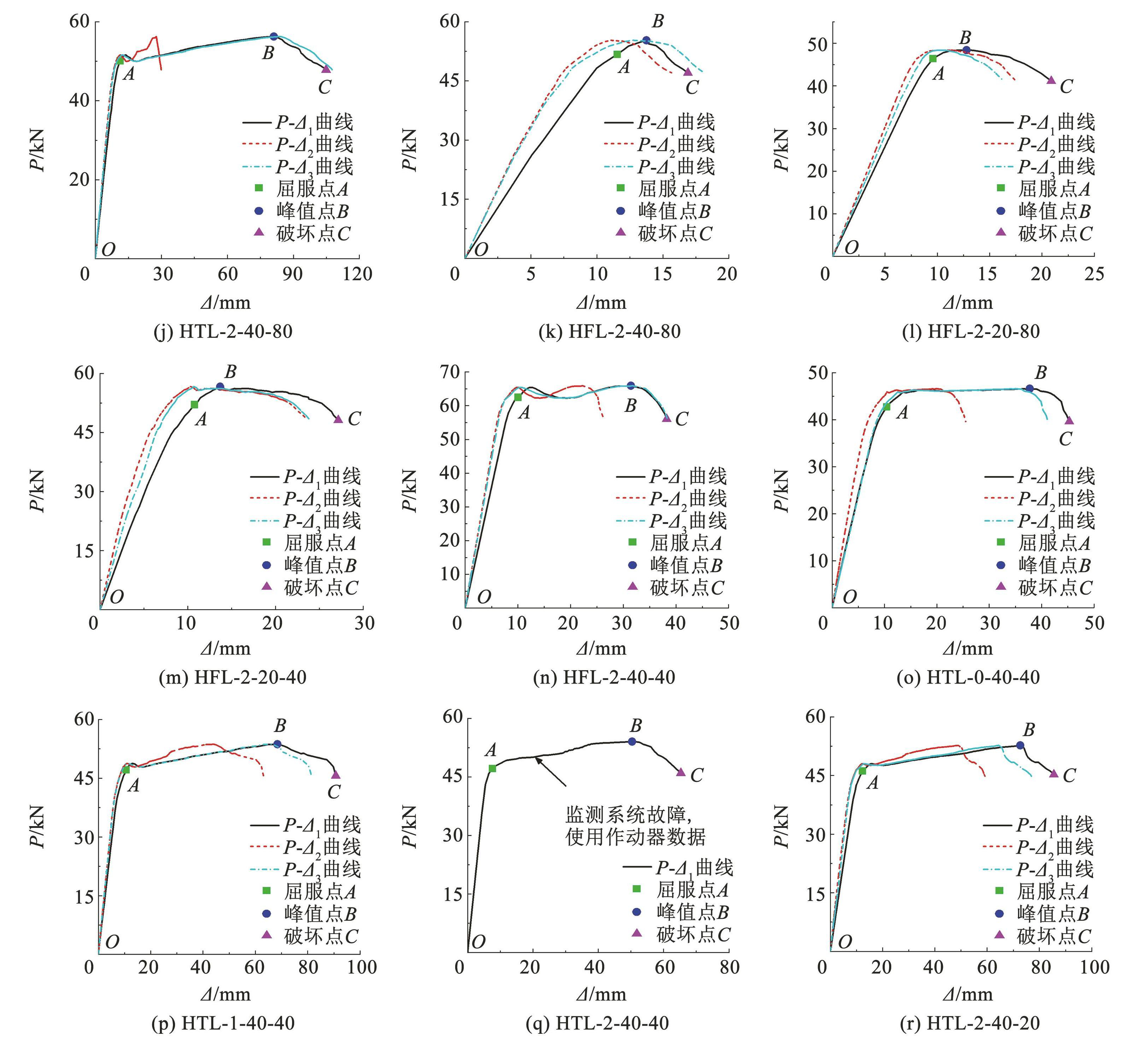
图3荷载-挠度曲线

Fig.3Load-deflection curves

多数试件

Δ

₁的增速大于

Δ

₂与

Δ

₃的增速，最终破坏时，（

Δ

₁-

Δ

₂）和（

Δ

₁-

Δ

₃）均大于 0，试件破坏对称性较好，如图4（a）所示。少部分试件的破坏集中在某一侧剪弯段，该侧分载点挠度增长迅速，即

Δ

₁的增速较

Δ

2 或

Δ

3 的增速更小。最终破坏时，（

Δ

₁-

Δ

₂）或（

Δ

₁-

Δ

₃）小于 0，试件发生非对称破坏，如图4（b）所示。如果梁跨中的弯曲效应较强，还可能出现某一侧分载点挠度增速与跨中挠度增速相似，且大于另一分载点挠度增速。最终破坏时，（

Δ

₁-

Δ

₂）或（

Δ

₁-

Δ

₃）趋近于 0，试件发生临界破坏，如图4（c）所示。表3给出了试件破坏对称性的类型。相比大剪跨比（λ 为 2.5 或 2.8）试件，小剪跨比试件（λ 为 1.5 或 1.7）的剪切作用更加显著，破坏主要集中在剪弯段，两个剪弯段的破坏更容易出现不对称性。因此，非对称破坏主要发生在小剪跨比的界面破坏试件中。

图4挠度分布类型

Fig.4Types of deflection distribution

表3试件性能指标

Tab.3 Performance indexes of specimens

注:由于监测系统故障，试件 HTS-2-40-20 和 HTL-2-40-40 仅获得作动器数据。

3 试件耗能分析

3.1 能量的定义与分类

基于实际的 P-

Δ

₁曲线，假定试件始终处于完全弹性状态，则 P 随

Δ

₁始终呈线性增加，称该状态下的 P-

Δ

₁ 曲线为理想 P-

Δ

₁ 曲线，如图5所示。 LCSSFRC 梁在外荷载（2P）作用下产生相应挠度，整个加载过程即外荷载做功的过程，P-

Δ

₁ 曲线包络面积的 2 倍即为外荷载所做的功。对于实际和理想状态下的 P-

Δ

₁曲线，外荷载所做的功分别记为 W 和 W′。如图5（a）所示，对于两种状态下的 P-

Δ

₁曲线，当

Δ

_i<

Δ

_y时，试件仅出现弹性变形，外荷载所做的功 W （ W′）均全部转化为试件的弹性变形能 W_ai（W′_ai）。 W_ai与 W′_ai的计算公式:

W = W^{'} = W_{a i} = W_{a i}^{'} = 0.5 \times (P_{i}^{2} / K_{0}) \times 2

(1)

K_{0} = P_{y} / Δ_{y}

(2)

式中:P_i为任意点 i 的荷载，K₀为初始弹性刚度，P_y为屈服点荷载，Δ_y为屈服点挠度。

A 点之后，实际与理想状态下的 P -

Δ

₁ 曲线开始出现差异。如图5（ b）所示，当

Δ

_i >

Δ

_y时，理想 P-

Δ

₁曲线所对应的试件，外荷载做功 W′仍仅转化为弹性变形能 W′_ai。但在实际的加载条件下，试件不再处于完全弹性状态，除弹性变形外，试件还会产生塑性变形。因此，外荷载做功 W 除转化为弹性变形能 W_ai外，还有一部分转化为塑性变形能 W_bi，计算公式如下:

W^{'} = W_{a i}^{'} = 0.5 \times K_{0} Δ_{i}^{2} \times 2

(3)

W = W_{a i} + W_{b i}

(4)

W_{a i} = 0.5 \times (P_{i}^{2} / K_{0}) \times 2

(5)

W_{c i} = W^{'} - W

(6)

式中:Δ_i为任意点 i 的挠度，K₀与 P_i的定义同前。可以看出，对于完全弹性和实际状态下的试件，外荷载做功存在一个差值。将这个差值定义为试件未能始终保持完全弹性状态而产生的能量损伤 W_ci，如图5（b）中深色区域所示。

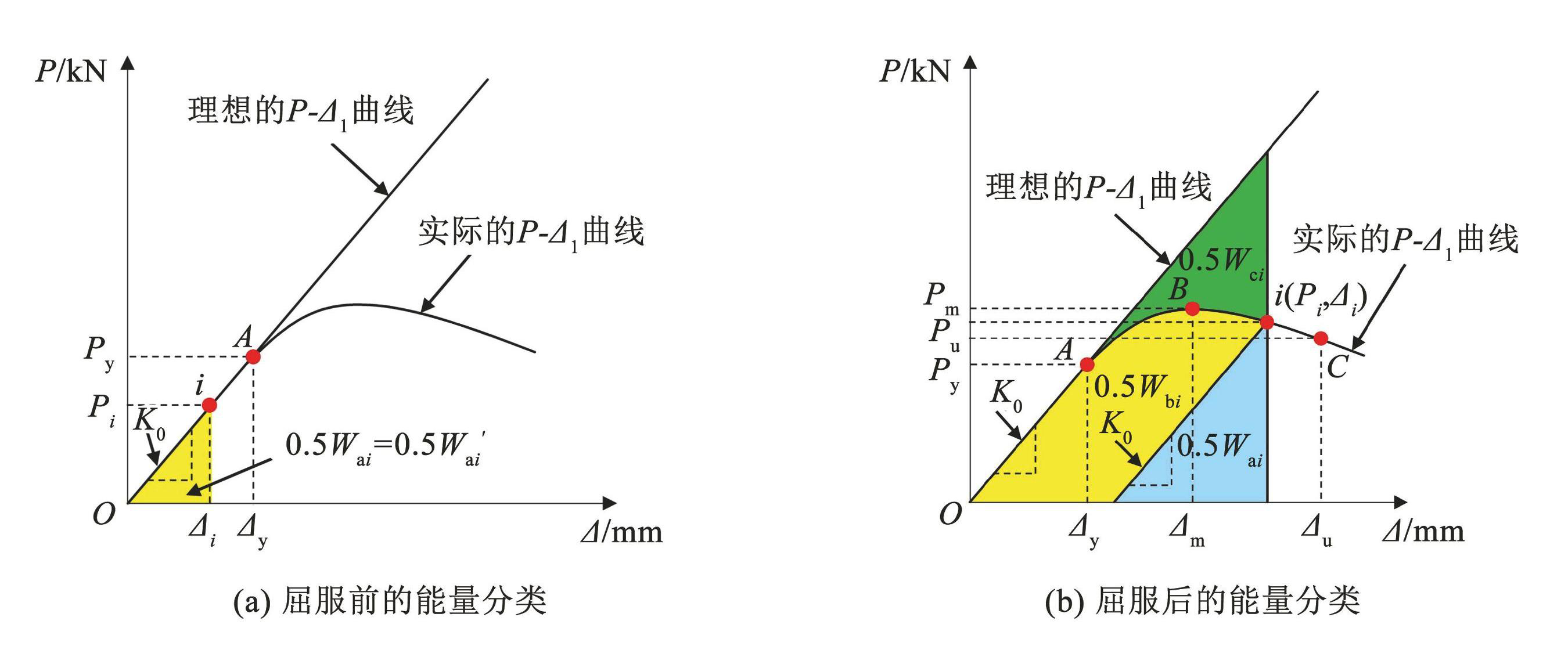
图5不同加载阶段的能量分类

Fig.5Energy classification at different loading stages

3.2 挠度退化系数

图6给出了 18 根试件 W_c随 W_b的变化曲线，可以看出，W_c的增长趋势较 W_b更加显著。这是由于在外荷载作用下，试件的整体性能逐渐退化，具体表现为损伤程度不断加重，耗能能力逐渐衰退。在此基础上，进一步讨论试件整体性能快慢退化的临界点，为结构设计和加固提供参考。如图7所示，根据能量损伤增量 ΔW_ci、能量耗散增量 ΔW_bi以及挠度增量 Δ_Δi之间的变化关系，采用相对能量损伤指数（ΔW′_c）来判断试件何时开始出现严重且迅速的性能退化，ΔW′_c的计算公式如下:

Δ W_{c i}^{'} = Δ W_{c i} / [(Δ W_{b i} / 100) Δ_{Δ_{i}}]

(7)

\{\begin{matrix} Δ W_{c i} = W_{c (i + 1)} - W_{c i} \\ Δ W_{b i} = W_{b (i + 1)} - W_{b i} \\ Δ_{Δ_{i}} = Δ_{i + 1} - Δ_{i} \end{matrix}

(8)

式中 Δ_i_{+ 1}与 Δ_i分别表示对应点的挠度。 ΔW′_c代表试件在单位挠度增量下，能量耗散（ W_b）每增加 100 kN·mm，试件能量损伤（ W_c）的增量。 ΔW′_c越大，试件在单位挠度下的能量损伤越严重，整体性能退化越严重。绘制 18 根试件的 ΔW′_c随 Δ 变化的曲线，如图8所示。

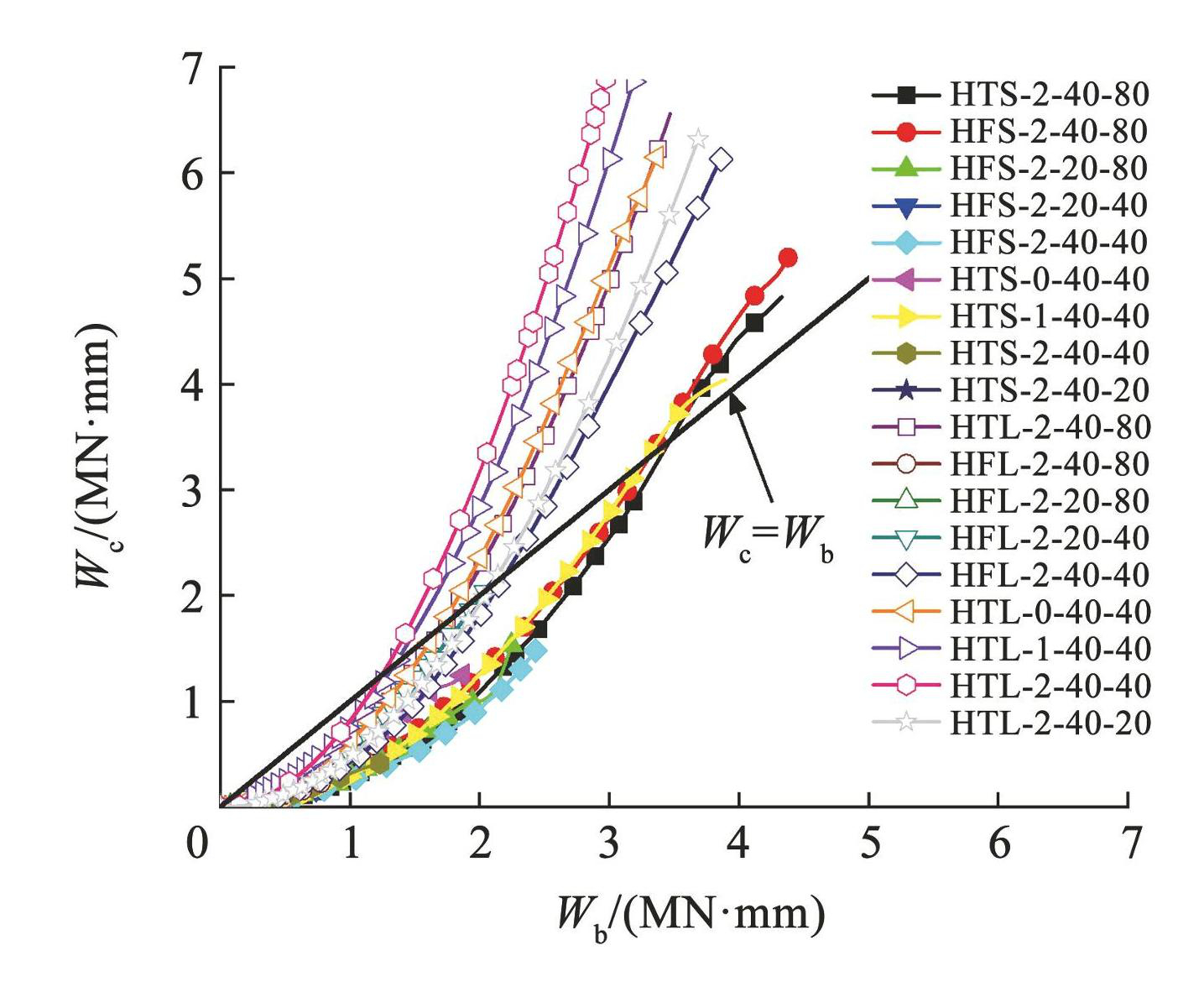
图6W_c-W_b曲线

Fig.6W_c-W_bcurves

图7ΔW_c与 ΔW_b的关系

Fig.7Relationship between ΔW_c and ΔW_b

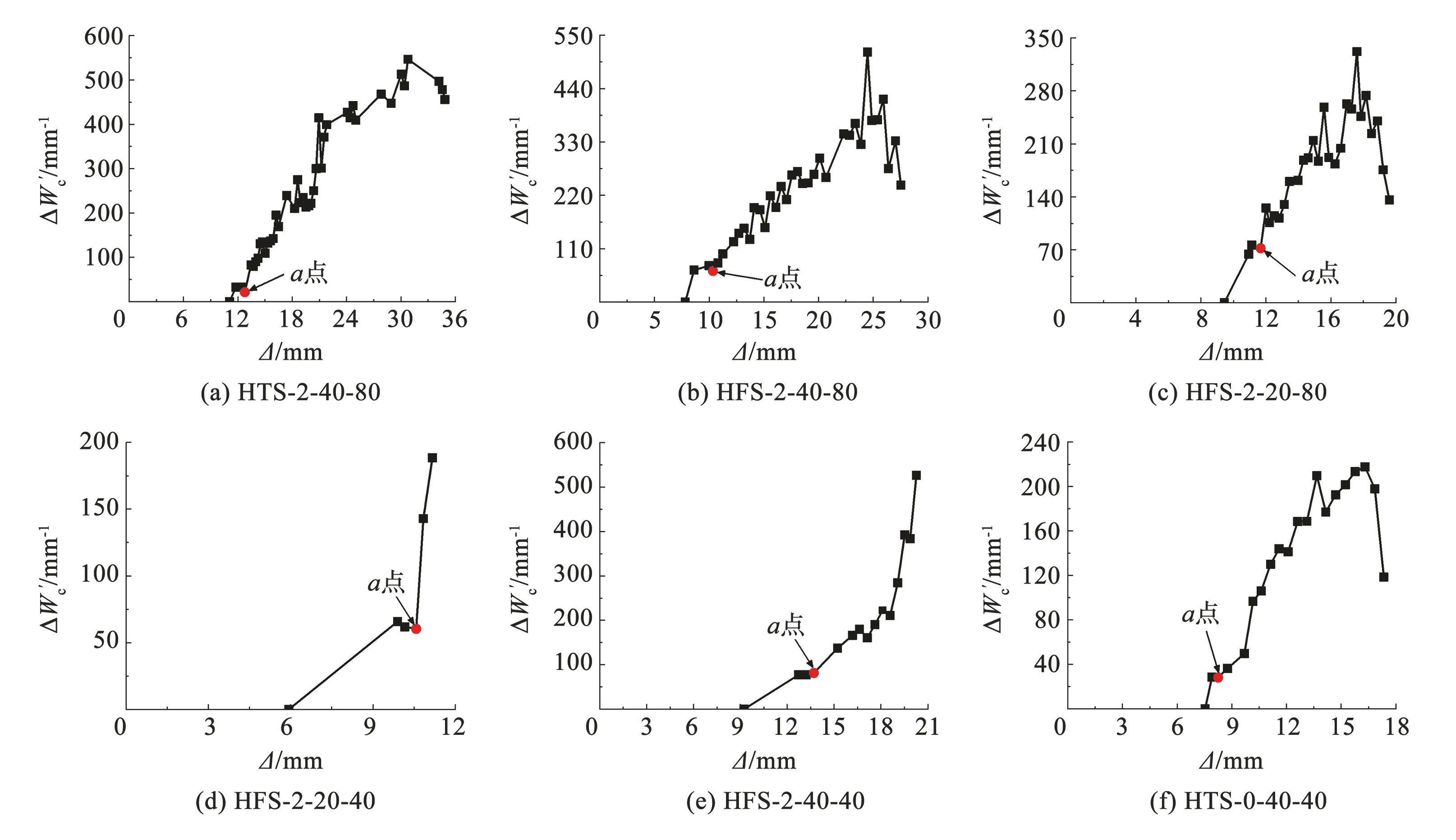
图8ΔW′_c-Δ 曲线

Fig.8ΔW′_c-Δ curves

分析 ΔW′_c-Δ 曲线可以看出，当 ΔW′_c从 0 增大至一定值后，曲线进入一个较为稳定的平台阶段。随着加载的继续进行，ΔW′_c-Δ 曲线的平台阶段自 a 点结束。 a 点之后，ΔW′_c增长较为迅速。因此，可以认为从 a 点开始，试件的整体性能出现较为严重且迅速的退化。根据各试件的 ΔW′_c-Δ 曲线，得 a 点对应的荷载与挠度（P_d、Δ_d）。基于试件整体性能开始出现严重退化时的挠度 Δ_d，得挠度退化系数 γ 计算公式为

γ = Δ_{d} / Δ_{u}

(9)

式中 Δ_u为破坏点挠度，具体计算结果见表3。

计算 γ 的峰度 K 和偏度 S:

K = \frac{1}{N - 1} \sum_{i = 1}^{N} {(\frac{γ_{i} - \bar{γ}}{σ})}^{4} - 3

(10)

S = \frac{1}{N} \sum_{i = 1}^{N} {(\frac{γ_{i} - \bar{γ}}{σ})}^{3}

(11)

式中:N 为试件总数（18），σ 为样本 γ 的标准差（0.225 5），

\bar{γ}

为样本 γ 的均值（46.24%）。得峰度 K 和偏度 S 分别为 0.60 和 0.28，γ 概率分布的陡峭程度（K），以及 γ 数据分布的偏斜方向和偏斜程度（S）均满足高斯分布的要求，可认为挠度退化系数 γ 服从高斯分布。图9给出了 n_i/ N 在各 γ 区间的分布情况，n_i为满足（ x -6.5%）≤γ≤（ x + 6.5%）的试件个数。 n_i / N 在各 γ 区间连续且随机分布，对其分布进行高斯拟合，所得拟合结果为

n_{i} / N = 0.0084 + 0.2234 e^{- \frac{(γ - μ)^{2}}{2 σ^{2}}} =

0.0084 + 0.2234 e^{- \frac{(y - 0.4382)^{2}}{2 \times 0.2962}}

(12)

式中:数学期望 μ = 0.438 2，标准差 σ = 0.229 6。

通过高斯拟合曲线，得 γ 在 90% 置信水平的置信区间为[0.105 6，0.806 1]，计算公式为

\frac{S_{D_{1.90 %} B D_{R 90 %} E_{R 90 %} E_{L 90 %}}}{S_{A B C F G}} = 0.90

(13)

式中:各点的定义如图9所示，S_ABCFG为点 A、B、C、F 和 G 所围成区域的面积，

S_{D_{L 90 %} B D_{R 90 %} E_{R 90 %} E_{L 90 %}}

同理。从结构安全的角度考虑，γ 的取值须小于 80.61%。考虑材料性能的充分利用，γ 的取值需大于 10.56%。基于数理统计的结果可以看出，当构件挠度最大大于 80% Δ_u时，构件整体性能也会开始出现严重且迅速的退化，须采取相应的加固措施。进一步地，通过挠度退化系数 γ 得预估退化挠度 Δ_d，p，对构件整体性能开始出现严重退化时的挠度进行预测，为结构加固提供参考，Δ_d，p计算公式为

Δ_{d, p} = γ Δ_{u} = 80 % Δ_{u}

(14)

式中 Δ_u的定义同前。

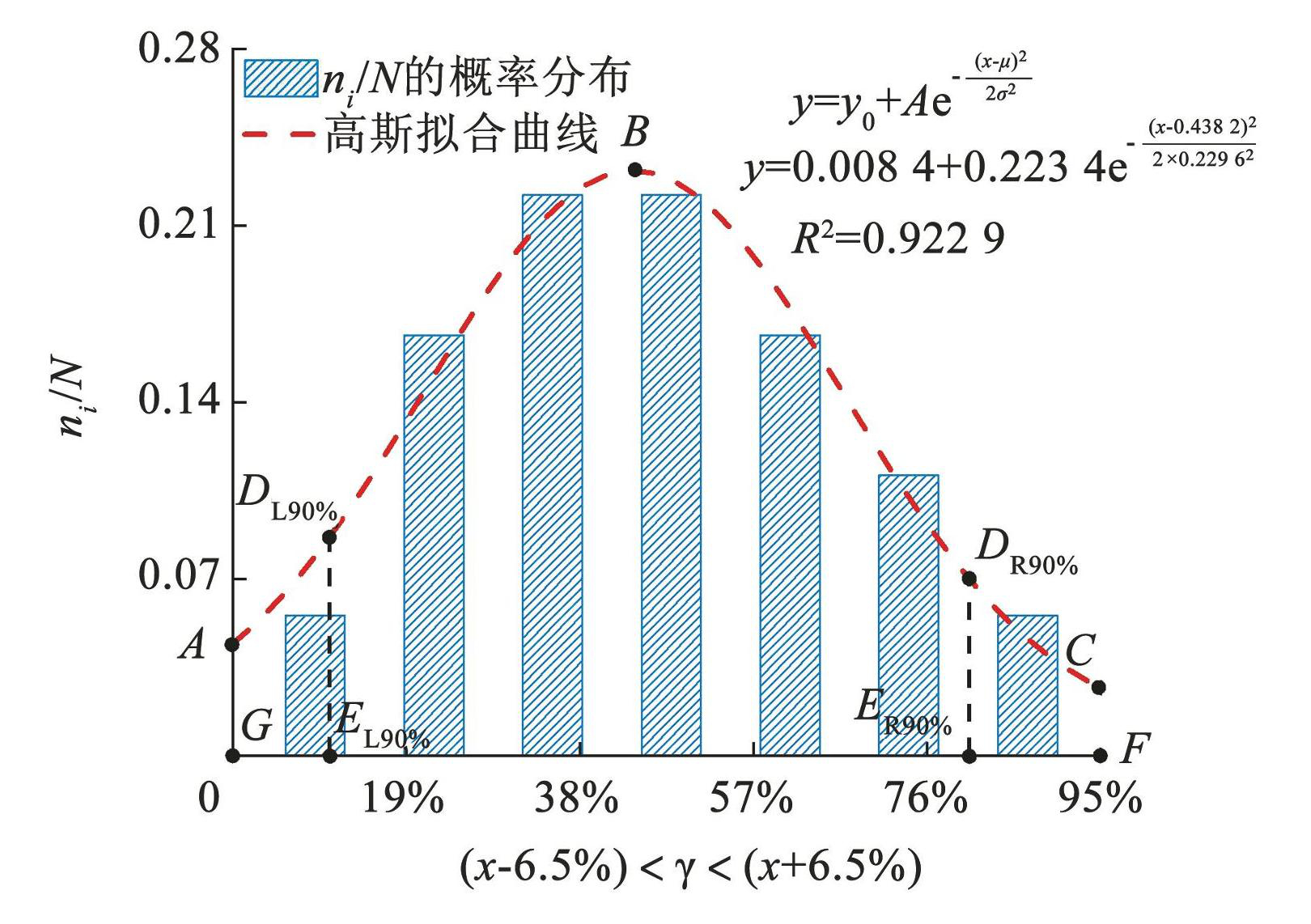
图9高斯分布拟合

Fig.9Gaussian distribution fitting

4 结论

1）小剪跨比试件（λ 为 1.5 或 1.7）主要发生界面破坏。随着 ρ_sf增大，界面脱黏得到控制，小剪跨比试件转而发生弯扭破坏。大剪跨比试件（λ 为2.5 或 2.8）的破坏模式主要取决于所配型钢的规格，配置 I14 型钢的试件，由于型钢所受“握裹效应”不足，在弯扭耦合作用下发生弯扭破坏。

2）多数试件的破坏对称性较好，而非对称破坏主要发生在小剪跨比的界面破坏试件中。这是由于相比大剪跨比试件，小剪跨比试件的剪切效应更加显著，破坏更容易集中在某一侧剪弯段，进而出现两个剪弯段的非对称破坏。

3）90% 置信水平下，当挠度最大发展至 80% Δ_u 时，LCSSFRC 构件也会开始出现严重且迅速的整体性能退化。可通过挠度退化系数 γ 对构件整体性能开始出现严重退化时的挠度进行预测，为结构设计和加固提供参考。

图1试验加载方式以及试件截面

Fig.1Test setup and cross section of specimens

下载: 全尺寸图片

图2试件的破坏模式

Fig.2Failure modes of specimens

下载: 全尺寸图片

图3荷载-挠度曲线

Fig.3Load-deflection curves

下载: 全尺寸图片

图4挠度分布类型

Fig.4Types of deflection distribution

下载: 全尺寸图片

图5不同加载阶段的能量分类

Fig.5Energy classification at different loading stages

下载: 全尺寸图片

图6W_c-W_b曲线

Fig.6W_c-W_bcurves

下载: 全尺寸图片

图7ΔW_c与 ΔW_b的关系

Fig.7Relationship between ΔW_c and ΔW_b

下载: 全尺寸图片

图8ΔW′_c-Δ 曲线

Fig.8ΔW′_c-Δ curves

下载: 全尺寸图片

图9高斯分布拟合

Fig.9Gaussian distribution fitting

下载: 全尺寸图片

表1型钢截面尺寸及力学性能

下载: 全尺寸图片

表2LCSSFRC 试件设计参数

下载: 全尺寸图片

表3试件性能指标

下载: 全尺寸图片

图1试验加载方式以及试件截面

Fig.1Test setup and cross section of specimens

图2试件的破坏模式

Fig.2Failure modes of specimens

图3荷载-挠度曲线

Fig.3Load-deflection curves

图4挠度分布类型

Fig.4Types of deflection distribution

图5不同加载阶段的能量分类

Fig.5Energy classification at different loading stages

图6W_c-W_b曲线

Fig.6W_c-W_bcurves

图7ΔW_c与 ΔW_b的关系

Fig.7Relationship between ΔW_c and ΔW_b

图8ΔW′_c-Δ 曲线

Fig.8ΔW′_c-Δ curves

图9高斯分布拟合

Fig.9Gaussian distribution fitting

表1型钢截面尺寸及力学性能

表2LCSSFRC 试件设计参数

表3试件性能指标

图1试验加载方式以及试件截面

Fig.1Test setup and cross section of specimens

图2试件的破坏模式

Fig.2Failure modes of specimens

图3荷载-挠度曲线

Fig.3Load-deflection curves

图4挠度分布类型

Fig.4Types of deflection distribution

图5不同加载阶段的能量分类

Fig.5Energy classification at different loading stages

图6W_c-W_b曲线

Fig.6W_c-W_bcurves

图7ΔW_c与 ΔW_b的关系

Fig.7Relationship between ΔW_c and ΔW_b

图8ΔW′_c-Δ 曲线

Fig.8ΔW′_c-Δ curves

图9高斯分布拟合

Fig.9Gaussian distribution fitting

表1型钢截面尺寸及力学性能

表2LCSSFRC 试件设计参数

表3试件性能指标

薛建阳, 周超锋, 刘祖强, 等. 型钢混凝土异形柱损伤行为及性能量化指标研究[J]. 土木工程学报,2020,53(2):1 XUE Jianyang, ZHOU Chaofeng, LIU Zuqiang,et.al.Research on damage behavior and quantitative indexes for steel reinforced concrete column with irregular section[J]. China Civil Engineering Journal,2020,53(2):1. DOI:10.15951/j.tmgcxb.2020.02.001

YUE Jianguang, QIAN Jiang, BESKOS D E. Seismic damage performance levels for concrete encased steel columns using acoustic emission tests and finite element analysis[J]. Engineering Structures,2019,189:471. DOI:10.1016/j.engstruct.2019.03.077

LAI Binglin, ZHANG Mingyang, ZHENG Xiaofeng,et al. Experimental study on the axial compressive behaviour of steel reinforced concrete composite columns with stay-in-place ECC jacket[J]. Journal of Building Engineering,2023,68:106174. DOI:10.1016/j.jobe.2023.106174

YANG Yong, XUE Yicong, YU Yunlong,et al. Experimental study on flexural performance of partially precast steel reinforced concrete beams[J]. Journal of Constructional Steel Research,2017,133:192. DOI:10.1016/j.jcsr.2017.02.019

SEO J, VARMA A H. Experimental behavior and design of steel plate composite-to-reinforced concrete lap splice connections[J]. Journal of Structural Engineering,2017,143(5):04017011. DOI:10.1061/(ASCE)ST.1943-541X.0001711

CHEN Chengcheng, CHEN Chienchung, SHEN Jiahau. Effects of steel-to-member depth ratio and axial load on flexural ductility of concrete-encased steel composite columns[J]. Engineering Structures,2018,155:157. DOI:10.1016/j.engstruct.2017.11.036

LAI Binglin, LIEW J Y R. Investigation on axial load-shorting behavior of high strength concrete encased steel composite section[J]. Engineering Structures,2021,227:111401. DOI:10.1016/j.engstruct.2020.111401

徐礼华, 李长宁, 李彪, 等. 循环受压状态下钢纤维混凝土一维弹塑性损伤本构模型研究[J]. 土木工程学报,2018,51(11):77 XU Lihua, LI Changning, LI Biao,et al.Investigation on 1D elastoplastic constitutive model of steel fiber reinforced concrete under uniaxial cyclic compression[J]. China Civil Engineering Journal,2018,51(11):77. DOI:10.15951/j.tmgcxb.2018.11.006

PAPACHRISTOFOROU M, ANASTASIOU E K, PAPAYIANNI I. Durability of steel fiber reinforced concrete with coarse steel slag aggregates including performance at elevated temperatures[J]. Construction and Building Materials,2020,262:120569. DOI:10.1016/j.conbuildmat.2020.120569

ZHANG Xiaoyong, LIN Xiang, CHEN Yu. Study on mechanical properties of steel fiber reinforced nano-concrete(SFRNC)after elevated temperature[J]. Composite Structures,2021,268:113941. DOI:10.1016/j.compstruct.2021.113941

RIVERA M, ENFEDAQUE A, ALBERTI M G,et al. Crackwidth-based sectional analysis of fiber-reinforced concrete applied to the structural design of the slab of a fly-over bridge[J]. Journal of Bridge Engineering,2022,27(1):04021095. DOI:10.1061/(ASCE)BE.1943-5592.0001793

SHARMA S, ARORA V V, KUMAR S,et al. Durability study of high-strength steel fiber-reinforced concrete[J]. ACI Materials Journal,2018,115(2):219. DOI:10.14359/51701122

TANG Kangkang, WILKINSON S. Corrosion resistance of electrified railway tunnels made of steel fibre reinforced concrete[J]. Construction and Building Materials,2020,230:117006. DOI:10.1016/j.conbuildmat.2019.117006

YUN H D, JEONG G Y, CHOI W C. Shear strengthening of high strength concrete beams that contain hooked-end steel fiber[J]. Materials,2021,15(1):17. DOI:10.3390/ma15010017

SAHOO D R, SHARMA A. Effect of steel fiber content on behavior of concrete beams with and without stirrups[J]. ACI Structural Journal,2014,111(5):1157. DOI:10.14359/51686821

YOO D Y, YUAN T, YANG J M,et al. Feasibility of replacing minimum shear reinforcement with steel fibers for sustainable highstrength concrete beams[J]. Engineering Structures,2017,147:207. DOI:10.1016/j.engstruct.2017.06.004

YAKOUB H E. Shear stress prediction:steel fiber-reinforced concrete beams without stirrups[J]. ACI Structural Journal,2011,108(3):304. DOI:10.14359/51682346

XU Shilang, ZHANG Xiufang, REINHARD H W. Shear capacity prediction of reinforced concrete beams without stirrups using fracture mechanics approach[J]. ACI Structural Journal,2012,109(5):706. DOI:10.14359/51684048

WU Kai, CHEN Feng, CHEN Chuyang,et al. Load-transfer mechanism and bond-stress components in steel and steel fiberreinforced concrete structure[J]. Journal of Structural Engineering,2019,145(12):04019160. DOI:10.1061/(ASCE)ST.1943-541X.0002441

WU Kai, LIN Shiqi, XUE Jianyang,et al. Failure mechanism and debonding analysis of steel and steel fiber-reinforced concrete composite beams[J]. ACI Structural Journal,2021,118(5):189. DOI:10.14359/51732828

聂建国, 王宇航, 樊健生, 等. 钢-混凝土组合梁加宽混凝土旧桥技术中组合横梁界面受力性能研究[J]. 土木工程学报,2012,45(3):99 NIE Jianguo, WANG Yuhang, FAN Jiansheng,et al.Mechanical behavior of the interface of composite cross beam in old concrete bridges widened with steel-concrete composite beam[J]. China Civil Engineering Journal,2012,45(3):99. DOI:10.15951/j.tmgcxb.2012.03.006

杨勇, 薛亦聪, 于云龙, 等. 部分预制装配型钢混凝土梁受力性能试验研究[J]. 土木工程学报,2018,51(4):1 YANG Yong, XUE Yicong, YU Yunlong,et al.Experimental research on mechanical performance of partially precast steel reinforced concrete beams[J]. China Civil Engineering Journal,2018,51(4):1. DOI:10.15951/j.tmgcxb.2018.04.001

WU Kai, YANG Yiheng, ZHANG Yanjie,et al. Experimental study on mechanical properties of locally composite steel and steel fiber reinforced concrete beams[J]. Structures,2023,58:105389. DOI:10.1016/j.istruc.2023.105389

中国建筑科学研究院. 普通混凝土配合比设计规程: JGJ 55—2011[S]. 北京: 中国建筑工业出版社,2011 China Academy of Building Research.Specification for mix proportion design of ordinary concrete: JGJ 55—2011[S]. Beijing: China Architecture & Building Press,2011

全国钢标准化技术委员会. 热轧型钢: GB/T 706—2016[S]. 北京: 中国标准出版社,2016 The Technical Committee on Steel of Standardization Committee of China.Hot rolled section steel: GB/T 706—2016[S]. Beijing: Standard Press of China,2016

LIU Chao, LV Zhenyuan, BAI Guoliang,et al. Experiment study on bond slip behavior between section steel and RAC in SRRC structures[J]. Construction and Building Materials,2018,175:104. DOI:10.1016/j.conbuildmat.2018.04.120

TONG Lewei, XIAO Shun, HE Lang,et al. Fatigue behavior of steel reinforced concrete(SRC)beams with different shear span-todepth ratios[J]. Engineering Structures,2018,166:339. DOI:10.1016/j.engstruct.2018.03.071

1 试验

2 破坏模式及荷载-挠度曲线

3 试件耗能分析

4 结论

友情链接LINKS