欢迎访问《哈尔滨工业大学学报》编辑部网站！

氯离子环境下RC桥墩时变抗震韧性分析

doi: 10.11918/202402021

聂莹慧，李镜培

同济大学土木工程学院,上海 200092

基金项目: 国家重点研发计划(2021YFB2600500)

详细信息

作者简介

聂莹慧(1996—),女,博士研究生;

李镜培(1963—),男,教授,博士生导师

通讯作者

李镜培,lijp2773@tongji.edu.cn

中图分类号: TU375

文献标识码: A

文章编号: 0367-6234(2025)03-0014-11

Time-dependent seismic resilience analysis of RC bridge piers in chloride service environments

NIE Yinghui ， LI Jingpei

College of Civil Engineering, Tongji University, Shanghai 200092 , China

摘要

为揭示结构全寿命周期内考虑时间效应的失效规律,针对分区腐蚀桥墩时变抗震韧性问题,围绕不同桥墩分区的腐蚀环境、材料特性和腐蚀过程,开展了钢筋面积、钢筋屈服强度及混凝土抗压强度等材料性能的时变退化规律研究。根据计算结果建立桥墩分区腐蚀有限元模型,结合增量动力分析(IDA)得到墩顶位移响应,基于概率需求模型及损伤界限值构建了桥墩地震易损性模型。进而利用 Pushover 分析,将桥墩抗震性能随服役时间的退化作为灾前时变性能指标,灾后的性能指标通过量化地震作用导致的桥墩瞬间功能损失以及恢复程度来表征,提出了考虑分区腐蚀环境桥墩全寿命抗震韧性计算模型。结果表明:浪溅区钢筋锈蚀速度明显大于水下区及大气区,桥墩服役 20 a 到 50 a 的韧性退化值约为 50 a 到 80 a 的韧性退化值的 2 倍。因此在桥墩服役前期,决策者可依据实际提出合理的震前加固措施来增强抗震韧性。

关键词

氯离子环境 / 桥墩 / 地震 / 易损性 / 韧性 / 全寿命

Abstract

To reveal the failure patterns considering time-dependent seismic resilience of bridge piers under zonal corrosion conditions throughout their life cycle, this study examines the time-varying degradation of key material properties, including rebar cross-sectional area, yield strength, and concrete compressive strength, under different corrosion environments and processes. Finite element models of zonally corroded piers were then established based on these computational results, and incremental dynamic analysis ( IDA ) was applied to obtain pier-top displacement responses. A seismic vulnerability model was constructed using a probabilistic demand model and damage threshold values. Furthermore, through Pushover analysis, the pre-earthquake time-dependent performance indicator was defined by the deterioration of pier seismic capacity over service time. The post-earthquake performance indicators were characterized by quantifying the instantaneous functional loss of the pier caused by seismic actions and subsequent recovery. Accordingly, a full life-cycle seismic resilience calculation model was proposed for piers, considering the partitioned corrosion environment. The results show that the corrosion rate of rebar in the splash zone is considerably higher than that in the underwater and atmospheric zones. Moreover, resilience degradation value of the bridge pier over a service period of 20 to 50 years is approximately twice that of the degradation value observed over 50 to 80 years. Thus, during the early service phase of piers, decision-makers can propose reasonable pre-earthquake reinforcement measures based on actual conditions to enhance seismic resilience.

Keywords

chloride environment / bridge piers / seismic / vulnerability / resilience / full life cycle

1 桥墩分区锈蚀退化模型 1.1 直角坐标系下氯离子分区扩散模型 1.2 钢筋锈蚀深度计算模型 1.3 钢筋性能退化 1.4 混凝土性能退化 2 易损性模型 2.1 损伤指标 2.2 易损性函数 3 韧性 3.1 性能指标 3.2 恢复模型 4 算例 4.1 选取地震动样本 4.2 桥墩有限元模型 4.3 氯离子腐蚀作用 4.4 灾前性能指标 4.5 灾后性能指标 4.6 全寿命周期韧性 5 结论

由于桥墩不同分区处氯离子质量分数、扩散系数和极限氯离子质量分数等参数的不同，内部钢筋的初始锈蚀时间及材料性能退化规律具有差异性。在地震作用下，桥梁工程的抗震性能降低，这种差异性材料性能的退化会放大结构的地震需求，最大损伤位置改变，桥墩地震失效机理也随之发生改变。因此，有必要对分区腐蚀桥墩进行全寿命抗震韧性分析。

桥墩多服役于锈蚀环境中，因此，许多学者针对氯离子在混凝土中的扩散方程开展研究，探讨了凝土表面氯离子质量分数、混凝土自身特性等的普遍性规律^[1-2]。在此基础上，一些学者综合考虑了水灰比、应力状态、温度、湿度和扩散系数时间依赖性等影响参数，对扩散方程进行了进一步修正^[3-4]。氯离子扩散至钢筋表面，破坏其钝化膜，钢筋锈蚀产生体积膨胀的锈蚀产物，其截面面积减少。基于此，国内外学者采用物理试验^[5-6]和理论分析方法^[7-8] 研究氯离子环境下钢筋锈蚀深度计算模型，描述了钢筋极限拉应变与锈蚀率之间的关系及各模型下的钢筋锈蚀速率发展规律，为钢筋锈蚀深度的计算提供理论依据。此外，锈蚀环境下钢筋混凝土力学性能也会发生变化。一些学者^[9-12] 考虑钢筋及混凝土性能在全寿命周期内的退化效应，分别基于试验及理论方法提出了氯离子锈蚀后的屈服强度模型及保护层混凝土抗压强度计算模型。上述文献研究对象的混凝土采用 C30 / C35 / C40（主要）/ C45 / C50（少量）等类型，而钢筋则采用 HRB335（主要）/ B450C（少量）等类型。

考虑钢筋锈蚀的影响有助于揭示氯离子服役环境下结构的抗震性能时变规律^[13-14]，例如文献^[15-16]将纵筋屈服作为极限状态，分别提出了基于大气氯化物腐蚀的桥墩全生命周期抗震可靠性评估模型及地震作用下腐蚀桥梁可靠性的定量评估框架。一些学者进一步将腐蚀结构的抗震性能分析拓展到易损性研究中^[17-19]。文献^[20-21]通过腐蚀钢筋原位测试及数值模拟对腐蚀桥墩展开地震性能分析，量化其地震易损性的变化规律。既有研究多集中于桥墩整体均匀锈蚀的情况，因此，基于数值模拟的方法，部分学者建立了考虑分区腐蚀桥墩退化问题的时变地震易损性模型^[22-24]。上述研究为分区腐蚀结构时变抗震性能分析提供了丰富了的理论支撑，但尚未从结构抗震韧性的角度，全面揭示分区腐蚀结构遭受地震灾害后的性能损伤程度及恢复性能的变化规律。

基于上述问题，本文首先依据 Fick 第二定律及法拉第定律建立桥墩分区锈蚀模型，进而结合概率需求分析方法得到了桥墩地震易损性模型。其次，围绕结构退化问题，将桥墩地震作用下的性能指标分为灾前性能指标和灾后性能指标。最后，依据修复函数得到氯离子服役环境下 RC 桥墩全寿命时变性能指标变化规律，进一步探讨在以 a 为时间尺度的全寿命韧性时变规律，以及以 d 为时间尺度的固定服役年限的韧性值，为后续有效评估潜在地震威胁和氯离子腐蚀劣化下桥墩的抗震韧性水平提供参考依据。本文流程如图1所示。

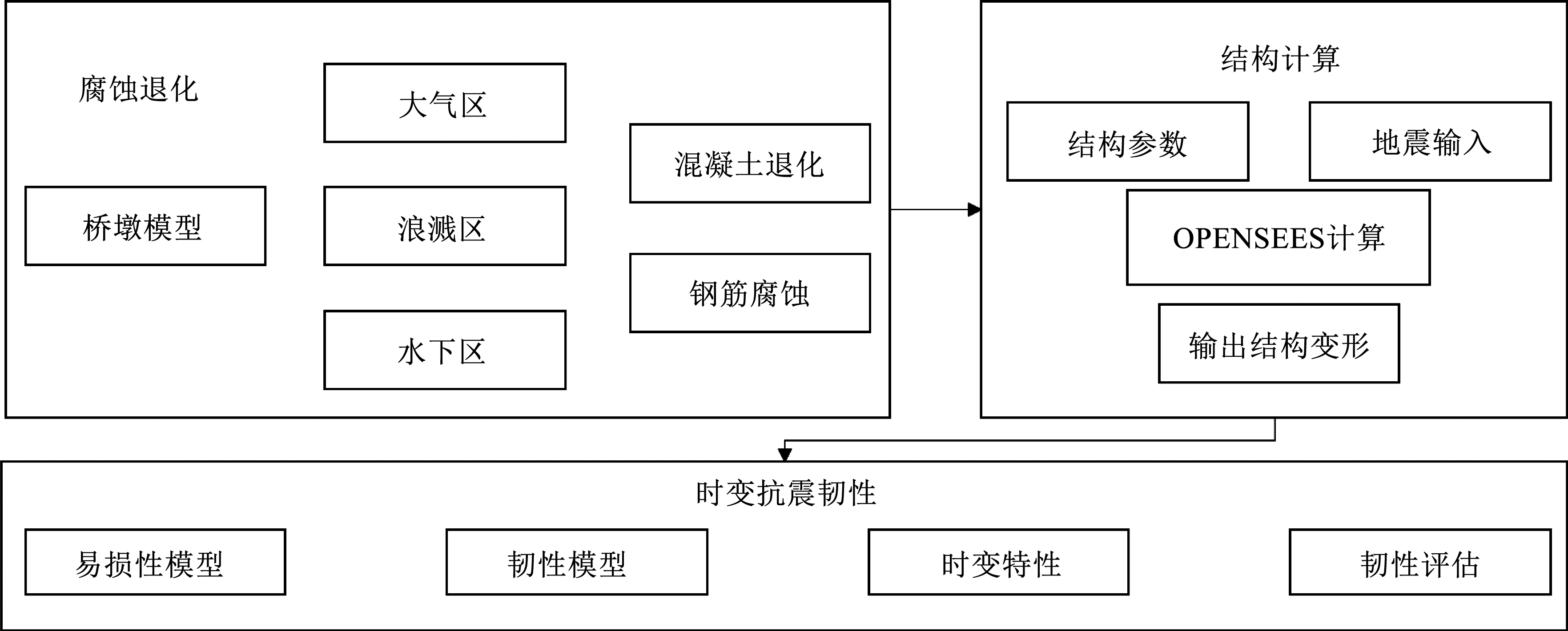
图1流程图

Fig.1Flow chart

1 桥墩分区锈蚀退化模型

桥梁震害主要表现为桥墩的倒塌破坏，氯离子环境下桥墩抗震性能退化问题是桥梁抗震研究的重点之一。以方形桥墩作为研究对象，首先介绍氯离子在直角坐标系下的扩散模型及钢筋锈蚀模型，并建立桥墩材料退化模型。

1.1 直角坐标系下氯离子分区扩散模型

基于氯离子在直角坐标系下的扩散方程，假设桥墩内初始自由氯离子质量分数为 0，表面氯离子质量分数恒为 C_s，得到任意扩散深度 x 处任意时刻 t 氯离子质量分数 C（x，t）表达式^[25]为

C (x, t) = C_{s} (1 - e r f \frac{x}{2 \sqrt{D t}})

(1)

式中:D 为氯离子扩散系数; erf（·）为误差函数，可以表示^[25]为

e r f (ε) = \frac{2}{\sqrt{π}} \int_{0}^{ε} e^{- t^{2}} d t

(2)

定义混凝土保护层内钢筋表面氯离子质量分数达到极限浓度的时间为初始锈蚀时间 T_i，假设钢筋表面位置处的极限氯离子质量分数为 C_th，即可据上式得到钢筋初始锈蚀时间。

本文考虑桥墩腐蚀环境的不同，依据文献^[26]，将桥墩划分为大气区、浪溅区及水位变动区、水下区 3 个部分。相应地，表面氯离子质量分数、扩散系数及极限氯离子质量分数值等，求解初始锈蚀时间的关键性参数的确定，也需考虑分区腐蚀环境的差异，确定方法^[27]为

D = D (t) = D_{0} k_{t} k_{c} k_{e} {(\frac{t_{0}}{t})}^{n}

(3)

式中:t₀为混凝土养护时间，取 28 d; n 为龄期系数; k_t、k_c和 k_e分别为考虑试验方法、环境和养护条件的影响系数; D₀为一定龄期的普通硅酸盐混凝土氯离子扩散系数，表达式^[27]为

D_{0} = 10^{- 12.06 + 2.4 (\frac{w}{b})}

(4)

其中

\frac{w}{b}

为水灰比。

1.2 钢筋锈蚀深度计算模型

基于钢筋初始锈蚀时间的计算结果，结合 Faraday 定律开展钢筋锈蚀深度规律研究，钢筋锈蚀量计算模型表达式^[3]为

\frac{d M_{loss}}{d t} = \frac{I_{corr} M_{F E}}{η F}

(5)

式中:M_FE为铁离子的原子量，取 M_FE =55.85 g / mol ^[28]; F 为法拉第常数; η 为化合价; t 为钢筋的锈蚀时间; I_corr为腐蚀电流，对于单位长度的桩，I_corr可以表示^[3]为

I_{c o r r} = π d_{0} i_{c o r r} (t)

(6)

i_{corr} (t) = 0.85 i_{corr, 0} {(t - T_{i})}^{- 0.29}, t ⩾ T_{i}

(7)

i_{c o r r, 0} = \frac{37.5 {(1 - \frac{w}{b})}^{- 1.64}}{c}

(8)

其中 d₀为初始钢筋直径; i_corr为腐蚀电流密度，采用文献^[8] 提出的腐蚀电流密度经验公式; i_corr，0 为初始腐蚀电流密度; c 为保护层厚度。

综上得钢筋锈蚀深度模型为

x = \frac{M_{loss}}{π ρ_{s} d_{0} L} = \int_{T_{i}}^{t} \frac{i_{corr} (t) L M_{F E}}{ρ_{s} η F} d t

(9)

其中 ρ_s为钢筋密度。

钢筋锈蚀深度为表征钢筋混凝土材料力学性能退化的重要参数，钢筋锈蚀对混凝土结构承载力的影响主要表现:1）锈胀裂缝引起混凝土中斜裂缝间骨料咬合力减弱，致使混凝土产生软化效应，抗压强度降低; 2）钢筋锈蚀后，钢筋有效面积减少，其屈服强度退化。接下来介绍腐蚀服役环境下钢筋和混凝土材料退化模型。

1.3 钢筋性能退化

采用文献^[6]建立的基于钢筋锈蚀率的钢筋性能退化模型，表达式为

f_{y} = (1 - β_{y} Q_{corr}) f_{y 0}

(10)

式中:f_y为退化后的钢筋屈服强度; β_y为屈服强度的折减系数，取 0. 005; f_y0为初始屈服强度; Q_corr为钢筋锈蚀率，其简化模型为

Q_{c o r r} (t) = \frac{d_{0}^{2} (t) - d_{0}^{2}}{d_{0}^{2}}

(11)

其中 d₀（t）为随服役时间锈蚀后的钢筋直径。

为简化分析条件，本文假设每根纵向钢筋受到的锈蚀损伤相同。

1.4 混凝土性能退化

随着锈蚀损伤的深化，锈蚀产物累积，裂缝发展至混凝土表面保护层，混凝土保护层顺筋开裂、导致混凝土剥落或者整体脱落，钢筋混凝土结构强度降低。文献^[29] 建立了锈蚀后保护层混凝土受压强度计算公式:

f_{corr} = \frac{f_{c}}{1 + K \frac{ε_{1}}{ε_{0}}}

(12)

式中:f_corr为锈胀后混凝抗压强度; f_c为未锈胀的混凝抗压强度; K 为与钢筋直径和粗糙度有关的系数，一般可取 0.1; ε₀为未锈胀混凝土峰值应变; ε₁为发生垂直于受力方向的锈胀后的混凝土平均拉应变，计算公式^[17]为

ε_{1} = \frac{b_{f} - b_{0}}{b_{0}} = \frac{n_{bars} ω}{b_{0}}

(13)

ω = 2 π (v_{r s} - 1) x

(14)

其中 b_f和 b₀为锈胀后和锈胀前的截面宽度; n_bars为纵筋数目; ω 为混凝土锈胀裂缝宽度^[17]，当 ω >3 mm时，ω 取 3 mm; v_rs为钢筋锈蚀体积膨胀系数，可取 3. 0。

2 易损性模型

2.1 损伤指标

针对结构地震易损性问题，基于变形破坏准则，采用文献^[30]提出的相对位移延性比作为损伤指标，以表征桥梁在不同状态下的损伤。相对位移延性比 μ_d定义为

μ_{d} = \frac{B}{B_{c y 1}}

(15)

式中:B 为墩顶响应的最大相对位移，B_cy1为第 1 次钢筋屈服开始时的墩顶相对位移。

通过比较各极限状态下桥墩的相对位移与第1 次钢筋屈服时桥墩的相对位移，可对桥墩的损伤状态进行分类。其中 μ_cy1为钢筋第一屈服位移延性比，μ_c为等效屈服位移延性比，μ_c4 对应于压应变达到 0. 004 时桥墩截面边缘混凝土的位移延性比依据。最大破坏位移延性比 μ_cmax定义为 μ_cmax= μ_c4 +3 ^[31]。

为确定各损伤状态的极限值，对桥墩底部截面进行了 M-ϕ（弯矩-曲率）分析。当混凝土压应变 ε_c = 0. 004 时，墩底截面等效屈服曲率 ϕ_y及墩底截面曲率 ϕ_c4 按规范提供的公式计算^[32]。计算得出 ϕ_y和 ϕ_c4分别为 2. 0、15.9 mm。随后，采用塑性铰区位移计算公式计算墩顶位移^[32] :

B_{c y} = \frac{1}{3} ϕ_{y} L^{2}

(16)

B_{c 4} = B_{c y} + B_{p} = \frac{1}{3} ϕ_{y} L^{2} + (L - \frac{L_{p}}{2}) θ_{p}

(17)

θ_{p} = L_{p} ϕ_{p} = L_{p} (ϕ_{c 4} - ϕ_{y})

(18)

L_{p} = 0.08 L + 0.022 f_{y} d_{s} ⩾ 0.044 f_{y} d_{s}, 或 L_{p} = \frac{2}{3} b_{s}

(19)

式中:L 为危险截面到拐点的距离，B_p为构件塑性位移需求，θ_p 为塑性铰区域的塑性转角，L_p为等效塑性铰长度，f_y为纵向钢筋抗拉强度标准值，d_s为纵筋直径，b_s为矩形截面的短边长度。

依据式（19）~（22），本研究计算得出 B_cy和 B_c4 的值分别为 7.28、19.70 cm。根据公路桥梁抗震设计规范^[32]，采用较为保守的 B_cy1 = 6. 0 cm 来计算各损伤状态下的桥墩相对位移延性比。

2.2 易损性函数

得到桥墩损伤指标后，按照规范反应谱选择地震动。为获桥梁结构的易损性曲线，一般需建立结构的有限元模型并对其进行大量非线性动力时程分析。因此，以峰值地面加速度（PGA）为地震动强度指标对所选取的地震波进行调整，对桥墩有限元模型进行 IDA 分析，获取墩柱地震响应，建立概率需求模型，假设结构构件的抗震能力和地震需求 D_s服从对数正态分布，则易损性函数可表示^[33]为

P [D ⩾ C ∣ I_{M}] = Φ (\frac{\ln \frac{\hat{D}}{D_{c}}}{\sqrt{β_{D ∣ I_{M}}^{2} + β_{c}^{2}}})

(20)

式中: D_c为结构抗震能力的中位值，采用 2.1 节的位移延性比来表达; β_c为结构抗震能力的对数标准差; D_s =

\hat{D}

ε，ε 为随机误差，假设其服从中位值为 1、对数标准差为

β_{D ∣ I_{M}}^{}

的对数正态分布;

\hat{D}

为地震需求 D_s的中位值，

\hat{D}

与地震动强度参数 I_M之间的关系为

\hat{D} = a I_{M}^{b}

(21)

其中 a 和 b 为未知参数，根据式（21）可将式（20）改写为

P [D ⩾ C ∣ I_{M}] = Φ (\frac{l n I_{M} - \frac{l n D_{c} - l n a}{b}}{\frac{\sqrt{β_{D ∣ I_{M}}^{2} + β_{c}^{2}}}{b}})

(22)

3 韧性

韧性是指系统在其服役期间，由于结构本身性能退化或遭受各种自然灾害时，能够维持其正常使用功能，并用最短时间和最小代价恢复甚至超过其原有功能的能力。单个地震作用下的韧性定义为

R = \frac{1}{Q (t_{0}) t_{R E}} \int_{t_{O E}}^{t_{O E} + t_{R E}} Q (t) d t

(23)

式中:t₀为初始时间，t_RE为修复时间，t_OE为地震发生时间，Q（t）为归一化的结构性能指标。

3.1 性能指标

围绕结构退化问题，将桥墩地震作用下的性能指标分为两类:灾前性能指标 Q₁ 和灾后性能指标 Q₂。灾前的性能指标采用抗震能力的退化进行表征:考虑氯离子侵蚀导致的桥墩结构性能退化，利用 Pushover 分析，将桥墩自身抗震性能随服役时间的退化作为时变性能指标 Q₁。灾后的性能指标通过量化地震作用导致的桥墩瞬间功能损失以及恢复程度来表征:假定地震发生在不同服役时间 t_i，初始的灾后性能指标 Q⁰₂（t_i），定义为 t_i时刻的灾前性能指标 Q₁（t_i），地震发生后，为量化桥墩瞬间功能损失，基于易损性曲线，定义桥梁处于不同损伤状态的概率乘以量化桥梁不同损伤状态离散值的损伤指数为灾后损伤性能，具体表达^[34]为

Δ Q = \sum_{i = 1}^{4} I_{{B D}_{i}} \times P [D S = {D S}_{i} ∣ I_{M}]

(24)

式中:ΔQ 为桥梁灾后损伤性能; I_BD 为桥梁损伤指数，取值见表1; P 为桥梁处于不同损伤状态的概率。灾后瞬时性能指标 Q₂可表示为

Q_{2} = Q_{2}^{0} - Δ Q

(25)

3.2 恢复模型

得到灾后瞬时性能指标后，结合恢复过程中的性能指标 Q₂（t_i），即完成氯离子服役环境下 RC 桥墩全寿命时变性能指标计算。因此，参考正负指数型函数及正弦型函数来描述桥梁遭受地震作用后的修复方式^[13]，采用 3 种修复函数的均值对桥墩进行性能修复预测，以桥墩在不同服役时间遭受地震灾害对应的灾前性能指标 Q₁（t_i）作为起始灾后性能指标 Q⁰₂（t_i）及桥墩修复完毕后的性能状态，震后桥梁的功能恢复过程表达^[13]为

Q (τ) = Q_{2} + H (τ) r_{f} (τ) (Q_{2}^{0} - Q_{2})

(26)

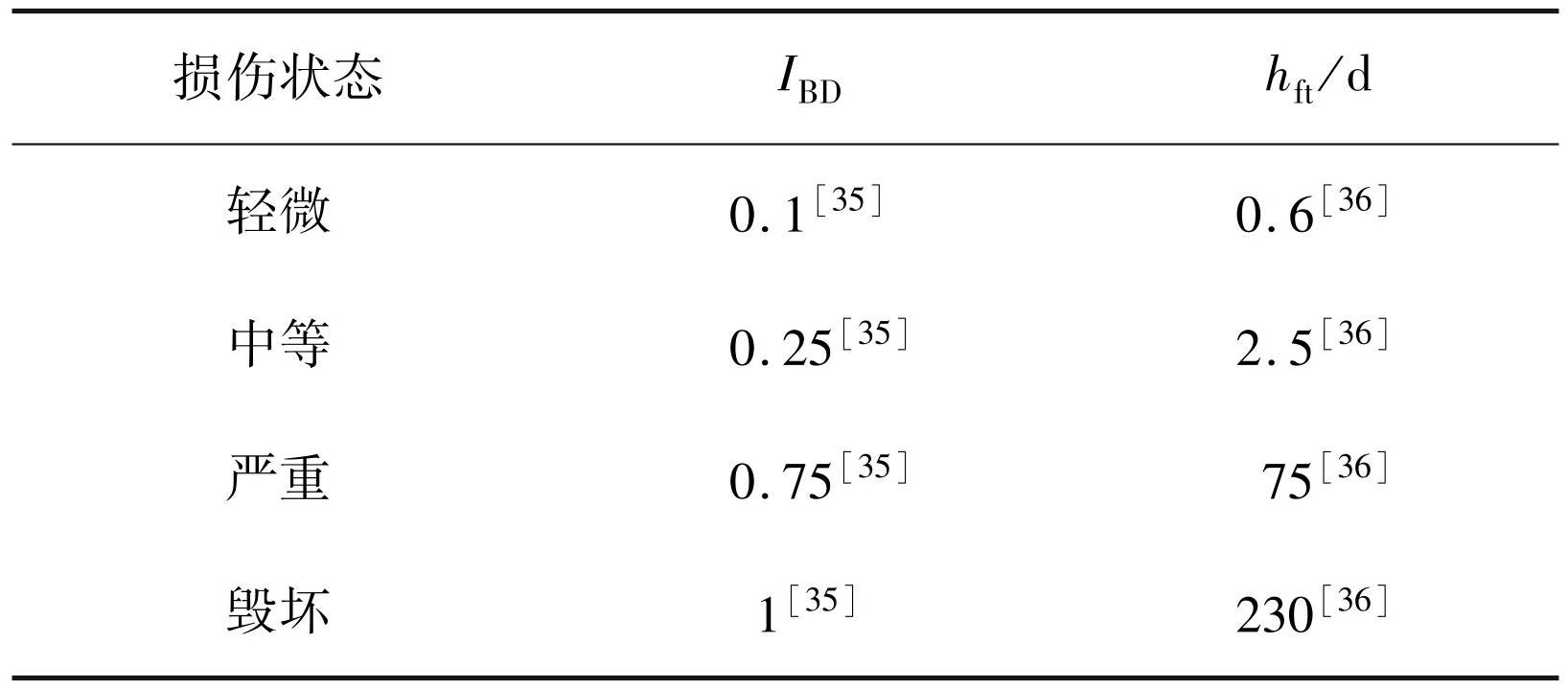
式中:Q₂为初始剩余性能，Q⁰₂ 为恢复完成时目标性能，H（τ）为 Heaviside 单位阶跃函数，r_f（τ）为恢复函数。不同损伤状态恢复需要的时间 h_ft见表1。不同服役时间桥墩灾后所需恢复时间可用 h_ft与桥梁处于不同损伤状态的失效概率的乘积和来计算。

表1不同损伤状态恢复时间及损伤指数离散值

Tab.1 Recovery time and bridge damage index for different damage states

4 算例

4.1 选取地震动样本

为对桥墩模型进行非线性动力时程分析，按规范^[37]反应谱选择地震动，具体依据的参数为:设防烈度为 7 度; 设计地震分组为第 2 组; 反应谱特征周期为 0.4 s; 场地类别为Ⅱ类; 频遇设防地震。从美国太平洋地震工程研究中心地震动数据库中筛选了 100 条天然地震动记录，所选 100 条地震波的反应谱如图2所示。

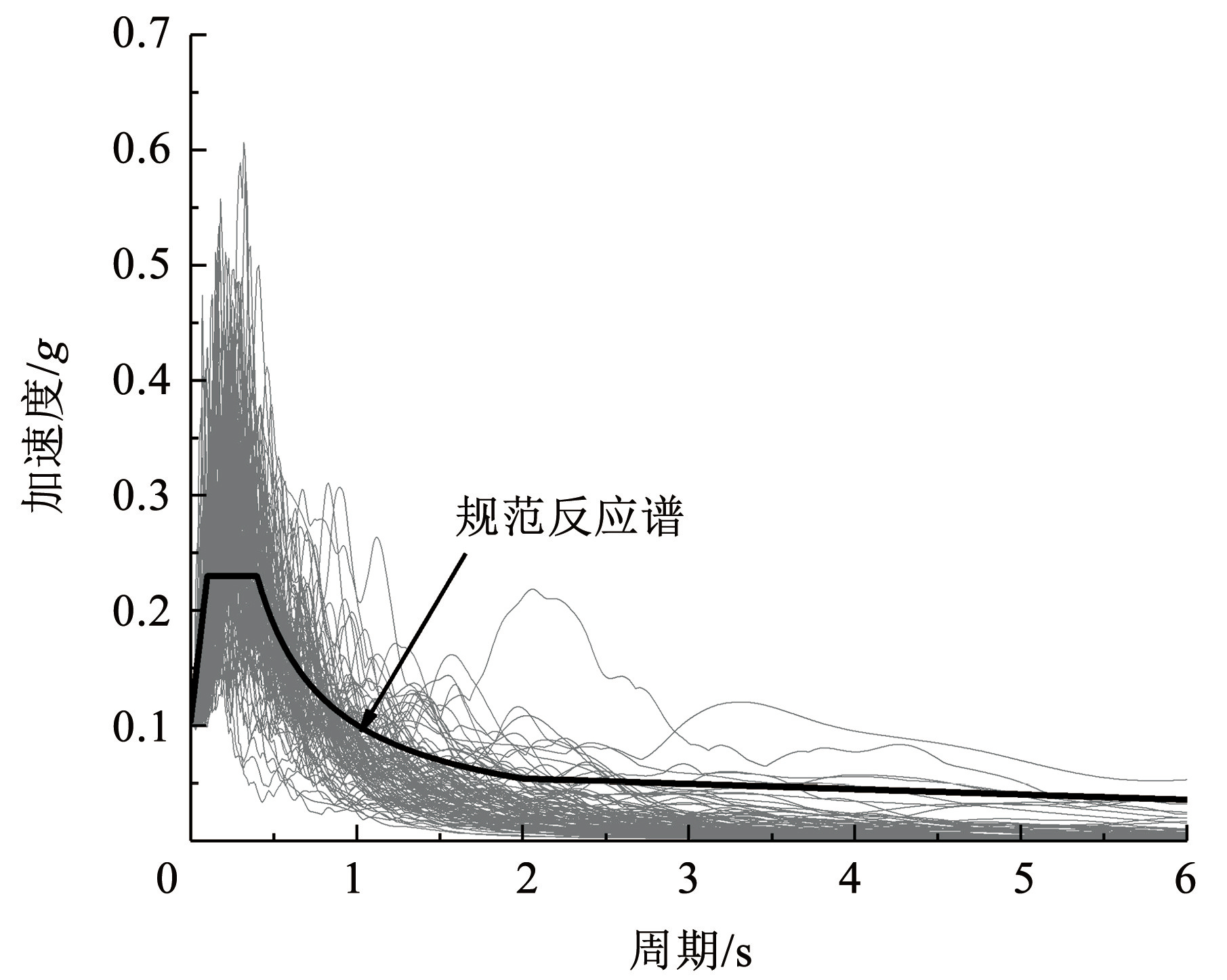
图2地震波反应谱

Fig.2Response spectrum of seismic waves

4.2 桥墩有限元模型

基于 OpenSees 对服役于潮汐环境中的某单柱式矩形墩进行建模，将桥墩划分为大气区（4 m）、浪溅区及水位变动区（2 m）、水下区（4 m）3 个部分，墩柱高 10 m，如图3（ b）所示。本次模拟忽略动水效应。截面采用边长为 1.5 m 的方形柱，其中混凝土保护层厚度为 50 mm，断面材料采用 C40 混凝土，断面内沿着边缘均匀配置 20 根 ϕ40HRB335 的钢筋，配筋率为 1.2%，钢筋混凝土密度 2 500 kg / m³，上部结构及支架简化为施加于桥墩上方竖向荷载 P，其大小为 2 000 kN。采用非线性力插值梁柱单元模拟墩柱，选择纤维模型对桥墩的截面进行定义，纤维截面划分方式如图3（a）。混凝土和纵筋分别采用 Concrete02 和 Steel01 单元定义。

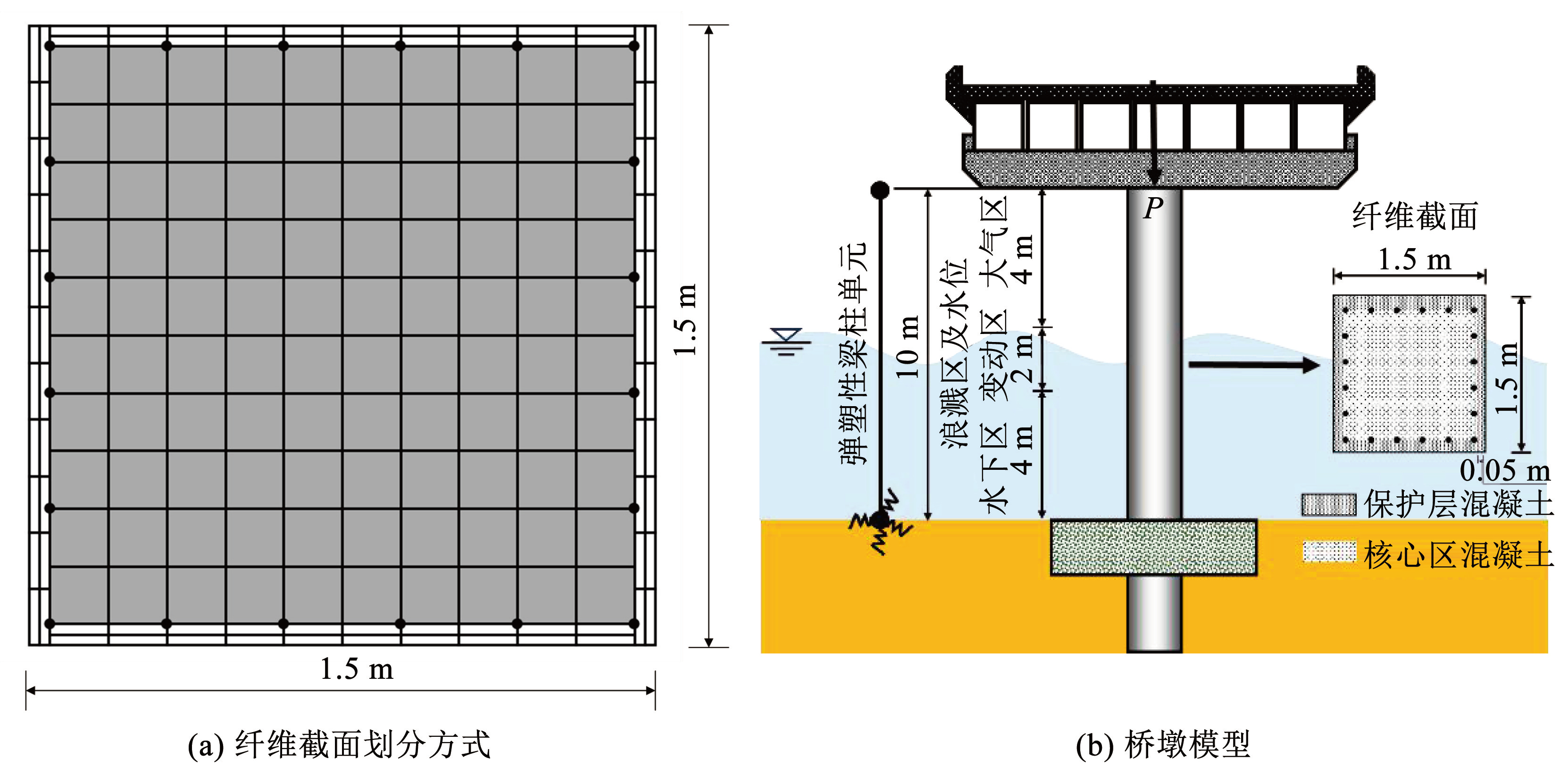
图3桥墩有限元模型

Fig.3Finite element model of the pier

4.3 氯离子腐蚀作用

桥墩锈蚀计算模型基本参数:大气区、浪溅区及水下区表面氯离子质量分数分别为 0.193%、 0.582%、0.770% ^[27]，法拉第常数 F 为 96 500 C/ mol，水灰比

\frac{w}{b}

为 0.4，试验方法影响系数 k_t为 1 ^[27]，大气区、浪溅区及水下区环境影响系数 K_c分别为 0.68、 0.92、1.32 ^[27]，养护条件影响系数 K_e为 1 ^[27]，大气区、浪溅区及水下区极限氯离子质量分数 C_th分别为 0. 070%、0.108%、0.308% ^[27]，混凝土龄期系数 n 为 0.37 ^[27]，铁离子的化合价 η 为 2.5，钢筋的密度 ρ_s为 7.85 g / cm³。

钢筋表面氯离子质量分数随时间变化规律如图4（a）所示，大气区 T_i_a、浪溅区及水位变动区 T_i_s、水下区 T_i_u 的桥墩中纵筋的初始锈蚀时间分别为 66.21、17.94、27.32 a。钢筋锈蚀深度随时间变化关系如图4（b）所示，进而根据钢筋混凝土材料退化模型，计算得到了在全寿命期内，钢筋屈服强度及截面面积的退化情况，以及混凝土抗压强度退化情况，如图5所示。由图4（ b）可知，在初始锈蚀时间之后，各个分区钢筋锈蚀深度不断增加，相应地，图5中材料性能在初始锈蚀时间之前并未退化，锈蚀发生后，随着锈蚀深度的增加，钢筋截面面积与屈服强度逐渐降低，与钢筋锈蚀深度变化一致。混凝土保护层抗压强度也逐渐降低，但在大气区、浪溅区、水下区服役时间分别为 111、63、72 a 后呈现不变趋势，这是由于在假设混凝土锈胀裂缝宽度最大为 3 mm，其达到3 mm 后，混凝土性能不再随时间变化。

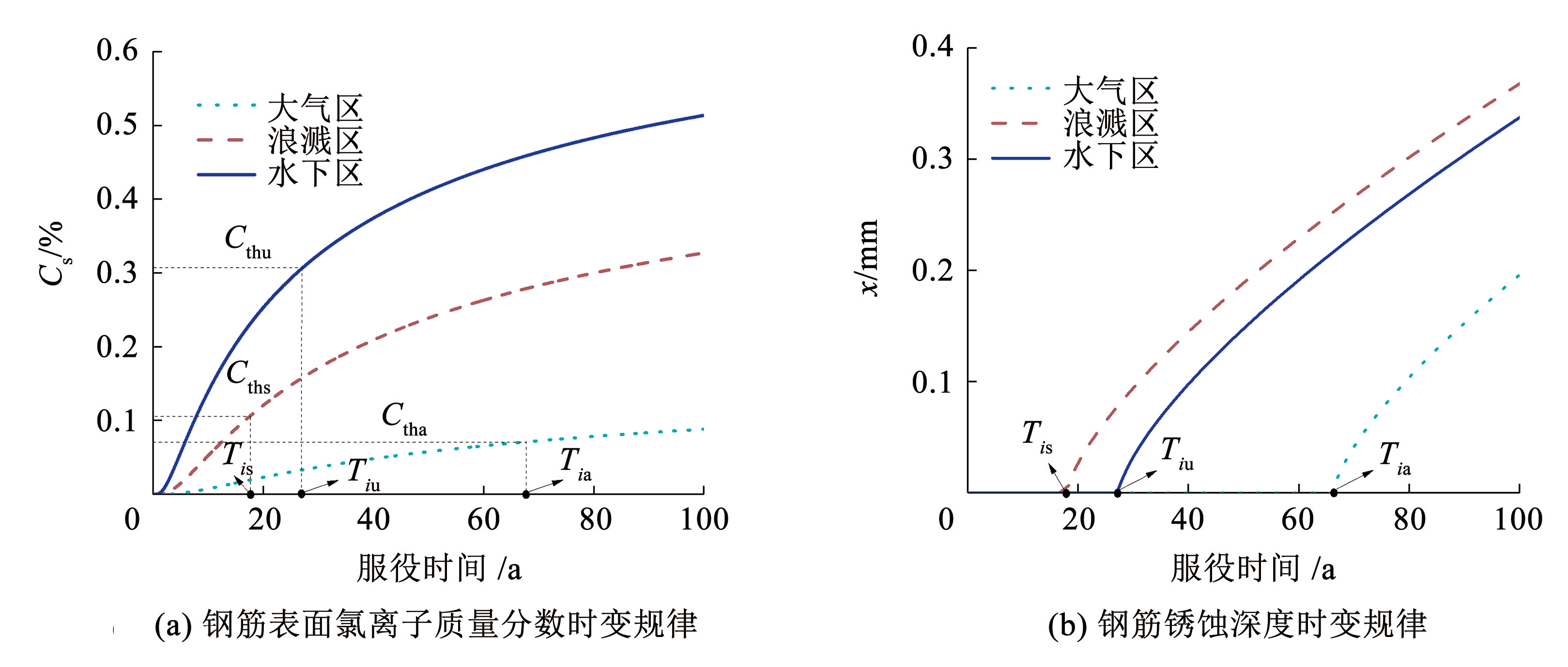
图4钢筋锈蚀规律

Fig.4The law of steel corrosion

图5桥墩材料性能退化规律

Fig.5Degradation patterns of bridge pier material properties

针对桥墩退化问题，根据材料性能时变规律对桥墩分别进行 Pushover 分析和震后性能分析，以获取灾前性能指标 Q₁和灾后性能指标 Q₂。

4.4 灾前性能指标

基于 Pushover 分析计算灾前性能指标 Q₁。为反应时间累积效应下的桥墩退化过程的抗震性能，本文考虑结构基本振型，采用 Pushover 法对腐蚀桥墩的时变受力性能进行分析。对桥墩施加均布水平位移荷载，以 0.3 mm 为间隔，逐步加载至 200 mm。用力-位移曲线来表征桥墩由弹性阶段进入弹塑性阶段的过程，如图6（a）所示。

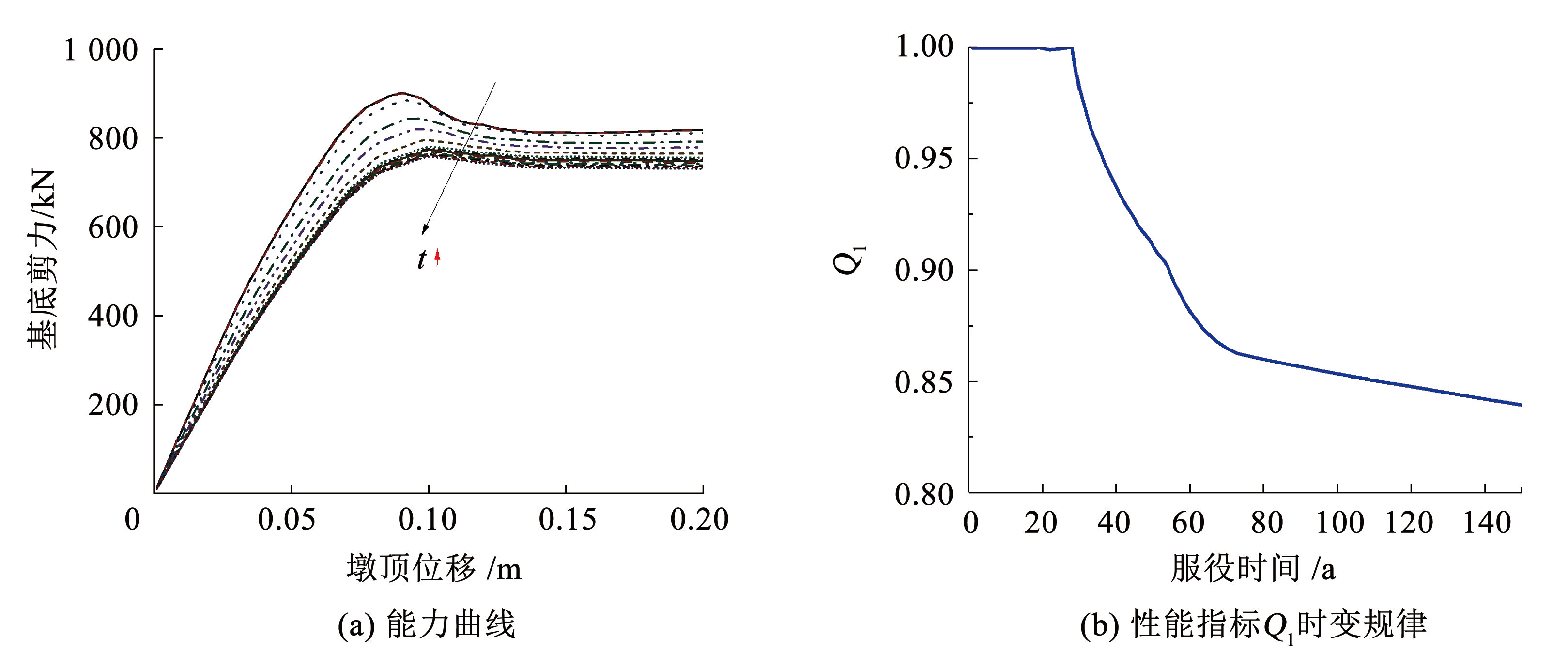
图6基于基底剪力比的灾前性能指标损失

Fig.6Pre-disaster performance loss indicators based on basal shear ratio

由图6（a）可知，随着墩顶水平位移的增加，桥墩由弹性状态逐步进入塑性状态，在墩顶水平位移达到 0. 09 m 后，混凝土产生明显损伤，结构软化，之后，钢筋继续承担剪力，基底剪力随墩顶水平位移的增大而平稳增大。随着服役时间的增加，同样的墩顶水平位移对应的基底剪力逐渐下降，这是由于桥墩服役于锈蚀环境导致的材料性能下降。

将基底剪力无量纲化，基底剪力比定义为不同服役时间基底剪力除以桥墩未退化时的基底剪力，故地震灾害发生前的性能损失采用基底剪力比的退化进行表征，性能指标 Q₁计算结果如图6（b）所示。由图可知，性能指标 Q₁在前 39 a 尚未退化，之后的服役年限产生了较大幅度的退化，72 a 后下降速度减慢。由于性能指标 Q₁ 完全基于氯离子侵蚀导致的桥墩结构性能退化得到，因此 Q₁的时变规律与图5桥墩材料性能退化规律类似。

4.5 灾后性能指标

基于上述模型计算得到桥墩在服役时间分别为 0、20、50、80 a 材料性能退化情况见表2。

表2材料性能退化

Tab.2 Deterioration of material properties

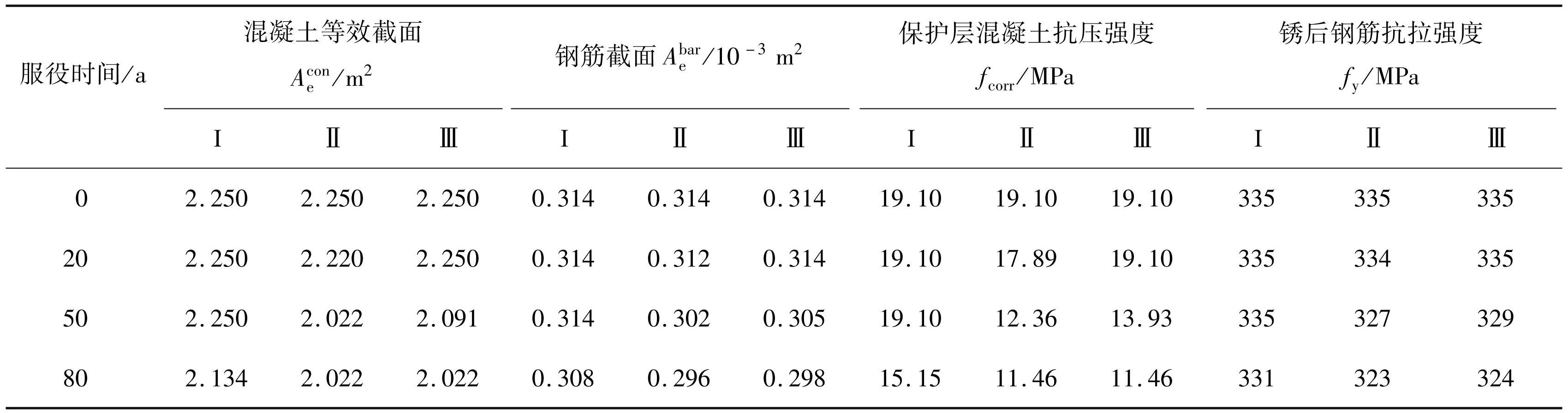
注:Ⅰ为大气区，Ⅱ为浪溅区，Ⅲ为水下区。

以峰值地面加速度 0. 05g 的增量步长对 4.1 节选取的 100 条地震波进行调幅，调幅为0.1g~1. 0g，对考虑材料性能退化的不同服役时间建立的桥墩有限元模型进行增量动力分析，得到不同强度地震作用下桥墩的时变响应。基于 2.1 节的位移延性模型，计算得到结构抗震能力的中位值 D_c 如表3所示，进而根据式（22）对桥墩进行地震易损性计算，结果如图7所示。

表3损伤界限

Tab.3 Damage boundaries

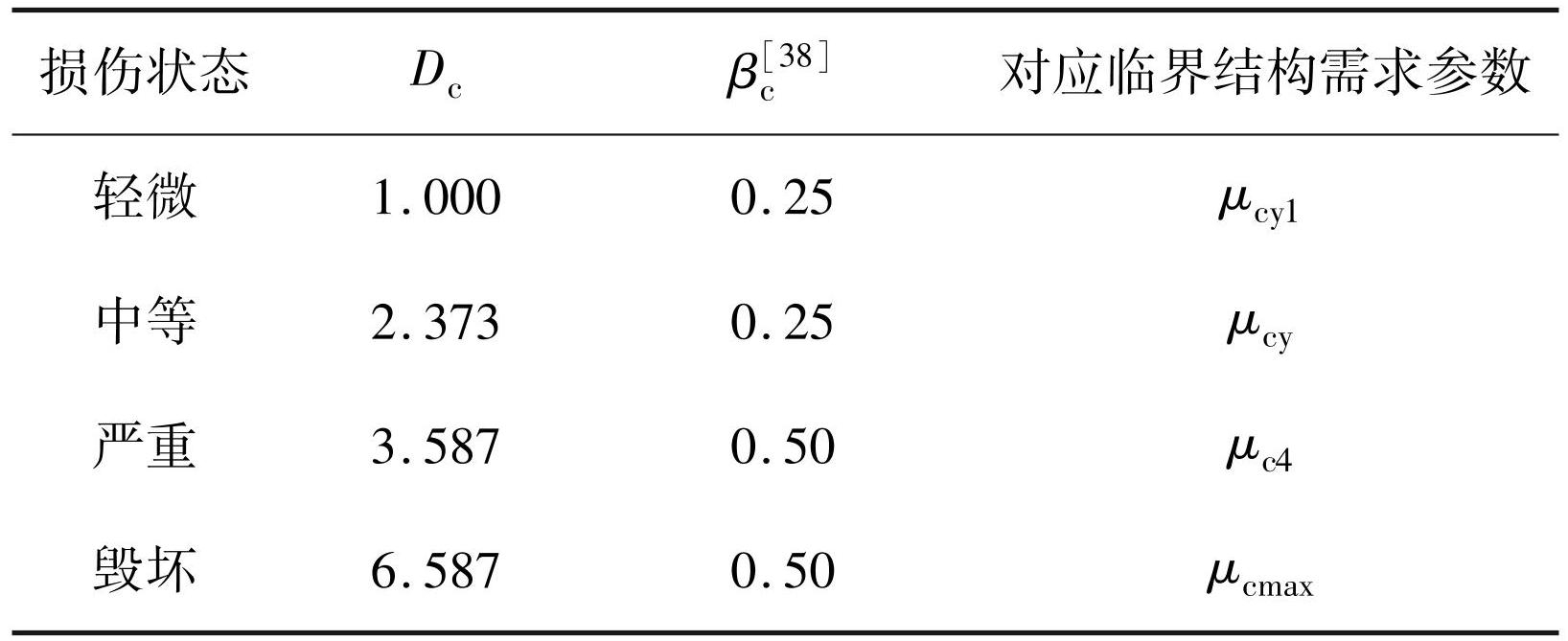
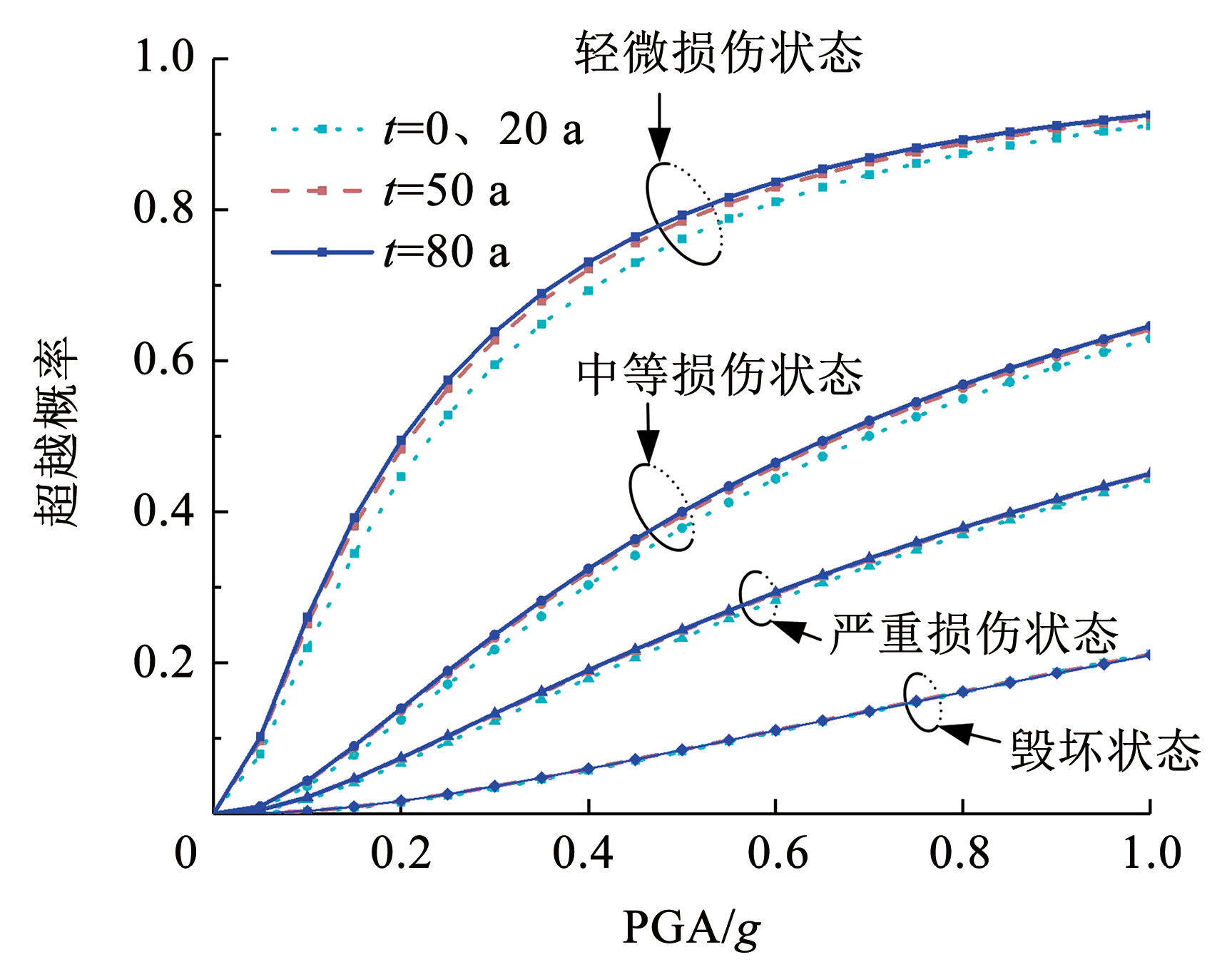
图7易损性曲线

Fig.7Fragility curve of pier

由图7可知，随着服役时间的增加，桥墩不同损伤状态的地震失效概率逐渐增大。以 PGA 为 0.6g 为例，当桥墩服役时间由 20 a 增长为 80 a 时，其轻微损伤状态的超越概率由 0.81 增大到了 0.84，这是由于钢筋的锈蚀导致桥墩材料性能退化，进一步导致桥墩抗震性能降低。值得注意的是，同一破坏状态下，桥墩服役 0 a 和 20 a 的地震易损性曲线差别不大。这是由于桥墩服役 20 a 时，对比于未锈蚀的状态，只有浪溅区及水位变动区产生了锈蚀退化现象，其承载能力仍大于荷载效应，故对桥墩性能影响不大。此外，在毁坏状态等级下，曲线几乎重合，这是由于当地震烈度达到足以使结构进入毁坏状态的范围时，结构本身即便因使用年限或者材料劣化等因素略有差异，也会全部进入全面破坏，概率曲线趋于饱和。

将不同服役时间对应的桥墩退结构化后的性能指标 Q₁值作为性能 2 的灾前性能初始值 Q⁰₂，地震波传至桥址的 PGA 为 0.6g 时，经计算得出灾后性能退化至 Q¹₂，假设灾后性能指标恢复至灾前状态，即 Q⁰₂，结合不同损伤状态恢复需要的时间及修复函数，得到桥墩全寿命周期性能曲线如图8所示。

图8桥墩全寿命周期性能曲线

Fig.8Life-cycle performance curve of the pier

由图8（a）可知，在全寿命周期内，由于服役时间的增加，桥墩材料性能退化，性能曲线逐渐降低。同时，本文假设传入桥址处地震波均为 0.6g，在不同时间节点发生地震时，桥墩损伤及恢复情况有较大差异:地震发生在桥墩服役时间为 20 a 及 80 a 时，修复时间分别为 38 d 和 40 d，且修复后的性能值分别为 1. 00 和 0.86。可见地震发生在桥墩服役时间较长的时间节点时，相比于比较短的时间节点，需要更多的时间来修复。

4.6 全寿命周期韧性

仅考虑氯离子侵蚀导致的桥墩结构性能退化，不考虑地震作用，根据韧性定义，在以 a 为单位的时间尺度内，韧性时变规律如图9所示。在服役前期，桥墩韧性基本保持恒定或轻微下降，随后韧性曲线开始以较缓的速率稳步降低，服役 40 a 至 140 a 期间，韧性值从 0.98 左右下降到约 0.89。由此可见，不同于地震等突发事件所造成的结构韧性急剧下降，氯离子侵蚀是一种长期渐进的损伤模式，长期积累效应不可忽视。

不同 PGA 作用下的桥墩恢复过程性能曲线如图10（a）所示，由图可知，当地震发生在同一桥墩服役时间时，随着 PGA 的增大，地震作用导致的性能退化程度显著，不同 PGA 作用下的韧性值变化规律亦佐证了此观点，如图10（ b）所示，相同服役年限下，桥墩韧性值随着 PGA 的增大而减小，例如当服役时间为 50 a 时，随着 PGA 从 0.1g 增大到 1. 0g，桥墩抗震韧性降低了 0.21。此外，不同的 PGA 作用下，桥墩服役 20 a 到 50 a 的韧性退化值远大于 50 a 到 80 a 的韧性退化值，大约为 2 倍。

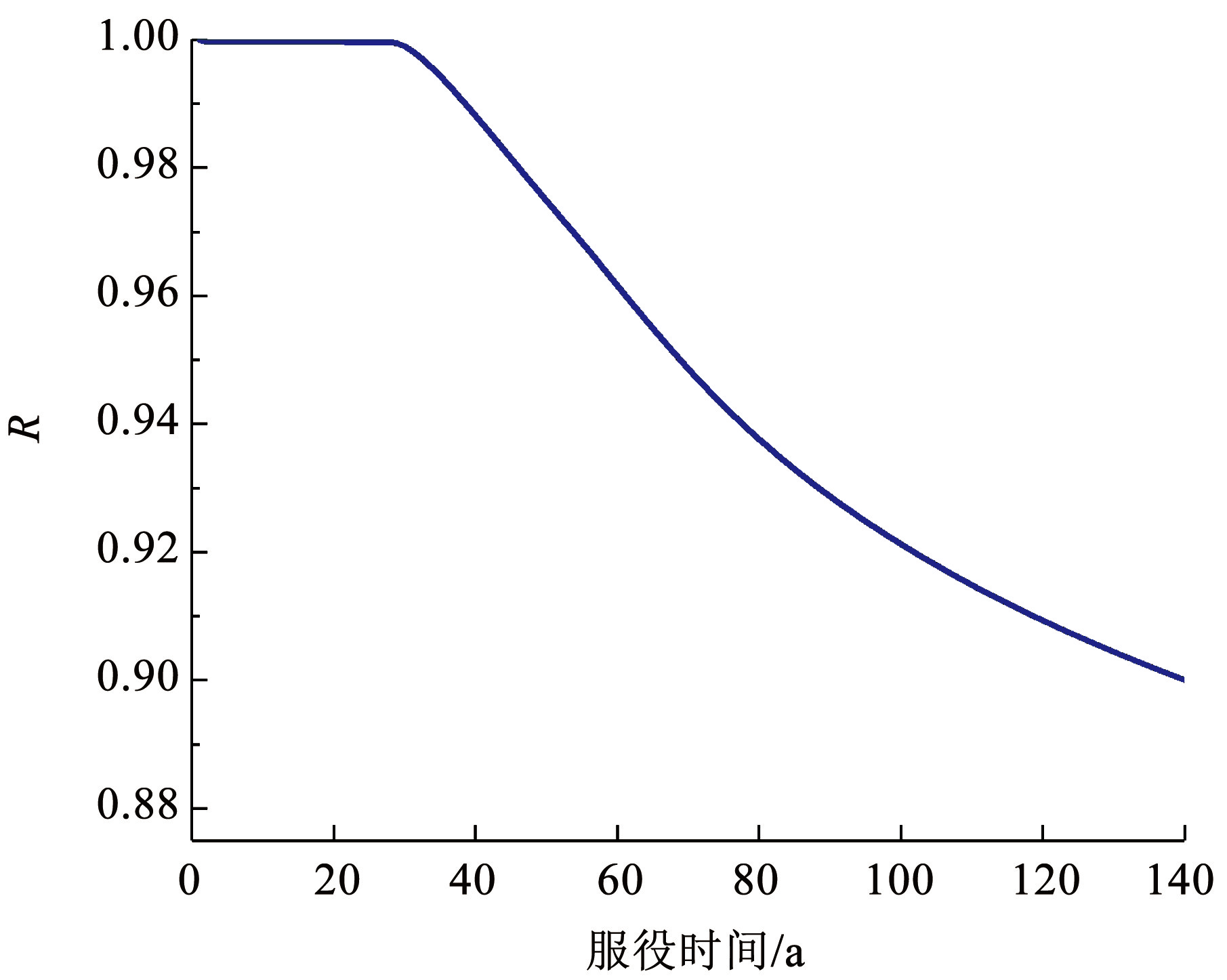
图9桥墩服役全寿命周期韧性时变规律

Fig.9Time-varying resilience patterns of bridge piers throughout thier service life

图10不同 PGA 作用下的桥墩恢复过程性能曲线及韧性规律

Fig.10Performance curves and resilience patterns of bridge piers under different PGAs loads during recovery process

5 结论

本文探讨了氯离子环境下分区腐蚀桥墩地震响应规律，基于概率需求分析构建了桥墩地震易损性模型，提出了分区腐蚀桥墩全寿命抗震韧性计算方法，主要结论如下:

1）钢筋锈蚀深度随服役时间的增大不断增加，材料性能下降，但混凝土裂缝并非无限增大。在本文研究模型中，大气区、浪溅区、水下区分别服役 111、63、72 a 后混凝土锈胀裂缝宽度呈不变趋势，混凝土等效截面及抗压强度不再继续降低，相比于大气区及水下区，浪溅区的服役环境更为恶劣。

2）由于腐蚀环境导致的材料性能劣化，墩顶水平位移对应的基底剪力随服役时间的增大而逐渐下降，桥墩不同损伤状态的地震失效概率逐渐增大。性能指标 Q₁在前 39 a 并未下降，之后产生了较大幅度的退化，降低了 0.14，72 a 后下降速度减慢，151 a 与 75 a 相比仅降低了 0. 03。

3）在全寿命周期内，性能曲线逐渐降低。地震发生于桥梁服役后期，需要更多的时间来修复，环境侵蚀对桥墩的抗震韧性削减作用显著。相同的时间间隔情况下，服役前期桥墩韧性下降更快，在本文的研究中，桥墩服役 20 a 到 50 a 的韧性退化值远大于 50 a 到 80 a 的韧性退化值，大约为 2 倍。可见在桥墩服役前期合理的恢复资源投入是提升系统恢复能力的有效手段，可以达到减少灾害长期影响的目的。

本文提出了考虑分区腐蚀环境桥墩全寿命抗震韧性计算模型，为后续如何有效评估潜在地震威胁下桥墩的抗震韧性水平提供参考依据。桥墩为交通基础设施的重要组成部分，下一步计划将其置于路网中作为关键节点，实现地震灾害下交通基础设施系统韧性评估。

图1流程图

Fig.1Flow chart

下载: 全尺寸图片

图2地震波反应谱

Fig.2Response spectrum of seismic waves

下载: 全尺寸图片

图3桥墩有限元模型

Fig.3Finite element model of the pier

下载: 全尺寸图片

图4钢筋锈蚀规律

Fig.4The law of steel corrosion

下载: 全尺寸图片

图5桥墩材料性能退化规律

Fig.5Degradation patterns of bridge pier material properties

下载: 全尺寸图片

图6基于基底剪力比的灾前性能指标损失

Fig.6Pre-disaster performance loss indicators based on basal shear ratio

下载: 全尺寸图片

图7易损性曲线

Fig.7Fragility curve of pier

下载: 全尺寸图片

图8桥墩全寿命周期性能曲线

Fig.8Life-cycle performance curve of the pier

下载: 全尺寸图片

图9桥墩服役全寿命周期韧性时变规律

Fig.9Time-varying resilience patterns of bridge piers throughout thier service life

下载: 全尺寸图片

图10不同 PGA 作用下的桥墩恢复过程性能曲线及韧性规律

Fig.10Performance curves and resilience patterns of bridge piers under different PGAs loads during recovery process

下载: 全尺寸图片

表1不同损伤状态恢复时间及损伤指数离散值

下载: 全尺寸图片

表2材料性能退化

下载: 全尺寸图片

表3损伤界限

下载: 全尺寸图片

图1流程图

Fig.1Flow chart

图2地震波反应谱

Fig.2Response spectrum of seismic waves

图3桥墩有限元模型

Fig.3Finite element model of the pier

图4钢筋锈蚀规律

Fig.4The law of steel corrosion

图5桥墩材料性能退化规律

Fig.5Degradation patterns of bridge pier material properties

图6基于基底剪力比的灾前性能指标损失

Fig.6Pre-disaster performance loss indicators based on basal shear ratio

图7易损性曲线

Fig.7Fragility curve of pier

图8桥墩全寿命周期性能曲线

Fig.8Life-cycle performance curve of the pier

图9桥墩服役全寿命周期韧性时变规律

Fig.9Time-varying resilience patterns of bridge piers throughout thier service life

图10不同 PGA 作用下的桥墩恢复过程性能曲线及韧性规律

Fig.10Performance curves and resilience patterns of bridge piers under different PGAs loads during recovery process

表1不同损伤状态恢复时间及损伤指数离散值

表2材料性能退化

表3损伤界限

图1流程图

Fig.1Flow chart

图2地震波反应谱

Fig.2Response spectrum of seismic waves

图3桥墩有限元模型

Fig.3Finite element model of the pier

图4钢筋锈蚀规律

Fig.4The law of steel corrosion

图5桥墩材料性能退化规律

Fig.5Degradation patterns of bridge pier material properties

图6基于基底剪力比的灾前性能指标损失

Fig.6Pre-disaster performance loss indicators based on basal shear ratio

图7易损性曲线

Fig.7Fragility curve of pier

图8桥墩全寿命周期性能曲线

Fig.8Life-cycle performance curve of the pier

图9桥墩服役全寿命周期韧性时变规律

Fig.9Time-varying resilience patterns of bridge piers throughout thier service life

图10不同 PGA 作用下的桥墩恢复过程性能曲线及韧性规律

Fig.10Performance curves and resilience patterns of bridge piers under different PGAs loads during recovery process

表1不同损伤状态恢复时间及损伤指数离散值

表2材料性能退化

表3损伤界限

余红发, 孙伟, 麻海燕, 等. 盐湖地区钢筋混凝土结构使用寿命的预测模型及其应用[J]. 东南大学学报(自然科学版),2002,32(4):638.YU Hongfa, SUN Wei, MA Haiyan,et al. Prediction model and application of service life of reinforced concrete structures in salt lake area[J]. Journal of Southeast University(Natural Science Edition),2002,32(4):638. DOI:10.3321/j.issn:1001-0505.2002.04.023

VAL D V, TRAPPER P A. Probabilistic evaluation of initiation time of chloride-induced corrosion[J]. Reliability Engineering & System Safety,2008,93(3):364. DOI:10.1016/j.ress.2006.12.010

SHAO Wei, NIE Yinghui, LIANG Fayun,et al. A novel comprehensive evaluation method for the corrosion initiation life of RC hollow piles in chloride environments[J]. Construction and Building Materials,2020,249:118801. DOI:10.1016/j.conbuildmat.2020.118801

陈妤, 刘荣桂, 付凯. 冻融循环下海工预应力混凝土结构的耐久性[J]. 建筑材料学报,2009,12(1):17.CHEN Yu, LIU Ronggui, FU Kai. Durability of offshore prestressed concrete structures under freeze-thaw cycles[J]. Journal of Building Materials,2009,12(1):17. DOI:10.3969/j.issn.1007-9629.2009.01.004

OU Yuchen, NGUYEN N D. Plastic hinge length of corroded reinforced concrete beams[J]. Aci Structural Journal,2014,111(5):1049

DU Y G, CHAN A H C, CLARK L A. Residual capacity of corroded reinforcing bars[J]. Magazine of Concrete Research,2005,57(3):135. DOI:10.1680/macr.2005.57.3.135

LIU T, WEYERS R W. Modeling the dynamic corrosion process in chloride contaminated concrete structures[J]. Cement and Concrete Research,1998,28(3):365. DOI:10.1016/S0008-8846(98)00259-2

VU K A T, STEWART M G. Structural reliability of concrete bridges including improved chloride-induced corrosion models[J]. Structural Safety,2000,22(4):313. DOI:10.1016/S0167-4730(00)00018-7

曹万林, 赵羽习, 叶涛萍. 再生混凝土结构长期工作性能研究进展[J]. 哈尔滨工业大学学报,2019,51(6):1. CAO Wanlin, ZHAO Yuxi, YE Taoping. Research progress on longterm working performance of recycled concrete structures[J]. Journal of Harbin Institute of Technology,2019,51(6):1

阳逸鸣, 彭建新, 张建仁. 考虑多因素作用下的RC梁抗力时空退化模型[J]. 哈尔滨工业大学学报,2017,49(9):58.YANG Yiming, PENG Jianxin, ZHANG Jianren. Spatiotemporal degradation model of RC beam resistance considering multiple factors[J]. Journal of Harbin Institute of Technology,2017,49(9):58. DOI:10.11918/j.issn.0367-6234.201611077

李超, 李宏男. 考虑氯离子腐蚀作用的近海桥梁结构全寿命抗震性能评价[J]. 振动与冲击,2014,33(11):8.LI Chao, LI Hongnan. Evaluation of life-cycle seismic performance of offshore bridge structures considering chloride ion corrosion[J]. Journal of Vibration and Shock,2014,33(11):8. DOI:10.13465/j.cnki.jvs.2014.11.013

VECCHIO F J, COLLINS M P. The modified compression-field theory for reinforced concrete elements subjected to shear[J]. Aci Structural Journal,1986,83(2):219. DOI:10.14359/10416

BIONDINI F, CAMNASIO E, TITI A. Seismic resilience of concrete structures under corrosion[J]. Earthquake Engineering & Structural Dynamics,2015,44(14):2445. DOI:10.1002/eqe.2591

RAJPUT A S, SHARMA U K. Corroded reinforced concrete columns under simulated seismic loading[J]. Engineering Structures,2018,171:453. DOI:10.1016/j.engstruct.2018.05.097

AKIYAMA M, FRANGOPOL D M, MATSUZAKI H. Life-cycle reliability of RC bridge piers under seismic and airborne chloride hazards[J]. Earthquake Engineering & Structural Dynamics,2011,40(15):1671. DOI:10.1002/eqe.1108

DOMANESCHI M, DE GAETANO A, CASAS J R,et al. Deteriorated seismic capacity assessment of reinforced concrete bridge piers in corrosive environment[J]. Structural Concrete,2020,21(5):1823. DOI:10.1002/suco.202000106

胡思聪. 考虑氯离子侵蚀的桥梁地震易损性及抗震加固策略研究[D]. 长沙: 湖南大学,2018. HU Sicong. Research on seismic vulnerability and seismic reinforcement strategy of bridges considering chloride ion erosion[D]. Changsha: Hunan University,2018

刘守苗. 氯离子腐蚀环境下RC桥墩抗震性能分析[D]. 长沙: 湖南大学,2015. LIU Shoumiao. Seismic performance analysis of RC bridge piers under chloride ion corrosion environment[D]. Changsha: Hunan University,2015

CUI Fengkun, ZHANG Haonan, GHOSN M,et al. Seismic fragility analysis of deteriorating RC bridge substructures subject to marine chloride-induced corrosion[J]. Engineering Structures,2018(155):61. DOI:10.1016/j.engstruct.2017.10.067

DE DOMENICO D, MESSINA D, RECUPERO A,et al. Seismic vulnerability assessment of reinforced concrete bridge piers with corroded bars[J]. Structural Concrete,2023,24(1):56. DOI:10.1002/suco.202200378

GHOSH J, PADGETT J E. Aging considerations in the development of time-dependent seismic fragility curves[J]. Journal of Structural Engineering,2010,136(12):1497. DOI:10.1061/(asce)st.1943-541x.0000260

成虎, 张存瑞, 邱开发, 等. 基于组合性能指标的立面差异化锈蚀桥墩时变抗震韧性研究[J]. 工程力学,2024,41(5):179.CHENG Hu, ZHANG Cunrui, QIU Kaifa,et al. Study on timevarying seismic resilience of facade differentiated corroded piers based on combined performance index[J]. Engineering Mechanics,2024,41(5):179. DOI:10.6052/j.issn.1000-4750.2022.05.0441

胡思聪, 王连华, 李立峰, 等. 非一致氯离子侵蚀下近海桥梁时变地震易损性研究[J]. 土木工程学报,2019,52(4):62.HU Sicong, WANG Lianhua, LI Lifeng,et al. Time-varying seismic vulnerability of offshore bridges under non-uniform chloride ion erosion[J]. Journal of Civil Engineering,2019,52(4):62. DOI:10.15951/j.tmgcxb.2019.04.006

谷音, 李晓芳. 考虑氯离子侵蚀的近海桥梁结构地震易损性分析[J]. 应用基础与工程科学学报,2019,27(5):1019.GU Yin, LI Xiaofang. Seismic fragility analysis of offshore bridge structures considering chloride ion erosion[J]. Journal of Applied Basic and Engineering Sciences,2019,27(5):1019. DOI:10.16058/j.issn.1005-0930.2019.05.007

XU Qiuhong, SHI Danda, SHAO Wei. Service life prediction of RC square piles based on time-varying probability analysis[J]. Construction and Building Materials,2019,227:116824. DOI:10.1016/j.conbuildmat.2019.116824

中华人民共和国交通运输部. 水运工程结构耐久性设计标准: JTS 153—2015[S]. 北京: 人民交通出版社,2015.Ministry of Transport of the People′s Republic of China. Standard for durability design of port and waterway engineering structure: JTS 153—2015[S]. Beijing: China Communications Press,2015

顾祥林, 张伟, 姜超, 等. 混凝土结构的环境作用[M]. 北京: 科学出版社,2021. GU Xianglin, ZHANG Wei, JIANG Chao,et al. Environmental effects of concrete structures[M]. Beijing: Science Press,2021

聂莹慧. 海洋环境下桩基的耐久性寿命预测与水平承载性能可靠度研究[D]. 上海: 上海海事大学,2021. NIE Yinghui. Durability life prediction and horizontal bearing performance reliability of pile foundation inmarine environment[D]. Shanghai: Shanghai Maritime University,2021

CORONELLI D, GAMBAROVA P. Structural assessment of corroded reinforced concrete beams:modeling guidelines[J]. Journal of Structural Engineering,2004,130(8):1214. DOI:10.1061/(asce)0733-9445(2004)130:8(1214)

HWANG H, 刘晶波. 地震作用下钢筋混凝土桥梁结构易损性分析[J]. 土木工程学报,2004,37(6):47.HWANG H, LIU Jingbo. Structural fragility analysis of reinforced concrete bridges under earthquake action[J]. Journal of Civil Engineering,2004,37(6):47. DOI:10.3321/j.issn:1000-131X.2004.06.009

HWANG H, LIU J B, CHIU Y H. Seismic fragility analysis of highway bridges[R]. Memphis: Center for Earthquake Research and Information, The University of Memphis,2001

中华人民共和国交通运输部. 公路桥梁抗震设计规范: JTG/T 2231-01—2020[S]. 北京: 人民交通出版社,2020.Ministry of Transport of the People′s Republic of China. Specifications for seismic design of highway bridges: JTG/T 2231-01—2020[S]. Beijing: China Communications Press,2020

郑凯锋, 陈力波, 庄卫林, 等. 基于概率性地震需求模型的桥梁易损性分析[J]. 工程力学,2013,30(5):8.ZHENG Kaifeng, CHEN Libo, ZHUANG Weilin,et al. Bridge vulnerability analysis based on probabilistic seismic demand model[J]. Engineering Mechanics,2013,30(5):8. DOI:10.6052/j.issn.1000-4750.2012.01.0027

ZHANG Mingyuan, YANG Xiangjie, ZHANG Juan,et al. Postearthquake resilience optimization of a rural " Road-bridge" transportation network system[J]. Reliability Engineering & System Safety,2022,225:108570. DOI:10.1016/j.ress.2022.108570

GUO Anxin, LIU Zhenliang, LI Suchao,et al. Seismic performance assessment of highway bridge networks considering post-disaster traffic demand of a transportation system in emergency conditions[J]. Structure and Infrastructure Engineering,2017,13(12):1523. DOI:10.1080/15732479.2017.1299770

HOLMES W, BORCHERDT R, BROOKSHIRE D,et al. HazusMH 2.1 technical manual-earthquake model[Z]. Washington DC: Federal Emergency Management Agency,2015

中华人民共和国住房和城乡建设部. 建筑抗震设计规范: GB 50011—2010[S]. 北京: 中国建筑工业出版社,2010.Ministry of Housing and Urban-Rural Development of the People′s Republic of China. Code for seismic design of buildings: GB 50011—2010[S]. Beijing: China Arehitecture & Building Press,2010

何双, 赵桂峰, 马玉宏, 等. 基于概率地震需求模型的隔震桥梁易损性对比[J]. 地震工程与工程振动,2014,34(6):1.HE Shuang, ZHAO Guifeng, MA Yuhong,et al. Vulnerability comparison of isolated bridges based on probabilistic seismic demand model[J]. Earthquake Engineering and Engineering Vibration,2014,34(6):1. DOI:10.13197/j.eeev.2014.06.1.hes.001

1 桥墩分区锈蚀退化模型

2 易损性模型

3 韧性

4 算例

5 结论

友情链接LINKS