欢迎访问《哈尔滨工业大学学报》编辑部网站！

基于FWD三参数的路基模量预测方法

doi: 10.11918/202301049

张磊^1,2 ，张定一¹ ，肖倩³ ，王龙⁴ ，姚鹏飞¹

1. 东南大学交通学院,南京 211189

2. 南京现代综合交通实验室,南京 211100

3. 交通运输部公路科学研究院,北京 100088

4. 哈尔滨工业大学交通科学与工程学院,哈尔滨 150090

基金项目: 国家自然科学基金(51778142) ；中交公路院科研项目(H202008201) ；中国民航机场建设集团项目(JSRDKYN20220307)

详细信息

作者简介

张磊(1977—),男,教授,博士生导师

通讯作者

张磊,lei800@163.com

中图分类号: U416.217

文献标识码: A

文章编号: 0367-6234(2025)03-0025-09

A prediction method of subgrade modulus based on three parameters of FWD

ZHANG Lei^1,2 ， ZHANG Dingyi¹ ， XIAO Qian³ ， WANG Long⁴ ， YAO Pengfei¹

1. School of Transportation, Southeast University, Nanjing 211189 , China

2. Nanjing Modern Multimodal Transportation Laboratory, Nanjing 211100 , China

3. Research Institute of Highway Ministry of Transport, Beijing 100088 , China

4. School of Transportation Science and Engineering, Harbin Institute of Technology, Harbin 150090 , China

摘要

为了建立能够客观准确评价既有路基承载能力状况的测算方法,改善路面模量反算软件因初值选取不唯一而导致的误差问题,建立了路面弹性层状体系有限元动力模型,基于相关性分析筛选优化了弯沉盆参数,提出了基于 BDI-F₂ -d₉的三参数路基模量预测模型;在此基础上形成多层路面模量反算新方法,并利用北京 RIOHTrack 环道的 4 种不同典型路面结构的实测数据对该模型的有效性和准确性进行验证。结果表明:应用所提出的 FWD 三参数预测模型计算得到的路基模量较常规反算方法更为准确,且与承载板实测值之间存在较好的线性关系(R² = 0. 9106),两者比值介于 0. 19 ~ 0. 28 之间,符合已有文献研究结论。以此路基模量预测值作为输入参数并利用沥青路面动力有限元模型能更加准确地模拟 FWD 测试动态过程,从而提高了路面各层模量的反算精度。研究成果为模量反算软件初值选取提供了参考,并为利用弯沉盆参数(DBP 指标)构建适用于实际工程的路基、路面模量反算方法提供了理论依据。

关键词

道路工程 / FWD 模型 / 非线性特性 / 路基模量反算

Abstract

In order to objectively evaluate the bearing capacity condition of the existing subgrade and to eliminate the deviation by the popular back-calculation software due to the initial parameter values. A finite element dynamic model of asphalt pavement was established and optimized the bending basin parameters based on correlation analysis screening, so as to propose a three-parameter subgrade modulus prediction model based on BDI-F₂ -d₉ . On this basis, a new method was developed to conduct a multi-layer pavement modulus back-calculation, and the effectiveness and accuracy of the model were verified by using the measured data of four different typical pavement structures of the Beijing RIOHTrack. The results showed that there is a good linear relationship (R² = 0. 9106) between the predicted subgrade modulus by proposed FWD three-parameter model and the measured value by the bearing plate. The ratio of them is between 0. 19 and 0. 28, which is consistent with the literature findings. Since this predicted subgrade modulus with more precision is utilized as an input parameter for the dynamic finite element model of asphalt pavement to simulate the real dynamic process of FWD testing, the more accurate results of the modulus of each layer of the pavement will produced by back-calculating. The research results provide the reference for the initial parameters value of modulus back-calculation software and provide the theoretical basis for back-calculation methods to calculate subgrade and each pavement modulus using DBP indexes as well.

Keywords

road engineering / FWD model / nonlinear characteristics / subgrade modulus back-calculation

1 路面结构动力有限元分析模型 1.1 路面动力响应分析基础理论 1.2 模型建立 1.2.1 模型尺寸 1.2.2 荷载条件 1.2.3 边界条件及网格划分 1.3 有限元模型校验 1.4 路面结构组合及材料参数 2 FWD 双参数模型建立 2.1 双参数诺谟图分析 2.2 BDI-F₂双参数的应用 3 既有 FWD 双参数模型的改进优化 3.1 DBP 指标构建 3.2 BDI-F₂-d₉三参数模型建立 4 基于 RIOHTrack 环道的多层路面模量反算方法验证 4.1 环道路面材料 4.2 基于 FWD 三参数模型的多层路面模量反算方法验证 4.2.1 实测弯沉的温度修正 4.2.2 路基模量非线性分析及逐层反算结果 5 结论

路基是公路的承重主体^[1-2]，目前国内常用路基回弹模量来表征路基的力学特性和抗变形能力^[3-4]，其测试方法通常为室内试验法和现场实测法。然而室内试验中试件受力状况与现场路基土的实际应力状态不一致; 现场实测法更是费时费力，操作繁琐，且测试结果为静态模量，应用场景不足^[5-6]。因此如何科学、快速、准确地计算出路基的回弹模量对评价路面结构承载能力至关重要。

FWD 自 20 世纪 80 年代提出以来，因弯沉参数中包含的丰富信息及广泛的适用性被道路工程领域普遍用于路面的结构状况评价。然而目前各国既有的 FWD 模量反算软件，大多以弹性层状体系为模型，采用的是静力分析方法。但 FWD 落锤仪在施加荷载时为动态荷载，因此为了更好地模拟实际 FWD 作用模式，应采用动力分析方法。同时模量反算软件反算结果受初值选取的影响较大，初值选取精度将直接影响反算精度^[7-9]，因此如何系统有效地确定初值，成为影响反算结果精度的重要因素。

基于上述存在的问题，国内外学者开始对弯沉盆参数（deflection basin parametres，DBP）展开研究，通过构建不同弯沉盆参数组合从而来表征路面各结构层的性能^[10-11]。其中文献^[12-13]针对柔性基层沥青路面，发现由基层损伤指数 BDI 和形状指数 F₂所组成的诺谟图可以表征路基模量，并提出可以用来表征基层和面层模量的 DBP 指标。相较而言，文献^[14]通过弹性多层体系的计算分析，建立了应用路表弯沉盆估算沥青路面结构各层应变的计算简式，但其研究仍基于静态理论，没有考虑到 FWD 的动态特性。文献^[15]利用 BDI 和 F₂两个参数确定土基模量，并基于此将计算得到的土基模量作为参数输入人工神经网络，从而得到其他结构层位的模量。文献^[16] 在有限元数值分析的基础上，利用 DBP 指标建立了基于直接弯沉指标 d₉ 和形状指标 F₈的路基模量预测模型。上述工作取得了较好的研究结论，但其反算结果目前还缺少实际验证。

基于此，本文通过建立沥青路面动力有限元数值分析模型，验证了基层损伤指数 BDI 和形状指数 F₂组成的路基模量双参数模型对于半刚性基层路面结构的适用性，同时克服该模型的局限性，提出了基于 BDI-F₂-d₉的三参数模型，并利用北京 RIOHTrack 环道对该模型的有效性和准确性进行了验证。研究成果为模量反算软件初值选取提供了参考，并为利用 DBP 指标构建适用于实际工程的路基模量反算提供了理论依据和技术保障。

1 路面结构动力有限元分析模型

1.1 路面动力响应分析基础理论

路面动力有限元模型以弹性层状体系为基本原理，弹性层状体系假设各结构层为连续、均质、各向同性的线弹性材料。通过在边界设置无限单元，保证最下一层为半无限空间体，在水平和竖直两个方向无限延伸。基于路面结构动力学得到的 Hamilton 变分原理基本平衡方程是研究路面动力荷载响应的核心，其方程形式为

M {\ddot{δ}}_{t} + C {\dot{δ}}_{t} + K δ_{t} = f (t)

(1)

其中:M、C 和 K 分别为质量、阻尼和刚度矩阵;

{\ddot{δ}}_{t}

、

{\dot{δ}}_{t}

和δ_t分别为加速度、速度和位移向量; f（t）为荷载向量。

本研究所采用阻尼模型为 Rayleigh 阻尼，常用方程形式为

C = α M + β K

(2)

\{\begin{matrix} α = \frac{2 ω_{1} ω_{2}}{ω_{1} + ω_{2}} δ \\ β = \frac{2 δ}{ω_{1} + ω_{2}} \end{matrix}

(3)

式中 α 和 β 的值由结构的阻尼比和固有频率决定，本研究阻尼比 δ 取 0. 05，通过对模型进行模态分析可得到二阶固有频率 ω₁和 ω₂。

本研究采用直接积分求解法，通过对加速度、速度和位移进行不断迭代，直至满足收敛条件，得出结果。为了得到较好的计算精度，本研究将时间步长限制在基本周期的 1 / 50 以内，荷载区域空间步长限制在 1 mm 以内。

1.2 模型建立

1.2.1 模型尺寸

为了更加准确地模拟 FWD 落锤实际的作用效应，同时考虑到计算效率以及路面模型的对称特性，本文采用空间轴对称模型来进行分析。模型层间接触状态设置为完全连续，通过对路面有限元模型的尺寸效应进行对比研究，最终确定模型水平长度为 10 m，纵向深度为 10 m（水平向侧边界和纵向底部边界都设置了无限单元）。

1.2.2 荷载条件

为简化方便，大多数学者通常采用半正弦曲线来模拟 FWD 加载过程，如图1（a）所示。为了更加真实地模拟实际的 FWD 荷载作用情况，本次加载根据路面实际采集的 FWD 荷载曲线进行^[17]，如图1（b）所示。其中荷载半径为 15 cm，所用 FWD 仪器 9 点传感器设置方案见表1。

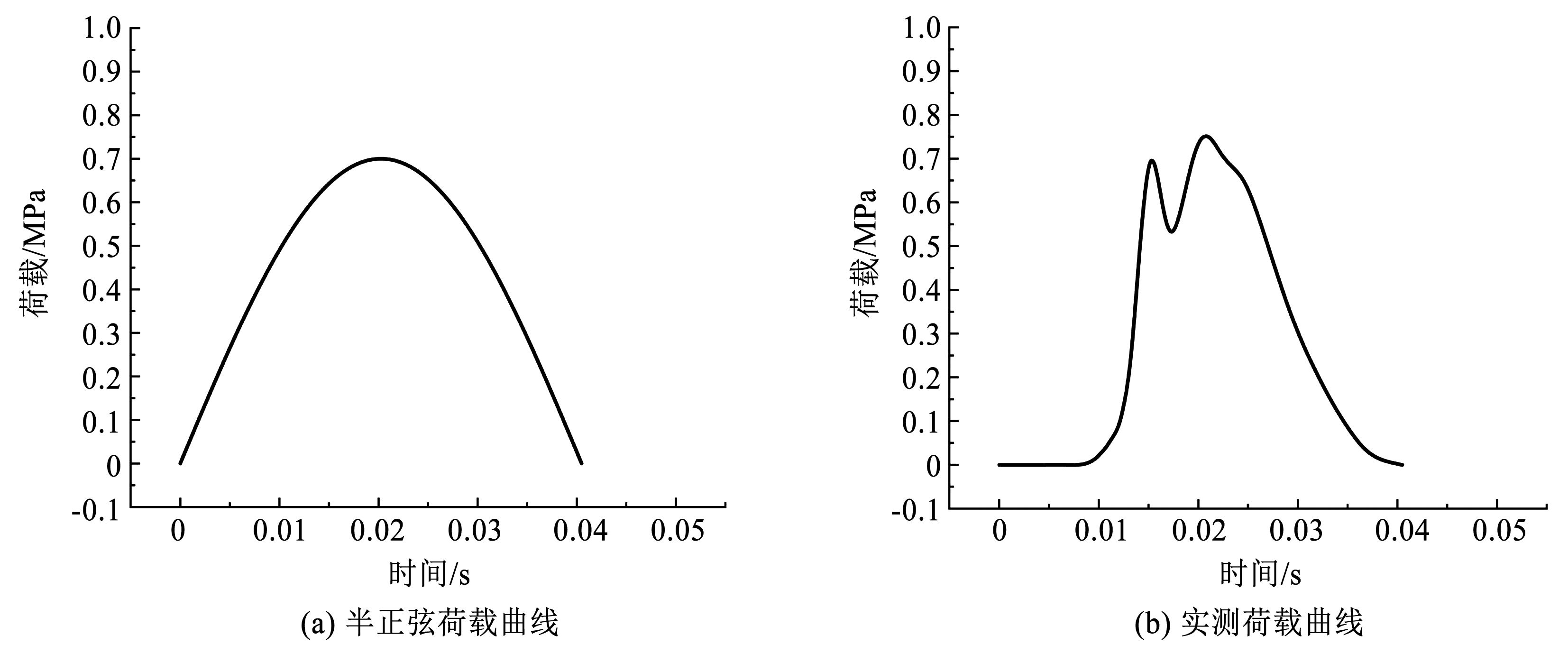
图1典型 FWD 荷载曲线

Fig.1Typical FWD load curve

表1传感器布设位置方案

Tab.1 Sensor placement scheme

1.2.3 边界条件及网格划分

如图2（a）所示，通过对比分析单自由度边界约束（侧面边界水平约束，底部边界竖向约束）和无限单元两种边界条件荷载作用中心的弯沉时程曲线可知，设置无限单元边界能够最大程度地减少由于边界条件设置导致的应力波反射现象，在模型水平以及竖直方向采用无限单元模拟实际路面的半无限结构边界状态，无限边界设置如图2（b）所示。

图2无限单元边界设置

Fig.2Infinite cell boundary setting

在网格划分时，FWD 荷载作用区域网格划分更加精细，每一层路面结构至少设置 4 层单元保证精度，除模型边界设置 CINAX4 轴对称无限单元外，其他部分均设置 CAX4R 单元。

1.3 有限元模型校验

根据上述模型建立原则，建立与美国航道试验站开发的 LEEPWIN 软件中的示例数据库相同的 3 层有限元模型，并将计算结果与示例数据库中的数据进行比较^[18]，精度满足要求，如图3所示。

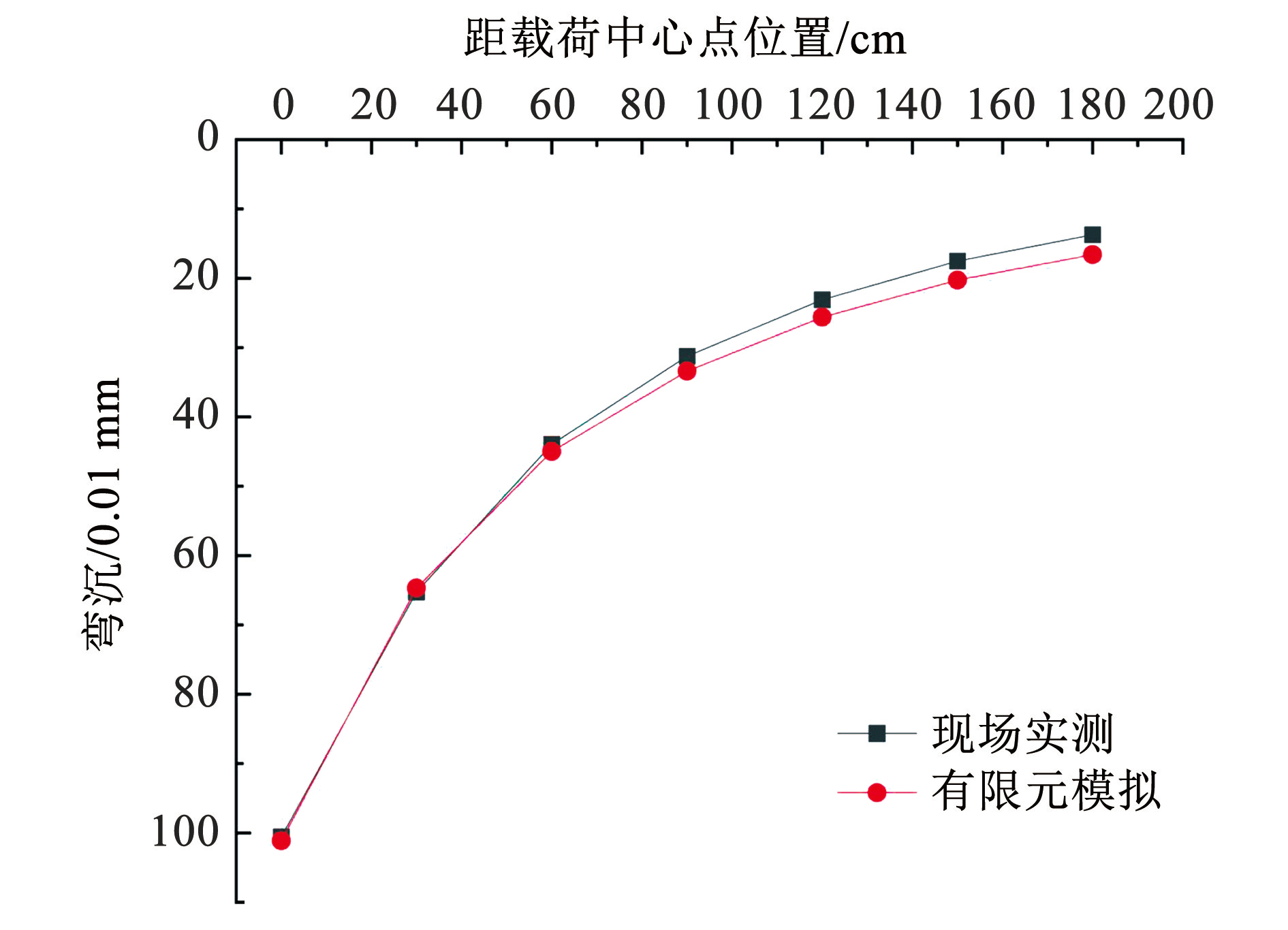
图3模型校验示意

Fig.3Schematic diagram of model calibration

1.4 路面结构组合及材料参数

将半刚性基层沥青路面简化为 3 层，根据中国高等级半刚性基层沥青路面实际情况及《公路沥青路面设计规范》相关规定，设置如表2所示的不同工况。

表2路面结构材料参数取值范围

Tab.2 Road surface structure material parameters to take the value range

2 FWD 双参数模型建立

2.1 双参数诺谟图分析

Y. Richard Kim 在分析柔性路面时，利用 BDI 和 F₂来预测土基模量。本文针对半刚性基层沥青路面，经过计算表明，BDI-F₂组成的诺谟图在上层结构模量及厚度不断变化时，仍可以用来表征路基模量，其中 BDI 和 F₂分别定义为

B D I = D_{3} - D_{5}

(4)

F_{2} = \frac{D_{3} - D_{6}}{D_{5}}

(5)

其中:D₃、D₅ 和 D₆ 分别为距离 FWD 荷载中心位置 30、60、90 cm 处的传感器弯沉。

图4（a）为路面结构层厚度保持不变，不断改变面层、基层的模量（不同的数据点）时不同土基模量（不同的图例表示）的双参数图。图4（ b）则为面层、基层模量保持不变，不断改变上部结构层厚度时不同土基模量的双参数图。通过图4中 BDI-F₂ 和土基模量 E_g关系曲线可以看到:即使上层结构的模量和厚度不断变化，相同土基模量构成的 BDI-F₂散点也会在同一曲线上。

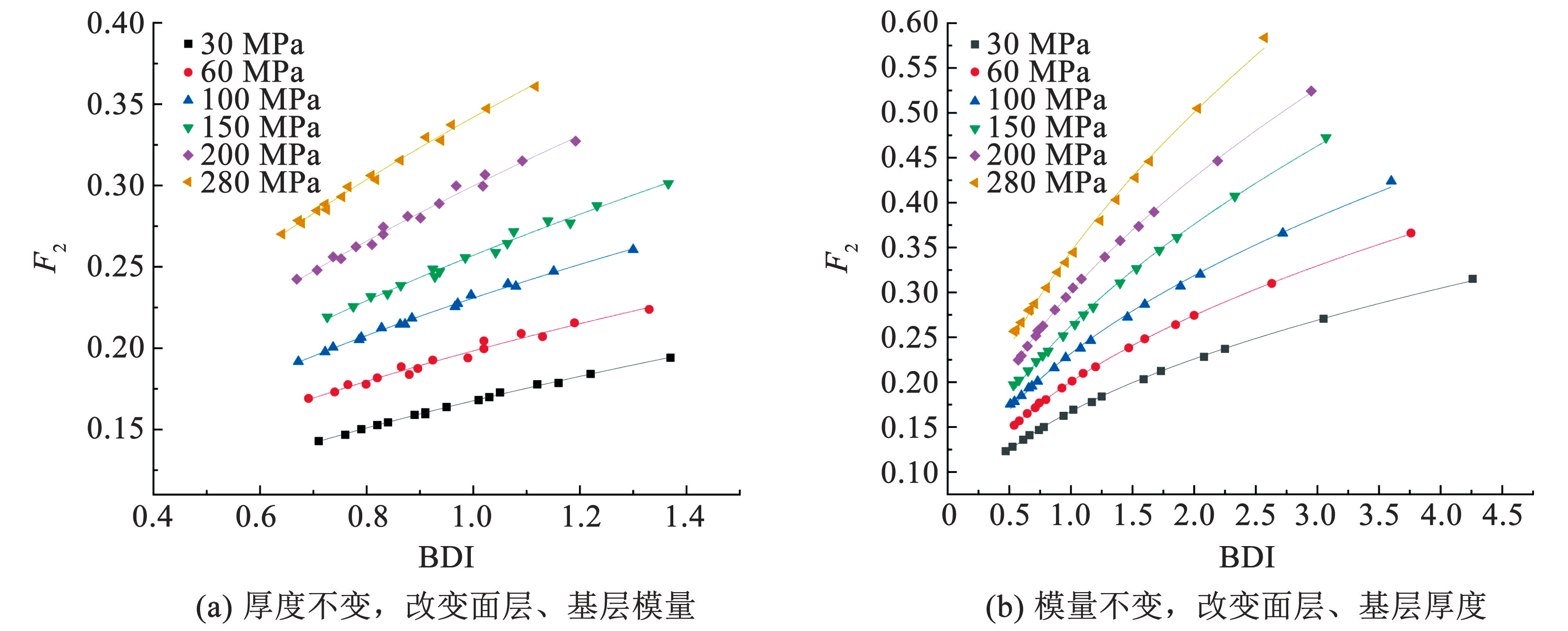
图4BDI-F₂诺谟分布

Fig.4BDI-F₂ Nomogram

图4仅显示了在固定厚度改变模量和固定模量改变厚度两种工况下 BDI、F₂的双参数与路基模量关系曲线，下面进一步拟合获取完整的函数关系式。

为便于应用，将不同土基模量的双参数拟合方程进行归一化处理，转化为如式（6）所示弯沉盆双参数土基模量标准方程:

E = a {B D I}^{b} F_{2}^{c}

(6)

式中:E 为土基模量; BDI、F₂ 为弯沉盆参数; a、b、c 为回归系数，分别取 4 838.347 3、-1.354 和 2.651 8; R² = 0.995 2。

由此可见，应用基于弹性层状体系建立的有限元动力模型，大量工况下的 FWD 弯沉模拟分析结果表明了该双参数路基模量预测模型的有效性，下面将进一步展开实际工程应用分析。

2.2 BDI-F₂双参数的应用

依托江苏省高速公路 A，借助 Dynatest 落锤式弯沉仪进行 FWD 现场检测，将实测并经温度修正后的弯沉盆数据代入双参数方程中，得到由 FWD 双参数公式反算的路基模量。同时，将 FWD 双参数反算得出的路基模量与对应 FWD 测点的路基顶面承载板测试值进行对比，结果如图5所示，其中左边阴影图反映路基反算模量数值大小的分布情况，中间箱线图反映了数据的分散聚集情况，右边正态分位数图反映数据正态分布情况，正态分位数图中的点代表不同点位的数据情况。图5中横坐标0.1、 0.2、0.4、0.6、0.8 和 0.9 代表数据点的位置关系，数据中值位于正中间，即坐标为 0.5，其他数据按间隔依次排列。 ± 0.67 为标准正态分布 0.75 所对应的分位数，通过查正态分布表可得。

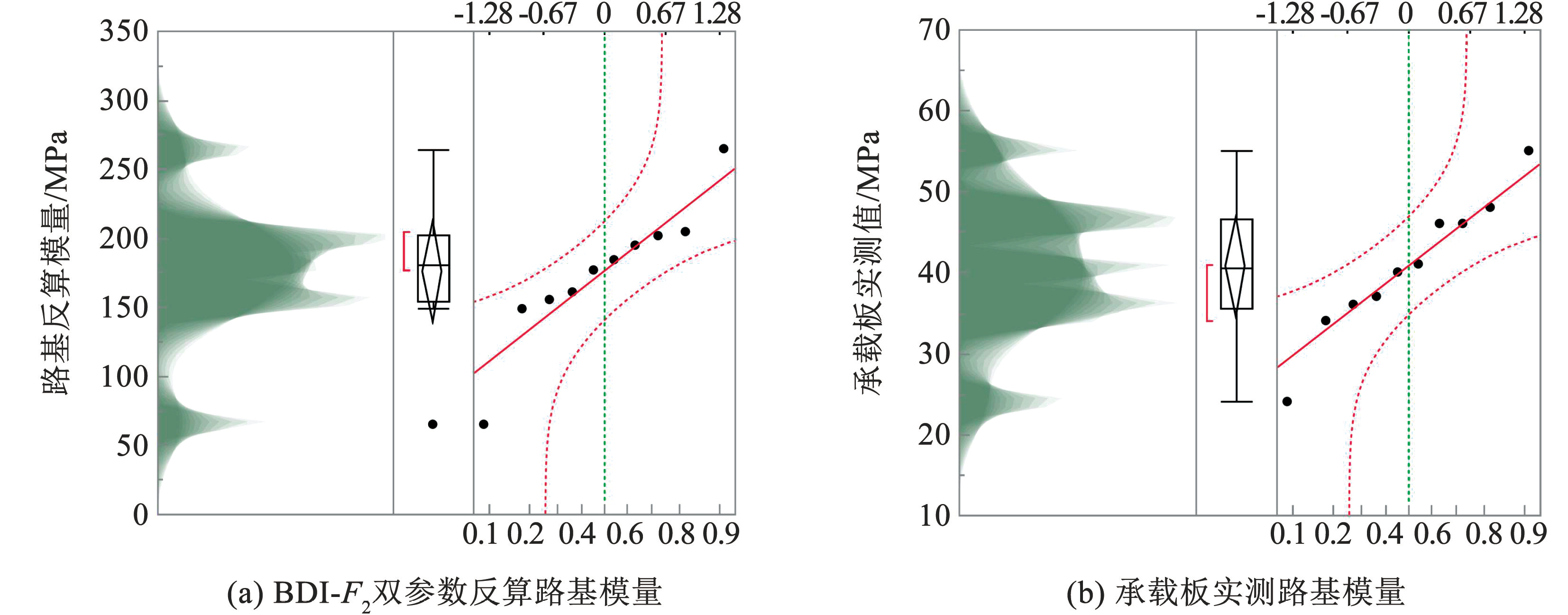
图5BDI-F₂双参数反算模量与承载板实测值对比

Fig.5Comparison of BDI-F₂ two-parameter back-calculated modulus and measured value of load-bearing plate

由图5可知，承载板测量得到的路基静态模量远小于 FWD 双参数反算得到的动态模量。观察阴影图可得两者大体趋势一致，但箱线图差别较大，经过计算得到两者的比值在 0.19~0.37 之间。通过建立两者之间的线性关系，如图6所示，两者具有一定的相关性，但相关性不够高（R² = 0.612 1）。通过分析，产生这一现象的可能原因有以下几点:1）双参数模型源于国外针对柔性路面的分析，其对中国半刚性路面结构实际工作状态的适用性尚待检验; 2）双参数模型仅包含了 3 个点位的弯沉（D₃、D₅和 D₆），虽然在数值模拟时，能很好地区分出路基模量，但是实际道路并非完全均匀，并且由于长期服役内部状态更加复杂，因此难以忽略这些未知因素导致的误差; 3）实际弯沉测量时，难免会有一些人为误差，导致测试结果的偏差。

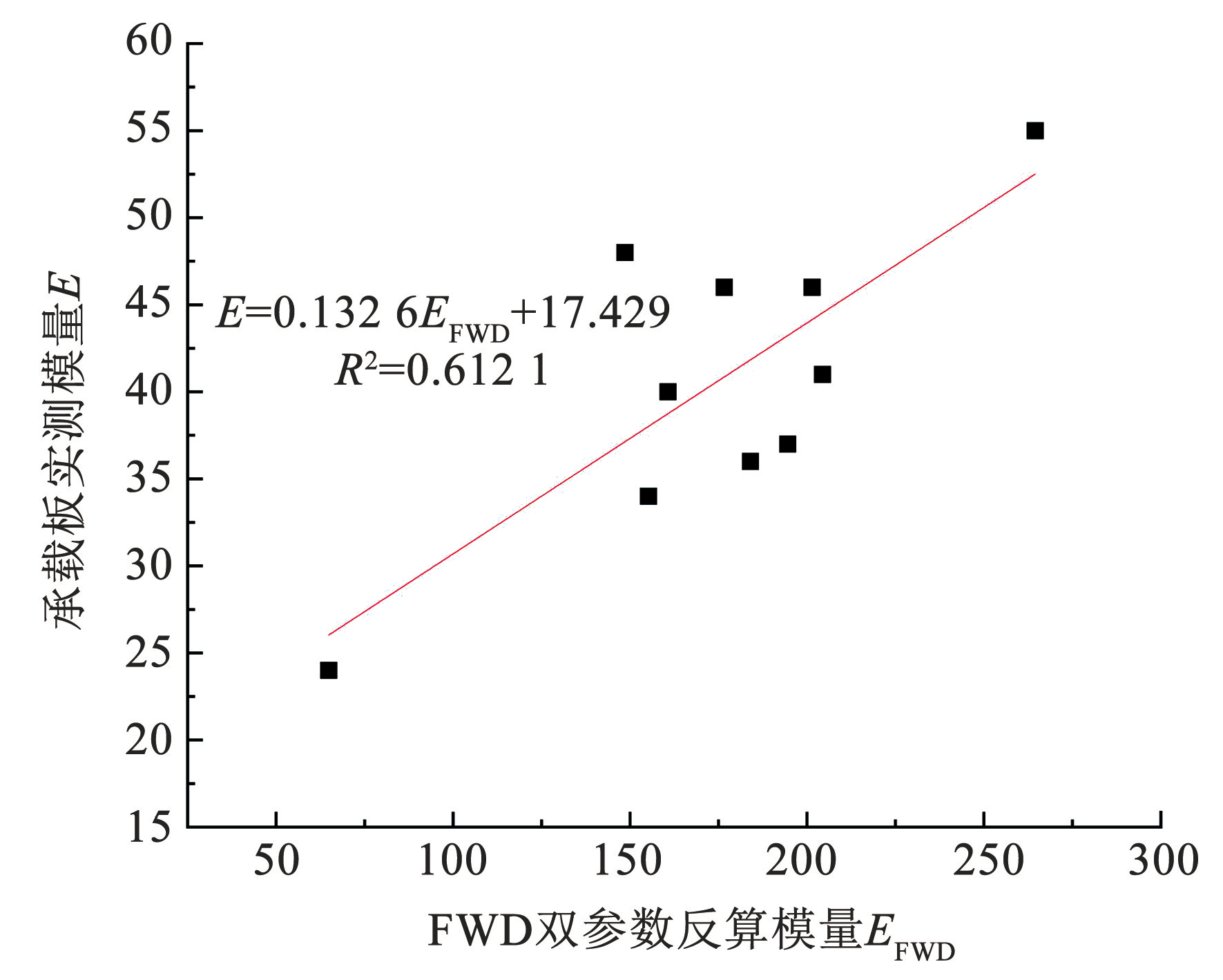
图6FWD 双参数反算模量与承载板实测值关系

Fig.6Relationship between FWD two-parameter back-calculated modulus and measured value of load-bearing plate

通过上述分析可知，BDI-F₂双参数模型在应用时，仅适用于测量精度非常高的工程和数值模拟，在实际工程应用时会存在一些误差，因此需要针对上述问题，对双参数模型进行优化，从而使其能够得到应用，下面就从如何添加能够全面反映半刚性路面结构实际状态的 FWD 弯沉盆参数等方面展开进一步研究。

3 既有 FWD 双参数模型的改进优化

3.1 DBP 指标构建

结合本文研究中使用的 Dynatest 落锤式 9 点弯沉仪布设方案，将 DBP 指标概括为以下 7 类:1）直接弯沉指标 d_i（i = 1~9）; 2）弯沉比指标 DR_i = d_i / d₁（i = 2~9）; 3）弯沉差指标 DD_i = d₁-d_i（i = 2~9）; 4）曲率指标 CI_i = d_i-d_i_{+ 1}（ i = 1~8）; 5）形状指标 F_i =（d_i_-1-d_i_{+ 1}）/ d_i（ i = 2~8）; 6）斜率指标 S_i =（d_i-d_i_{+ 2}）/（ r_i_{+ 2}-r_i）（ i = 1~7）; 7）面积类指标 AREA =（5d₁-2d₃-2d₅-d₆）/ 2。

将上述有限元模拟获取的计算结果，通过回归分析可得到路基模量与不同 DBP 指标的相关性。按照相关性系数由大到小排列为直接弯沉指标 d₉（R² = 0.981）、曲率指标 CI₈（R² = 0.941）、斜率指标 S₇（R² = 0.908）、形状指标 F₈（R² = 0.885）、弯沉比指标 DR₉（ R² = 0.879）、面积指标 AREA（ R² = 0.821）、弯沉差指标 DD₉（R² = 0.352）。

3.2 BDI-F₂-d₉三参数模型建立

以 BDI-F₂双参数模型为基础，同时以上述 DBP 指标的相关性为依据，分别取相关性大于 0.9 的参数 d₉（ R² = 0.981）、C_I8（ R² = 0.941）和 S₇（ R² = 0.908），通过逐步回归分析，依次增加相关参数，从而调用更多弯沉点的信息，实现对双参数模型的优化。

按照上述方法首先加入与路基模量相关性最高的直接弯沉指标 d₉，构造 BDI-F₂-d₉三参数模型，模型方程为

E = a {B D I}^{b} F_{2}^{c} d_{9}^{d}

(7)

根据上述模型方程可知，该模型具有 3 个自变量，一个因变量，通过编写 python 脚本，利用编程实现对上述模型的回归。通过回归得到系数 a = 2 365.592 5、b =-0.170 6、c =0.811 0、d =-1.225 1，R² = 0.988 5。利用优化后的 BDI-F₂-d₉模型对实测弯沉数据进行反算，结果如图7所示。

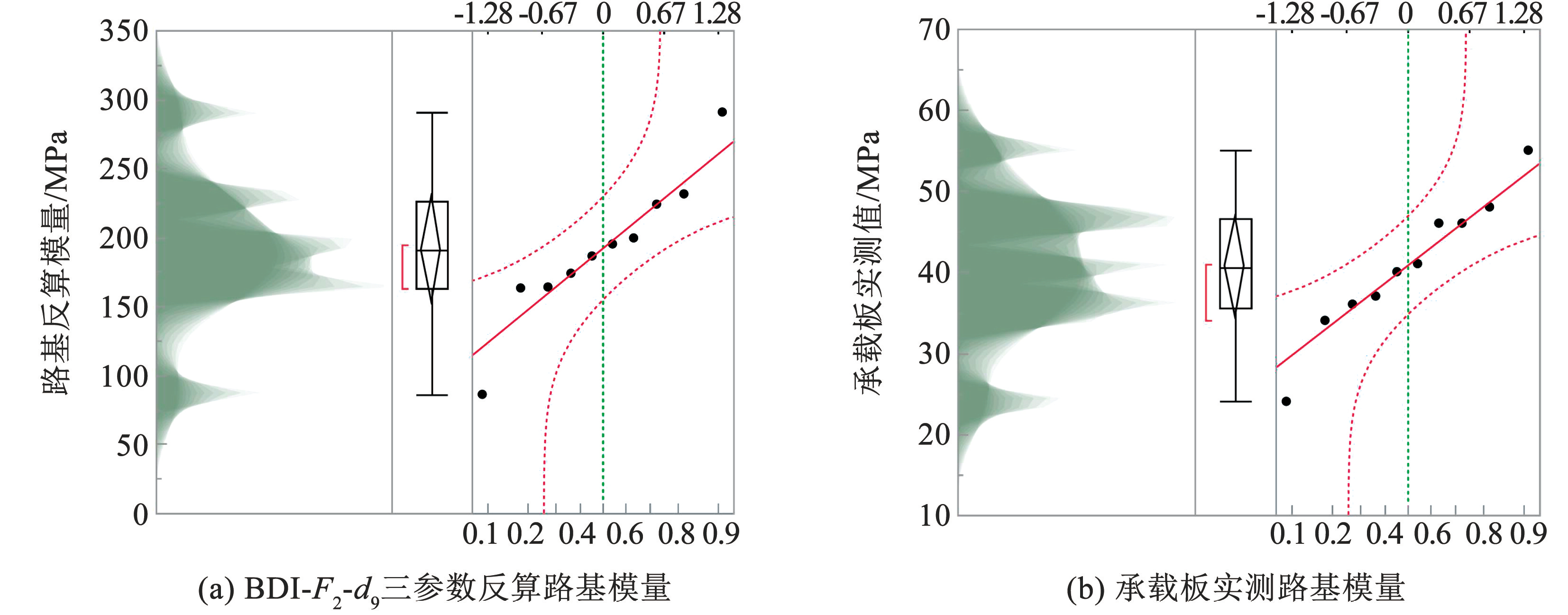
图7BDI-F₂-d₉三参数反算模量与承载板实测值对比

Fig.7Comparison of BDI-F₂-d₉ three-parameter back-calculated modulus and measured value of load-bearing plate

通过对比图7（a）和图7（b）可知，利用 BDI-F₂-d₉三参数模型反算得到的路基模量与承载板实测值之间阴影分布大体一致，箱线分布也趋同，反算效果更好。建立两者之间的线性关系，如图8所示，相关性大幅提高，达到了 R² = 0.910 6。两者之间的比值位于 0.19~0.28 之间，这一结果与文献^[19] 的基于现场实测数据的研究成果一致，且离散性相比双参数模型有显著降低，稳定性大幅提高。

图8FWD 三参数反算模量与承载板实测值关系

Fig.8Relationship between FWD three-parameter back-calculated modulus and measured value of load-bearing plate

在 BDI-F₂-d₉三参数模型的基础上，再分别加入参数 CI₈和 S₇。由于此前的 BDI-F₂-d₉三参数模型相关性已较高，新参数的加入对该模型的相关性提升有限，如图9所示，且随着参数的加入该模型的复杂度以及计算量会大幅提升，因此综合考虑选择 BDI-F₂-d₉作为最终的优化模型参数。

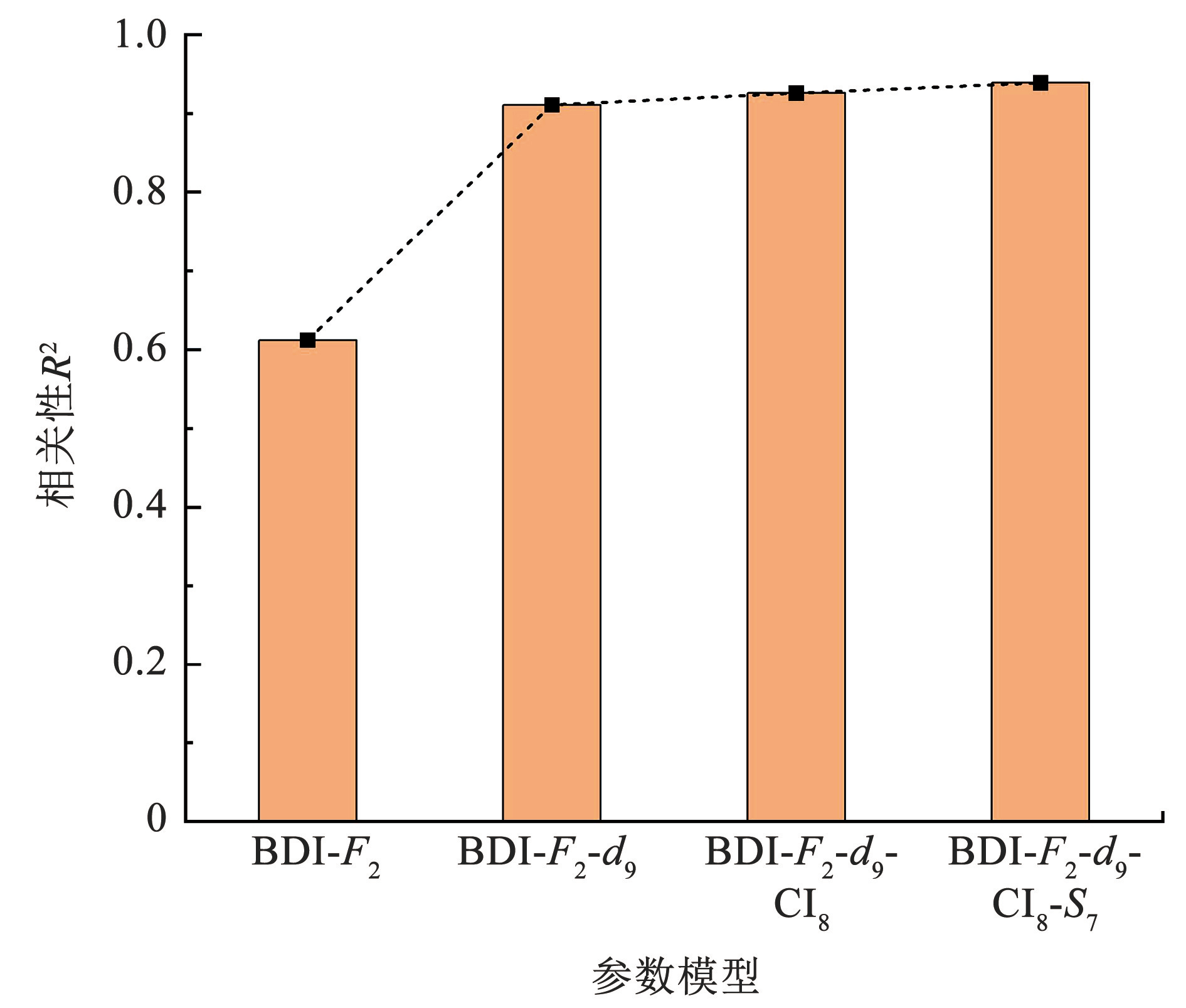
图9逐步优化过程中各模型的相关性

Fig.9Correlation of the models in the stepwise optimization process

4 基于 RIOHTrack 环道的多层路面模量反算方法验证

基于 FWD 三参数的路基模量预测模型的应用之一就是利用现场 FWD 检测数据确定路面各层的弹性模量，具体方法:首先，基于既有公路表面的 FWD 测试数据，采用上述预测模型计算路基模量，然后建立与该路段相应的路面结构有限元动力模型，并将由预测模型获得的路基模量作为输入参数，在此基础上变化路面各层的模量的取值，以实测 FWD 弯沉数据为基准，搜索使动力模拟计算弯沉值与实测值相差最小的那组路面模量组合（包括面层、基层，路基为上述预测模型推算值），即为多层路面模量反算值。下面结合工程示例，阐明基于 FWD 三参数模型的多层路面模量反算方法的主要步骤，本研究的基础数据来源于北京大杜社公路材料腐蚀与工程安全国家野外科学观测研究站^[20]。

4.1 环道路面材料

限于篇幅，本节选取了 RIOHTrack 环道具有代表性的 4 种典型路面结构 STR2（强基薄面型路面结构）、STR4（复合式路面结构）、STR7（常用半刚性基层结构）和 STR17（厚沥青混凝土路面结构）进行验证，4 种路面结构示意如图10所示。本文所用数据为 2016 年环道实测数据，此时环道刚竣工使用，层间接触状态良好。图中 AC 代表沥青混合料; LCC 代表贫混凝土; CBG 代表水泥稳定级配碎石; CS 代表水泥稳定土。

图104 种路面结构示意

Fig.10Schematic diagram of the four pavement structures

4.2 基于 FWD 三参数模型的多层路面模量反算方法验证

4.2.1 实测弯沉的温度修正

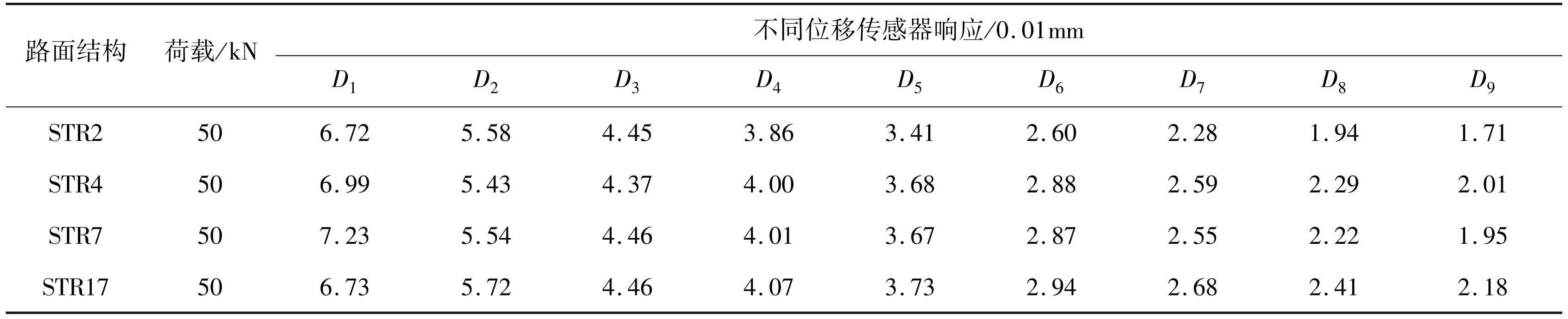
本节借助文献^[21-22] 在弯沉温度修正的相关成果对 STR2、STR4、STR7 和 STR17 在 2016 年进行实测的弯沉数值进行温度修正，消除温度带来的反算误差，修正后 4 种路面结构的路表弯沉见表3。

表34 种典型路面结构温度修正后路表弯沉

Tab.3 Four typical pavement structure temperature-corrected road surface bending settlement

4.2.2 路基模量非线性分析及逐层反算结果

RIOHTrack 环道在铺筑过程中，对每一层顶部都进行了 FWD 测试，本节基于这些测试数据对 4 种不同路面结构进行逐层模量反算。由于土基等粒料类材料并不是线弹性材料，其在车辆荷载作用下会表现出较强的应力依赖性^[23]。在逐层反算过程中，荷载位置的不断变化将导致土基受到的应力也在不断变化，体现在模量上就是路基模量也会不断变化。经过研究发现，路基土等粒料材料的模量会随着所受应力的减小而逐渐增大。正是由于路基的这种非线性特性，在进行路基模量反算的过程中，无法把路基看作单独的个体去根据路基顶面弯沉进行反算，而应该把路基看作路面结构的一部分，充分考虑非线性对路基模量的影响。

本节利用第 3 节提出的基于 FWD 三参数模型的路基模量反算方法，根据面层弯沉指标对路基模量进行反算。为检验反算精度，在保证路基模量不变的情况下，根据底基层、基层和面层弯沉盆，利用有限元软件分别反算各层模量，最后将反算模量得到的理论弯沉盆与实际弯沉盆进行匹配，从而验证本文得到的路基模量反算方法的有效性。经计算，4 种不同路面结构的反算结果见表4，验证弯沉盆如图11所示。该方法不仅充分考虑了路基材料的非线性特性，还充分利用了底基层、基层以及面层实测弯沉盆数据，避免单一弯沉盆误差带来的反算精度影响。根据图11结果可知，利用本章所构建的 FWD 三参数模型来进行路基模量反算，并以此逐层反算出的路面各结构层模量所得理论弯沉与实测弯沉吻合结果较好，其中仅有距离落锤正下方 30 cm 处的第 2 个弯沉点位误差较大，这是由于该点为 “惰性弯沉点” ^[24]所导致。

表44 种路面结构各层位反算结果

Tab.4 Back-calculation results for each layer of the four pavement structures

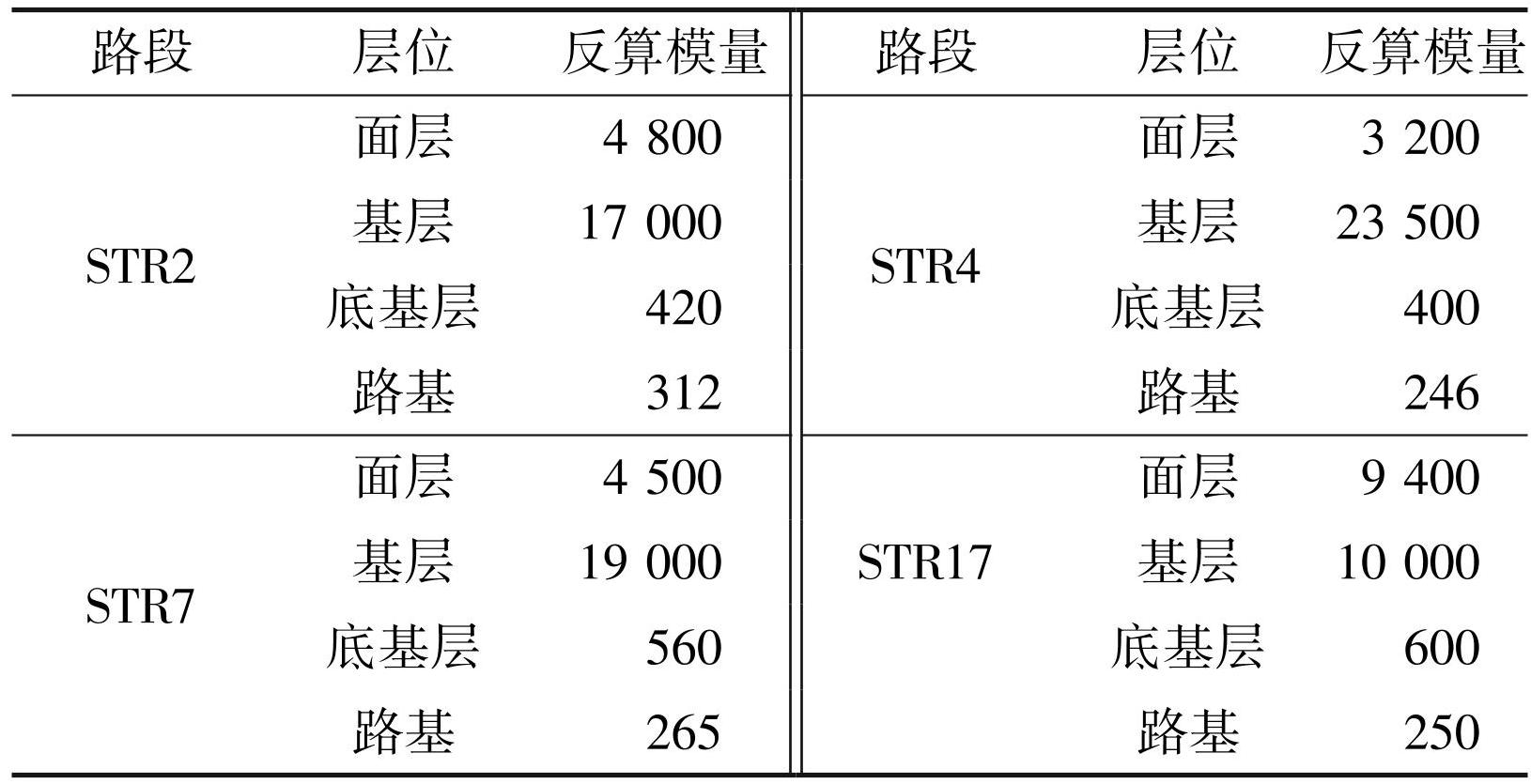
以 STR7 为例，根据分析对比其2016 年、2017 年和 2018 年 3 a 的弯沉盆变化趋势可知，在 2016 年刚施工完成后所测的弯沉盆中，前三点的弯沉变化更趋于线性变化。但随着时间的延长，第 1 点和第 3 点均出现逐渐变大的趋势，而第 2 点作为惰性弯沉点则变化很小，由此前 3 点的弯沉变化趋势逐渐呈现出指数型变化，即斜率绝对值由大逐渐减小，如图12所示，这与本文所得到的理论弯沉盆前三点的变化趋势相同，因此可以说明本文反算结果的有效性与准确性。

图114 种路面结构反算结果验证

Fig.11Verification of back-calculation results for four pavement structures

图12惰性弯沉点示意

Fig.12Schematic diagram of inert bending and sinking point

5 结论

本文建立了路面弹性层状体系有限元动力模型，提出准确性更高、适用于中国半刚性路面的基于弯沉盆三参数的路基模量预测模型。在此基础上形成多层路面模量反算新方法，并通过对比 RIOHTrack 环道实测弯沉值，验证了该方法的有效性和准确性。具体结论如下:

1）FWD 弯沉盆双参数模型只需计算 BDI 和 F₂ 两个参数，便可以唯一确定土基模量，但该模型源于国外针对柔性路面的研究，采用中国半刚性路面实测数据预测时精度显著降低，需要改进和优化。

2）不同弯沉盆参数指标与路基模量相关系数由大到小排序为直接弯沉指标 d₉、曲率指标 CI₈、斜率指标 S₇、形状指标 F₈、弯沉比指标 DR₉、面积指标 AREA、弯沉差指标 DD₉。

3）FWD 三参数模型路基模量预测值与承载板实测值之间线性关系良好（R² = 0.910 6），且两者比值介于 0.19~0.28 之间，与文献实测结果吻合，较之双参数模型更准确。

4）作为多层路面模量反算的输入参数，该路基模量推算值更为准确，加之动力有限元模型能够准确地模拟 FWD 测试动态过程，从而大幅提高了路面各层模量的反算精度。该方法为客观评价既有路基的承载能力状况、准确反算半刚性路面面层模量提供了依据。

图1典型 FWD 荷载曲线

Fig.1Typical FWD load curve

下载: 全尺寸图片

图2无限单元边界设置

Fig.2Infinite cell boundary setting

下载: 全尺寸图片

图3模型校验示意

Fig.3Schematic diagram of model calibration

下载: 全尺寸图片

图4BDI-F₂诺谟分布

Fig.4BDI-F₂ Nomogram

下载: 全尺寸图片

图5BDI-F₂双参数反算模量与承载板实测值对比

Fig.5Comparison of BDI-F₂ two-parameter back-calculated modulus and measured value of load-bearing plate

下载: 全尺寸图片

图6FWD 双参数反算模量与承载板实测值关系

Fig.6Relationship between FWD two-parameter back-calculated modulus and measured value of load-bearing plate

下载: 全尺寸图片

图7BDI-F₂-d₉三参数反算模量与承载板实测值对比

Fig.7Comparison of BDI-F₂-d₉ three-parameter back-calculated modulus and measured value of load-bearing plate

下载: 全尺寸图片

图8FWD 三参数反算模量与承载板实测值关系

Fig.8Relationship between FWD three-parameter back-calculated modulus and measured value of load-bearing plate

下载: 全尺寸图片

图9逐步优化过程中各模型的相关性

Fig.9Correlation of the models in the stepwise optimization process

下载: 全尺寸图片

图104 种路面结构示意

Fig.10Schematic diagram of the four pavement structures

下载: 全尺寸图片

图114 种路面结构反算结果验证

Fig.11Verification of back-calculation results for four pavement structures

下载: 全尺寸图片

图12惰性弯沉点示意

Fig.12Schematic diagram of inert bending and sinking point

下载: 全尺寸图片

表1传感器布设位置方案

下载: 全尺寸图片

表2路面结构材料参数取值范围

下载: 全尺寸图片

表34 种典型路面结构温度修正后路表弯沉

下载: 全尺寸图片

表44 种路面结构各层位反算结果

下载: 全尺寸图片

图1典型 FWD 荷载曲线

Fig.1Typical FWD load curve

图2无限单元边界设置

Fig.2Infinite cell boundary setting

图3模型校验示意

Fig.3Schematic diagram of model calibration

图4BDI-F₂诺谟分布

Fig.4BDI-F₂ Nomogram

图5BDI-F₂双参数反算模量与承载板实测值对比

Fig.5Comparison of BDI-F₂ two-parameter back-calculated modulus and measured value of load-bearing plate

图6FWD 双参数反算模量与承载板实测值关系

Fig.6Relationship between FWD two-parameter back-calculated modulus and measured value of load-bearing plate

图7BDI-F₂-d₉三参数反算模量与承载板实测值对比

Fig.7Comparison of BDI-F₂-d₉ three-parameter back-calculated modulus and measured value of load-bearing plate

图8FWD 三参数反算模量与承载板实测值关系

Fig.8Relationship between FWD three-parameter back-calculated modulus and measured value of load-bearing plate

图9逐步优化过程中各模型的相关性

Fig.9Correlation of the models in the stepwise optimization process

图104 种路面结构示意

Fig.10Schematic diagram of the four pavement structures

图114 种路面结构反算结果验证

Fig.11Verification of back-calculation results for four pavement structures

图12惰性弯沉点示意

Fig.12Schematic diagram of inert bending and sinking point

表1传感器布设位置方案

表2路面结构材料参数取值范围

表34 种典型路面结构温度修正后路表弯沉

表44 种路面结构各层位反算结果

图1典型 FWD 荷载曲线

Fig.1Typical FWD load curve

图2无限单元边界设置

Fig.2Infinite cell boundary setting

图3模型校验示意

Fig.3Schematic diagram of model calibration

图4BDI-F₂诺谟分布

Fig.4BDI-F₂ Nomogram

图5BDI-F₂双参数反算模量与承载板实测值对比

Fig.5Comparison of BDI-F₂ two-parameter back-calculated modulus and measured value of load-bearing plate

图6FWD 双参数反算模量与承载板实测值关系

Fig.6Relationship between FWD two-parameter back-calculated modulus and measured value of load-bearing plate

图7BDI-F₂-d₉三参数反算模量与承载板实测值对比

Fig.7Comparison of BDI-F₂-d₉ three-parameter back-calculated modulus and measured value of load-bearing plate

图8FWD 三参数反算模量与承载板实测值关系

Fig.8Relationship between FWD three-parameter back-calculated modulus and measured value of load-bearing plate

图9逐步优化过程中各模型的相关性

Fig.9Correlation of the models in the stepwise optimization process

图104 种路面结构示意

Fig.10Schematic diagram of the four pavement structures

图114 种路面结构反算结果验证

Fig.11Verification of back-calculation results for four pavement structures

图12惰性弯沉点示意

Fig.12Schematic diagram of inert bending and sinking point

表1传感器布设位置方案

表2路面结构材料参数取值范围

表34 种典型路面结构温度修正后路表弯沉

表44 种路面结构各层位反算结果

SYED M, GUHARAY A, GOEL D. Strength characterisation of fiber reinforced expansive subgrade soil stabilized with alkali activated binder[J]. Road Materials and Pavement Design,2022,23(5):1037

周纯秀, 崔洪海, 张中丽, 等. 改良碳酸盐渍土路基填料的力学性质[J]. 哈尔滨工业大学学报,2022,54(9):93. ZHOU Chunxiu, CUI Honghai, ZHANG Zhongli,et al. Mechanical properties of improved carbonate soil roadbed filler[J]. Journal of Harbin Institute of Technology,2022,54(9):93

李鹏. 道路工程弯沉检测技术研究进展[J]. 市政技术,2022,40(9):210. LI Peng. Research on deflection detection technology of road engineering[J]. Journal of Municipal Technology,2022,40(9):210

张锋, 臧宏阳, 冯德成, 等. 模量不均匀路基上的沥青路面动力响应研究[J]. 土木工程学报,2018,51(3):115. ZHANG Feng, ZANG Hongyang, FENG Decheng,et al. Moving truck-induced dynamic response of asphalt pavement supported by subgrade with non-uniform modulus[J]. China Civil Engineering Journal,2018,51(3):115

ASMAH H, NUR I M, HALIL C,et al. Comparative study on using static and dynamic finite element models to develop FWD measurement on flexible pavement structures[J]. Construction and Building Materials,2018,176(10):583

王中将. 基于BISAR的半刚性基层沥青路面结构设计研究[J]. 市政技术,2021,39(3):34. WANG Zhongjiang. Research on structural design of asphalt pavement with semi-rigid based on BISAR[J]. Journal of Municipal Technology,2021,39(3):34

邱欣, 杨青, 游庆龙. 基于FWD动态弯沉盆参数的沥青路面模量反演分析[J]. 长安大学学报(自然科学版),2013,33(6):42. QIU Xin, YANG Qing, YOU Qinglong. Back analysis on modulus of asphalt pavements based on FWD dynamic deflection basin parameters[J]. Journal of Chang′ an University(Natural Science Edition),2013,33(6):42

HAKIM B A, CHEUNG L W, ARMITAGE R J. Use of FWD data for prediction of bonding between pavement layers[J]. International Journal of Pavement Engineering,1999,1(1):49

STEFAN A R, METCALF J B. The errors in pavement layer moduli backcalculation due to improper modeling of layer interface condition[J]. Journal of the Transportation Research Board,2003,1639(2):36

SUNNY D G, VINOD K A, RAKESH K. Comparative studies of lightweight deflectometer and Benkelman beam deflectometer in low volume roads[J]. Journal of Traffic and Transportation Engineering(English Edition),2016,3(5):438

曹志坡, 梁乃兴, 曹源文. 路面结构综合模量连续检测方法[J]. 哈尔滨工业大学学报,2020,52(3):90. CAO Zhipo, LIANG Naixing, CAO Yuanwen. Method for continuously testing pavement structural composite modulus[J]. Journal of Harbin Institute of Technology,2020,52(3):90

KIM Y R, LEE Y C, RANJITHAN S R. Flexible pavement condition evaluation using deflection basin parameters and dynamic finite element analysis implemented by artificial neural networks[J]. Symposium on Nondestructive Testing of Pavements and Backcalculation of Moduli,2000,3(10):514

LEE Y C, KIM Y, RANJITHAN S. Dynamic analysis-based approach to determine flexible pavement layer moduli using deflection basin parameters[J]. Transportation Research Record Journal of the Transportation Research Board,1998,1639(4):36

丰晓, 唐伯明, 李锦华. FWD 应用于沥青路面结构承载能力的非破损评价[J]. 同济大学学报(自然科学版),1996,24(5):520. FENG Xiao, TANG Boming, LI Jinhua. FWD applied to non-breakage evaluation of structural load carrying capacity of asphalt pavement[J]. Journal of Tongji University(Natural Science),1996,24(5):520

谢辉, 郭忠印, 丛林. 基于人工神经网络的沥青路面模量评估[J]. 同济大学学报(自然科学版),2007,35(8):1044. XIE Hui, GUO Zhongyin, CONG Lin. Artificial neural networkbased evaluation of layer modulusof asphalt pavement[J]. Journal of Tongji University(Natural Science),2007,35(8):1044

罗启添, 邱欣, 杨青. 基于FWD路表动态弯沉盆参数的路基模量评价研究[J]. 公路工程,2011,36(2):4. LUO Qitian, QIU Xin, YANG Qing. Evaluation study on subgrade modulus based on FWD dynamic deflection basin parameters[J]. Highway Engineering,2011,36(2):4

孙应钦. 基于动态弯沉反演的既有高速公路路面结构性能评价研究[D]. 南京: 东南大学,2021. SUN Yingqin. Research on structural performance evaluation of existing highway pavement based on dynamic bending and settlement inversion[D]. Nanjing: Southeastern University,2021

查旭东. 基于同伦方法的路面模量反算的研究[D]. 西安: 长安大学,2001.ZHA Xudong. Study on the back-calculation of pavement modulus based on the Tonglen method[D]. Xi′an: Chang′an University,2001

邱欣. 基于FWD的半刚性基层沥青路面模量参数反演及校正方法研究[D]. 上海: 同济大学,2009. QIU Xin. Research on inversion and correction method of modulus parameters of semi-rigid base asphalt pavement based on FWD[D]. Shanghai: Tongji University,2009

WANG Xudong, ZHOU Guangli, LIU Haiyan,et al. Key points of RIOHTRACK testing road design and construction[J]. Journal of Highway and Transportation Research and Development(English Edition),2020,14(4):1

宋小金, 樊亮. 基于FWD的沥青路面动态弯沉温度修正系数[J]. 土木工程学报,2018,51(3):123. SONG Xiaojin, FAN Liang. Temperature correction coefficient for dynamic deflection of asphalt pavement based on FWD[J]. China Civil Engineering Journal,2018,51(3):123

宋小金, 曾梦澜, 王林. 沥青路面动态弯沉值的温度修正方法研究[J]. 公路交通科技,2016,33(1):22. SONG Xiaojin, ZENG Menglan, WANG Lin. A method of temperature correction for asphalt pavement dynamic deflection[J]. Journal of Highway and Transportation Research and Development,2016,33(1):22

王旭东, 周兴业. 基于材料非线性的沥青路面结构当量力学分析方法[J]. 中国公路学报,2019,32(8):25. WANG Xudong, ZHOU Xingye. Equivalent mechanical method for asphalt pavement structure based on material nonlinearity[J]. China Journal of Highway and Transport,2019,32(8):25

朱洁, 孙立军. 沥青路面三层结构模量反演最佳反演点的确定[J]. 同济大学学报(自然科学版),2017,45(2):203. ZHU Jie, SUN Lijun. Determination of optimal backcalculation point for three layer structure modulus backcalculation of asphalt pavement[J]. Journal of Tongji University(Natural Science),2017,45(2):203

1 路面结构动力有限元分析模型

2 FWD 双参数模型建立

3 既有 FWD 双参数模型的改进优化

4 基于 RIOHTrack 环道的多层路面模量反算方法验证

5 结论

友情链接LINKS