摘要
大悬臂预应力混凝土盖梁(以下简称大悬臂 PC 盖梁)通常会在悬臂根部设置折线段来保证结构的受力性能,但尚未有合理的折线段尺寸设计依据。为此,通过将附加折线段等效为弧线段,提出了折线段大悬臂 PC 盖梁的剪应力计算理论;针对大悬臂 PC 盖梁的折线段尺寸设计问题进行了 1∶ 4 的缩尺模型试验,分析了折线段对悬臂根部剪应力分布及受力性能的影响;并根据结构弯剪受力强度要求,给出了不同盖梁悬臂长度、受压边倾角及预应力水平等设计参数下的最小折线段长度比计算公式。结果表明:所提出的折线段变截面梁剪应力计算理论能较好地反映折线段设置对剪应力纵向分布带来的影响,顶缘最不利受力位置由悬臂根部转变为变受压边倾角处,随着折线段长度比的增加,盖梁顶底缘应力峰值均有所降低,需要通过控制折线段尺寸来保证结构受压边底缘的强度要求。所给出的最小折线段长度比计算公式对不同设计参数的大悬臂 PC 盖梁均能保证其有效精度,具有一定的实用性。
Abstract
Large cantilever prestressed concrete bent caps (hereinafter referred to large cantilever PC bent caps) typically incorporate corbels at the root of the cantilever to ensure the mechanical behavior. However, there is currently a lack of a rational framework for determining the appropriate size of these corbels. In this paper, the shear stress calculation theory of large cantilever PC bent caps with corbels is proposed by equating the corbels to arc segments; a 1∶ 4 scaled model experiment is carried out to analyze the influence of corbels on the shear stress distribution and stress performance of the cantilever root; The formula for calculating the minimum corbel length ratio under different design parameters of compression edge inclination, cantilever lengths and prestressing level is given according to the bending and shear strength requirements. The findings indicate that the shear stress calculation theory proposed in this study for variable cross-section beams with corbels provides a more accurate representation of the impact of corbels on the longitudinal distribution of shear stress. Additionally, the most critical location for shear stress has shifted from the cantilever root to the changing position of bottom inclination. Furthermore, as the corbel length ratio increases, the stress peaks at the upper and bottom edges of the beams decrease. Therefore, it is essential to control the size of the corbel to ensure the strength of the compression edges. The formula for the minimum corbel length ratio, as presented in this paper, ensures its effective accuracy when applied to large cantilever PC bent caps with varying parameters. This formula demonstrates practicality in construction applications.
随着车流量的日益增大,城市桥梁需要保证足够行车道宽度的同时最大限度地减小对桥下道路通行的影响,大悬臂 PC 混凝土盖梁比较完美地解决了这一问题,但其结构自重及上部荷载会在悬臂根部产生较大的负弯矩[1-3],影响结构的承载效率。不同于大跨连续刚构桥,大悬臂 PC 盖梁通常由于截面尺寸限制无法布置足够的预应力来抵消上部荷载在悬臂根部产生的不利影响[4-5],因此会在设计时考虑在根部区域设置折线段保证结构的受力性能,诸如中山西环高速公路大悬臂盖梁、成都二环路大悬臂盖梁以及京雄高速花瓶式桥墩盖梁等都设置了相应的折线段构造。
目前国内外针对变截面梁附加剪应力提出了较多的计算理论及简化方法,但对于带有附加折线段的变截面悬臂梁剪应力分布规律研究较少,也缺少折线段设置的相关理论基础与设计准则。关于变截面梁剪应力,文献[6-7]推导出任意变截面梁剪应力计算的一般公式,证明了变截面梁的弯矩及轴力会引起附加剪应力; 文献[8]通过大比例变截面模型梁静力加载试验验证了传统剪应力公式对变截面梁不再适用,弯矩、轴力的方向对腹板上的剪力可能造成不利影响; 文献[9-11]发现变截面梁由弯矩产生的附加剪应力是自平衡的,由弯矩产生的附加剪应力大小与弯矩大小和截面高度变化率有关; 文献[12]提出了变截面梁受非均匀弯曲时的剪应力计算理论及分布规律; 文献[13]将弯矩与轴力引起的附加剪应力积分成为相应的合力,引入剪应力分项系数来研究各内力引起的剪应力的贡献,简化了剪应力的计算方法。上述这些研究成果大多假设悬臂梁梁底的高度变化率保持不变,而折线段的设置改变了大悬臂盖梁悬臂根部区域的应力分布规律,同时根部的弯剪双向受力状态使得折线段带来的剪应力变化不能被忽视,国内外学者也普遍认为大跨变截面梁的结构剪应力分布规律对分析结构的屈曲变形及挠度控制有着十分重要的力学意义[14-19],这也说明了盖梁悬臂根部的受力性能与折线段长度的设置密切相关; 目前关于内衬混凝土对箱梁剪切及扭转性能的研究较多[20],但对于折线段长度取值的研究较少,一般在进行折线段设计时通常在拟定好盖梁各部分尺寸的基础上假定折线段尺寸并进行受力性能验算直至满足设计要求,通过试算方法确定折线段的尺寸,并未有相关的折线段设计依据,但不当的折线段尺寸设计会导致截面高度增加,在减小了桥下净空的同时影响结构外观,甚至不得不增加桥面标高,例如狮子洋通道工程的桥墩大悬臂长度已达 19.5 m,悬臂根部截面高度高达 5.8 m; 没有合理的折线段尺寸设计依据给折线段大悬臂变截面 PC 盖梁的应用与推广带来了诸多困难。
为了给出合理的折线段尺寸设计依据,明确折线段设计准则,有必要对带有附加折线段的大悬臂变截面 PC 盖梁开展试验研究以及受力分析,探究折线段对于盖梁悬臂根部应力分布规律及受力性能的影响,基于悬臂根部受力性能与折线段尺寸的对应关系,确定不同盖梁参数条件下能够保证大悬臂盖梁结构强度要求的合理折线段尺寸,在此基础上给出折线段尺寸的设计依据。
1 变截面梁折线段长度比设置理论
大悬臂盖梁根部底缘为结构压应力最大的位置,不同于等截面梁,轴力与弯矩引起的附加剪应力使得变截面梁悬臂根部横截面上的最大剪应力出现在中性轴以下区域或梁底缘处,这导致悬臂根部底缘处的第一主应力由剪应力控制,折线段的设置会使得悬臂根部的剪应力纵向分布产生改变,若折线段尺寸设置不当,则会使得悬臂根部底缘的结构受力存在风险。为了明确折线段的尺寸设置依据,必须先明确折线段变截面梁的剪应力分布规律,对设有折线段的变截面悬臂梁剪应力计算理论进行推导。
1.1 折线段变截面梁剪应力计算方法
如图1所示的折线段变截面梁,一般悬臂段梁底倾角为 β,折线段梁底倾角为 α,将横截面上描述应力计算点竖向位置 y 的坐标原点取在悬臂根部顶缘处,取折线段变截面梁的微段 dx,微段两端截面重心连线的水平倾角为 γ,则作用在微段两端的内力平衡可以表达为
(1)
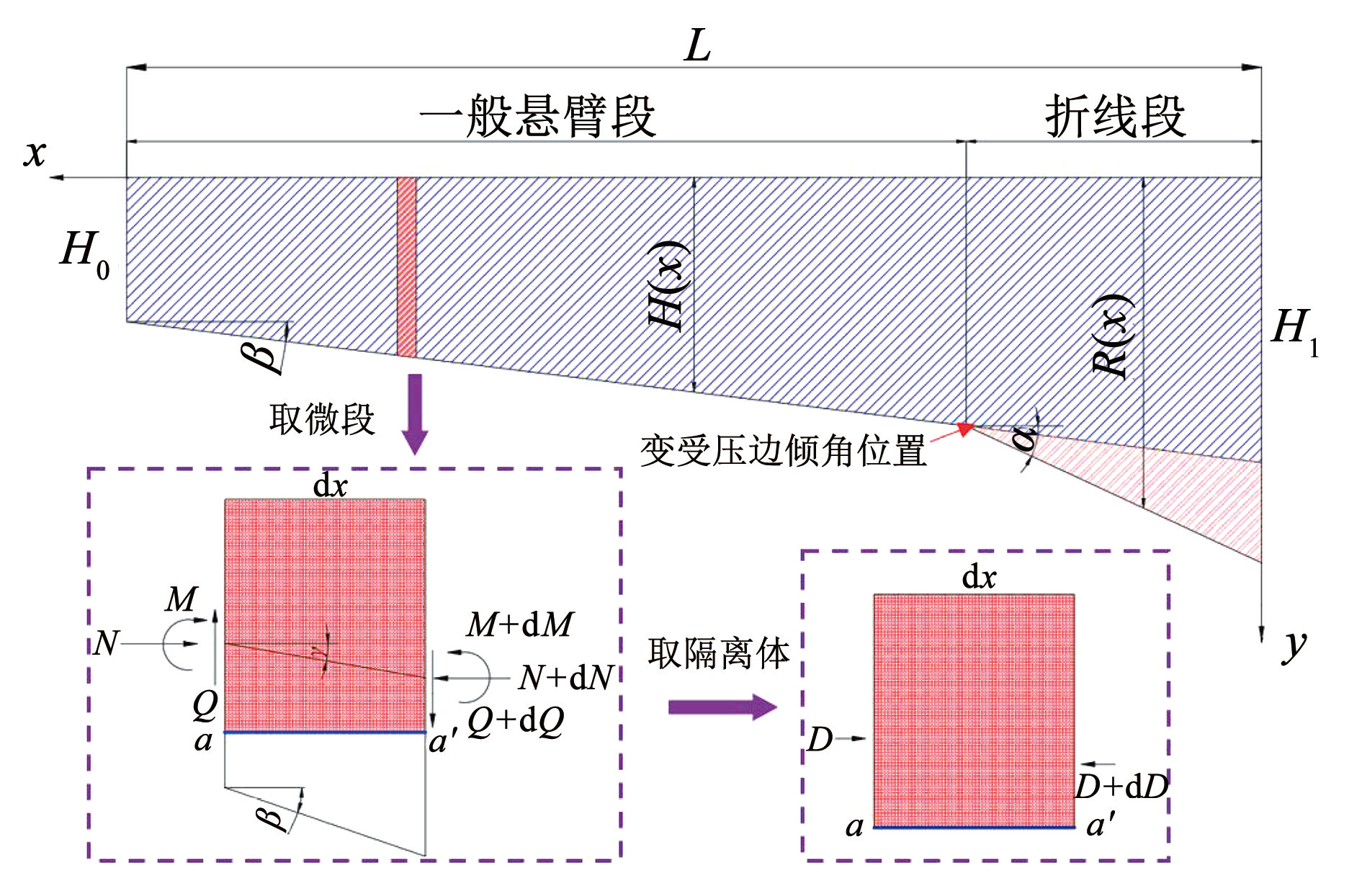
图1折线段大悬臂盖梁微段受力简图
Fig.1Sketch of the forces in the micro-section of a large cantilevered bent cap with a corbel
所取微段横截面上距梁顶为 y 的纵向纤维的正应力为
(2)
式中:A、I 分别为横截面面积及其重心轴的惯性矩,yc为横截面重心至梁顶距离。
为了计算横截面上任意点处 ξ 的剪应力 τ,在微段上截出水平截面 aa′以上部分为分离体,横截面高度的变化使分离体两端所受压力作用点位置不同,由水平方向平衡条件,可以得到
(3)
式中:b 为剪应力计算点处的横截面宽度,D 为横截面上剪应力计算点以上区域的水平合力。
不同高度位置处的正应力 σ(y)沿纵向的分布规律相同,因此上式可表示为
(4)
由于折线段位置的应力一阶导数并不连续变化,导致式(4)在折线段位置并不适用,本文通过将折线段等效为弧线段的方式来保证合力 D 与应力 σy 在纵向方向上的连续性,由此可以通过式(3)来计算截面上的剪应力。
如图2所示的长度为 L 的折线段变截面悬臂梁,折线段区域长度为 L1 ,悬臂端部梁高为 H0,根部梁高为 H1,截面高度为 H(x)。在 L1~L 区域内,与一般变截面悬臂梁相同,截面高度以 β 作为受压边倾角均匀过渡,在 O~L1 折线段之内,折线段变受压边倾角为 α,折线段高度为 h′(x),折线段根部高度为 h1。折线段等效为弧线段后,弧线段的区域长度由 L1 变化为 x1,截面高度由 H(x)变化为 R(x),弧线段高度为 R′(x),弧线段根部高度仍保持为 h1 不变。
图2折线段变截面悬臂梁剪应力计算等效模型
Fig.2Equivalent model for shear stress calculation of variable cross-section cantilever beams with corbels
为避免采用圆弧方程或三次项在悬臂根部的截面变化率过大,设等效弧线段的高度 R(x)为二项式 Ax2 + Bx + C,等效弧线段在悬臂根部的高度 h1 与折线段相同,且整个弧线段对悬臂根部产生的弯矩与原折线段相同,同时根据附加折线段与变截面梁底部交界位置的截面高度与截面变化率相同,最终得到等效弧线段的边界条件:
(5)
联立 4 个边界,求解得到等效弧线段高度表达式参数:
(6)
确定等效弧线段后,由弧线段连续边界可将式(3)简化为
(7)
式中:Aa 为剪应力计算点以上的横截面积,y 为剪应力计算点至梁顶的距离,Sa 为 Aa 对重心轴的静面积矩。
将式(7)代入式(3),同时联立式(2),忽略轴力变化时可以得到
(8)
式(8)为任意变截面梁剪应力的一般计算公式,当截面宽度不沿着跨度方向变化,Aa、Sa 的偏导为 0 时,式(8)可以改写为
(9)
式(9)只需代入计算位置的内力即可求得相应剪应力,但大悬臂变截面悬臂盖梁在重力荷载集度作用下的内力较大,目前在计算变截面内力时大多将变截面梁的高度及刚度等效为等截面梁去计算,折线段的设置会导致变截面梁的刚度在变受压边倾角附近位置(折线段与一般变截面梁交界位置,后文统称变受压边倾角位置)存在突变,为了精确分析折线段对应力分布规律的影响,不能再简单地采用等效计算方法,需要对变截面悬臂梁重力荷载集度作用下的内力公式进行推导。
如图3所示,为求任意位置处 x = x0 的弯矩,取 x0~L 之内的变截面梁作为隔离体,假设隔离体每个微段上的重力荷载集度为 q(x)dx,则 x0 处的弯矩为
(10)
剪力的计算取变截面梁 O~x0 部分为隔离体,以悬臂根部的剪力 Q1q0减去隔离体的剪力得到计算截面的剪力 Q1q(x):
(11)
(12)
式中:γ 为变截面梁材料容重,b 为变截面梁截面宽度,H0 +(L-x)tan β 为变截面梁在 x 截面位置截面高度的表达式。
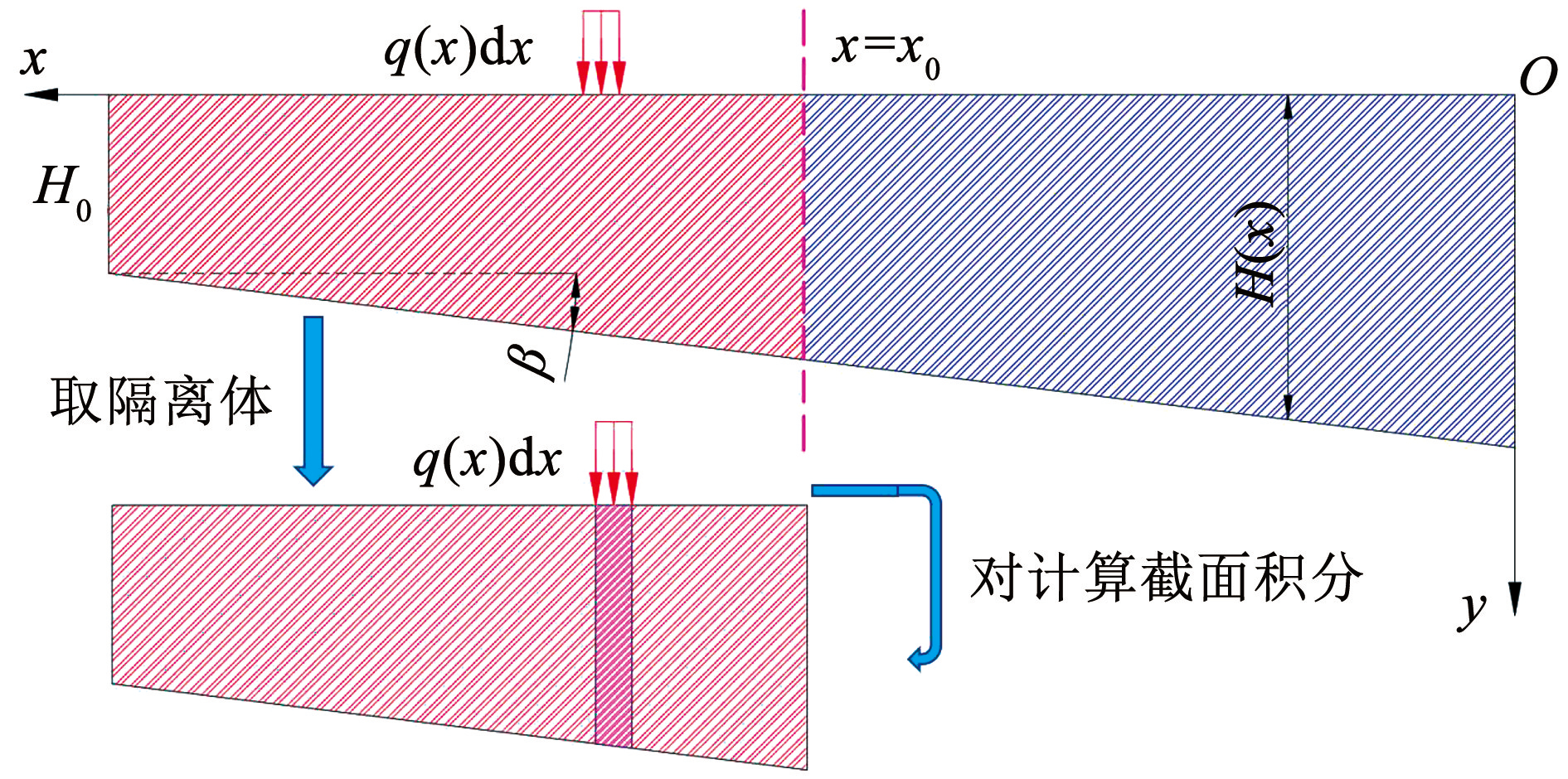
图3重力荷载集度作用下内力计算示意
Fig.3Schematic diagram of internal force calculation under gravity load
将上述弯矩及剪力计算公式积分,并令 x = x0,可得
(13)
1.2 合理折线段尺寸程序编制
假设大悬臂盖梁悬臂端部的受压边倾角为 β,一般悬臂段与折线段交界位置的受压边倾角 α = 2β,则悬臂根部的折线段高度 H1 可以根据受压边倾角 β 以及折线段长度 L1 确定。而受压边倾角 β 作为大悬臂盖梁的设计参数,则折线段设计尺寸的关键参数即为折线段长度 L1。为了体现折线段长度 L1 与盖梁悬臂长度 L 的相关性,定义最小折线段长度比 λ = L1 / L,以折线段长度 L1 与盖梁悬臂长度 L 的比值来作为折线段设计的关键参数,通过明确最小折线段长度比的设计可以确定折线段尺寸的最优解。
为了计算能保证盖梁受力性能的最小折线段长度比 λ,以同时保证大悬臂盖梁变受压边倾角位置顶缘及悬臂根部底缘的强度要求为目标函数,编写程序计算得到不同设计参数下大悬臂盖梁的最小折线段长度比,具体的迭代流程(图4)如下:
1)输入大悬臂盖梁设计参数受压边倾角 βi、预压应力 N(i,j)以及悬臂长度 L(i,j,k)。大悬臂盖梁的关键设计参数在于其悬臂长度 L,折线段高度与折线段悬臂端受压边倾角 β 控制,而折线段长度的设置同样与盖梁横截面上的预应力水平 N 相关,因此确定大悬臂盖梁设计参数变量为 L、β、N。在程序开始迭代前依次输入 3 个设计参数变量受压边倾角 βi、预应力 N(i,j)以及悬臂长度 L(i,j,k),并根据程序计算判定情况在设计范围内迭代参数,以达到覆盖通用大悬臂盖梁工程设计参数组合的目的。
2)计算不同参数变量下的对应荷载工况 [P(i,j,k,m) ]。在进行迭代时,需要按照当前的大悬臂盖梁设计参数受压边倾角 βi、横截面预应力水平 N(i,j) 以及悬臂长度 L(i,j,k)来计算对应的荷载工况 [P(i,j,k,m) ]。在考虑安全富余度的基础上,当悬臂根部顶缘应力大于所使用混凝土材料抗拉强度时,[P(i,j,k,m)]为保证受压边倾角顶缘强度要求的荷载工况; 当悬臂根部底缘应力大于所使用混凝土材料抗压强度时,[P(i,j,k,m) ]为保证悬臂根部底缘强度要求的荷载工况。
3)计算最小折线段长度比 λ(i,j,k,m)。确定对应盖梁参数组合 βi、N(i,j)、L(i,j,k)的荷载工况[P(i,j,k,m)] 后,设定初始最小折线段长度比 λ 为 0. 05,最小折线段长度比增量为 0. 001。 λ top (i,j,k,m)为保证变受压边倾角位置顶缘第一主应力小于抗拉强度的顶缘最小折线段长度比; λ bot (i,j,k,m)为保证悬臂根部底缘第一主应力小于抗拉强度的底缘最小折线段长度比。在所有受压边倾角 βi、预压应力水平 N(i,j) 以及悬臂长度 L(i,j,k)的设计参数组合全部循环完成后,输出所有的顶底缘最小折线段长度比 λ top (i,j,k,m)、λ bot (i,j,k,m)。
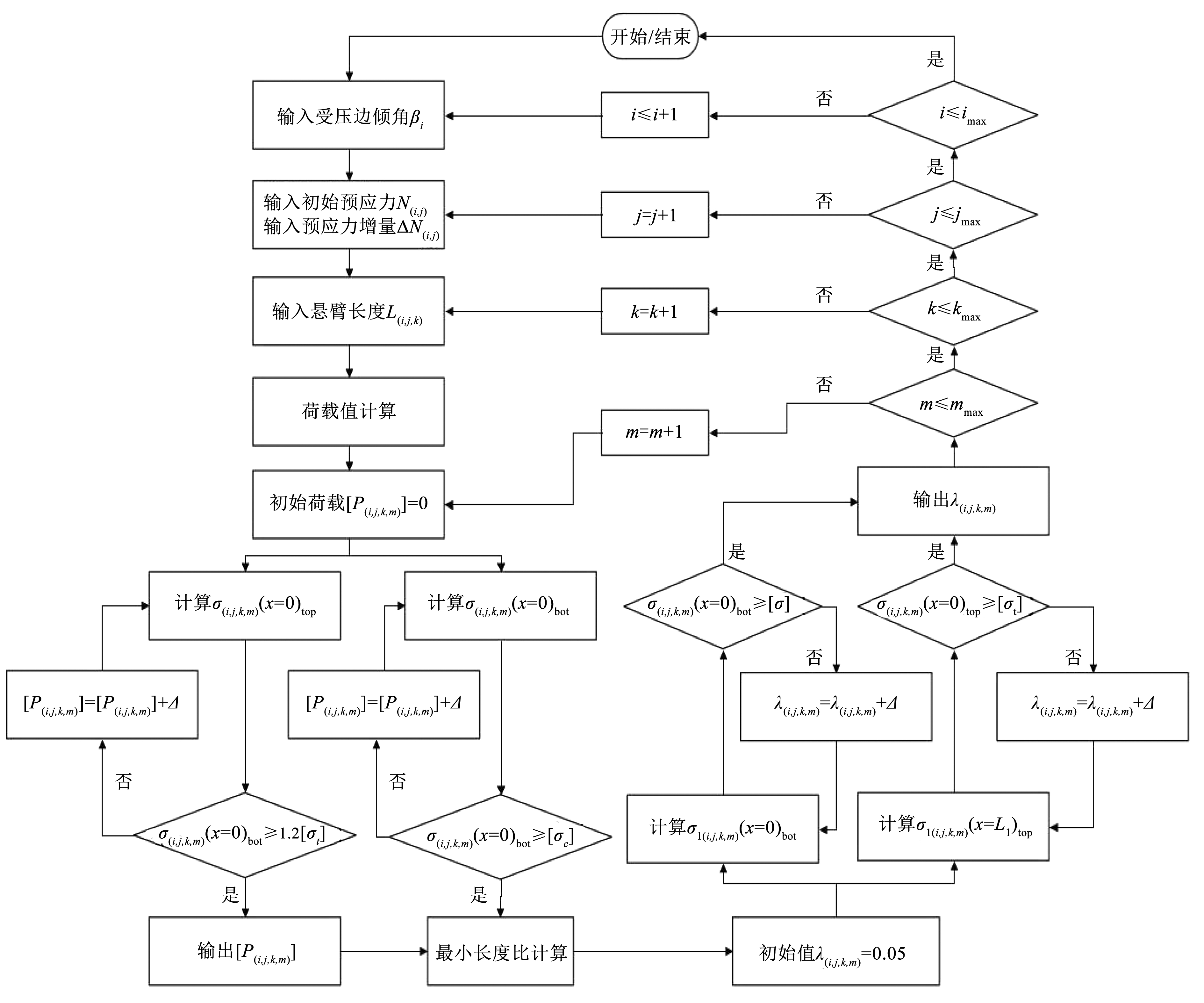
图4最小折线段长度比计算迭代流程
Fig.4Iterative flowchart for the calculation of the minimum corbel length ratio
2 折线段大悬臂变截面 PC 盖梁试验
本文依托京雄高速花瓶式桥墩,按照 1∶ 4 缩尺比设计了并制作了两片试验模型来探究大悬臂变截面 PC 盖梁的应力分布及受力性能,并将其中一片针对剪应力研究分析的试验模型数据与前述的折线段变截面梁剪应力计算理论进行对比验证。
2.1 大悬臂 PC 盖梁试验缩尺模型
2.1.1 试验缩尺模型设计
大悬臂 PC 盖梁缩尺模型的具体尺寸布置如图5所示,缩尺模型由一般变截面悬臂段、附加折线段以及跨中段组成,缩尺模型悬臂段长度 L = 3 m,折线段区域长度 L1 = 0.8 m,跨中段长度为 L2 = 2.5 m; 缩尺模型采用截面宽度 b = 0.4 m 的矩形截面,悬臂端部截面高度 H0 = 0.4 m,悬臂根部截面高度 H1 = 1 m; 一般变截面段区域的受压边倾角 β = 7.8°,折线段区域受压边倾角 α = 15.6°。
缩尺模型采用抗压强度为 29.3 MPa,抗拉强度为 1.73 MPa 的 C40 混凝土浇筑,每立方米混凝土由 540 kg 水泥、174 kg 水、621 kg 中砂、1 024 kg 粗骨料、60 kg 粉煤灰以及 11.4 kg 外加剂拌合而成。为了保证结构受力的安全性,试件共设置了两排共 3 根 15.2 mm × 4 的预应力束,以抵消自重及加载带来的负弯矩,预应力束特性见表1。
2.1.2 加载方案
本次缩尺模型试验采用千斤顶顶推反力架的方式给顶缘 15 × 60 cm 的加载区域施加面荷载,同时在中跨段设置分配梁来保证缩尺模型悬臂根部的固结边界,试验加载及边界布置如图6所示。
表1预应力配束表
Tab.1 Configuration of prestressing tendons
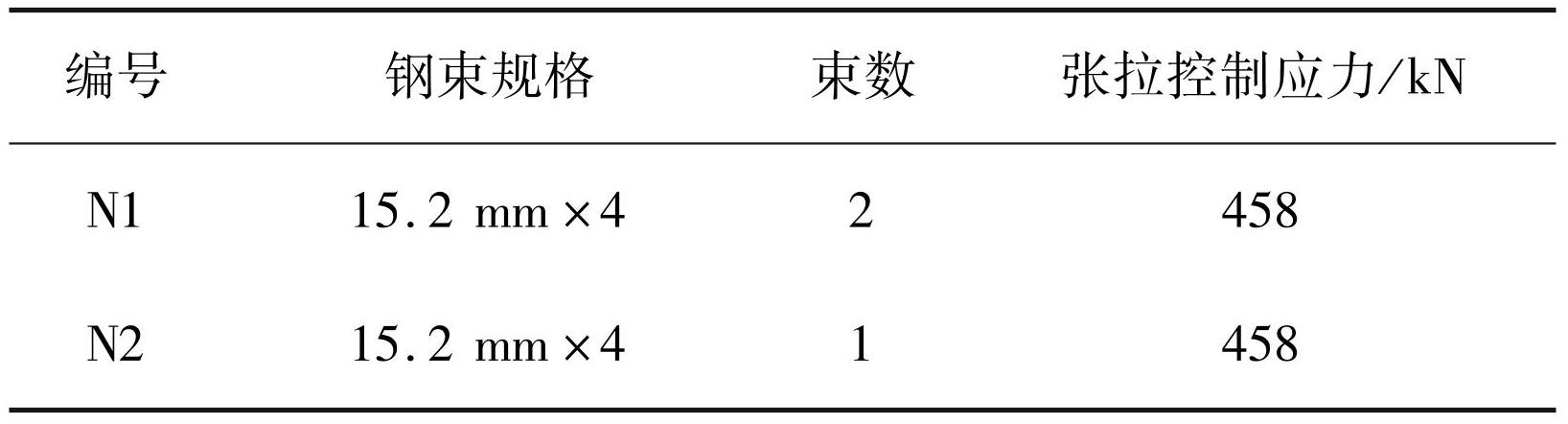
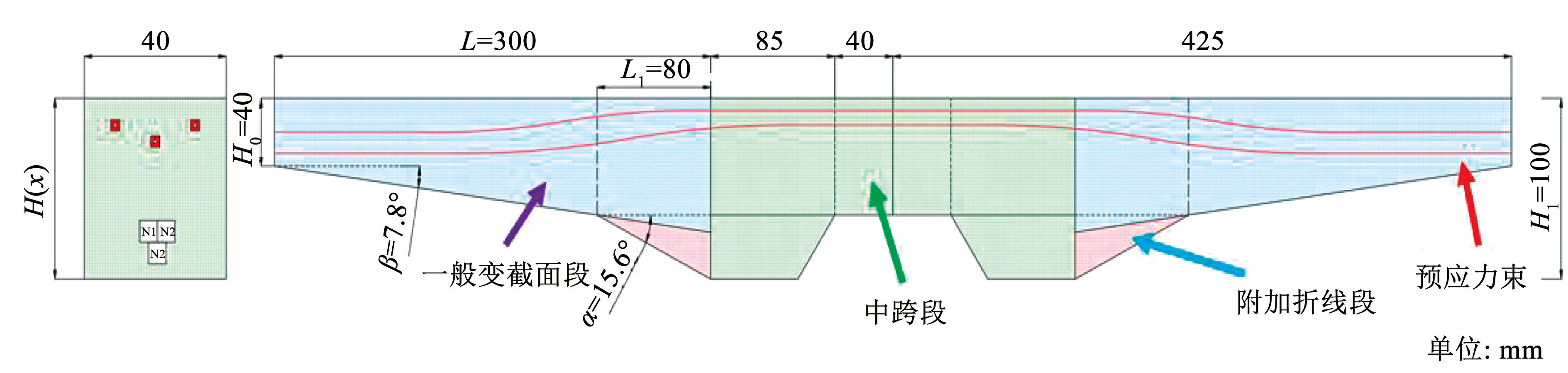
图5缩尺模型尺寸及预应力布置
Fig.5Dimensions of the scaled model and prestressing arrangement
图6试验加载及测点布置
Fig.6Loading and measurement point layout of the experiment
为了获得各工况下的纵向剪应力分布规律,在缩尺模型左右侧悬臂的 7 个关键截面上布置 45°应变花,应变测点编号分别为 C1~C12(左侧悬臂),C15~C23(右侧悬臂)。其中左侧悬臂应变测点测量由一般悬臂段 L / 2 位置至变受压边倾角右侧区域的剪应力分布,右侧悬臂应变测点则为左边测点的对称增补点,其余 T1~T7 测量缩尺模型顶面正应力,A1~A7 测量缩尺模型侧面顶缘正应力,B1~B6 测量缩尺模型侧面底缘正应力。在缩尺模型顶缘中心线上布置 7 个大量程百分表测量作为位移测点,其中 N1、N7 布置于缩尺模型的悬臂端部下缘位置测量悬臂端部的位移; N2、N6 测量变受压边倾角处的位移。
2.2 有限元模型与试验裂缝发展
如图7所示,在 ANSYS 中建立了大悬臂折线段矩形变截面悬臂梁缩尺模型的实体有限元。混凝土使用 SOLID65 单元、普通钢筋与预应力筋采用 LINK8 单元进行模拟; 在悬臂端部及加载区域设置采用 SOLID45 单元模拟的预应力锚垫板与加载垫块避免局部应力过大导致不收敛的情况发生。在跨中顶部区域以及支座底部位置施加固结边界,在加载垫块上施加对应于试验荷载的面荷载进行加载。
提取有限元模型悬臂端部位移随荷载变化的数据,与试验 N1、N7 测点的荷载位移曲线进行对比,对比结果如图7(b)所示。
有限元的荷载位移曲线与试验结果基本吻合,加载过程中的测点位移变化基本一致。本文在对试验进行数值仿真时未考虑预应力损失,而缩尺试验试件在预应力张拉锚固及运输过程中存在预应力损失,因此导致其开裂荷载 150 kN 小于有限元模拟的开裂荷载 160 kN,而有限元开裂阶段的刚度要略小于试验构件的刚度,因此有限元最终的极限荷载值 525 kN 要略小于试验的实际极限荷载 540 kN。
如图8( a)所示,当试验的悬臂端部荷载达到 450 kN 时,与临界斜裂缝相交的竖向箍筋 SV11 的应力迅速增加,悬臂端部荷载达到 500 kN 时,竖向箍筋 SV11 与水平腹筋 SH14 的应力均达到屈服强度极限,而由于钢筋塑性变形的发展,临界裂缝不断加宽并继续向变受压边倾角延伸,如图8( b)所示,悬臂端部荷载达到 525 kN 时,B5 混凝土的测点应力达到抗压极限强度,变受压边倾角位置混凝土在剪压复合作用下达到极限强度破坏。
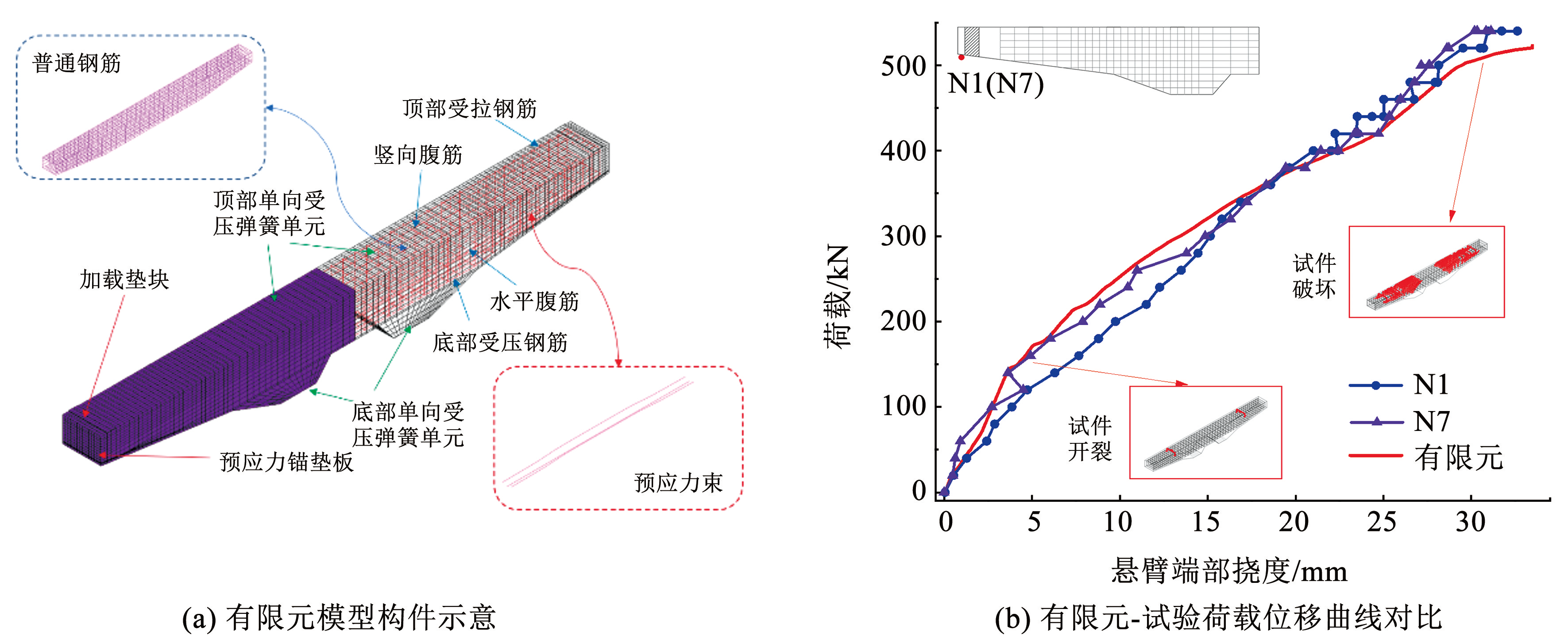
图7有限元模型示意图及荷载位移曲线对比
Fig.7Schematic diagram of finite element model and comparison of load-displacement curves
如图8(c)所示,缩尺模型早期裂缝以受弯裂缝为主,顶面与侧面均为变受压边倾角位置最先出现裂缝,且发展最为迅速。当裂缝发展到后期时,呈现以变受压边倾角位置裂缝为中心,悬臂端部与悬臂根部区域裂缝向变受压边倾角位置斜向发展的剪弯裂缝形态,折线段变截面梁的变受压边倾角处为应力最大区域。分析 400 kN 荷载下,一般悬臂端区域 L / 2 截面和悬臂根部区域 L / 2 截面的混凝土剪应力与正应力竖向分布绘制如图9所示。有限元模型中的混凝土单元失效后刚度很小,应力在开裂区域几乎为 0,而一旦进入未开裂区域混凝土应力则相应急剧增长,但主要以压应力为主。受压区内的剪弯斜裂缝主要由剪应力控制,观察 L / 2 悬臂截面和变受压边倾角截面的主拉应力分布曲线,在一般悬臂端区域 L / 2 截面高度 300 mm 和悬臂根部区域 L / 2 截面高度 500 mm 的裂纹尖端区域附近,混凝土主拉应力突然增大至接近 C40 混凝土的抗拉强度的峰值,说明在中性轴以下一定范围内,结构的开裂主要由剪应力控制,其破坏形态表现为混凝土的脆性斜拉破坏,而在底部的混凝土受压区,其承受剪应力的同时还承受较大的纵向压应力,斜裂缝无法贯穿,最终破坏表现为试验的弯剪复合作用下的剪压破坏。
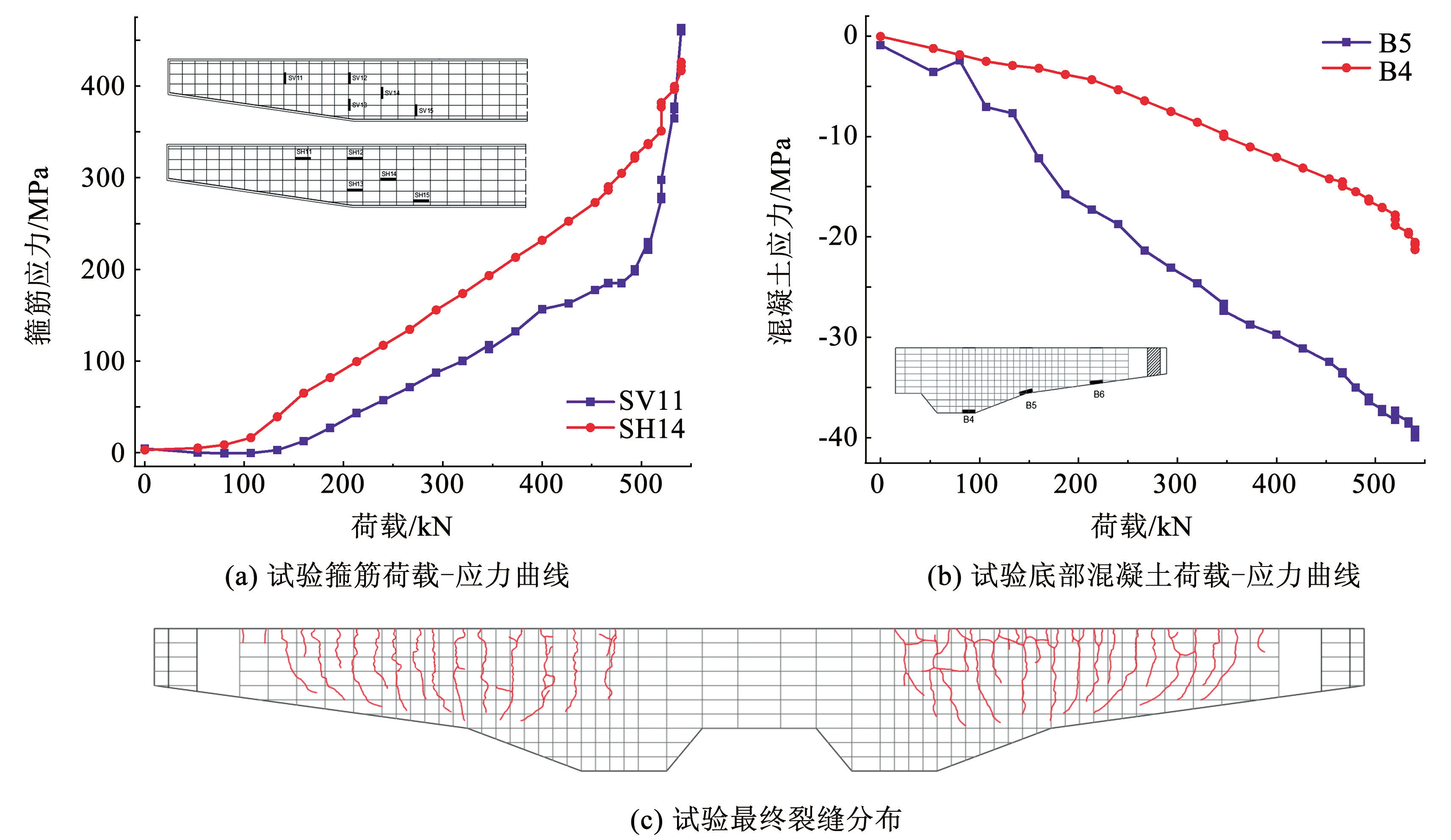
图8试验裂缝分布及部分测点荷载应力曲线
Fig.8Distribution of experimental cracks and stress-strain curves of some measuring points
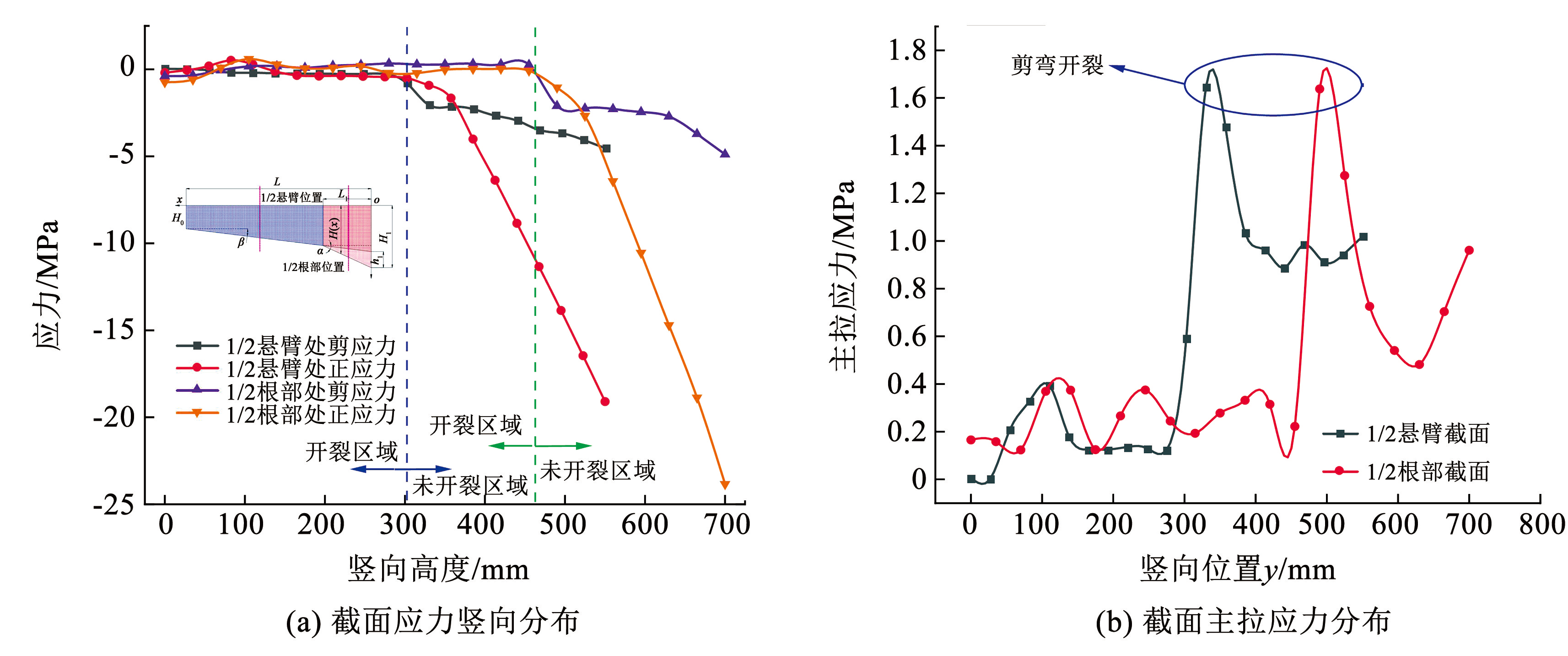
图9400 kN 荷载下混凝土应力
Fig.9Stress distribution of certain concrete sections under a400 kN load
2.3 剪应力对比
选取试验过程中未开裂荷载等级下的混凝土应变测点(C1~C12,C15~C23)数据进行整理,与本文理论解析解及有限元模型对应荷载下的剪应力纵向分布进行对比,结果如图10所示。
图10剪应力纵向分布对比
Fig.10Comparison of longitudinal distribution of shear stress
悬臂段剪应力的纵向分布呈现二段式特点,折线段的设置使得剪应力在变受压边倾角附近出现拐点,折线段区域剪应力变化率也相较一般变截面区域有所增加,由式(9)可知变截面梁的剪应力与弯矩变化率相关,折线段曲率的改变引起了折线段区域的弯矩及应力变化率的相应改变。
在悬臂端部 0.25 m 之内,由理论公式计算得到的剪应力与有限元结果误差较大,由于在边界处预设初应变模拟预应力容易存在误差,同时悬臂端部位置所受集中荷载及自重效应较小,预应力所占比重相对较大,导致此处有限元的剪应力计算结果与理论计算结果误差较大。由对比结果可以看出,除去有限元悬臂端部的边界影响误差,在盖梁缩尺模型的其他纵向分布区域,本文理论解析解与有限元计算值以及试验实际的剪应力分布在数值及分布规律上均吻合较好,验证了本文折线段变截面悬臂梁应力计算理论的有效性。
2.4 正应力对比
将 T1~T7 顶部测点在不同荷载等级下的数据进行整理,与有限元及理论计算得到的正应力纵向分布进行对比,对比结果如图11所示。
图11正应力纵向分布对比
Fig.11Comparison of longitudinal distribution of stress
悬臂段顶缘正应力分布规律与剪应力相似,在变受压边倾角位置正应力达到最大值后便不再继续增加,并由于截面高度变化率的增加开始减小。相较无折线段,折线段最大正应力的分布区域及数值均有所差异,在安全性上有所提高。
由对比结果可以看出,有限元的纵向应力分布在悬臂端部锚固区域同样与正应力理论计算值差异较大,在一般变截面悬臂段及折线段区域,试验值、理论解析解及有限元计算值三者之间在数值及变化规律上基本吻合。
3 折线段对结构受力的影响
3.1 折线段设置对应力分布的影响
折线段在增加盖梁悬臂根部抗弯性能的同时改变了折线段区域的剪应力分布,由于悬臂根部处于弯剪共同受力的状态,为了综合考虑结构在正应力及剪应力复合作用下的受力性能,计算接近试验开裂荷载时折线段盖梁的剪应力空间分布,分析附加折线段对结构受力带来的影响。
试验中预压轴力 N = 900 kN,悬臂端部的集中荷载 P = 150 kN 时构件开裂,通过本文理论计算得到的试验缩尺模型在不同截面位置及截面高度下的剪应力分布如图12所示,正应力分布如图13所示,由于不同截面位置的截面高度不同,因此在绘图中统一用截面高度百分比来表示。
折线段变截面悬臂梁顶缘与底缘的剪应力分布在悬臂端部与悬臂根部区域有着较大的差异性。在悬臂端部区域附近,结构剪应力竖向分布与材料力学相似,呈现截面中性轴位置剪应力最大,截面顶部及底部剪应力最小的分布规律; 当截面位置过渡至悬臂根部区域时,剪应力的竖向极值由截面中性轴位置向顶缘偏移,最大剪应力出现在截面底缘区域,悬臂根部位置的截面底缘处结构剪应力达到最大值。
图12折线段变截面悬臂梁剪应力分布
Fig.12Distribution of shear stress in variable cross-section cantilever beam with a corbel
图13折线段变截面悬臂梁正应力分布
Fig.13Distribution of stress in a variable cross-section cantilever beam with a corbel
由有无折线段的变截面悬臂梁正应力对比可以看出,折线段的存在改善了悬臂根部的受力性能,折线段区域截面高度的增加不仅提高了悬臂根部的抗弯惯性矩,也因为预应力偏心距的增大而增强了预应力效应。悬臂根部顶缘正应力由 2.37 MPa 减小至 1. 06 MPa,整个悬臂根部区域的顶缘最大正应力由悬臂根部位置转移至变受压边倾角位置,最大正应力数值降低 0.72 MPa,如图14所示。
折线段顶缘受力性能主要由拉应力控制,折线段区域顶缘的拉应力及第一主应力分布规律在有无折线段上存在明显差异,而第三主应力分布则并未受到明显影响。折线段的设置使得悬臂根部顶缘的第一主应力由 2.4 MPa 减小至 1.1 MPa,避免了悬臂根部的开裂,提高了悬臂根部的受力储备。
图14折线段变截面悬臂梁主应力分布
Fig.14Distribution of principal stress in a variable cross-section cantilever beam with a corbel
折线段悬臂根部底缘的受力同样由第一主应力控制,第三主应力在受压边倾角位置处开始下降,最大应力远小于受压破坏极限,而悬臂根部底缘由于是受压区域,第一主应力主要由剪应力控制,因此剪应力的增加也导致了第一主应力剧烈增大。当悬臂端部的集中荷载增大到接近极限荷载(525 kN)的 480 kN 时,悬臂梁底缘应力沿纵向的分布规律如图15所示。
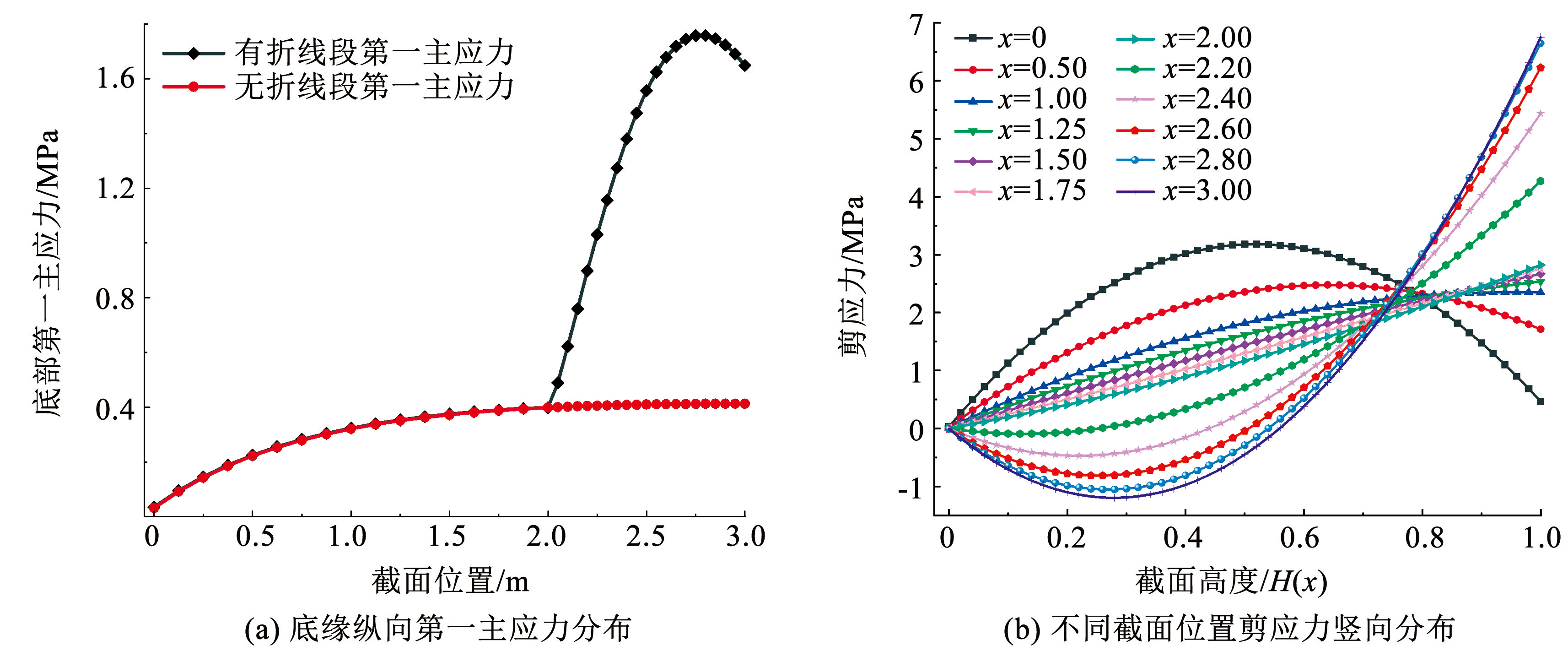
图15底缘纵向第一主应力及竖向剪应力分布规律
Fig.15Distribution laws of the first principal stress along the bottom edge and the vertical shear stress
由变截面梁剪应力计算公式可知,梁底缘由剪力引起的剪应力为 0,此时的剪应力全部由轴力与弯矩提供,当计算截面位于悬臂端部区域时,变截面悬臂梁的弯矩较小,因此底缘剪应力也较小,而随着计算截面靠近根部,底缘剪应力也逐渐增大,剪应力最大区域也由中性轴位置转移至底缘位置。且由于弯矩的增加,在截面中性轴附近的剪应力也由剪力控制转变为由弯矩控制,数值上也由正值最终转变为负值。
当荷载值较大时,折线段区域的底缘最大剪应力已经达到 5.7 MPa,接近无折线段最大剪应力数值(3 MPa)的两倍,这使得有折线段变截面悬臂梁悬臂根部底缘相较无折线段变截面悬臂梁成为了一个危险受力区域,此时最大第一主应力达到 1.76 MPa,已经超过了混凝土的受拉允许值,而无折线段的最大第一主应力则稳定在 0.4 MPa,远小于有折线段的最大第一主应力数值。
如前文所述,受剪构件的合理破坏形态是受压区边缘混凝土在剪压复合作用下的剪压破坏,但如果折线段设置不当,则会导致受压区边缘混凝土在剪压破坏前首先因剪应力控制的第一主应力达到抗拉极限强度而开裂,因此有必要对折线段的设置长度进行研究,以保证折线段在改善根部受力性能的同时不会有开裂风险。
3.2 折线段长度对结构受力的影响
由 3.1 节的分析可知,悬臂根部顶部及底部的受力均由第一主应力控制,令折线段长度比 λ = L1 / L,分析不同折线段长度比(0~0.45)下,悬臂根部区域结构顶底缘第一主应力的变化规律,计算结果如下:
如图16所示,随着折线段长度比的增加,悬臂梁变受压边倾角位置也逐渐由悬臂根部向端部转移,顶缘最大第一主应力的数值也逐渐下降; 悬臂梁底缘第一主应力分布随着折线段长度比的变化也有所变化,当折线段长度比较小时,底缘第一主应力呈现在变受压边倾角位置突然增大的趋势,而当折线段长度比增加,第一主应力由变受压变倾角位置至悬臂根部开始逐渐过渡变化,这种过渡的应力分布无疑对结构更为有利。

图16不同折线段长度比的纵向第一主应力分布规律
Fig.16Distribution law of the first principal stress with different ratios of line segment lengths
4 附加最小折线段长度比
按照 1.2 节所述的最小长度比计算迭代流程,本文在迭代计算时,选取变受压边倾角 β 为 5°~10°,预压应力 N 随着悬臂长度变化对应的值为 600~7 200 kN,悬臂长度 L 值为 5~20 m。根据图4流程拟合得到的不同参数组合下的顶底缘最小折线段长度比 λ 如图17所示。
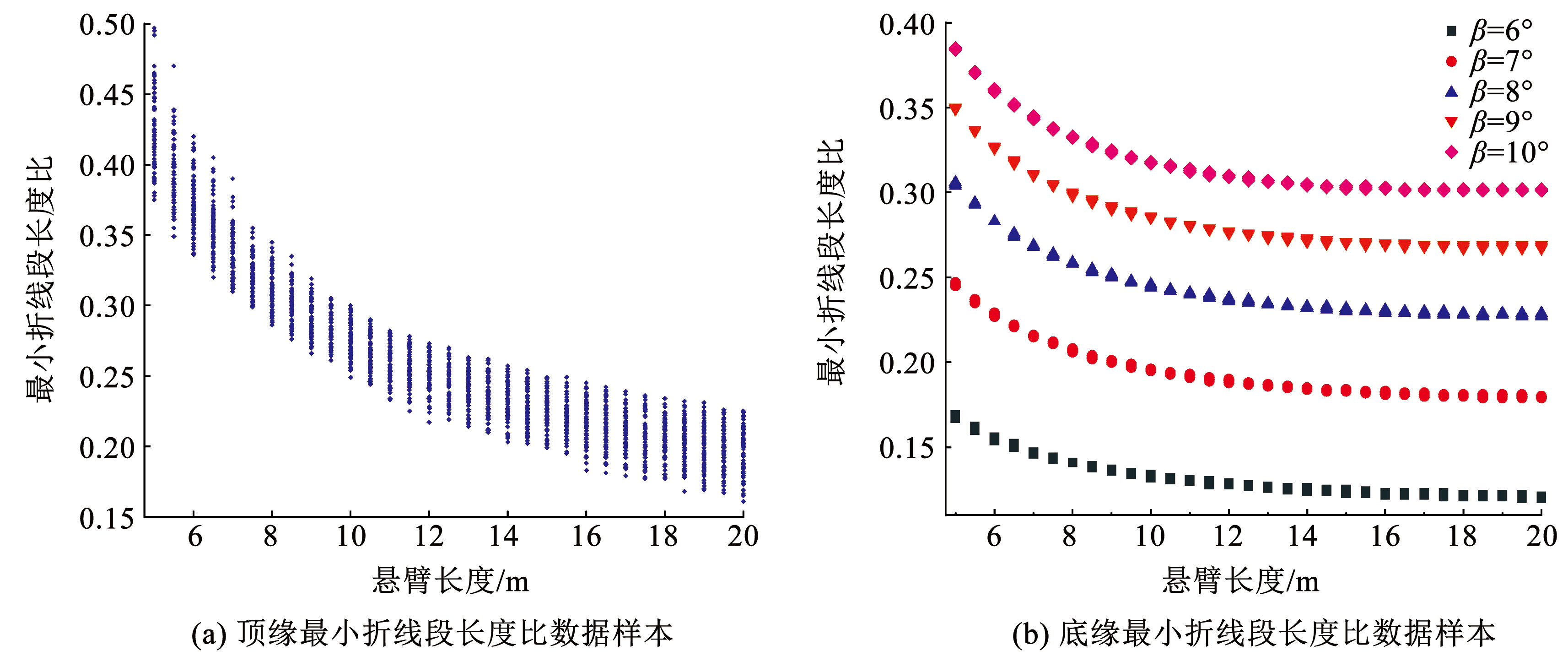
图17最小折线段长度比数据样本
Fig.17Sample of the ratio of minimum corbel lengths
由图17(a)可以看出,顶缘悬臂长度与最小折线段长度比呈现指数函数 的数学关系,当预压应力水平 N 不同时,函数的整体曲线形状变化并不明显,但在数值上表现出差异,可以确定预压应力水平 N 主要与函数的截距 C 相关; 受压边倾角 β 变化带来了函数曲线形状及数值上的差异,因此受压边倾角 β 与函数的变化参数 A、C 都有相关性。在拟合函数时,首先确定不同受压边倾角 β 下的参数 A,确定 A 后再进行截距与受压边倾角 β 及预压应力水平 N 之间多元函数关系式的拟合,最终得到顶缘最小折线段长度比 λtop与悬臂长度 L、受压边倾角 β、预压应力 N 之间的函数表达式:
(14)
式(14)与数据样本之间的拟合效果对比如图17(a)所示,由公式计算得到的最小折线段长度比基本维持在数据样本的区间之内,拟合值与数据样本之间的误差维持在 ± 6% 之内,验证了最小折线段长度比计算公式的有效性。
图18拟合效果
Fig.18Fitting effect
由图17( b)可以看出,当悬臂长度 L 在 5~15 m之间时,悬臂长度 L 与底缘最小折线段长度比 λ 之间呈现二次函数的数学关系,当悬臂长度 L 为 15~20 m 时,底缘最小折线段长度比 λ 则基本趋于定值。在拟合函数时,主要分析 5~15 m 悬臂长度间数据样本,不同的预应力水平 N 对底缘最小折线段长度比 λ 的数值影响并不明显,不同受压边倾角 β 下的底缘最小折线段长度比 λ 曲线基本只呈现出一条曲线的趋势,而受压边倾角 β 的变化对函数曲线形状的影响不明显,但在函数数值上的差异巨大,因此确定二次函数的参数主要与受压边倾角 β 相关,最终得到底缘最小折线段长度比 λbot与悬臂长度 L、受压边倾角 β 之间的函数表达式为
(15)
分析底缘最小折线段长度比 λbot拟合效果可以看出,所选取的函数形式与数据样本分布规律基本相同,且在不同受压边倾角 β 下的拟合曲线与样本数据曲线基本相符,拟合值与数据样本之间误差在 ± 4% 之内,验证了底缘最小折线段长度比计算公式的有效性。
在进行折线段尺寸设计时,可以分别依据式(14)、(15)计算得到顶底缘最小折线段长度比,并选取较小的数值以作为折线段尺寸设计参数以保证大悬臂 PC 盖梁结构整体的受力性能。
5 结论
1)通过将折线段等效为弧线段,推导了带有附加折线段的大悬臂变截面 PC 盖梁剪应力计算理论; 该理论计算得到的纵向剪应力分布得到了缩尺模型试验测试结果及有限元解析解的有效验证,能较好地反映折线段对盖梁剪应力分布带来的影响。
2)附加折线段使得盖梁顶缘最不利受力位置由悬臂根部转变为变受压边倾角处,盖梁底缘的开裂受剪应力控制,需要通过控制折线段尺寸来保证结构弯剪受力下的强度要求; 随着折线段长度的增加,顶底缘应力峰值均有所降低,底缘变受压边倾角处第一主应力由突然增大转变为过渡变化至悬臂根部,对结构更为有利。
3)按照顶缘最不利受力位置不开裂及保证受压边底缘强度要求的准则,考虑盖梁悬臂长度、受压边倾角及预应力水平的影响,给出了大悬臂 PC 盖梁最小折线段长度比的计算公式,公式在不同盖梁设计参数下均能保证其有效精度,具有一定的实用性。








