摘要
钢-混组合桥面板的混凝土铺装层设计参数多由工程经验确定,针对因缺乏明确的受力机制分析而容易导致其结构开裂或不经济的问题,根据正交异性钢-混组合桥面板构造特点,将混凝土铺装层横桥向受力比拟为弹性地基上的无限长梁, 建立了轮载下混凝土层横桥向效应的理论分析模型,推导了混凝土层横桥向弹性变形、受力和有效作用范围的解析式。以实际正交异性钢-混组合桥面构造为原型,设计和实施了足尺模型静载试验,还进行了空间有限元仿真分析,结果证明了弹性地基梁比拟模型的合理性。因横隔板和刚性混凝土层约束,偏载下 U 肋扭转变形可忽略不计;轮载横桥向有效作用范围不超过 5 个 U 肋中心距。基于有限元的参数分析表明:栓钉布置和横隔板对混凝土层横桥向受力影响很显著。在所提的混凝土铺装层设计参数取值范围内,提出的横桥向受力计算公式适用于正交异性钢混组合桥面设计。
Abstract
The design parameters are primarily determined empirically for the concrete overlay of steel-concrete composite bridge decks, as the lack of a clear stress analysis mechanism can lead to structural cracking or inefficiency. The transverse performance of the concrete overlay was simulated as a infinitely long beam on an elastic foundation based on the characteristics of orthotropic composite bridge deck. A theoretical analysis model was first established for the transverse behavior of the concrete overlay under wheel load, and the formulas were derived for the deformation, load, and effective range of the wheel load. A full-scale model static load test was then designed and conducted according to the practical orthotropic composite bridge deck. A corresponding spatial finite element model was also established, and the theoretical, experimental, and finite element results were compared to validate the accuracy of the proposed mechanical model. Due to the constraints imposed by the diaphragm and the rigid concrete layer, the torsional deformation of the U-rib under eccentric loading can be neglected. The effective range of the wheel load is limited to the span of 5 U-ribs. Parameter analysis indicated that both the arrangement of studs and transverse diaphragms have a significant influence on the transverse deflection of the concrete overlay. Within the range of commonly used design parameters, the proposed calculation formula is applicable to the design of steel-concrete composite bridge decks.
铺装层损坏和钢桥面构造疲劳开裂等病害[1-3] 是公路正交异性钢桥面常见的病害,威胁桥梁长期安全服役,其主因是桥面构造在轮载作用处显著的局部变形效应[4-7]。在钢桥面上铺设刚性混凝土层,形成共同受力的钢-混组合桥面板,既提高了顶板刚度,扩散了轮载作用,降低了关键细节的疲劳应力,又减小局部变形效应,降低了铺装层的开裂风险,应用越来越广泛[8-11]。一般认为,组合桥面实际上是 3 个结构体系组合受力:1)纵桥向受力是将桥面板与纵肋组成的结构系看成主梁的一部分参与主梁共同受力(第一、二体系受力); 2)横桥向受力控制着轮载下桥面板疲劳行为[12-13],具有显著的局部受力特征(第三体系受力)。由于正交异性组合钢桥面纵肋间距一般远小于横隔板间距,纵、横桥向受力行为极为不同,铺设其上的混凝土层呈明显的双向受力特征,两个受力方向都可能控制混凝土层极限状态。混凝土层与正交异性钢桥面已成为共同受力的组合结构,在双向受力模式主导下,若混凝土铺装层仍然只按纵桥向受力(第一、二体系)进行计算和设计,其失效行为评估势必与桥面实际行为产生较大偏差,已有工程实践[14] 表明,即使是高性能混凝土铺装层,仍出现了开裂病害。前期的研究[15-16]表明:轮载下混凝土铺装层受力行为控制着钢-混组合桥面板的疲劳极限状态,尤其是横桥向受力。因此混凝土层轮载横桥向受力机理研究非常必要,可为混凝土层设计提供理论依据。
国内外的研究[17-19]多基于试验和有限元模拟,通过调整混凝土层几何、材料、力学和配筋参数,在不增加自重情况下,改善钢桥面构造细节的疲劳性能和铺装层的抗裂性能。文献[8] 通过闭口肋钢UHPC 组合梁的纵向受弯试验研究表明,UHPC 层配筋会提高其抗裂强度。文献[20] 对钢-UHPC 轻型组合桥面横向抗弯开裂性能的正交试验也表明了配筋率对开裂应力的影响最大。混凝土层厚度及其配筋率影响组合桥面板的安全服役和经济性,但这些混凝土层关键参数的取值缺乏力学基础和理论计算公式。目前采用的有限元方法和试验模型工作量大,研究过程类似黑箱,成果缺乏统一性和广泛的适应性,工程应用不便,一定程度上成为组合桥面应用的“瓶颈”,亟待力学模型直观、计算精度较高、工程实用性更强的混凝土层受力计算分析理论。弹性地基梁比拟法应用广泛、理论成熟,公式简便,适用于分析正交异性组合桥面混凝土层的结构行为[21]。因此本文以典型正交异性钢-混组合桥面板构造为研究对象,首先通过理论推导建立轮载下混凝土层的弹性地基梁比拟分析模型,然后依托实际桥梁工程设计和实施了足尺模型静载试验,并进行了相应的空间有限元仿真分析,基于数值模拟和实测值完善所提出的混凝土层横桥向受力计算公式,并基于有限元模型对横隔板布置、剪力钉刚度及布置和轮载分布及加载位置等开展参数研究。
1 弹性地基梁比拟模型
1.1 基本假设
以单个轮载作用范围内的正交异性钢-混组合桥面板为研究对象,横隔板间距为 L,U 肋中心距为 d,tc和 ts分别为混凝土层和钢顶板厚度,如图1( a)所示。纵桥向上轮载 P 作用于距离横隔板 αL 处,轮压接地形状为矩形,a0和 b0为接地长度和宽度,压力分布均匀且取值为 σ0。根据正交异性梁格法的思路,将混凝土层横桥向受力状态比拟为弹性地基上的无限长梁,即混凝土层横桥向受力模式等效为多个 U 肋弹性支承的宽度为 b 的无限长混凝土梁,如图1(b)所示。混凝土尺寸定义为:厚度 tc,宽度 b。 U 肋尺寸定义为:板厚 t1,高度 h1,上、下口宽分别为 d1和 d2。单 U 肋和混凝土梁(宽为 b)绕各自中性轴的抗弯惯性矩定义为 Is、 Ic,如图2( b)和 3(b)所示。为简化计算,假定如下:1)不考虑材料缺陷,钢材和混凝土均为理想线弹性材料,弹性模量分别为 Es和 Ec; 2)不考虑 U 肋扭转变形; 3)钢-混组合桥面满足小变形假设; 4)钢-混界面光滑,无摩阻效应; 5)轮压荷载是局部均布荷载 σ0,故忽略等厚混凝土层竖向压缩、扭转、剪切变形及掀起效应。
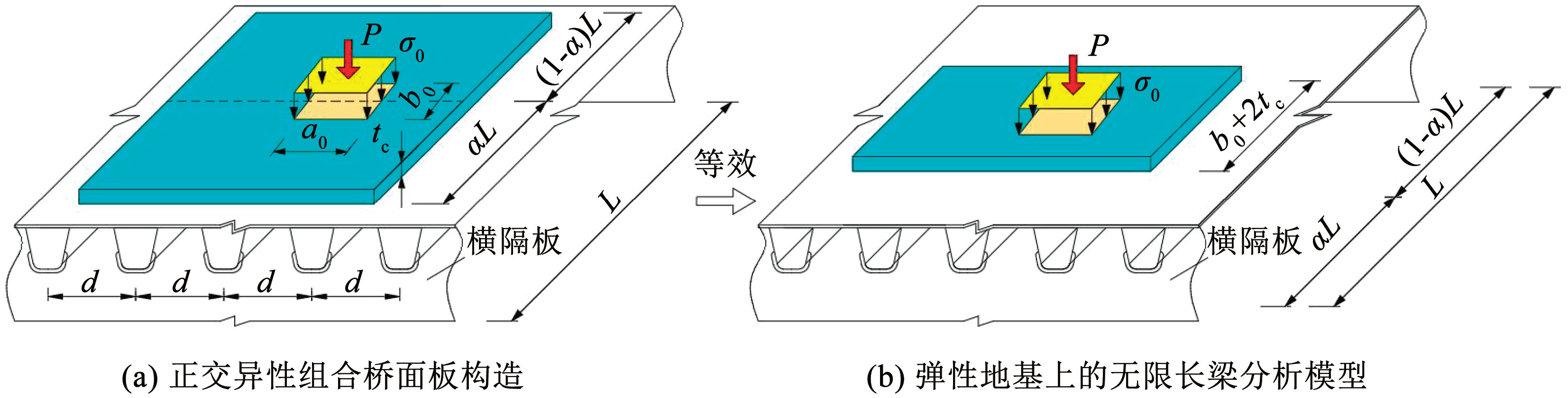
图1正交异性钢-混组合桥面板混凝土层弹性地基梁比拟模型
Fig.1Analogous mechanical model of elastic foundation beam for concrete overlay of composite bridge deck
1.2 模型推导
根据文献[21],混凝土层纵桥向上轮载有效作用范围以45°扩散角确定,故混凝土梁宽度 b 确定为
(1)
式中:b 为无限长混凝土梁的纵桥向宽度,b0为轮载纵桥向接地宽度,tc为混凝土层厚度。
正交异性钢桥面 U 肋纵桥向受到横隔板和顶板的约束,实际约束情况介于简支和固结之间,为简化计算,假定相邻两侧横隔板对 U 肋纵桥向的约束为固结,如图2(a)所示。同时引入挠度修正系数 η以考虑边界条件及荷载的差异,因此图2(b)所示的单 U 肋在集中力 P 作用下的作用点处(c 点)挠度为
(2)
当轮载位于横隔板上方时,仍可将相邻横隔板的约束视为固结,并按图2(a)进行计算。将横桥向上的多U肋等效为均匀连续分布的弹性地基( 弹簧),如图3(a)和 3(b)所示,由式(1)可得 c 点的弹性压缩系数为
(3)
式中:k 为弹性地基(弹簧)的弹性压缩系数; η 为挠度修正系数,可通过实验或有限元模拟确定。
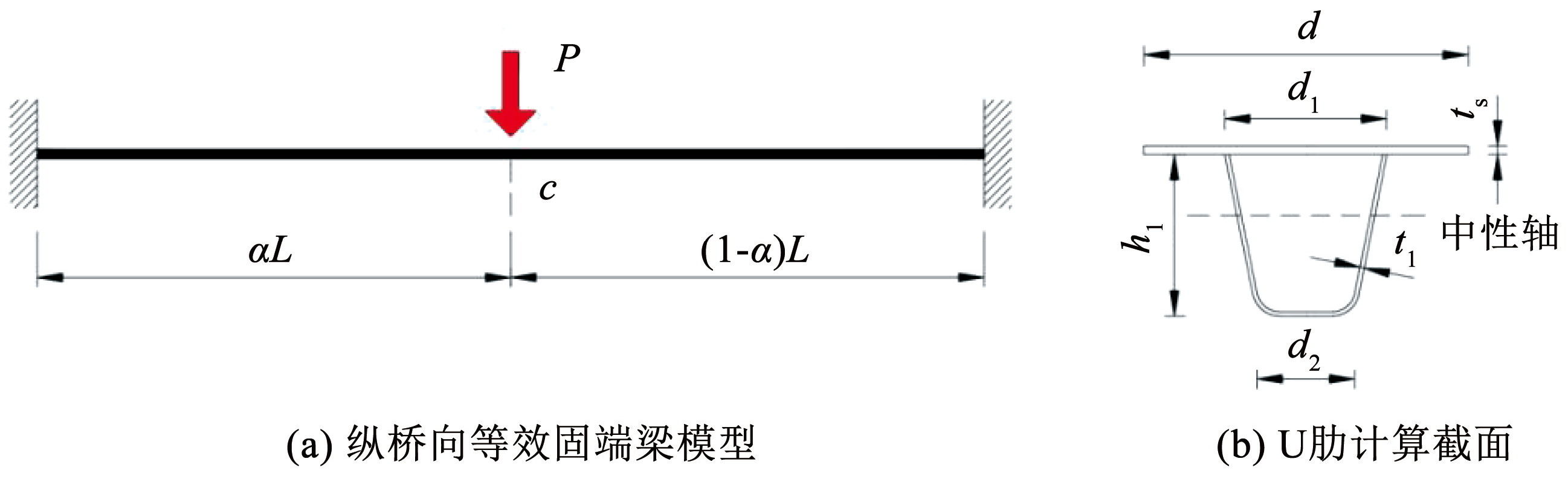
图2正交异性钢桥面的弹性地基模型
Fig.2Elastic foundation model for orthotropic steel bridge deck
图3(c)和 3(d)为混凝土梁变形与受力的弹性地基梁比拟模型,根据文献[22],钢桥面反力与弹性压缩系数间的关系为
(4)
式中 p 为钢桥面对混凝土梁的作用分布( 地基反力)。

图3混凝土层的弹性地基梁模型
Fig.3Elastic foundation beam model for concrete overlay
混凝土层竖向挠度 y、轮载 P 和地基反力 p(x)的关系满足方程:
(5)
式(5)可整理为
(6)
与桥面混凝土层平面尺寸相比,轮载分布尺寸很小,为得到简化的解析解,将轮载 P 视为集中力,因此根据弹性地基梁中的无限长梁的解法,式(6)的解(x≥0)为
(7)
根据对称性原理,可得到挠曲线的另外一半(x <0)。根据式(7)中的变形曲线,可求得任一截面相应的弯矩 M,剪力 Q 为
(8)
根据式(6),混凝土梁挠度随 x 增加而快速衰减,当 x = S 时,y = 0,可认为轮载影响已经很小,即
(9)
式中 S 为轮载一侧的有效作用范围。
因此根据式(9),可求得轮载一侧的有效作用范围为
(10)
由式(6)和式(8)可见,混凝土梁的弯矩 M 与 λ 和 k 成反比,即当 k 取最小值时,混凝土梁所受弯矩最大,受力状态最不利。因此根据式(3),当 α = 0.5(两道横隔板正中间)时,k 取最小值,即
(11)
将式(11)代入式(7)和式(8),即可得到混凝土层横桥向最不利变形和受力情况。
2 组合桥面足尺模型试验
2.1 试验设计与变形测量
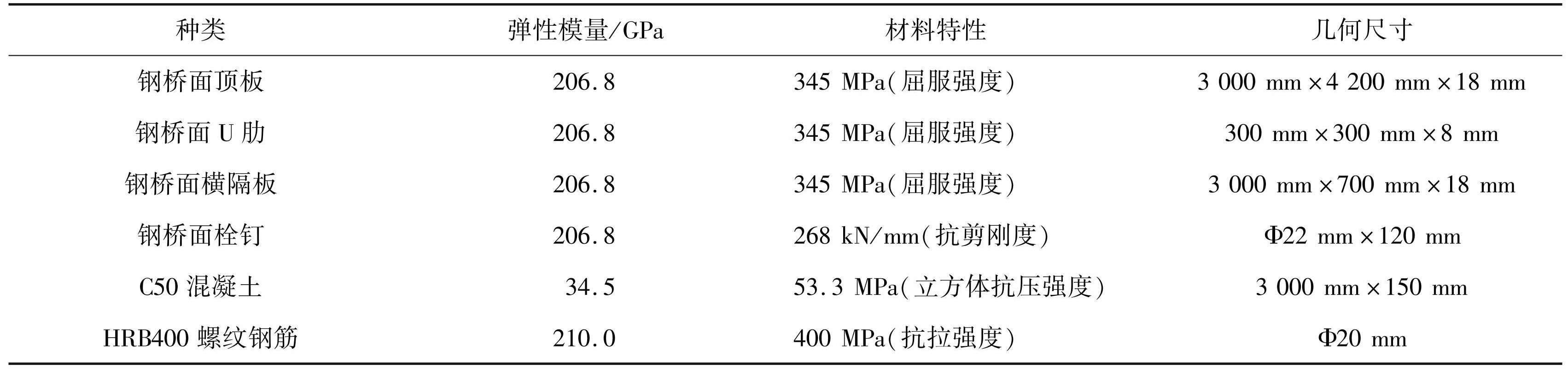
依据实桥构造设计[16] 和中国公路钢桥设计规范[23],设计和实施了整体尺寸为 4.2 m × 3 m × 0.7 m的正交异性钢-混组合桥面板足尺模型静力试验,如图4所示,具体材料和几何参数见表1。试验模型为间距 2 m 横隔板横向加劲,U 肋纵向加劲,上铺 150 mm 厚 C50 混凝土层的组合桥面构造。钢材为 Q345qE,混凝土层内铺设有直径 20 mm、纵横向间距 150 mm、竖向间距 100 mm 的 HRB400 钢筋组成的双层钢筋网。钢混界面上剪力钉纵横向间距均为 300 mm,通过推出试验[24] 获得的抗剪刚度为 268 kN/ mm。在跨中横隔板处正上方中部通过 MTS 作动器进行分级加载,加载垫块为( 300 mm × 300 mm)厚 30 cm 的弹性橡胶垫,施加荷载最大值 P 为100 kN。模型端部两道横隔板两端各设置一个面积为 200 mm × 300 mm 的支撑,共 4 个支撑。
图4足尺试验模型
Fig.4Full-scale test setup
表1试件材料性能
Tab.1 properties of specimen
为全面测量轮载下桥面变形情况,纵桥向上分别在 3 道横隔板处(截面 H1、H2 和 H3),跨中横隔板左右各 0.5 m 处( 截面 C1 和 C2),设置精度 0. 001 mm的电子位移计,如图5所示。横桥向上每个 U 肋底部布置两测点测量其扭转情况,U 肋中间的顶板中间布置一个测点,每个横截面共计 14 个测点。试验过程中还对混凝土层与钢顶板之间的滑移进行了监测,结果发现界面滑移很小,可忽略不计。
2.2 有限元模型
根据图4(a)和表1中的几何和力学参数,基于大型软件 ANSYS 17. 0 建立正交异性钢混组合桥面足尺模型的空间有限元模型,如图6所示。考虑到轮载值不大,模型结构处于线弹性状态,混凝土不会开裂,钢混界面不产生摩擦滑移(钢混界面摩擦系数取 0),配筋率不影响混凝土弹性量,故为简化模型忽略这些影响因素。钢结构和混凝土均采用线弹性、各向同性单元模拟,分别为 SHELL 63(泊松比取 0.3)及 SOLID 65(泊松比取 0.2)单元; 栓钉采用弹簧单元 COMBIN 14 模拟。基于多点约束法(MPC)模拟钢混界面的滑移变形,其中接触对采用 CONTA 175 和 TARGE 170 单元,约束设置为具有平移自由度,无转动自由度。为保证计算精度,采用试错法确定网格划分尺寸: U 肋为 5 mm,其他钢构造为 10 mm,混凝土层为 25 mm。按照模型与支座间的接触面积进行约束,在桥面施加均布面荷载。
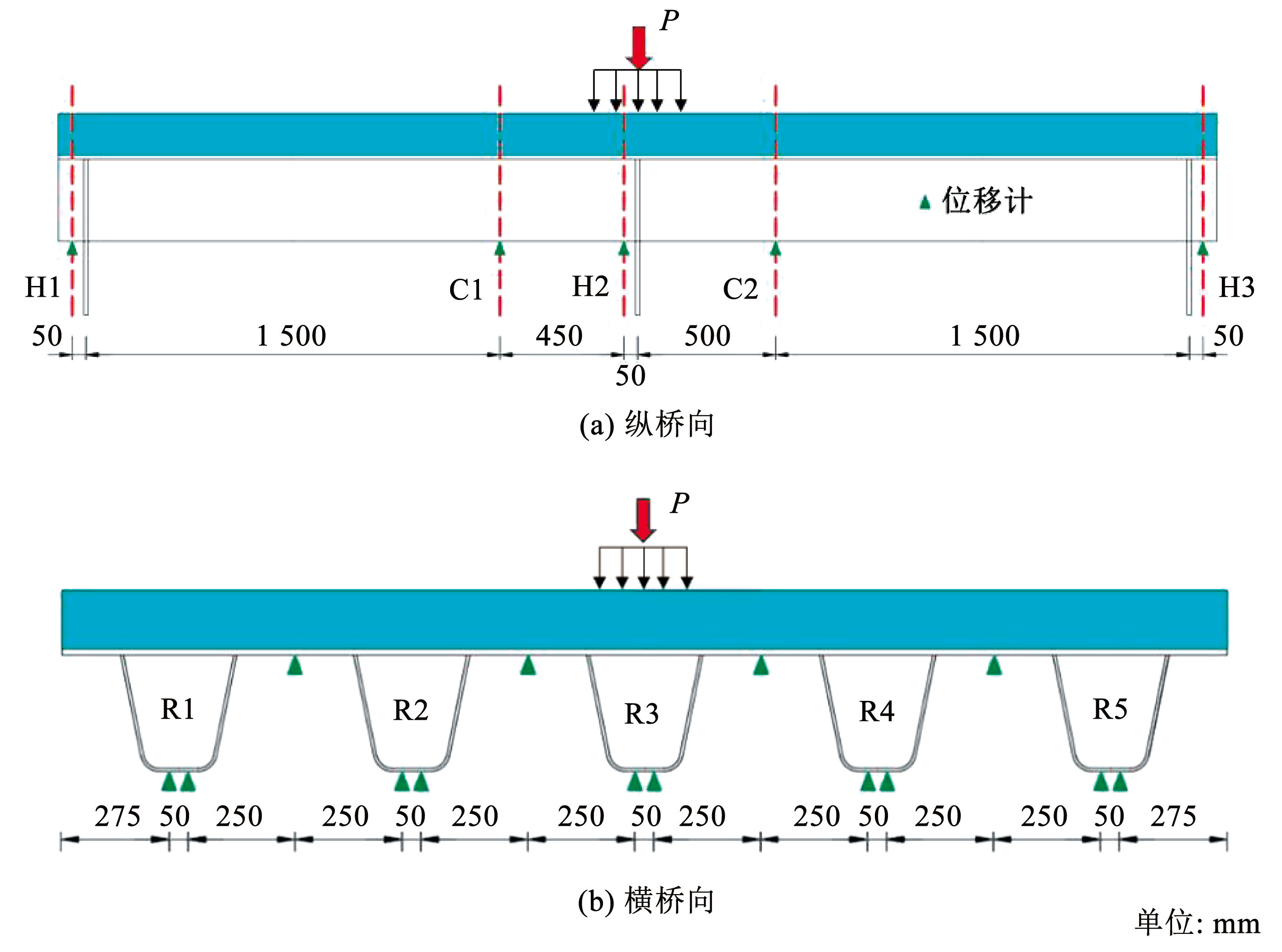
图5位移测点布置
Fig.5Displacement measurement

图6有限元模型
Fig.6FE model
2.3 混凝土层局部变形分析
图7(a)对比分析了 100 kN 轮载作用下混凝土层沿横桥向的竖向位移(挠度)分布的实测值、有限元值和理论值(η = 0.8)。由于式(7)不考虑钢混界面的剪力钉,最大挠度理论值比相应试验值稍大,两者差异在 5% 以内,由于挠度实测值较小,位移计测试误差影响较大,沿横桥向挠度分布的实测值与理论值及有限元值吻合良好,表明所提出的理论模型和有限元模型可合理反映轮载下混凝土层横桥向受力行为。图7(b)为跨中 C1(无横隔板)和 H2(有横隔板处)两个截面的横桥向挠度值,两个 U 肋(R3 和 R4)底部位移测点的挠度差约为 0. 02 mm,说明横隔板和刚性混凝土层约束了 U 肋扭转,轮载下扭转变形很小,可忽略不计。
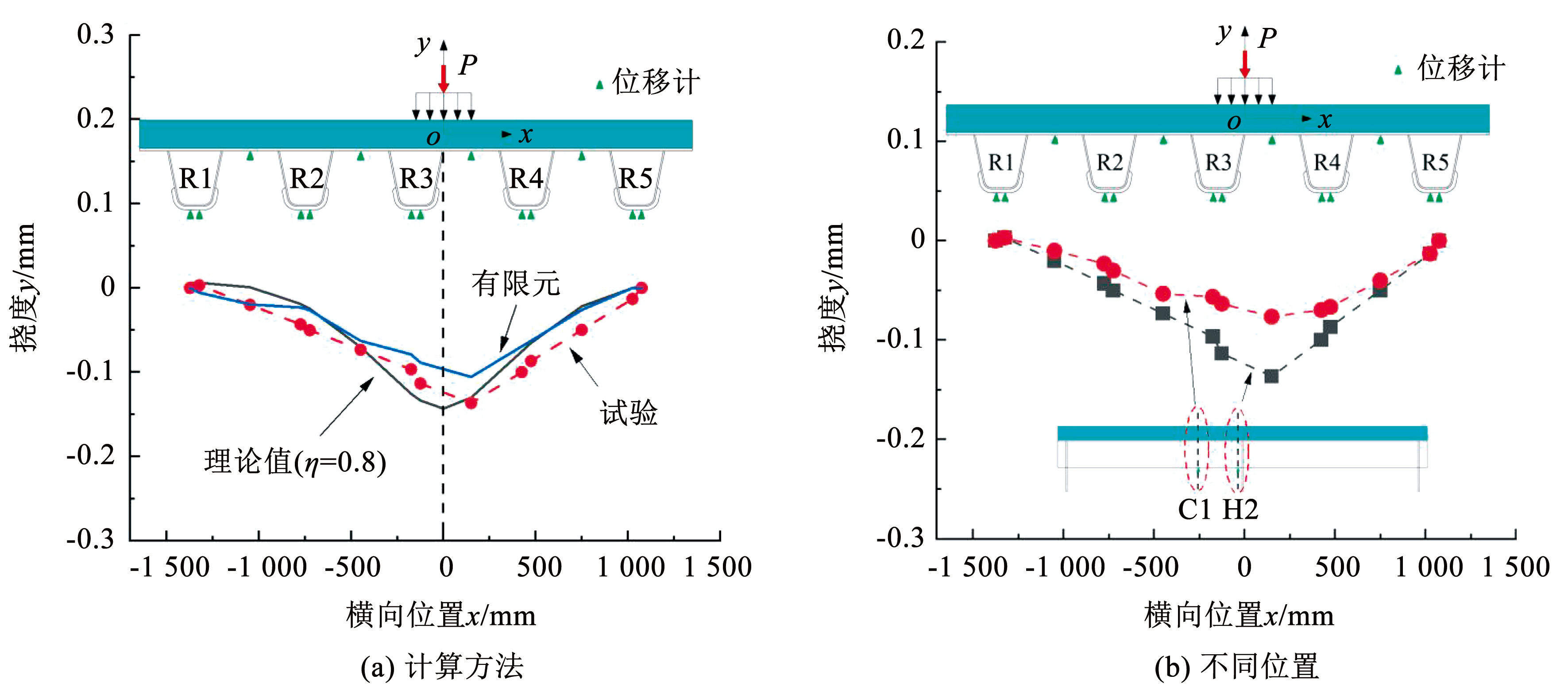
图7混凝土层横桥向挠度分布比较
Fig.7Transverse displacement curves of concrete overlay
在试验模型的设计参数取值条件下,根据式(10)确定不同的混凝土层厚度(30~200 mm)时轮载(集中力)两侧的有效作用范围与 U 肋间距的比值为 2S / d,如图8所示,在混凝土厚度不超过 200 mm时,轮载横桥向有效作用范围不超过 5 个 U 肋中心距范围,因此试验模型几何尺寸可以包含轮载的横桥向作用范围。

图8轮载的横桥向有效作用范围确定
Fig.8Effective loading range along transverse bridge direction
3 参数分析
为分析轮载分布、剪力钉和边界条件对混凝土层横向受力行为的影响,拓展上述足尺试验模型的有限元模型进行参数分析,采用混凝土层横桥向挠度分布的变化来表征影响效应。为尽可能模拟实桥条件下混凝土层横桥向变形行为,在其他参数不变情况下,将试验模型(单跨)增加到含四道横隔板的三跨正交异性钢-混组合桥面构造,如图9所示。根据上述实际桥面构造和中国公路钢桥规范[21] 确定钢桥面板各项设计参数取值,混凝土强度等级为 C50。轮载仍为100 kN,加载面积为300 mm ×300 mm。采用三跨有限元模型进行参数分析时,研究参数在取值范围内变化,而其余设计参数取自上述试验模型。
图9多跨有限元分析模型
Fig.9FE model for multiple-span specimen
3.1 横隔板
横隔板约束 U 肋的扭转变形,增加了钢桥面横向刚度,对混凝土层横桥向挠度分布有影响,图10分析了轮载正下方有无横隔板两种情况下的混凝土层横桥向挠度分布,结果表明横隔板的影响很显著,无横隔板情况下的挠度是有横隔板的 3 倍。因此混凝土层横桥向挠度最大处为两道横隔板中间位置,该处也是其横桥向受力的最不利位置。

图10横隔板的影响
Fig.10Effect of crossbeam
3.2 剪力钉布置
为考虑钢混界面剪力钉的摩阻效应,选取 3 种栓钉布置间距:150 mm × 150 mm,300 mm × 300 mm,450 mm × 450 mm,及 3 种不同抗剪刚度进行对比分析,如图11所示。当间距从 150 mm × 150 mm 增加到 450 mm × 450 mm 后,U 肋 R3 处挠度增加约 50%,钢混界面剪力钉布置越多,其对混凝土层的挠度和受力消减作用越大,对混凝土层受力越有利。当抗剪刚度由 74 kN/ mm 增加到 401 kN/ mm,U 肋 R3 处挠度降低了约 30%。本文提出的理论模型未考虑剪力钉对混凝土层变形和受力的有利作用,偏于保守,后续可参考文献[25]和进行更大比例尺多跨模型试验,考虑摩阻效应来完善弹性地基梁比拟模型。
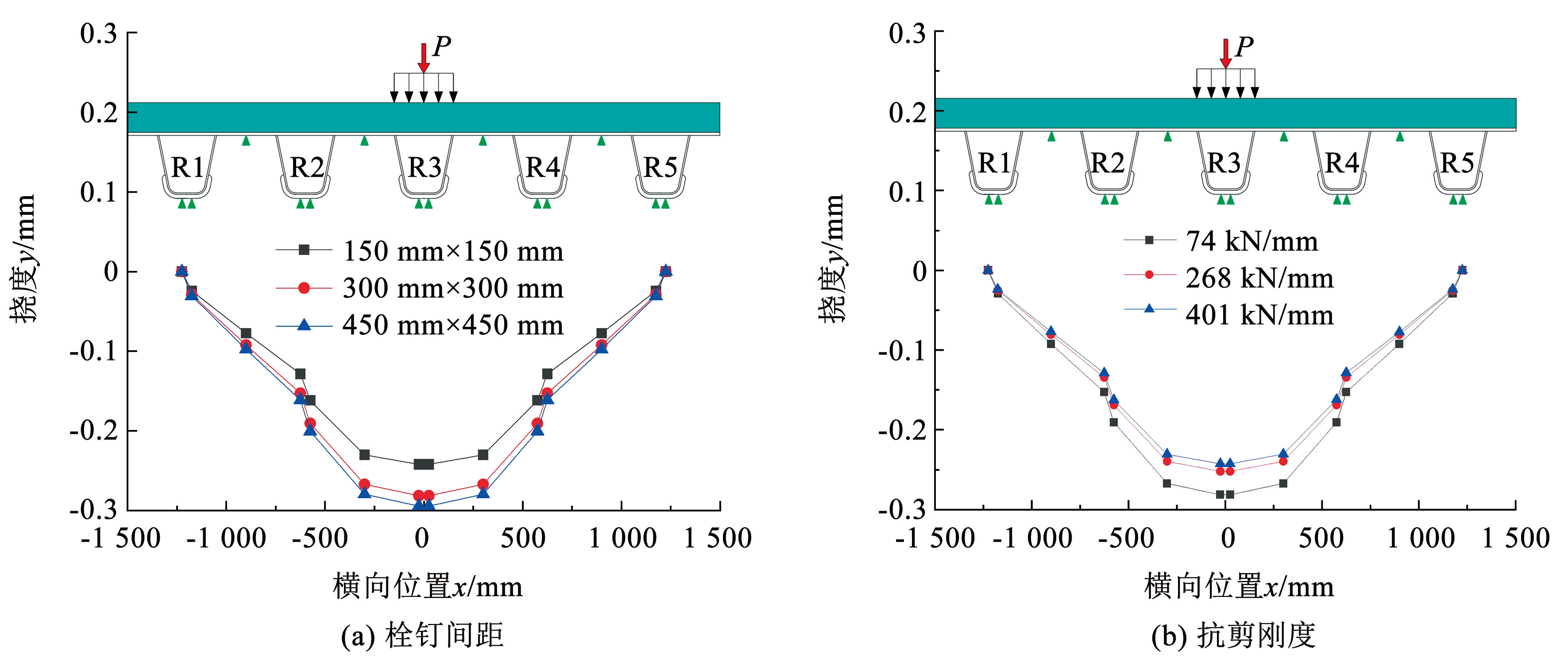
图11剪力钉的影响
Fig.11Effect of shear connector
3.3 轮载分布及横向加载位置
为考虑轮载分布及加载位置的影响,选取两种典型轮载分布尺寸:300 mm × 300 mm(试验模型)和 600 mm × 200 mm(规范建议)进行对比分析,如图12(a)所示。轮载均为 100 kN 情况下,轮载分布面积越大,混凝土层变形较小,但所研究的两种轮载分布下最大挠度差不到 0. 01 mm,可见轮载分布影响很小。图12( b)为相同轮载分布( 300 mm × 300 mm)、不同加载位置条件混凝土层横向上挠度分布。 3 种典型加载位置条件下(U 肋中心和偏心加载,肋间中心加载),混凝土层最大挠度基本相同,只是分布有少许差异,原因是轮载偏心加载引起的一定程度的 U 肋扭转。考虑到轮载值不大,横隔板及刚性混凝土层对 U 肋的约束很强,挠度差异不大。
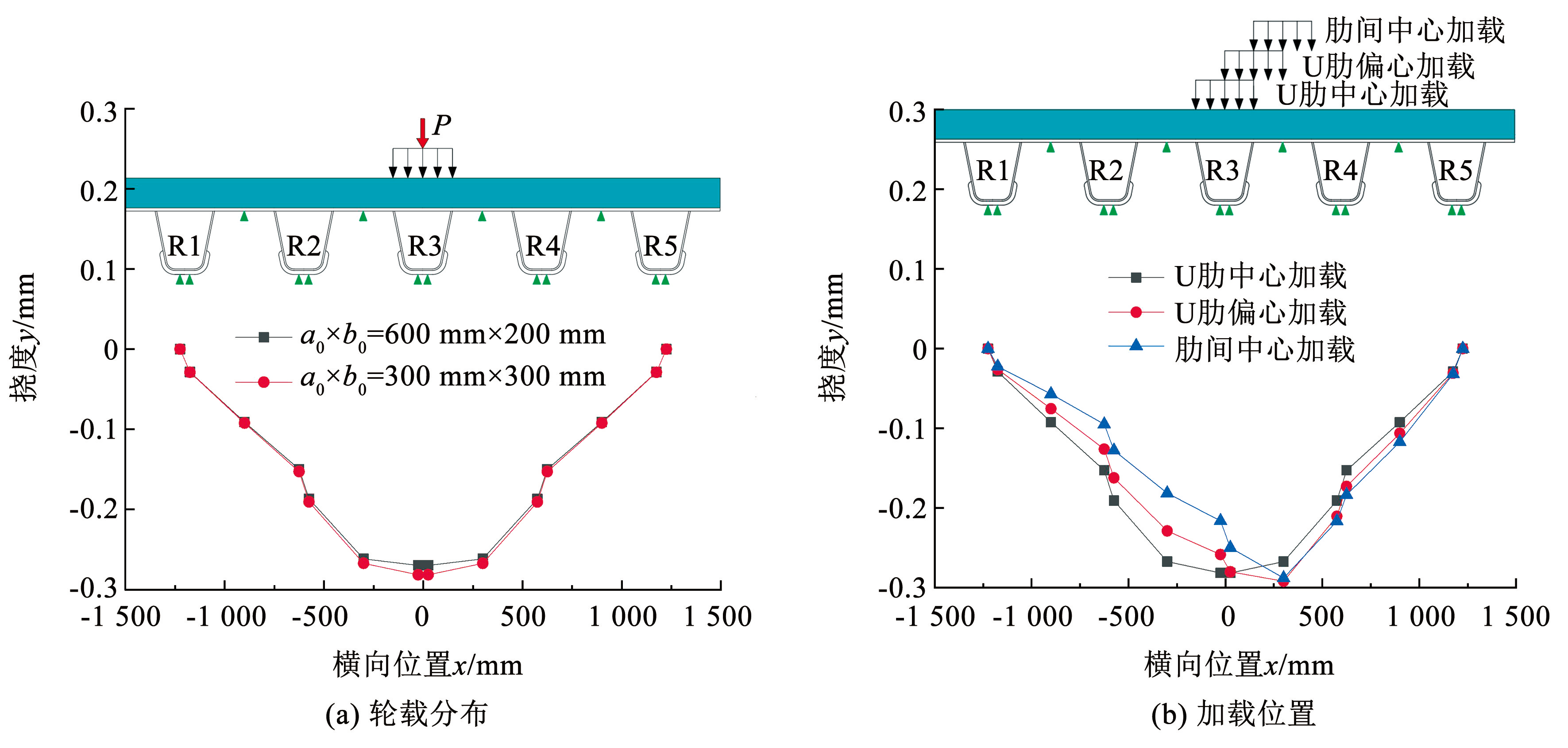
图12轮载分布及加载位置的影响
Fig.12Effect of wheel-loading distribution and position
4 结论
通过对轮载下正交异性钢-混组合桥面板混凝土层横桥向的弹性变形和受力行为的理论分析和试验研究,得出如下结论:
1)基于弹性地基梁比拟方法提出了正交异性钢-混组合桥面板混凝土层轮载横向受力响应模型,经与相应足尺模型试验结果对比表明:混凝土层横桥向挠度分布理论值略大于试验值和有限元值,挠度修正系数可取 0.8,可简便计算轮载下混凝土层横桥向力学响应,为钢-混组合桥面板设计和计算提供理论支撑。
2)轮载在混凝土层板内产生的最大横桥向挠度出现在两道横隔板正中间,是混凝土层受力最不利部位。横隔板和刚性混凝土铺装层有效约束了 U 肋扭转,偏载下 U 肋扭转变形可忽略不计。轮载横桥向有效作用范围不超过 5 个 U 肋中心距。
3)参数分析表明,混凝土层变形随横隔板间距增大而增大,但随剪力钉布置加密和抗剪刚度增加而减小。由于横隔板和刚性混凝土铺装层对 U 肋扭转的强大约束,混凝土层变形对轮载分布及加载位置的变化不敏感。

