摘要
为解决快速路合流区的交通拥堵和安全问题,保障智能网联车辆(connected and automated vehicle,CAV)在快速路合流区高效、安全、舒适、稳定地行驶,采用深度强化学习方法之 DQN(deep q-network)算法,综合考虑车辆行驶安全性、高效性与舒适性等因素,建立了用于神经网络训练的奖励函数模型,提出了快速路合流区 CAV 换道决策方法。应用开源自动驾驶仿真场景 highway-env,搭建快速路合流区仿真环境,对其主线路段及匝道进行仿真试验。仿真试验结果表明:相比于智能驾驶人模型(intelligent driver model,IDM)和 highway-env 中换道决策方法,采用所提出的快速路合流区 CAV 换道决策方法时,CAV 能够快速达到 22. 22 m/ s 行驶的稳定状态,同时避免频繁换道及加减速行为,并优化了车头时距,很大程度上提高了交通流运行效率和乘车舒适性。研究成果在智能交通领域中,可为智能网联环境下城市快速路合流区的车辆通行提供了一种新方法,为未来智能网联车辆的换道提供了决策方法。
Abstract
In order to tackle traffic congestion and safety issues in expressway merging areas and to ensure efficient, safe, comfortable, and stable travel of connected and automated vehicles ( CAVs) in these areas, this study employs the DQN ( deep q-network) algorithm from deep reinforcement learning. By considering factors such as vehicle safety, efficiency, and comfort, a reward function model for neural network training has been established, and a CAV lane-change decision-making method for merging areas has been proposed. Using the open-source highway-env simulation scenario, a simulation environment for expressway merging areas has been set up, and experiments have been conducted on the mainline and ramps. The results of the simulation experiments show that compared to the intelligent driver model (IDM) and the lane-change decision-making method in highway-env, the proposed CAV lane-change decision-making method enables CAVs to quickly reach a stable driving state at a speed of 22. 22 m / s. It also reduces frequent lane changes and acceleration / deceleration behaviors, and optimizes the time-headway between vehicles. This significantly improves the efficiency of traffic flow and ride comfort. The research findings provide a new method for vehicle traffic management in urban expressway merging areas under intelligent networked conditions. They also offer a decision-making approach for lane changes in future connected and automated vehicles.
随着机动车拥有量的不断提升,城市交通拥堵日益严重,为了解决这一问题,人们以高速公路的建设理念在城市中打造立体交通,从而建设了城市快速路[1]。但城市机动车保有量的进一步增长造成了城市快速路流量的急剧增加,主线车流与匝道车流形成的交通冲突问题,使合流区经常发生交通拥堵状况,交通流运行风险随之提高[2]。智能网联车辆的发展对于解决城市快速路合流区交通安全、拥堵问题有着巨大的影响。且在 CAV 的发展阶段中,深度强化学习( deep reinforcement learning,DRL)领域的进步极大推动了自动驾驶决策技术的发展[3]。因此,本文将利用深度强化学习方法建立快速路合流区 CAV 换道决策方法,为进一步解决快速路合流区的交通拥堵问题提供新的方法和思路。
彭浩楠等[4]利用逆强化学习方法,实现神经网络对最优轨迹规划的学习。朱冰等[5] 通过实际测量驾驶数据的方式,针对车辆纵向行为对神经网络进行训练。高振海等[6] 采用实际驾驶数据训练逆强化学习算法模仿驾驶员的行为。以上研究都显示了机器学习和逆强化学习在自动驾驶车辆轨迹规划和行为模仿中的应用潜力。
李伟东等[7] 提出结合决策层和控制层的双层强化学习模型训练神经网络以提高算法的计算效率。刘卫国等[8] 通过分布式训练的方法提升系统的计算速度。 Wang 等[9] 通过在多个驾驶演示数据集上并行异步执行多个监督学习过程提高强化学习训练阶段的初始性能和收敛速度。宋晓琳等[10] 结合模仿学习与强化学习构建智能车辆换道策略提升决策速度。以上研究都体现了在智能车辆领域,如何通过不同的方法和技术提高强化学习算法的效率和性能,提高其在实际道路环境中的适应性和安全性。
张志勇等[11] 改进双延迟深度确定性策略梯度算法提高 Q 值的估计精度,以提高并道决策的准确性。杨顺等[12]通过对多种特征数据进行卷积的方式训练神经网络,提高自动驾驶车辆运行速度和偏移控制效果。张雪峰等[13] 提出双决斗深度 Q 网络强化学习模型对神经网络进行训练来进行智能网联车辆换道决策。谷梦路等[14] 提出一种结合随机森林算法和深度 Q 网络算法的 ICV 汇入控制模型,提高 ICV 在与高速公路主线上的传统人工驾驶车辆交互时的汇入效率和成功率。姚福星等[15] 提出一种基于混合专家模型的智能网联汽车换道决策方法,实现连续控制、高安全、高可靠的自适应高速换道。以上研究都表明了深度强化学习算法的改进和应用对于提升自动驾驶和智能网联车辆的决策能力具有重要作用。通过精确的 Q 值估计、高效的特征提取和稳定的决策机制,可以显著提高车辆的自主驾驶性能。
张羽翔等[16]采用强化学习方法学习决策参数,在奖励函数中考虑了安全性、当前驾驶员的意愿和平均人类驾驶风格。这项研究表明,强化学习可以为自动驾驶车辆提供一种有效的决策学习框架,尤其是在需要综合考虑多种因素时。通过设计的奖励函数,可以在不牺牲安全性的前提下,使自动驾驶车辆的行为更加符合人类的期望和习惯。
综上所述,在智能网联车辆的研究领域,尤其是针对城市快速路合流区的行驶策略,尽管已有一些研究运用深度强化学习方法[17-19],但主要聚焦于车辆行驶效率及安全性等方面,少有研究考虑驾驶过程中的稳定性及乘客舒适性等因素。
本文采用了 DQN 算法[20],并对其奖励函数进行了创新性的改进。在设计奖励函数时,本文不仅关注于提升车辆的期望速度,以确保在城市快速路上的高效通行,同时也将行驶安全性和乘客乘车舒适性纳入考量。通过这种多维度的奖励设计,本文旨在实现一个综合性的优化目标:在确保车辆快速通过路段的同时,兼顾行车安全和乘客的良好乘车体验。
1 CAV 换道决策方法
1.1 换道决策场景及研究对象
本文研究场景为城市快速路合流区,行驶车辆包括目标 CAV 和环境车辆,如图1所示。 CAV 能与道路传感通信控制设施(即路侧单元,road side unit,RSU)网联通信,并受其控制,而环境车辆则由路侧单元通过传感器雷达等监测其行驶信息。在此场景下,当目标 CAV 位于匝道时,需结合车辆的行驶安全、速度和加速度,考虑并入主线的最佳时机; 当目标 CAV 位于主线时,会受到匝道车辆并入行为和其他主线车辆行驶状态的影响。因此,本文将基于马尔科夫性,设置深度强化学习的奖励函数,以保障目标 CAV 在合流区中不同类型道路上行驶时的安全、高速和稳定。
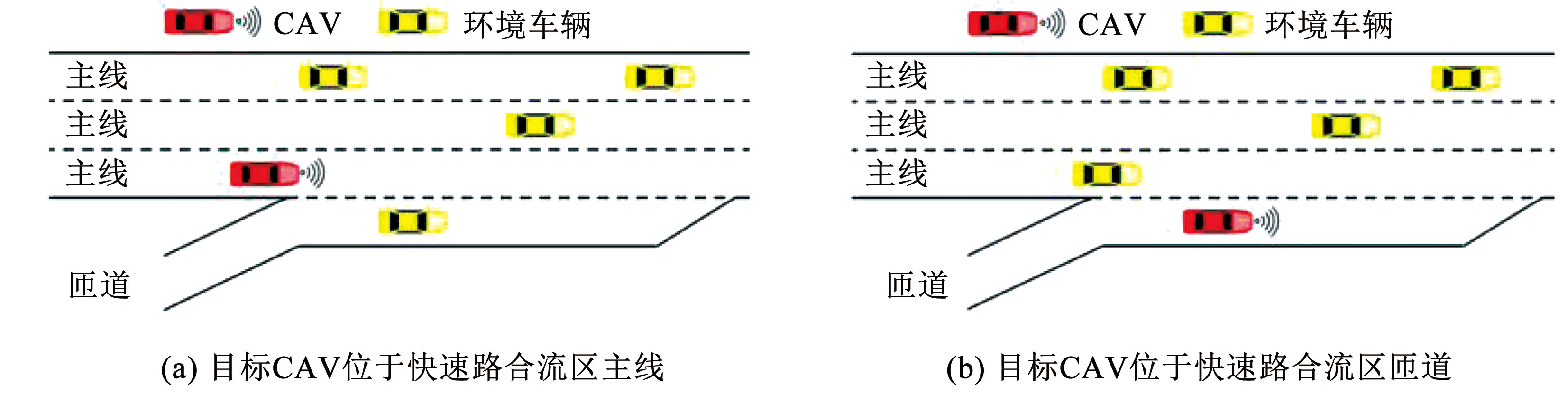
图1快速路合流区
Fig.1Merging area of expressway
1.2 换道决策思路与流程
本文针对 CAV 换道决策过程主要考虑目标 CAV 位于快速路合流区主线和匝道两个场景。目标车辆(主车)首先判断处于哪种行驶环境。若为快速路合流区主线,则进一步判断前方车辆是否处于影响自身保持原车道行驶的范围内,此影响范围通过比较目标车辆以期望速度在期望超车总时间 18 s [21]内的行驶距离是否大于前车在此段时间的行驶距离,若小于则前车处于影响范围内,反之前车则不处于影响范围内。若前车未在影响范围内,目标车辆继续保持原车道行驶; 若在影响范围内,目标车辆继续判断前方车辆的速度是否大于自身速度,若前车速度大于主车速度,则目标车辆保持原车道行驶; 反之,目标车辆进入换道判断阶段。首先由最小安全距离计算模型[22] 判断换道是否安全,若不安全,则放弃换道,减速跟随前方车辆; 若安全,进一步通过对比奖励值决定换道方向,最终完成换道。以此方式往复循环,直至主车到达目的地。若为快速路合流区匝道,本文只考虑合流区入口。目标车辆到达合流区起点时开始判断换道是否安全,若不安全,则继续保持原车道行驶,此情况下,如果目标车辆到达合流区终点,则以“先到先服务”的原则进行强制换道,即在主线后车与合流区终点的间距满足最小安全距离、可以安全实现减速或停车让行的情况下,目标车辆忽略速度、乘车舒适度等因素采取换道行为并入主线,避免造成匝道的排队拥堵情况; 若安全,则通过对比奖励值判断最佳的换道时机,完成换道,进入快速路合流区主线。换道决策流程如图2所示。

图2快速路合流区智能网联车辆换道决策流程
Fig.2Lane change decision-making process of intelligent networked vehicles in expressway merging area
2 基于马尔科夫过程的奖励函数
2.1 奖励函数构建
马尔科夫决策过程(Markov decision processes,MDPs)[23-24]作为强化学习的数学基础,通常由状态空间、动作空间、状态转移矩阵、奖励函数以及折扣因子等组成。本文通过马尔科夫决策过程建立奖励函数,并通过训练神经网络确定折扣因子。最终利用 DQN 算法评估最优动作价值,即 CAV 在快速路合流区行驶的最优决策。
在马尔科夫过程的基础上增加奖励函数 R 和衰减系数 γ,表示为( S,P,R,γ)。 R 是一个奖励函数,S 状态下的奖励是某一时刻(t)处在状态 s 的下一个时刻(t + 1)能获得的奖励期望,具体形式为
(2)
基于此,从 t 时刻开始所得到的折扣回报总和为
(3)
式中折扣因子 γ 代表了对未来奖励的折扣。 γ 越大,代表更重视未来奖励; 相反,γ 越小,则更重视近期奖励。
在城市快速路场景中,智能网联车辆(目标车辆)在不同的道路环境,即状态 si下将选择不同的驾驶行为 ai,每个驾驶行为得到相应的奖励或惩罚 ri,使得目标车辆进入下一个状态 si + 1 ,以此循环往复得到最优的驾驶决策,流程如图3所示。其中,状态 si∈S,行为 ai∈A,奖励 ri∈R。
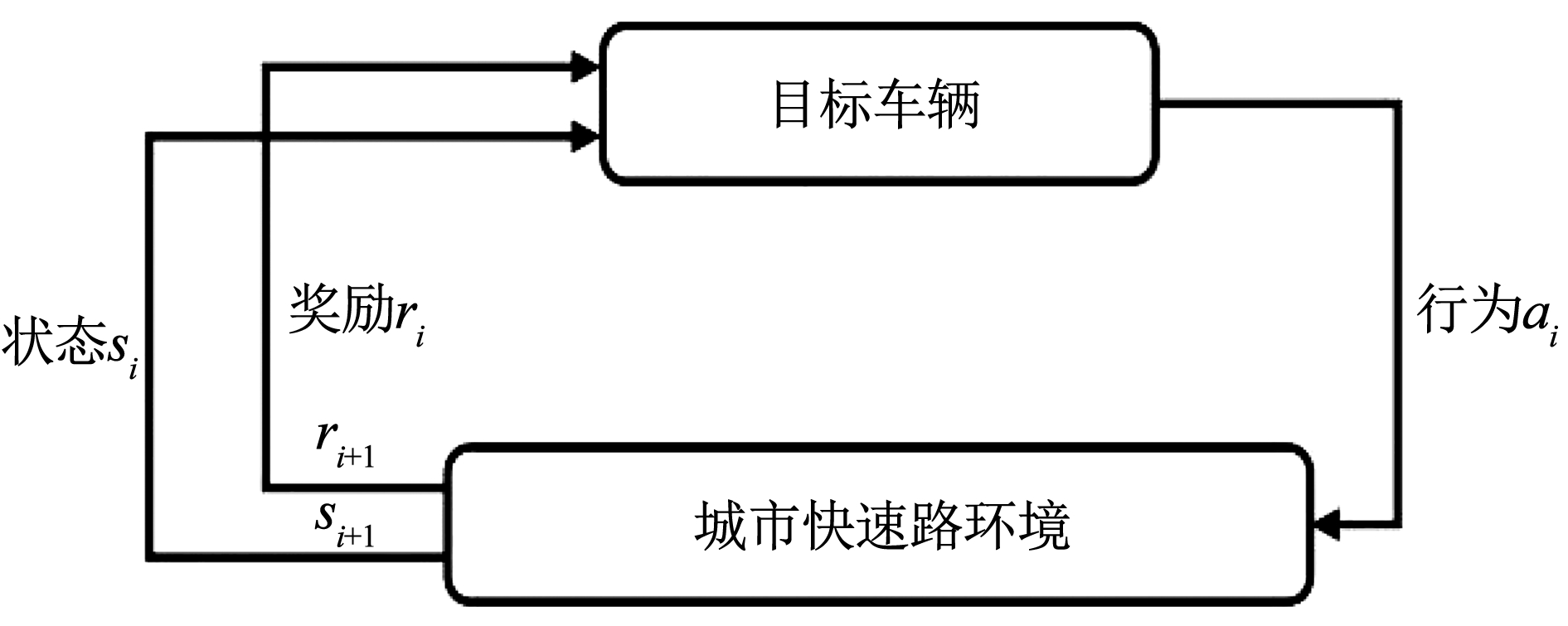
图3智能网联车辆强化学习流程
Fig.3Reinforcement learning process for connected and automated vehicles
2.1.1 快速路合流区主线的奖励函数设计
当目标车辆位于快速路合流区的主线时,其在行驶过程中的主要需求为更短的通行时间、更舒适的乘坐体验和更安全的驾驶行为。因此,在奖励值的计算中,本文主要考虑以下 4 个方面的奖励。
1)速度奖励 Rv。当目标车道前车在影响主车的距离范围内时,主车速度 vMV与目标车道前车的速度 vFV之比。考虑目标车辆可能在换道期间与前车发生追尾事故,通过最小安全距离模型计算换道安全距离,若不满足换道安全条件,则速度奖励的折扣因子为 0,目标车辆将放弃追求更高的车速,保持安全条件下的跟驰行为:
(4)
2)可接受减速度奖励(针对前车)Rb1。当目标车道前车在影响主车的距离范围内时,主车可接受减速度 bMV与目标车道前车减速度 bFV之比:
(5)
3)可接受减速度奖励(针对后车)Rb2。当目标车道后车在影响主车的距离范围内时,主车可接受减速度 bMV与目标车道后车减速度 bLV之比:
(6)
4)安全距离奖励 Rd。换道临界间隙 sCG与行驶安全距离 ssafe之比:
(7)
Rv值越高,代表车辆的换道行为将会获得更高的行驶速度; Rb1和 Rb2值越高,代表车辆的换道行为对于乘客来说更加舒适; Rd值越高,代表车辆的换道行为更安全。综上,奖励函数从速度、安全以及舒适性三方面综合考虑车辆换道行为产生的影响。
Rb1和 Rb2的计算方法是利用 SITRAS 模型[25] 判断是否可以换道,分为两个条件:1)主车跟随目标车道前车的减(加)速度是否大于主车可接受的减速度; 2)目标车道后车跟随主车时的减速度是否大于目标车道后车可接受的减速度。减速度计算公式为
(8)
式中:bn为车辆 n 在 t 时刻可接受的减速度,D 为预定的转向或障碍物的位置,xn为车辆 n 在 t 时刻的位置,vn为车辆 n 的期望速度,bLC为车辆愿意接受的减速度的平均值,θ 为司机的风险系数。
目标车辆行驶决策的奖励具体形式为
(9)
式中:折扣因子 λ 代表了对不同奖励的折扣,用以平衡各奖励之间的相互影响。其中 λv为速度奖励折扣因子,λb1为可接受减速度奖励(针对前车)折扣因子,λb2为可接受减速度奖励(针对后车)折扣因子,λd为安全距离奖励折扣因子。
为保障交通流安全,便于神经网络进行计算,设置偏置项 w1作为车辆发生碰撞的惩罚; 设置偏置项 w2作为车辆频繁换道的惩罚来保障乘客乘车的舒适性; 设置偏置项 w3作为车辆出界的惩罚。则奖惩机制下的神经网络计算函数具体形式为
(10)
2.1.2 快速路合流区匝道的奖励函数设计
当目标车辆处于快速路匝道时,车辆在到达换道终止点前必须完成换道,否则匝道将产生排队拥堵现象。因此,在快速路合流区环境中,匝道上的车辆换道时无需考虑主车速度与目标车道前车速度之间的关系,则 t 时刻所得到的奖励具体形式为
(11)
因为匝道处车辆行驶入主路仅需进行一次换道,所以无需考虑车辆的频繁换道行为,所以对于在合流区的匝道车辆,仅需设置偏置项 w1、w3,所以此环境下神经网络计算函数具体形式为
(12)
2.2 奖励函数参数设置
深度强化学习方法之深度 Q 网络(DQN)结合 Q 学习和深度神经网络,利用训练后的神经网络确定目标体在某一状态下执行动作的期望奖励。 DQN 算法的神经网络结构需要根据问题的性质进行设计,即需要通过调整学习率等参数来提高算法的学习效率。
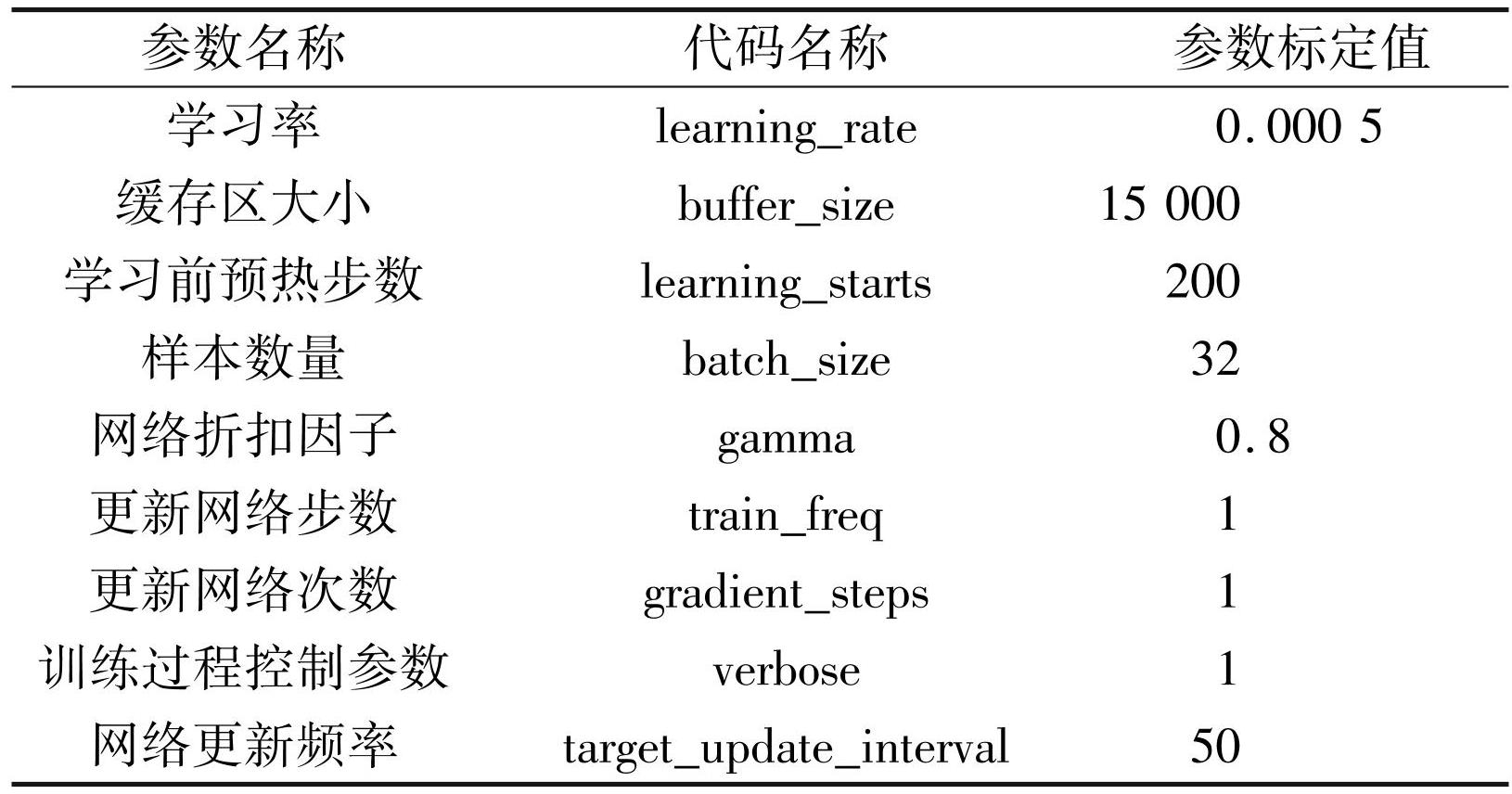
神经网络是一种模仿生物神经网络的结构和功能的数学模型,在本文用于对目标车辆的行为进行识别、预测和执行。参考文献[6-7],设置神经网络架构包含两个隐藏层,每个隐藏层有 256 个神经元,通过设置学习率控制权重更新的步长,设置经验回放缓冲区存储智能体的经验,设置折扣因子用于未来奖励的当前价值,设置 tensor board 用来监控训练过程。具体参数设定值见表1。
表1神经网络参数设置
Tab.1 Neural network parameter setting
折扣因子用于平衡神经网络中的各项奖励,确保模型在学习时不会只关注某一特定行为,形成适用多种情况的策略。奖励值的偏高或偏低都会导致目标车辆偏重某一方面而忽略其他,从而造成目标车辆运行过程中奖励值突变,即受到惩罚。本文设置不同数值的 5 组折扣因子,对比目标车辆运行期间其奖励值的变化情况如图4所示。
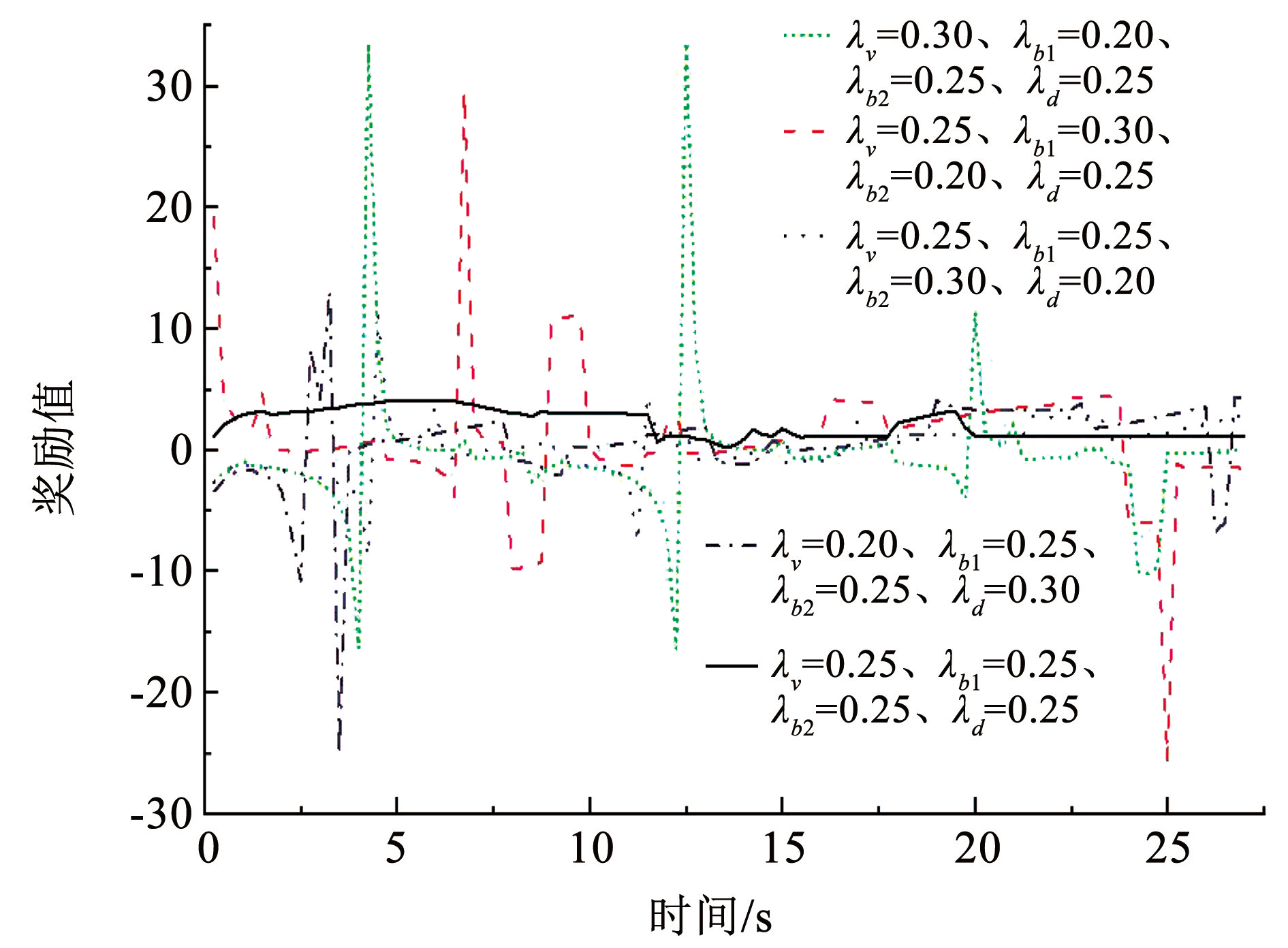
图4奖励值变化曲线
Fig.4Reward value change curve
可知,当各折扣因子均为 0.25 时,目标车辆在运行过程中所获的奖励值变化最为平稳,即在此条件下目标车辆可以平等地考虑每个驾驶行为,此时各项奖励均有效。因此确定各项奖励折扣因子 λi 取值见表2。
表2折扣因子设置
Tab.2 Discount factor setting

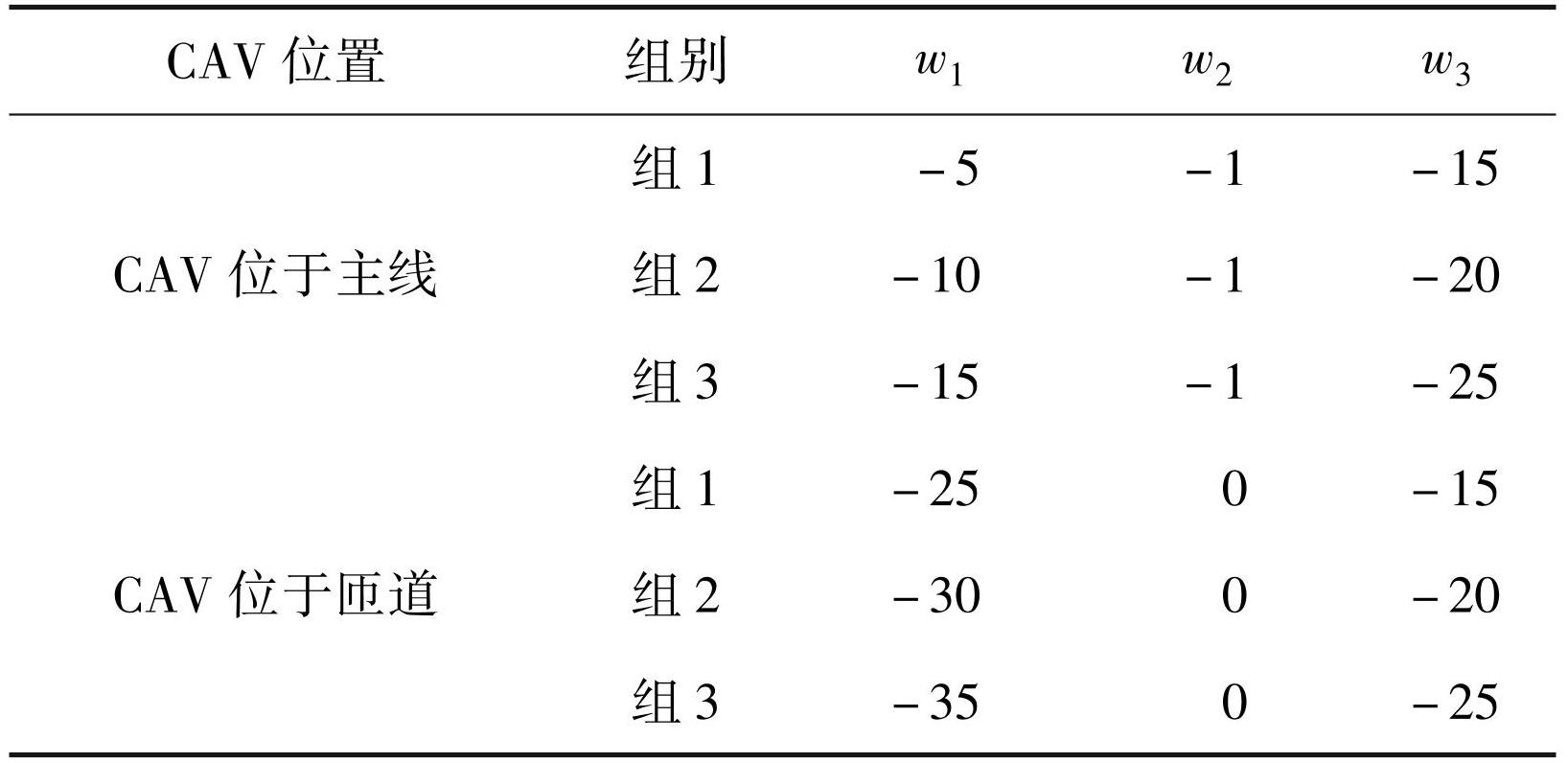
偏置项有助于神经网络模型更快收敛,提高计算效率,减少过拟合。目标车辆的表现受多种因素影响,需要通过训练和仿真测试来调整偏置项值,以明确任务目标,避免低效学习,并应对环境复杂性。因此,需要综合考量不同组 wi取值下完成有限的训练次数后目标车辆的平均碰撞发生率、平均车速和平均换道次数确定偏置项值。其中,碰撞发生率设为 1 × 10 6 组随机仿真试验中目标车辆发生碰撞的概率。各组偏置项取值见表3。其中,3 组的事故发生率分别为 24%、16%、13%,CAV 位于主线时的平均车速分别为 21.39、22.21、15. 07 m / s,CAV 位于匝道时的平均车速分别为17.48、18.32、15.51 m / s,CAV 位于主线时的平均换道次数分别为 3.1、2.6、 1.2,CAV 位于匝道时的平均换道次数均为 3。可见,组 2 的事故发生率较组 1 低 0. 08%,且在平均车速更高的同时换道次数更少,因此组 2 设置值优于组 1; 组 3 的事故发生率虽然较组 2 低 0. 03%,但因过度考虑车辆运行的稳定性而忽略了运行效率,因此大幅度降低了车速,且事故发生率相差不大,所以组 2 设置值优于组 3。最终选取组 2 设置值作为奖励函数的偏置项设置值。
表3偏置项设置
Tab.3 Offset item setting
3 CAV 换道决策方法验证
3.1 仿真环境搭建
为了验证本文 CAV 换道决策的可行性,依托Python 搭建仿真试验环境,考虑城市快速路的建设规范,以及车辆行驶时的不同环境,搭建快速路合流区。参考《城市快速路设计规程》 设置 3 条主线车道和 1 条匝道,合流区长度为 80 m,单车道宽度为 3.5 m,主线限速为 80 km / h,匝道限速为 40 km / h,试验车道总长度为510 m,试验部分匝道长度为150 m。
在上述设置条件下,依托 Python 搭建的城市快速路合流区仿真试验环境能够模拟不同的驾驶场景,其中目标 CAV 可能位于合流区的主线或匝道,如图5所示。图5( a)中,目标 CAV 位于合流区主线,图5(b)中,目标 CAV 位于合流区匝道的情况。除目标车辆外,环境中其他车辆均采用 IDM 模型[26]进行控制。此外,为简化研究,参考文献[27] 对车辆特征以及车辆跟驰模型的参数进行标定,车辆长度为 5 m,车辆宽度为 1.8 m,最大加速度为 1.4 m / s 2,最大减速度为 3 m / s 2,舒适减速度为 2 m / s 2,车辆间最小安全距离为 2 m,司机风险系数为 1。

图5快速路合流区仿真环境
Fig.5Simulation environment of expressway merging area
3.2 试验方案
在开源自动驾驶仿真场景 highway-env 中,原 DQN 算法配置的奖励函数主要侧重于 3 个关键目标:提升目标 CAV 的速度,尽量保持在最右侧车道行驶,并避免与其他车辆发生碰撞( 简称 VRL 策略)。而在改进的 DQN 算法中,奖励函数进一步考虑了提供舒适的减速度,并减少目标 CAV 的频繁换道和加减速行为,同时确保目标 CAV 与其他车辆之间保持安全的行驶距离(简称 VBSD 策略)。在这个仿真环境中,其他车辆采用智能驾驶模型进行模拟。
针对目标 CAV 在合流区的不同位置,设置了不同的起始速度范围:当目标 CAV 位于合流区主线时,其起始速度设置在 50~70 km / h 之间; 当目标 CAV 位于合流区匝道时,其起始速度设置在 20~40 km / h之间。此外,设定仿真环境中其他车辆的数量为 10 辆,且控制仿真环境的空间占有率在 10.78%。整个仿真的总时长设定为 50 s,在这段时间内持续记录仿真运行的数据。分别在以下 4 种场景训练神经网络模型:VRL 策略下,目标车辆位于快速路合流区主线和匝道的场景; VBSD 策略下,目标车辆位于快速路合流区主线和匝道的场景。每种场景迭代 1 × 10 8 个回合,每个回合起始于目标 CAV 进入试验路段起点,终止于目标 CAV 到达试验路段终点,完成所有迭代后将获得适应不同策略的神经网络模型。
在模型训练完成后,进行仿真模拟。在奖励函数设计中设置了速度奖励、可接受减速度奖励、安全距离奖励以控制 CAV 更高速且平稳地行驶,因此在仿真试验中收集目标车辆和环境车辆的行驶速度、加速度、与前车的车头时距数据,以及仿真过程中的换道次数。通过这些数据,可以对不同策略下的神经网络模型进行对比分析,从而评估 VRL 和 VBSD 策略在实际仿真环境中的表现效果,验证本文所设计奖励函数的可行性。
3.3 主线仿真结果分析
3.3.1 车速和加速度对比分析
为避免数据集偏差,神经网络训练完成后分别进行了 4 组速度和加速度的随机场景仿真试验。通过不同的交通环境和条件来检验模型的泛化和性能一致性,确保结论的可靠性。试验结果如图6和图7所示。
对试验数据进行分析,在采用 VBSD 策略的情况下,目标车辆在 4 种不同的场景中能够在仿真开始后的 11、13、11、11 s 时达到 22.22 m / s 的速度,并在此速度水平上保持稳定行驶。与此同时,加速度在这些场景中均保持在 0 值附近的小幅波动。相比之下,VRL 策略下的目标车辆在仿真开始后的 46、 27、27、32 s 时速度达到 22.22 m / s,但在此期间存在超速行为,表明神经网络模型对车辆行驶的控制出现了问题。在 VRL 策略中,尽管目标车辆的加速度在某些时段保持稳定,但经常出现急剧增加或减少的情况,这可能导致乘客体验不佳。
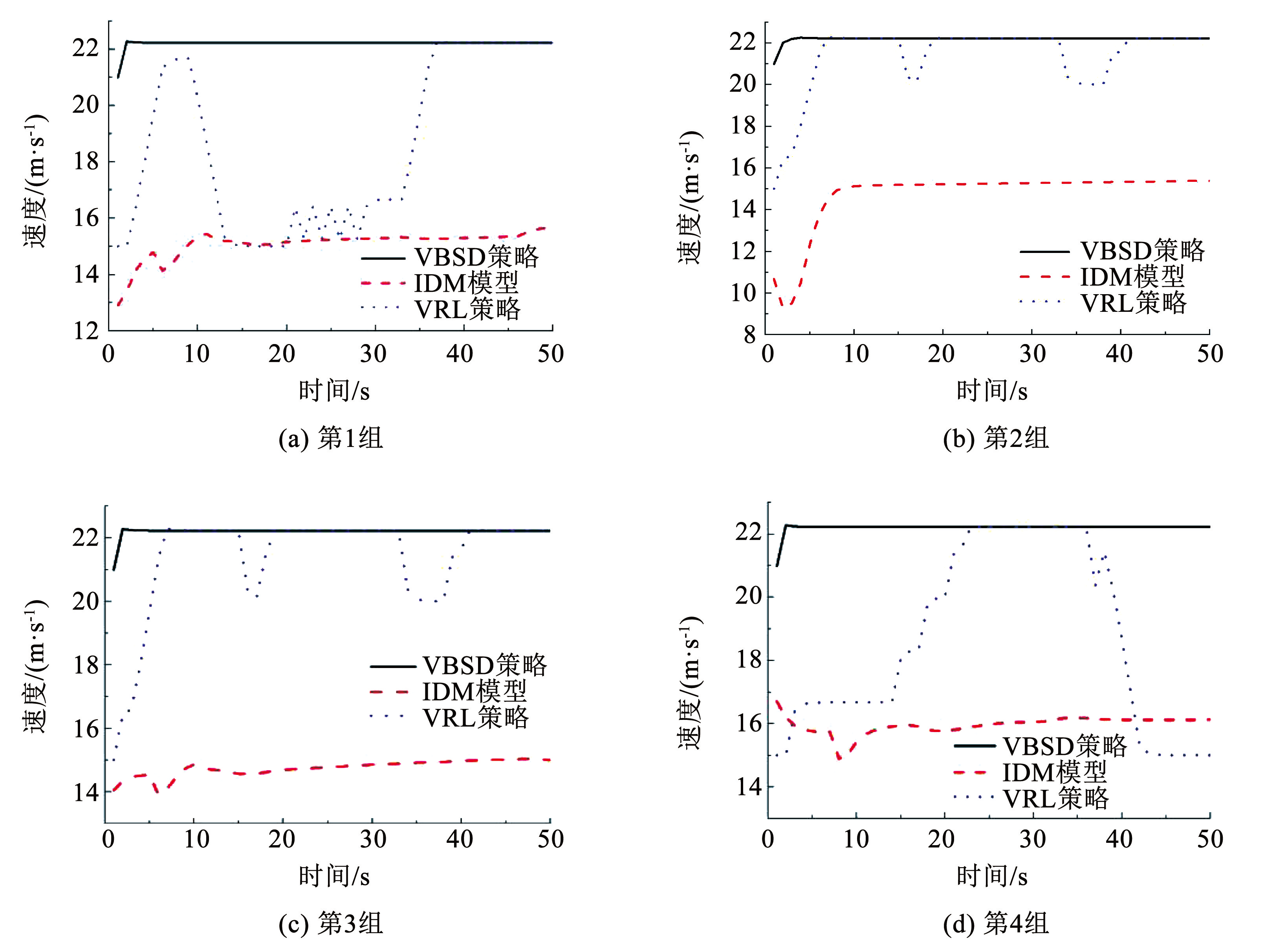
图6合流区主线车辆速度对比
Fig.6Comparison of the speed of the main line vehicles in the merging area
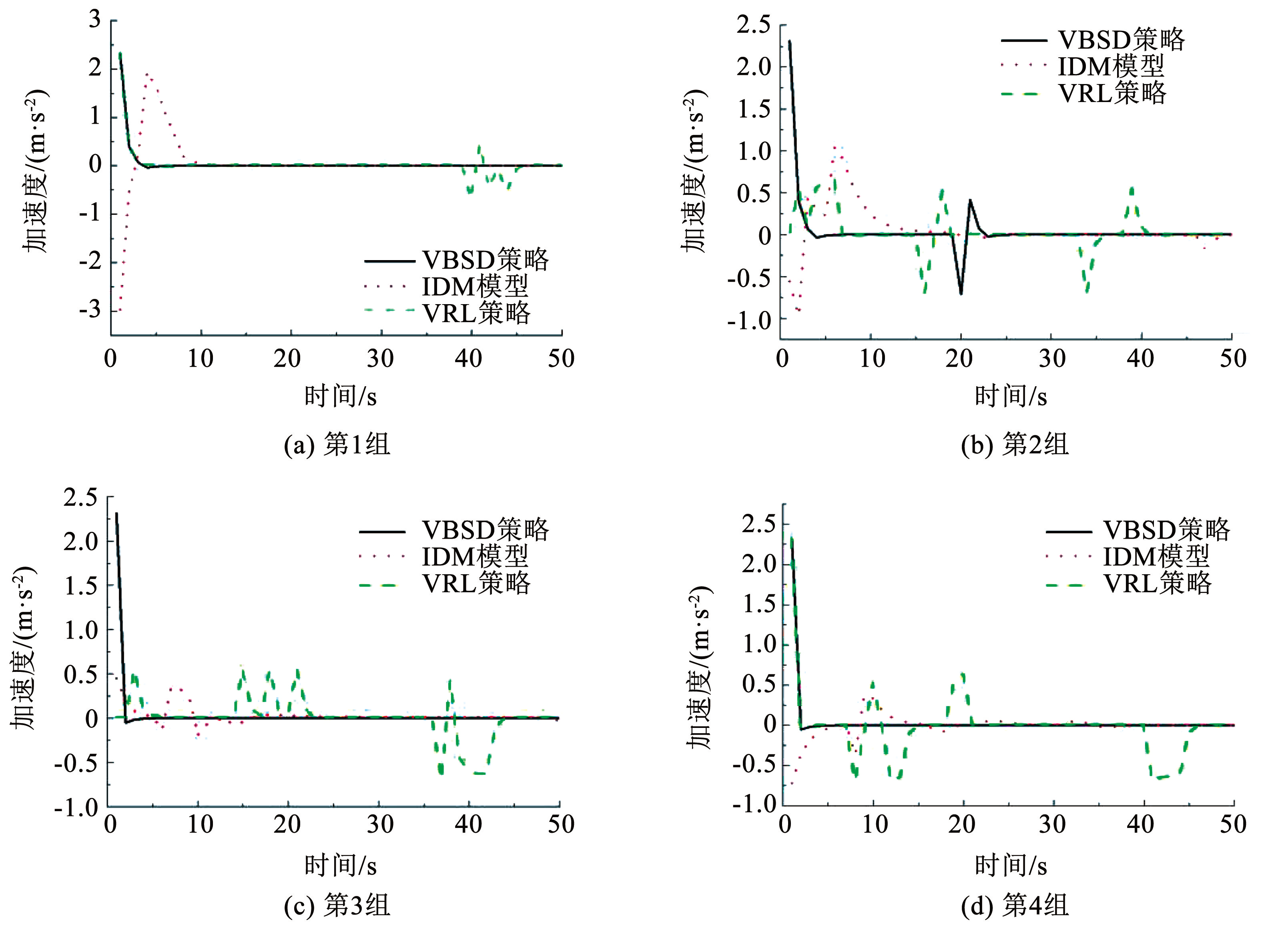
图7合流区主线车辆加速度对比
Fig.7Comparison of the acceleration of the main line vehicles in the merging area
VBSD 策略在与 VRL 策略和 IDM 模型比较时,具有以下优势:与 VRL 和 IDM 相比,VBSD 能控制车辆以更高速度行驶; VRL 策略下车辆速度和加速度波动较大,可能影响乘客舒适度; VBSD 策略能维持车辆期望速度,并保持速度和加速度稳定,这种稳定性在提升行驶效率的同时,也为乘客提供了更舒适的乘车体验。因此,VBSD 在提升行驶效率和乘客舒适度方面都优于 VRL 和 IDM。
3.3.2 换道次数对比分析
换道次数是影响乘车舒适性的重要因素之一,频繁的换道会导致乘客感到不适。为了提高乘车舒适性,CAV 需要在确保安全的前提下,尽量避免不必要的换道行为。本文进行了 5 组随机仿真试验,统计每次仿真试验中车辆行驶过程的换道次数,并定义连续换道次数为目标 CAV 在行驶中连续执行了两次及以上换道行为的次数,无效换道次数为目标 CAV 在前方无车辆影响其行驶的情况下执行换道行为的次数,见表4。
表4CAV 主线行驶过程换道次数统计
Tab.4 Statistics on lane changes during the running of the CAV main line
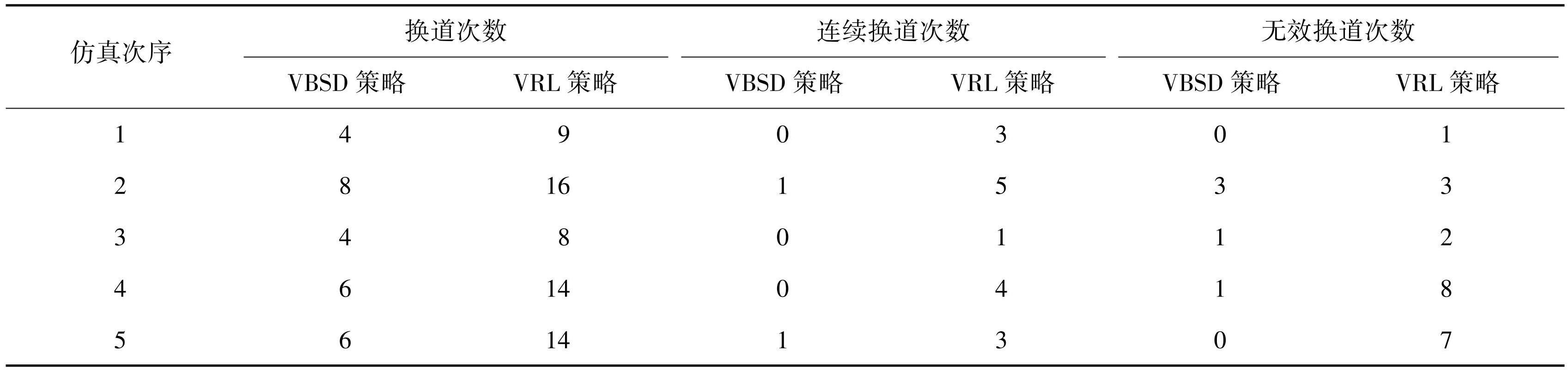
根据表4所获数据进行系统分析,在换道次数方面,VBSD 策略控制下的 CAV 平均换道次数为 5.6 次,VRL 策略控制下的 CAV 平均换道次数为 12.2 次,VBSD 策略相较 VRL 策略降低了 54.10%; 在连续换道次数方面,VBSD 策略控制下的 CAV 平均连续换道次数为0.4 次,VRL 策略控制下的 CAV 平均连续换道次数为 3.2 次,VBSD 策略相较 VRL 策略降低了87.50%; 在无效换道次数方面,VBSD 策略控制下的 CAV 平均无效换道次数为 1. 0 次,VRL 策略控制下的 CAV 平均无效换道次数为 4.2 次,VBSD 策略相较 VRL 策略降低了 76.19%。综上所述,VBSD 策略在以下方面优于 VRL 策略:能更有效地减少频繁和无效的换道行为; 提高了行车安全性和乘客乘车舒适度,可为乘客提供更佳的乘车体验。
3.3.3 车头时距分析
分别采用 VRL 策略与 VBSD 策略进行两组随机的仿真模拟试验,仿真结果如图8所示,图8(a)、 8(b)分别为目标车辆位于快速路合流区主线的两种不同随机场景。
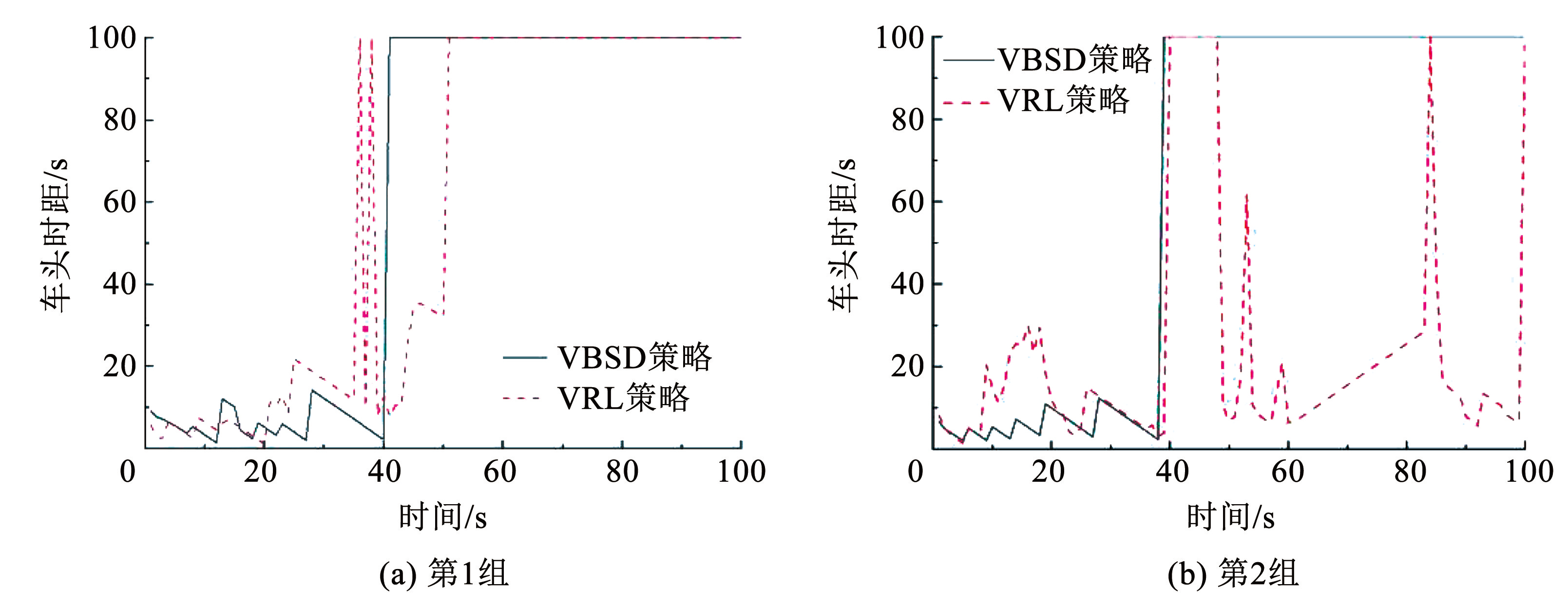
图8合流区主线车头时距对比
Fig.8Comparison of the time distance between the front of the main line in the confluence area
根据试验数据,VBSD 策略中目标车辆与前车车头时距在两种场景中分别于仿真开始 41 s 和 39 s 后进入持续平稳状态; VRL 策略中此车头时距分别于仿真开始 51 s 和 40 s 后进入平稳状态,且随后仍有车头时距的大幅波动。综上,VBSD 策略相较于 VRL 策略有以下优势:能更长时间维持车辆无影响行驶,优化了行驶环境; 减少换道行为,提升了乘客舒适性; 解决了 VRL 策略中车头时距突增突降导致的行驶不稳定问题; 通过改进,显著提高了神经网络计算和车辆行驶的稳定性。
3.4 匝道仿真结果分析
3.4.1 车速和加速度对比分析
同主线车速和加速度仿真试验分析,对目标车辆位于匝道的情况分别进行 4 组随机场景速度仿真试验和 4 组随机场景加速度仿真试验,试验结果如图9、10所示。

图9合流区匝道车辆速度对比
Fig.9Comparison of vehicle speeds on ramps in merging areas
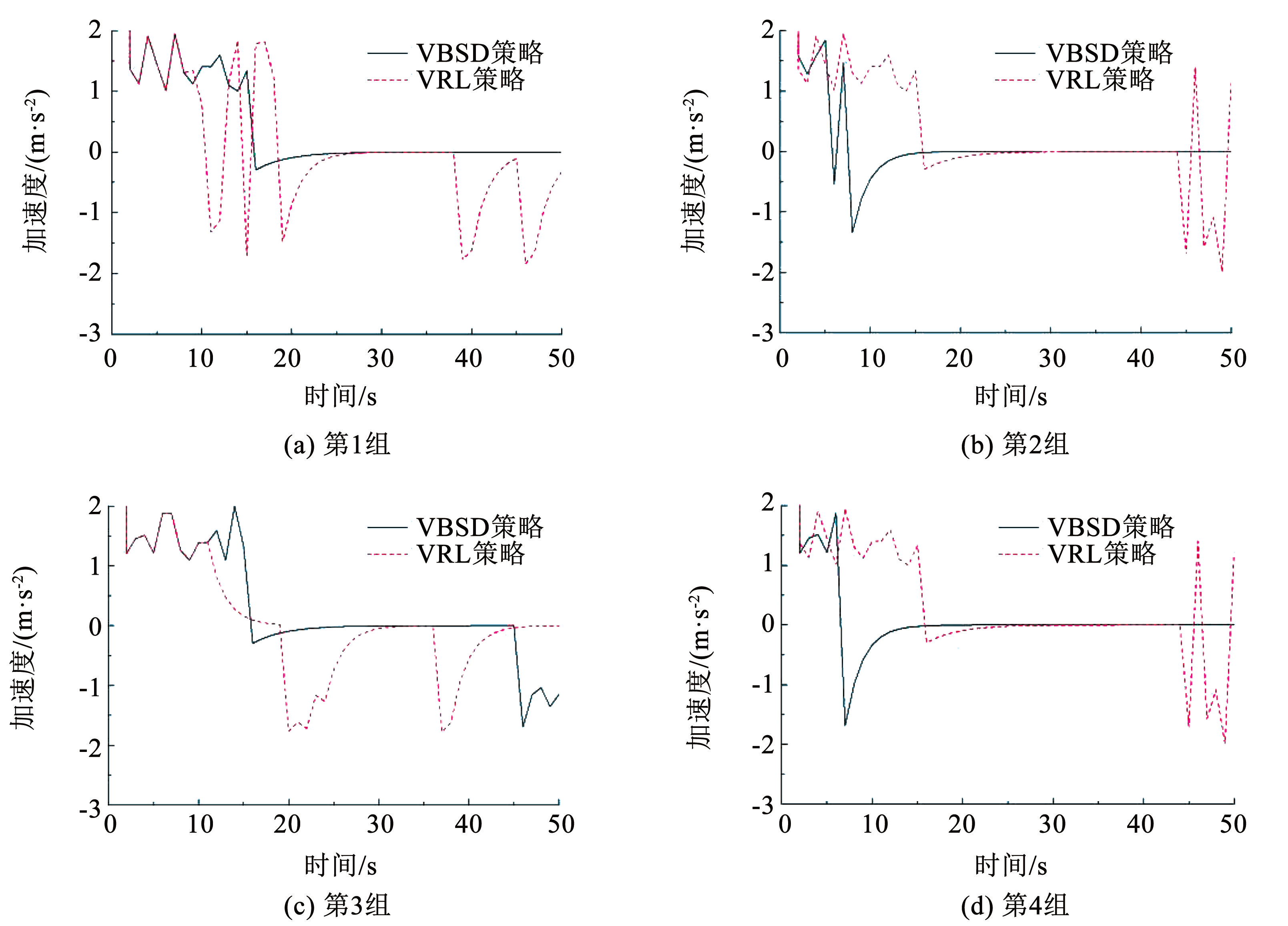
图10合流区匝道车辆加速度对比
Fig.10Comparison of vehicle acceleration at the ramp in the merging area
对试验数据进行分析,在采用 VBSD 策略的情况下,目标车辆在 4 种不同的场景中均能在仿真开始后的 36、15 s 时达到大约 22 m / s 的最高速度,并在此速度下保持稳定行驶。在这一策略控制下,加速度基本维持在 0 值附近,仅出现小幅波动。相比之下,VRL 策略下的目标车辆在稳定运行时的最高速度仅达到 15 m / s,且在车辆有机会高速运行时,速度和加速度都会发生较为剧烈的波动。在相同场景的对比中,VBSD 策略在以下方面优于 VRL 策略和 IDM 跟驰模型:能更有效地控制车辆长时间高速行驶; 在匝道行驶阶段,能更好地控制加速度变化,减少乘客不适; 驶入主线后,能维持车辆稳定高速行驶,提升乘车体验。
3.4.2 换道次数对比分析
为比较 VBSD 策略和 VRL 策略在 CAV 从匝道并入主线时的稳定性和舒适度,记录仿真试验中的换道次数、连续换道次数和无效换道次数,来量化评估两种策略的影响。换道次数统计见表5。
表5CAV 由匝道并入主线换道次数统计
Tab.5 Statistics on the number of CAV lane changes from ramp to main line
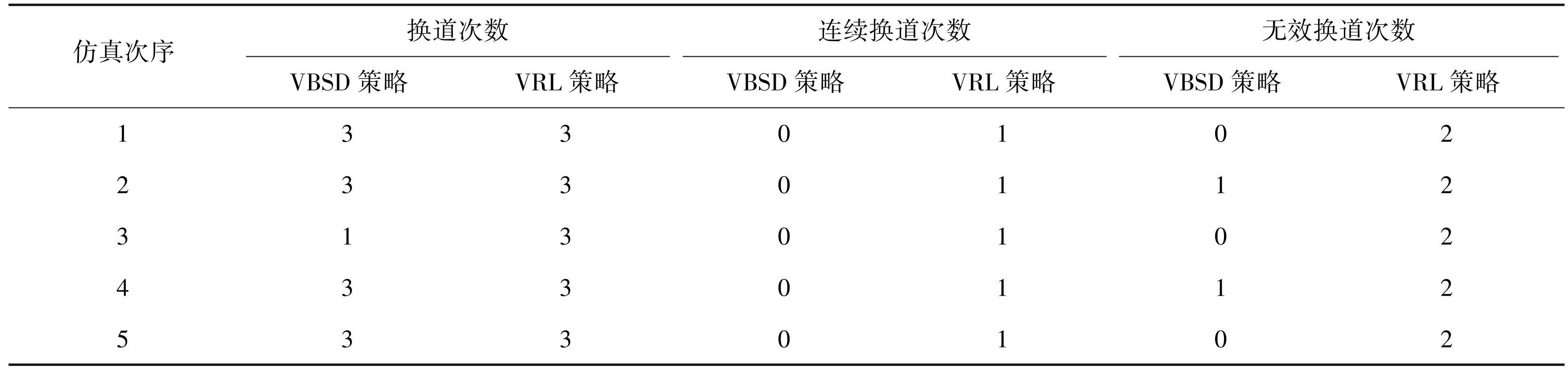
根据表5所获数据进行统计分析,在换道次数方面,VBSD 策略控制下的 CAV 在 5 次仿真试验中平均换道次数为2.6 次,VRL 策略控制下的 CAV 在 5 次仿真试验中平均换道次数为 3 次,VBSD 策略相较 VRL 策略降低了 13.33%; 在连续换道次数方面,VBSD 策略控制下的 CAV 在 5 次仿真试验中不存在连续换道行为,VRL 策略控制下的 CAV 在 5 次仿真试验中平均连续换道次数为 1 次,VBSD 策略相较 VRL 策略降低了 100%; 在无效换道次数方面,VBSD 策略控制下的 CAV 在 5 次仿真试验中平均无效换道次数为 0.4 次,VRL 策略控制下的 CAV 在 5 次仿真试验中平均无效换道次数为两次,VBSD 策略相较 VRL 策略降低了 80%。
综上所述,VBSD 策略在 CAV 匝道并入主线时比 VRL 策略更高效和稳定,主要优势如下:提升了行车安全性和乘客舒适度; 减少了并入行为对主线交通流的负面影响; 通过优化并入过程,减少了交通拥堵,提高了道路网络运行效率; 能确保乘客享受到平稳且安全的乘车体验。
3.4.3 车头时距分析
分别采用 VRL 策略与 VBSD 策略进行两组随机的仿真模拟试验,仿真结果如图11所示,图11(a)、11(b)分别为目标车辆位于快速路合流区匝道的两种不同随机的场景。
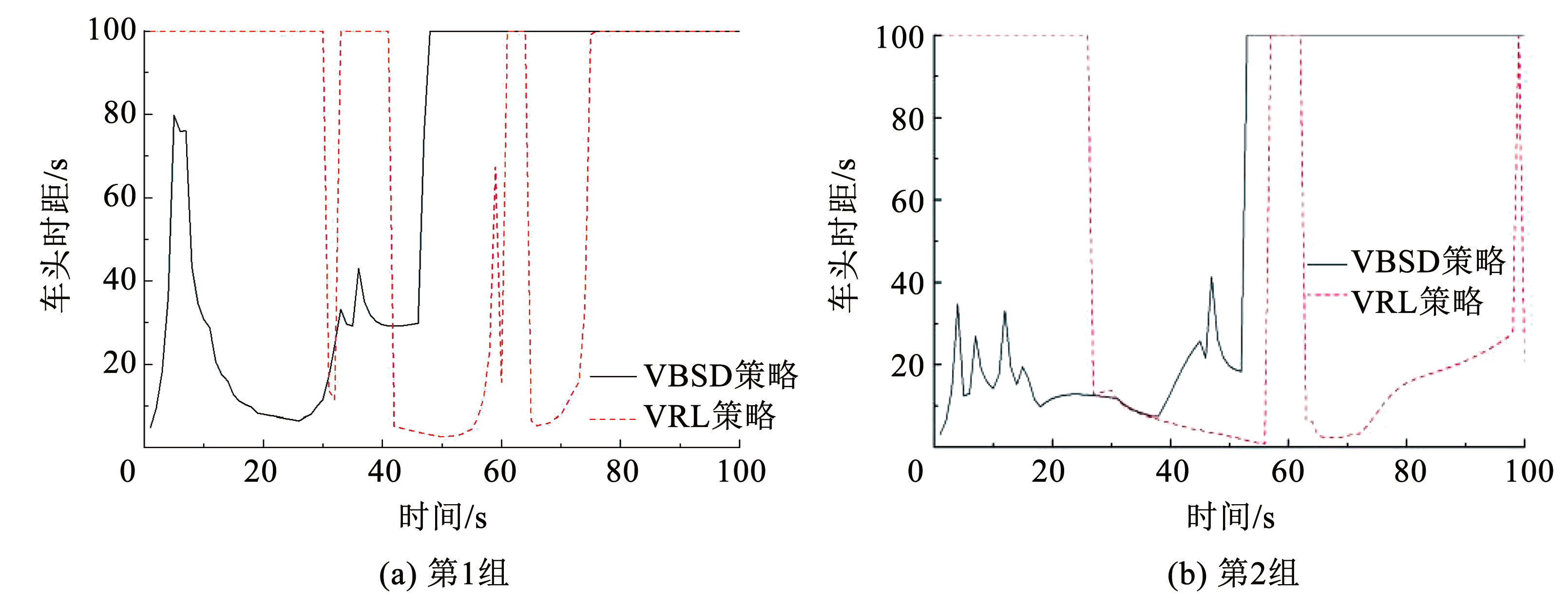
图11合流区匝道车头时距对比
Fig.11Comparison of the time distance between the front of the ramp in the merging area
由此可知,VBSD 策略在匝道行驶时与 VRL 策略相比,有以下优势:能保持更小的车头时距,避免交通流速率降低; 完成换道后,目标车辆能快速进入稳定行驶状态,保持前方无影响车辆。
4 结论
本文针对智能网联车辆在城市快速路合流区的驾驶行为进行了深入研究,主要考虑 CAV 在合流区主线和匝道两种不同环境下的行驶状态。结合马尔科夫过程对深度强化学习中的 DQN 算法进行创新性改进,提出了 VBSD 换道决策方法,该策略不仅考虑通行效率,还兼顾了行驶的稳定性和乘客的舒适性。利用 Python 搭建了仿真试验平台验证所提出的 VBSD 策略,得出如下研究结论:
1)引入马尔科夫过程理论,对 DQN 算法的奖励函数进行了改进设计,实现了算法的优化。
2)构建快速路合流区的仿真环境,使得单一智能体能够在该环境中进行有效的仿真测试。
3)VBSD 策略显著提升了 CAV 在快速路合流区的行驶表现。在主线上,使车辆高速且稳定行驶,减少无效换道,提升乘车体验; 在匝道上,使车辆保持较短车头时距,为解决拥堵提供了理论支持; 并入主线时,使车辆执行高效换道; 并入后,使车辆进入高速稳定状态,解决了状态衔接问题。
本文的研究成果为智能网联车辆在城市快速路合流区的通行提供了新的方法和思路,但仍有待进一步探索。未来的研究将更深入地分析目标 CAV 对整体交通流的影响,并考虑多智能体构成的复杂交通流。
