摘要
为探究冻融循环条件下非饱和黄土中铅离子的迁移规律,开展了吸附试验及冻融循环条件下铅离子迁移土柱试验, 并基于热-质守恒原理建立了非饱和土中污染物迁移的耦合数学模型,同时利用 COMSOL Multiphysics 多物理场仿真软件对模型进行数值求解,结合土柱试验评估了耦合模型的可靠性,探讨了各物理量的变化规律。结果表明:冻融循环条件下,土柱温度变化滞后于循环温度的变化,虽然冻融循环使土体渗透性明显减弱,液态水通量急剧下降,但液态水通量减小并未完全阻碍污染物向冻结区迁移,离子扩散作用还会导致土体冻结区出现污染物,进而引起冻结区土体污染物吸附浓度增长,96 h 时土柱顶端污染物质量浓度达 0. 204 g / L,污染物吸附浓度达 3. 62 × 10-7 kg / kg;冻融循环条件下污染物结晶出现在土柱下部, 结晶体积分数最大值维持在 4% 左右,同时污染物结晶产生的膨胀量约占土体总位移的 9% 左右,远小于冰晶体膨胀位移量; 负温梯度减小,污染物溶解度增大,析出的污染物晶体部分重新溶解,部分冰晶体也重新融化,两者叠加使土柱顶点位移呈波浪式缓慢增长。
Abstract
In order to explore the migration law of lead ions in unsaturated loess under freeze-thaw cycle condition, this paper conducted adsorption experiment and soil column experiment on lead ion migration under freeze-thaw cycle condition. Based on the principle of heat mass conservation, a coupled mathematical model for pollutant migration in unsaturated soil was established. At the same time, the COMSOL multiphysics simulation software was used to numerically solve the model. The reliability of the coupled model was evaluated in combination with soil column experiment, and the variation laws of various physical quantities were explored. Research has shown that under the freeze-thaw cycling condition, the temperature change of the soil column lags behind the change in cycling temperature. Although freeze-thaw cycling significantly reduces soil permeability and sharply decreases liquid water flux, the decrease in liquid water flux does not completely hinder the migration of pollutants to the freezing zone. Ionic diffusion can also cause pollutants to appear in the frozen zone of the soil, leading to an increase in the adsorption concentration of pollutants in the frozen zone. At 96 hours, the mass concentration of pollutants at the top of the soil column reached 0. 204 g / L, and the adsorption concentration of pollutants reached 3. 62 × 10-7 kg / kg; Under freeze-thaw cycle condition, pollutant crystallization occurs at the lower part of the soil column, with a maximum crystal volume content of around 4% . At the same time, the expansion caused by pollutant crystallization accounts for about 9% of the total soil displacement, which is much smaller than the expansion displacement of ice crystals. The negative temperature gradient decreases, the solubility of pollutants increases, and some of the precipitated pollutant crystals dissolve again. Some of the ice crystals also melt again, and the combination of the two causes the displacement of the soil column vertex to slowly increase in a wave like manner.
Keywords
中国西部地区分布有大面积季节性冻土,随着经济发展,中国工业污水排放量逐年增长。各地污水处理装置在环保政策引导下逐步配套,但由于资金制约,西部地区装置配备仍显滞后,工业污水乱排现象时有发生,由此引起土壤重金属污染,影响居民健康及生态安全,例如:2009 年陕西宝鸡化工污染引起数十名儿童血铅超标[1]; 2013 年甘肃白银利用铅污染水灌溉导致近千亩耕地失效[1]。
冻融循环条件下非饱和土中水分迁移涉及复杂的水-热-力耦合,土体受重金属污染后,还伴有重金属盐吸附、结晶及吸水膨胀,理化过程更加复杂,针对上述问题的研究主要聚焦于两方面:一是冻土水-热耦合,文献[2]提出了冻土水-热耦合模型; 文献[3]以文献[2]中构建的理论模型为基础,首次提出冻土中存在未冻水,并提出未冻水含量与温度间的经验公式,虽然以经验公式估算未动水含量的精度有待商榷,但该观点对后续研究产生了较大影响; 文献[4]考虑土体水分迁移及结晶对孔隙水压的影响,构建了以温度、孔隙率及位移为变量的土体水-热-力耦合模型,模型引入了冰透镜形成和消失的判断准则,但该模型耦合关系复杂,数值求解难度大; 文献[5] 通过修正 Clapeyron 方程得到了孔隙水冻结温度与孔隙半径间的关系,建立了冻土导水系数与未冻水含量间的数学表达式,为计算冻土中水-热传输提供了较精准的参数。二是冻土水-热-盐-力耦合,文献[6]探讨了负温条件下土体盐分结晶的热力学过程,计算了结晶应力; 文献[7]基于盐分的 Henry 线性吸附效应,构建了冻融循环条件下滨海含盐土水-盐-热-力多场耦合模型,探讨了盐分、压力、温度及水分等因素对液相通量及土体压缩性的影响; 文献[8]对重金属污染冻土中未冻溶液含量与浓度间的数学关系进行了试验研究,发现重金属离子主要存在于未冻水中; 文献[9]提出了用冻结锋面移动使悬浊液中金属离子排除的“低温净化法”; 文献[10]基于冻融试验清洗重金属污染土,研究了冻融作用对土体微观结构的影响,探明了冻融-淋洗使土体脱重金属盐的作用机理。
综上所述,已有研究多考察单向冻结条件下土体中的热-质传输机理,但单纯的单向冻结工况并不多见; 少数研究考虑了冻融交替,却忽略了汽态水的影响; 土体对金属离子均有一定程度的吸附[11],同时土体或离子类别不同,吸附模型及对应的吸附系数也不相同[11],而已有研究对黄土吸附铅离子少有涉及。本文通过吸附试验确定黄土对铅离子的吸附类型,进行冻融循环条件下非饱和黄土中铅离子迁移土柱试验,并构建水-热-汽-污染物-力多场耦合数学模型,全面考虑水分冻结、蒸发及污染物的 Langmuir 吸附效应,并对土体的弹性模量进行了合理修正,研究成果可为西部地区重金属污染防控提供理论借鉴。
1 试验
1.1 吸附试验
试验材料:兰州市区黄土,取土深度 50 cm,测得土样体积含水率为 0.11,干密度 ρd = 1 560 kg / m 3,最大干密度 ρmax = 1 880 kg / m 3,土样颗粒级配曲线如图1所示。土样物理参数:土粒相对密度 Gs = 2.7,最优含水率 wopt = 13.7%,液限 wL = 25.4%,塑限 wp = 12.6%,pH = 6.8。土样中各元素质量分数: w(Si)= 33.5%,w(Ca)= 18.6%,w(Mg)= 3.6%,w(Na)= 0.9%,w(K)= 2.4%,w( Fe)= 6.2%,w(Al)= 10.3%。
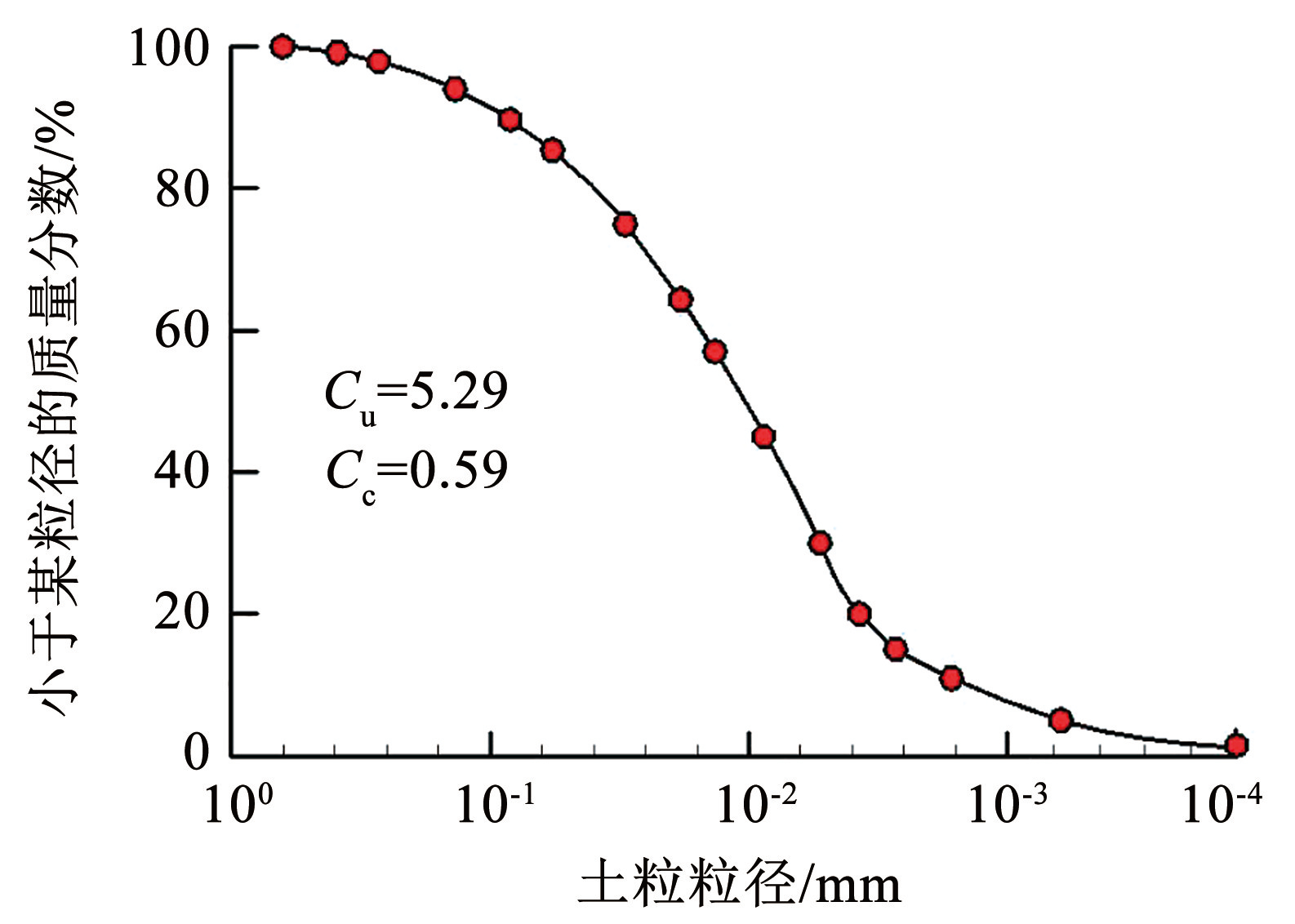
图1土样颗粒级配曲线
Fig.1Particle-size distribution curve of soil sample
试验方案:电子天秤称 5 组质量 2 g 的土样,分别在温度为 273、283、293 K 条件下,将 25 mL 初始质量浓度分别为 100、120、150、180、200 mg / L 的硝酸铅试剂同土样一起倒入 5 支试管,用玻璃棒搅拌试管中溶液 30 min,静置 30 min,重新搅拌,循环 5 次后用离子色谱仪测定试管上部溶液铅离子质量浓度,结果见表1。利用式(1)计算铅离子吸附量[12] :
(1)
式中:Cs为土样对铅离子的吸附量,C0为初始质量浓度,C 为上部溶液质量浓度,V 为溶液体积,m 为土样质量。
描述土体对重金属离子吸附效应的常用模型为 Langmuir 非线性吸附[11],可表示为
(2)
式中:α 为非线性吸附常数,mg / L; β 为最大吸附量,mg / g。
按式(2)对试验数据进行拟合,结果见表2,计算得 Langmuir 模型参数 α 及 β 见表3,β 与温度 T 的拟合关系为
表1铅离子吸附试验数值
Tab.1 Experimental value of Pb ion adsorption
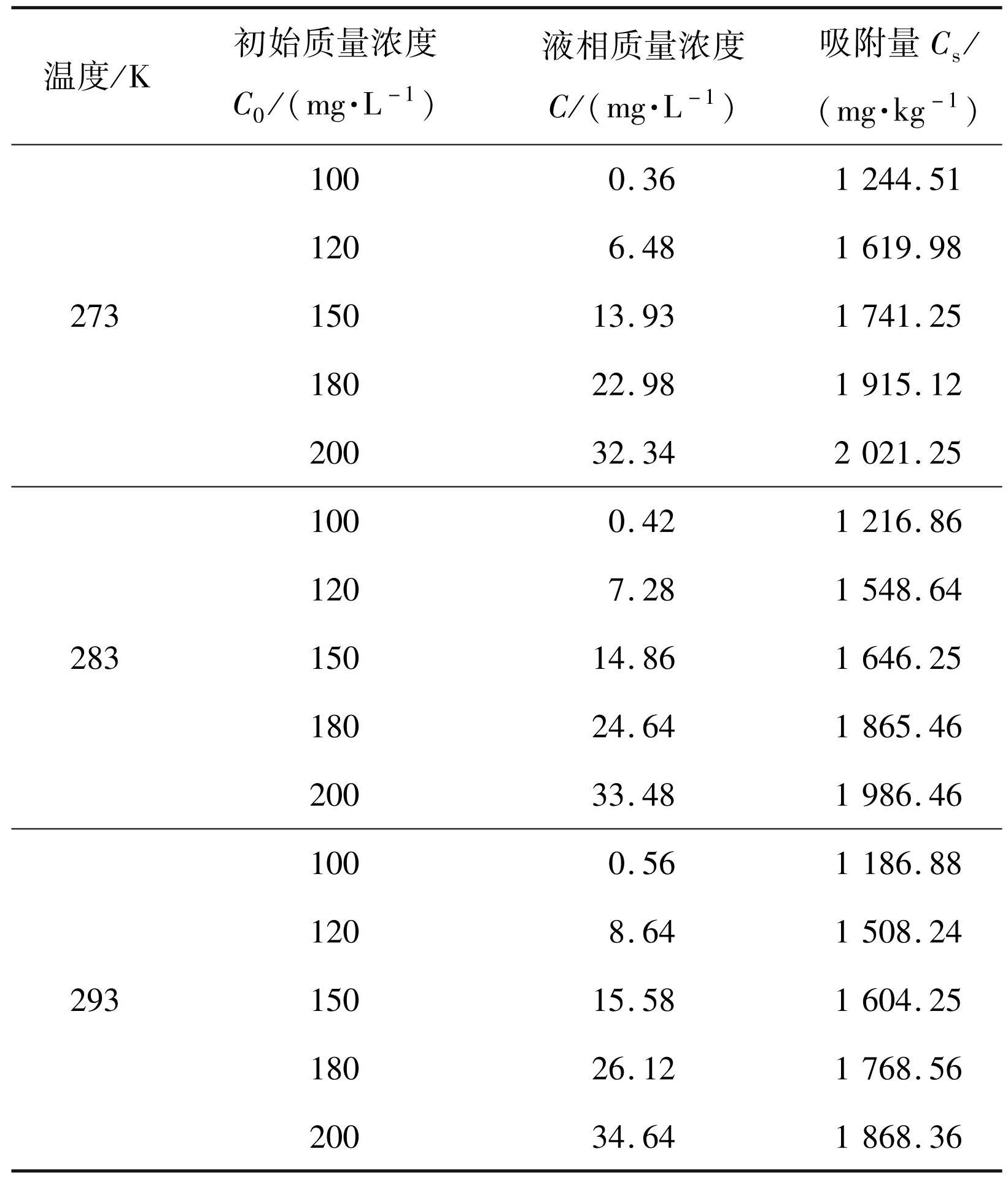
表2拟合结果
Tab.2 Fitting results

表3吸附系数
Tab.3 Adsorption coefficient

1.2 铅离子迁移土柱试验
目标污染物乙酸铅((CH3 COO)2 Pb)为易溶性重金属盐,其溶解度 S(g / 100 g)与温度 T(K)的关系可表示[13]为
(3)
试验装置:内部直径为 20 cm,高度为 36 cm 的钢化玻璃柱; 5TE 传感器,探针长 0.12 m,可同步测定土体温度、体积含水率及电导率,温度精度 ± 0. 01℃,体积含水率( VWC)精度 ± 1%,电导率精度 ± 0. 01 dS / m; CR1000 动态数据采集系统,可同时采集温度、体积含水率、土体电导率数据; 振筛机; 温度计等。
传感器电导率标定:配制质量浓度分别为 10、30、 50、70、90、110、130、150 g / L 的 8 组乙酸铅溶液样品,将 4 个传感器探头分别浸入 8 组溶液中,进行电导率标定,标定结果见表4,各组标定结果求均值后与各组污染物溶液质量浓度值进行线性拟合,拟合结果如图2所示。
表4传感器电导率标定结果
Tab.4 Calibration results of sensor conductivity
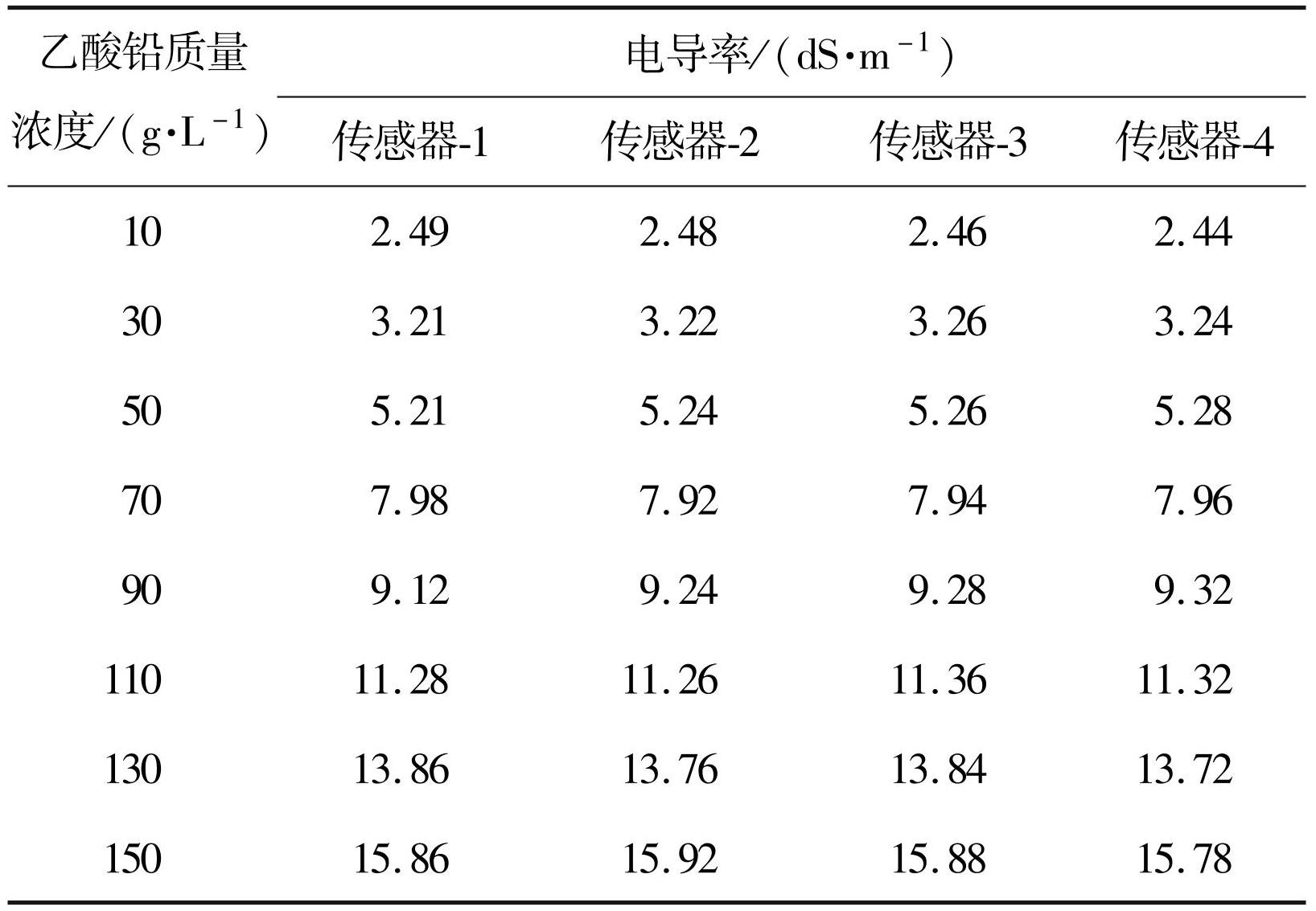
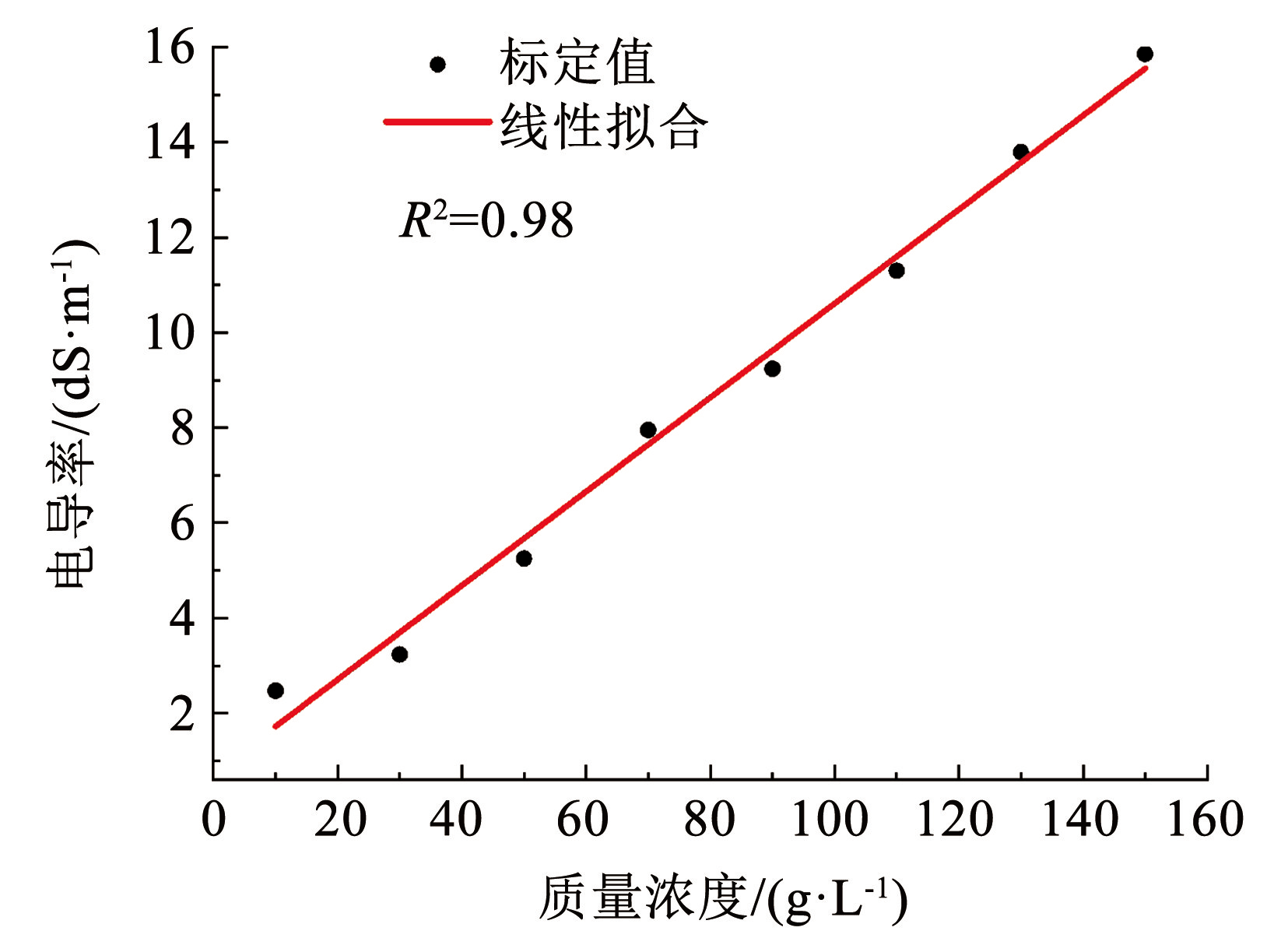
图2电导率与浓度的关系
Fig.2The relationship between conductivity and concentration
试验方案:去除自然状态下黄土中的杂质,用振筛机过滤粒径大于2 mm 的土颗粒,将土体加热10 h使其完全干燥,再向土体中加入清水,将其配置成体积含水率为0.2 的试验土样,塑料薄膜覆盖土样静置 10 h 后通过控制压实度将土样分 3 层填入钢化玻璃柱,最终形成高为35 cm 的土柱,土柱预热至286.15 K(13℃),分别在距离土柱底面 5、9、19、29 cm的 4 个位置插入传感器,用保温棉包裹土柱以免其与周围环境产生热量传递,土柱上、下端放置冷浴盖板,试验关键设备及装置连接示意如图3所示。 12 月份至次年 1 月份间兰州市温度变化为-10.6~6.4℃,因此土柱上盖板循环温度设为T(t)=-2-9cos(2πt/ 24)+ 273.15,循环温度正温峰值为 280.15 K(7. 0℃),负温峰值为 262.15 K(-11. 0℃),下盖板为常温 283.15 K(13℃)。由式(3)知286.15 K(13℃)时乙酸铅溶解度为16.3 g,因此土柱底部施加质量浓度为 150 g / L 的乙酸铅溶液污染源,使土柱底部浸润溶液达到饱和状态后启动数据采集系统,每10 min 采集1 次数据,试验持续96 h。
图3试验装置及连接示意
Fig.3Schematic diagram of test device connection
2 耦合模型
本文假定土体为连续、各向同性弹性体。水分以液态及水汽形式迁移,不考虑结合水的影响和冰晶迁移; 土体与外界空气相通[14]。
2.1 水分质量守恒方程
冻融循环条件下非饱和土中水分质量守恒方程可表示为
(4)
式中:ql和 qv分别为液态水和水汽通量,m/ s; M 为水的摩尔质量,kg / mol; MC为结晶乙酸铅摩尔质量,kg / mol; θte为总等效体积含水率,可表示为
(5)
(6)
(7)
其中:θl、θv、θi、θc 分别为液态水体积分数、汽态水体积分数、体积含冰量及污染物结晶体积分数; ρl、ρv、ρi分别为液态水密度、汽态水密度及冰密度,kg / m 3; ns为土体孔隙率。
非饱和土中液态水迁移由基质吸力及温度梯度共同引起,基于 Richards 方程[14],液态水通量可表示为
(8)
式中:qlh为水势梯度作用下的液态水通量,m/ s; qlT为温度梯度作用下的液态水通量,m/ s; y 为竖向坐标,m,向上为正; h 为压力水头,m; Klh为水势梯度作用下非饱和土导水系数,m/ s; KlT为温度梯度作用下非饱和土导水系数,m 2 /(K·s); T 为温度,K。
基于 Fick 定律,土体中水汽通量受水汽密度影响,水汽密度又由基质吸力及温度梯度控制[14],则非饱和土中水汽通量可表示为
(9)
式中:qvh、qvT分别为非饱和土基质吸力作用下的水汽通量和温度梯度作用下的水汽通量,m/ s; Kvh为水势梯度作用下非饱和土水汽传导系数,m/ s; KvT为温度梯度作用下非饱和土水汽传导系数,m 2 /(K·s)。
结合式(5)~(7),则非饱和土中水分质量守恒方程可表示为
(10)
2.2 VG 模型
本文利用 VG 模型描述冻结条件下土体的土水特征关系[15],可表示为
(11)
(12)
考虑土体冻结过程中冰晶体对液态水传导的阻滞效应[16],则基质吸力作用下非饱和土导水系数 Klh可表示为
(13)
(14)
式中:Ks为饱和土体导水系数,m/ s; I 为阻抗因子; Se为土体有效饱和度; θr为土体残余含水率; θs为土体饱和含水率; α 为土体进气值的倒数,m-1; l、ml、n 为模型参数,满足 ml =1-1/ n。
温度梯度作用下非饱和土导水系数 KlT 可表示[17]为
(15)
式中:GlT为温度对土体颗粒吸附水表面张力影响的增益因子,取值为7. 0; γ0为 283.15 K 时土颗粒表面水张力,取值为 71.89 g / s 2 ; γ 为土颗粒表面水张力,J/ s 2,可表示为
(16)
水势梯度作用下非饱和土汽态水传导系数 Kvh可表示[17]为
(17)
式中:M 为水的摩尔质量,kg / mol; R 为通用气体常数,J/(mol·K); g 为重力加速度,m/ s 2; D = τθvDa为土体水汽扩散系数,m 2 / s,其中为土体弯曲因子,; ρvs为饱和水汽密度,kg / m 3; ρv为水汽密度,kg / m 3; Hr为空气相对湿度[17],。 ρvs、ρv可分别表示为
(18)
(19)
温度梯度作用下非饱和土水汽传导系数 KvT可表示[18]为
(20)
(21)
式中:η 为水汽增强因子; fc为土体黏粒比例,fc取值为 0.2。
(22)
(23)
式中:a、b 为回归参数,a、b 取值分别为 6.9、0.47; Tf为土体孔隙溶液冻结温度,K。
2.3 能量守恒方程
(24)
(25)
(26)
(27)
式中:Cp为非饱和土总体积热容,J/(m 3·K); Cs、Cl、Ci 分别为土体基质、液态水及冰的体积热容,J/(m 3·K); Lw为液态水蒸发潜热,J/ kg; Lf为液态水冻结潜热,J/ kg; Lc为污染物结晶潜热,J/ kg; λ 为土体总导热系数; λs、λl、λi、λa分别为土体基质、液态水、冰及空气的导热系数,W/(m·K)。
2.4 污染物迁移方程
冻融循环条件下非饱和土中污染物迁移方程可表示[11]为
(28)
式中:C 为污染物质量浓度,g / L; D1 = D0 τ + αL v 为水动力弥散系数,m 2 / s; 为孔隙水渗流速度,m / s; αL为土体纵向弥散度,m; τ 为土体弯曲因子; D0为纯水中污染物的扩散系数,m 2 / s; Is为单位时间单位体积土体吸附的污染物质量,kg /(m 3·s)[11],可表示为
(29)
(30)
式中:λ1、λ2分别为正反应速率常数及逆反应速率常数,λ1、λ2取值分别为 2. 0 ×10 -6 s-1、5. 0 ×10-6 s-1。
2.5 本构方程
土体变形由土体孔隙液态水相变为冰晶体产生的体积膨胀、溶解度下降引起的污染物结晶膨胀及温度变化引起的土体基质收缩共同引起[16],土体有效应力 σ 可表示为
(31)
(32)
(33)
式中:ε、εi、εc、εT 分别为土体总应变、冻结膨胀应变、结晶膨胀应变和温度应变; αi、αc、αT、T0 分别为液态水冻结膨胀系数、结晶膨胀系数、热膨胀系数和参考温度,αi、αc、αT 、T0 取值分别为 0. 09、0. 015、 2. 0 × 10-6、273.15 K [20]; E 为修正后的冻结污染土弹性模量,MPa; E0为未冻土弹性模量[21],E0取值为 2. 0 × 10 6 MPa。
土体变形在各方向相等,可表示为
(34)
式中:εxv、εyv、εzv为变形引起的正应变; γxyv、γyzv、γzxv 为变形引起的切应变。
2.6 污染物体积分数 θc及冻结温度 Tf
非饱和土中乙酸铅溶液达到溶解度后,温度继续降低,乙酸铅将结晶形成三水合乙酸铅[13],可表示为
(35)
降温过程引起土体孔隙中液态水含量和溶解于水的乙酸铅含量同时减小,则土体孔隙中溶解于水的乙酸铅浓度 Cj 可表示[16]为
(36)
三水合乙酸铅析出后,可将其分为无水乙酸铅和结晶水两部分[16],降温过程中析出的乙酸铅晶体体积分数 θc可表示为
(37)
式中 ρc为结晶乙酸铅密度,kg / m 3。
污染物溶液冻结温度 Tf可表示[22]为
(38)
式中:T0 为纯水冻结温度,K; R 为理想气体常数,J/(mol·K); Li为水-冰相变潜热,J/ kg。
结合 Pitzer 模型可得[22]
(39)
将式(39)代入式(38),则冻结温度 Tf可表示为
(40)
式中:cw为液态水摩尔浓度,cw取值为 55.6 mol / m 3; kf为污染物对液态水冻结温度的降低系数,kf取值为 1.86(kg·K)/ mol; C 为污染物质量浓度,g / L; Mc为乙酸铅摩尔质量,kg / mol。
式(10)、(24)、(28)、(30)、(31)构成冻融循环条件下非饱和土中污染物迁移的多场耦合方程组,基本未知量为 θ、T、C、Cs、u。结合本文所建数学模型,利用 COMSOL Multiphysics 软件对前文已完成的铅离子迁移土柱试验进行数值模拟,数值计算模型如图4所示,计算参数[12,16,20] :液态水密度 ρl、土体密度 ρs、冰密度 ρi、结晶乙酸铅密度 ρc分别为 1 000、 1 560、917、1 250 kg / m 3; 土体基质体积热容 Cs、液态水体积热容 Cl、冰体积热容 Ci分别为 1 003、4 100、 2 000 J/(m 3·K); 土体基质导热系数 λs、液态水导热系数 λl、冰导热系数 λi、空气导热系数 λa分别为 1.38、0.55、0.22、0.1 W/(m·K); 水摩尔质量 M、乙酸铅摩尔质量 Mc、乙酸铅晶体摩尔质量 MC分别为 0. 018、0.325、0.343 kg / mol; 污染物扩散系数 D0、通用气体常数 R、液态水冻结潜热 Lf、污染物结晶潜热 Lc分别为 2. 0 × 10-8 m 2 / s、8.34 J/(mol·K)、3.34 × 10 5 J/ kg、7.3 × 10 4 J/ kg; 土体最大含水率 θs、残余含水率 θr、土体进气值倒数 α、纵向弥散度 αL、饱和导水率 Ks、孔隙率 ns 分别为 0.49、0. 001、1.54 m-1 、 0.3 m、2.2 × 10-8 m / s、0.49; VG 模型参数 n、l 分别为 2. 0、0.5。
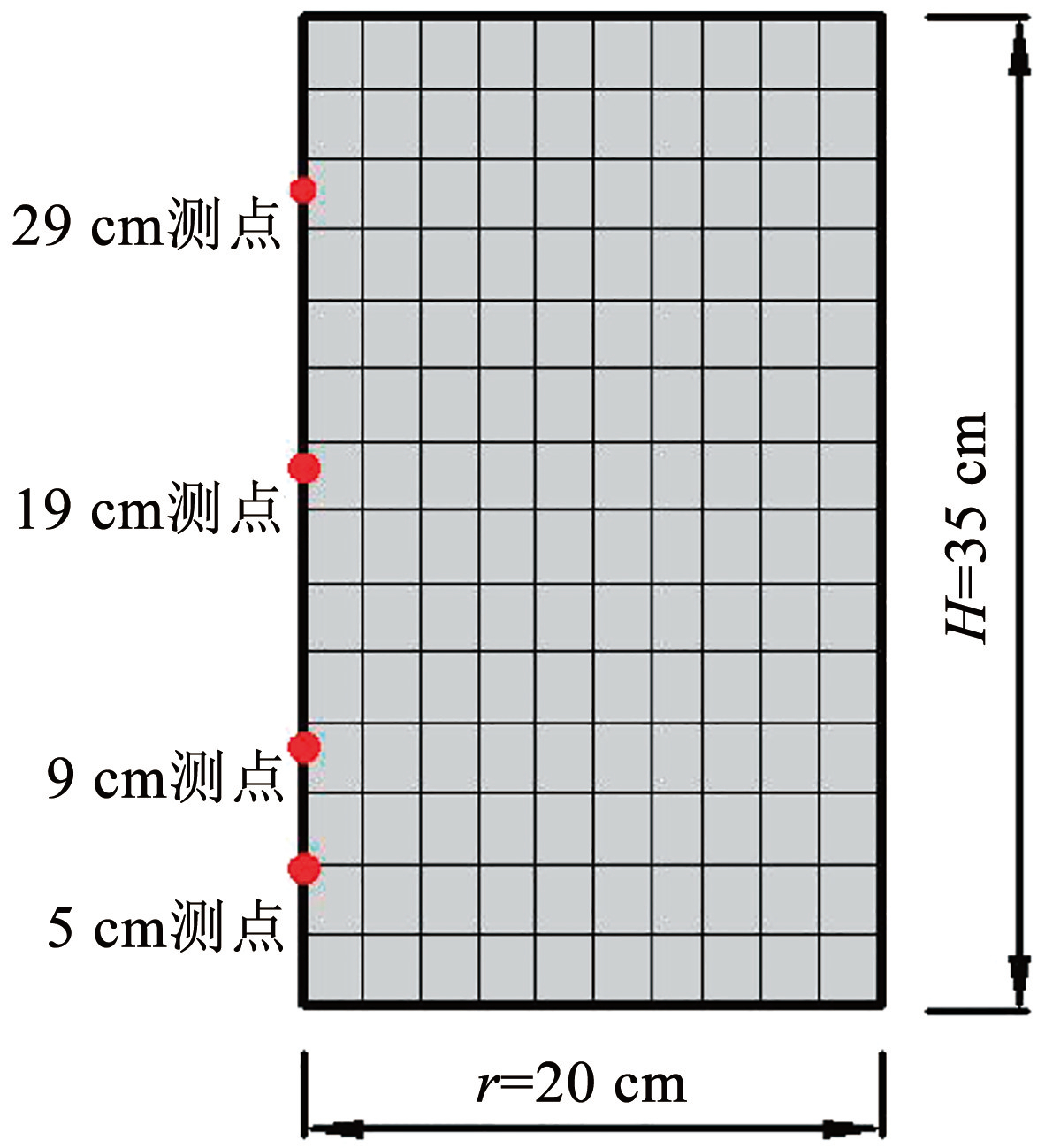
图4数值计算模型
Fig.4Numerical model
初始条件:体积含水率 θl为 0.2,位移 u、质量浓度 C 及吸附浓度 Cs均为0,温度 T 为286.15 K。
边界条件:上边界处温度 T 与前文试验时上盖板循环温度相同,即 T( t)=-2-9cos(2πt / 24)+ 273.15; 下边界处体积含水率 θl、质量浓度 C 及温度 T 分别为 0.48、150 g / L 及 286.15 K,位移 u 及吸附浓度 Cs均为 0。
2.7 结果对比
图5为利用 COMSOL Multiphysics 软件对前文土柱试验过程进行数值模拟后,4 个观测点处温度、污染物浓度及液态水体积分数计算值与实测值的对比,由图5可知数值计算结果与试验结果吻合度较高,表明本文构建的数学模型可较好地反映冻融循环条件下非饱和黄土中铅离子的迁移规律。本文研究涉及水分、浓度、温度、位移及吸附效应等多物理场的耦合,耦合效应使液态水及污染物沿土柱高度方向自下而上迁移。
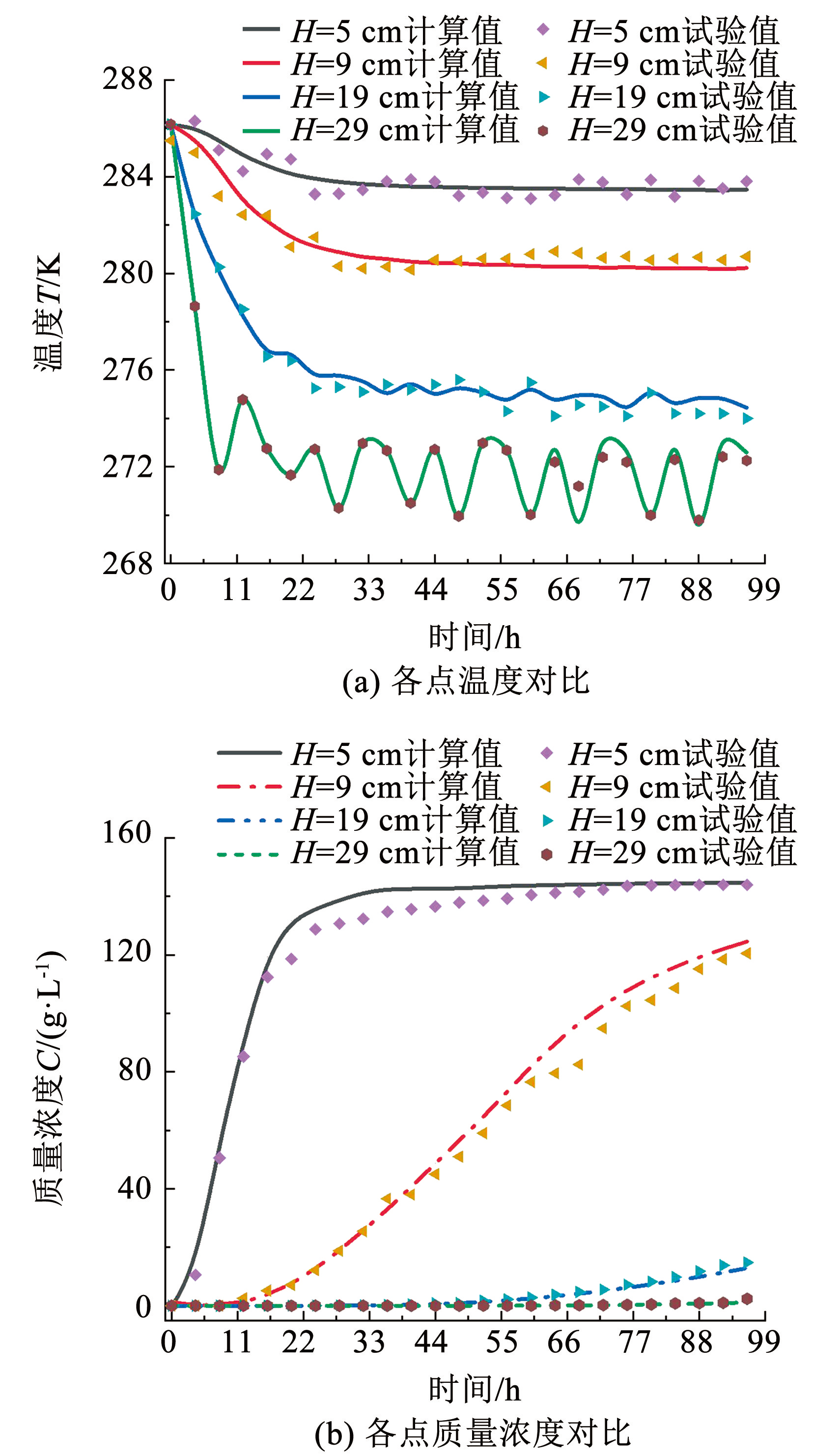
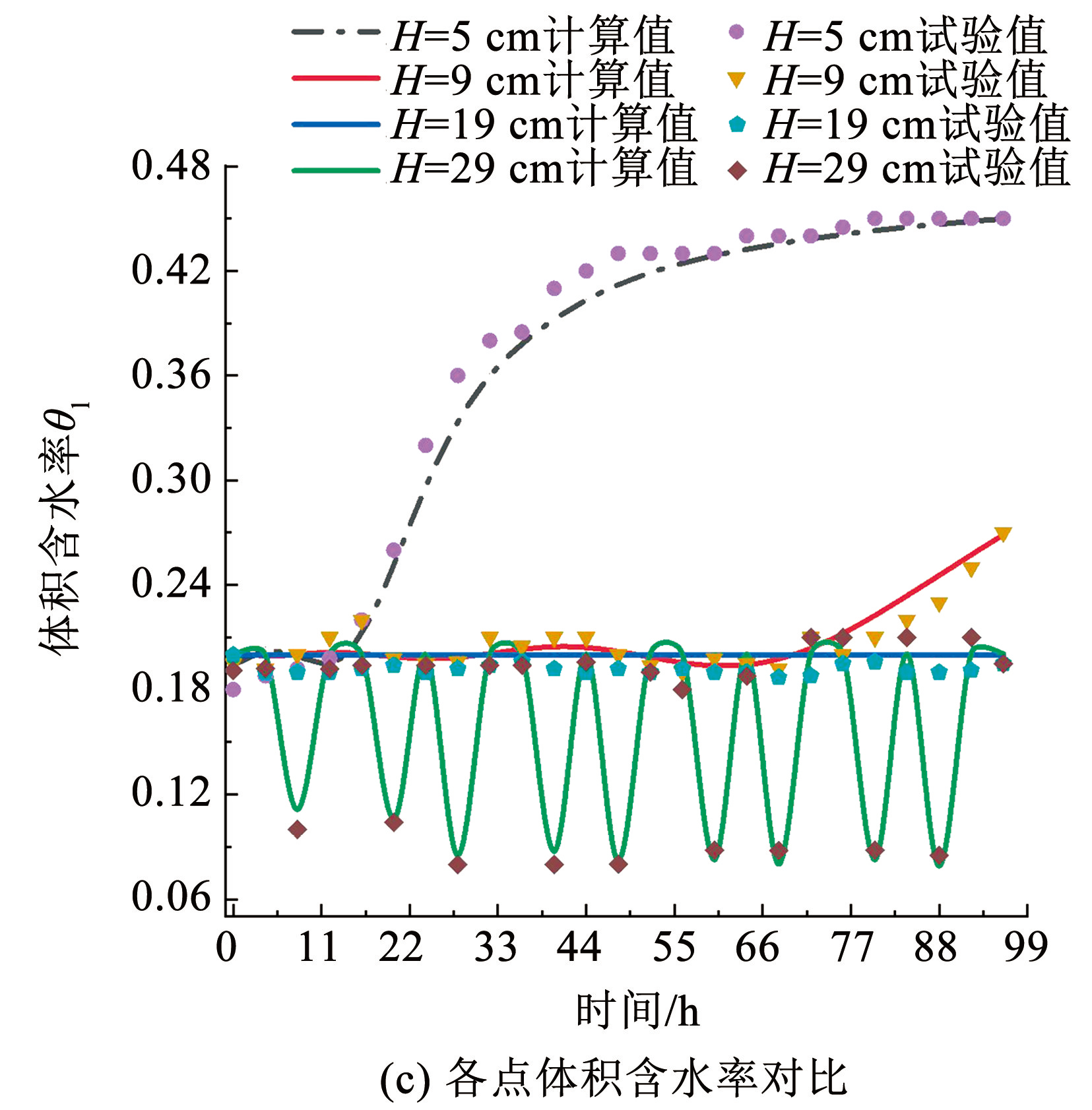
图5温度、质量浓度及体积含水率对比
Fig.5Comparison of temperature, concentration, and volumetric water content
图6~9 分别为不同时刻土柱中温度、质量浓度、吸附浓度及污染物结晶体积分数变化云图,以 24 h 为例,循环温度达到负温峰值,但土柱上部温度还未降到负温峰值,因此可知土柱温度变化明显滞后于外界循环温度的变化,同时在土柱上部形成 “冻结夹心层”,“冻结夹心层” 随时间增长缓慢向下迁移; 基质吸力和温度梯度共同影响使污染物溶液沿土柱高度方向逐渐向上迁移; 由于吸附效应,污染物吸附浓度沿土柱高度方向也逐渐增大; 冻融循环条件下污染物结晶出现在土柱下部,整个过程中,污染物结晶体积分数最大值维持在 4% 左右。

图6温度变化云图
Fig.6Cloud maps of temperature
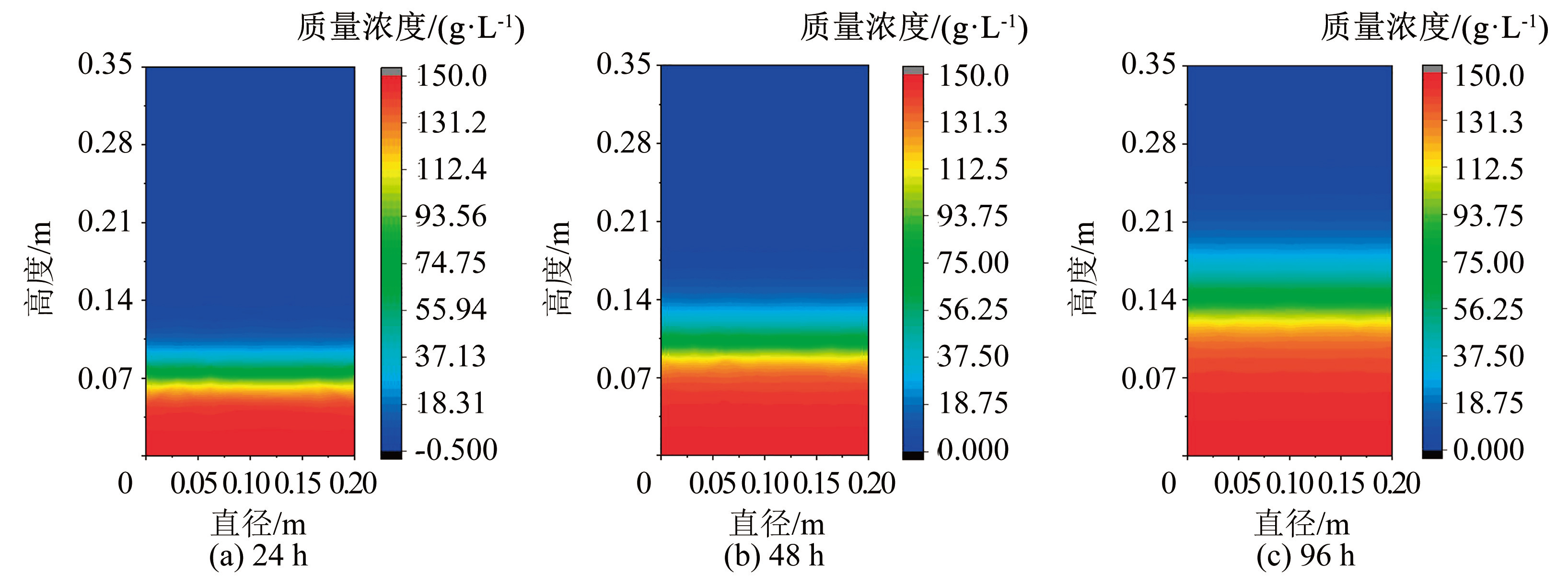
图7质量浓度变化云图
Fig.7Cloud maps of mass concentration
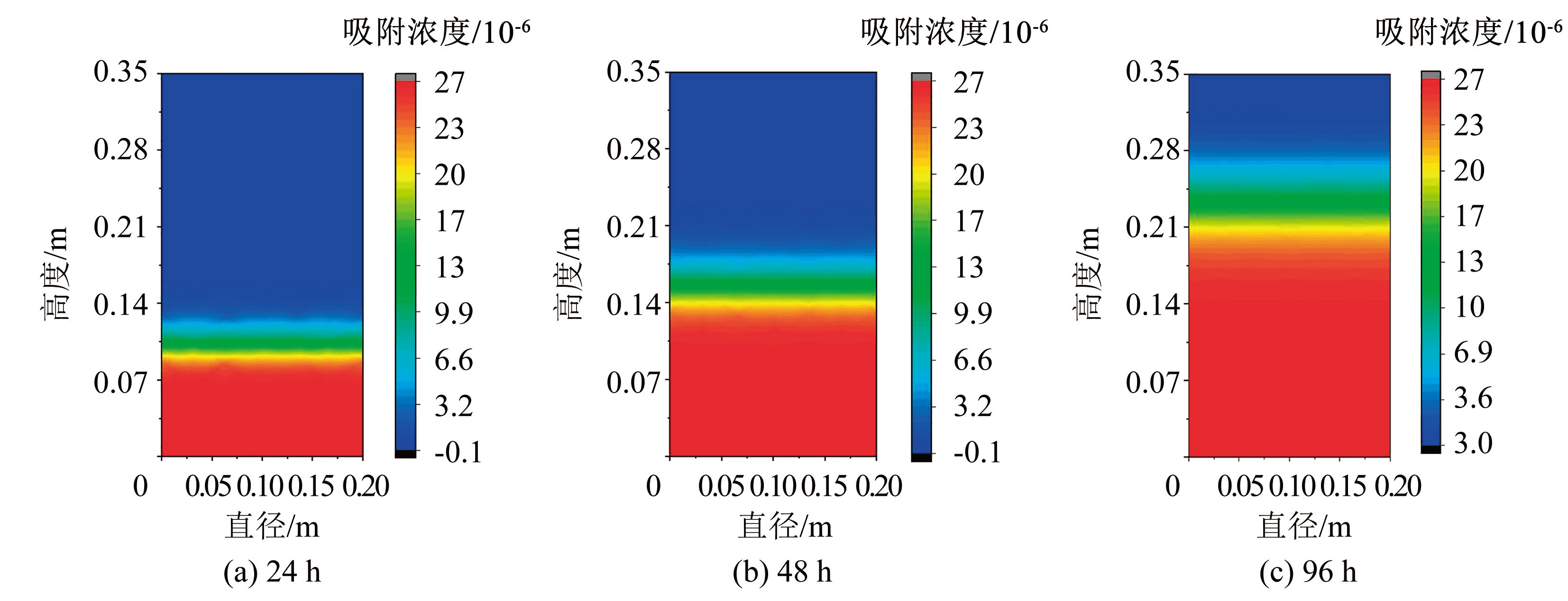
图8吸附浓度变化云图
Fig.8Cloud maps of adsorption concentration

图9污染物结晶体积分数变化云图
Fig.9Cloud maps of crystalline volume content of pollutants
3 结果分析
3.1 液态水迁移及土体渗透性
图10为水分迁移变化曲线,由图10可知土柱底部施加污染源后,在温度梯度和基质吸力的共同作用下,污染物溶液沿土柱底部向上迁移,初期液态水通量较大,同时具有较强烈的波动性,随时间增长,未冻区土体饱和度逐渐增大,液态水通量逐渐减小,且波动性减弱; 顶部冻融循环温度使土柱中形成冻结区,孔隙水冻结削弱了土体的渗透性能,阻碍污染物溶液向上传递。图11为不同时刻土体导水系数变化曲线,由图11可知土柱顶面施加冻融循环温度后,土体基质吸力减小,导水系数急剧下降。
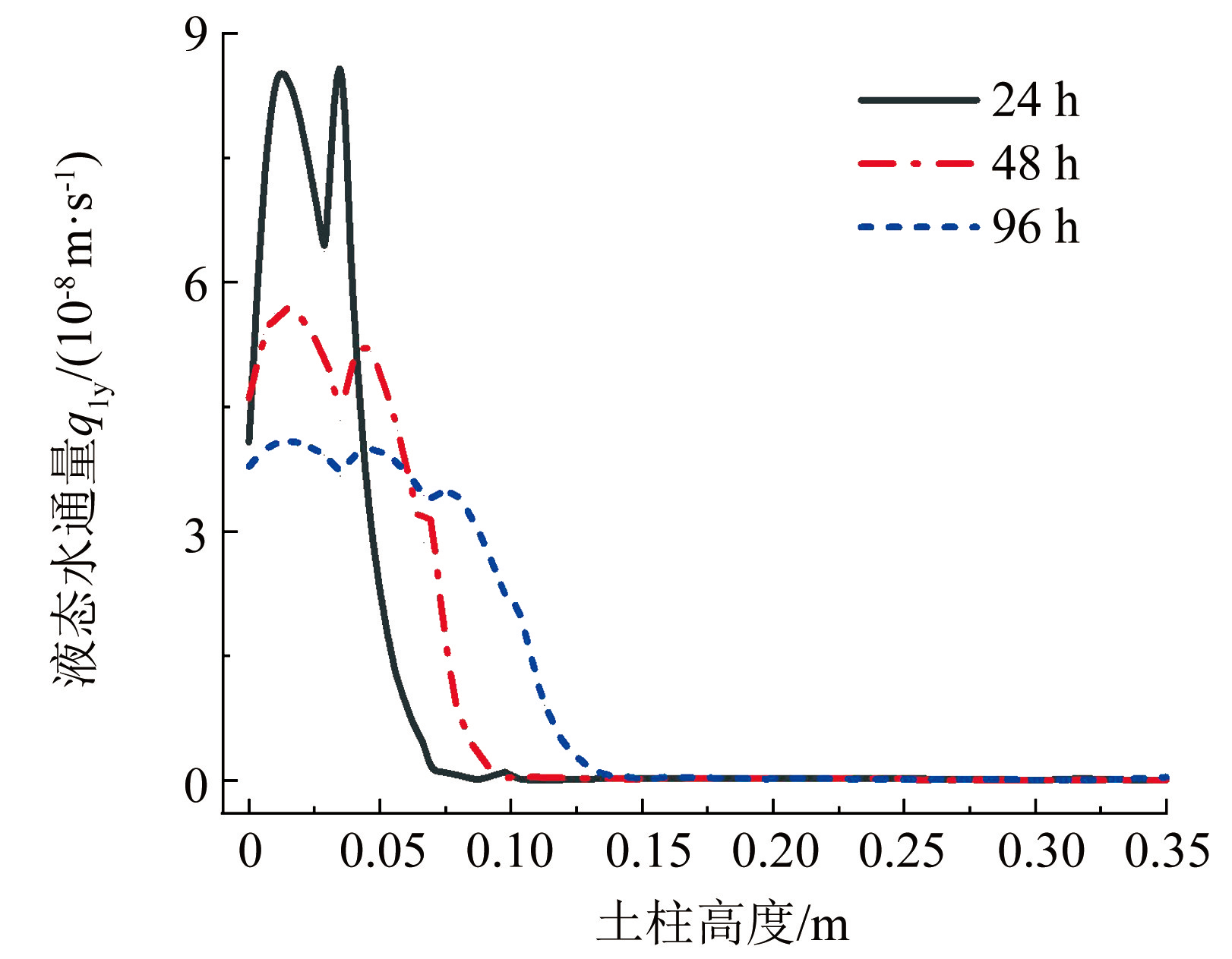
图10液态水通量变化曲线
Fig.10Liquid water flux variation curve
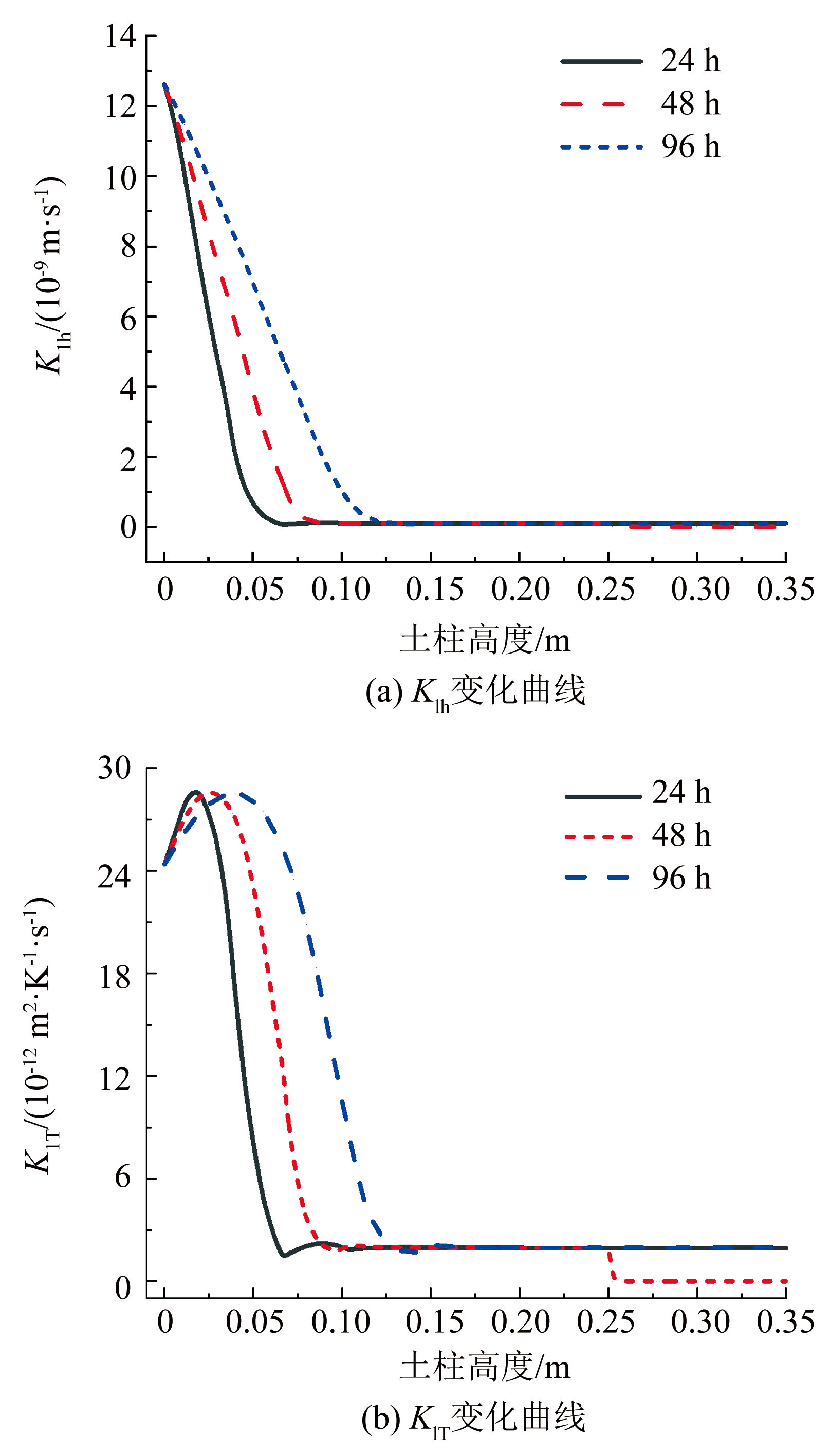
图11土体导水系数变化曲线
Fig.11Soil hydraulic conductivity variation curve
3.2 污染物迁移
图12为土柱高度方向污染物质量浓度及吸附浓度变化曲线,由图12(a)可知,土柱底部施加定质量浓度污染源后,基质吸力使污染物溶液沿土柱高度方向向上迁移,由于冻融循环作用,土体孔隙水逐渐冻结,土体导水性能急剧降低,已有学术观点认为液态水是污染物迁移的主要媒介[23],非饱和土中污染物迁移遵循“盐随水来,盐随水去”的规律[11,23],按此规律,冻融循环作用下土柱中出现冻结层,由于冻结层的阻隔,液态水不能继续向上迁移,失去液态水的携带,污染物也停止迁移,冻结层及以上区域中不会出现污染物。但观察图12(b)可知,土柱顶端污染物质量浓度还随时间缓慢增大,96 h 土柱顶端污染物质量浓度为 0.204 g / L,土体渗透性急剧下降并未完全阻隔污染物迁移,分析原因为:污染物迁移由两部分叠加,随液态水的对流迁移和污染物自身的离子扩散,冻结区液态水对流迁移急剧下降,但污染物还可在离子扩散作用下继续向上迁移,导致冻结区及以上部分出现污染物。
由图12(c)可知,污染物溶液沿土柱高度方向逐渐向上迁移,正温区域污染物与土体颗粒充分接触,土体颗粒吸附点位占满后吸附浓度达到定值; 负温区出现污染物的原因是扩散作用,扩散量虽小,但扩散作用速度较慢,使污染物有充足时间与土体接触,从而使冻结区吸附浓度增大。由图12(d)可知,土柱顶端污染物吸附浓度也随时间逐渐增长,96 h 土柱顶端吸附浓度达到 3.62 × 10-7。
3.3 土体变形
图13为土柱位移变化曲线,由图13( a)可知,在液态水冻结膨胀、污染物结晶膨胀及温度应变的共同作用下,土柱整体处于拉伸变形状态。由图13(b)可知,整个冻融循环过程中若不考虑污染物结晶膨胀时土柱顶点位移最大值为 1.13 mm,考虑污染物结晶膨胀时顶点位移增大了 9%,为 1.23 mm,由此可知,与冰晶体膨胀量相比,污染物结晶膨胀对土体位移影响不明显; 负温作用下,在冰晶体及污染物结晶的双重影响下土柱顶点位移先逐渐增大,当温度循环至正温后,部分冰晶体重新融化,同时污染物溶解度增大,前期析出的污染物晶体部分重新溶解于水,因此,土柱顶点位移由于融陷效应又逐渐减小,依此规律往复循环,顶点位移总体呈波浪式缓慢增大。
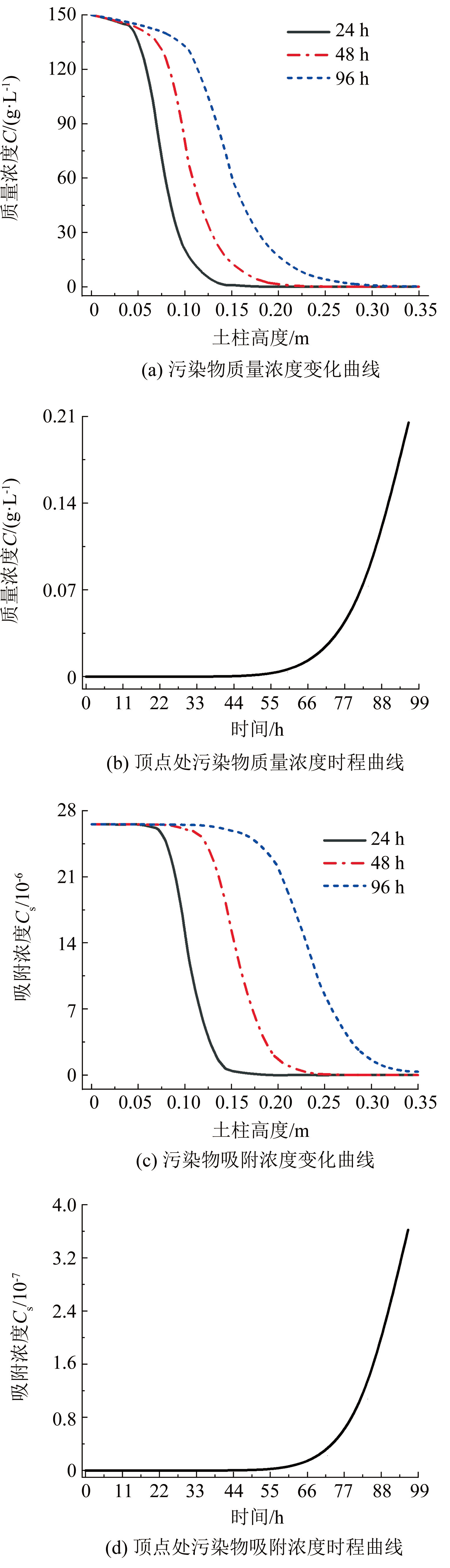
图12污染物迁移变化曲线
Fig.12Pollutants migration change curve
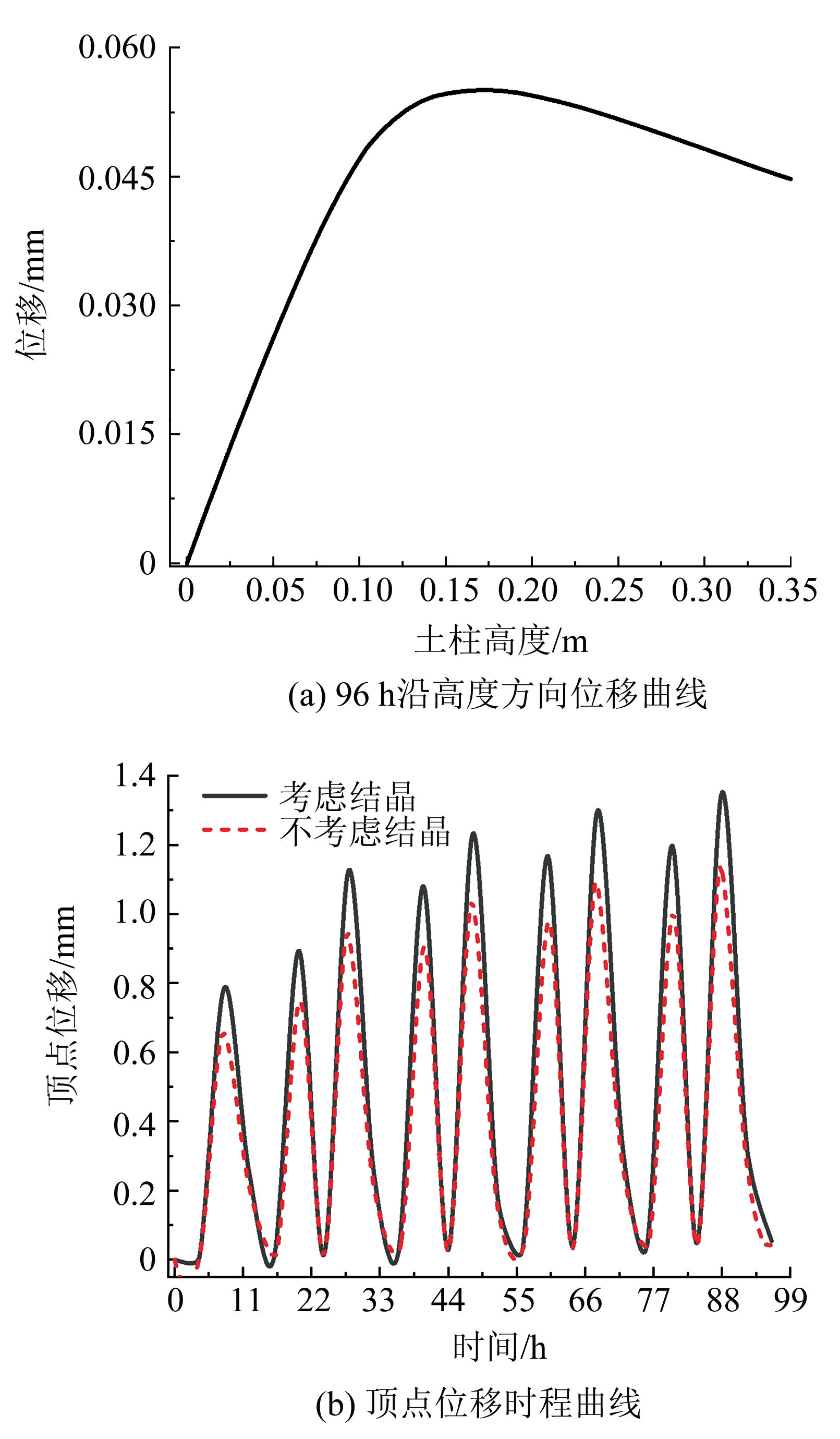
图13位移变化曲线
Fig.13Displacement change curve
4 结论
本文开展了黄土对铅离子的吸附试验及冻融循环条件下铅离子在黄土中的迁移土柱试验,并基于热-质守恒原理构建了非饱和土中污染物迁移的耦合数学模型,通过 COMSOL Multiphysics 仿真软件对模型进行数值求解,评估了模型的可靠性,探讨了各物理量的变化规律,得到如下主要结论:
1)冻融循环条件下,土体温度变化滞后于外界循环温度的变化,土柱上部形成“冻结夹心层”,“冻结夹心层”随时间增长缓慢向下迁移; 冻融循环条件下污染物结晶出现在土柱下部,且结晶体积分数最大值维持在 4% 左右。
2)冻融循环条件下,土体渗透性减弱,作为污染物传递主要媒介的液态水对流通量急剧下降,但并不能完全阻滞污染物的传递,扩散作用还会引起土体冻结区出现污染物,进而引起冻结区土体中污染物吸附浓度增大,96 h 时土柱顶端污染物质量浓度值达 0.204 g / L,污染物吸附浓度值达 3.62 ×10-7。
3)乙酸铅结晶膨胀引起的位移约占土体总位移的 9% 左右,但与冰晶体膨胀量相比,其对土体总位移影响较小; 负温条件下,在冰晶体及污染物结晶的共同作用下,土柱顶点位移先逐渐增大,当温度循环至正温后,部分冰晶体融化,析出的污染物晶体也部分重新溶解,导致土柱顶点位移又逐渐减小,依此规律往复循环,但顶点位移总体呈波浪式缓慢增长。

