摘要
为探明开采过程中采空区典型岩体碎胀-储水演化特性及内在机制,基于自主研发的岩石三轴流固耦合试验系统推导了岩样碎胀、储水系数同步测试方法,针对粗砂岩、粉砂岩和泥岩开展了三轴加载岩样全应力应变过程碎胀-储水系数测定试验,并采用核磁共振成像同步获取了岩石内部裂隙空间分布情况。结果表明:3 类岩样的碎胀、储水系数随加载进程逐渐增大并趋于稳定,对应应力应变曲线 4 个阶段呈阶段性梯度变化。其中,储水系数随着应变变化呈现较好的双参数 Weibull 分布。初始孔隙度在一定程度上影响着新生裂隙扩展形态及岩样储水空间,随着岩样初始孔隙度增大,储水系数在峰前 80% 及以前呈线性增大关系,之后呈指数增大关系。基于碎胀系数计算的储水系数理论值和试验实测值演化规律一致但数值具有明显差异,最大差值可达 0. 7% ,具有明显的“先碎胀后储水”特征。岩样的碎胀、储水系数受应力加载与初始孔隙度的耦合影响,在加载初期由初始孔隙度主导,逐渐过渡至应力主导,最终由应力及岩体孔裂隙贯穿程度共同决定。
Abstract
To explore the broken expansion and water storage evolution characteristics and internal mechanism of typical rock masses in goafs during mining, a synchronous test method of broken expansion coefficient and water storage coefficient based on a self-developed rock triaxial fluid-solid coupling test system was developed. A triaxial loading test was conducted on rock samples of coarse sandstone, siltstone, and mudstone to determine the broken expansion and water storage coefficients in complete stress-strain process, and the spatial distribution of internal fractures in the rock was synchronously obtained via nuclear magnetic resonance imaging. The results show that the broken expansion and water storage coefficients of the three types of rock samples gradually increase and tend to stabilize with the loading process, and the corresponding stress-strain curve shows a phased gradient change in four stages. Among them, the water storage coefficient exhibits a good Weibull distribution with strain variation. The initial porosity affects the expansion morphology of newly formed fractures and the water storage space of rock samples to some extent. As the initial porosity of rock samples increases, the water storage coefficient shows a linear increasing relationship before 80% prepeak, and then an exponential increasing relationship. The theoretical value of the water storage coefficient calculated based on the expansion coefficient is consistent with the evolution law of the experimental measured value, but the difference in value can reach up to 0. 7% , indicating a clear characteristic of first broken expansion followed by water storage. The broken expansion and water storage coefficient of rock samples are influenced by the coupling effect of stress loading and initial porosity. In the initial stage of loading, the initial porosity dominates, gradually transitioning to stress dominance, and is ultimately determined by both stress and the degree of penetration of rock pores and fractures.
中国是全球最大的煤炭生产和消费国,煤炭的主体能源地位较长时期内不会发生改变[1]。西部矿区煤矿规模开采与环境保护之间的矛盾关系使 “绿色矿山”推进迫在眉睫[2]。以顾大钊院士为首的学者推行的采空区储水工程,可有效改善矿区缺水现状,成为西部生态脆弱区水资源保护利用的有效途径[3-4]。采空区垮落岩体孔裂隙是煤矿地下水库主要储水空间,研究典型顶板覆岩的碎胀与储水特性对揭示地下水库储水结构形成机理具有重要科学意义。
国内外学者对采空区破碎岩体的碎胀特性开展了系列研究,并取得了一定的研究成果。针对碎胀系数演化规律,文献[5]讨论了采空区岩体碎胀系数对灌浆钻孔尺寸预测精度的影响; 文献[6] 利用自制的承压破碎煤体渗流及自燃测试装置,开展压实试验,分析了破碎煤体在应力场、温度场和水分环境共存的条件下碎胀系数的演化特征; 文献[7] 对软弱破碎围岩进行了二次成岩压实,通过试验研究将成岩过程分为压实破碎和固结二次成岩两个阶段,并分析了压实破碎阶段的力学机制; 文献[8]对矸石开展单轴压缩试验和破碎后压实试验,探讨了压实过程中应变、碎胀系数、压实度与应力的关系。
随着研究的不断深入,学者们发现不同性质岩体的碎胀特性差异明显,如文献[9-11]对煤、页岩和砂岩 3 种岩样进行破碎,结合压实过程中的应力-应变关系,分析了粒径、强度对破碎岩石应力-碎胀系数演化规律影响; 文献[12]对顶板砂岩、砂质泥岩和泥岩进行破碎并开展压实试验,分析了岩石强度、块径、压实应力对碎胀特性的影响; 文献[13-14] 开展了不同块度砂岩、泥岩和煤的碎胀与压实变形试验,阐述了尺寸效应对煤岩碎胀与压实变形的影响,并通过模型试验揭示了饱水岩石压实特性,明确垮落岩体应力-碎胀系数关系。
为进一步揭示破碎岩体的储水机理,学者们逐步聚焦碎胀系数与岩体物理力学之间的定量关系,如文献[15]研究了采空区垮落岩体强度与碎胀系数的关系,明确了两者之间的数学表达式; 文献[16]采用数学方法建立垮落岩体碎胀系数计算模型; 文献[17]通过数值模拟研究了煤层开采覆岩动态破坏过程中采空区垮落岩体碎胀效应; 文献[18]基于采空区垮落岩体碎胀特性分区特征,推导出相应的碎胀系数公式; 文献[19]采用室内实验与理论分析相结合的方法,探讨了煤岩体强度、粒径级配、时间与碎胀系数的定量关系。
上述研究的对象多为破碎岩体,且大多数学者以垮落带和裂隙带孔隙率等同于储水系数,对顶板岩层整个应力应变过程中的碎胀和储水特性的同步演化规律鲜有研究[20-21]。垮落带和裂隙带孔隙率是理想状态下的最大储水系数,但实际工程中,由于岩体所处的应力状态和破碎程度不同,一些未贯通或较小的孔隙无法进行储水[21]。采空区垮落岩体的破坏过程是揭示储水通道演化机制的关键,碎胀及储水系数的耦合演化规律对地下水库结构形成具有重要影响。基于此,本文依托典型矿区,采用自主研发的岩石三轴流固耦合试验系统,推导了岩样碎胀、储水系数同步测试方法,研究 3 种典型地下水库岩体全应力应变过程中的碎胀-储水特性演化规律,获取各类岩体不同应力阶段碎胀-储水系数的定量关系,为煤矿采空区地下储水工程奠定理论基础。
1 试验
1.1 测试原理
针对现有试验方法无法同时测量试样的碎胀和储水系数的难题,本文基于自主研发的岩石三轴流固耦合试验仪,提出了岩样碎胀、储水系数同步测试方法,具体原理如图1所示。试样在三轴加载条件下逐渐变形、失稳直至破坏,由于水可视为不可压缩的流体,当试样变形产生碎胀现象时将挤出围压腔中的水,同时轴向水头将对试样加载产生的孔裂隙进行渗流补压。基于实时测量的仪器围压腔及流固耦合腔体内注水体积变化,可以计算试样的实时体应变、碎胀与储水系数参数值。
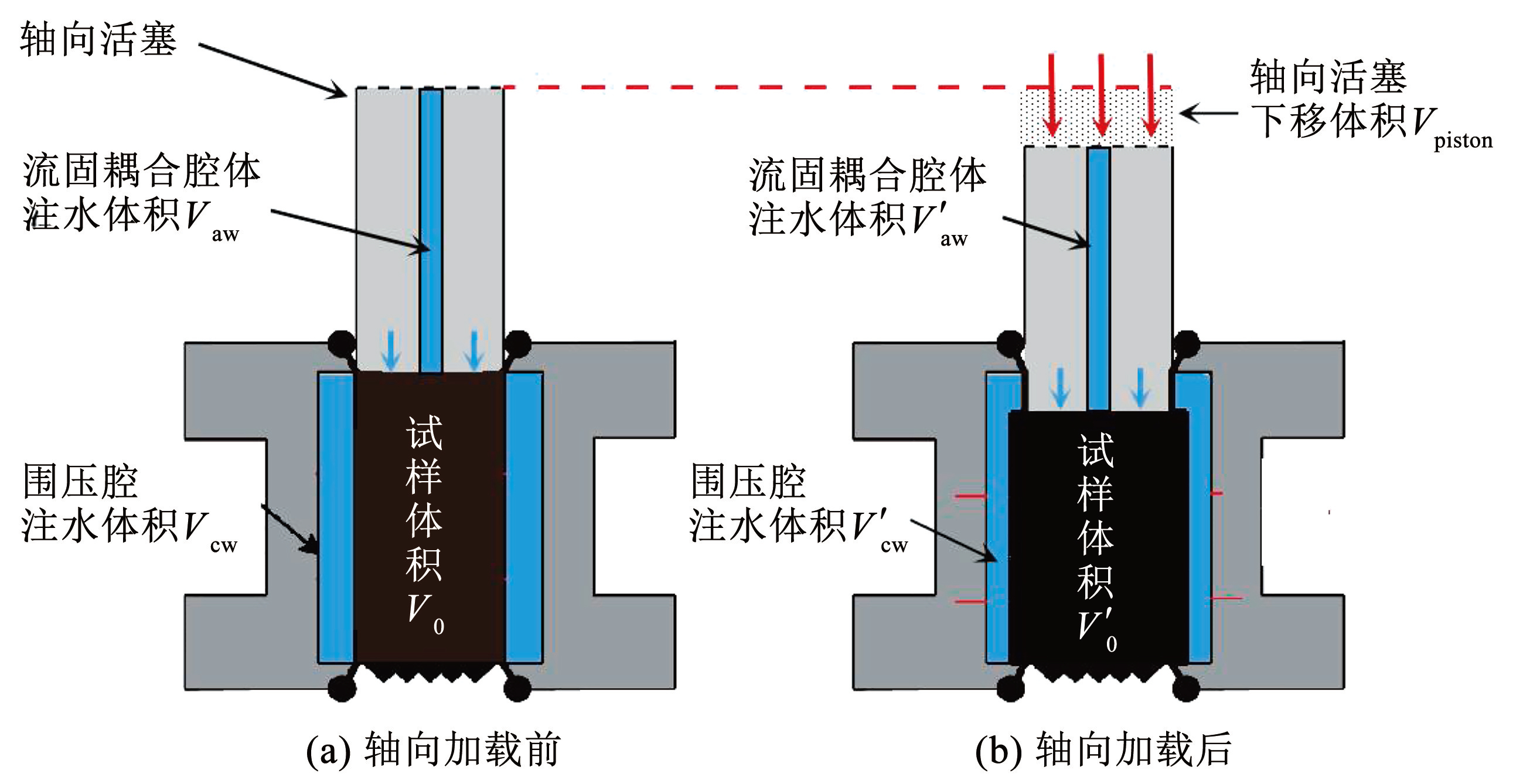
图1碎胀和储水系数同步测试原理
Fig.1Synchronous testing principle of broken expansion and water storage coefficient
本文采用式(1)、(2)计算试验中试样的实时碎胀系数 Kp和实时储水系数 β。
(1)
(2)
式中:Kp为试样的碎胀系数; V0、V′0 分别为试样加载前后的实时体积; Vcw、V′cw分别为加载前后试验仪围压腔的注水体积; Vaw、V′aw分别为加载前后流固耦合腔体内的注水体积; Vpiston为轴向活塞下移体积; β0为初始储水系数,通过饱水试验测得。
1.2 试验仪器
上述自主研发的岩石三轴流固耦合试验仪,主要包括信息采集模块、自平衡三轴加载模块、流体注入控制模块[22]。轴向载荷由伺服压力机施加,并通过活塞杆传递给试样。活塞杆中间设有沿轴心方向的孔道,并且在活塞外表面开孔与轴心孔道联通,形成自平衡结构,避免了高压流体注入后在活塞杆底部产生反力造成的试验误差和安全隐患。仪器可进行流固耦合作用下岩石的单轴加载、三轴加载和渗透率测定试验,试验过程中可精确测量试件轴向应力与应变、环向应力与应变、碎胀与储水系数等相关参数。
将岩石三轴流固耦合试验仪耦合集成于 MacroMR12-150C-1 型核磁共振测试分析系统,如图2所示。与传统机型相比,该仪器采用了独立的脉冲控制模块及射频收发电路,进一步提高了脉冲序列的准确性和核磁共振信号的信噪比,保证了仪器的整体稳定性。仪器配套有核磁孔径分析和成像识别软件,配合流固耦合试验仪可对不同应力阶段岩样进行孔隙度和孔径分布测试,并获取岩样的孔裂隙分布图像。

图2岩石三轴流固耦合试验仪整体结构及原理
Fig.2Structure and principle of rock triaxial fluid-solid coupling test system
1.3 试样制备
基于内蒙古东胜煤田上湾煤矿地质调查资料,选取粗砂岩、粉砂岩及泥岩 3 类不同岩性岩体,并根据相关试验规范制作标准圆柱型(Φ50 × 100 mm)试样。为了得到具有统计特征的试验结果,避免原生裂隙含量差异对试验结果的干扰,同类试样取自同一岩块,且在试验前对制作的标准试样进行超声波检测,根据试样的超声数据挑选波速相近的试样进行试验。
1.4 试验流程
试验聚焦岩样在全应力应变过程中的碎胀-储水特性,具体试验步骤:1)参考文献[23]的饱水试样制样方法,将试样没水浸泡 14 d,定期称重,制成饱水试样; 2)将饱水试样放置于岩石三轴流固耦合试验仪腔体内部并组装好试验仪,控制伺服压力机向试样施加 2 kN 的预紧压力; 3)连接恒速恒压泵,通过恒压模式分别向围压腔和流固耦合腔体内部注入稳定水压。为了让水流尽快的填充试样储水空间,以降低时间对储水效果的影响,选择较大的渗透压 1 MPa。为保证垮落带岩体的低围压状态,并保证围压与渗透压有足够压差以保证试验效果,围压选择 1.5 MPa [17]; 4)以 0.1 mm / min 的位移加载速度轴向加载直至试样失稳破坏,确保恒速恒压泵流体注入及回压的反应时间,实时记录加载过程中双缸恒速恒压泵在恒压模式下的流量参数; 5)加载过程中,对峰前强度 20%、40%、60%、80%、100% 和峰后强度 80%、40% 应力状态下的试样进行孔隙结构测试并利用核磁共振系统扫描成像(图3)。
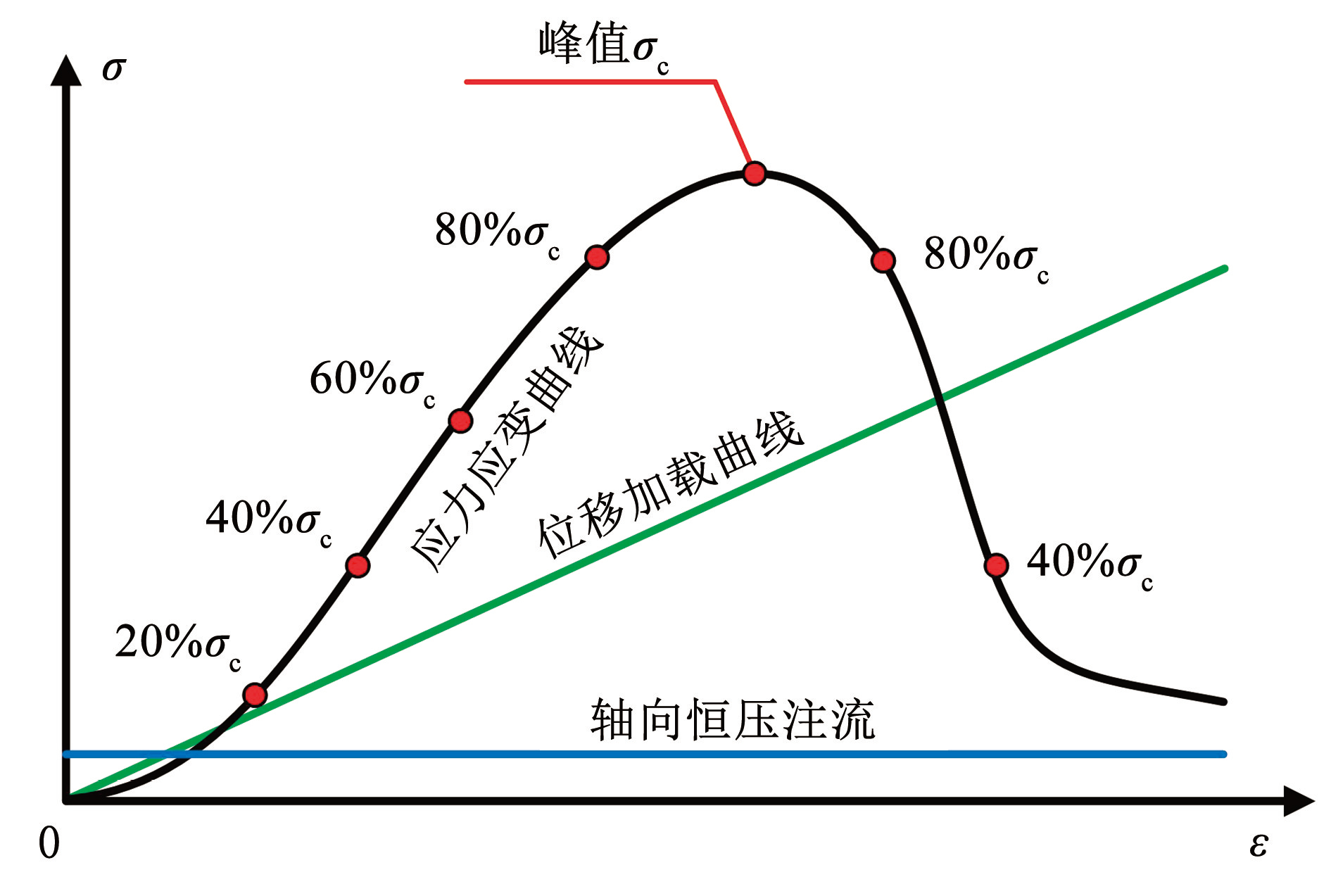
图3应力加载点分布
Fig.3Distribution of stress loading points
2 试验结果与分析
2.1 全应力应变碎胀-储水系数演化规律
试验获取了 3 类岩样在三轴流固耦合加载过程中的应力、应变和流量等数据,并计算了岩体的碎胀系数和储水系数。碎胀系数的倒数和储水系数均可反映岩体的储水能力,二者和应力应变曲线的耦合规律如图4所示。为更好地阐明典型应力阶段不同岩样储水系数变化规律,选择达到峰前强度 20%、 40%、60%、80%、100% 和峰后强度 80%、40% 应力状态点处的储水系数进行耦合分析,不同应力阶段储水系数变化如图5所示。

图4各类试样全应力应变过程碎胀与储水系数变化曲线
Fig.4Variation curves of broken expansion and water storage coefficient during complete stress-strain process
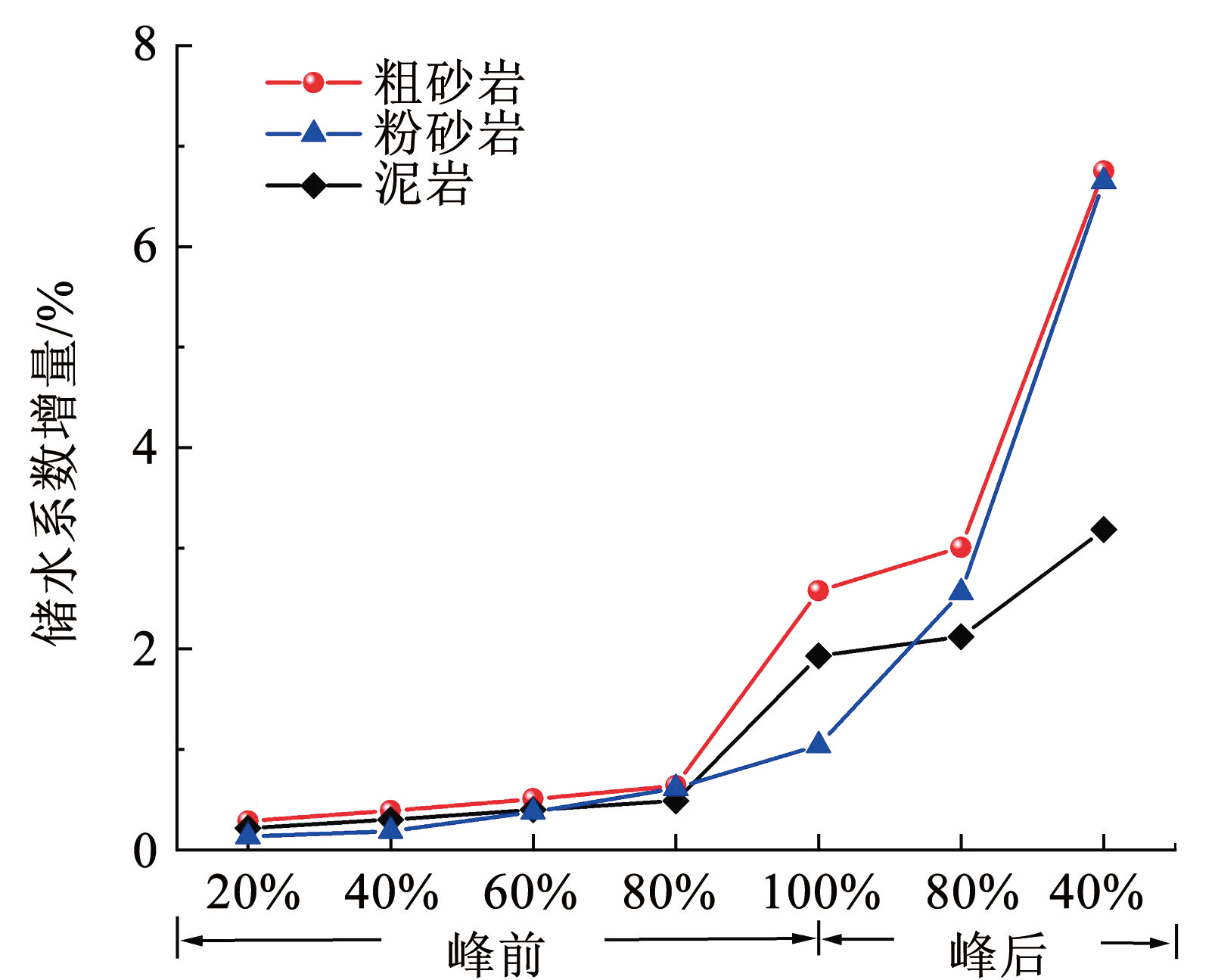
图5不同应力阶段岩样储水系数
Fig.5Water storage coefficient of rock samples at different stress stages
由于碎胀系数倒数和储水系数变化规律基本一致,此处仅就储水系数进行分析。在整个加载变形过程中,3 类岩样的储水系数均逐渐增大并最终趋于稳定。对应应力应变曲线的 4 个典型阶段,储水系数也呈阶段性梯度变化。粗砂岩、粉砂岩和泥岩的初始储水系数分别为 2.18%、1.97% 和 1.11%。在岩样的压密和弹性变形阶段(80% 以前),3 类岩样的储水系数随着应力的增大缓慢增长,增长幅度均在 0.2%~0.5% 之间波动; 在岩样的屈服变形阶段(80%~峰值强度),3 类岩样的储水系数显著增长,粗砂岩、粉砂岩和泥岩的储水系数分别增长至 4.78%、3. 01% 和 3. 04%,增长率分别为 119.3%、 52.8% 和 175.5%,在此阶段,初始储水系数较小的泥岩的储水系数超过了孔隙度较大的粉砂岩; 在岩样的破坏阶段(峰值破坏~峰后 40%),3 类岩样的储水系数继续快速增长,储水系数分别增长至 8.96%、8.45% 和 4.29%,增长率分别为 311. 0%、 328.9%和286.5%; 在进入破坏后压实阶段后,3 类岩样的储水系数随着应力的增大缓慢增长并趋于稳定,侧面说明储水系数在全应力应变过程中存在最大值。
对于加载产生碎胀变形的试样,其储水空间主要为加载过程产生的孔裂隙结构。损伤变量是材料内部不可逆的细观结构变化在宏观上的表述[24-25]。借鉴常规混凝土的损伤变量来表征试样的储水系数变化规律,利用双参数的 Weibull 分布公式(式 3)对该曲线进行拟合[26]。拟合曲线和拟合结果如图6和表1所示,函数关系式拟合的相关系数均大于 0.95,表明拟合相似度良好。需要说明的是,式(3)是基于岩体轴向变形计算储水系数的经验公式,而工程现场中岩体变形是可以获取的参数,因此该公式具有一定的实用性。
(3)
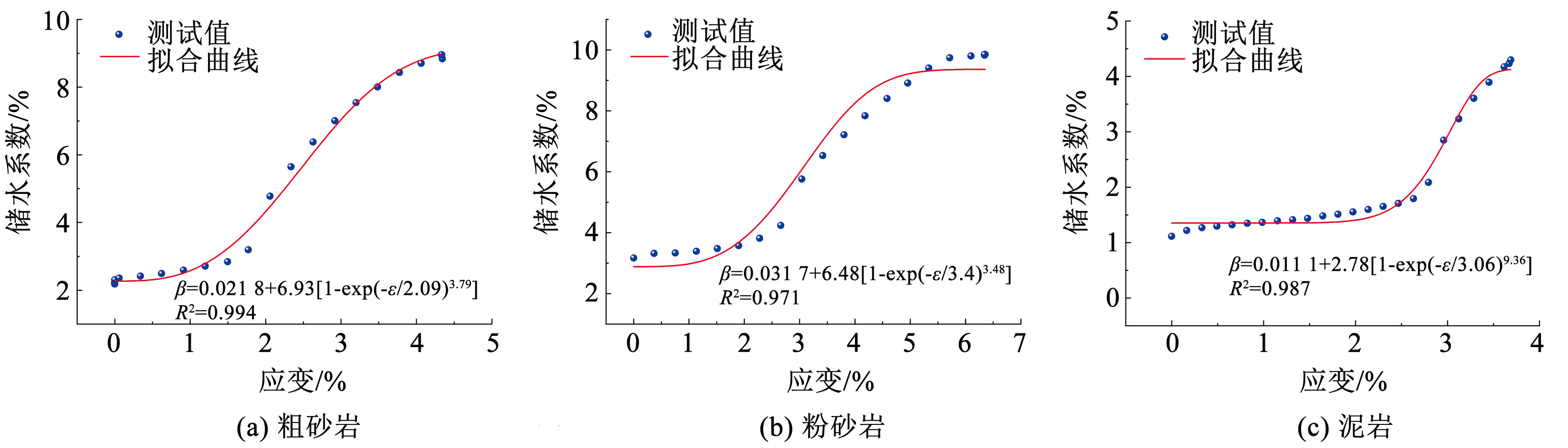
图6破碎岩石储水系数与应变拟合关系曲线
Fig.6Fitting curves between water storage coefficient and strain of broken rock
表1破碎岩石储水系数与应变拟合关系
Tab.1 Fitting relationship between water storage coefficient and strain of broken rock

2.2 全应力应变过程碎胀-储水系数差异分析
目前,大多数学者直接将储水系数与碎胀系数关联起来。文献[20] 总结了储水系数与采空区破碎岩体碎胀系数二者之间的关系:
(4)
式(4)没有考虑岩体的初始储水系数,本文对其进行改进,得到了全应力应变过程中基于碎胀系数的储水系数计算公式:
(5)
通过式(5)计算得到的储水系数称之为理论值,试验中直接测试获取的称为测试值。本文 3 类岩样的储水系数理论值与实测值随应变的变化关系如图7所示。从图7中可以看出,储水系数理论值与实测值具有较好的相关性,随着应变增大,均表现为由缓慢增长至急剧增长并最终趋于稳定。此外,3 类岩样在压密阶段的储水系数理论值低于实测值,而在压密阶段以后储水系数理论值均高于实测值。
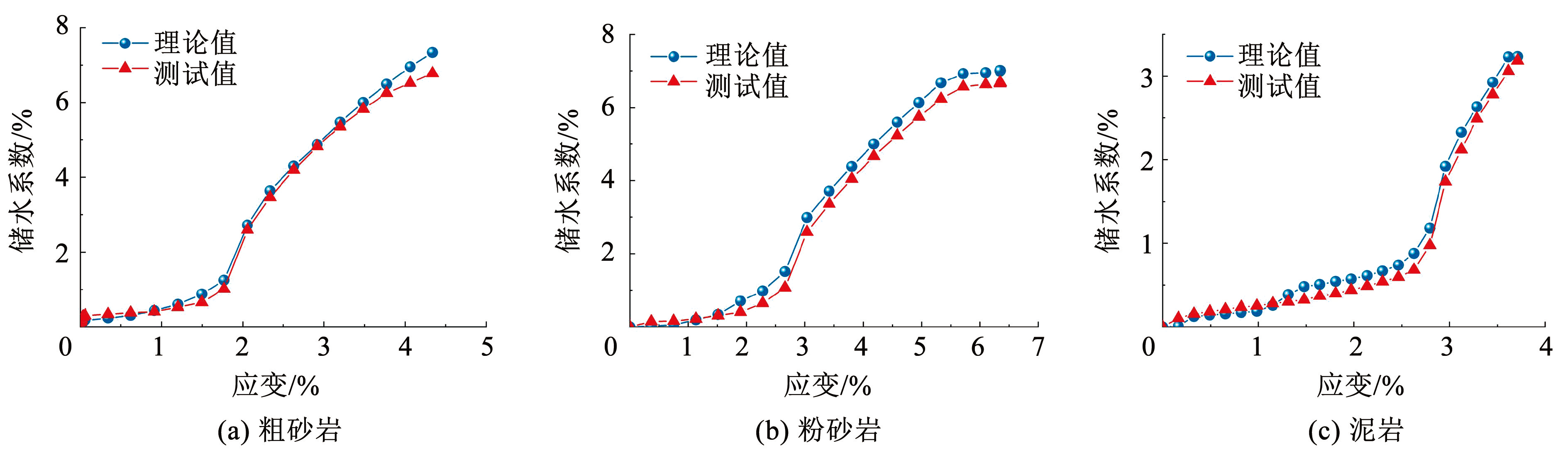
图73 类岩样储水系数理论值与实测值对比
Fig.7Comparison between theoretical and measured water storage coefficients of three rock samples
为了更直观地表述储水系数理论值和实测值之间的差异,将 3 类岩样储水系数理论值与实测值的差值绘制成图8,其中蓝色区域高度即为二者差值。从图8中可以看出,粗砂岩与粉砂岩的最大差值约 0.7%,泥岩的最大差值约 0.3%,差值数值约占岩样最终储水系数的 10%。在岩体的压密阶段,理论值和实测值的差值为负值。原因是在此阶段岩石未产生碎胀变形,储水系数理论值基本不变。但由于初始 1 MPa 流体压力的原因,水体会进一步渗流充填孔隙并达到新的饱水状态,导致储水系数实测值增大。随着应力进一步加载,储水系数差值很快趋于正值并不断增大,并于峰值破坏处达到最大值。
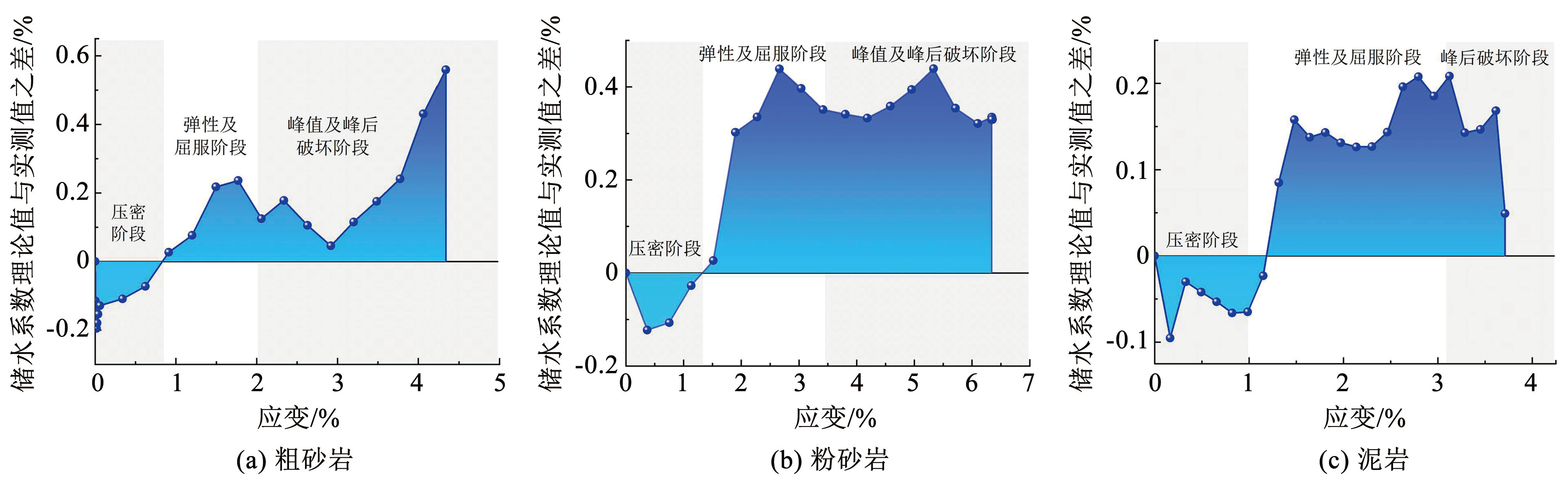
图83 类岩样储水系数理论值与实测值之差
Fig.8Difference between calculated and measured water storage coefficients of three rock samples
造成上述现象的原因为储水系数理论值是基于实测的碎胀系数得到的,它更多地反映出岩石的体积变化对储水系数的影响。而储水系数测量值能直接表征岩石内部真实储水情况。二者之间的差异本质是岩石的碎胀特性与储水特性之间的差异,反映了岩石在碎胀-储水过程存在转化效率问题。理想状态下,岩石碎胀产生的导水裂隙可完全作为储水通道。但在实际中,新生孔裂隙的空间分布位置对储水性能有很大影响,如远离轴向水头产生的孔裂隙,其达到饱和储水状态就需要较长渗流时间。另一方面在应力的作用下,原生孔裂隙压密闭合,影响着流体进入,由此造成储水系数实测值偏低。由此可见,储水特性相较于碎胀特性在时间上具有滞后性,即先碎胀后储水,这种情况在工程现场中也是同样存在并值得注意的。
2.3 不同岩性试样初始孔隙分布和储水系数关系分析
在三轴加载试验开始前,测试得到了 3 类岩样的初始孔隙分布,以及在不同应力阶段对应的储水系数,如图9所示。图9中,岩样孔隙分布特征通过 T2弛豫分布曲线中的谱峰数量、高度、形状和宽度表征,T2值越大表示孔隙尺寸越大,峰面积越大表示该区间内的孔隙数量越多[29]。从图9可以看出,粗砂岩、粉砂岩的初始孔隙度较大,分别为 14.4%、 13.93%,泥岩初始孔隙度较小,为 6. 00%。从图10可以看出,随着岩样初始孔隙度增大,储水系数呈增大趋势。在峰前 80% 应力阶段及以前,初始孔隙度和储水系数基本呈正相关线性关系。在峰前 80% 应力阶段以后,两者不再呈线性关系,3 类岩样的储水系数均急剧增长,但最终储水系数从大到小仍然是粗砂岩、粉砂岩和泥岩。
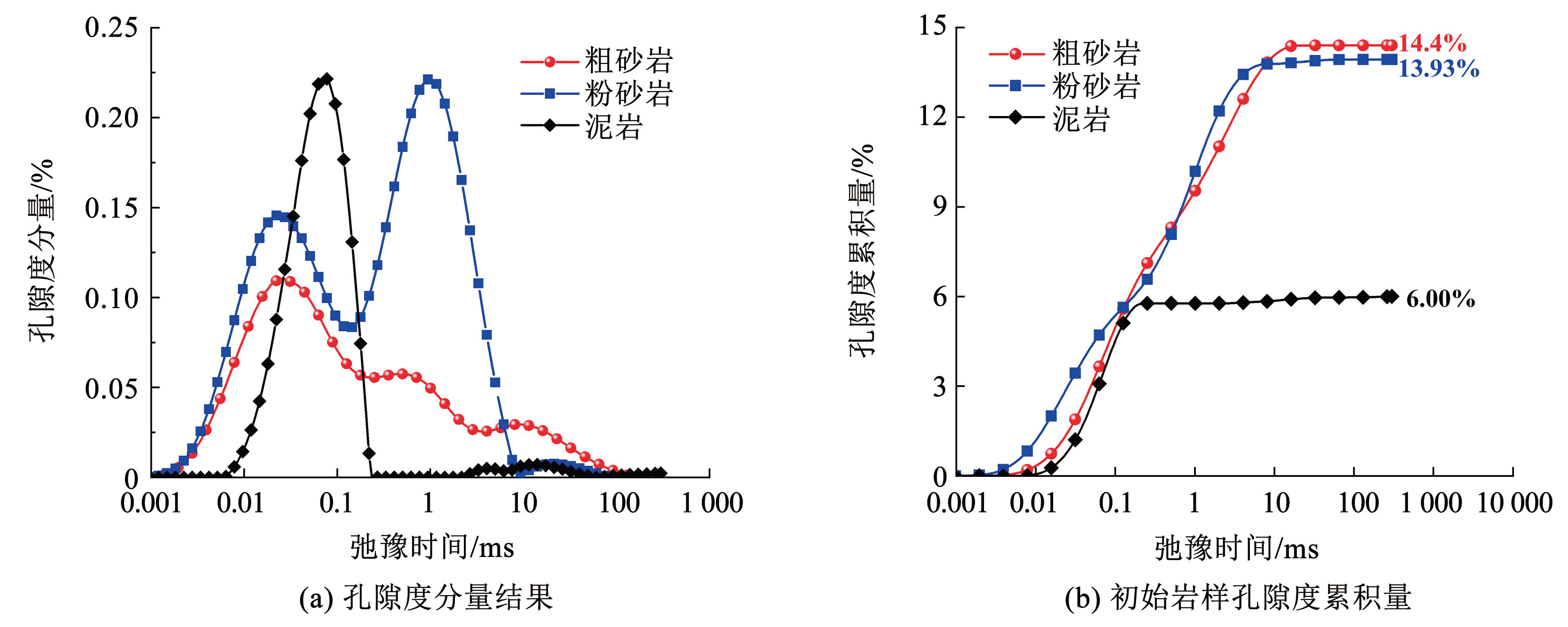
图93 类试样初始孔隙度测试结果
Fig.9Test results of initial porosity for three rock samples
初始孔隙度反映了原生孔隙、裂隙的发育程度,在一定程度上影响着新生裂隙扩展形态。如图9所示,与初始孔隙度较小的泥岩相比,初始孔隙度较大的粗砂岩和粉砂岩的 T2谱峰值较大,且谱峰之间连续性较好。这说明两类岩体的中孔和大孔占比较高,初始孔裂隙之间的连通性较好,有利于再生裂隙发育,形成储水空间。
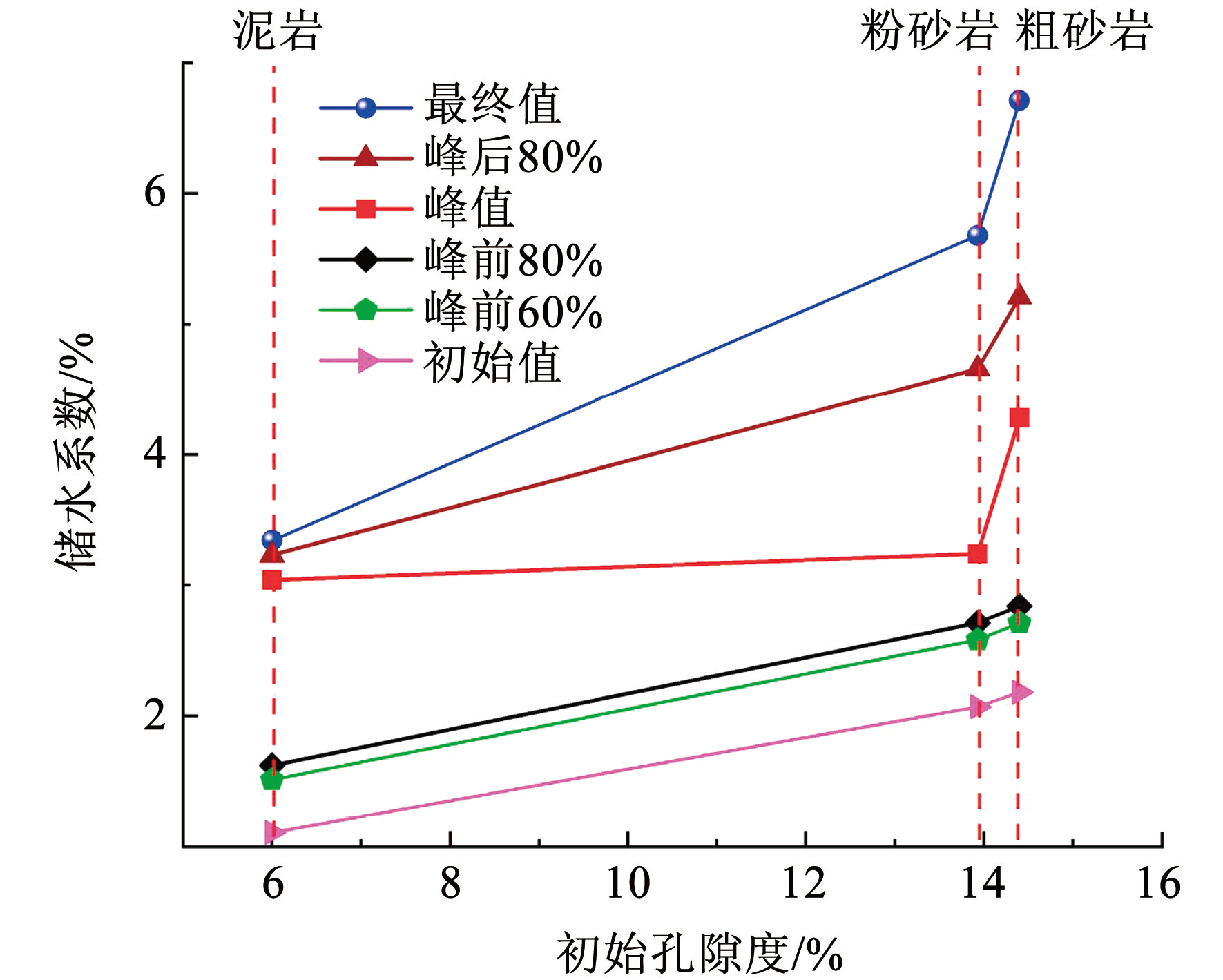
图10不同应力阶段岩样的初始孔隙度和储水系数
Fig.10Initial porosity and water storage coefficient of rock samples at different stress stages
3 不同应力阶段岩体储水系数演化机制分析
为了更直观地阐述全应力应变过程中岩体储水系数演化机理,对不同应力阶段岩体的孔隙度变化进行分析,如图11所示。利用核磁共振波谱成像技术,获取了不同应力阶段岩样内部孔裂隙结构及空间分布。以粗砂岩为例,利用核磁共振技术对不同应力加载阶段下的试样进行成像,分别得到沿试样纵向和横向方向的核磁图像,如图12所示。图12中,蓝色为背景颜色,红色像素点表示充满流体的孔隙空间,颜色越深表示孔径越大。
从图11中可以看出,在峰前 20%~60% 应力阶段,岩体的储水系数基本无变化,原因是此时的岩样处于弹性变形阶段,其初始孔裂隙为主要储水空间。随着加载进程的推进,在峰前 80% 阶段原生孔裂隙进一步发育,并伴随着新生微小裂隙的产生,造成储水系数的缓慢增大。上述阶段岩体内部虽然有较多孔裂隙发育,但从图11的孔隙度曲线和图12可以看出,此阶段并没有产生大的裂隙,因此储水系数没有大的变化,岩体的储水系数仍然由初始孔隙度决定。当应力加载进入峰值破坏阶段,岩体发生脆性破坏,内部产生较大裂隙,岩体孔隙度迅速增大,储水系数也发生了跳跃式增长。此阶段,初始孔隙度最小的泥岩孔隙率增大率最大,其储水系数(1.928%)首次超过了粉砂岩的储水系数(1. 070%),应力的主导作用逐渐明显。当应力进一步加载,进入峰后 80% 和 40% 阶段,此阶段 3 类岩体的孔隙度均不再发生大的变化,但是储水系数却仍然快速增大。从图12可以看出,此阶段虽然没有较大的新生裂隙,但是在应力的持续作用下岩体碎胀程度进一步增大,裂隙继续扩展并滑移贯通形成主断裂面,因此储水系数呈现数量级的增长。纵观整个应力阶段,岩体储水系数的变化由初始孔隙度主导,逐渐过渡至应力主导,最终由应力及岩体孔裂隙的位置和贯穿程度共同决定。
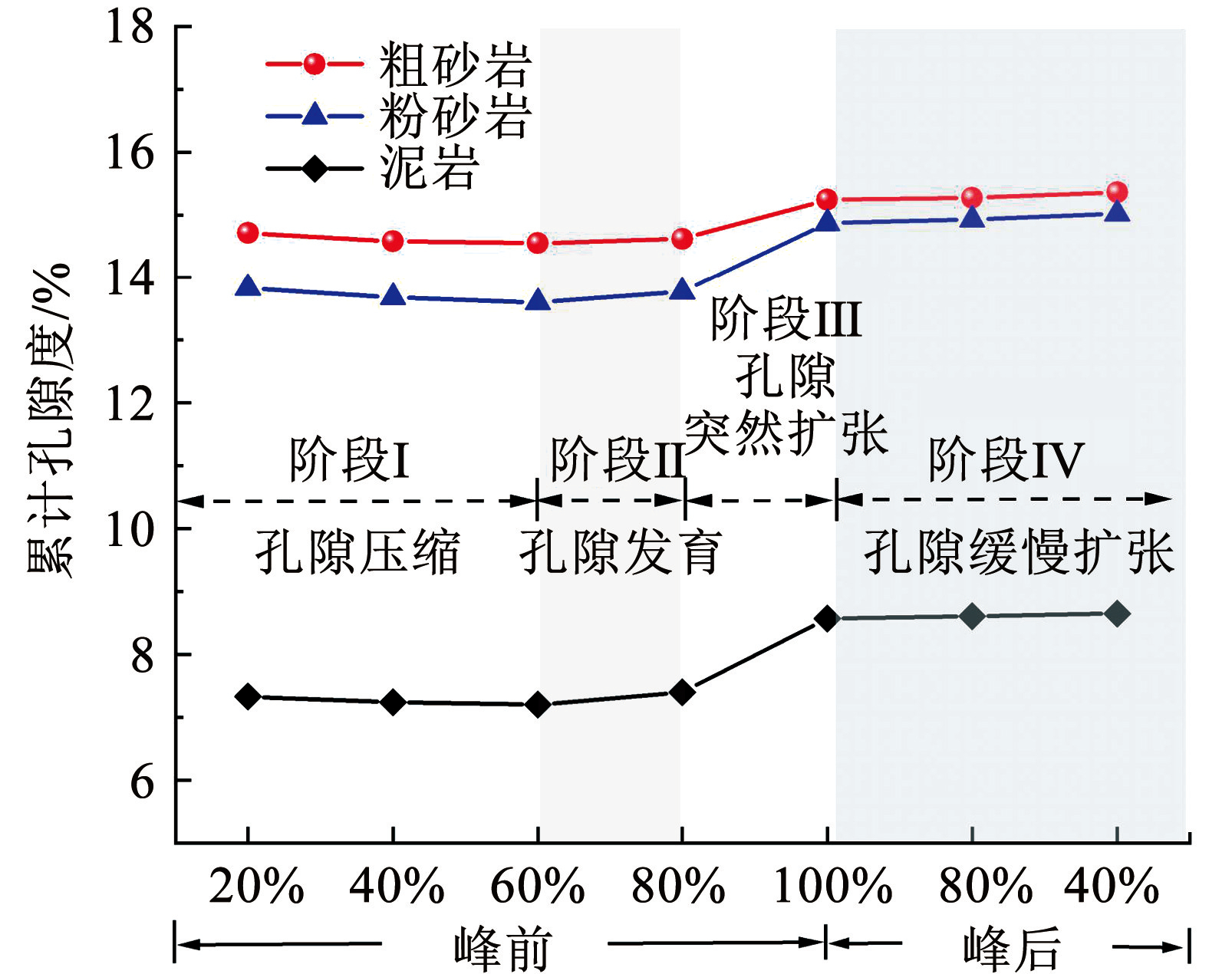
图11不同应力阶段岩样的孔隙度演化规律
Fig.11Porosity evolution of rock samples at different stress stages
图12粗砂岩全应力应变过程核磁共振成像图
Fig.12NMR imaging diagram of coarse sandstone in complete stress-strain process
4 结论
1)基于自主研发的岩石三轴流固耦合试验系统及提出的岩样碎胀、储水系数同步测试方法,获取了粗砂岩、粉砂岩和泥岩在全应力应变过程中碎胀-储水特性,发现 3 类岩样的碎胀、储水系数均随加载进程逐渐增大并最终趋于稳定,且对应应力应变曲线的 4 个典型阶段呈阶段性梯度变化。其中,储水系数随着应变变化呈现较好的双参数 Weibull 分布。
2)基于碎胀系数计算的储水系数理论值和试验实测值演化规律一致但数值具有明显差异。 3 类岩样在压密阶段的储水系数理论值低于实测值,而在压密阶段以后储水系数理论值均高于实测值,最大差值可达0.7%,具有明显的“先碎胀后储水”特征。
3)初始孔隙度在一定程度上影响着新生裂隙扩展形态及岩样储水空间。随着岩样初始孔隙度增大,储水系数呈增大趋势,在峰前 80% 应力阶段及以前呈线性关系,之后呈指数关系。
4)借助基于核磁共振波谱成像技术获取的岩样内部裂隙结构及空间分布演化规律,对不同应力阶段岩体储水系数演化机制进行了分析,发现岩体储水系数首先由初始孔隙度主导,逐渐过渡至应力主导,最终由应力及岩体孔裂隙贯穿程度共同决定。

