欢迎访问《哈尔滨工业大学学报》编辑部网站！

三维重构黏弹性半空间体上多层板连续上坡路面动力学响应

doi: 10.11918/202304011

李少奇¹ ，严战友^2,3 ，崔永昌¹ ，侯雪可¹ ，王子俊³ ，乔博³

1. 石家庄铁道大学交通运输学院,石家庄 050043

2. 省部共建交通工程结构力学行为与系统安全国家重点实验室 (石家庄铁道大学),石家庄 050043

3. 石家庄铁道大学土木工程学院,石家庄 050043

详细信息

作者简介

李少奇(1998—),男,硕士研究生;

严战友(1984—),男,博士,副教授

通讯作者

严战友,yanzhanyou@163.com

中图分类号: U416.01;O344.3

文献标识码: A

文章编号: 0367-6234(2025)03-0129-10

Dynamic response of continuous uphill pavement withmulti-layer plate on viscoelastic half-space foundation on a 3D reconstructed

LI Shaoqi¹ ， YAN Zhanyou^2,3 ， CUI Yongchang¹ ， HOU Xueke¹ ， WANG Zijun³ ， QIAO Bo³

1. School of Transportation, Shijiazhuang Tiedao University, Shijiazhuang 050043 , China

2. State Key Laboratory of Mechanical Behavior in Traffic Engineering Structure and System Safety(Shijiazhuang Tiedao University), Shijiazhuang 050043 , China

3. School of Civil Engineering, Shijiazhuang Tiedao University, Shijiazhuang 050043 , China

摘要

为研究行驶车辆对山区道路所造成的动力学响应,利用随机正弦波叠加法以 MATLAB 联合 TruckSim 软件重构了三维路面不平度模型,采用黏弹性半空间体上无限大多层板模型模拟路基结构,通过三轴重型车辆连续上坡工况对车-路相互作用三向力及车辆行驶过程进行分析,使用自行编制的广义积分计算程序对 4 层板路面垂向位移进行求解。结果表明:相比 2D 路面,3D 路面的纵向力与横向力最大值、均方根均相差较大,其中 3D 路面比 2D 路面横向力高出 42. 95% ;车辆行驶于圆形缓和坡道时,车-路相互作用的三向力出现明显改变,其中,通过凹形坡道时纵向力最大值超出整个过程纵向力平均值的 6 倍,横向力有先增加、后减小、再增加、最后趋于平稳的一个过程;多个轮胎对道路产生的位移影响不是每个轮胎作用的简单相加,需要根据轮胎位置、作用距离等综合考虑。研究结果可为重型车辆连续上坡、通过拱形桥、涵洞等多个工况提供技术指导。

关键词

三维路面 / 黏弹性半空间 / 无限大多层板 / 连续上坡 / 三向力 / 垂向位移

Abstract

The study investigates dynamic response of vehicles driving on mountainous roads by developing a three-dimensional ( 3D) road roughness model using the random sine wave superposition method, integrated with MATLAB and TruckSim software. The roadbed structure is modeled as an infinite multi-layer plate on a viscoelastic half-space foundation. The three-dimensional interaction forces between the vehicle and the road, as well as the vehicle′s driving dynamics, are analyzed during the continuous uphill operation of a three-axle loaded vehicle. A self-developed generalized integral calculation program is employed to determine the vertical displacement of a four-layer pavement. The results reveal significant differences between 3D and 2D pavement models in terms of the maximum and root mean square values of longitudinal and lateral forces, with the lateral force on 3D pavement being 42. 95% higher than on 2D pavement. When navigating circular ramps, the three-dimensional interaction forces exhibit notable variations. Specifically, when traversing a concave ramp, the peak longitudinal force can exceed the average longitudinal force by up to six times, while the lateral force demonstrates a pattern of initial increase, followed by a decrease, another increase, and eventual stabilization. Furthermore, the displacement impact of multiple tires on the road is not simply additive but must be evaluated based on factors such as tire position and effective distance. The findings provide valuable technical insights for the operation of heavy vehicles in scenarios involving continuous slope climbing, arch bridges, and culverts.

Keywords

3D pavement / viscoelastic half-space / infinite multi-layer plate / continuously climb slopes / three-dimensional force / vertical displacement

1 二维路面车路耦合描述 1.1 路面谱时域模型 1.2 车-路相互作用的动力学描述 1.3 轮胎接地状态描述 1.4 多层板地基动力响应解析解 2 三维路面重构 2.1 模型建立 2.2 动力响应分析 3 三维重构连续上坡路段动力学应用 3.1 模型建立 3.2 动力响应分析 3.3 4 层板位移响应分析 3.3.1 算法验证 3.3.2 工程应用 4 结论

近年来，为实施乡村振兴战略，山区新建公路里程日创新高。然而，山区道路复杂多变，尤其道路不平顺现象较城市道路更具有害性。山区公路最常见道路类型为连续上、下坡，不仅要考虑车辆动力问题，还要将车辆所受向心力和离心力计算在内，这是车辆安全、舒适行驶于山间道路最先解决的技术难题。

研究路面结构动力学响应要同时考虑车辆荷载、道路结构以及车-路耦合状态三个方面。国内外，在使用解析法研究路面结构动力学响应时，一般将车辆荷载简化为移动恒载或简谐荷载，将路面结构简化为黏弹性地基（ Winkler 或 Kelvin）上的 Kirchhoff 薄板^[1-2]。文献^[3-5]研究了移动荷载作用下 Winkler（或 Kelvin）地基上无限大 Kirchhoff 薄板的动力响应，给出了板瞬态和稳态挠度的积分解析解。文献^[6]研究了移动荷载下黏弹性半空间体上双层板的动力响应，同时对材料参数、板层厚度对响应的影响进行了进一步研究。文献^[7]建立了弹性地基上多层条形板在各种静荷载作用下内力系数的数学模型和计算方法，证明了无穷代数方程组的正则性，并得到了相应的估计。将荷载简化虽然使复杂理论达到计算简便效果，但对工程应用精度问题大打折扣。研究车荷载下道路动力学响应关键在于构造模型得到轮胎与路面接触力，这需要对路面不平度进行研究。用来描述路面不平度方法有很多，主要有谐波叠加法、白噪声法、小波分析法、AR 模型法以及分形方法等，但以往研究中大多基于二维路面谱。文献^[8]指出使用二维路面谱得出轮胎与路面之间摩擦系数存在缺陷，提出立体视觉在路面三维纹理重建中的应用，恢复了路面三维不平度。文献^[9]通过实验明确了可指导工程应用的路面摩擦等特征指标，并得到三维路面数据，但研究车路耦合动力学响应所需的三维路面模型未给出。文献^[10]基于分形理论提出一种三维路面谱重构方法，验证应用三维路面谱仿真车路间动力学行为比使用二维路面不平度有着更高精度。

车轮-路面耦合接触状态对其动力响有着重要影响。文献^[11] 将静态轮胎压力密度分布函数改进为随时程变化的动态函数，提高轮胎模型准确性的同时又进一步改善了其接地应力精确度。文献^[12]将车辆行驶应用在湿滑路面，通过实验测试提出胎面橡胶-湿滑路面摩擦行为数值分析方法。随着计算机技术的迅速发展，Adams、 CarSim / TruckSim 等软件在车路动力学分析上运用的越来越广泛。文献^[13]使用 ADAMS 软件建立 1 / 4 悬架车轮动力学模型，提出车轮质量不平衡会对车辆性能产生较大影响，并利用 ADAMS / Vibration 模块对单个车轮不平衡质量进行了振动分析。文献^[14] 使用 TruckSim 软件构建卡车在长下坡 T 形路口底部转弯模型，研究车辆转向失稳机理并提出道路因素与车辆安全速度阈值关系。

综上，目前对于三维路面谱的研究较少，将其运用到工程案例中的文献更是屈指可数。本文基于随机正弦波叠加法重构了 3D 路面模型，并将其数据导入 TruckSim 软件，模拟车辆在连续上坡路段行驶的动力学行为。通过分析三轴重型车辆在连续上坡路段行驶过程，阐述了受圆形缓和坡道产生离（向）心力以及三向力变化现象。最后，将垂向力代入黏弹性半空间地基上 4 层板模型位移解析解，得到道路内部受车辆载荷而引起的位移响应。

1 二维路面车路耦合描述

1.1 路面谱时域模型

国际标准化组织与中国国家标准均建议路面不平度的功率谱密度 G_q（n），用下式^[15]拟合:

G_{q} (n) = G_{q} (n_{0}) {(\frac{n}{n_{0}})}^{- w}, n > 0

(1)

式中:n 为空间频率，为波长的倒数; n₀ = 0.1 m^-1为参考频率; G_q（n₀）为参考频率 n₀ 下的路面功率谱密度值，也称为路面不平度系数; w 为频率指数，等于双对数坐标上斜线的斜率，取决于路面功率谱密度的频率结构，一般情况下 w = 2。

在描述路面的起伏程度时，采用随机正弦波叠加法对路面不平度进行拟合^[16] :

q (x) = \sum_{i = 1}^{m} \sqrt{2 G_{q} (n_{m i d - i}) Δ n_{i}} s i n (2 π n_{m i d - i} + θ_{i})

(2)

式中:x 为路面纵向位移，θ_i 为[0，2π] 内均匀分布的相互独立的随机变量; n_mid-i为将频率区间分成 m 个小区间后每一个小区间的中心频率。

将上式扩展到路面上任一点（x，y），可得

\begin{matrix} q (x, y) = \sum_{i = 1}^{m} [\sqrt{2 G_{q} (n_{m i d - i}) Δ n_{i}} . \\ \sin (2 π n_{m i d - i} \sqrt{x^{2} + y^{2}} + θ_{i} (x, y))] \end{matrix}

(3)

式中:θ_i（x，y）为路面上任意点（x，y）处属于[0，2π] 内的随机数。

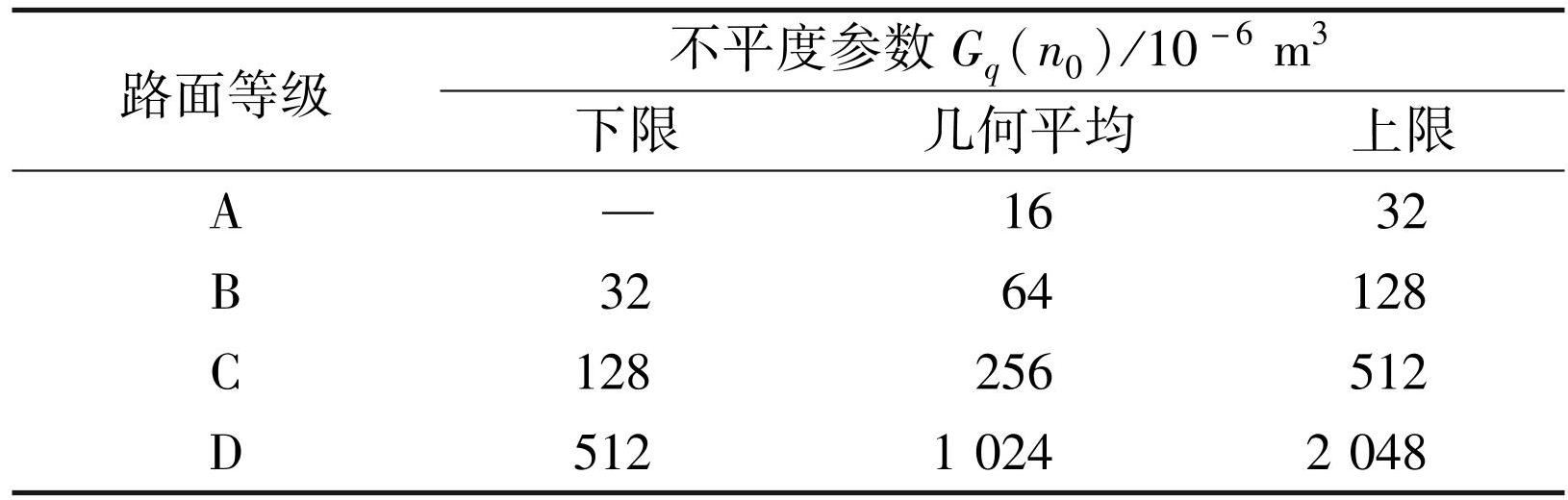
路面等级参数一般可分为 8 个等级，用来表示路面不平顺程度，表1仅列出 A~D 级路面等级参数^[15]。

表1GB/ T7031—2005 标准 A~D 路面等级参数

Tab.1 A-D pavement grade parameters of GB/ T7031—2005 standard

基于随机正弦波叠加法可得到 C 级路面不平度的位移功率谱密度（PSD），联合上、下限以及几何平均值绘制了时间频率下的位移 PSD 图形，如图1所示。从图中可以看出:C 级路面不平度的位移 PSD 围绕其平均值的位移 PSD 上下波动且大部分处于上、下限位移 PSD 的之间，由此可证明该路面数值模拟的正确性。

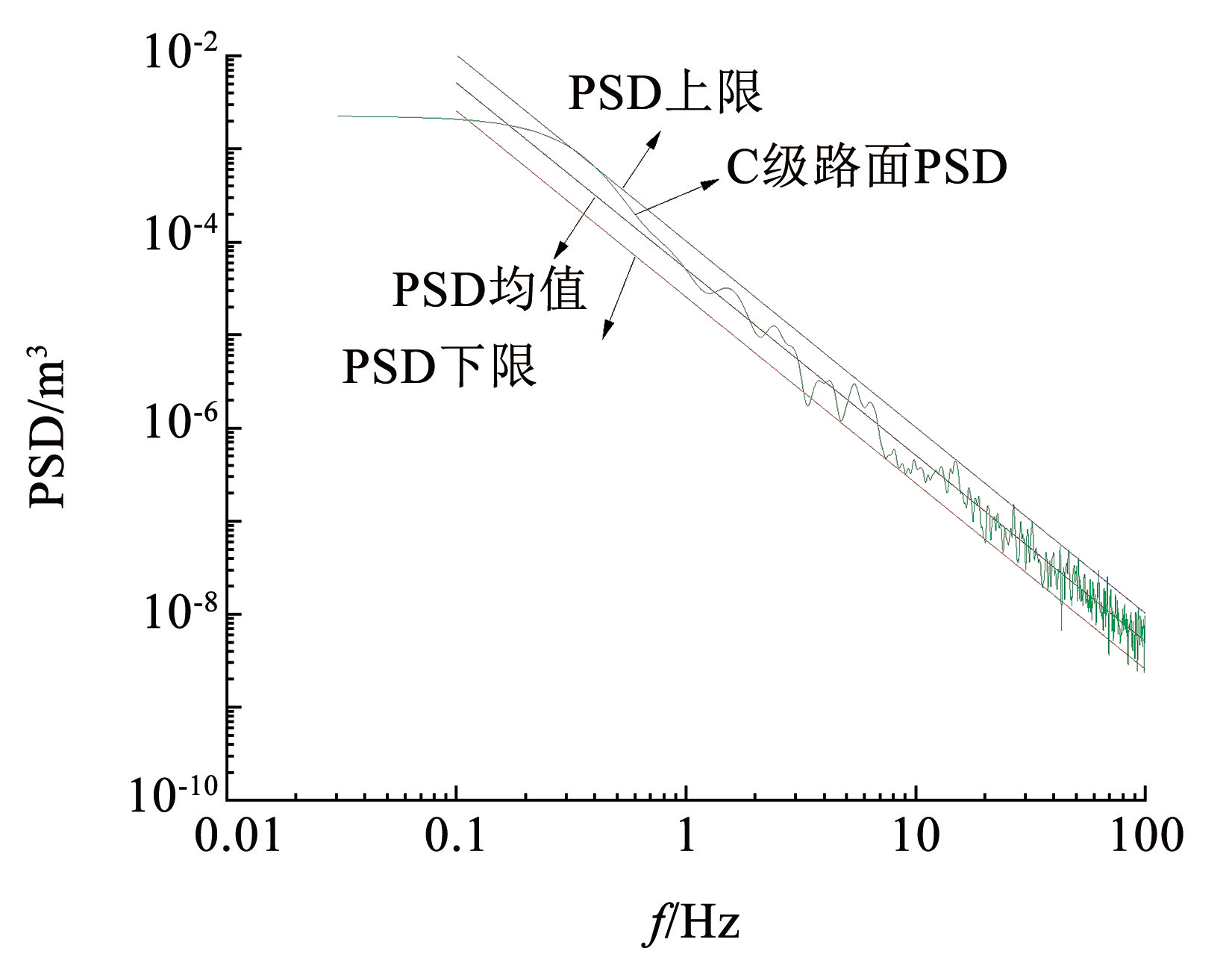
图1C 级路面不平度位移功率谱密度

Fig.1Displacement power spectral density of class C pavement roughness

1.2 车-路相互作用的动力学描述

图2（a）为一重型卡车的三轴半车辆模型，由于轮胎阻尼较小且为方便研究，基于车前轮给出图2（b）所示两个自由度 z₁、z₂ 上的垂向振动模型。根据牛顿第二定律和达朗贝尔原理，建立车辆-道路相互作用平衡微分方程组:

\{\begin{matrix} m_{2} {\ddot{z}}_{2} + c_{s z} ({\dot{z}}_{2} - {\dot{z}}_{1}) + k_{s z} (z_{2} - z_{1}) = 0 \\ m_{1} {\ddot{z}}_{1} + c_{s z} ({\dot{z}}_{1} - {\dot{z}}_{2}) + k_{s z} (z_{1} - z_{2}) + k_{t z} (z_{1} - q_{z}) = 0 \end{matrix}

(4)

式中:m₁、m₂分别为非簧载与簧载质量; q_z 为基于水平路面的垂向路面不平度; k_tz、k_sz分别为车轮与悬架在垂向上刚度; c_sz为悬架阻尼。

由动力学关系，可得轮胎垂向荷载:

\{\begin{matrix} F_{d z} = k_{t z} (q_{z} - z_{1}) \\ F_{z} = F_{d z} + F_{s z} \end{matrix}

(5)

其中:F_z为轮胎垂向荷载，由 F_dz动载荷和 F_sz = Mg 静态载荷两部分组成。

纵向振动时车辆与轮胎近似看成刚性连接，可简化为图2（ c）所示的基于车前轮纵向振动模型^[17]。车路耦合纵向振动方程为

(m_{1} + m_{2}) \ddot{x} + k_{t x} (x - q_{x}) = 0

(6)

式中:k_tx 为车轮在垂向上刚度，q_x 为纵向路面不平度。

车辆行驶在不平路面，重力对路面产生的竖向静载荷 Mg 被分成垂向载荷 Mgcos α 和纵向载荷 Mgsin α，如图2（d）所示。

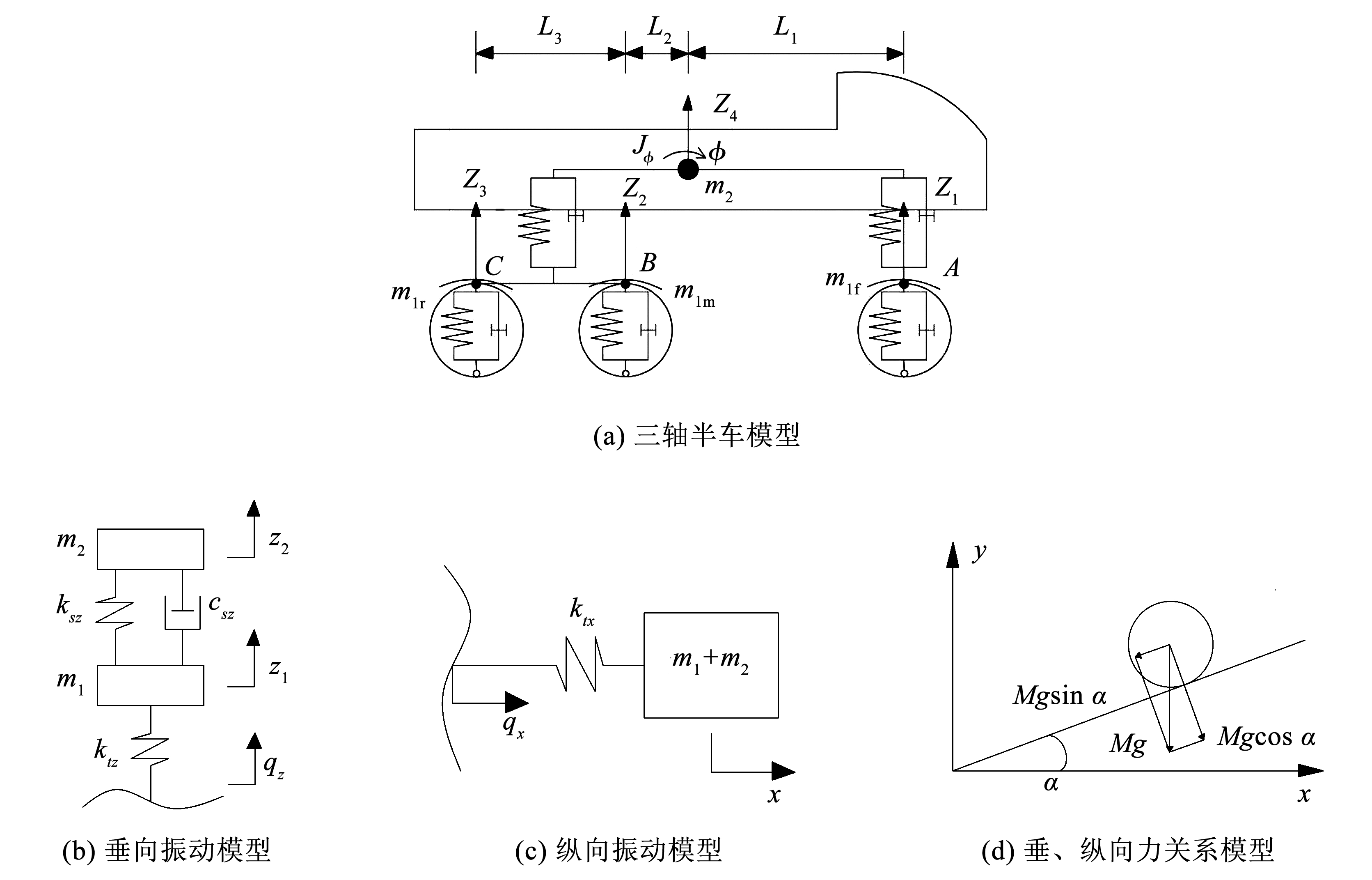
图2三轴重型车及其振动模型

Fig.2Three axle heavy-duty vehicle and its vibration model

1.3 轮胎接地状态描述

轮胎接地形状可近似为长、宽分别为 0.6L、 0.4L的矩形和两个以 0.3L 为半径的半圆组成^[18]，如图3（a）所示。本文采用矩形均布荷载模拟轮胎对路面的作用，即为图中阴影部分。假设车辆以速度 v 沿 x 轴正向匀速运动，轮胎荷载 F（x，y，t）均匀分布在矩形区域{-l₁≤x≤l₁，-l₂≤x≤l₂ }内，对于路面的稳态响应，该荷载可表示为

F (x, y, t) = \frac{F_{0}}{4 l_{1} l_{2}} [l_{1}^{2} - (x - v t)^{2}] H (l_{2}^{2} - y^{2})

(7)

式中:H（·）为单位阶跃函数，F₀ 为路面所受垂向（或纵向）载荷的大小。

图3（b）、3（c）分别为车辆分别行驶于凸、凹形圆坡道所受离心力和向心力示意。图中，F_z 为路面受到的车轮垂向力; F_n、F′_n 分别为离心力与向心力，大小均可用 mv² / r 表示; 车速 v 与圆形坡道相切。

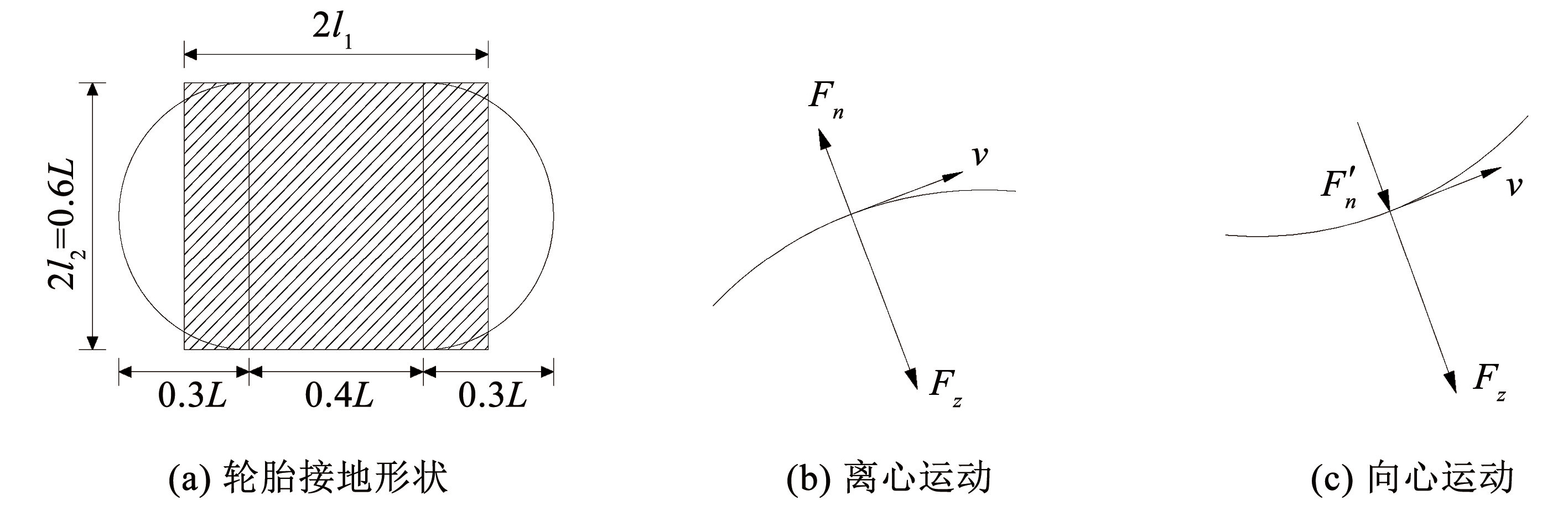
图3轮胎接地状态

Fig.3Tire contact with the ground

1.4 多层板地基动力响应解析解

图4为黏弹性半空间体上无限大多层板模型。图4中最下一层为黏弹性半空间体，其上为无限大多层板。

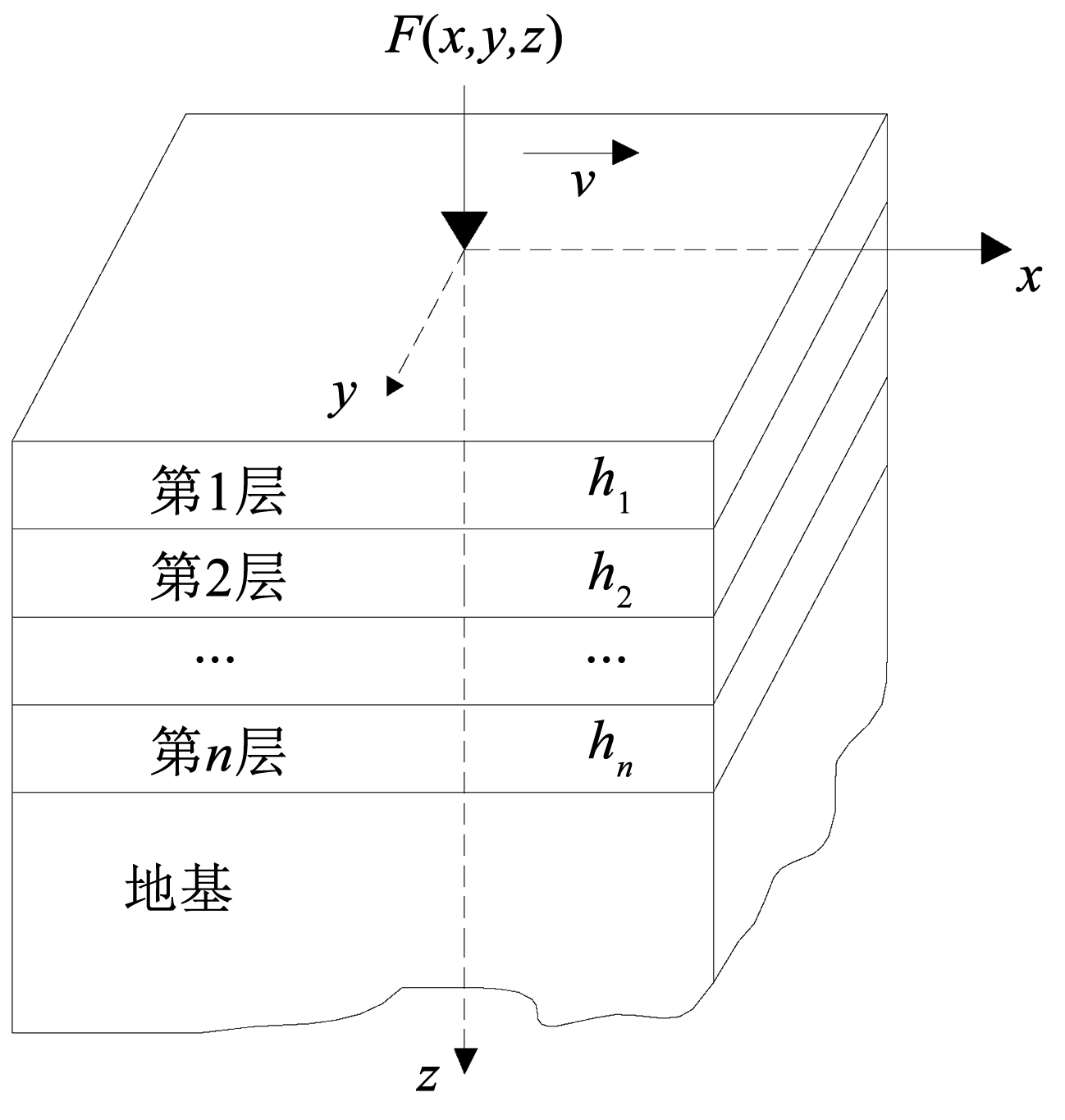
图4黏弹性半空间体上无限大多层板

Fig.4An multi-layer plate on viscoelastic half-space foundation

黏弹性半空间体的密度、泊松比、弹性模量分别用 ρ、 μ、 E、 λ、 G 表示; x，y，z 3 个方向的位移用 u_i（u_x，v_y，w_z）表示，则均质各向同性黏弹性半空间体以位移表示的控制方程为

(λ + G) \nabla (\nabla \cdot u_{j}) + G \nabla^{2} u_{j} = ρ \frac{\partial^{2} u_{j}}{\partial t^{2}}

(8)

其中:λ、G 为 Lamé 常数，λ = μE/ [（1 + μ）（1-2μ）]，G = E /（2 + 2μ）;

\nabla^{2} = \frac{\partial^{2}}{\partial r^{2}} + \frac{1}{r} \frac{\partial}{\partial r} + \frac{\partial^{2}}{\partial z^{2}}

为拉普拉斯算子，r 为研究位置到 z 轴距离大小。

假设板和板、板和黏弹性半空间体之间均为光滑接触，各层板的厚度、弹性模量、泊松比和密度分别为 h_i、E_i、μ_i、ρ_i（i = 1，2，···，n），其最上层板上表面受到 F（x，y，t）的移动荷载，P（x，y，t）为黏弹性参考半空间体作用于板的垂向反力，参考文献^[5]，可推得以多层板垂向位移表示的运动微分方程:

\begin{matrix} D (\frac{\partial^{4} w_{z b}}{\partial x^{4}} + \frac{\partial^{4} w_{z b}}{\partial y^{4}}) + 2 (D_{x y} + 2 D_{k}) \frac{\partial^{4} w_{z b}}{\partial x^{2} \partial y^{2}} + \\ m_{b} \frac{\partial^{2} w_{z b}}{\partial t^{2}} = F (x, y, z) - P (x, y, t) \end{matrix}

(9)

式中:w_zb为多层板垂向位移;

m_{b} = \sum_{i = 1}^{n} ρ_{i} h_{i}

为多层板单位面积质量; D_xy为多层板弯曲刚度，D_k 为多层板扭转刚度，表达式为

\{\begin{matrix} D = \int_{h_{0} - h_{1}}^{h_{0}} \frac{E_{1}}{1 - μ_{1}^{2}} z^{2} d z + \int_{h_{0} - h_{1} - h_{2}}^{h_{0} - h_{1}} \frac{E_{2}}{1 - μ_{2}^{2}} z^{2} d z + \\ \dots + \int_{(h_{0} - \sum_{i = 1}^{n} h_{i})}^{(h_{0} - \sum_{i = 1}^{n - 1} h_{i})} \frac{E_{n}}{1 - μ_{n}^{2}} z^{2} d z \\ D_{x y} = \int_{h_{0} - h_{1}}^{h_{0}} \frac{E_{1} μ_{1}}{1 - μ_{1}^{2}} z^{2} d z + \int_{h_{0} - h_{1} - h_{2}}^{h_{0} - h_{1}} \frac{E_{2} μ_{2}}{1 - μ_{2}^{2}} z^{2} d z + \\ \dots + \int_{(h_{0} - \sum_{i = 1}^{n} h_{i})}^{(h_{0} - \sum_{i = 1}^{n - 1} h_{i})} \frac{E_{n} μ_{n}}{1 - μ_{n}^{2}} z^{2} d z \\ D_{k} = \int_{h_{0} - h_{1}}^{h_{0}} \frac{E_{1}}{2 (1 + μ_{1})} z^{2} d z + \int_{h_{0} - h_{1} - h_{2}}^{h_{0} - h_{1}} \frac{E_{2}}{2 (1 + μ_{2})} z^{2} d z + \\ \dots + \int_{(h_{0} - \sum_{i = 1}^{n - 1} h_{i})}^{(h_{0} - \sum_{i = 1}^{n - 1} h_{i})} \frac{E_{n}}{2 (1 - μ_{n})} z^{2} d z \end{matrix}

(10)

式中 h₀为多层板中性层距最上层板上表面距离，由中性层上应力为零可推得表达式为

\begin{matrix} h_{0} = [E_{1} h_{1}^{2} + E_{2} (2 h_{1} + h_{2}) h_{1} + E_{3} (2 h_{1} + 2 h_{2} + h_{3}) h_{3} + \\ \dots + E_{n} (2 \sum_{i = 1}^{n - 1} h_{i} + h_{n}) h_{n}] / [n \sum_{i = 1}^{n} (E_{i} h_{i})] \end{matrix}

(11)

为实现函数的时域和频域转换，定义三维 Fourier 正、逆变换:

\{\begin{matrix} \bar{f} (k_{1}, k_{2}, ω) = \\ \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} f (x, y, t) e^{- j (k_{1} x + k_{2} y + ω t)} d x d y d t \\ f (x, y, t) = \\ \frac{1}{(2 π)^{3}} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \bar{f} (k_{1}, k_{2}, ω) e^{- j (k_{1} x + k_{2} y + w t)} d k_{1} d k_{2} d ω \end{matrix}

(12)

根据 Helmholtz 定理、三维 Fourier 变换^[6]，得到黏弹性半空间体上多层板模型在直角坐标系下三向（垂向、纵向和横向）位移矢量:

\{\begin{matrix} {\bar{u}}_{x} = \frac{j}{G Δ} [- k_{1} (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) e^{- B_{p} z} + 2 k_{1} B_{p} B_{s} e^{- B_{s} z}] \\ {\bar{v}}_{y} = \frac{j}{G Δ} [- k_{2} (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) e^{- B_{p} z} + 2 k_{2} B_{p} B_{s} e^{- B_{s^{z}}}] \\ {\bar{w}}_{z} = \frac{j}{G Δ} [B_{p} (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) e^{- B_{p} z} - 2 B_{p} (k_{1}^{2} + k_{2}^{2}) e^{- B_{s} z}] \end{matrix}

(13)

式中:j 为虚数单位，j² =-1;

Δ = [(k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) + D_{1} B_{p} / G] (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) - 2 B_{p} (2 B_{s} + D_{1} / G) (k_{1}^{2} + k_{2}^{2})

;

B_{p}^{2} = k_{1}^{2} + k_{2}^{2} - k_{p}^{2}; B_{s}^{2} = k_{1}^{2} + k_{2}^{2} - k_{s}^{2}; k_{p} = ω / C_{p}; k_{s} = ω / C_{s}

;

C_{p} = \sqrt{（ λ + 2 G ） / ρ}

为纵波（ P 波）波速;

C_{s} = \sqrt{G / ρ}

为横波（S 波）波速。

利用 Green 函数和广义 Duhamel 积分^[6]，得到车辆移动荷载作用下黏弹性半空间体上多层板模型的三向位移:

\{\begin{matrix} u_{x} = \frac{j F_{0}}{(2 π)^{2} G} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \frac{\sin (k_{1} l_{1})}{k_{1} l_{1}} \frac{\sin (k_{2} l_{2})}{k_{2} l_{2}} \cdot \frac{1}{Δ} [- k_{1} (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) e^{- B_{p} z} + 2 k_{1} B_{p} B_{s} e^{- B_{s}^{z}}] \cdot e^{j [k_{1} (x - v t) + k_{2} y]} d k_{1} d k_{2} \\ v_{y} = \frac{j F_{0}}{(2 π)^{2} G} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \frac{\sin (k_{1} l_{1})}{k_{1} l_{1}} \frac{\sin (k_{2} l_{2})}{k_{2} l_{2}} \cdot \frac{1}{Δ} [- k_{2} (k_{1}^{2} + k_{2}^{2} + B_{s}^{2}) e^{- B_{p} z} + 2 k_{2} B_{p} B_{s} e^{- B_{s} z}] \cdot e^{j [k_{1} (x - v t) + k_{2} y]} d k_{1} d k_{2} \\ w_{z} = \frac{F_{0}}{(2 π)^{2} G} \int_{- \infty}^{+ \infty} \int_{- \infty}^{+ \infty} \frac{\sin (k_{1} l_{1})}{k_{1} l_{1}} \cdot \frac{\sin (k_{2} l_{2})}{k_{2} l_{2}} \cdot \frac{1}{Δ} [B_{p} (k_{1}^{2} + k_{1}^{2} + B_{s}^{2}) e^{- B_{p} z} - 2 B_{p} (k_{1}^{2} + k_{2}^{2}) e^{- B_{s} z}] \cdot e^{j [k_{1} (x - v t) + k_{2} y]} d k_{1} d k_{2} \end{matrix}

(14)

2 三维路面重构

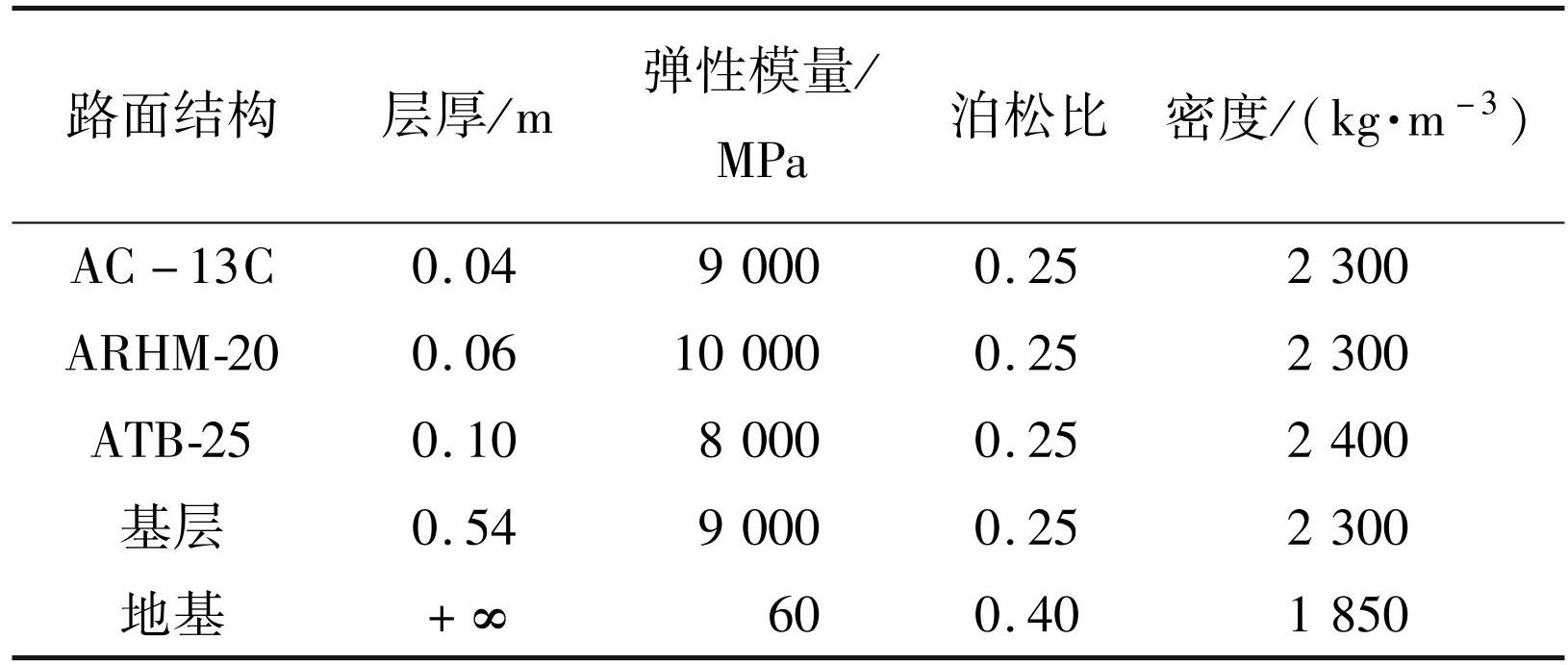
前文已给出黏弹性半空间体上多层板三向位移的解析解，编写 MATLAB 程序^[19] 完成对黏弹性半空间体上多层板的位移响应仿真。实际上，采用面层、基层、底基层、垫层等 4 层板足以满足工程需要。本文以太行山高速涞曲段路面结构为例^[20]，黏弹性半空间体 4 层板结构材料参数取值见表2。三轴车辆参数参考文献^[21]:前车轮质量 500 kg，中、后车轮质量 725 kg，车身质量 28 500 kg，前中轴间距 4 m，中后轴间距 1.4 m，前悬架阻尼 11 200（ kN·s）/ m，后悬架阻尼 33 420（ kN·s）/ m，前悬架刚度 1 577 kN/ m，后悬架刚度 4 724 kN/ m，前轮刚度 3 146 kN/ m，中、后轮刚度 4 724 kN/ m。

表2路面结构的材料参数

Tab.2 Material parameters of pavement structure

2.1 模型建立

为更准确模拟路面工况，通过 MATLAB 联合 TruckSim 软件对 C 级路面进行三维重构，如图5所示。

图5（a）采用随机正弦波叠加法模拟 1 000 m 长路面的不平度，正、负值分别表示高出和低于水平路面基准线，该值始终围绕 0 值上下波动，最大可达 17.9 mm。图5（ b）在上述基础上设置路面宽度为 6 m，建立了 3D 路面不平度模型。图5（ c）为 TruckSim 软件路面模型设置窗口，在路面模型（ geometry）选项下的道路线型（ centerline geometry）、路面纵向不平度（ centerline elevation）和横向不平度（ off-center elevation）分别进行下列操作:设置 1 000 m 直行单车道、导入二维及三维 C 级路面数据。图5（ d）为输入三轴货车模型参数后得到的车辆-路面模型，其行驶速度设置为 36 km / h。

2.2 动力响应分析

根据 2.1 节所建立的车-路模型，得到如图6所示的车路相互作用动力响应。图6（a）中直线与曲线分别代表设定车辆行驶速度和车辆实际行驶在不平路面上的速度，可以看出不平路面车速围绕其设定速度上下波动。最大值与最小值分别为 36. 046、 35.955 km / h，二者均与设定速度偏差 0.13%。以车辆左前轮为例，将二维和三维路面数据分别导入 TruckSim 软件得到图6（ b）~6（ d），分别表示车辆载荷施加在不平路面上所产生的垂向、纵向和横向力。表3给出仿真结果的最大值和均方根值。通过最大值比较，三维路面比二维路面三向力分别高出 3.54%、82.61%、42.95%。通过均方根值比较，三维路面比二维路面三向力分别高出 0. 05%、 15.23%、6.54%。可见，相比 2D 路面，3D 路面的纵向力与横向力最大值、均方根均相差较大，此结论验证了重构 3D 路面对研究车-路动力响应的重要性。

图5MATLAB/ TruckSim 联合重构 C 级三维路面

Fig.5MATLAB/ TruckSim joint reconstruction of C-level 3D pavement

图6车-路相互作用动力响应

Fig.6Vehicle and road interaction dynamic response

表3三向力最大值和均方根值

Tab.3 Maximum and root mean square values of three-dimensional forces

3 三维重构连续上坡路段动力学应用

3.1 模型建立

基于第 2 节研究方法，对三轴重型车辆在连续上坡路面时动力学响应进行研究，如图7所示。图7（a）描述了一条水平距离为 100 m 的道路纵向剖面，其中蓝色线形表示路面，纵坐标表示路面高程。两端上坡路段相对水平路面上升角度均为 15°，中间有一段长为 30 m 的水平路段，3 条路段均通过半径为 38.64 m 的缓和圆形坡道联结。将 3D 路面不平度数据导入 TruckSim 软件中，得到如图7（b）所示的 3D 车-路连续上坡模型。图7（c）为车辆整个运动过程车速变化时程曲线，给定该车初始速度为 16 m / s。在 2.7~5. 0 s 时，车辆行驶于水平路段，速度增加; 在 0~2.7 s 及 5. 0~10. 0 s 时，车辆分别行驶于包含缓和圆形坡道的一、二级上坡路段，速度减小。

图7车辆连续上坡模型

Fig.7Vehicle continuous uphill model

3.2 动力响应分析

由 3.1 节车辆连续上坡模型，得到图8所示的车-路相互作用三向力（分别为垂向力、纵向力和横向力）随时间变化曲线。

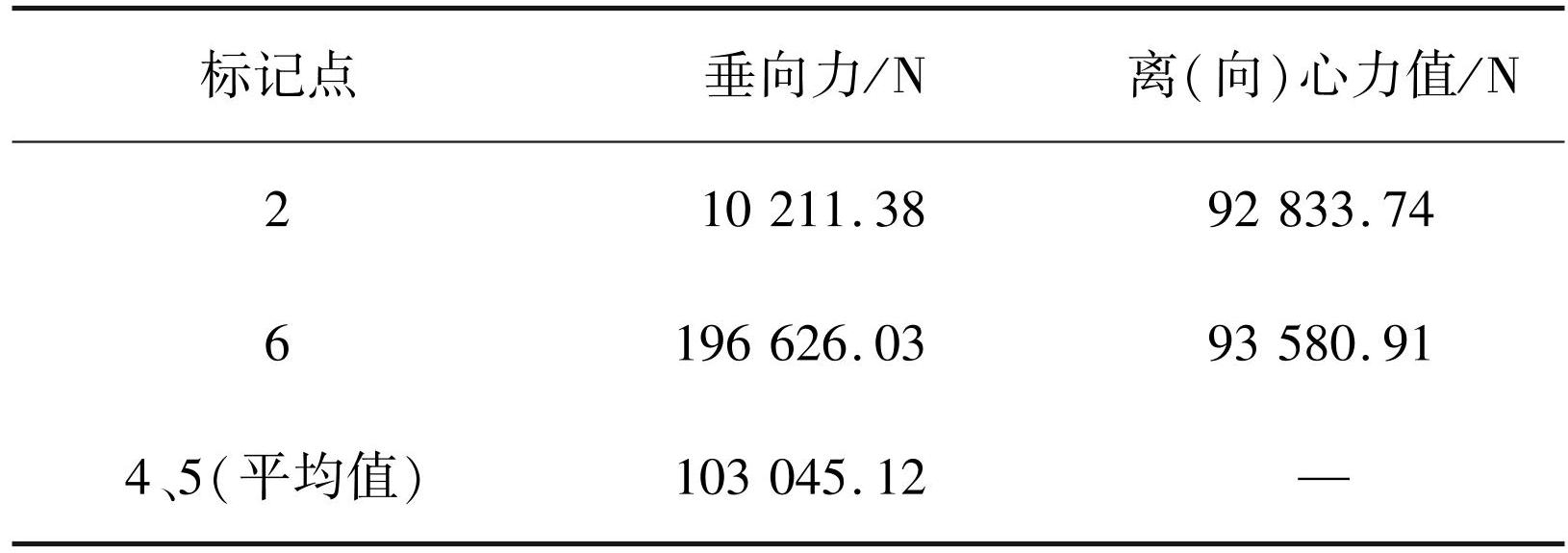
图8（a）为垂向力时程曲线，对关键时刻点作了 7 处圆形标记。标记 1（1.56 s 处）为车前轮驶入凸形圆坡道时刻，标记 2（2. 00 s 处）为车后轮驶入该坡道时刻，用时共 0.44 s，此期间平均速度为 12. 01 m / s。经计算行驶距离为 5.284 m，这与前后轮距 5.4 m 仅相差 2.15%，由此可验证该模型的精确性。标记 2~3 是车体完全位于凸形圆坡道的时间段。标记 3、4 分别为车前轮与车后轮驶出凸形圆坡道时刻。标记 5、7 分别为第 2 次上坡车前轮驶入与驶出凹形坡道时刻，用时 0.83 s，比标记 1~3 少用时 0. 02 s。此外，标记 2、6 分别为整个过程垂向力最小与最大处，这与车辆行驶于两个圆形缓和坡道位置分别受到离心力与向心力有关。表4列出了水平路段处垂向力及凸、凹形圆弧坡道处离、向心力数值，离心力值（9 283.374 N）是向心力值（9 358. 091 N）的 99.20%; 该重型车通过相同半径凸、凹形圆弧坡道平均速度分别为 11.70、11.95 m / s，根据离/ 向心力公式，前者为后者 95.86%。通过两组数据对比，离心力均比向心力小，除受速度影响外，路面不平度也是造成该差异的一个原因。

图8（b）、8（ c）分别为纵向力和横向力时程曲线。从图中圈出部分可以看出:通过凸形圆坡道纵向力减小，而通过凹形圆坡道纵向力增加，最大可达到 6 923.32 N，超出平均值的 6 倍; 通过凸、凹形圆坡道时，横向力均有先增加后减小再增加，最后趋于平稳的一个过程。最大值是平均值的 2.34 倍，通过二级坡道的凹形圆坡道时横向力甚至改变了方向（图中已作标注）。

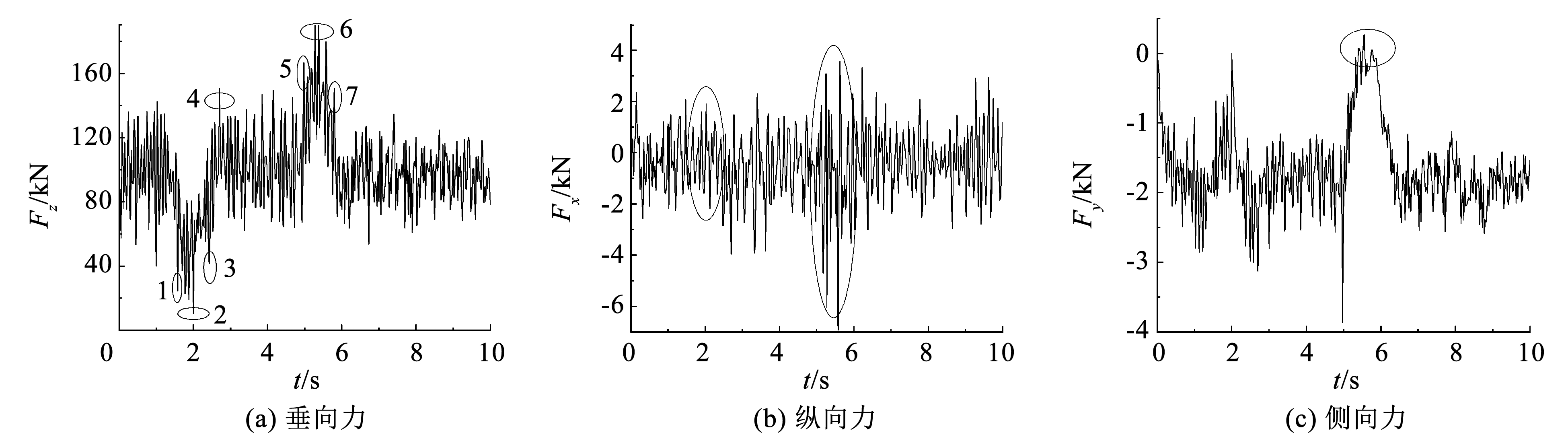
图8三向力

Fig.8Three directional force

表4垂向力及离/ 向心力

Tab.4 Vertical force and separation / centripetal force

3.3 4 层板位移响应分析

3.3.1 算法验证

Hung 等曾采用直接积分变换法，计算了黏弹性半空间体的动力响应^[22]。其中 v = 50 km/ h，F = 50 kN，G = 20 MPa，μ = 0.25，ρ = 2 000 kg / m³，ξ = 0. 02。应用第 2 节方法编制的 MATLAB 程序进行验证，如图9所示。通过黏弹性半空间体在（0，0，1）点垂向位移时程响应结果比较可见，本文方法与 Hung 的计算结果一致，可用于后续研究。

3.3.2 工程应用

下面基于车辆形行驶于水平路段工况，对垂向力作用于 4 层板道路造成位移影响进行研究。

图10（a）为各层板板底垂向位移随路面下深度变化曲线，图中 x = 0 m 表示垂向力作用位置，这也是产生垂向位移最大位置处。从图中还可以看出: 垂向位移变化率由 x = 0 位置向两边方向逐渐减小，表现为中间陡、两边缓的“ v”字形; 道路表面及各层板板底最大垂向位移分别为 0.201 86、0.201 31、 0.203 6、0.198 55、0.186 88 mm，相对路表依次减小了 0.272%、0.743%、1.640%、7.421%。图10（b）为第 4 层板板底在多个轮胎联合作用下位移响应，以前侧轮胎作为参照位置，前、中、后轮胎对该位置的 4 层板板底产生垂向位移大小分别为0.187、 0.117、0. 093 mm，相比最大值依次减小了 37.4%、 50.3%。图11（a）、11（b）分别基于单轮和双轮，绘制第 4 层板板底 3D 垂向位移云图，在描述受力位置及周围位移变化上更为直观，其最大位移分别为 0.187、0.316 5 mm，双轮共同作用比单轮作用增大 69.25%。

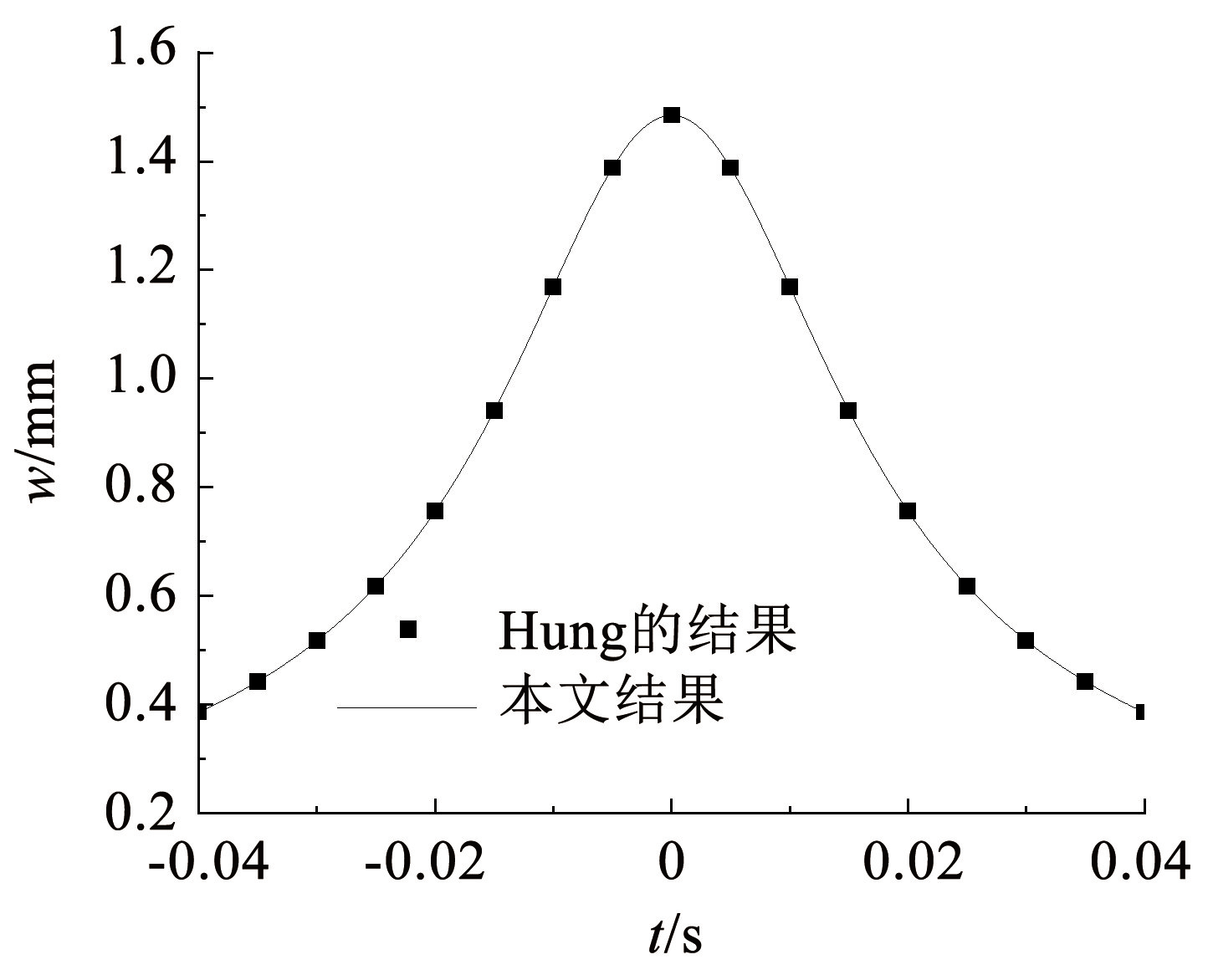
图9垂向位移结果比较

Fig.9Comparison of vertical displacement results

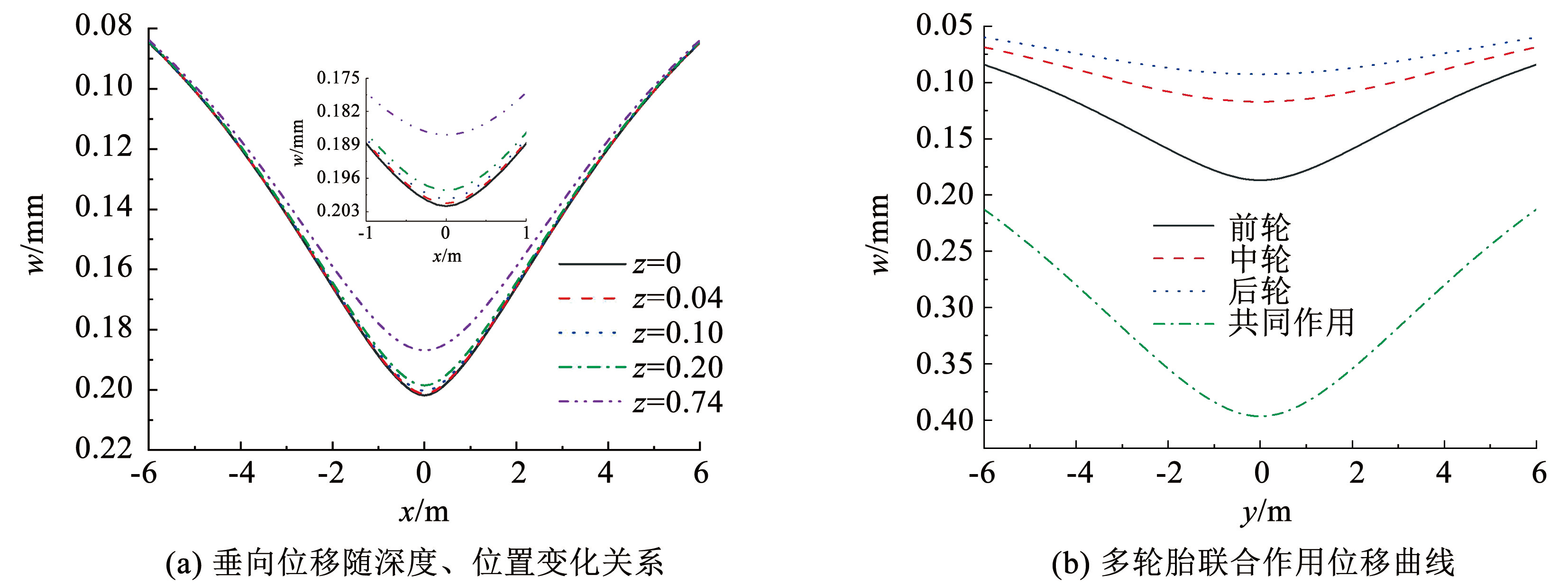
图10垂向位移响应

Fig.10Vertical displacement response

图114 层板板底垂向位移云图

Fig.11Displacement nephogram of vertical displacement at the bottom of the four-layer plate

4 结论

本文通过随机正弦波叠加法构建 2D 和 3D 路面模型，将 3D 路面模型运用到连续上坡路段并分析车-路相互作用的三向力，最后以水平路段为例分析了垂向力对 4 层板道路位移的影响，得到如下结论:

1）相比 2D 路面，3D 路面的纵向力与横向力最大值、均方根均相差较大，其中 3D 路面比 2D 路面横向力高出 42.95%，重构 3D 路面对研究车-路动力响应非常重要。

2）除受速度影响外，路面不平度也是车辆行驶时产生离（向）心力的一个原因。

3）车辆行驶于圆形缓和坡道时，车-路相互作用的三向力出现明显改变。其中，通过凹形坡道时纵向力最大值超出整个过程纵向力平均值的 6 倍，横向力有先增加、后减小、再增加、最后趋于平稳的一个过程。

4）多个轮胎对道路产生的位移影响不是每个轮胎作用的简单相加，需要根据轮胎位置、作用距离等综合考虑。

图1C 级路面不平度位移功率谱密度

Fig.1Displacement power spectral density of class C pavement roughness

下载: 全尺寸图片

图2三轴重型车及其振动模型

Fig.2Three axle heavy-duty vehicle and its vibration model

下载: 全尺寸图片

图3轮胎接地状态

Fig.3Tire contact with the ground

下载: 全尺寸图片

图4黏弹性半空间体上无限大多层板

Fig.4An multi-layer plate on viscoelastic half-space foundation

下载: 全尺寸图片

图5MATLAB/ TruckSim 联合重构 C 级三维路面

Fig.5MATLAB/ TruckSim joint reconstruction of C-level 3D pavement

下载: 全尺寸图片

图6车-路相互作用动力响应

Fig.6Vehicle and road interaction dynamic response

下载: 全尺寸图片

图7车辆连续上坡模型

Fig.7Vehicle continuous uphill model

下载: 全尺寸图片

图8三向力

Fig.8Three directional force

下载: 全尺寸图片

图9垂向位移结果比较

Fig.9Comparison of vertical displacement results

下载: 全尺寸图片

图10垂向位移响应

Fig.10Vertical displacement response

下载: 全尺寸图片

图114 层板板底垂向位移云图

Fig.11Displacement nephogram of vertical displacement at the bottom of the four-layer plate

下载: 全尺寸图片

表1GB/ T7031—2005 标准 A~D 路面等级参数

下载: 全尺寸图片

表2路面结构的材料参数

下载: 全尺寸图片

表3三向力最大值和均方根值

下载: 全尺寸图片

表4垂向力及离/ 向心力

下载: 全尺寸图片

图1C 级路面不平度位移功率谱密度

Fig.1Displacement power spectral density of class C pavement roughness

图2三轴重型车及其振动模型

Fig.2Three axle heavy-duty vehicle and its vibration model

图3轮胎接地状态

Fig.3Tire contact with the ground

图4黏弹性半空间体上无限大多层板

Fig.4An multi-layer plate on viscoelastic half-space foundation

图5MATLAB/ TruckSim 联合重构 C 级三维路面

Fig.5MATLAB/ TruckSim joint reconstruction of C-level 3D pavement

图6车-路相互作用动力响应

Fig.6Vehicle and road interaction dynamic response

图7车辆连续上坡模型

Fig.7Vehicle continuous uphill model

图8三向力

Fig.8Three directional force

图9垂向位移结果比较

Fig.9Comparison of vertical displacement results

图10垂向位移响应

Fig.10Vertical displacement response

图114 层板板底垂向位移云图

Fig.11Displacement nephogram of vertical displacement at the bottom of the four-layer plate

表1GB/ T7031—2005 标准 A~D 路面等级参数

表2路面结构的材料参数

表3三向力最大值和均方根值

表4垂向力及离/ 向心力

图1C 级路面不平度位移功率谱密度

Fig.1Displacement power spectral density of class C pavement roughness

图2三轴重型车及其振动模型

Fig.2Three axle heavy-duty vehicle and its vibration model

图3轮胎接地状态

Fig.3Tire contact with the ground

图4黏弹性半空间体上无限大多层板

Fig.4An multi-layer plate on viscoelastic half-space foundation

图5MATLAB/ TruckSim 联合重构 C 级三维路面

Fig.5MATLAB/ TruckSim joint reconstruction of C-level 3D pavement

图6车-路相互作用动力响应

Fig.6Vehicle and road interaction dynamic response

图7车辆连续上坡模型

Fig.7Vehicle continuous uphill model

图8三向力

Fig.8Three directional force

图9垂向位移结果比较

Fig.9Comparison of vertical displacement results

图10垂向位移响应

Fig.10Vertical displacement response

图114 层板板底垂向位移云图

Fig.11Displacement nephogram of vertical displacement at the bottom of the four-layer plate

表1GB/ T7031—2005 标准 A~D 路面等级参数

表2路面结构的材料参数

表3三向力最大值和均方根值

表4垂向力及离/ 向心力

SUN L. Steady-state dynamic response of a kirchhoffs slab on viscoelastic kelvin′ s foundation to moving harmonic loads[J]. Journal of Applied Mechanics,2007,74(6):1212

CAO Z G, BOSTRÖM A. Dynamic response of a poroelastic halfspace to accelerating or decelerating trains[J]. Journal of Sound and Vibration,2013,332(11):2777

KIM C W, KAWATANI M, KIM K B. Three-dimensional dynamic analysis for bridge-vehicle interaction with roadway roughness[J]. Computers and Structures,2005,83(19/20):1627

KIM S M. Influence of horizontal resistance at plate bottom on vibration of plates on elastic foundation under moving loads[J]. Engineering Structure,2004,26(4):519

YANG S P, LI S H, LU Y J. Investigation on dynamical interaction between a heavy vehicle and roadpavement[J]. Vehicle and System Dynamics,2010,48(8):923

李皓玉, 齐月芹, 刘进. 移动荷载下黏弹性半空间体上双层板的动力响应[J]. 岩土力学,2013,34(增刊 1):28. LI Haoyu, QI Yueqin, LIU Jin. Dynamic responses of a two-layer plate on viscoelastic half-space foundation under moving loads[J]. Rock and Soil Mechanics,2013,34(Sup.1):28

MIRSAIDOV M, MAMASOLIEV Q. Contact problems of multilayer slabs interaction on an elastic foundation[J]. IOP Conference Series: Earth and Environmental Science,2020,614(1):012089

GENDY E A, SHALABY A, SALEH M,et al. Stereo-vision applications to reconstruct the 3D texture of pavement surface[J]. International Journal of Pavement Engineering,2011,12(3):546858

LIU Q F. Three-dimensional pavement surface texture measurement and statistical analysis[D]. Winnipeg: University of Manitoba,2015

路永婕, 李振宇, 怀文青, 等. 基于分形理论的三维路面谱重构及在多体动力学软件中的应用[J]. 图学学报,2019,40(2):328. LU Yongjie, LI Zhenyu, HUAI Wenqing,et al. Reconstruction of three-dimensional pavement spectrum based on fractal theory and its application in multi-body dynamics software[J]. Journal of Graphics,2019,40(2):328

LU Yongjie, ZHANG Junning, YANG Shaopu,et al. Study on improvement of LuGre dynamical model and its application in vehicle handling dynamics[J]. Journal of Mechanical Science and Technology,2019,33(2):545

周海超, 王国林, 姜震, 等. 湿滑状态下轮胎路面摩擦特性的数值分析方法[J]. 机械工程学报,2020,54(21):117. ZHOU Haichao, WANG Guolin, JIANG Zhen,et al. Numerical analysis method for friction characteristics of tire-pavement under wet slip condition[J]. Journal of Mechanical Engineering,2020,54(21):117

LI Xiaoyong. Kinetic analysis of the unbalanced masses of wheel based on ADAMS[J]. Applied Mechanics and Materials,2014,2963:494

ZHANG Shibo, LIU Yishan, LI Pingfei,et al. Study of instability mechanisms of trucks turning right at long downhill T-junctions based on TruckSim simulation[J]. PloS ONE,2023,18(3):e0282779

全国机械振动与冲击标准化技术委员会. 机械振动道路路面谱测量数据报告: GB/T7031—2005[S]. 北京: 中国标准出版社,2006.National Technical Committee for Standardization of Mechanical Vibration and Impact. Mechanical vibration—Road surface profiles—Reporting of measured data: GB/T7031—2005[S]. Beijing: China Standards Publishing House,2006

JIANG Jiacheng, LI Peiqing, CHEN Yikai,et al. Ride comfort of heavy vehicles based on key response characteristics of multibody dynamics[J]. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics,2021,235(4):553

石晓辉, 蒋欣, 赵军, 等. 不平路面车路耦合动载研究[J]. 中国科技论文,2018,13(4):408. SHI Xiaohui, JIANG Xin, ZHAO Jun,et al. Research on vehicleroad coupling dynamic load on uneven pavement[J]. China Sciencepaper,2018,13(4):408

李皓玉. 车辆与路面相互作用下路面结构动力学研究[D]. 北京: 北京交通大学,2011. LI Haoyu. Research on dynamics of pavement structure due to vehicle and pavement Interaction[D]. Beijing: Beijing Jiaotong University,2011

KREINES M G, KREINES E M. Matrix models of texts:models of text collections[J]. Mathematical Models and Computer Simulations,2020,12(5):779

严战友, 赵晓林, 赵国芳, 等. 整车多轮动载作用下沥青路面动力响应[J]. 中国公路学报,2020,33(8):119. YAN Zhanyou, ZHAO Xiaolin, ZHAO Guofang,et al. Dynamic response of asphalt pavement under multi-wheel dynamic load[J]. Journal of China Highway,2020,33(8):119

张步云, 戴涛, TAN C A, 等. 悬架系统振动特性的非平稳虚拟激励法研究[J]. 振动. 测试与诊断,2022,42(2):227. ZHANG Buyun, DAI Tao, TAN C A,et al. Research on the nonstationary virtual excitation method of suspension system vibration characteristics[J]. Journal of Vibration, Measurement & Diagnosis,2022,42(2):227

HUNG H H, YANG Y B. Elasitc waves in visco-elastic half-space generated by various vehicle loads[J]. Solid Dynamics and Earthquake Engineering,2001,21(1):1

1 二维路面车路耦合描述

2 三维路面重构

3 三维重构连续上坡路段动力学应用

4 结论

友情链接LINKS