摘要
第四代建筑的阳台上覆盖了大量绿植,其气动外形发生明显改变,来流受到绿植的扰动使得建筑表面风压变化更复杂。为探究绿植对高层建筑风压非高斯特性的影响,通过刚性模型测压试验,对不同覆植面积下建筑外立面极值风压和标准化风压系数的概率分布进行分析,给出了非高斯风压的经验判断标准和分布特征,揭示了绿植对建筑外立面极值风压的影响规律。分析结果表明:绿植的存在改变了来流在建筑迎风面分离点位置,使得边缘测点由非高斯性转化为高斯性,侧风面风压均表现出非高斯性,受绿植影响较小;窄面上的极值风压受绿植影响较小,而布置在相对较宽外立面上的绿植对该区域流场影响更大,不同绿化率作用下极值风压降低作用更明显;绿植对建筑极值风压的降低作用随覆植面积的增加先增大后减小,覆植面积为 13. 5% 时风荷载降低作用最大。研究结果可为类似结构抗风设计提供参考。
Abstract
The balconies of fourth-generation buildings are covered with a large number of vegetations, resulting in a noticeable alteration of their aerodynamic profiles. The airflow is disturbed by the vegetation, leading to more complex variations in wind pressure on the building surfaces. To investigate the influence of vegetations on the non-Gaussian characteristics of wind pressure on high-rise buildings, rigid model pressure tests were conducted to analyze the probability distribution of extreme wind pressures and standardized wind pressure coefficients on the building facade under different coverage areas of vegetations. Empirical criteria and distribution characteristics for non-Gaussian wind pressures were provided, revealing the influence of vegetation on extreme wind pressures on the building facades. The results indicate that the presence of vegetations changes the separation point position of incoming flow on the windward side of the building, causing the edge measurement points to transform from non-Gaussian to Gaussian. Conversely, crosswind wind pressure shows non-Gaussian, which is less affected by vegetations. The extreme wind pressure on narrow surfaces is less affected by vegetations, while vegetations arranged on relatively wide facades have a greater impact on the flow field in the area. The reduction of extreme wind pressure is more significant under different vegetation coverage rates. Furthermore, the effectiveness of greenery in reducing extreme wind pressures initially increases with the coverage area, reaching its maximum reduction effect at a coverage of 13. 5% . The results can provide reference for wind-resistant design of similar structures.
高层建筑表面风压作为建筑抗风性能设计的重要依据,直接关系到建筑风荷载和建筑围护结构的安全,一直备受国内外学者关注[1-4]。近年来,为了满足低碳、环保、舒适等住房新要求,在阳台上种植树木,形成以垂直绿化为特点的第四代建筑正在受到越来越多国家的青睐,如意大利米兰的垂直森林[5]、南京明发财富中心[6]、成都七一城市森林花园[7]等。为了满足布置绿植的空间要求,此类建筑阳台和层高远大于常规建筑,且外立面往往被大量绿植包裹,外立面形式的改变会影响建筑的表面风压分布,进而可能影响建筑表面风荷载。第四代建筑在未来的城市生态中占据重要地位,为保证此类建筑的抗风性能安全,有关绿植对高层建筑表面风压影响规律的研究亟待进行。
现阶段,有关建筑表面风压受绿植影响的研究主要集中在绿植对低矮房屋的挡风作用和对风环境的影响方面。文献[8]基于风洞试验数据分析了不同类型树木影响下低矮房屋外立面非高斯风压分布特性及变化情况。文献[9]对比了不同大小绿植对小区风场的拖曳作用,结果表明拖曳作用与植被大小成正比。文献[10]将树木阻力参数化,通过 CFD 数值模拟研究了城市地区树木对行人高度风舒适度的影响,以蒲福风力等级( beaufort wind force scale,BWS)为舒适性判断依据,结果表明树木可使 BWS 值下降 1~3 个等级,有效改善了行人的风舒适度。
绿植对高层建筑的风压影响研究仍处于探索阶段,其影响机理尚不明确。文献[11] 通过测压和 HFBB 测力试验研究了树木对建筑风荷载的影响,发现绿植降低了迎风面和背风面的平均和极值风压,但该研究绿植布置形式较为单一。此外,既有研究表明,高层建筑的表面风压往往伴随着强烈的非高斯特性[12-16]。文献 [17 ] 通过大涡模拟( large eddy simulation,LES)分析了某超高层建筑表面风压,发现位于分离流动区域的脉动风压本质上是非高斯的; 也有学者发现高层建筑背风面中下部及侧风面边缘处风压的非高斯特性明显更强[18-19],且风压非高斯特性与风向角密切相关[20]。风压的非高斯特性会极大影响建筑表面的极值风压,因此在进行高层建筑维护结构抗风计算时需要关注风压的非高斯特性。
外立面形式不同会显著影响建筑表面风压的非高斯分布。文献[21] 探究了竖向肋条布置对建筑外立面风压非高斯特性分布的影响,试验结果表明竖向肋条使得侧风面非高斯性测点减少,背风面无明显变化; 文献[22]通过风洞试验发现水平隔板可以减小高层建筑局部风压的偏度和峰度,从而削弱其非高斯特性。文献[23] 通过风洞试验研究了高层建筑表面风压系数的概率特征,发现分离区测点风压母体接近伽马(Gamma)分布。文献[24-25] 基于风压时程的高阶矩,划分了建筑表面非高斯区域。绿植显著改变了第四代建筑外立面形式,其风压非高斯特性如何尚无定论,亟需加以研究。
因此,基于上述研究的不足,以某高层建筑为研究背景,利用风洞试验对不同绿植覆盖面积下建筑外立面风压系数的概率分布特征进行深入分析,通过概率分布拟合选取非高斯风压最优母体分布,基于 Sadek-Simiu 法获得风压非高斯特性的极值分布,揭示绿植对第四代建筑极值风压的影响规律,研究结果可为类似高层建筑抗风设计提供参考。
1 风洞试验
1.1 风洞试验模型
试验在长沙理工大学风工程与风环境研究中心高速试验段进行,高速试验段宽 4 m,高 3 m,采用刚性模型整体测压,试验缩尺比 1∶ 100,模型在风洞中的阻塞比小于 5%。如图1(a)所示,建筑模型核心区尺寸为 39.2 m × 26 m × 100 m,其中,阳台外伸 3 m,阳台围墙高 1 m; 如图1(b)所示,宽面 W、E 每层布置了 5 个测点,窄面 N、S 每层布置了 3 个测点,共有 13 层测点。采用圆柱体绿植模型模拟绿植对外立面的遮挡作用,忽略绿植在风荷载下的微小变形,绿植模型整体高 0. 06 m,其中树冠高 0. 04 m,直径为 0. 02 m,绿植与阳台之间采用刚性连接。通过尖劈和粗糙元模拟了 B 类地貌,风速和湍流度剖面如图1(c)所示,试验中模型顶部高度处来流风速为 10 m / s,风压采样频率为 331.5 Hz,每个测点获得 20 000 个采样数据,风向角为 0°~180°,间隔 15°,共采集了 13 个风向角的风压数据。
1.2 数据处理
为分析结构在不同绿植覆盖面积作用下表面风压特性的变化规律,定义绿化率 R 为
(1)
式中:A1 为绿植在外墙立面的投影面积,A0 为建筑外立面面积。
风压系数是结构风压的无量纲表现形式,平均风压系数 Cpmean定义为
(2)
(3)
式中:Cpi为测点 i 处的无量纲风压系数; pi 为测点 i 处的风压值; p∞ 为参考点的静压力值; ρ 为空气密度,取1.225 kg / m 3; VH 为参考高度处的风速,H = 1 m; N 为风压时程数据总数。
极值风压系数 定义为
(4)
式中: 为极大/ 小值风压系数,为测点 i 的平均风压系数,为脉动风压系数,g 为峰值因子。
图1风洞试验模型
Fig.1Wind tunnel test model
2 第四代高层建筑风压特性
2.1 风压非高斯特性判断
高斯信号的概率密度函数可以由低阶矩(期望和方差)描述,对于非高斯信号,概率分布通常表现出非对称特性,一般用高阶统计量偏度( skewness)和峰度(kurtosis)描述其概率分布的偏离和陡峭程度,偏度 Sk 和峰度 Ku 定义为
(5)
(6)
文献[26]通过风洞试验对双幕墙矩形建筑脉动风压进行了分析,给出了高斯风压的经验判断标准,当结构上监测点风压系数时程的偏度和峰度同时满足| Sk | <0.4、2.3 <Ku <3.7 时,可视为该区域基本符合高斯分布。文献[27] 通过试验对一标准 CAARC 建筑模型表面风压进行分析,表明当测点风压系数满足 | Sk | <0.5、Ku <3.5 时,为高斯测点。文献[28]结合试验数据,认为划定非高斯区域的标准为| Sk | >0.2、 | Ku | >3.5。对于第四代建筑,阳台上布置的绿植显著改变了建筑外立面气动外形,来流到达外立面之前受到绿植的干扰将会使得风压脉动特性发生一定变化,上述标准对于该种结构风压的非高斯划分的适用性情况尚不清楚。
图2为不同绿化率时建筑外立面 0°到 90°风向角下风压系数高阶矩偏度-峰度散点分布图,不难发现,随着绿化率的增大,高阶矩散点图分布范围更加集中,不同风向角下负偏度测点总数大于正偏度测点总数,且负偏度值远大于正偏度值,表明负压区风压表现出强非高斯特性的机率更大,从而产生不利风荷载。各绿化率测点的峰度值基本大于 2.3,符合文献[26]的非高斯判断下限标准,以该标准为基础,进一步分析其峰度上限和偏度判断标准的适用性。
2.2 概率分布拟合
为进一步检验文献[26] 非高斯标准对第四代建筑的适用性,对该标准范围附近测点的标准化风压系数概率分布进行拟合,如图3所示,给出了 0° 风向角下 2 / 3 建筑高度处典型测点(见图1(b))标准化风压系数概率分布拟合曲线。图3(a)、4(a)分别为无绿植时侧风面中轴线测点 210 标准化风压系数概率分布拟合曲线及风压系数时程,标准化风压系数概率分布直方图左侧数值变化范围大于右侧,有明显的“拖尾”现象,风压系数在 0~1 之间的概率密度大于所有的拟合曲线值,表现出高峰度特征; 图3(b)为迎风面边缘测点 212 的概率分布拟合曲线,不难看出风压系数分布较为均匀,与 Normal 分布曲线拟合较好,其风压系数时程(图4(b))基本关于 0 轴上下对称分布,表现出高斯特性; 图3(c)测点 219 与图3( a)测点 210 的概率分布特征基本相同,表现出明显的非高斯特性。
图2高阶矩偏度-峰度散点分布
Fig.2High order moment skewness-kurtosis scatter plot

图3典型测点概率分布拟合
Fig.3Probability distribution fitting diagram of typical measurement points
如图3(a)和图3(c),测点210 和219 受到直方图带宽的影响不能直观判断出概率分布拟合曲线优劣,因此通过概率图相关系数法[29] 来进行曲线拟合优度检验。图5为 2 / 3 建筑高度处不同绿化率下建筑外立面典型测点风压概率分布拟合曲线相关系数值,整体上来说,各绿化率下 Normal 分布相关系数值基本上小于其他分布,表明大部分测点表现出非高斯特性; 对比所有测点相关系数值发现 GEV 分布和 Gamma 分布的相关系数值保持“优势”的概率较大。因此,非高斯风压母体分布更适合用 GEV 分布和 Gamma 分布来描述。
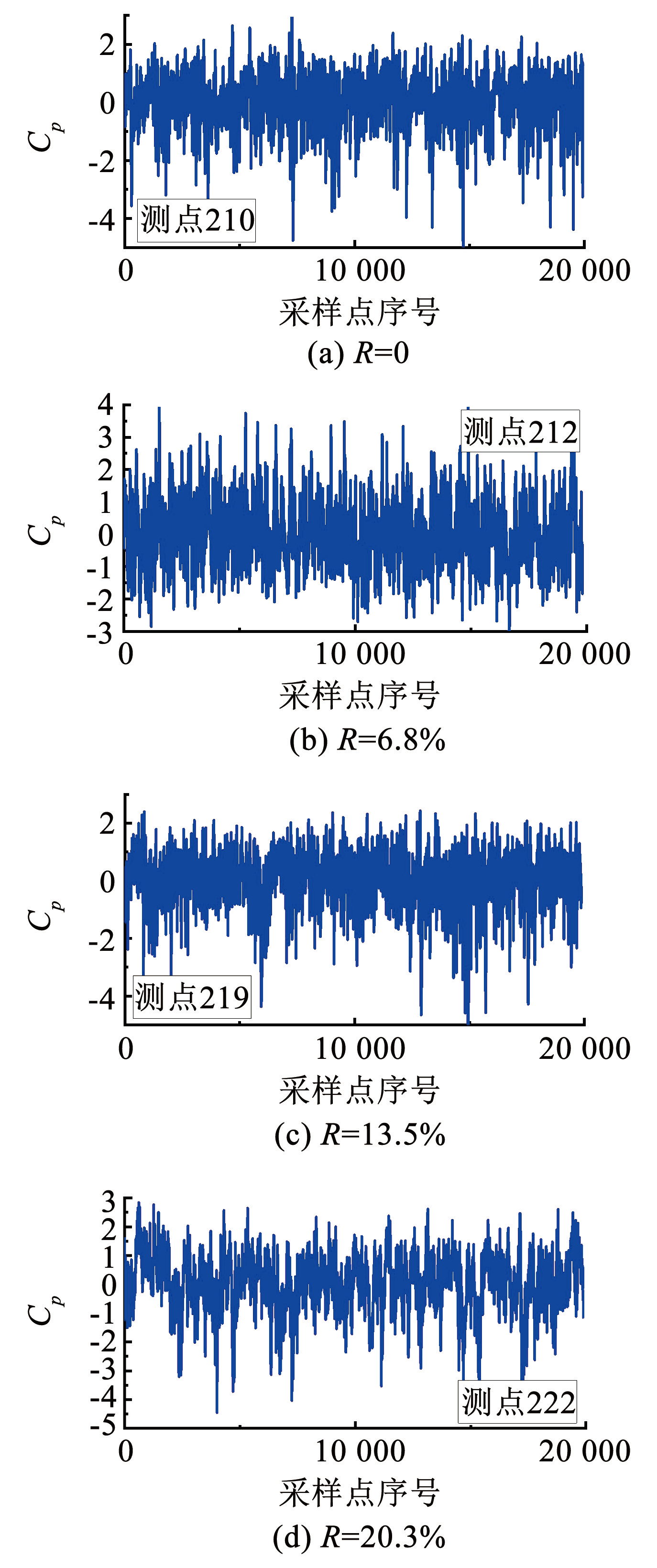
图4典型测点风压系数时程
Fig.4Wind pressure coefficient time history of typical measurement points
通过对全风向角、不同绿化率下所有测点风压的概率分布拟合及拟合优度检验结果进行统计分析,给出了第四代建筑风压非高斯判断经验标准,即当偏度和峰度值同时满足| Sk | <0.4、2.5 <Ku <3.5 时,可认为该风压表现出高斯特性,经过统计分析,该判断标准的准确率为 92%。
2.3 非高斯风压测点分布
图6~8 为 0°风向角时建筑外立面测点风压高斯性判断结果,不难看出:1)R = 6.8% 时迎风面非高斯性测点最多,此时绿植对来流的扰动较大; 此外,绿植的存在改变了迎风面边缘分离点位置,使得边缘测点由非高斯性转化为高斯性。 2)侧风面为分离流运动区,均表现出非高斯特性,且绿植对其影响较小。 3)背风面顶部高斯测点随着绿化率的增大先增多后减少,最后再次增多,绿植对三维流有较大影响,导致背风面顶部非高斯特性区域有较大波动。
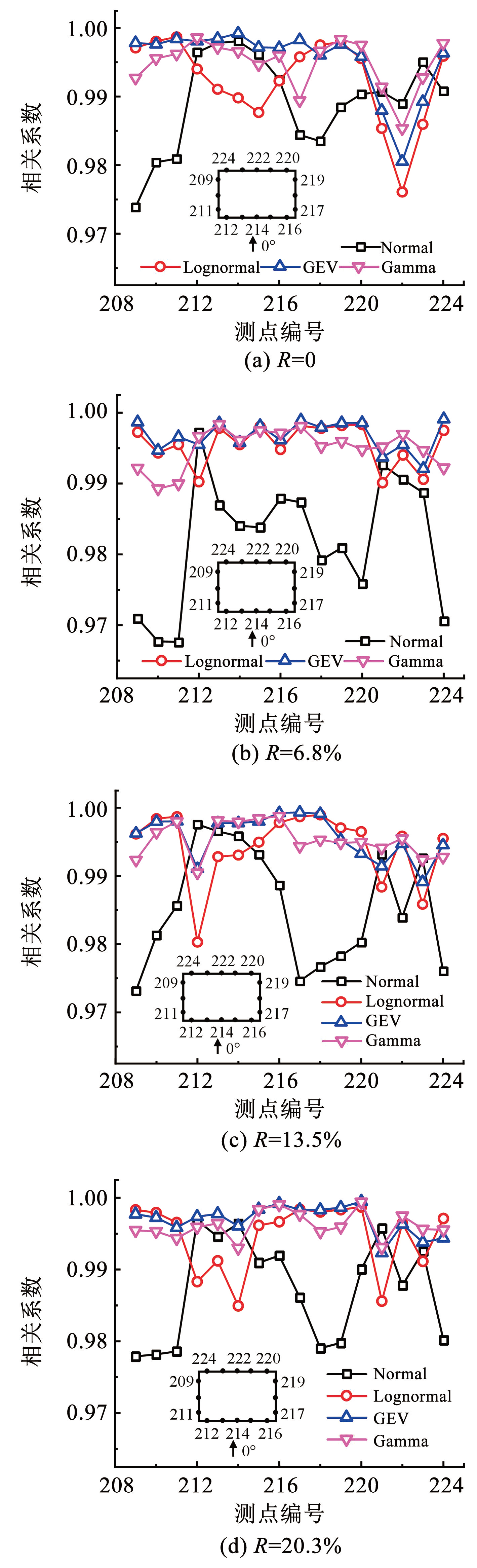
图5概率分布相关系数
Fig.5Correlation coefficient of probability distribution
2.4 基于最优母体分布的 Sadek-Simiu 法峰值因子分析
文献[30]基于标准高斯过程提出的峰值因子法被广泛应用于高斯风压极值的求解。对于非高斯风压,常表现出高峰度、高偏度特征,其概率分布更容易出现“拖尾现象”,从而导致极值风压更大,引起结构破坏。文献[29] 建立了高斯过程与非高斯过程的映射关系,对非高斯信号处理有较好的适用性,受到广泛应用[31-33]。
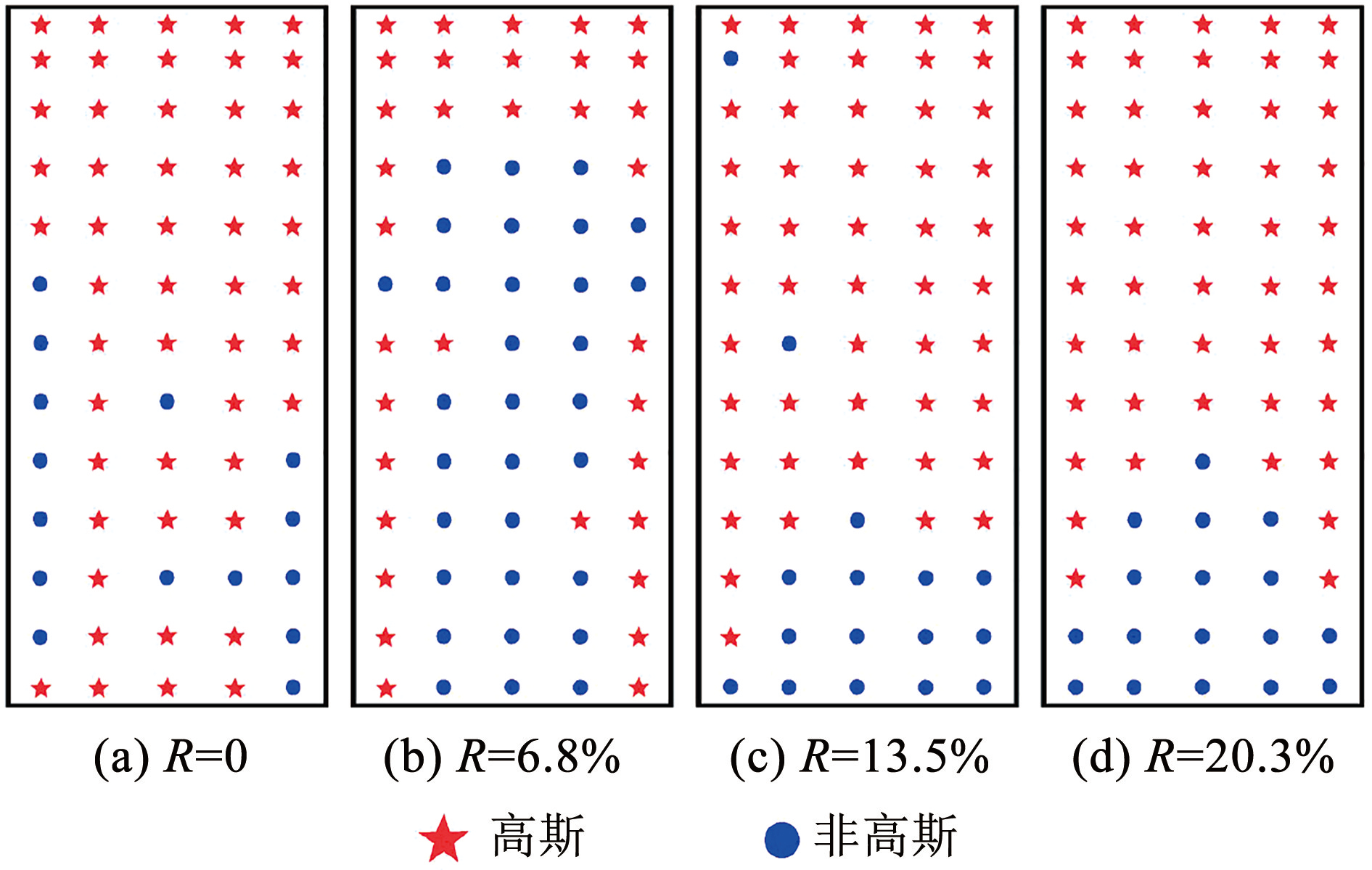
图6迎风面测点高斯性判断(0°)
Fig.6Gaussianity assessment for windward side measurement points (0°)
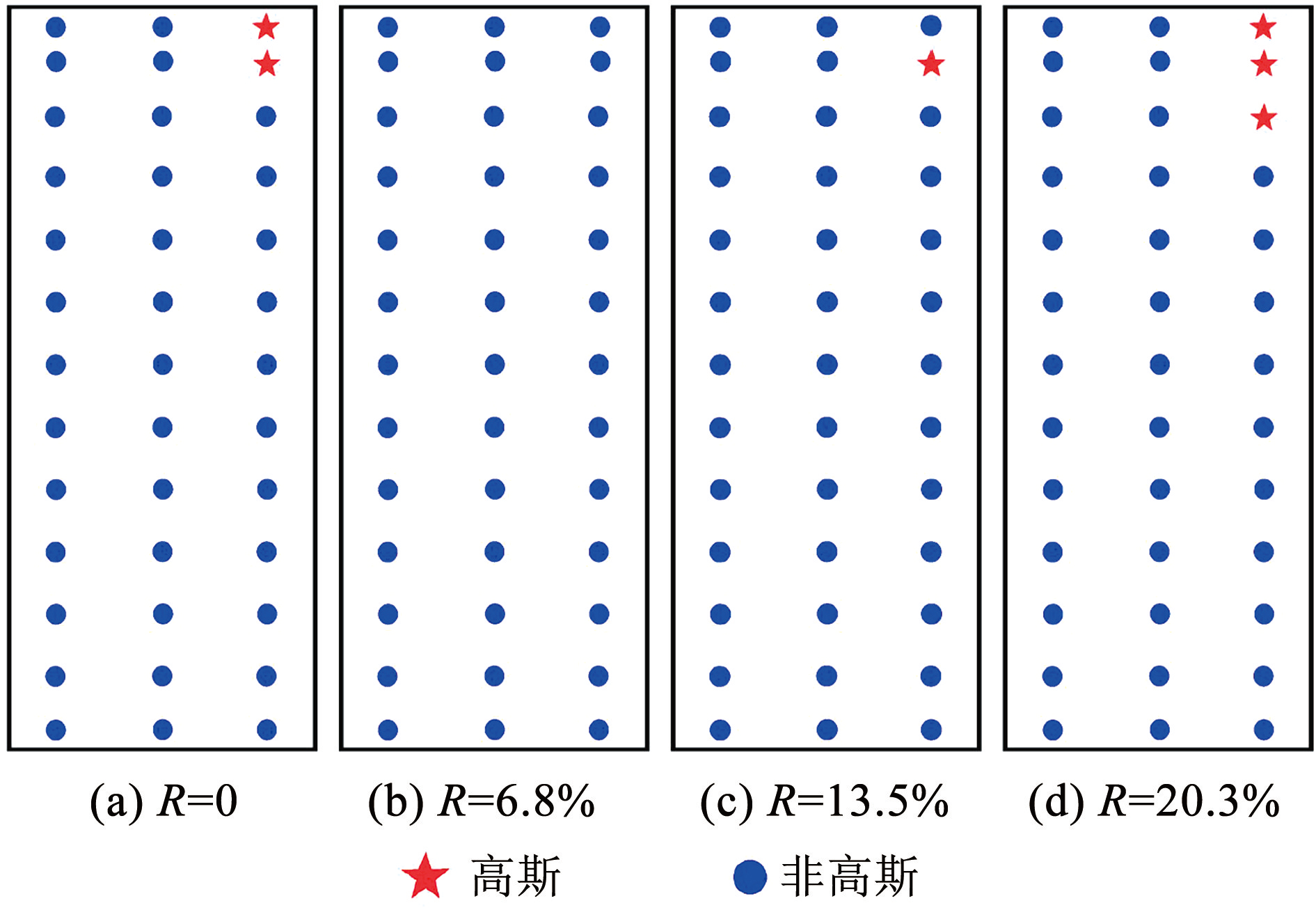
图7左侧面测点高斯性判断(0°)
Fig.7Gaussianity assessment for left side measurement points (0°)
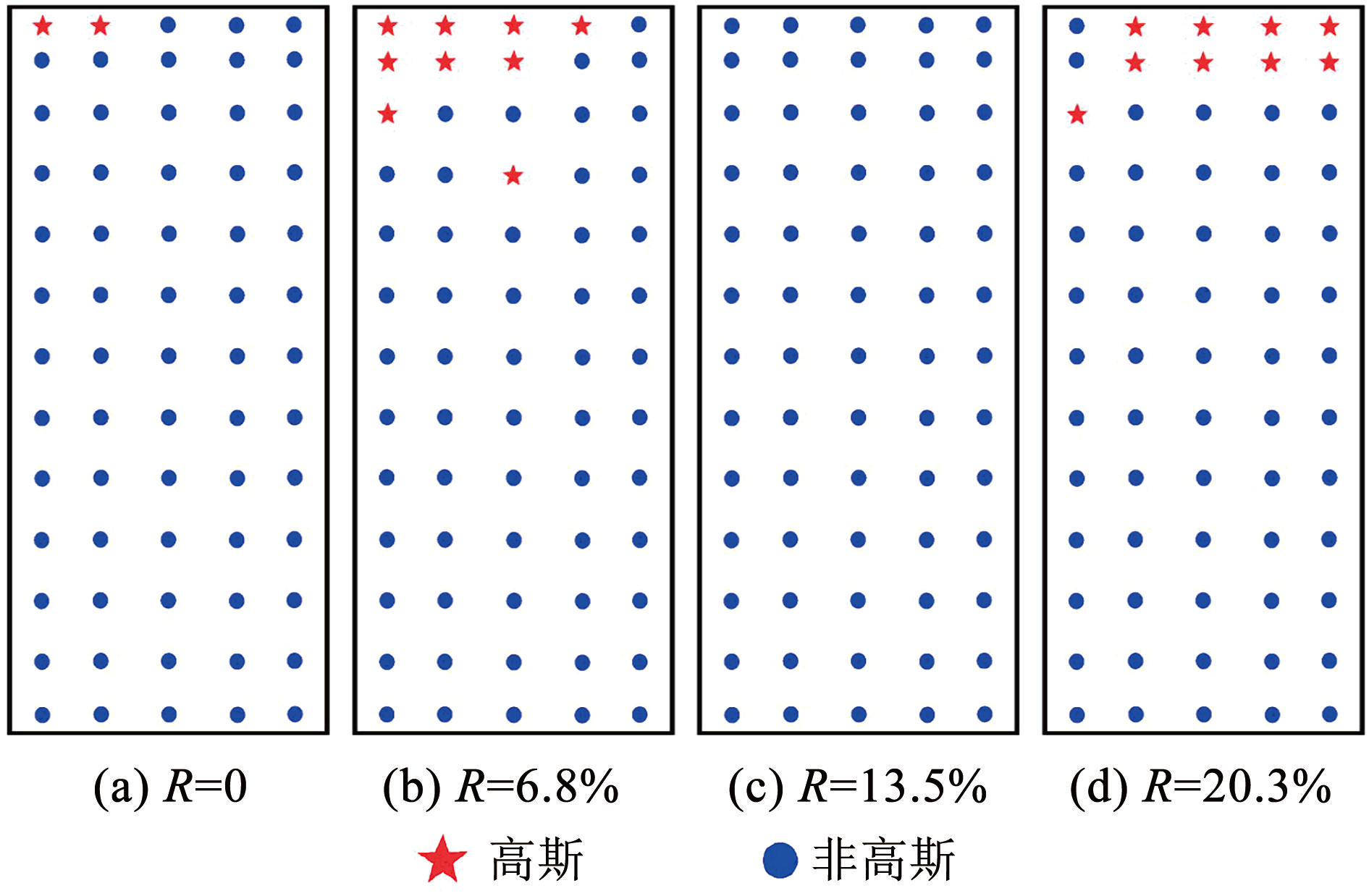
图8背面测点高斯性判断(0°)
Fig.8Gaussianity assessment for leeward side measurement points (0°)
本研究基于 Sadek-Simiu 非高斯风压峰值因子计算方法,通过拟合的最优母体分布,对每个测点的峰值因子进行精细化分析。图9为不同绿化率影响下峰值因子变化对比结果,其中 OM 代表最优分布母体,是经过 2.2 节拟合优度检验的最佳母体分布。不难发现,以 Lognormal 为风压母体分布计算出的峰值因子整体上最大,以 Normal 为风压母体通过 Sadek-Simiu 法计算出的峰值因子均小于峰值因子法结果; 同一测点不同绿化率下最优母体分布不同,导致峰值因子有较大波动。整体上来说,不同母体分布对应的峰值因子均远大于规范[34] 值 2.5,且绿植对风压母体分布有较大改变。
图9不同绿化率影响下峰值因子分布
Fig.9Peak factor distribution under different vegetation coverage rates
3 绿植影响下建筑极值风压分布
为整体分析绿植对建筑外立面极值风压的影响,将外立面每层极值风压求均值。如图10所示,45°时,侧风面 N 极大值风压受绿化率影响有较大波动,R = 6.8% 时绿植对极大值负压的降低作用大于其他绿化率; 迎风面 W 极大值风压随绿化率的增大先减小后增大,R = 13.5% 时绿植对正压的降低作用最大; 背风面 E 与侧风面 N 变化规律相同,R = 6.8% 时绿植对极大值负压的降低作用最大。整体上,宽面迎风时,绿植降低了外立面极大值风压。
由图11可看出,90°时背风面 N 极大值风压受绿植影响波动较大,绿植增大了背风面负压; 侧风面 W 和 E 的极大值负压随绿化率的增大而增大,窄面迎风时,绿植的拖拽作用随绿化率的增大而增大,平均风压的微量减小与脉动风压的急剧降低组合后导致负压增大; 由于绿植布置有误差,导致侧风面 W 和 E 的极大值负压变化曲线不完全对称。总的来说,窄面迎风时,绿植会增大建筑侧风面的负压,且随着绿化率的增大有增大趋势,但风压系数绝对值较小,设计时可忽略其影响。
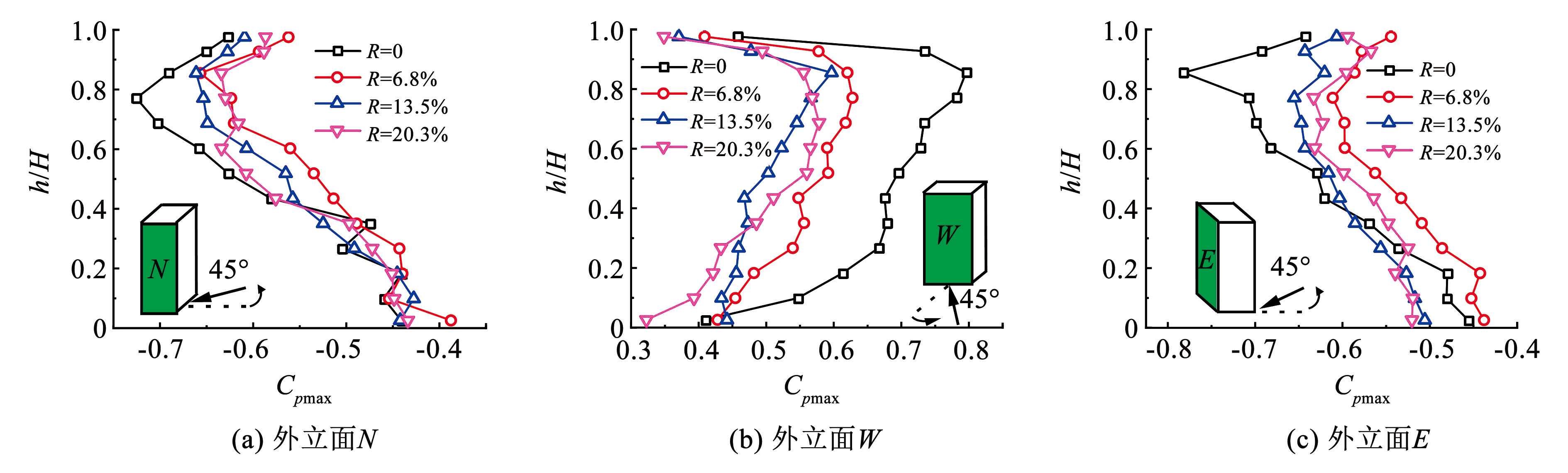
图10外立面极大值风压系数(45°)
Fig.10Maximum wind pressure coefficient of exterior facade (45°)
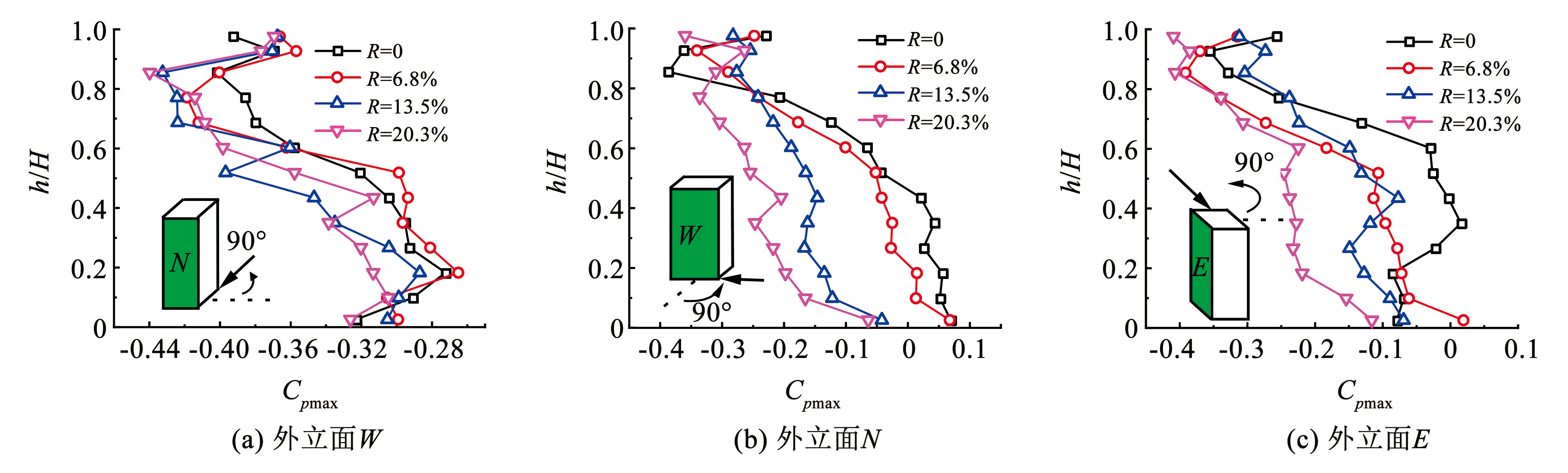
图11外立面极大值风压系数(90°)
Fig.11Maximum wind pressure coefficient of exterior facade (90°)
图12为 45°风向角时绿植影响下外立面极小值风压系数变化曲线。侧风面 N 的极小值负压随着绿化率的增大单调递减; R = 20.3% 时,绿植对迎风面 W 表现出遮挡作用,降低了负压,其他绿化率均增大了负压,来流在绿植与外墙立面之间的通道被加速,同时也会受到绿植的遮挡拖拽,两者互相影响,导致迎风面 W 极小值风压变化受绿植影响规律不明显; 背风面 E 负压随绿化率的增大先减小后增大,R = 13.5% 时绿植对负压降低作用最大。整体上,绿植降低了外立面的极小值负压,且降低作用随绿化率的增大呈非线性变化。
图13为 90°时外立面极小值风压变化曲线。不同绿化率的绿植对背风面 N 极小值负压均有抑制作用; 侧风面 W 和 E 极小值负压随着绿化率的增大而减小,随着绿化率的增大,外立面“粗糙度” 增加,绿植的拖拽作用增大,风压脉动特性降低,导致峰值因子和脉动风压下降,平均风压起主导作用,造成极小值风压降低。总的来说,窄面迎风时,绿植对外立面极小值负压的降低作用随着绿化率的增大而增大。

图12外立面极小值风压系数(45°)
Fig.12Minimum wind pressure coefficient of exterior facade (45°)
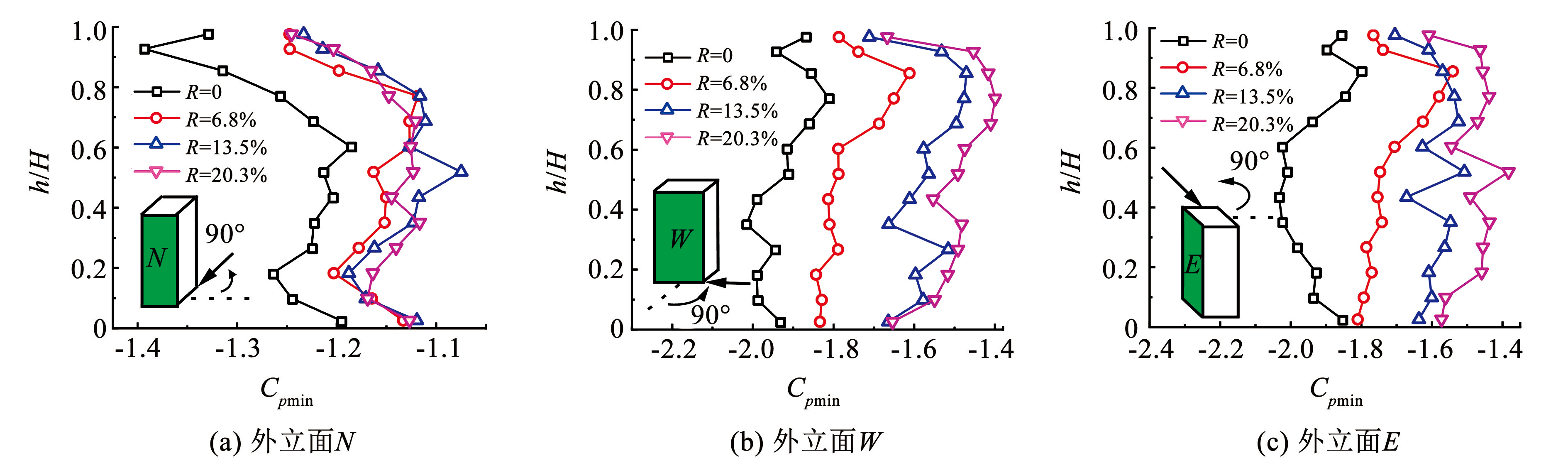
图13外立面极小值风压系数(90°)
Fig.13Minimum wind pressure coefficient of exterior facade (90°)
4 结论
本文通过风洞测压试验,研究了不同绿植覆盖面积下高层建筑外立面风压的非高斯特性变化,基于 Sadek-Simiu 法分析不同风压母体分布对峰值因子的影响,揭示了不同覆植面积下建筑外立面极值风压的变化规律,得到以下结论:
1)基于试验数据,给出了第四代建筑高斯风压的判断标准,当偏度和峰度同时满足 | Sk | <0.4、 2.5 <Ku <3.5 时,可认为该风压表现出高斯性,且广义极值分布(GEV)和伽马分布(Gamma)更适合做第四代建筑非高斯风压母体分布。
2)绿植的存在改变了建筑迎风面分离点位置,使得迎风面边缘测点由非高斯性转化为高斯性; 侧风面风压均表现出非高斯性,且受绿植影响较小。
3)与无绿植结构相比,窄面上的极值风压受绿植影响较小,而布置在相对较宽外立面上的绿植对该区域流场影响更大,不同绿化率下极值风压降低作用更明显,设计时应引起关注。
4)绿植对建筑外立面极值风压的影响与风向角有关,整体来说,绿植对极值风压的降低作用随绿化率的增大先增大后减小,绿化率 R = 13.5% 时对风荷载的降低作用最大。



