欢迎访问《哈尔滨工业大学学报》编辑部网站！

球面爆轰波下不同孔径耦合装药孔壁压力沿炮孔轴向分布特征

doi: 10.11918/202311089

楼晓明^1,2 ，林杰^1,2 ，王新龙³ ，刘怀宇³ ，王广³

1. 福州大学紫金地质与矿业学院,福州 350108

2. 福州大学爆破技术研究所,福州 350108

3. 乌拉特后旗紫金矿业有限公司,内蒙古巴彦淖尔 015500

基金项目: 国家自然科学基金(51679093,51374112)

详细信息

作者简介

楼晓明(1972—),男,教授

通讯作者

林杰,Linjie2021@126.com

中图分类号: TB41

文献标识码: A

文章编号: 0367-6234(2025)03-0148-12

Characteristics of axial distribution of borehole wall pressure along the borehole of coupled charges with different borehole diameters under spherical detonation wave

LOU Xiaoming^1,2 ， LIN Jie^1,2 ， WANG Xinlong³ ， LIU Huaiyu³ ， WANG Guang³

1. Zijin College of Geology and Mining, Fuzhou University, Fuzhou 350108 , China

2. Institute of Explosin Technology, Fuzhou University, Fuzhou, 350108 , China

3. Wulate Houqi Zijin Mining Co.,Ltd., Bayannur 015500 , Inner Mongolia, China

摘要

为分析岩石爆破孔壁压力沿炮孔轴向分布的特征,采用理论分析、模型试验和有限元模拟相结合的方法,对不同孔径耦合装药炮孔轴向孔壁压力进行研究。首先基于球面爆轰波理论,建立炮孔内爆轰作用模型;以爆轰波与孔壁的入射角和炮孔直径关系为基础,推导出各阶段爆轰作用下的孔壁压力理论计算公式,得到不同孔径的孔壁压力沿炮孔轴向孔壁的变化曲线。为验证理论分析的合理性,进一步利用混凝土厚壁圆筒模型试验,运用高速多路动态应变测试系统对孔壁压力进行监测,同时建立不同炮孔直径的有限元数值模拟,获得不同孔径炮孔孔壁压力沿炮孔轴向分布结果,并将模型试验和数值模拟结果与理论分析结果进行了对比分析。研究结果表明:耦合装药孔壁压力沿炮孔轴向方向呈现不均匀分布,起爆点近区孔壁压力急剧增大,达到最大压力峰值后开始衰减,最后孔壁压力趋于平稳波动的特征;炮孔直径与孔壁压力存在正相关,最大压力峰值和平稳波动阶段孔壁压力随炮孔直径增大而增大;在 d = 40 mm 炮孔轴向孔壁压力的理论计算值与模型试验、数值模拟结果相对误差均较小,验证了理论分析的合理性。

关键词

球面爆轰波 / 孔壁压力 / 耦合装药 / 模型试验 / 数值模拟

Abstract

In order to analyze the characteristics of axial distribution of borehole wall pressure along the borehole in rock blasting, the axial distribution of borehole wall pressure along the borehole of coupled charges with different borehole diameters was studied by combining theoretical analysis, model testing, and finite element simulation. Firstly, based on the theory of spherical detonation wave, a model of the detonation wave propagation in the borehole was established. Based on the relationship between the incidence angle of the detonation wave and the diameter of the borehole, the theoretical calculation formula of the borehole wall pressure under different propagation stages of detonation was derived, and the change curve of the borehole wall pressure along the axial borehole wall with different borehole diameters was obtained. In order to verify the rationality of the theoretical analysis, the concrete thick wall cylinder model test was further used to monitor the pressure of the borehole wall by using a high-speed multichannel dynamic strain test system. Meanwhile, finite element numerical simulation of different borehole diameters was established to obtain the axial distribution of borehole wall pressure results of different borehole diameters. And the model test and numerical simulation results were compared with the theoretical analysis results. The results show that the coupled charge borehole wall pressure presents an uneven distribution along the axial direction of the borehole, and the borehole wall pressure near the detonation point increases sharply, begins to decrease exponentially after reaching the maximum peak pressure, and finally tends to fluctuate steadily. There is a positive correlation between the borehole wall pressure and the borehole diameter. The maximum peak pressure and the stable fluctuation stage of the borehole wall pressure increase with the borehole diameter. The relative error between the theoretical calculation value of the axial borehole wall pressure at d =40 mm and the results of the model test and numerical simulation is small, which verifies the rationality of the theoretical analysis.

Keywords

spherical detonation wave / pressure of borehole wall / coupling charge / model test / numerical simulation

1 爆轰波与孔壁作用模型建立 2 孔壁压力峰值沿炮孔轴向分布理论计算 2.1 爆轰波正规斜反射作用 2.2 爆轰波马赫反射作用 2.3 孔壁压力峰值轴向分布特征 3 炮孔轴向孔壁压力模型试验 3.1 试验方案 3.2 试验模型制备 3.3 试验系统 3.4 模型试验结果与分析 4 数值模拟 4.1 有限元模型构建 4.2 材料与状态方程参数 4.3 数值模拟结果分析 4.3.1 不同孔径孔壁初始冲击压力沿炮孔轴向分布 4.3.2 数值模拟结果合理性分析 5 结论

柱状耦合装药爆破广泛应用于地下矿山采场中，作用于孔壁的压力峰值，直接影响岩石粉碎区范围及爆破破坏程度，是进行岩石爆破破坏分析的关键参数之一^[1]。不同孔径炮孔的装药量不同，导致在炮孔孔壁上的初始冲击压力峰值分布不同，进而导致周围岩石的破坏范围及破碎效果存在差异。因此，开展不同孔径耦合装药炮孔孔壁初始冲击压力轴向分布特征的研究，对提高破岩效果、优化孔网参数和设计装药结构具有重要意义。

国内外众多学者从理论计算、数值模拟和模型试验等不同研究方法出发，对炮孔孔壁压力进行了相关的研究。文献^[2-3]根据声学近似原理，推导耦合装药条件下柱状药包爆炸孔壁冲击压力计算公式。文献^[4]利用冲击波的基本关系式，考虑爆炸冲击波正入射的形式作用到孔壁上，得到孔壁的初始冲击压力计算公式，结果表明不同阻抗岩石对孔壁压力大小存在正相关。文献^[5]分析炸药爆轰和岩体破坏运动过程，构建孔壁压力简化计算模型，并基于理想气体状态方程得到各阶段孔壁压力随时间变化的函数。文献^[6]推导爆炸冲击波与弹性壁碰撞后压力增大倍数的理论解，提出孔壁压力峰值计算方法。但上述计算公式的结果是某一定值，即炮孔轴向孔壁上任一点的冲击压力均相同，不能反应孔壁压力沿炮孔轴向方向上分布的实际情况。文献^[7-8]考虑炸药性能和岩石介质条件，提出了一种小耦合系数装药爆破孔壁压力峰值计算方法。众多学者采用数值模拟方法研究爆破孔壁压力特性^[9-11]。文献^[12] 通过 ANSYS / LS-DYNA 对柱状装药爆破进行数值模拟，对孔壁初始压力的数值模拟结果与模型试验实测值、理论计算值进行对比分析，结果表明数值模拟值相对于实测值的平均误差较小，二者变化趋势较一致，实测值受到反射应力波的干扰，使得理论公式计算值较小于模拟值和实测值。文献^[13]以水泥砂浆试块为研究对象，利用超动态应变测试系统研究了不同耦合装药爆破试验，得到炮孔周围介质中爆炸压力的分布特性。文献^[14]采用锰铜压阻传感器对耦合装药条件下水泥砂浆等介质的孔壁压力进行了试验，并与理论值对比分析验证测试方法的可行性。这些研究成果在数值模拟和模型试验上提供了参考。总体上，对炮孔孔壁压力的研究基本是均值压力，无法体现孔壁压力沿炮孔轴向分布的特征。但在柱状耦合装药起爆时，爆轰波在炮孔内以球面波的形式进行传播，并与孔壁发生斜入射作用，使得轴向孔壁压力分布存在不均匀特征，在这方面的研究比较少，因此，柱状耦合装药孔壁压力沿炮孔轴向分布特征需要深入研究。

本文在孔壁压力峰值理论计算研究成果的基础上，针对不同孔径耦合装药炮孔孔壁压力峰值沿炮孔轴向分布的计算问题，采用球面爆轰波理论，构建爆轰作用模型并考虑爆轰波与孔壁的入射角和炮孔直径的的影响，推导了不同孔径下孔壁压力峰值沿炮孔轴向分布计算公式，进一步开展混凝土厚壁圆筒模型试验和不同孔径的三维数值模拟试验，获得两者的试验结果与理论计算值进行对比分析，验证理论公式的合理性，并确定不同孔径炮孔孔壁压力峰值沿炮孔轴向分布特征。

1 爆轰波与孔壁作用模型建立

耦合装药柱状炮孔孔底起爆后，爆轰波沿炮孔轴向进行传播叠加作用。在孔内传播过程中，爆轰波波阵面曲率半径 R 随着传播距离 l 的增大而增大，但传播至某一极限距离 l_m后，曲率半径趋于恒值 R_m ^[15]。建立炮孔内爆轰波传播模型，其中 H 为孔底中心起爆点，d 为炮孔直径，如图1所示。

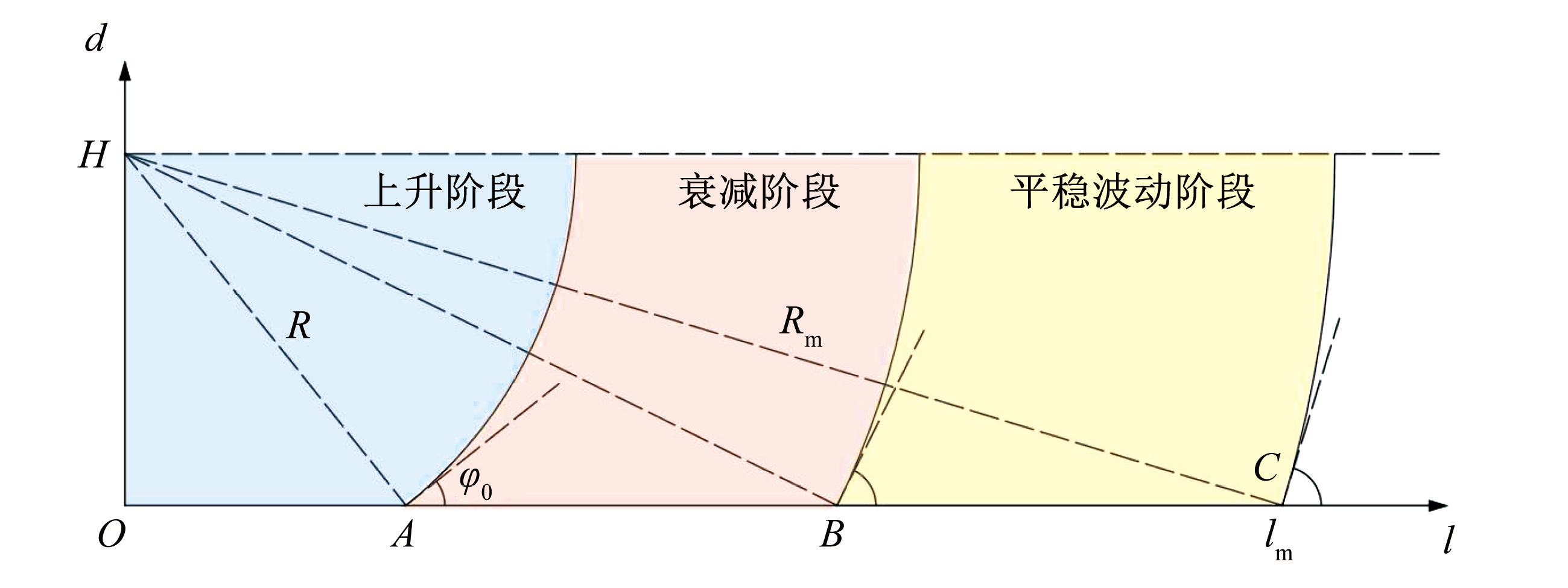
图1爆轰波在炮孔内传播过程

Fig.1Propagation process of detonation wave in borehole

当炸药起爆后，爆轰波以球面波传播，与炮孔孔壁发生斜反射作用。随着炸药爆轰传播，波阵面曲率半径增大，首先在起爆点近区 OA 段与孔壁发生冲击，此时爆轰波波阵面的入射角较小，可视为爆轰波与孔壁发生正规斜反射阶段。之后爆轰波沿炮孔进一步传播，波阵面曲率半径和爆轰波孔壁入射角都进一步增大，此时爆轰波在 AC 段发生马赫反射作用。其中马赫反射作用存在衰减阶段和平稳波动阶段，即 AB 阶段和 BC 阶段。在 BC 阶段后，由于炮孔长径比已经很大，此时爆轰波入射角变化不大，可以忽略不计，因此可视为以恒定入射角与孔壁发生斜反射作用直至爆轰完成。

2 孔壁压力峰值沿炮孔轴向分布理论计算

当爆轰波传至炸药与岩石的分界面处时，必然在介质中产生冲击波并会形成反射波。若考虑各反射波的叠加作用，理论计算结果难以求解，因此本文仅考虑球面爆轰波传播叠加作用在孔壁上的冲击压力。

2.1 爆轰波正规斜反射作用

为研究方便，以爆轰波与孔壁接触点为原点建立相对坐标系，正规斜反射结构^[15]如图2所示。 OI 为斜爆轰波波阵面，与炮孔孔壁的夹角为 φ₀，OV 为反射回爆轰产物的反射冲击波波阵面，与初始孔壁的夹角为 φ₂; OT 为传入岩石中的透射冲击波波阵面。这样，斜爆轰波、斜反射冲击波、斜透射冲击波和炮孔孔壁将整个区域分为 5 个区域:0 区为未爆炸药，1 区为斜爆轰波后爆轰产物区，2 区为反射冲击波后爆轰产物区，m₀ 区为初始介质，m 区为透射冲击波冲击波后介质区。

图2爆轰波的正规斜反射

Fig.2Regular oblique reflection of detonation wave

斜爆轰波可以视作与斜爆轰波法向速度相同的正爆轰波和斜爆轰波切向速度相同的均匀流动叠加而成，因此有

u_{0 n} = q_{0} s i n φ_{0} = D

(1)

式中:u₀_n为斜爆轰波法向速度，m / s; q₀ 为均匀流场速度，m / s; D 为炸药爆轰波波速，m / s。

爆轰波波阵面 OI 的法向上有质量、动量和能量守恒有

\{\begin{matrix} ρ_{0} u_{0 n} = ρ_{1} u_{1 n} \\ p_{1} - p_{0} = ρ_{0} q_{0 n} (u_{1 n} - u_{0 n}) \\ \frac{1}{2} u_{1 n}^{2} + e_{1} + p_{1} v_{1} = \frac{1}{2} u_{0 n}^{2} + e_{0} + p_{0} v_{0} \end{matrix}

(2)

式中:ρ₀为炸药装药密度，g / cm³; ρ₁为爆轰波波后产物密度，g / cm³; u₁_n为爆轰波波后产物流动的法向速度，m / s; p₀为爆轰波波前压力，GPa; p₁为爆轰波波后压力，GPa; v₀为比体积，v₀ = 1 / ρ₀; v₁为爆轰产物比体积，v₁ = 1 / ρ₁; e₀为炸药内能，

e_{0} = \frac{p_{0} v_{0}}{k - 1}

; e₁为 C-J 状态内能，

e_{1} = \frac{p_{1} v_{1}}{k - 1}

。

由式（1）、（2）和 C-J 状态条件可以确定 1 区爆轰波产物状态参数:

\{\begin{matrix} p_{1} = \frac{1}{k + 1} ρ_{0} D^{2} \\ ρ_{1} = \frac{k + 1}{k} ρ_{0} \\ c_{1} = \frac{k}{k + 1} D \end{matrix}

(3)

式中:k 为爆轰产物绝热指数; c₁为爆轰产物声速，m/ s。

2区为斜反射冲击波后的区域，其流动满足平行于介质面的条件，流动方向与斜反射冲击波波阵面的夹角为 φ₂ + δ; 1 区流动方向与斜反射冲击波波阵面的夹角为 φ₂ + θ。其中，1 区流动方向 θ 可表示为

t a n θ = \frac{\tan φ_{0}}{1 + k (1 + {t a n}^{2} φ_{0})}

(4)

反射冲击波 OV 向流动方向上，采用质量、动量和能量守恒有

\{\begin{matrix} ρ_{1} u_{1 n} = ρ_{2} u_{2 n} \\ p_{2} - p_{1} = ρ_{1} u_{1 n} (u_{1 n} - u_{2 n}) \\ e_{2} - e_{1} = \frac{1}{2} (p_{2} + p_{1}) (v_{2} + v_{1}) \end{matrix}

(5)

式中:ρ₂ 为反射冲击波波后产物密度，g / cm³; u₁_n和 u₂_n分别为爆轰波波后产物和反射冲击波波后产物质点法向速度，m / s; p₂为反射冲击波压力，GPa; v₂为反射冲击波波后产物比体积。

在式（5）中 D₂、p₂、v₂和 e₂为 4 个待求解量，求解时需引入第 4 个方程。结合在起爆点近区爆轰时间极短不考虑爆轰产物膨胀，引入分子排斥作用的凝聚体状态方程^[16] :

\{\begin{matrix} p_{i} = \frac{A}{v_{i}^{k}} \\ e_{i} = \frac{A}{(k - 1) v_{i}^{k - 1}} \end{matrix}

(6)

结合式（6）可确定斜反射冲击波在波阵面前后压力比的函数关系:

\frac{p_{2}}{P_{1}} = \frac{2 k}{k + 1} M_{1}^{2} {s i n}^{2} (φ_{2} + θ) - \frac{k - 1}{k + 1}

(7)

式中 M₁ 为 1 区流动速度 mach 数，

M_{1}^{} = \sqrt{1 + {(\frac{k + 1}{k})}^{2} {c o t}^{2} φ_{0}}

。

在斜反射冲击波后的 2 区和斜透射冲击波后的 m 区，在分界面上满足压力相等的条件，可得到斜爆轰波入射时孔壁压力，即起爆点近区正规斜反射阶段孔壁压力计算公式:

p_{I} = [\frac{2 k}{k + 1} M_{1}^{2} {s i n}^{2} (φ_{2} + θ) - \frac{k - 1}{k + 1}] \frac{1}{k + 1} ρ_{0} D^{2}

(8)

上式中关键参数为入射角和反射角取值，入射角 φ₀和反射角 φ₂之间存在函数关系^[15] :

\frac{\tan φ_{2}}{\tan [φ_{2} + a r c t a n (\frac{\tan φ_{0}}{k {t a n}^{2} φ_{0} + k + 1})]} = \frac{k - 1}{k + 1} + \frac{2 k^{2}}{k + 1} . \frac{1}{k^{2} + (k + 1)^{2} {c o t}^{2} φ_{0} {s i n}^{2} [φ_{0} + a r c t a n (\frac{\tan φ_{0}}{k {t a n}^{2} φ_{0} + k + 1})]}

(9)

在已知 k 的情况下，只要确定入射角，采用数值迭代法，即可求出反射角。应当说明，随着爆轰波进行正规斜反射爆轰，入射角度不断增大，当入射角大于某一临界角时，得不到实数解。对式（9）迭代求解可知，当入射角达到 45°附近时，反射角无实数解，此时，孔壁压力在炮孔轴向上达到峰值，对应位置与起爆点的距离称为峰值距离 l_A，峰值距离与炮孔直径有关。

因此，可联合式（8）和式（9）求得爆轰波斜入射炮孔孔壁初始压力。

2.2 爆轰波马赫反射作用

爆轰波传播达到峰值距离 l_A后，其不再进行正规斜反射。实验证明，大于临界入射角后，爆轰波在孔壁上会发生反射波脱离，在孔壁上出现马赫杆^[15]，其结构如图3所示。

以爆轰波与孔壁界面接触点为原点建立相对坐标系。 OI 为斜爆轰波波阵面，其中 OO′为马赫杆波阵面，O′I 与孔壁初始界面的入射角为 φ₀，O′V 为反射冲击波波阵面，与孔壁初始界面的夹角为 φ₂; 在三波点 O′后存在一道涡旋面 O′G。其余与正规斜反射作用标记相同。此时，整个区域分为 6 个区域: 3 区为马赫杆后过度压缩的爆轰产物区，其余 5 个区与正规斜反射作用分区相同。

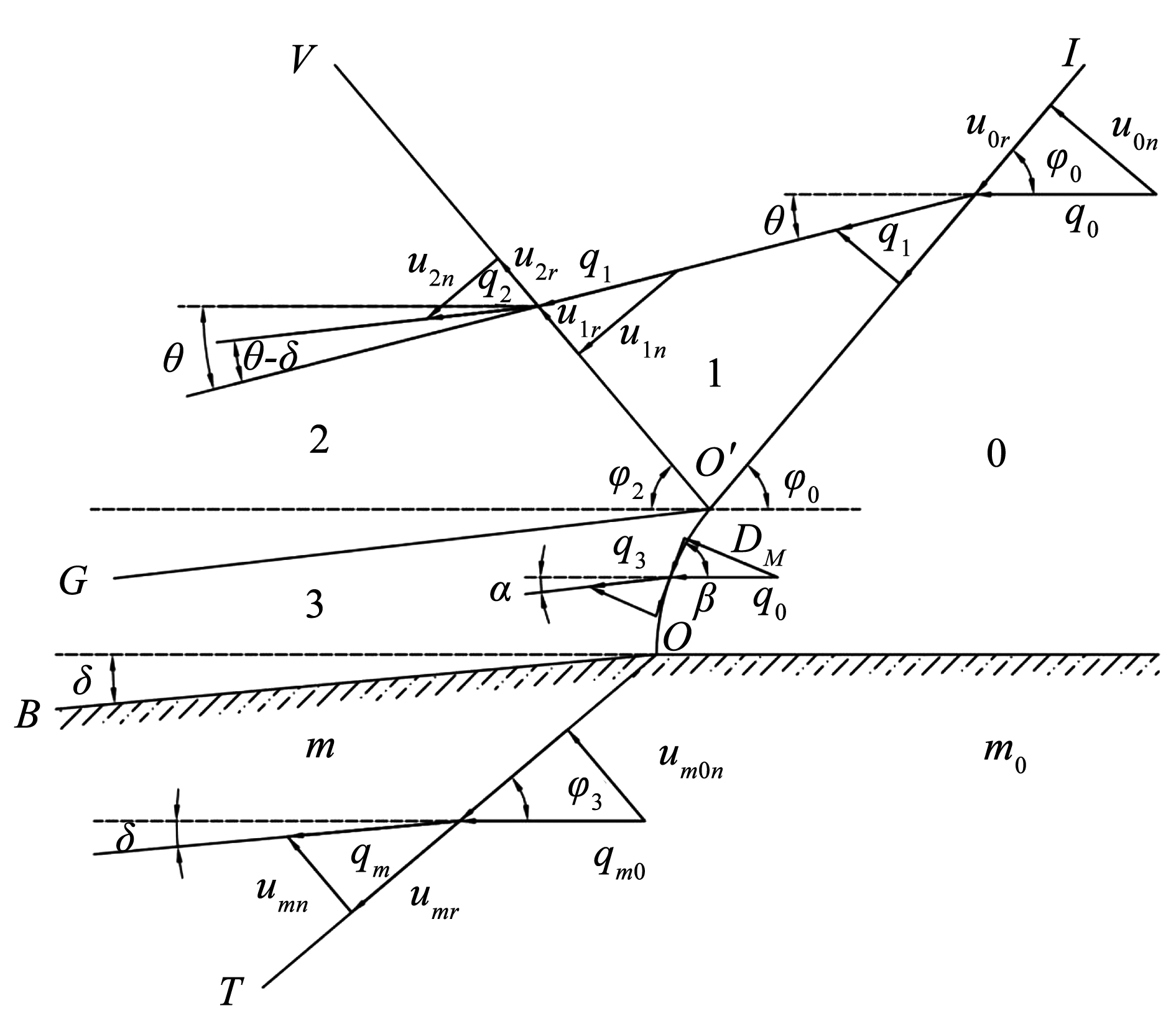
图3爆轰波的马赫反射

Fig.3Mach reflection of detonation wave

对于马赫杆波阵面法向上仍满足基本方程:

\{\begin{matrix} ρ_{0} D_{M} = ρ_{3} (D_{M} - q_{3}) \\ p_{3} - p_{0} = ρ_{0} D_{M} q_{3} \\ e_{3} - e_{0} = \frac{1}{2} (p_{3} + p_{0}) (v_{0} + v_{3}) + η Q_{v} \end{matrix}

(10)

式中:q₃为马赫杆前后法向流动速度变化量，m / s; η 为过度压缩系数，一般取 η = 1.1~1.2; Q_v为正常爆轰释放的能量，

Q_{v} = \frac{p_{1} v_{0}}{2 （ k - 1 ）}

。

对于马赫杆前法向速度有

D_{M} = q_{0} s i n β = \frac{D s i n β}{\sin φ_{0}}

(11)

有式（6）、（10）、（11）可得

\{\begin{matrix} \frac{p_{3}}{p_{1}} = \frac{\sin^{2} β}{\sin^{2} φ_{0}} (1 + \sqrt{1 - \frac{η {s i n}^{2} φ_{0}}{\sin^{2} β}}) \\ \frac{ρ_{0}}{ρ_{3}} = \frac{1}{k + 1} (k + \sqrt{1 - \frac{η {s i n}^{2} φ_{0}}{\sin^{2} β}}) \end{matrix}

(12)

根据波面上切向速度相等以及质量守恒的关系，有

t a n (β + α) = \frac{ρ_{0}}{ρ_{3}} t a n β

(13)

将式（12）代入式（13）可得到 3 区流动转折角 α 关系式:

t a n α = \frac{(1 + \sqrt{1 - \frac{η {s i n}^{2} φ_{0}}{\sin^{2} β}}) t a n β}{1 + k + (k + \sqrt{1 - \frac{η {s i n}^{2} φ_{0}}{\sin^{2} β}}) {t a n}^{2} β}

(14)

从式（12）、（14）可以看出，若已知 k、φ₀ 和 η，3 区的参数和流动转折角都是 β 的函数。在 3 区和 2 区的漩涡面压力相等，流动方向一致; 在 3 区和 m 区分界面上压力相等，有

\begin{matrix} {s i n}^{2} φ_{3} (1 - \frac{a s i n φ_{0}}{D s i n φ_{3}}) = \\ \frac{b ρ_{0} {s i n}^{2} β}{(k + 1) ρ_{m 0}} (1 + \sqrt{1 - \frac{η {s i n}^{2} φ_{0}}{\sin^{2} β}}) \end{matrix}

(15)

由式（12）、（13）、（14）、（15），以及根据马赫杆不同位置，可以确定 β，然后进一步确定 3 区的的 p₃、ρ₃等参数。但由于上述计算公式过于复杂，难以确定数值解，所以采用近似求解，得到爆轰波马赫反射作用阶段下的孔壁压力:

p_{II} = [\frac{1}{\sin^{2} φ_{2}} + \frac{1}{\sin φ_{2}} {(\frac{1}{\sin^{2} φ_{2}} - 1)}^{\frac{1}{2}}] \frac{1}{k + 1} ρ_{0} D^{2}

(16)

2.3 孔壁压力峰值轴向分布特征

随着爆轰波沿炮孔轴向传播叠加，入射角与距起爆点某一距离孔壁存在函数关系 f（l）。由图1所示，确定入射角函数关系式:

φ_{0} = a r c t a n \frac{l}{r}

(17)

式中:l 为孔壁某点位置距起爆点的距离，mm; r 为炮孔半径，mm。

理论和试验研究表明，炸药爆速与装药直径的关系^[2]为

D = D_{H} (1 - \frac{a}{d})

(18)

式中:D 为炸药的实际爆速; D_H为炸药的理想爆速; d 为炮孔直径; a 为爆轰反应区厚度，一般取炸药临界直径的 1 / 2 ^[17]。

将式（17）、（18）代入式（8）、（16）中，可得到连续耦合装药炮孔轴向孔壁压力计算公式:

p = \{\begin{matrix} \{\frac{2 k}{k + 1} [1 + {(\frac{k + 1}{k})}^{2} {c o t}^{2} (\arctan \frac{l}{r})] {s i n}^{2} (φ_{2} + θ) - \frac{k - 1}{k + 1}\} \frac{1}{k + 1} ρ_{0} D^{2}, 0 < l ⩽ l_{A} \\ [\frac{1}{\sin^{2} (\arctan \frac{l}{r})} + \frac{1}{\sin (\arctan \frac{l}{r})} {(\frac{1}{\sin^{2} (\arctan \frac{l}{r})} - 1)}^{\frac{1}{2}}] \frac{1}{k + 1} ρ_{0} D^{2}, l > l_{A} \end{matrix}

(19)

由上述分析可知在确定炸药参数和炮孔直径后，可由上述理论推导公式求得炮孔轴向孔壁上任一点的初始冲击压力的大小。结合下文的模型试验和数值模拟参数数据，以直径为 40、60、80、100 mm 炮孔为对象，基于 MATLAB 软件编程求解拟合，得到球面爆轰波下连续耦合装药孔壁初始冲击压力沿炮孔轴向变化，如图4所示。

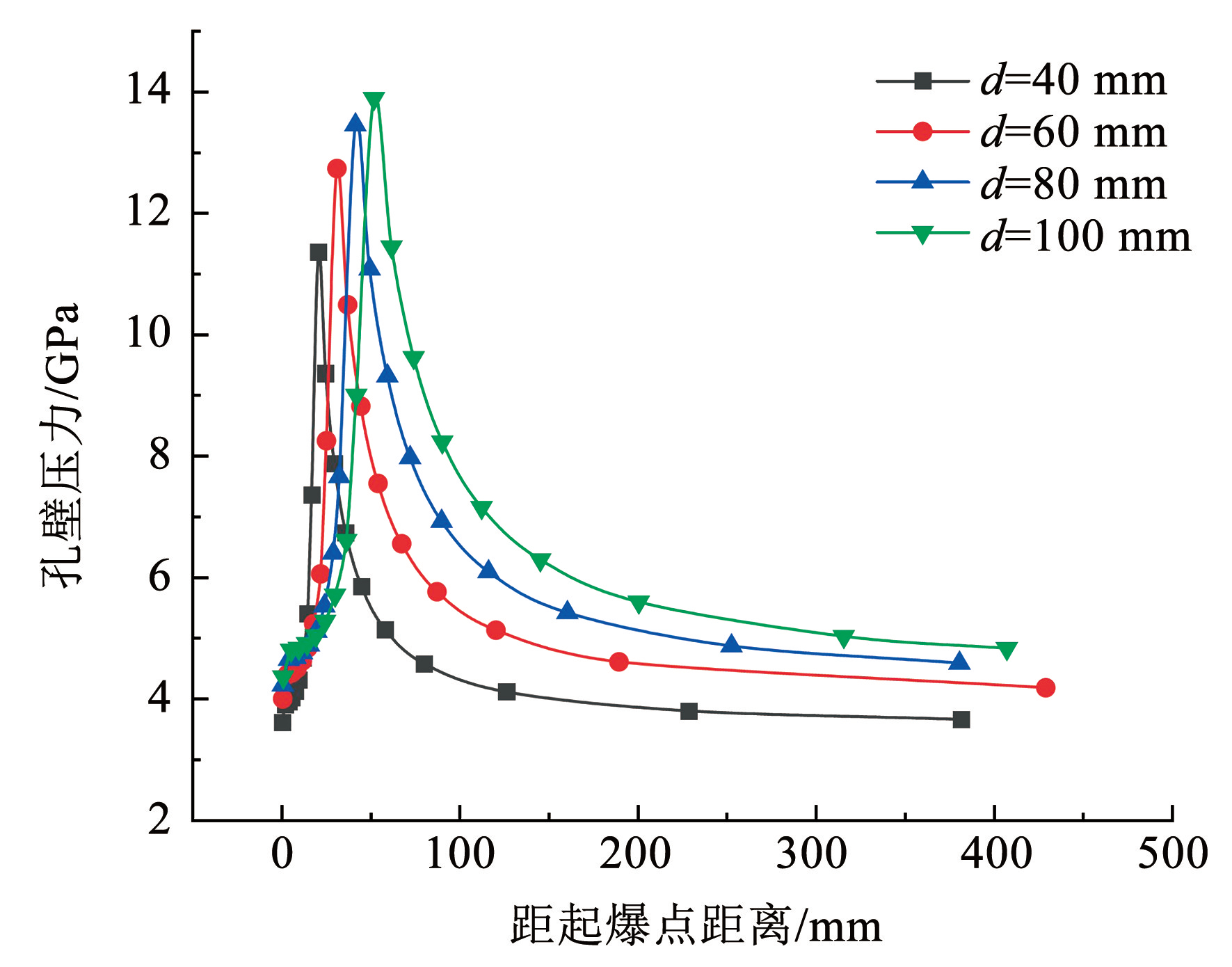
图4不同炮孔直径下孔壁压力峰值沿炮孔轴向分布理论曲线

Fig.4Theoretical curve of axial distribution of borehole wall peak pressure under different borehole diameters

由图4可以看出，炸药爆炸后孔壁压力峰值沿炮孔轴向呈现非均匀分布，在峰值距离处达到孔壁压力最大峰值，爆轰波在达到峰值距离前，与孔壁发生正规斜反射作用，孔壁压力急剧增大; 在峰值距离后发生马赫反射作用，孔壁压力沿炮孔轴向开始衰减，最后进入平稳波动阶段孔壁压力趋于稳定。同时，不同孔径下孔壁压力峰值分布趋势具有相似性，但特征存在差异，随着炮孔直径的增大，孔壁压力最大峰值和平稳阶段的孔壁压力逐渐增大; 峰值距离也随炮孔直径的增大而增大。

3 炮孔轴向孔壁压力模型试验

岩石爆破中炸药爆炸作用于孔壁的过程十分复杂，因此需要开展试验来进一步验证。但矿山现场无法在岩石内布置传感器，所以通过制作满足矿山岩石力学参数的混凝土厚壁圆筒模型来开展爆破试验，监测孔壁初始冲击压力沿炮孔轴向分布情况，达到与理论计算结果相互验证的目的。由于试验条件有限，因此本文选取炸药使用量最少的直径 40 mm 的炮孔开展模拟试验。

3.1 试验方案

试验采用混凝土厚壁圆筒模型作为载体，应变砖作为传感器，利用高速多路动态应变测试系统，实现对连续耦合装药孔壁压力沿炮孔轴向分布的监测。混凝土厚壁圆筒模型的尺寸为直径 200 mm × 高度700 mm，模型中心为直径 40 mm × 长度 600 mm 的空孔。装药长度为 400 mm，堵塞长度为 200 mm。应变砖在模型空孔内侧等间距布置，孔底起爆点处布置第1 个监测点，记为为 N₁，各监测点间隔 50 mm，沿孔壁轴向依次布置监测点 N₂~N₉，N₉为炸药和堵塞接触点处的监测点，共计9 个监测点，如图5所示。

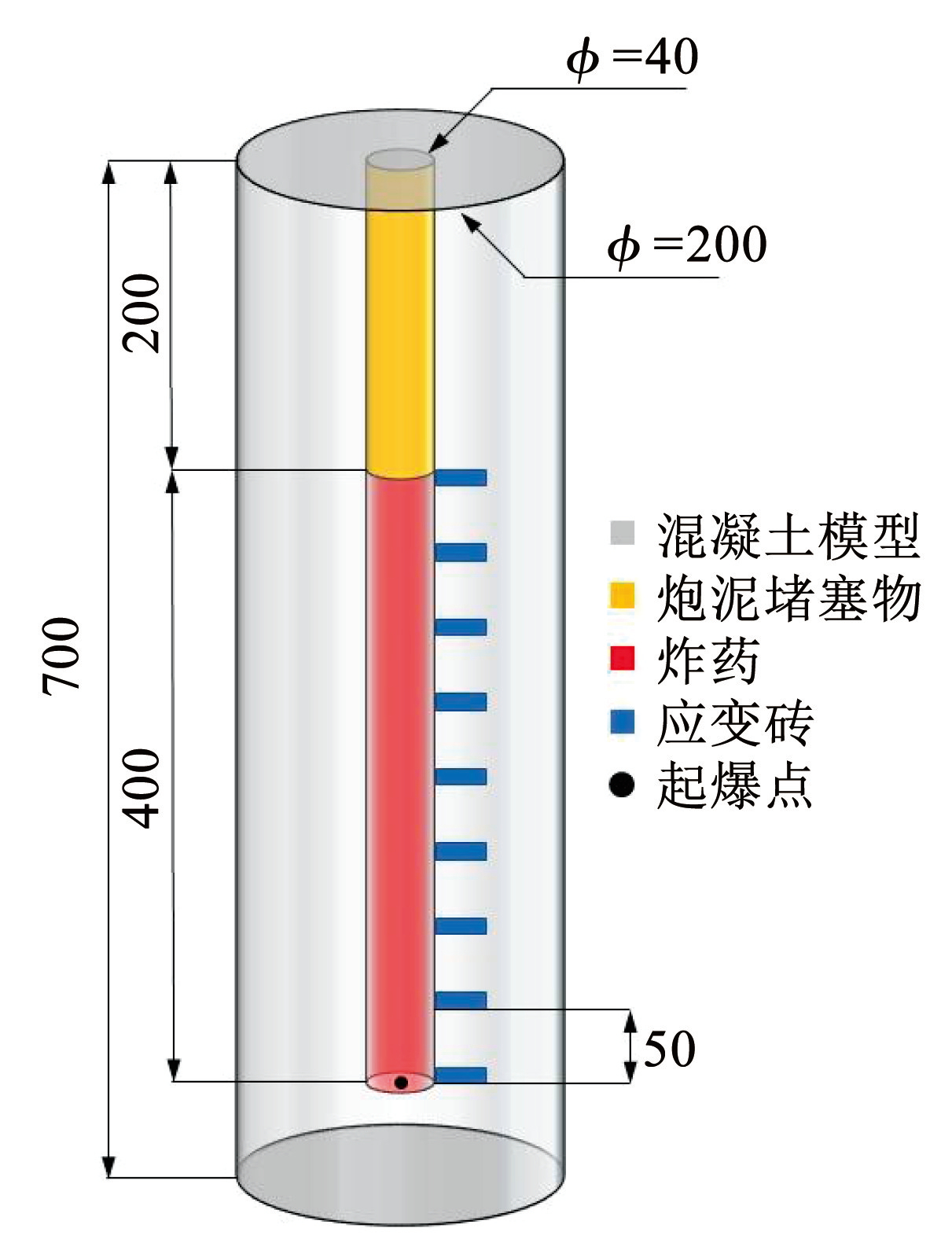
图5模型尺寸和应变砖布置（mm）

Fig.5Model size and strain brick layout (mm)

为了满足模型试验的爆炸动力相似^[18-20]，本试验确定采用2 号岩石乳化炸药，装药密度为1.20 g / cm³，采用导爆管雷管孔底起爆。为减少模型试验监测结果的误差，相同装药结构进行两次爆破试验。

3.2 试验模型制备

试验制备主要包括应变砖和混凝土炮孔模型。应变砖规格为 20 mm × 20 mm × 60 mm，使用材料为 42.5 号普通硅酸盐水泥、干燥细沙（直径不超过 3 mm）和水。水泥、细沙、水的配比为 0.8∶ 1. 0∶ 0.5。使用中空塑料模具制作，浇筑前在模具内表面均匀喷涂脱模剂，以减小脱模阻力和缩短凝固时间。电阻应变计脚线与引线采用十字绞合连接，连接处使用锡焊进一步固定，并使用热熔收缩胶套确保在浇筑过程中的防水绝缘效果，应变砖制作及应变计连接如图6所示。应变计粘贴前，需采用细砂纸对应变砖进行打磨，并使用无水乙醇擦拭干净，确保粘贴处平整、无异物。使用胶水将应变计粘贴到应变砖上，确保胶层均匀无气泡达到完全耦合状态。胶水固化后在应变计表面刷涂环氧树脂，起到在浇筑过程中对应变计的防护作用，应变砖成品如图7所示。在应变计粘贴前后都需要对其电阻值进行检测，确保电阻值在允许误差范围内，保证试验数据的可靠性。

图6应变砖制作过程

Fig.6Process of making strain brick

图7应变砖成品实物

Fig.7Physical of formed strain brick

混凝土模型内层模具采用直径为 40 mm、长度为600 mm 的 PVC 管，外层模具采用直径为 200 mm、长度为 700 mm 的 PVC 管，模型底部厚为 100 mm，上部堵塞长度设置为 200 mm。混凝土模型的材料及配比与应变砖的制作相同，从而使得二者具有相同的密度和波阻抗^[21]，确保模型试验的可靠性。模型浇筑前，应变砖根据试验方案布置在内层管壁上，并在圆筒模型内喷涂脱模剂，使得孔壁整齐光滑。模型浇筑完成后，在 12~14 h 内对内层模具进行拆除，在 24~36 h 内对外层模具进行拆除。在标准养护体条件下，即温度为 20℃ ± 2℃，湿度为 95% 下进行28 d 的养护工作^[22]，如图8所示。在混凝土模型固化后需要再对应变砖电阻值检测，确保每个应变砖在允许误差范围内才可进行试验。应当说明，混凝土模型的基本力学参数与矿山岩石力学参数满足相似试验要求。

图8厚壁圆筒模型实物照片

Fig.8Physical model of thick wall cylinder

3.3 试验系统

本试验系统主要有传感装置、信号采集装置和数据分析装置构成。传感装置是制备的含有 BX120-2AA 型电阻应变计的应变砖，并按试验方案将应变砖布置在相应位置进行浇筑; 信号采集装置由 KD7901 桥盒、KD6009A 型应变放大器和超动态应变测试工作站组成; 试验测试系统和测试流程如图9所示。

测试原理为试验系统测得的电压信号，根据式（20）确定相应的应变值后，再利用胡克定律式（21）计算得到测点应力峰值，即孔壁压力峰值。

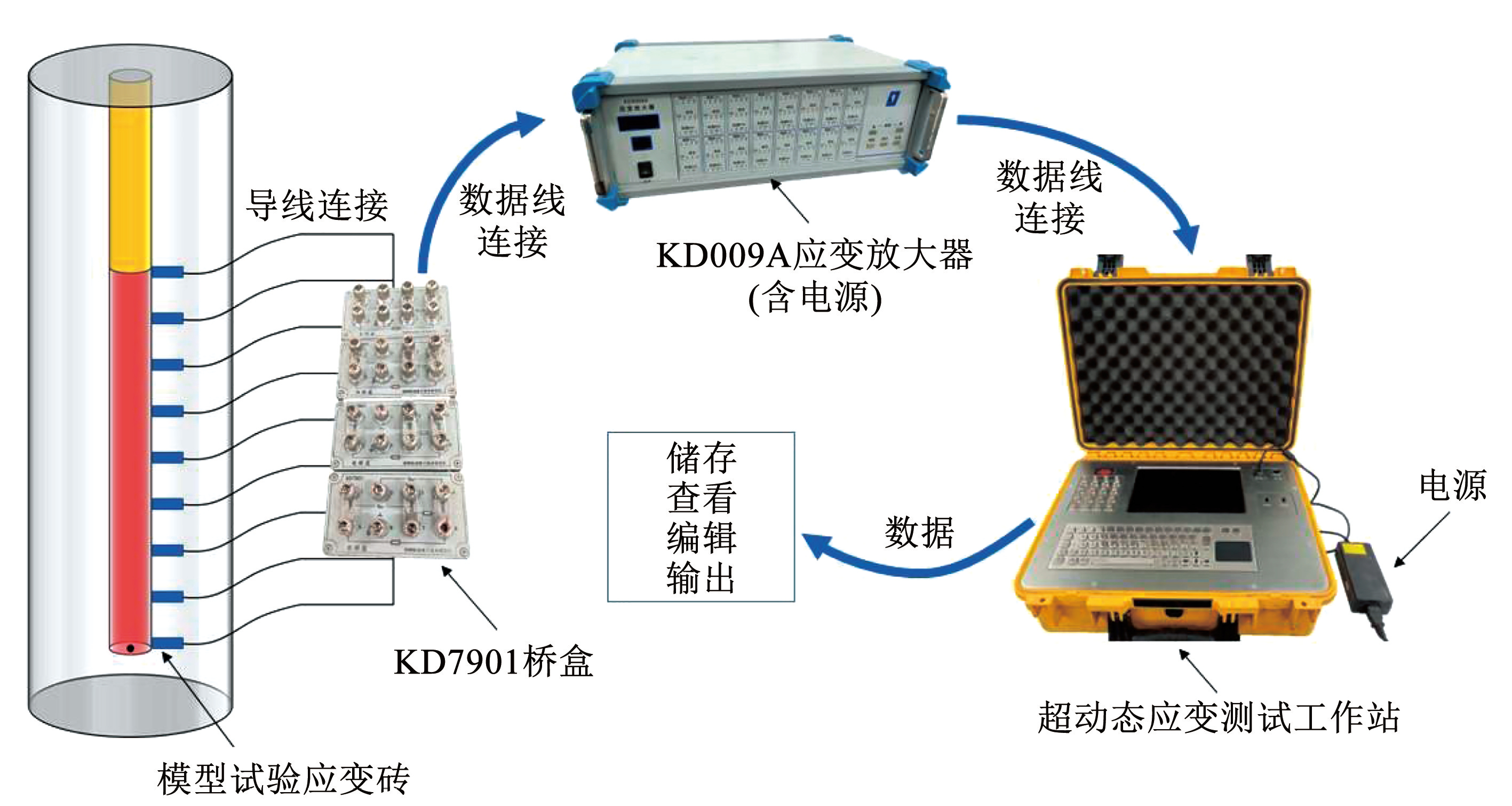
图9试验测试系统及流程

Fig.9Test system and process

ε = \frac{4 \times U \times 10^{6}}{K \times U_{0} \times n \times G}

(20)

σ = E ε

(21)

式中:U 为输出的峰值电压，V; K 为电阻应变计的灵敏度系数; U₀为应变放大器的桥压，V; n 为使用的桥臂数; G 为应变放大器的增益; E 为试件的弹性模量，GPa。

3.4 模型试验结果与分析

完成混凝土厚壁圆筒模型爆破试验，试验系统测量并记录电压信号变化，以 N₁监测点为例，电压信号实测曲线如图10所示，图中横、纵坐标分别为时间、电压，对应单位分别为 μs 和 V。根据各监测点的电压信号曲线选取最大电压峰值，并按照测试原理计算得到两次模型试验孔壁压力峰值数据，本文采用两次试验数据的平均值进行分析研究见表1。

对连续耦合装药的混凝土厚壁圆筒模型爆破试验数据进行处理分析，得到各监测点的最大压力峰值，进一步与理论计算值对比分析，如图11所示。

由图11分析可知，在模型试验中，炸药爆炸在起爆点处 N₁的孔壁压力为 3.552 1 GPa; 在 N₁至 N₂ 阶段，孔壁压力急剧增大，此时爆轰波已完成正规反射作用。在 N₂测点处达到最大孔壁压力为 5.328 5 GPa，随后爆轰波进行马赫反射，孔壁压力急剧下降，N₃ 测点处孔壁压力为 3.947 2 GPa，随后孔壁压力趋于 3.767 4 GPa 并平稳波动。总体上，模型试验的孔壁压力沿炮孔轴向分布趋势为:爆炸后，孔壁压力急剧增大，当达到最大压力峰值后，孔壁压力迅速衰减，并会趋于稳定波动。模型试验与理论计算的变化趋势基本一致。

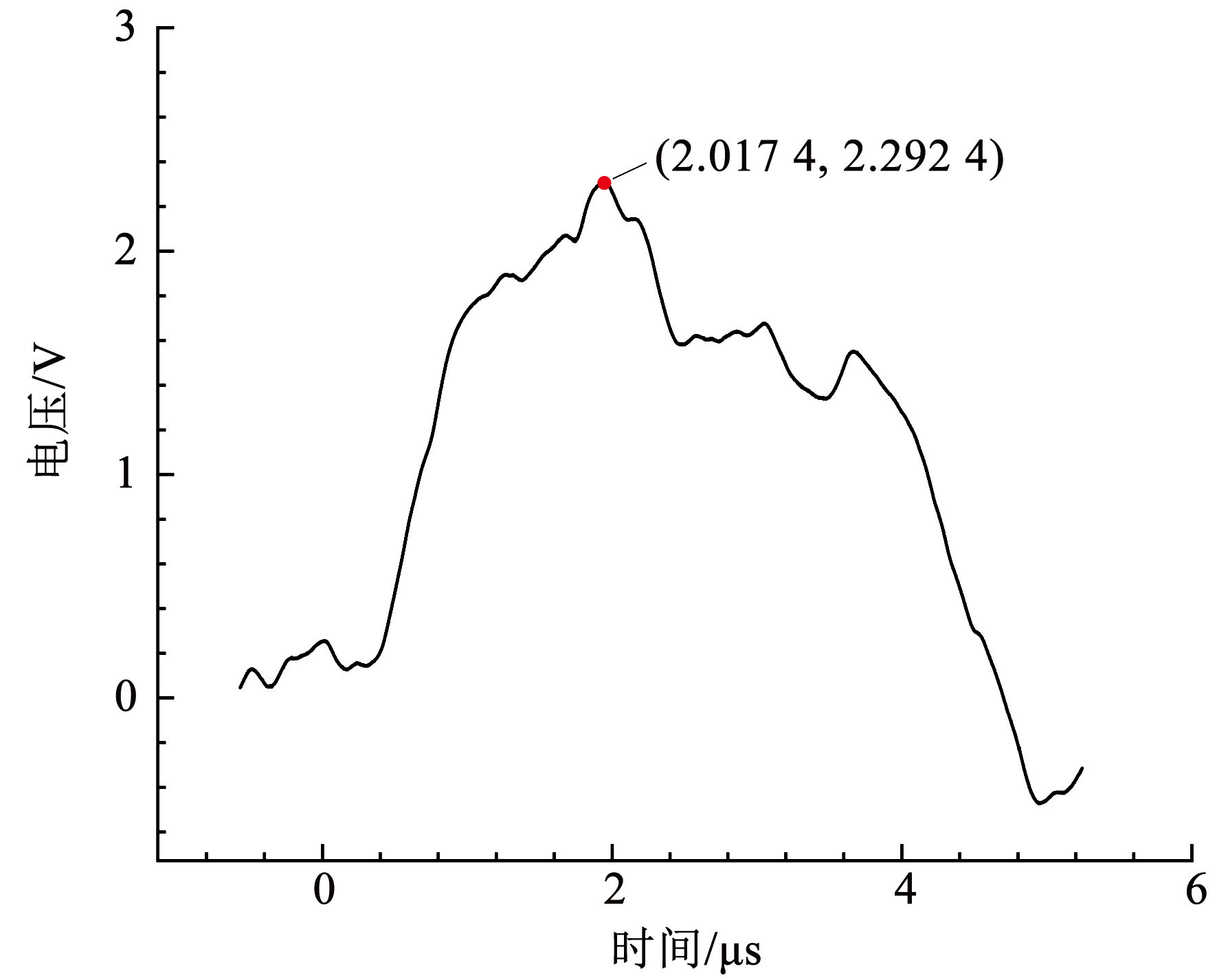
图10电压信号的实测曲线

Fig.10Measured curve of voltage signal

表1爆破试验轴向孔壁各测点压力测试结果

Tab.1 Test results of each measuring point of axial borehole wall in model blasting test

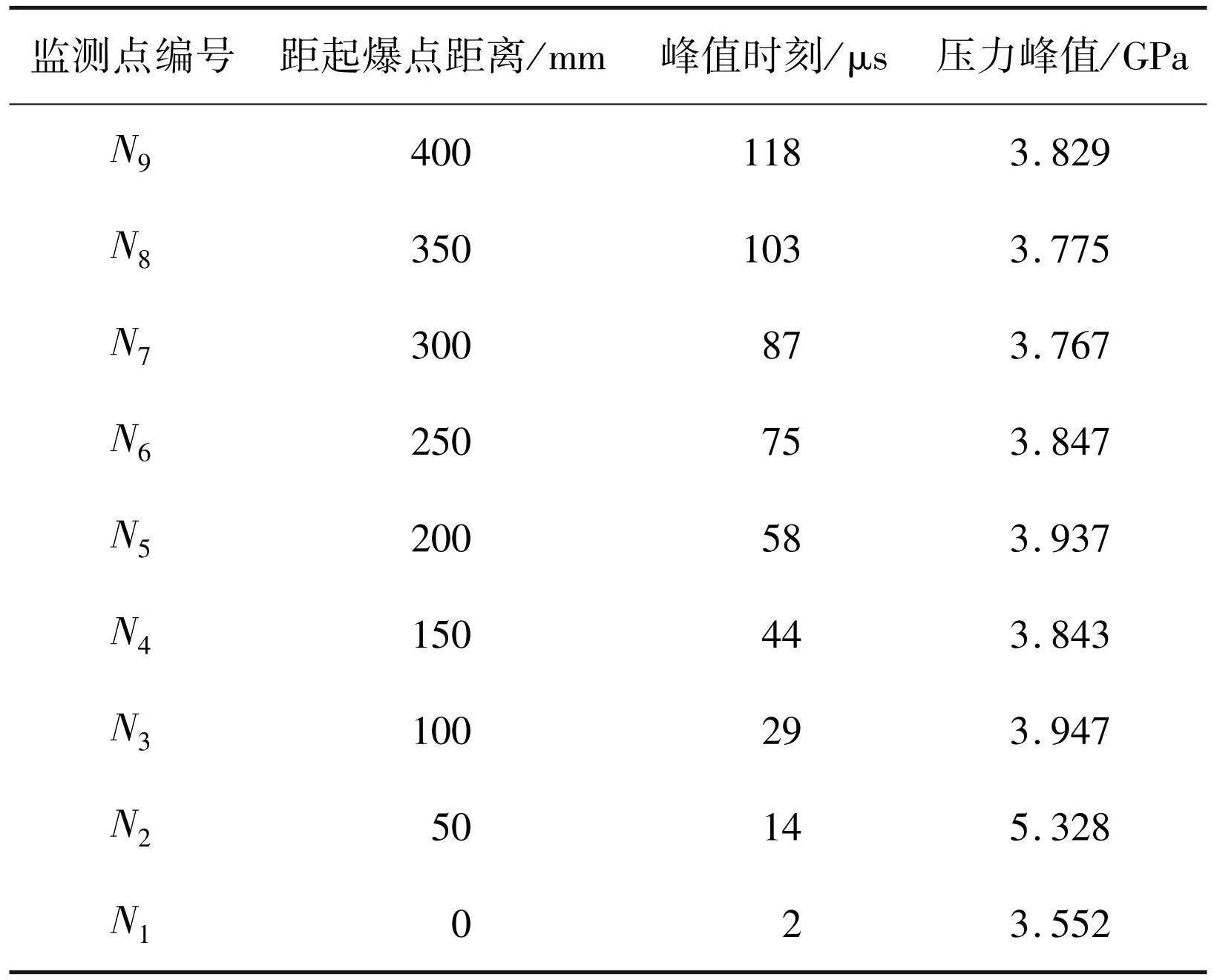
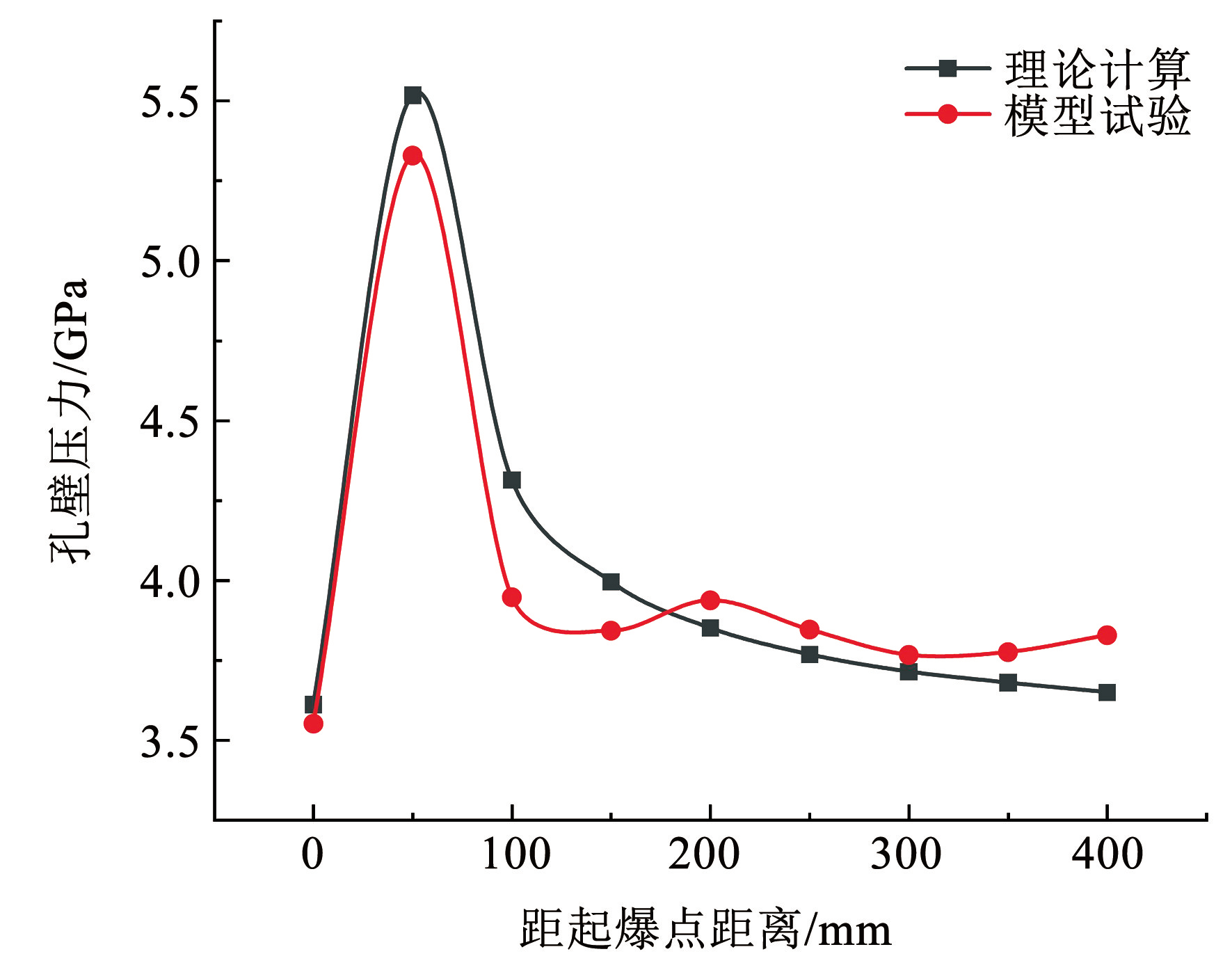
图11理论-试验轴向孔壁压力峰值趋势对比

Fig.11Comparison of peak pressure of axial borehole wall in theoretical calculation and experimental results

对理论计算和模型试验中孔壁压力沿炮孔轴向变化趋势差异进行分析。模型试验中 N₂ 测点处孔壁压力非理论上的最大压力峰值，这是受到应变砖尺寸的限制，无法在起爆点近区布置更多的测点进行监测。相较于理论计算，模型试验结果在 N₃~N₉ 阶段有明显的波动，例如，在 N₇~N₉处孔壁压力峰值出现增大波动，N₉处孔壁压力为 3.828 6 GPa，高于理论计算值 3.650 2 GPa，其原因是在爆轰波传播至孔口堵塞时，在炸药-堵塞界面会形成反射冲击波在孔壁处产生了叠加作用。

由上述分析可知，连续耦合装药孔壁压力沿炮孔轴向分布是非均匀的，孔壁压力在起爆点近区出现急剧增大，到达最大压力峰值后开始衰减，最后趋于平稳波动。通过计算可知，模型试验在 N₂测点处孔壁压力峰值与理论计算值的相对误差为 3.536 6%，在平稳波动阶段 N₄~N₉处平均误差为 2.794 1%，理论计算与试验结果基本吻合。

4 数值模拟

模型试验中马赫反射作用阶段的孔壁压力基本与理论分析相同，但在起爆点近区的正规斜反射作用阶段，由于受到应变砖尺寸的限制，不能布置密集的监测点，需要对正规反射作用阶段进一步探究，因此通过数值模拟手段开展研究，对模型试验相互补充验证，同时，进一步探究不同炮孔直径条件下孔壁初始冲击压力沿炮孔轴向分布特征。

4.1 有限元模型构建

根据模拟试验方案，利用 ANSYS / LS-DYNA 有限元软件建立数值模型。模型外层尺寸为直径 200 mm × 高度 700 mm 圆筒，中心空孔直径分别为 40、60、80、100 mm，空孔高度为 600 mm，堵塞长度为 200 mm。炮孔采用连续耦合装药结构，装药长度为 400 mm，起爆点位于炮孔孔底中心，共建立 4 个不同炮孔直径的数值模型，如图12所示。

图12数值模型及剖面（d = 40 mm）

Fig.12Diagram of numerical simulation model and section (d = 40 mm)

4.2 材料与状态方程参数

混凝土单元类型设置为 SOLID 单元，材料关键字为∗MAT_JOHNSON_HOLMQUIST_CERAMICS ^[23-26]，数值模拟力学材料与模型试验材料保持一致，力学参数见表2。现场采用渣土进行堵塞，炮孔堵塞材料采用关键字为∗MAT_SOIL_AND_FOAM ^[27] 材料定义，材料参数见表3。炸药为与模型试验相同的乳化炸药，炸药模型关键字为 ∗ MAT _ HIGH _ EXPLOSIVE_BURN ^[28-29]，采用 JWL 状态方程^[30-31]，炸药及其状态方程的参数见表4。

表2混凝土的物理力学参数

Tab.2 Physical and mechanical parameters of concrete

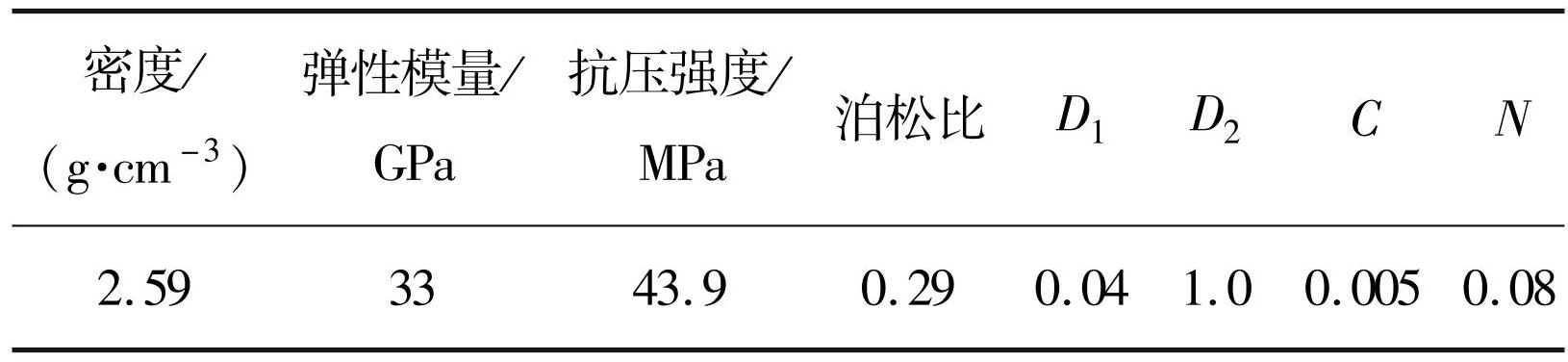
表3炮孔堵塞物材料参数

Tab.3 Parameters of the stemming material

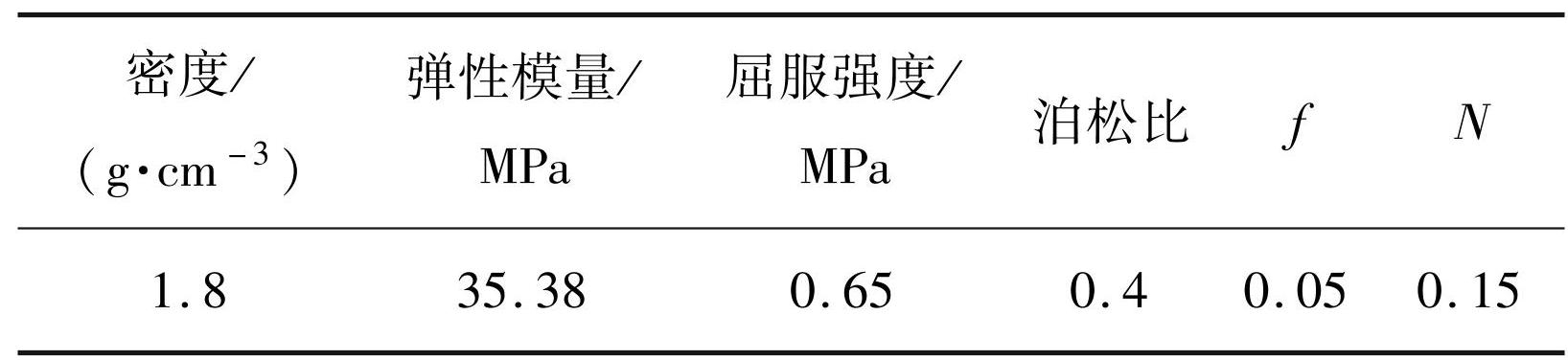
表4炸药材料参数

Tab.4 Parameters of explosives

4.3 数值模拟结果分析

4.3.1 不同孔径孔壁初始冲击压力沿炮孔轴向分布

为确定孔壁压力峰值，在模型中沿炮孔轴向孔壁选取监测点。在距起爆点 100 mm 内间隔10 mm 选取监测点，依次记为 P₁~P₁₁，其余监测点沿轴向孔壁间隔 25 mm 均匀选取，依次记为 P₁₂~P₂₃，共计 23 个监测点，如图13所示。

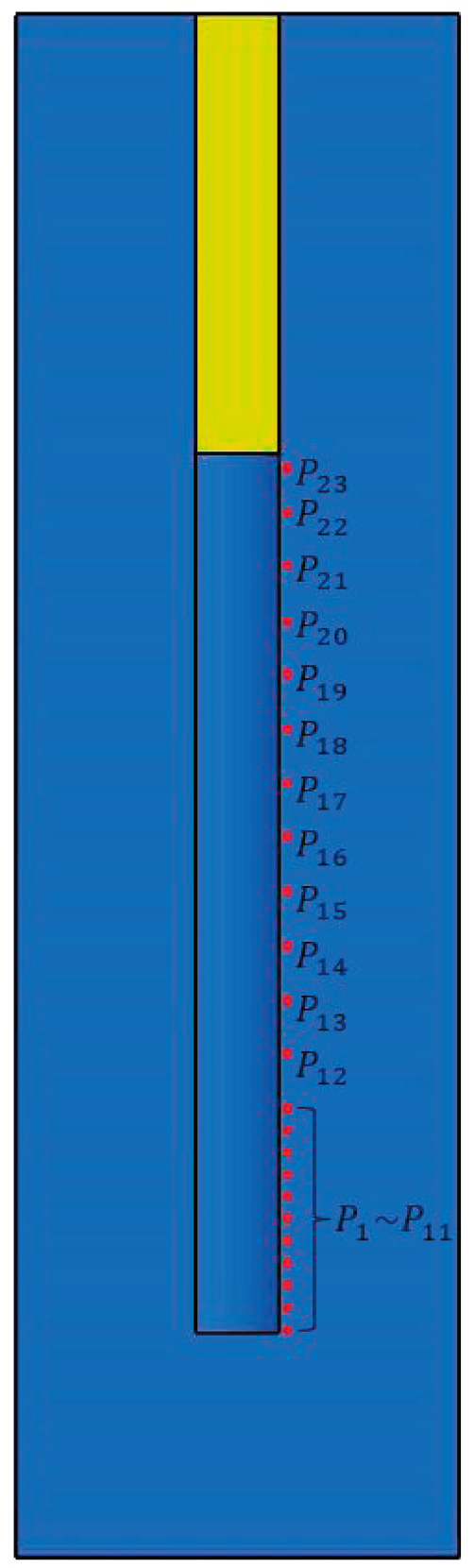
图13数值模拟监测点布置

Fig.13Layout of monitoring point in numerical simulation

对各监测点的压力峰值进行拟合处理，得到不同炮孔直径时的孔壁压力峰值沿炮孔轴向分布情况，如图14所示。

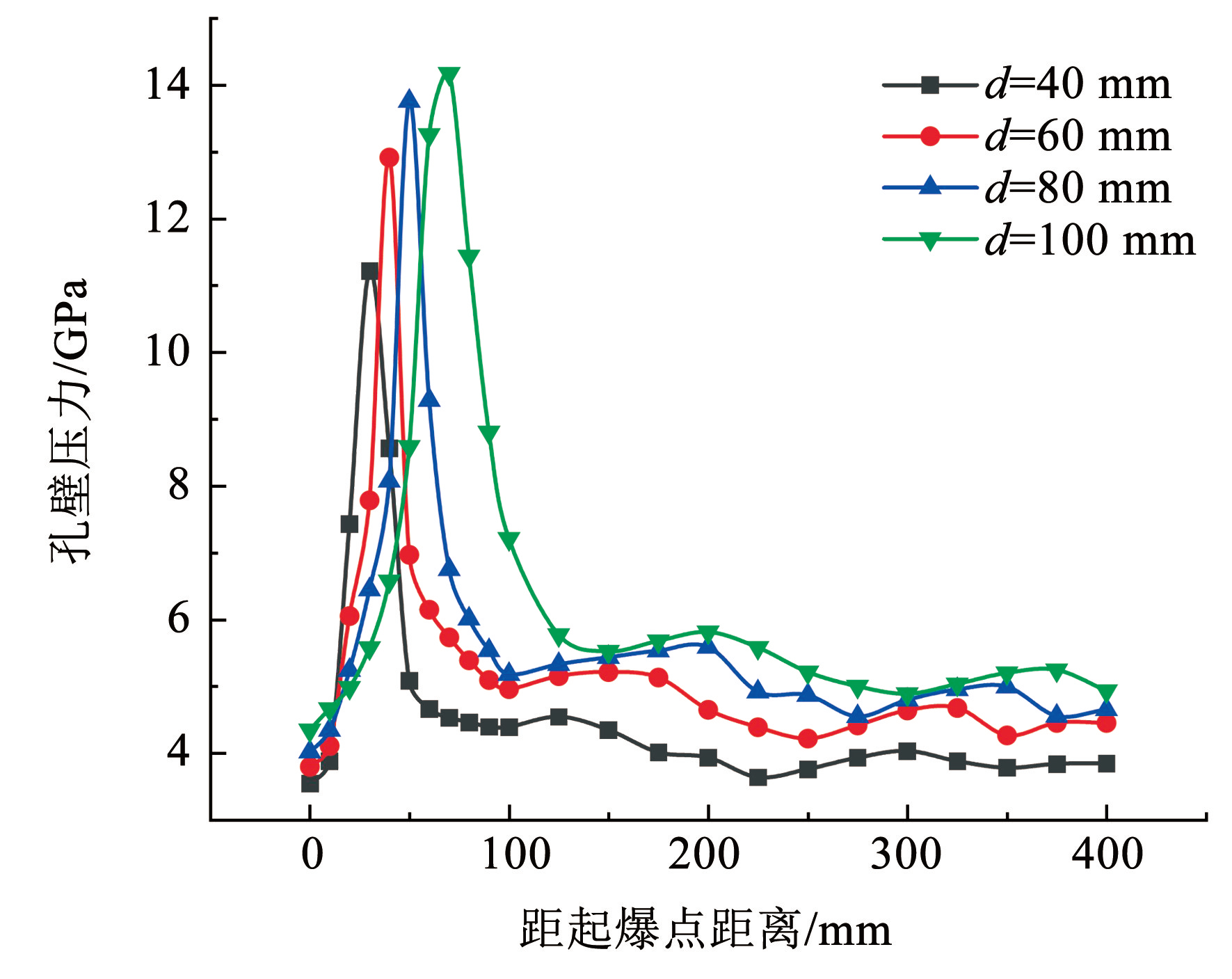
图14不同炮孔直径下轴向孔壁压力峰值曲线

Fig.14Variation curve of peak pressure of axial borehole wall under different hole diameters

分析图14可知，整体上，孔壁初始冲击压力在起爆点近区急剧增大，到达峰值后开始衰减，最后趋于平稳波动，孔壁初始冲击压力沿炮孔轴向分布上呈现出非均匀分布。随着炮孔直径的增大，孔壁压力峰值和平稳波动时的孔壁压力也不断增大，d = 40 mm 时，孔壁压力峰值为 11.213 3 GPa，在 3.638 3~4.513 1 GPa之间波动，d = 60 mm 时，孔壁压力峰值为 12.915 8 GPa，在 4.217 8~5.133 5 GPa 之间波动。同时，孔壁压力峰值和进入平稳波动前的拐点出现的位置距起爆点的距离随孔径增大也不断延后。不同孔径时的数值模拟结果的孔壁压力沿炮孔轴向分布趋势以及峰值大小均与理论计算结果基本相吻合。

4.3.2 数值模拟结果合理性分析

将 d = 40、60、80、100 mm 的 4 种数值模拟结果与相对应的理论计算值进行对比，得到二者的孔壁压力峰值对比图，如图15所示。同时，选取 d = 40 mm 的理论、模拟和试验三者的在相同测点处的孔壁压力进行对比分析，如图15所示。

观察图15可知，在 4 种不同炮孔直径下，数值模拟与理论计算的轴向孔壁压力变化趋势基本一致，孔壁压力最大峰值和平稳波动阶段孔壁压力大小相对吻合。由于篇幅有限，选取 d = 40 mm 对比结果进行详细分析，见图15（ a），在距起爆点近区 0~40 mm 孔壁上，爆轰波发生正规反射作用，孔壁压力随距离急剧增大，达到最大压力峰值 11.213 3 GPa，与理论计算结果相对误差为 5.591%。由于数值模拟中网格密度和材料的变形特性，导致数值模拟的峰值距离大于理论计算的结果; 在距起爆点 40~100 mm 孔壁阶段，压力峰值开始衰减，在 100 mm 测点附近出现拐点，孔壁压力衰减至 4.367 9 GPa 左右，数值模拟与理论计算结果基本吻合; 在距起爆点 100 mm 后的孔壁上，孔壁压力在 3.637 2~4.513 1 GPa之间波动，是模型外边界面的反射叠加作用导致，与理论计算值相比，各测点压力峰值的平均误差为 4.601%。数值模拟结果与理论计算结果基本吻合，相互验证了二者的合理性。

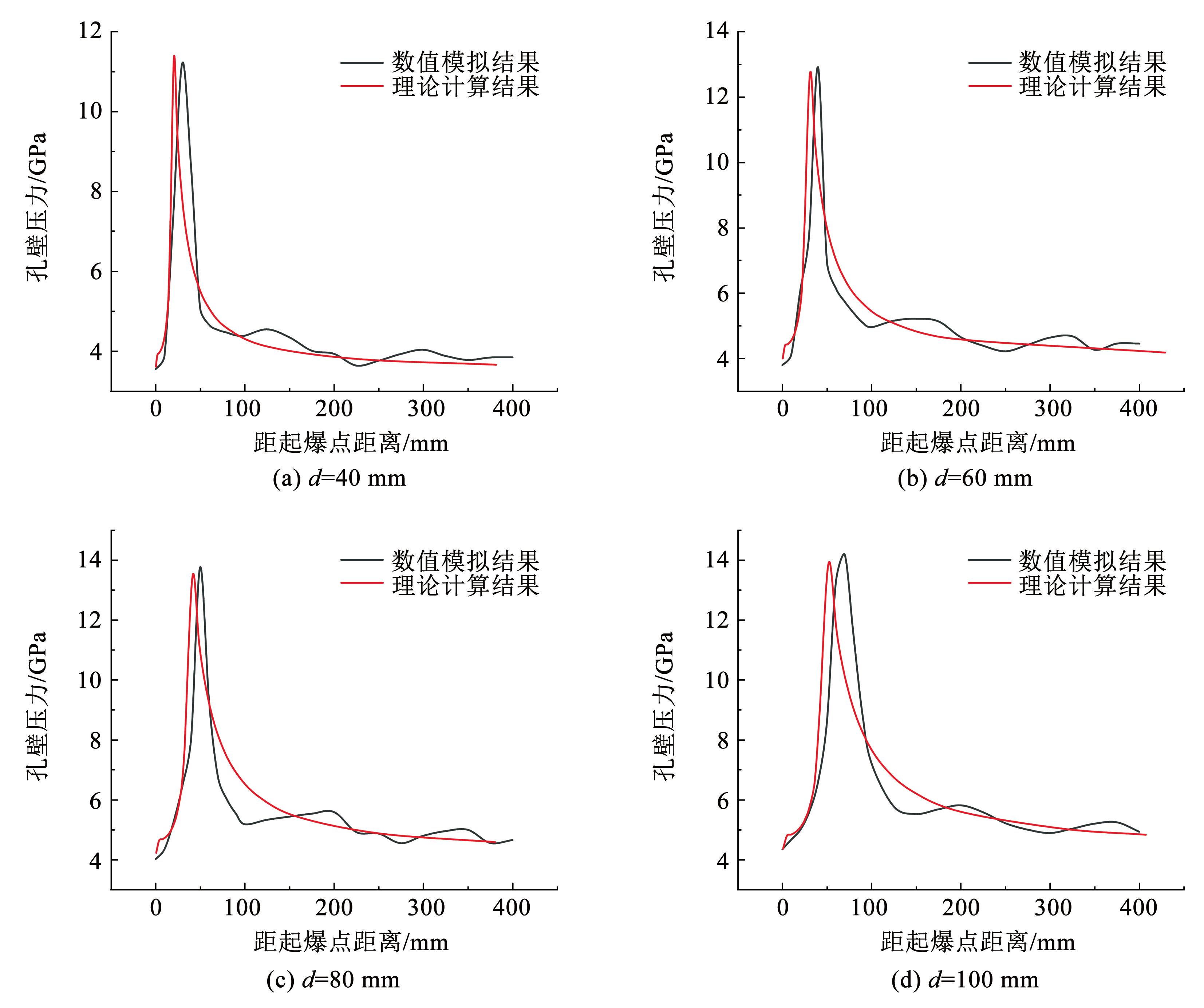
图15模拟-理论孔壁压力峰值对比

Fig.15Comparison of peak pressure of borehole wall in numerical simulation and theoretical calculation

由图16可以看出，在炸药爆炸起爆点 N₁处，数值模拟与模型试验的孔壁压力峰值分别为 3.700、 3.552 1 GPa，误差为 3.999%; 在 N₂ 处达到测点的最大压力峰值，数值模拟孔壁压力为 5. 080 4 GPa，稍低于理论计算值和模型试验结果，误差分别为 8.591 8% 和 4.882%。在 N₄~N₉平稳波动阶段，数值模拟的孔壁压力在 4 GPa 左右波动，与模型试验结果、理论计算值基本吻合，平均误差分别为3.362 6% 和 2.403 1%。在各测点处的数值模拟孔壁压力峰值与模型试验监测结果基本吻合，进一步验证了数值模拟结果的准确性，说明了本文理论计算公式的可靠性。

5 结论

本文基于球面爆轰波传播条件下，通过理论计算、模型试验和数值模拟等方法，对连续耦合装药孔壁压力沿炮孔轴向分布特征进行研究，得到以下结论:

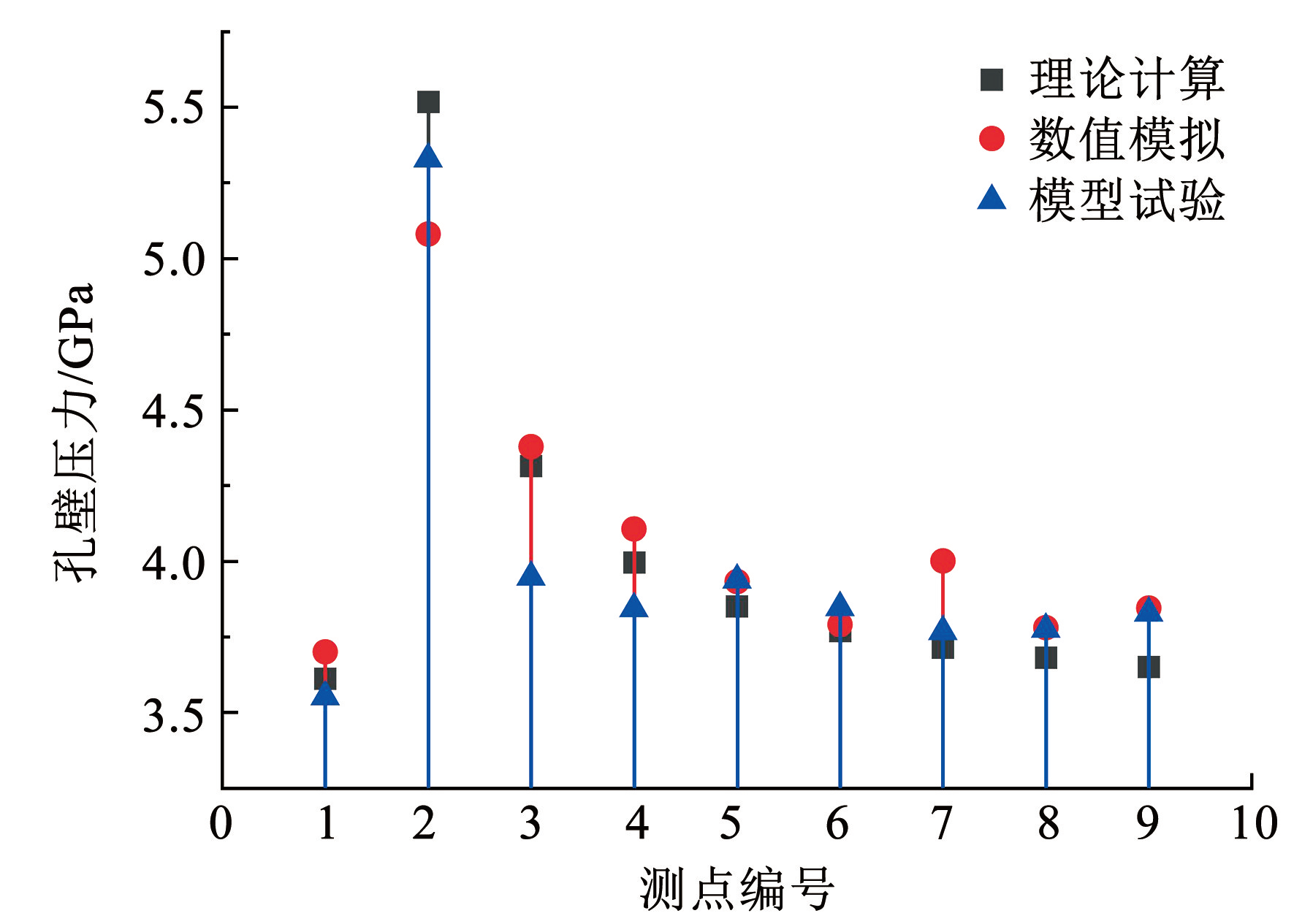
图16各测点的孔壁压力峰值（d = 40 mm）

Fig.16Peak pressure of borehole wall at each measuring point (d = 40 mm)

1）在球面爆轰波下，连续耦合装药孔壁初始冲击压力沿炮孔轴向方向呈现不均匀分布的特征; 在起爆点近区孔壁压力急剧增大，达到最大压力峰值后开始衰减，最后孔壁压力趋于平稳波动; 理论计算结果与数值模拟的孔壁压力沿炮孔轴向分布趋势吻合良好。

2）沿炮孔轴向的孔壁压力峰值与炮孔直径呈正相关，孔壁最大压力峰值和平稳波动阶段的孔壁平均压力随着炮孔直径增大而增大; 出现最大压力峰值的位置也随着炮孔直径增大而延后。

3）在 d = 40 mm 炮孔孔壁压力理论计算的最大压力峰值与数值模拟结果的相对误差为 5.591%，平稳波动阶段孔壁压力平均相对误差为 4.601%; 与模型试验各测点孔壁压力相比，理论计算值的相对误差始终保持在 9% 以内，理论计算结果分别与数值模拟、模型试验结果相互验证，确定了基于球面爆轰波的轴向孔壁初始冲击压力理论计算公式的合理性。

图1爆轰波在炮孔内传播过程

Fig.1Propagation process of detonation wave in borehole

下载: 全尺寸图片

图2爆轰波的正规斜反射

Fig.2Regular oblique reflection of detonation wave

下载: 全尺寸图片

图3爆轰波的马赫反射

Fig.3Mach reflection of detonation wave

下载: 全尺寸图片

图4不同炮孔直径下孔壁压力峰值沿炮孔轴向分布理论曲线

Fig.4Theoretical curve of axial distribution of borehole wall peak pressure under different borehole diameters

下载: 全尺寸图片

图5模型尺寸和应变砖布置（mm）

Fig.5Model size and strain brick layout (mm)

下载: 全尺寸图片

图6应变砖制作过程

Fig.6Process of making strain brick

下载: 全尺寸图片

图7应变砖成品实物

Fig.7Physical of formed strain brick

下载: 全尺寸图片

图8厚壁圆筒模型实物照片

Fig.8Physical model of thick wall cylinder

下载: 全尺寸图片

图9试验测试系统及流程

Fig.9Test system and process

下载: 全尺寸图片

图10电压信号的实测曲线

Fig.10Measured curve of voltage signal

下载: 全尺寸图片

图11理论-试验轴向孔壁压力峰值趋势对比

Fig.11Comparison of peak pressure of axial borehole wall in theoretical calculation and experimental results

下载: 全尺寸图片

图12数值模型及剖面（d = 40 mm）

Fig.12Diagram of numerical simulation model and section (d = 40 mm)

下载: 全尺寸图片

图13数值模拟监测点布置

Fig.13Layout of monitoring point in numerical simulation

下载: 全尺寸图片

图14不同炮孔直径下轴向孔壁压力峰值曲线

Fig.14Variation curve of peak pressure of axial borehole wall under different hole diameters

下载: 全尺寸图片

图15模拟-理论孔壁压力峰值对比

Fig.15Comparison of peak pressure of borehole wall in numerical simulation and theoretical calculation

下载: 全尺寸图片

图16各测点的孔壁压力峰值（d = 40 mm）

Fig.16Peak pressure of borehole wall at each measuring point (d = 40 mm)

下载: 全尺寸图片

表1爆破试验轴向孔壁各测点压力测试结果

下载: 全尺寸图片

表2混凝土的物理力学参数

下载: 全尺寸图片

表3炮孔堵塞物材料参数

下载: 全尺寸图片

表4炸药材料参数

下载: 全尺寸图片

图1爆轰波在炮孔内传播过程

Fig.1Propagation process of detonation wave in borehole

图2爆轰波的正规斜反射

Fig.2Regular oblique reflection of detonation wave

图3爆轰波的马赫反射

Fig.3Mach reflection of detonation wave

图4不同炮孔直径下孔壁压力峰值沿炮孔轴向分布理论曲线

Fig.4Theoretical curve of axial distribution of borehole wall peak pressure under different borehole diameters

图5模型尺寸和应变砖布置（mm）

Fig.5Model size and strain brick layout (mm)

图6应变砖制作过程

Fig.6Process of making strain brick

图7应变砖成品实物

Fig.7Physical of formed strain brick

图8厚壁圆筒模型实物照片

Fig.8Physical model of thick wall cylinder

图9试验测试系统及流程

Fig.9Test system and process

图10电压信号的实测曲线

Fig.10Measured curve of voltage signal

图11理论-试验轴向孔壁压力峰值趋势对比

Fig.11Comparison of peak pressure of axial borehole wall in theoretical calculation and experimental results

图12数值模型及剖面（d = 40 mm）

Fig.12Diagram of numerical simulation model and section (d = 40 mm)

图13数值模拟监测点布置

Fig.13Layout of monitoring point in numerical simulation

图14不同炮孔直径下轴向孔壁压力峰值曲线

Fig.14Variation curve of peak pressure of axial borehole wall under different hole diameters

图15模拟-理论孔壁压力峰值对比

Fig.15Comparison of peak pressure of borehole wall in numerical simulation and theoretical calculation

图16各测点的孔壁压力峰值（d = 40 mm）

Fig.16Peak pressure of borehole wall at each measuring point (d = 40 mm)

表1爆破试验轴向孔壁各测点压力测试结果

表2混凝土的物理力学参数

表3炮孔堵塞物材料参数

表4炸药材料参数

图1爆轰波在炮孔内传播过程

Fig.1Propagation process of detonation wave in borehole

图2爆轰波的正规斜反射

Fig.2Regular oblique reflection of detonation wave

图3爆轰波的马赫反射

Fig.3Mach reflection of detonation wave

图4不同炮孔直径下孔壁压力峰值沿炮孔轴向分布理论曲线

Fig.4Theoretical curve of axial distribution of borehole wall peak pressure under different borehole diameters

图5模型尺寸和应变砖布置（mm）

Fig.5Model size and strain brick layout (mm)

图6应变砖制作过程

Fig.6Process of making strain brick

图7应变砖成品实物

Fig.7Physical of formed strain brick

图8厚壁圆筒模型实物照片

Fig.8Physical model of thick wall cylinder

图9试验测试系统及流程

Fig.9Test system and process

图10电压信号的实测曲线

Fig.10Measured curve of voltage signal

图11理论-试验轴向孔壁压力峰值趋势对比

Fig.11Comparison of peak pressure of axial borehole wall in theoretical calculation and experimental results

图12数值模型及剖面（d = 40 mm）

Fig.12Diagram of numerical simulation model and section (d = 40 mm)

图13数值模拟监测点布置

Fig.13Layout of monitoring point in numerical simulation

图14不同炮孔直径下轴向孔壁压力峰值曲线

Fig.14Variation curve of peak pressure of axial borehole wall under different hole diameters

图15模拟-理论孔壁压力峰值对比

Fig.15Comparison of peak pressure of borehole wall in numerical simulation and theoretical calculation

图16各测点的孔壁压力峰值（d = 40 mm）

Fig.16Peak pressure of borehole wall at each measuring point (d = 40 mm)

表1爆破试验轴向孔壁各测点压力测试结果

表2混凝土的物理力学参数

表3炮孔堵塞物材料参数

表4炸药材料参数

叶志伟, 陈明, 李桐, 等. 小不耦合系数装药爆破孔壁压力峰值计算方法[J]. 爆炸与冲击,2021,41(6):119.YE Zhiwei, CHEN Ming, LI Tong,et al. A calculation method of the peak pressure on borehole wall for low decoupling coefficient charge blasting[J]. Explosion and Shock Waves,2021,41(6):119. DOI:10.11883/bzcyj-2020-0185

王文龙. 钻眼爆破[M]. 北京: 煤炭工业出版社,1984

张永琦. 矿山爆破技术与安全[M]. 北京: 煤炭工业出版社,1991

杜俊林, 罗强, 宗琦. 空气不耦合装药爆破孔壁冲击压力分析[J]. 西安科技大学学报,2005,25(3):306.DU Junlin, LUO Qiang, ZONG Qi. Analysis on preliminary shock pressure on borehole of air-de-coupling charging[J]. Journal of Xi′an University of Science and Technology,2005,25(3):306. DOI:10.3969/j.issn.1672-9315.2005.03.009

张馨, 孙金山, 张湘平, 等. 钻孔爆破炮孔孔壁压力计算模型[J]. 爆破,2021,38(3):1. ZHANG Xin, SUN Jinshan, ZHANG Xiangping,et al. Calculation model of blasthole pressure[J]. Blasting,2021,38(3):1

陈明, 刘涛, 叶志伟, 等. 轮廓爆破孔壁压力峰值计算方法[J]. 爆炸与冲击,2019,39(6):103.CHEN Ming, LIU Tao, YE Zhiwei,et al. Calculation methods for peak pressure on borehole wall of contour blasting[J]. Explosion and Shock Waves,2019,39(6):103. DOI:10.11883/bzycj-2018-0171

叶志伟, 陈明, 李桐, 等. 一种水耦合轮廓爆破孔壁压力峰值的简化计算方法[J]. 岩土力学,2021,42(10):2808.YE Zhiwei, CHEN Ming, LI Tong,et al. A simplified method for calculating peak pressure of borehole wall under water-coupling contour blasting[J]. Rock and Soil Mechanics,2021,42(10):2808. DOI:10.16285/j.rsm.2021.0094

叶志伟, 陈明, 魏东, 等. 不耦合装药爆破孔壁压力峰值的实验研究[J]. 爆炸与冲击,2021,41(5):115.YE Zhiwei, CHEN Ming, WEI Dong,et al. Experimental study on the peak pressure of borehole wall in decoupling charge blasting[J]. Explosion and Shock Waves,2021,41(5):115. DOI:10.11883/bzycj-2020-0004

宗琦, 程兵, 汪海波. 偏心不耦合装药孔壁压力与损伤效应数值模拟[J]. 爆破,2019,36(3):76. ZONG Qi, CHENG Bing, WANG Haibo. Numerical simulation of pressure on borehole wall and damage effect with eccentric decouple charge[J]. Blasting,2019,36(3):76

刘玉丰, 方芳, 李海谦, 等. 不耦合装药结构爆炸孔壁压力分布特性的数值模拟[J]. 矿冶工程,2022,42(5):30. LIU Yufeng, FANG Fang, LI Haiqian,et al. Numerical simulation of pressure distribution of blastholes with decoupled charges[J]. Mining and Metallurgical Engineering,2022,42(5):30

甯尤军, 江成, 杨正. 爆炸应力波作用下岩石双孔爆破的数值模拟[J]. 黑龙江科技大学学报,2016,26(6):705.NING Youjun, JIANG Cheng, YANG Zheng. Numerical simulation of two-hole blasting of rock under effect of explosion-induced stress waves[J]. Journal of Heilongjiang University of Science and Technology,2016,26(6):705. DOI:10.3969/j.issn.2095-7262.2016.06.024

余德运, 刘殿书, 李洪超, 等. 柱状装药炮孔壁初始压力数值模拟及误差分析[J]. 爆破,2015,32(4):26.YU Deyun, LIU Dianshu, LI Hongchao,et al. Numerical simulation and error analysis of preliminary shock pressure on borehole wall in columnar blasting[J]. Blasting,2015,32(4):26. DOI:10.3963/j.issn.1001-487X.2015.04.006

宗琦, 罗强. 炮孔水耦合装药爆破应力分布特性试验研究[J]. 实验力学,2006,21(3):393.ZONG Qi, LUO Qiang. Experimental study on distribution character of blasting stress when boreholes with water-couple charge[J]. Journal of Experimental Mechanics,2006,21(3):393. DOI:10.3969/j.issn.1001-4888.2006.03.022.

凌伟明. 岩石爆破炮孔孔壁压力的试验研究[J]. 矿冶,2004,21(4):13.LING Weiming. Experimental research on explosion pressure on the wall of a borehole in rock[J]. Mining and Metallurgy,2004,21(4):13. DOI:10.3969/j.issn.1005-7854.2004.04.004

孙新利, 蔡星会, 姬国勋, 等. 内爆冲击动力学[M]. 西安: 西北工业大学出版社,2011

张守种. 爆炸与冲击动力学[M]. 北京: 兵器工业出版社,1993

谢平, 王梦想, 武建, 等. 装药直径对煤矿岩巷掘进爆破效果的影响[J]. 煤矿爆破,2020,38(5):9.XIE Ping, WANG Mengxiang, WU Jian,et al. Influence of charge diameter on blasting effect in coalmine rock roadway excavation[J]. Coal Mine Blasting,2020,38(5):9. DOI:10.3969/j.issn.1674-3970.2020.05.003

单仁亮, 黄宝龙, 蔚振廷, 等. 岩巷掘进准直眼掏槽爆破模型试验研究[J]. 岩石力学与工程学报,2012,31(2):256.SHAN Renliang, HUANG Baolong, YU Zhenting,et al. Model test of quasi-parallel cut blasting in rock drivage[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(2):256. DOI:10.3969/j.issn.1000-6915.2012.02.004

刘鑫, 杨军, 唐红亮. 同时起爆的双孔台阶模型试验研究[J]. 岩石力学与工程学报,2020,39(12):2460.LIU Xin, YANG Jun, TANG Hongliang. Experimental study on simultaneous initiation in double-hole bench model[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(12):2460. DOI:10.13722/j.cnki.jrme.2020.0283

费鸿禄, 王明玉, 魏世众, 等. 不同因素影响下混凝土立柱爆破效果的模型试验研究[J]. 爆破器材,2023,52(2):56.FEI Honglu, WANG Mingyu, WEI Shizhong,et al. Model test study on blasting effect of concrete column under different influencing factors[J]. Explosive Materials,2023,52(2):56. DOI:10.3969/j.issn.1001-8352.2023.02.009

马建军, 熊祖钊, 段卫东, 等. 工程爆破模拟试验的相似律[J]. 武汉科技大学学报(自然科学版),2001,24(2):170.MA Jjainjun, XIONG Zuzhao, DUAN Weidong,et al. Similarity law in simulation test of engineering blasting[J]. Journal of Wuhan University of Science and Technology,2001,24(2):170. DOI:10.3969/j.issn.1674-3644.2001.02.020

楼晓明, 王振昌, 陈必港, 等. 空气间隔装药孔壁初始冲击压力分析[J]. 煤炭学报,2017,42(11):2875.LOU Xiaoming, WANG Zhenchang, CHEN Bigang,et al. Initial shock pressure analysis for hole wall with air-decked charge[J]. Journal of China Coal Society,2017,42(11):2875. DOI:10.13225/j.cnki.jccs.2017.0919

杨仁树, 赵勇, 方士正, 等. 起爆方式对间隔装药应力场分布及裂纹扩展的影响[J]. 工程科学学报,2023,45(5):714.YANG Renshu, ZHAO Yong, FANG Shizheng,et al. Effect of the detonation method on the stress field distribution and crack propagation of spacer charge blasting[J]. Chinese Journal of Engineering,2023,45(5):714. DOI:10.13374/j.issn2095-9389.2022.03.03.006

宋帅, 杜闯, 李艳艳. 超高性能混凝土HJC本构模型参数确定及应用[J]. 爆炸与冲击,2023,43(5):57.SONG Shuai, DU Chuang, LI Yanyan. Determination and application of the HJC constitutive model parameters for ultra-high performance concrete[J]. Explosion and Shock Waves,2023,43(5):57. DOI:10.11883/bzycj-2022-0343

康耕新, 颜海春, 张亚栋, 等. 接触爆炸下混凝土墩破坏效应试验与数值模拟[J]. 兵工学报,2024,45(1):144.KANG Gengxin, YAN Haichun, ZHANG Yadong,et al. Test and numerical calculation of concrete obstacle damage effect under contact explosion[J]. Acta Armamentarii,2024,45(1):144. DOI:10.12382/bgxb.2022.0397

张社荣, 宋冉, 王超, 等. 碾压混凝土HJC动态本构模型修正及数值验证[J]. 振动与冲击,2019,38(12):25.ZHANG Sherong, SONG Ran, WANG Chao,et al. Modification of a dynamic constitutive model-HJC model for roller-compacted concrete and numerical verfication[J]. Journal of Vibration and Shock,2019,38(12):25. DOI:10.13465/j.cnki.jvs.2019.12.004

孙善政, 卢浩. 侧向爆炸作用下土中钢-混凝土竖井结构破坏模式研究[J]. 振动与冲击,2023,42(14):64.SUN Shanzheng, LU Hao. Failure mode of a steel-concrete shaft structure in soil under the action of lateral explosion[J]. Journal of Vibration and Shock,2023,42(14):64. DOI:10.13465/j.cnki.jvs.2023.14.008

骆浩浩, 杨仁树, 马鑫民, 等. 石禄铁矿扇形中深孔爆破块度分布特征研究[J]. 采矿与安全工程学报,2023,40(2):371.LUO Haohao, YANG Renshu, MA Xinmin,et al. Study on the distribution characteristics of deep hole blasting in the fan-shaped hole of Shilu Iron Mine[J]. Journal of Mining and Safety Engineering,2023,40(2):371. DOI:10.13545/j.cnki.jmse.2022.0159

刘江超, 高文学, 张声辉, 等. 水间隔装药孔壁爆炸应力分布规律[J]. 兵工学报,2021,42(12):2646.LIU Jiangchao, GAO Wenxue, ZHANG Shenghui,et al. Distribution law of explosion stress on hole wall of water interval charge[J]. Acta Armamentarii,2021,42(12):2646. DOI:10.3969/j.issn.1000-1093.2021.12.012

刘帅, 王卫华, 张恒根, 等. 岩体单孔爆破损伤的三维数值模拟研究[J]. 工程爆破,2023,29(1):10.LIU Shuai, WANG Weihua, ZHANG Henggen,et al. Threedimensional numerical simulation of single hole blasting damage in rock mass[J]. Engineering Blasting,2023,29(1):10. DOI:10.19931/j. EB.20210186

吴再海, 安龙, 齐兆军, 等. 基于 LS-DYNA 与PFC联合的岩体爆破数值模拟方法分析[J]. 采矿与安全工程学报,2021,38(3):609.WU Zaihai, AN Long, QI Zhaojun,et al. The numerical simulation method of rock mass blasting based on PFC combined with LSDYNA[J]. Journal of Mining & Safety Engineering,2021,38(3):609. DOI:10.13545/j.cnki.jmse.2020.0133

1 爆轰波与孔壁作用模型建立

2 孔壁压力峰值沿炮孔轴向分布理论计算

3 炮孔轴向孔壁压力模型试验

4 数值模拟

5 结论

友情链接LINKS