欢迎访问《哈尔滨工业大学学报》编辑部网站！

湿地湖泊相黏土胶结结构性与各向异性本构模型

doi: 10.11918/202312049

朱楠^1,2,3,4,5 ，诸葛爱军^1,2,3,4,5 ，喻志发^1,2,3,4,5 ，朱耀庭^1,2,3,4,5 ，李雨润^6,7

1. 中交天津港湾工程研究院有限公司,天津 300222

2. 港口岩土工程技术交通行业重点实验室,天津 300222

3. 天津市港口岩土工程技术重点实验室,天津 300222

4. 中交集团岩土工程重点实验室,天津 300222

5. 中交第一航务工程局有限公司,天津 300461

6. 河北工业大学土木与交通学院,天津 300401

7. 河北省土木工程技术研究中心,天津 300401

基金项目: 国家自然科学基金(51778207) ；中国交通建设集团有限公司科技研发项目(2021-207-03019)

详细信息

作者简介

朱楠(1987—),男,博士,高级工程师

通讯作者

李雨润(1978—),reddemon_love@126.com

中图分类号: TU43

文献标识码: A

文章编号: 0367-6234(2025)03-0160-11

A structured and anisotropic constitutive model considering bonding for marshy-lacustrine clay

ZHU Nan^1,2,3,4,5 ， ZHUGE Aijun^1,2,3,4,5 ， YU Zhifa^1,2,3,4,5 ， ZHU Yaoting^1,2,3,4,5 ， LI Yurun^6,7

1. Tianjin Port Engineering Institute Co., Ltd. of CCCC First Harbor Engineering Co., Ltd., Tianjin 300222 , China

2. Key Laboratory of Port Geotechnical Engineering, Ministry of Communications, PRC, Tianjin 300222 , China

3. Key Laboratory of Port Geotechnical Engineering of Tianjin, Tianjin 300222 , China

4. Key Laboratory of Geotechnical Engineering of CCCC, Tianjin 300222 , China

5. CCCC First Harbor Engineering Co., Ltd., Tianjin 300461 , China

6. School of Civil and Transportation Engineering, Hebei University of Technology, Tianjin 300401 , China

7. Civil Engineering Technology Research Center of Hebei Province, Tianjin 300401 , China

摘要

湿地湖泊相黏土由湖泊湿地或古湖泊湿地干缩形成,具有明显的胶结特性、结构性及初始各向异性。为了有效描述湿地湖泊相黏土的应力-应变关系及屈服特性,建立了考虑胶结强度演化、结构性及初始各向异性影响的土体弹塑性本构模型。基于纯剪切应力路径下胶结强度 p′_r 的变化规律,以及等向压缩条件下屈服面与胶结强度 p′_r 的对应关系,提出了适用于等向压缩、纯剪切及压缩剪切共同作用 3 种应力状态的胶结强度演化规律;基于修正剑桥模型理论框架,引入了胶结强度演化规律,并考虑体积应变硬化和剪切应变硬化的影响对硬化规律进行改进;引入各向异性参数 η_NCL ,对 p′-q 平面进行极坐标变换来反映初始各向异性的影响;采用相关联流动法则,建立了土体的胶结结构性和各向异性本构模型。所有的模型参数均可通过固结压缩试验、三轴试验及 K₀固结试验获得。模型预测与试验对比结果表明:所提出的模型能够合理地描述胶结强度及结构性与初始各向异性对土体应力-应变特性及屈服特性的影响,可以有效反映加载过程中土体胶结强度的渐进退化,以及在卸载应力路径下胶结强度对土体抗拉强度的提高作用。该模型考虑了胶结强度特性、结构性和各向异性的影响,可以更好地表征湿地湖泊相黏土的力学响应。

关键词

胶结强度 / 结构性 / 初始各向异性 / 硬化规律 / 本构模型 / 湿地湖泊相黏土

Abstract

Marshy-lacustrine clays with bonding characteristic, soil structure and initial anisotropy were formed by shrinkage of lake wetlands and ancient lake wetlands. In order to effectively describe the stress-strain relationship and yield characteristics of marshy-lacustrine clays, an elastic-plastic constitutive model of soil taking into account evolution of bonding strength, soil structure and initial anisotropy effects was established. A bonding strength evolution law used for three stress states including isotropic compression, shear and a combined action of compression and shear was proposed, based on the variation law of bonding strength under shear stress path and the corresponding relationship between yield surfaces and bonding strength with isotropic compression. On the basis of the Modified Cambridge model, the hardening law was improved by considering the evolution law of bonding strength and the influence of volumetric strain hardening and shear strain hardening. To reflect the effect of initial anisotropy, anisotropic parameters η_NCL was introduced and polar coordinate transformation was performed for the p′- q space. A structured and anisotropic constitutive model considering bonding for soil was presented by using the correlated flow rule. All parameters of the structured and anisotropic constitutive model considering bonding can be obtained through isotropic compression tests, triaxial test, and K₀ consolidation tests. The comparison between model predictions and experimental results shows that the proposed model can reasonably capture the influences of bonding strength, soil structure and initial anisotropy on the stress-strain and yield characteristics of marshy-lacustrine clays. The structured and anisotropic constitutive model considering bonding for marshy-lacustrine clays can effectively reflect the gradual degradation of bonding strength during loading and the improvement of bonding strength on soil tensile strength under unloading stress path. This model takes into account the influence of bonding strength, soil structure and anisotropy, which can reasonably characterize the mechanical response of marshy-lacustrine clays.

Keywords

bonding strength / soil structure / initial anisotropy / hardening law / constitutive model / marshy-lacustrine clay

1 湿地湖泊相黏土的结构特征及胶结特性 2 胶结结构性和各向异性本构模型 2.1 硬化规律 2.2 屈服函数 2.3 应力-应变关系 3 本构模型的验证及参数分析 3.1 本构模型参数的确定 3.2 模型参数 3.3 本构模型参数的敏感性分析 3.4 模型预测结果 4 结论

湖泊湿地或古湖泊湿地在中国广泛分布^[1]，气候变化和人类活动导致大量的湖泊湿地干缩或消失，原有饱和湖相沉积物在湖泊湿地干缩后重新固结，形成湿地湖泊相黏土^[2]。湿地湖泊相黏土在沉积过程中形成一定的土体初始结构和胶结连接，使土体具有结构性、初始各向异性和胶结特性。土的结构性和初始各向异性改变了土体的应力-应变特性和屈服面形态，而土的胶结特性使黏性土具有黏聚强度和一定的抗拉强度。如何在土体本构关系中反映土的结构性、初始各向异性和胶结特性影响，是合理表征湿地湖泊相黏土应力-应变特性的关键问题。

土的结构性本构模型是天然沉积黏土本构关系研究的首要问题。沈珠江院士指出“土的结构性本构模型的建立是 21 世纪土力学研究的重点” ^[3]。目前，建立土体结构性本构模型的主要方法包括: 1）为重塑土模型增加一个结构破损规律来反映土体结构性的退化，进而建立土的结构性本构模型（Vatsala 等^[4]，Baudet 等^[5]，Zhu 等^[6]）; 2）建立结构性土的参考屈服面，通过屈服面的变化来表征土体结构性的演化过程（ Rounania 等^[7]，Asoaka 等^[8]; Nakano 等^[9]，王立忠等^[10]）; 3）构建土的结构性参数，通过结构性参数的变化来描述加载过程中土体结构性的衰减过程（Liu 等^[11]，李吴刚等^[12]）; 4）将土体视为由结构完整的原状土或土块、结构完全破损的扰动土及软弱带组成的混合物，采用不同的本构模型分别进行表征（沈珠江^[13-15]，刘恩龙等^[16]）。上述方法从不同角度描述了加载过程中土体结构性的衰减，核心思想是建立原状土与重塑土力学指标或力学响应之间的定量关系，通过定量关系变化反映土体结构性的演化过程。

除了土的结构性外，考虑初始各向异性影响也是天然沉积黏土本构模型的研究热点。当前学者们主要采用旋转初始屈服面、引入各向异性参数等方法考虑 K₀ 固结诱发的初始各向异性影响（ Wheeler 等^[17]，Asoaka 等^[8]，Nakano 等^[9]，王立忠等^[10]，魏星等^[18]，于亚磊等^[19]），将 p′-q 应力空间中的椭圆形屈服面旋转一定角度，以 K₀线或 NCL 为对称轴，以 K₀线或 NCL 的夹角 θ_K₀和 θ_NCL为各向异性参数，或构建各向异性张量 α_ij及应力诱导各向异性参数 ζ 来描述椭圆屈服面的旋转特征。

在土的结构性和各向异性模型基础上，近年来对土体胶结特性本构的研究逐渐深入。与结构性本构模型类似，通过建立胶结强度参数或胶结强度演化规律来反映土体胶结的影响，引入结构性本构模型中来建立胶结结构性本构模型（ Suebsuk 等^[20]，Horpibulsuk 等^[21]，陈波等^[22]，孙凯等^[23]，万征等^[24-25]）。特别地，有学者提出了胶结强度与体积应变、剪切应变的双对数关系，建立了结构性软土的双对数胶结本构模型（刘鹏等^[26]）; 或将静止的临界状态线（CSL）扩展为移动临界状态线（MCSL），将结构性土统一硬化（UH）模型扩展为胶结结构性土统一硬化（UH）模型（祝恩阳等^[27]）。综上，上述工作分别针对土的结构性、初始各向异性和胶结特性本构模型开展，但同时考虑结构性、初始各向异性和胶结特性影响的土体本构模型尚未有相关报道。

为了合理反映湿地湖泊相黏土的应力-应变特性，建立土的胶结结构性和各向异性本构模型，基于课题组前期对湿地湖泊相黏土应力-应变及屈服特性的研究工作，提出了能够反映等向压缩、纯剪切及压缩剪切共同作用影响的胶结强度演化规律，并基于修正剑桥模型理论框架，考虑结构性和初始各向异性影响，引入提出的胶结强度演化规律，构建了考虑胶结强度演化、体积应变硬化和剪切应变硬化影响的改进硬化规律，最终通过旋转屈服面、引入各向异性参数及坐标变换来表征初始各向异性的影响，建立了湿地湖泊相黏土的胶结结构性和各向异性本构模型。

1 湿地湖泊相黏土的结构特征及胶结特性

湿地湖泊相黏土的物理力学指标见表1^[28]，黏聚力 c 较高为 28.7 kPa，表明湿地湖泊相黏土具有较明显的胶结特性，固结压缩曲线由文献^[29]中得到（图1），采用 Butterfield 双对数压缩曲线法^[30] 确定土体的结构屈服应力 p′_y = 107.89 kPa，而土体上覆压力 p′_c = 91.65 kPa，两者之比为 1.18，表明湿地湖泊相黏土具有较明显的结构强度。湿地湖泊相黏土的微观结构如图2所示^[28]，可见土颗粒之间和土团粒之间存在胶结联结，表明土体具有明显的胶结特性。而在土体结构屈服破坏后（图2（ b）），片状大颗粒和土团粒被压碎，胶结联结破坏，孔隙被压缩，破碎的颗粒重新集聚成新的结构形式。上述结果表明，当应力水平超过湿地湖泊相黏土的结构屈服应力后，土体结构发生破坏和重组，土体的胶结和组构相应改变，进而影响强度和变形特性。

表1湿地湖泊相黏土的物理力学指标^[28]

Tab.1 Physical and mechanical indexes of marshy-lacustrine clays

图1湿地湖泊相黏土双对数压缩曲线^[29]

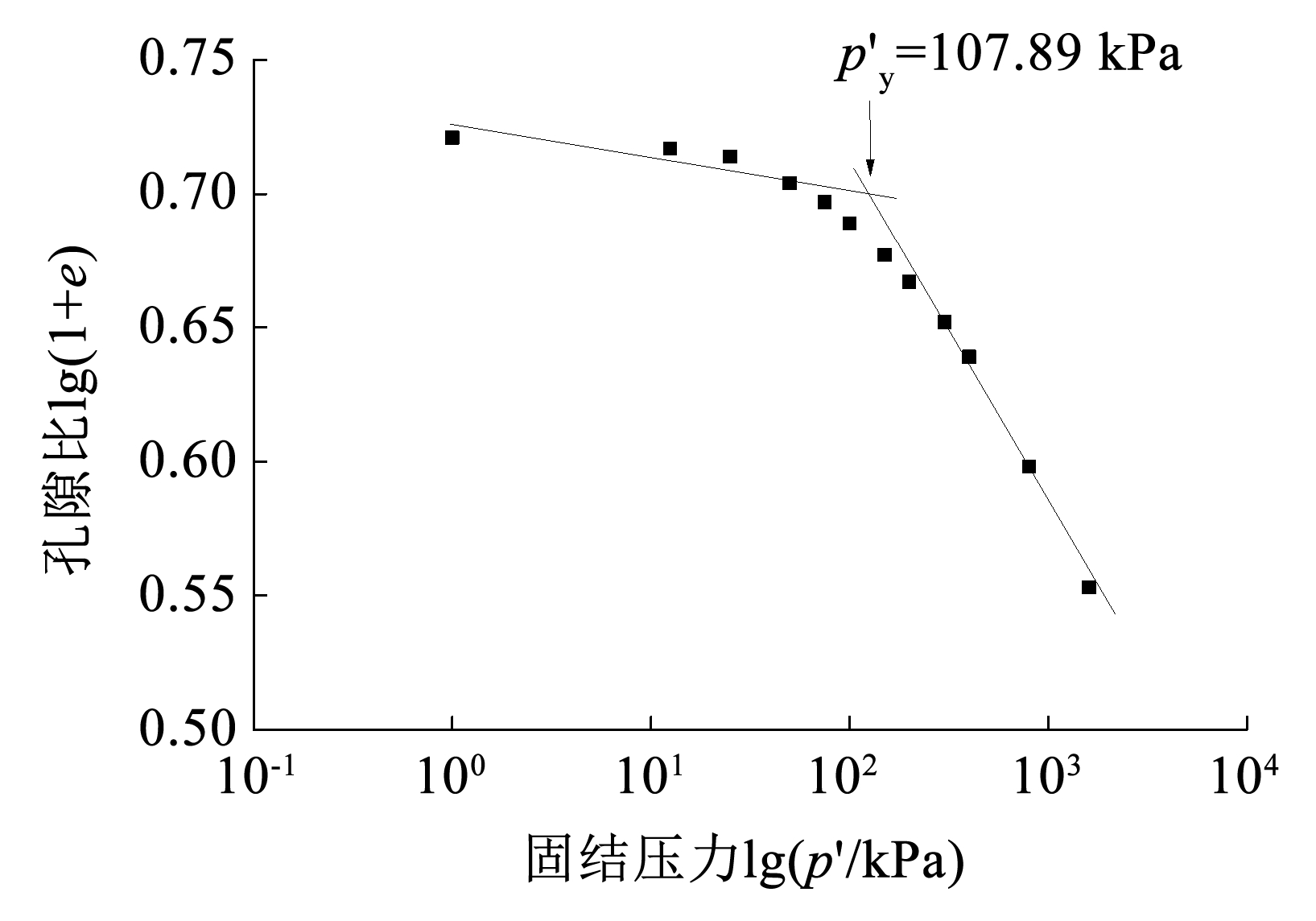
Fig.1Double logarithmic consolidation compression curve of marshy-lacustrine clays

图2湿地湖泊相黏土结构屈服破坏前后微观结构变化^[28]

Fig.2Microstructure for marshy-lacustrine clays before and after structural yield

有研究表明，土体的胶结强度 p′_r由 p′-q 平面中临界状态线 CSL 与 p′轴交点在原点左侧的截距确定^[22]。为研究 p′_r的演化规律，开展土体等 p′纯剪切应力路径试验，探讨纯剪切条件下土体 p′_r的变化规律，采用英国 GDS 三轴仪进行，初始 K₀ 固结应力 p′ = 57.29 kPa，偏应力 q = 44.96 kPa，剪切控制速率 Δq = 0.1 kPa / min，试验土样物理力学性质见表1，试验结果如图3、4所示。

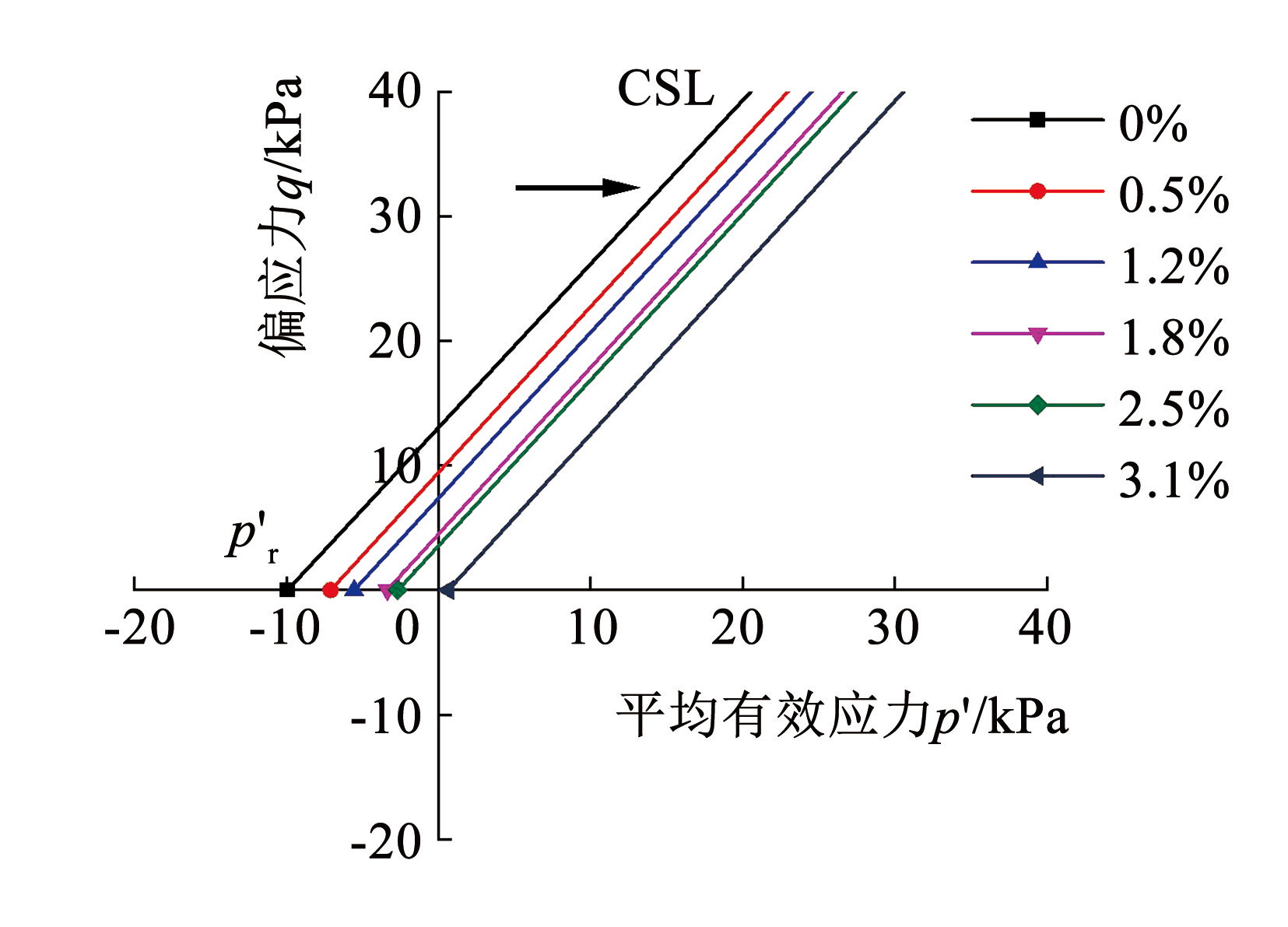
图3不同塑性剪切应变下土体的临界状态线

Fig.3Critical state lines under different plastic shear strains

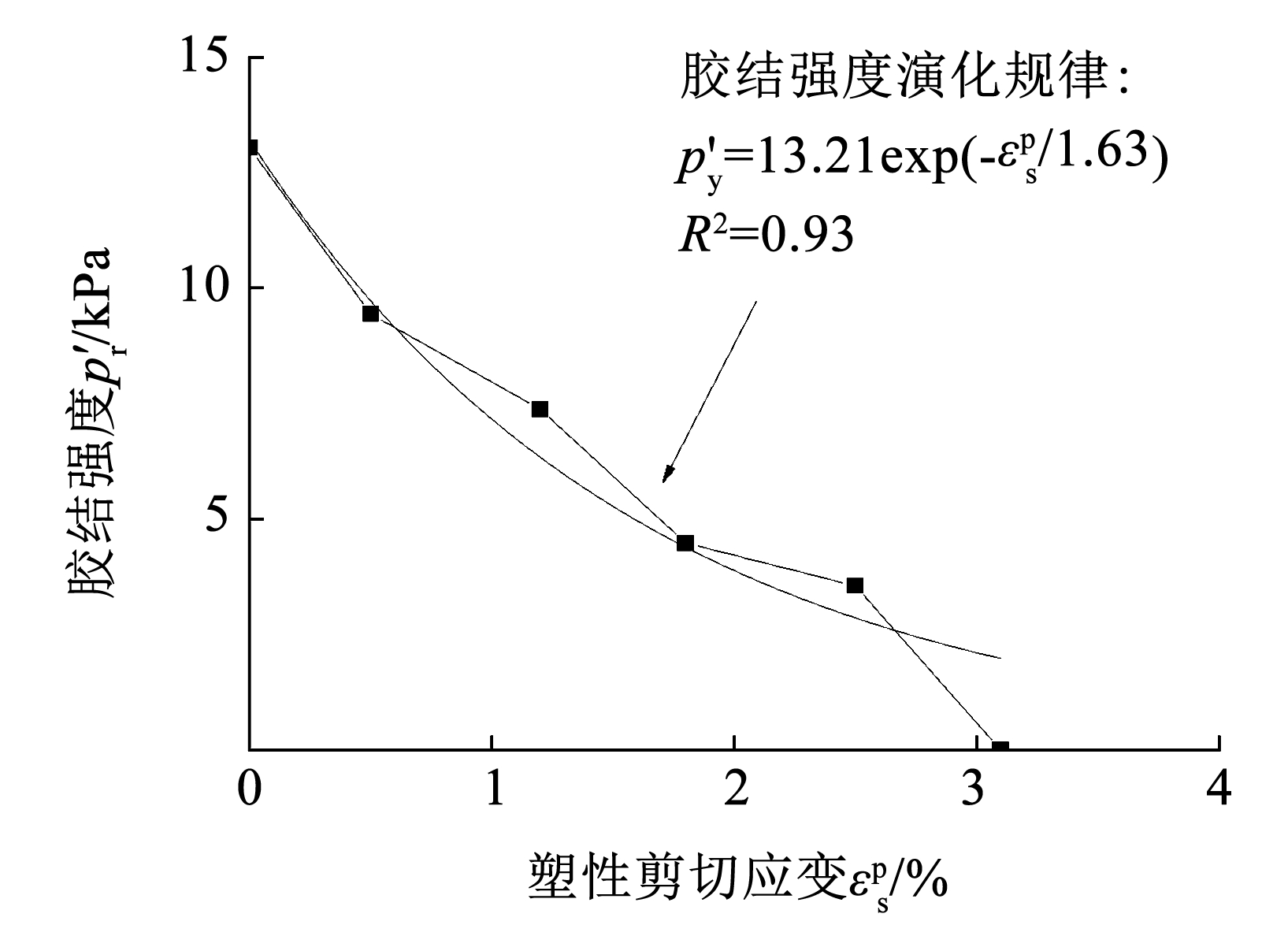
图4塑性剪切应变与胶结强度关系

Fig.4Relationship between plastic shear strains and bonding strength

由等 p′应力路径试验可得到纯剪切过程中临界状态线 CSL 的演化过程（图3）。在偏应力 q 达到屈服点后，CSL 随塑性剪切应变

ε_{s}^{p}

的增加而向右移动，CSL 与原点的截距逐渐变小，p′_r 也逐渐退化。根据试验结果建立

ε_{s}^{p}

与 p′_r的定量关系，二者呈指数型负相关关系（图4），与 Suebsuk ^[20] 的结论一致。分析可知，在纯剪切条件下，土体微观结构颗粒、土团粒之间的胶结连接发生渐进破坏，胶结强度逐渐衰减，许多研究表明^[20，22]这一衰减规律呈指数函数形式，与本文试验结果一致。因此，本文中纯剪切条件下胶结强度演化规律采用式（1）形式表示，即

p_{r i}^{'} = p_{r 0}^{'} e x p (- k ε_{s}^{p}), k > 0

(1)

式中 k 为拟合参数。

进一步，考虑等向压缩条件下土体的胶结强度演化规律。土体微观结构变化表明，在固结压缩条件下，胶结联结在加载后逐渐发生破坏^[31]。此外，众多学者的研究表明^[20-24，27]，当土体处于等向压缩状态时，随着固结压力增大，胶结强度 p′_r（大小为屈服面左端点与 p′-q 平面原点的截距）在 p′-q 空间中沿 p′轴向原点 O 移动，土体的屈服面从 p′₁逐渐演化为 p′₅，如图5所示。

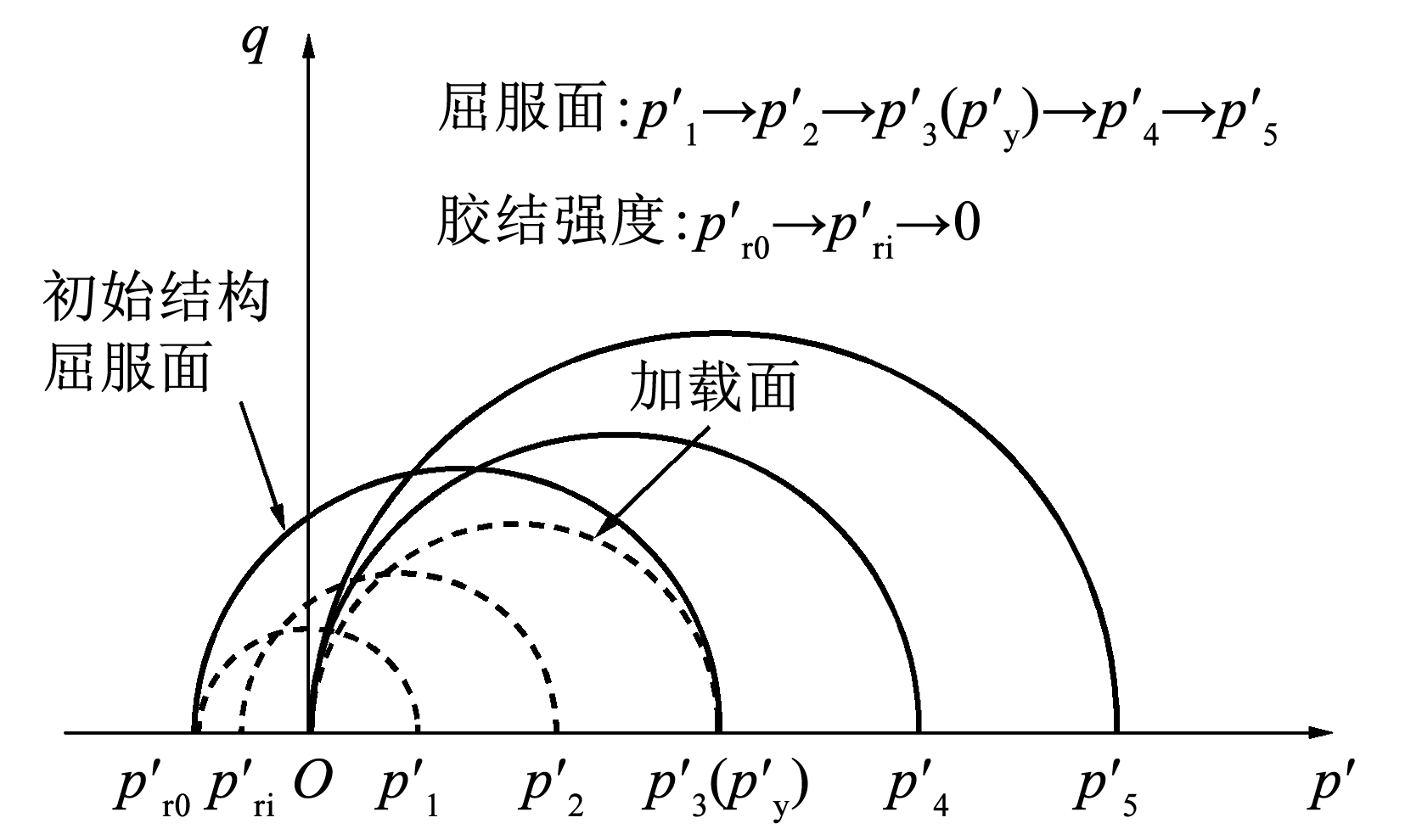
图5土的结构屈服面与胶结强度的演化过程

Fig.5Evolutions of structured yield surface and bonding strength for soils

由图5可知，胶结强度 p′_r从初始胶结强度 p′_r0逐渐退化为 0，而屈服面的右端点从 p′₁逐渐增大至 p′_y，p′_r与屈服面右端点 p′的变化一一对应。因此，在等向压缩条件下，可用 p′-q 空间中当前应力 p′沿 p′轴向结构屈服应力 p′_y的移动速率来反映 p′_r 的衰减速率，即以当前应力 p′与 p′_y之差与 p′_y的比值来反映等压缩条件下胶结强度的演化规律:

p_{r}^{'} = p_{r 0}^{'} (\frac{p_{y}^{'} - p^{'}}{p_{y}^{'}}) = p_{r 0}^{'} (1 - \frac{p^{'}}{p_{y}^{'}})

(2)

将式（2）与式（1）结合，得到能够分别反映等向压缩、纯剪切及压缩剪切共同作用 3 种应力状态下胶结强度变化的胶结强度演化规律:

p_{r}^{'} = \{\begin{matrix} p_{r 0}^{'} (1 - \frac{p^{'}}{p_{y}^{'}}) e x p (- k ε_{s}^{p}), p^{'} < p_{y}^{'} \\ 0, p^{'} ⩾ p_{y}^{'} \end{matrix}

(3)

式中:p′_y为结构屈服应力，p′_r0为初始胶结强度，

ε_{s}^{p}

为塑性剪切应变，k 为拟合参数。在 p′ <p′_y 时，土体的胶结强度存在，胶结强度根据式（3）的规律衰减; 在 p′≥p′_y 时，土体发生结构屈服破坏，胶结强度完全消失 p′_r = 0。

2 胶结结构性和各向异性本构模型

2.1 硬化规律

考虑湿地湖泊相黏土的结构特性及胶结特性，在等向压缩条件下，当固结压力 p′小于结构屈服应力 p′_y时，屈服前弹性段曲线斜率为 κ₀，κ₀ 受不同类型土的结构性大小影响，同时考虑原状土具有的胶结强度 p′_r影响，在弹性阶段土体的压缩模型可表示为

e = e_{0} - κ_{0} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{0}^{'} + p_{r}^{'}})

(4)

此时，土体的体积应变仅为弹性体应变:

ε_{v} = ε_{v}^{e} = - \frac{Δ e}{1 + e_{0}} = \frac{κ_{0}}{1 + e_{0}} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{0}^{'} + p_{r}^{'}})

(5)

当固结压力增大至 p′_y时，对应的孔隙比 e 为

e_{y} = e_{0} - κ_{0} l n (\frac{p_{y}^{'} + p_{r}^{'}}{p_{0}^{'} + p_{r}^{'}})

(6)

式中:e₀为初始孔隙比，e_y为结构屈服时的孔隙比，Δe 为附加孔隙比，κ₀为土体结构屈服前的压缩曲线斜率，p′₀为先期固结压力，p′_y为结构屈服应力。

在固结压力超过 p′_y 后，土体进入弹塑性阶段，压缩曲线斜率为 λ_s，回弹曲线斜率为 κ_s，结构屈服后土体孔隙比为

e_{x} = e_{y} - λ_{s} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(7)

附加孔隙比 Δe 与弹性附加孔隙比 Δe^e可分别表示为

Δ e = - λ_{s} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(8)

Δ e^{e} = - κ_{s} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(9)

则弹性体积应变

ε_{v}^{e}

和总体积应变 ε_v 分别为

ε_{v}^{e} = - \frac{Δ e^{e}}{1 + e_{0}} = \frac{κ_{s}}{1 + e_{0}} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(10)

ε_{v} = - \frac{Δ e}{1 + e_{0}} = \frac{λ_{s}}{1 + e_{0}} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(11)

塑性体积应变

ε_{v}^{p}

为

ε_{v}^{p} = ε_{v} - ε_{v}^{e} = - \frac{Δ e^{p}}{1 + e_{0}} = \frac{λ_{s} - κ_{s}}{1 + e_{0}} l n (\frac{p_{x}^{'} + p_{r}^{'}}{p_{y}^{'} + p_{r}^{'}})

(12)

由式（ 12）整理得到土体的硬化规律，借鉴 Collins 等^[32]提出的符合热力学耗散原理的本构模型，在硬化规律中引入式（3），将硬化规律拓展为考虑胶结强度演化、体积应变硬化和剪切应变硬化影响的改进硬化规律，表达式为

p_{x}^{'} = (p_{y}^{'} + p_{r}^{'}) e x p [(ε_{v}^{p} + η_{N C L} ε_{s}^{p}) \frac{1 + e_{0}}{λ_{s} - κ_{s}}] - p_{r}^{'}

(13)

式中:λ_s和 κ_s分别为结构屈服后土体压缩曲线的斜率和回弹曲线的斜率，η_NCL为 NCL 线的斜率。

2.2 屈服函数

相比修正剑桥模型的屈服面，湿地湖泊相黏土的屈服面在 p′-q 平面向原点左侧平移，且逆时针旋转一定角度^[28]，截距即为胶结强度 p′_r（图6），则考虑胶结影响的临界状态线公式为

q = M (p^{'} + p_{r}^{'})

(14)

式中:M 为湿地湖泊相黏土临界状态线的斜率，p′_r为土体的胶结强度，由式（3）计算。

根据魏汝龙^[33] 对修正剑桥模型屈服面的描述方法，屈服函数可表示为

{(\frac{q}{β})}^{2} + {(\frac{p^{'} - γ p_{x}^{'}}{α})}^{2} = p_{x}^{' 2}

(15)

其中:

α p_{x}^{'} = \frac{1}{2} (p_{x}^{'} + p_{r}^{'})

(16)

β p_{x}^{'} = M α p_{x}^{'} = \frac{1}{2} M (p_{x}^{'} + p_{r}^{'})

(17)

γ p_{x}^{'} = p_{x}^{'} - α p_{x}^{'} = \frac{1}{2} (p_{x}^{'} - p_{r}^{'})

(18)

将式（16）~（18）代入式（15）中，整理得到屈服函数表达式为

f = q^{2} + M^{2} p^{' 2} - M^{2} p^{'} p_{x}^{'} + M^{2} p^{'} p_{r}^{'} - M^{2} p_{x}^{'} p_{r}^{'}

(19)

Wheeler 等^[17]研究表明，天然黏土的初始屈服面以 NCL 线为对称轴。因此，假设湿地湖泊相黏土的初始屈服面（胶结结构性和各向异性屈服面）以 NCL 线为对称轴，本文通过采用各向异性参数 η_NCL 以及将胶结结构性屈服面旋转一定角度 ω 来反映土体初始各向异性的影响。由文献^[17]可知，NCL 线斜率 η_NCL 与天然沉积土的 K₀线斜率

η_{K_{0}}

有如下关系:

η_{N C L} = \frac{η_{K_{0}}^{2} + 3 η_{K_{0}} - M^{2}}{3}

(20)

式中

η_{K_{0}}

为 K₀固结线斜率，计算公式为

η_{K_{0}} = \frac{3 (1 - K_{0})}{1 + 2 K_{0}}

(21)

其中:K₀为湿地湖泊相黏土的侧向土压力系数，由原状土的 K₀固结试验确定，初始屈服面的旋转角度 ω 通过 ω = arctan η_NCL确定。

通过坐标变换来考虑土体初始各向异性的影响，旋转角度为 ω，p′-q 平面坐标变换公式为

p^{' *} = p^{'} c o s ω + q s i n ω

(22)

q^{*} = - p^{'} s i n ω + q c o s ω

(23)

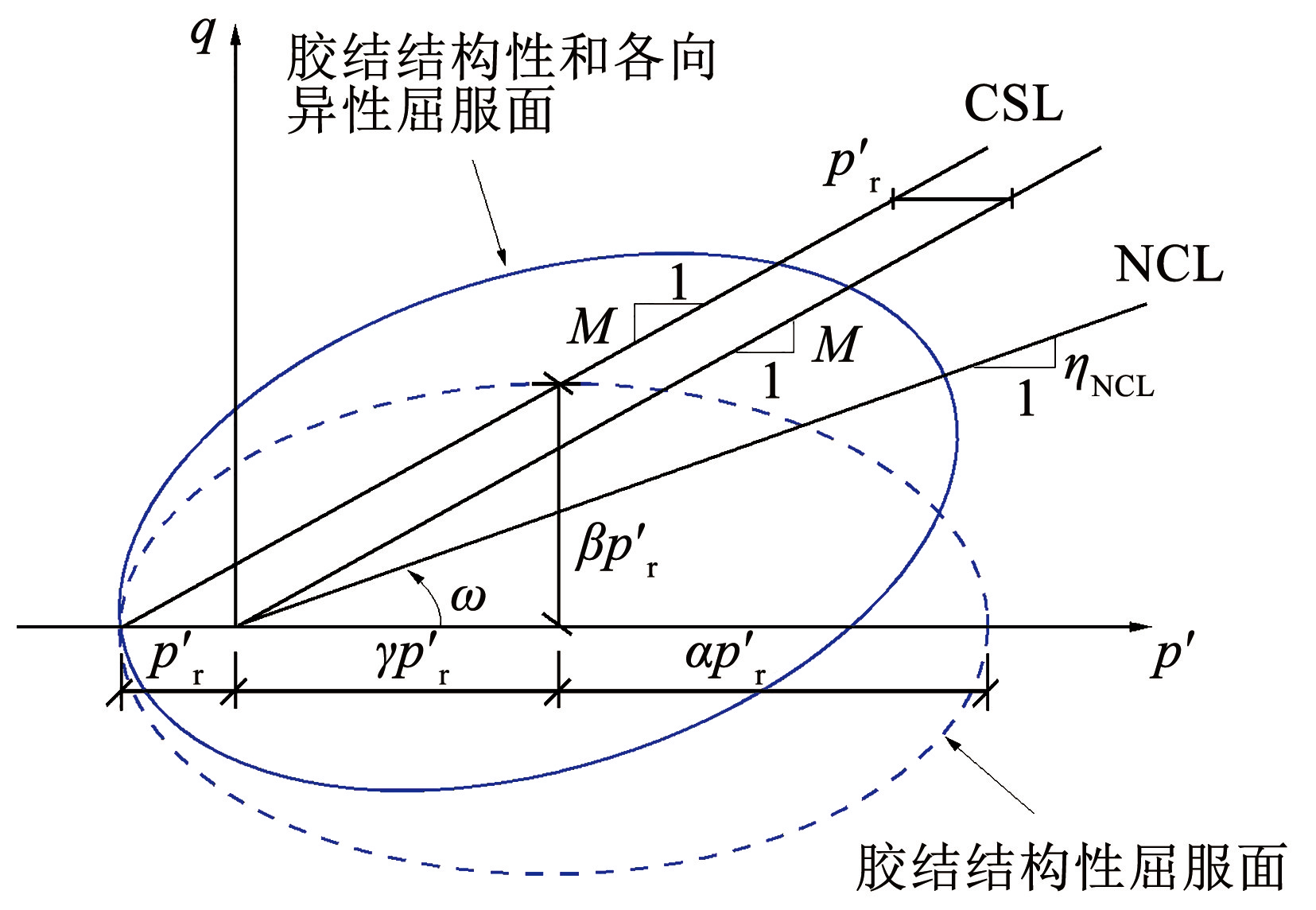
图6湿地湖泊相黏土胶结结构性和各向异性屈服面

Fig.6Diagram of structured and anisotropic yield surface considering bonding of marshy-lacustrine clay

首先假设式（19）中的 p′、q 变为p′^∗、q^∗，再将式（22）和式（23）代入屈服函数式（19），最后将硬化规律式（13）和胶结强度演化规律式（3）代入屈服函数式（19），整理后屈服函数为

\begin{matrix} f = {(- p^{'} s i n ω + q c o s ω)}^{2} + M^{2} {(p^{'} c o s ω + q s i n ω)}^{2} - M^{2} (p^{'} c o s ω + q s i n ω) p_{y}^{'} e x p [(ε_{v}^{p} + η_{N C L} ε_{s}^{p}) \frac{1 + e_{0}}{λ_{s} - κ_{s}}] - \\ M^{2} \{(p^{'} c o s ω + q s i n ω + p_{y}^{'}) e x p [(ε_{v}^{p} + η_{N C L} ε_{s}^{p}) \frac{1 + e_{0}}{λ_{s} - κ_{s}}] - 2 (p^{'} c o s ω + q s i n ω)\} p_{r o}^{'} (1 - \frac{p^{'} c o s ω + q s i n ω}{p_{y}^{'}}) e x p (- k ε_{s}^{p}) + \\ M^{2} \{1 - e x p [(ε_{v}^{p} + η_{N C L} ε_{s}^{p}) \frac{1 + e_{0}}{λ_{s} - κ_{s}}]\} p_{r 0}^{' 2} {(1 - \frac{p^{'} c o s ω + q s i n ω}{p_{y}^{'}})}^{2} e x p (- 2 k ε_{s}^{p}) \end{matrix}

(24)

2.3 应力-应变关系

研究^[34]表明，天然黏土的塑性应变增量与塑性势面正交性较好，结合湿地湖泊相黏土的塑性流动特性^[28]，因此本文模型采用相关联流动法则，表达式为

d ε_{v}^{p} = d λ \frac{\partial f}{\partial p^{'}}

(25)

d ε_{s}^{p} = d λ \frac{\partial f}{\partial q}

(26)

根据一致连续性条件，对式（24）求全微分，有

d f = \frac{\partial f}{\partial p^{'}} d p^{'} + \frac{\partial f}{\partial q} d q + \frac{\partial f}{\partial ε_{v}^{p}} d ε_{v}^{p} + \frac{\partial f}{\partial ε_{s}^{p}} d ε_{s}^{p} = 0

(27)

由相关联流动法则，整理后得到的塑性标量因子 dλ 可表示为

d λ = - \frac{\frac{\partial f}{\partial p^{'}} d p^{'} + \frac{\partial f}{\partial q} d q}{\frac{\partial f}{\partial ε_{v}^{p}} \frac{\partial f}{\partial p^{'}} + \frac{\partial f}{\partial ε_{s}^{p}} \frac{\partial f}{\partial q}}

(28)

对屈服函数式（24）求偏导，推导 df 中的各分项表达式，为了对公式进行简化，进行如下代换:

A = e x p [(ε_{v}^{p} + η_{N C L} ε_{s}^{p}) \frac{1 + e_{0}}{λ_{s} - κ_{s}}]

(29)

B = p^{'} c o s ω + q s i n ω

(30)

C = - p^{'} s i n ω + q c o s ω

(31)

并且令

p_{r 0}^{'} (1 - \frac{p^{'}}{p_{y}^{'}}) e x p (- k ε_{s}^{p}) = p_{r}^{'}

，整理后，有

\begin{matrix} \frac{\partial f}{\partial p^{'}} = - 2 C s i n ω + M^{2} [2 (B + p_{r}^{'}) - (p_{y}^{'} + p_{r}^{'}) A] c o s ω - \\ M^{2} [2 (B + p_{r}^{'}) - (B + p_{y}^{'} + 2 p_{r}^{'}) A] \cdot \\ p_{r 0}^{'} (\frac{\cos ω}{p_{y}^{'}}) e x p (- k ε_{s}^{p}) \end{matrix}

(32)

\begin{matrix} \frac{\partial f}{\partial q} = 2 C c o s ω + M^{2} [2 (B + p_{r}^{'}) - (p_{y}^{'} + p_{r}^{'}) A] s i n ω - \\ M^{2} [2 (B + p_{r}^{'}) - (B + p_{y}^{'} + 2 p_{r}^{'}) A] \cdot \\ p_{r 0}^{'} (\frac{\sin ω}{p_{y}^{'}}) e x p (- k ε_{s}^{p}) \end{matrix}

(33)

\frac{\partial f}{\partial ε_{v}^{p}} = - \frac{1 + e_{0}}{λ_{s} - κ_{s}} M^{2} A (B + p_{r}^{'}) (p_{y}^{'} + p_{r}^{'})

(34)

\begin{matrix} \frac{\partial f}{\partial ε_{s}^{p}} = - η_{N C L} \frac{1 + e_{0}}{λ_{s} - κ_{s}} M^{2} A (B + p_{r}^{'}) (p_{y}^{'} + p_{r}^{'}) + \\ M^{2} k p_{r}^{'} [(B + p_{y}^{'} + 2 p_{r}^{'}) A - 2 (B + p_{r}^{'})] \end{matrix}

(35)

根据胡克定律，弹性应力应变-关系可表达为

\{\begin{matrix} d ε_{v}^{e} \\ d ε_{s}^{e} \end{matrix}\} = [C^{e}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\} = [\begin{matrix} \frac{1}{K} & 0 \\ 0 & \frac{1}{3 G} \end{matrix}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\}

(36)

其中弹性体积模量 K 和弹性剪切模量 G 分别为

K = \frac{E}{3 (1 - 2 v)} = \frac{1 + e_{0}}{κ_{0}} p^{'}

(37)

G = \frac{E}{2 (1 + v)} = \frac{3 (1 - 2 v)}{2 (1 + v)} \frac{1 + e_{0}}{κ_{0}} p^{'}

(38)

由相关联法则，塑性应力-应变关系式为

\{\begin{matrix} d ε_{v}^{p} \\ d ε_{s}^{p} \end{matrix}\} = [C^{p}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\} = [\begin{matrix} C_{11}^{p} C_{12}^{p} \\ C_{21}^{p} C_{22}^{p} \end{matrix}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\}

(39)

则土体的弹塑性应力-应变关系式为

\{\begin{matrix} d ε_{v} \\ d ε_{s} \end{matrix}\} = [C^{e p}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\} = [\begin{matrix} C_{11}^{p} + \frac{1}{K} & C_{12}^{p} \\ C_{21}^{p} & C_{22}^{p} + \frac{1}{3 G} \end{matrix}] \{\begin{matrix} d p^{'} \\ d q \end{matrix}\}

(40)

其中弹塑性柔度矩阵为

[C^{e p}] = [\begin{matrix} C_{11}^{p} + \frac{1}{K} & C_{12}^{p} \\ C_{21}^{p} & C_{22}^{p} + \frac{1}{3 G} \end{matrix}] = [\begin{matrix} - \frac{\frac{\partial f}{\partial p^{'}} \frac{\partial f}{\partial p^{'}}}{\frac{\partial f}{\partial ε_{v}^{p}} \frac{\partial f}{\partial p^{'}} + \frac{\partial f}{\partial ε_{s}^{p}} \frac{\partial f}{\partial q}} + \frac{1}{K} & - \frac{\frac{\partial f}{\partial p^{'}} \frac{\partial f}{\partial q}}{\frac{\partial f}{\partial ε_{v}^{p}} \frac{\partial f}{\partial p^{'}} + \frac{\partial f}{\partial ε_{s}^{p}} \frac{\partial f}{\partial q}} \\ - \frac{\frac{\partial f}{\partial q} \frac{\partial f}{\partial p^{'}}}{\frac{\partial f}{\partial ε_{v}^{p}} \frac{\partial f}{\partial p^{'}} + \frac{\partial f}{\partial ε_{s}^{p}} \frac{\partial f}{\partial q}} & - \frac{\frac{\partial f}{\partial q} \frac{\partial f}{\partial q}}{\frac{\partial f}{\partial ε_{v}^{p}} \frac{\partial f}{\partial p^{'}} + \frac{\partial f}{\partial ε_{s}^{p}} \frac{\partial f}{\partial q}} + \frac{1}{3 G} \end{matrix}]

(41)

3 本构模型的验证及参数分析

3.1 本构模型参数的确定

本文模型共有 17 个模型参数，均有明确物理意义，全部参数都可由固结压缩试验、三轴试验及 K₀固结试验获得:1）K、G、 υ 为弹性参数，其中 υ 取 0.33，K 和 G 由原状土等向压缩加卸载试验结果根据式（37）和式（38）计算得到; 2）e₀、M、λ_r、κ_r为修正剑桥模型参数，e₀为土体的初始孔隙比，M 为 p′-q 应力空间中临界状态线 CSL 的斜率，采用不同固结压力的三轴试验确定，λ_r和 κ_r分别为重塑土的压缩曲线及回弹曲线斜率，由重塑土的一维压缩试验得到; 3）λ_s、κ_s、κ₀、p′₀、p′_y、Δe_y为描述土体结构性的参数，λ_s 和 κ_s分别为原状土在结构屈服后压缩曲线和回弹曲线的斜率，κ₀为原状土在结构屈服前弹性段压缩曲线的斜率，p′₀为初始平均有效应力，根据上覆土层的有效自重应力确定，p′_y为土的结构屈服应力，Δe_y 为固结压力等于结构屈服应力时原状土与重塑土孔隙比之差，前述参数均可由原状土压缩曲线采用双对数法确定，如图1所示; 4）p′_r0、k 为反映胶结强度演化的参数，p′_r0 为初始胶结强度，由三轴试验得到的 p′-q 应力空间中临界状态线 CSL 与原点的截距确定，k 为纯剪切条件下胶结强度 p′_r 演化速率相关的参数，由三轴试验拟合确定; 5）湿地湖泊相黏土的初始屈服面以 NCL 线为对称轴，采用 NCL 线的斜率 η_NCL和初始屈服面的旋转角度 ω 来反映初始各向异性的影响，η_NCL采用式（20）由 η_K₀计算得到，η_K₀采用式（21）由 K₀计算得到，ω 通过反正切函数 ω = arctan η_NCL计算确定。

3.2 模型参数

通过一维压缩试验和 K₀固结应力路径试验对本文提出的模型进行验证，同时以修正剑桥模型（MCC 模型）的模拟结果作为对比，分析本文模型的预测效果，并对模型的主要参数进行敏感性分析，模型的材料参数见表2。

3.3 本构模型参数的敏感性分析

结构屈服应力 p′_y对预测结果的影响如图7所示，提高结构屈服应力 p′_y后，土体压缩曲线拐点的位置右移，在结构屈服后各压缩曲线的斜率基本相同，表明增大 p′_y提高了土体压缩曲线发生转折时的结构屈服应力，但不会影响结构屈服后土体的压缩性。

表2模拟预测所需的土体模型参数

Tab.2 Parameters of soil model for simulation and prediction

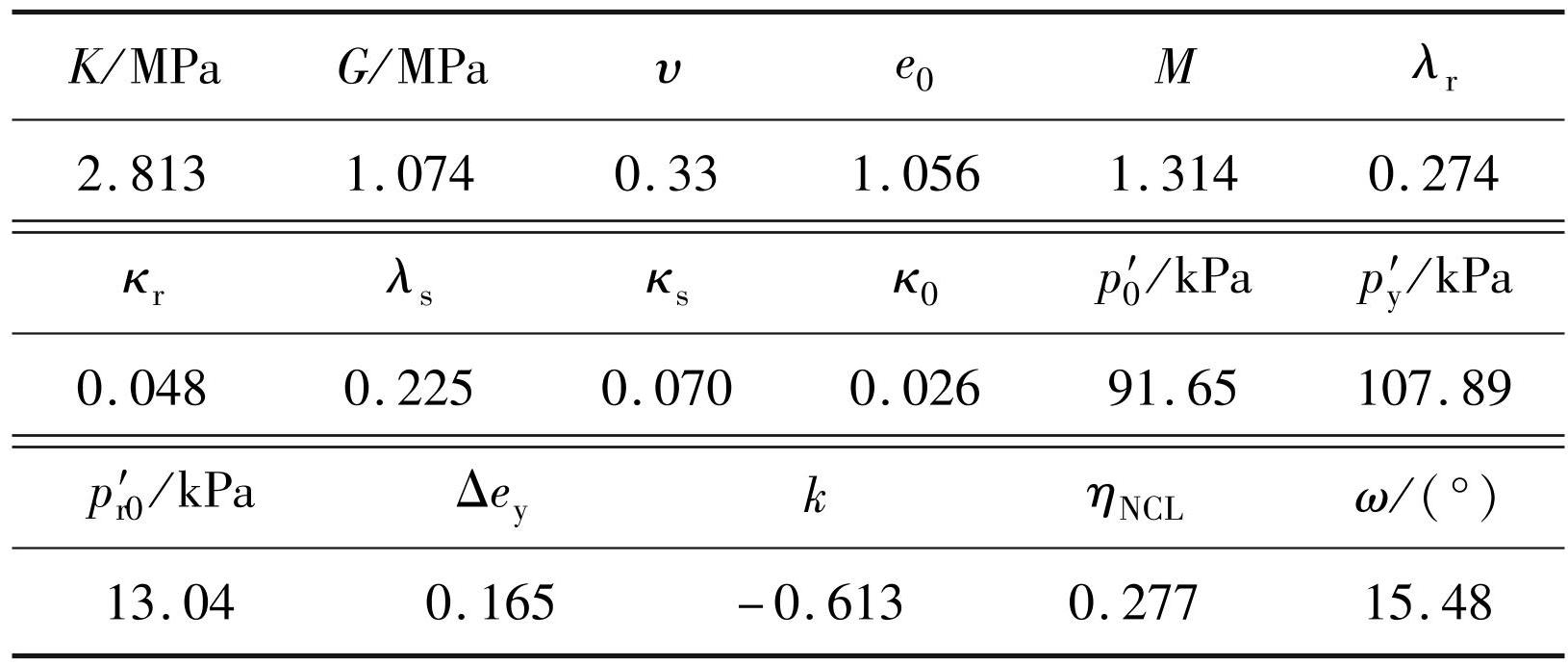
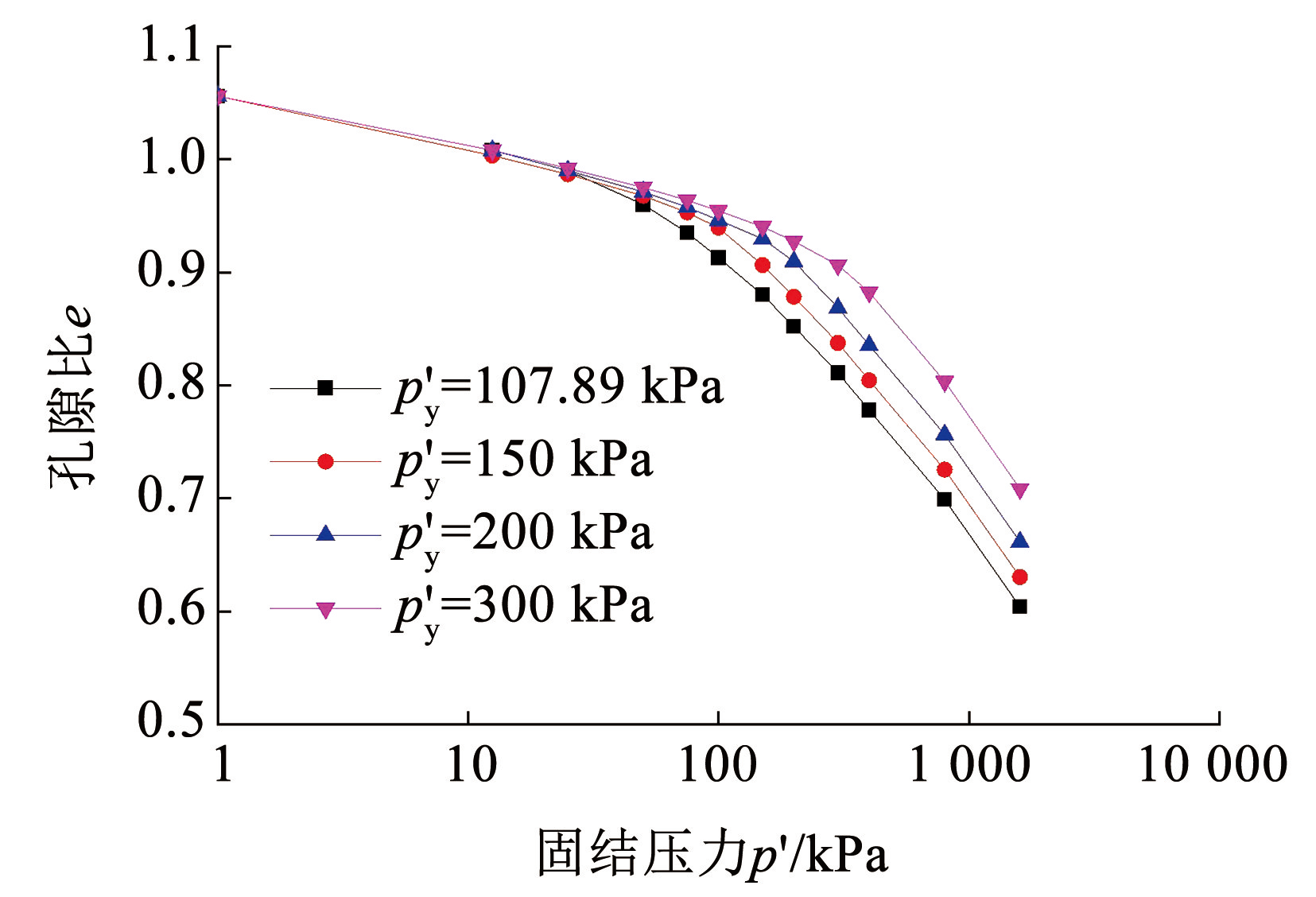
图7p′_y对一维压缩特性的影响

Fig.7Influences of p′_y on one-dimensional compressive characteristics of marshy-lacustrine clay

图8为胶结强度演化参数 k 对预测结果的影响，可见土体偏应力 q 随着 k 的减小而增加，表明减小 k 会提高土体的抗剪强度，但各应力-应变曲线在后半段斜率基本相同，表明 k 对结构屈服后对土体偏应力 q 增长速率的影响较小。

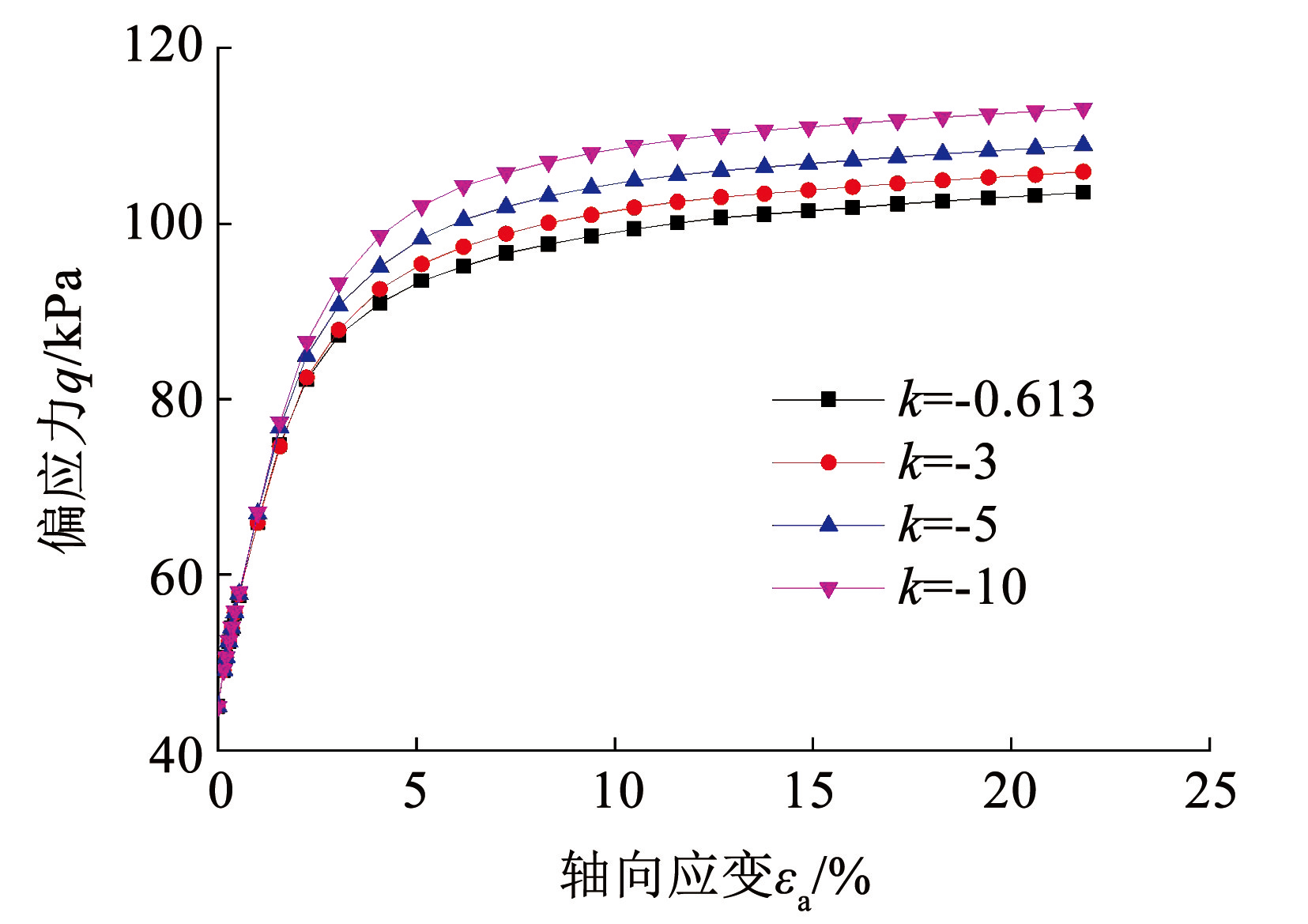
图8k 对 TCD3 应力路径下应力-应变曲线的影响

Fig.8Influences of k on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

图9为初始胶结强度 p′_r0对土体应力-应变曲线的影响，随着 p′_r0提高，土体偏应力 q 明显增大，但在偏应力 q 达到峰值后各应力-应变曲线基本平行，表明此时胶结强度已经不再发挥作用。

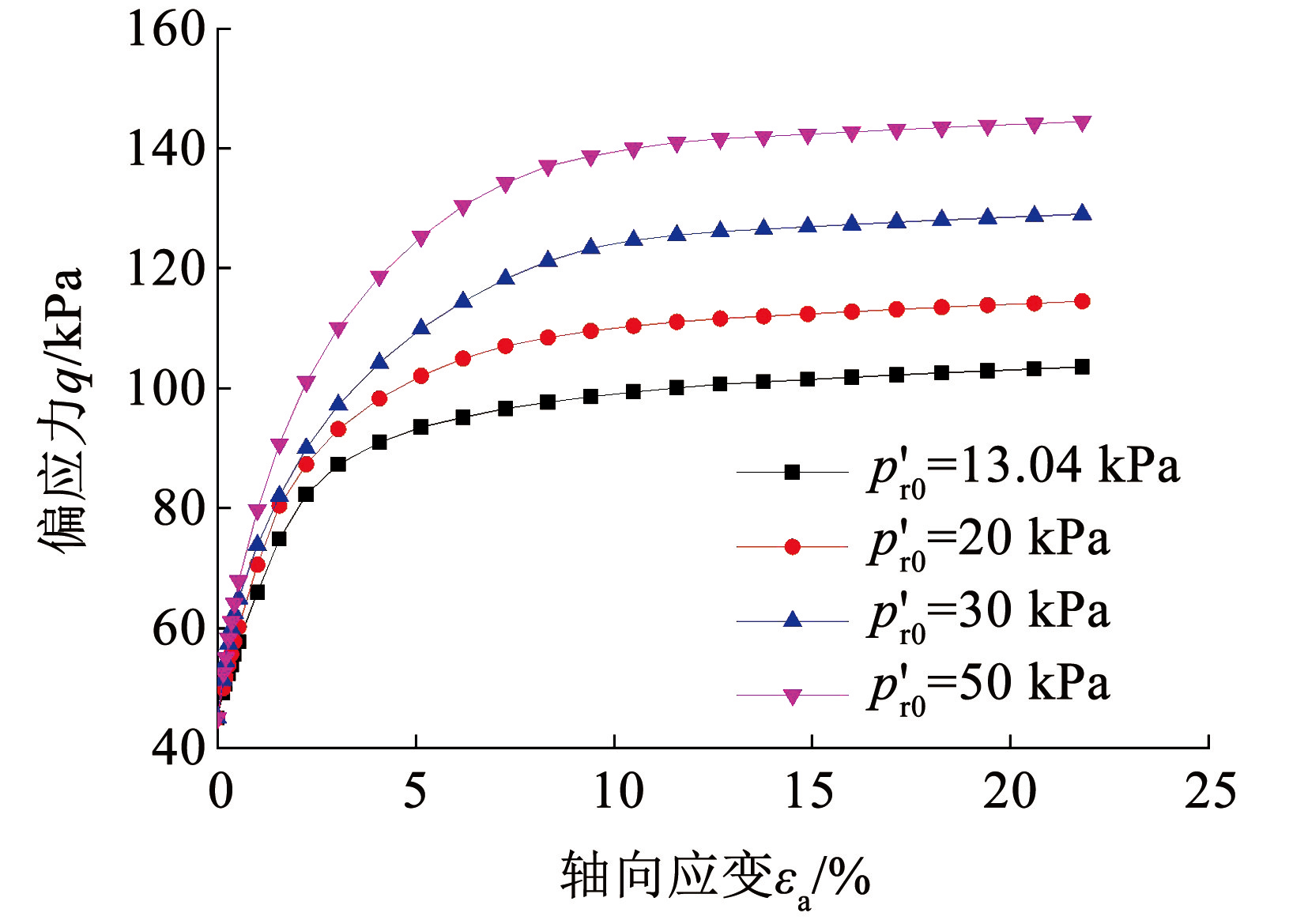
图9p′_r0对 TCD3 应力路径下应力-应变曲线的影响

Fig.9Influences of p′_r0 on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

3.4 模型预测结果

图10为本文模型和 MCC 模型的预测结果与一维压缩试验的结果对比，可见本文模型能够模拟原状土的非线性压缩特性; 预测的压缩曲线位于 MCC 模型的压缩曲线上方，反映了结构性对土体刚度的提高作用; 本文模型的压缩曲线相比 MCC 模型更接近试验结果，预测效果更好。

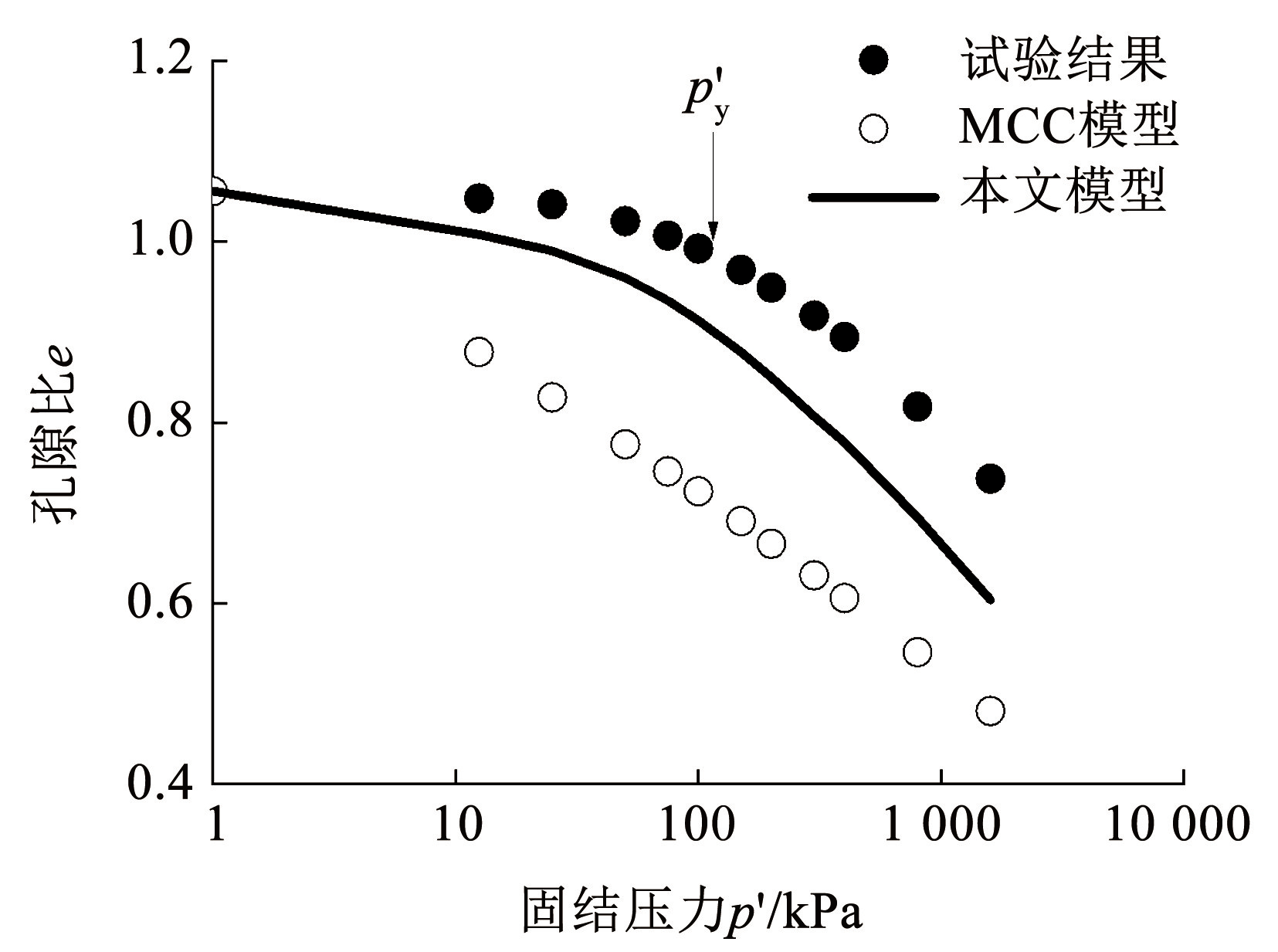
图10一维固结压缩试验结果对比

Fig.10Comparison of results for one-dimensional consolidation tests

通过 K₀固结应力路径试验来验证本文模型对不同应力路径下土体应力-应变特性的预测效果，应力路径试验方案如图11所示。

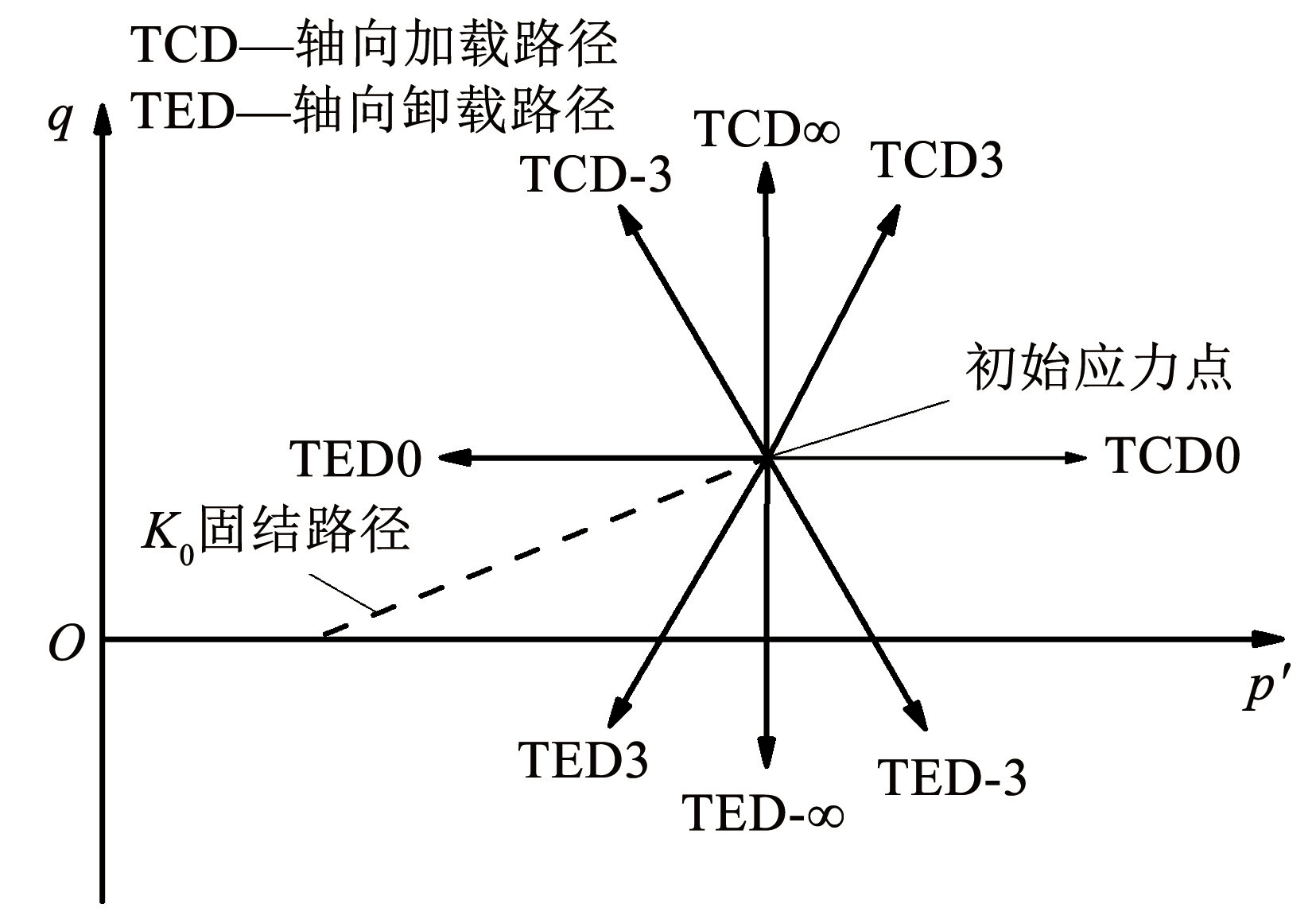
图11应力路径试验方案示意

Fig.11Schematic diagram of scheme of stress path tests

图12~14 为轴向加载应力路径（TCD3、TCD-3、 TCD∞）下本文模型及 MCC 模型预测结果与试验结果的对比，可见在不同的轴向加载应力路径下，本文模型的预测结果与试验结果较为吻合。相比 MCC 模型，本文模型反映了结构性对土体强度的提高作用，同时在偏应力 q 接近屈服强度（曲线拐点）后，应力-应变曲线的上升速度减慢，表明随着加载的进行土体的结构性逐渐退化，土的结构性提供的结构强度逐渐减小，在偏应力 q 达到屈服强度后土的结构强度基本消失。

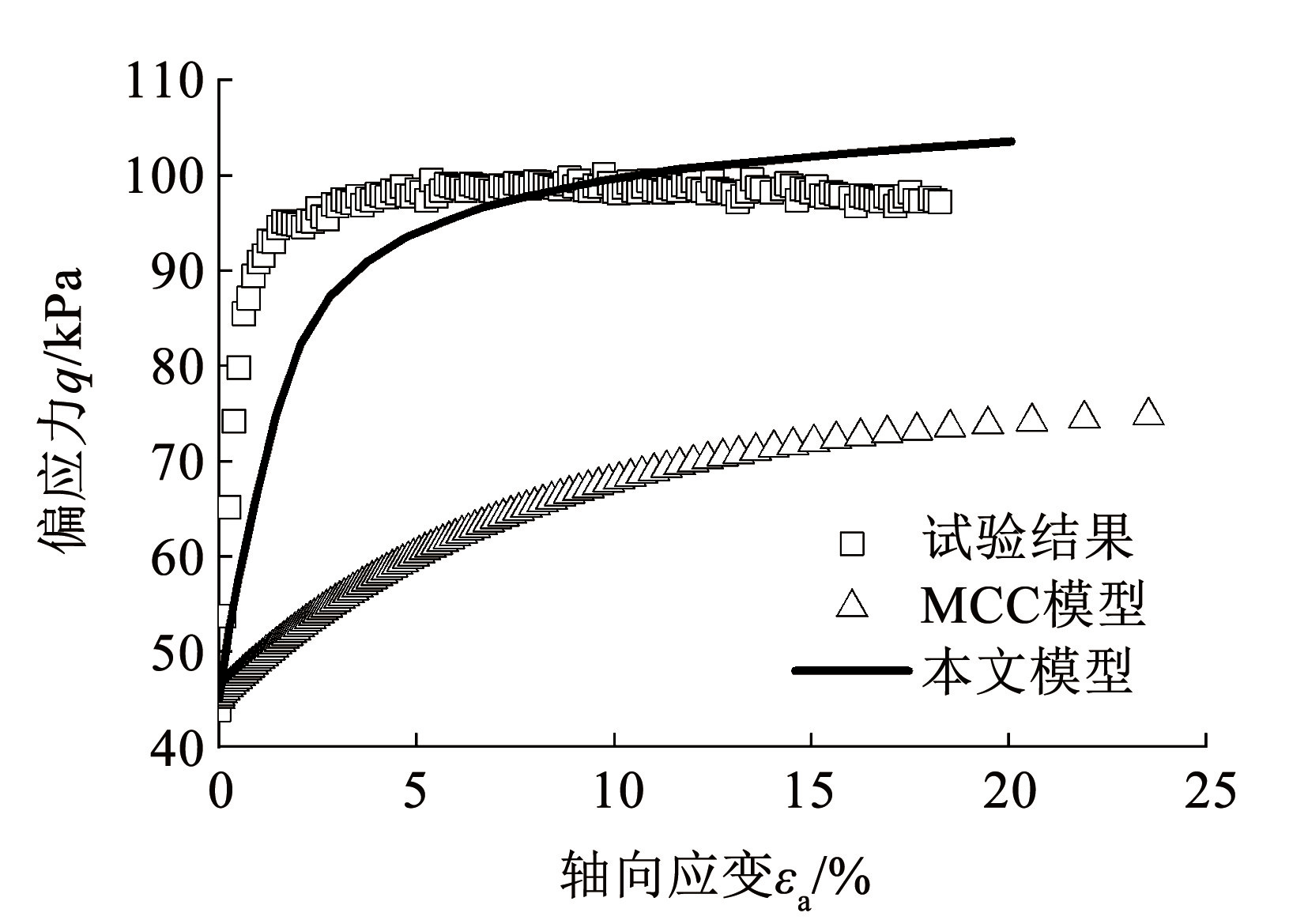
图12TCD3 应力路径三轴试验结果对比

Fig.12Comparison of results of TCD3 stress path triaxial tests

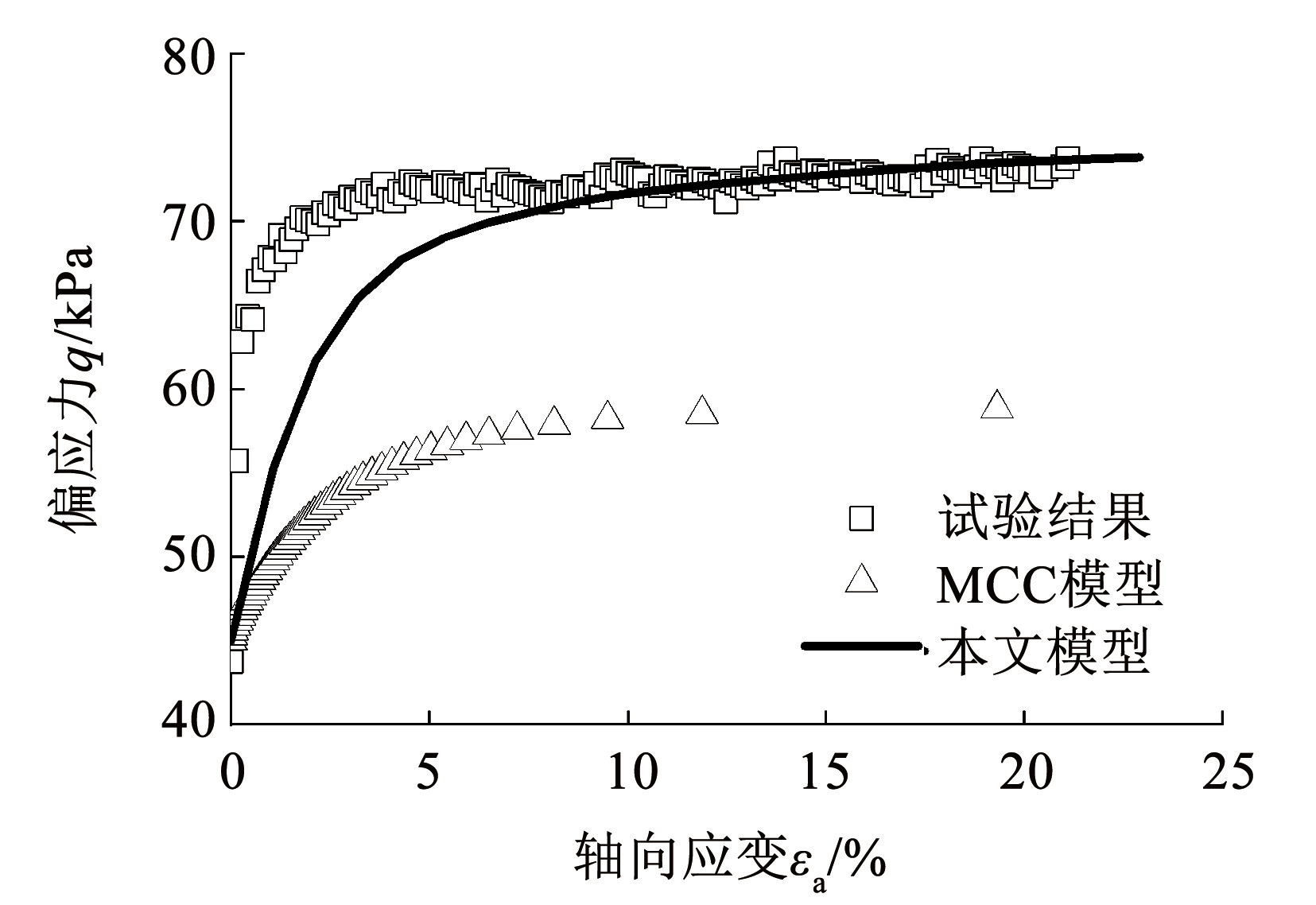
图13TCD-3 应力路径三轴试验结果对比

Fig.13Comparison of results of TCD-3 stress path triaxial tests

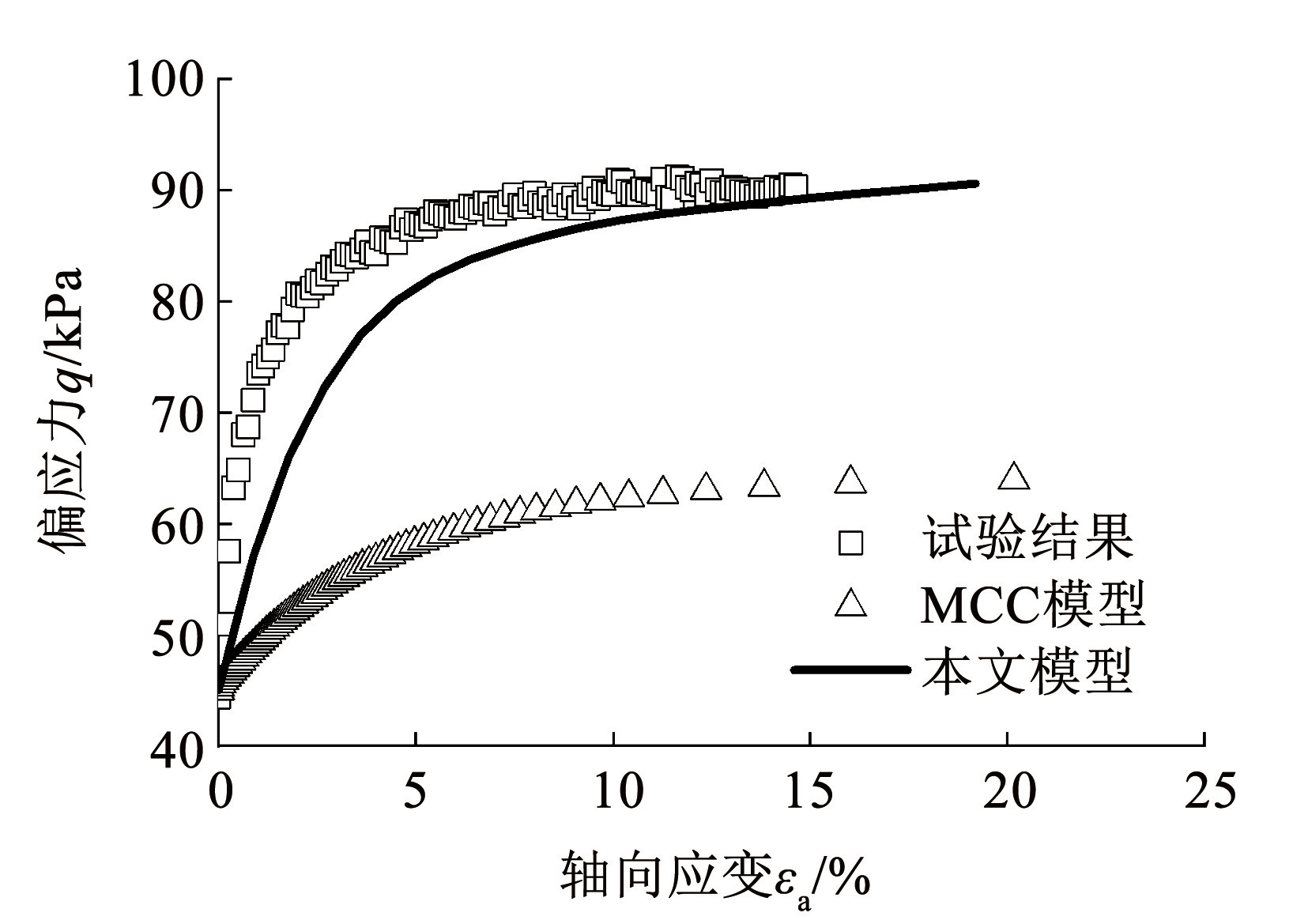
图14TCD∞ 应力路径三轴试验结果对比

Fig.14Comparison of results of TCD∞ stress path triaxial tests

图15、16为轴向卸载应力路径试验（TED-3 和 TED-∞）的试验结果与本文模型及 MCC 模型预测结果的对比，可见由于本文模型考虑了胶结强度的影响，在轴向拉伸条件下具有比 MCC 模型更高的强度，并且预测的应力-应变曲线相比 MCC 模型与试验结果更为接近。

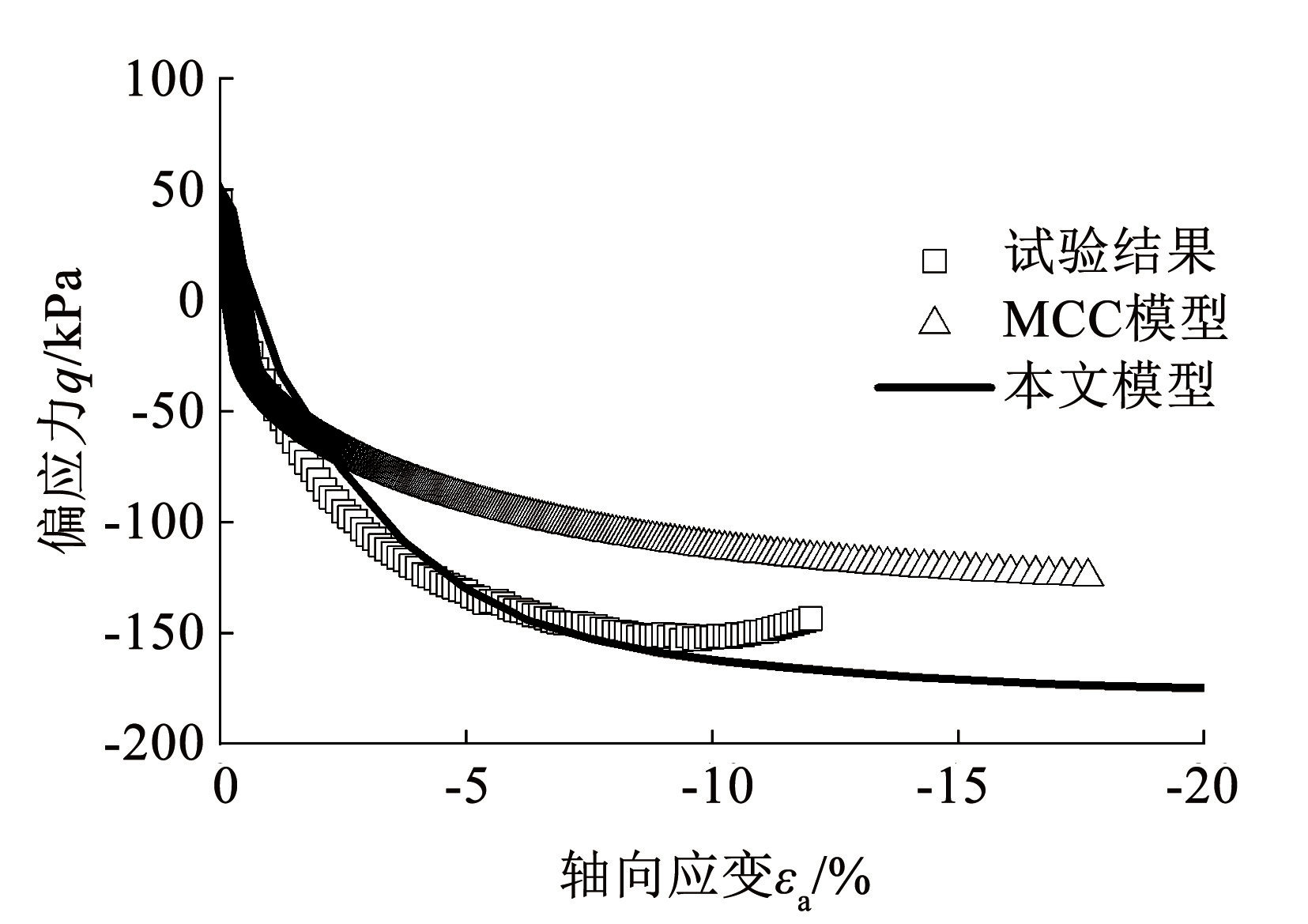
图15TED-3 应力路径三轴试验结果对比

Fig.15Comparison of results of TED-3 stress path triaxial tests

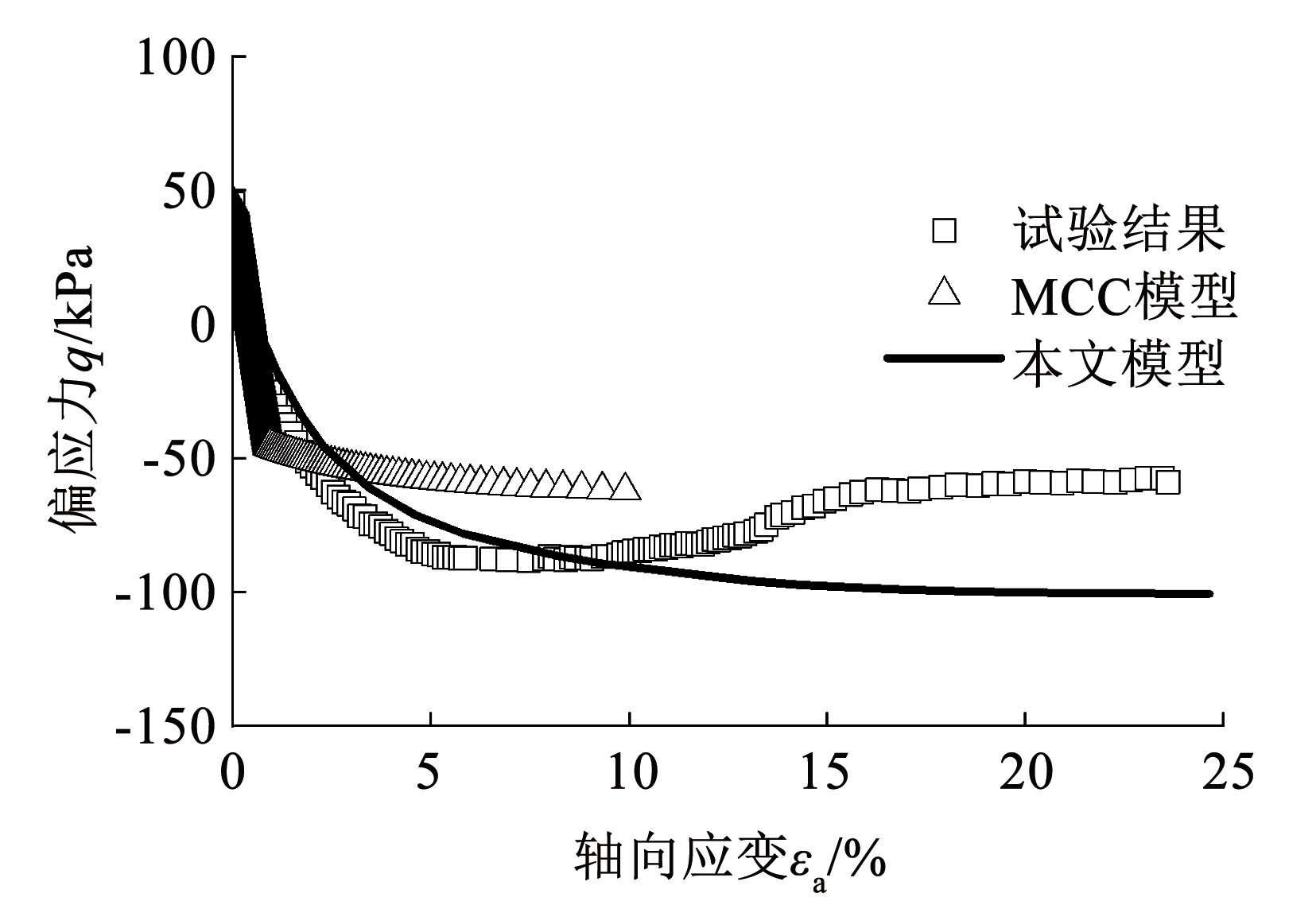
图16TED-∞ 应力路径三轴试验结果对比

Fig.16Comparison of results of TED-∞ stress path triaxial tests

由图10、12~16 的本文模型与 MCC 模型和试验结果对比可见，本文模型计算结果与 MCC 模型的结果存在较大差异，分析可知，由于 MCC 模型仅反映了基本的重塑土压缩和强度特性，而本文模型在 MCC 模型基础上考虑了结构性对刚度的提高作用，减小了相同应力下的土体变形; 此外，本文模型在 MCC 模型基础上反映了结构性和胶结特性对土体强度的提高作用，因此本文模型应力-应变曲线的屈服强度大大高于 MCC 模型的屈服强度。最后，本文模型计算的结果曲线与试验结果仍有一定偏差，这是由于原状土在取样运输及试验过程中造成的扰动损伤导致的，后续将采取措施进行修正。

图17土样取自连云港沿海地区，土样为海积相软土，为灰-灰绿色流塑淤泥及淤泥质黏土，属于高液限黏性土，具有较强的结构性。连云港软土的基本物理学指标及结构性和各向异性参数见表3。

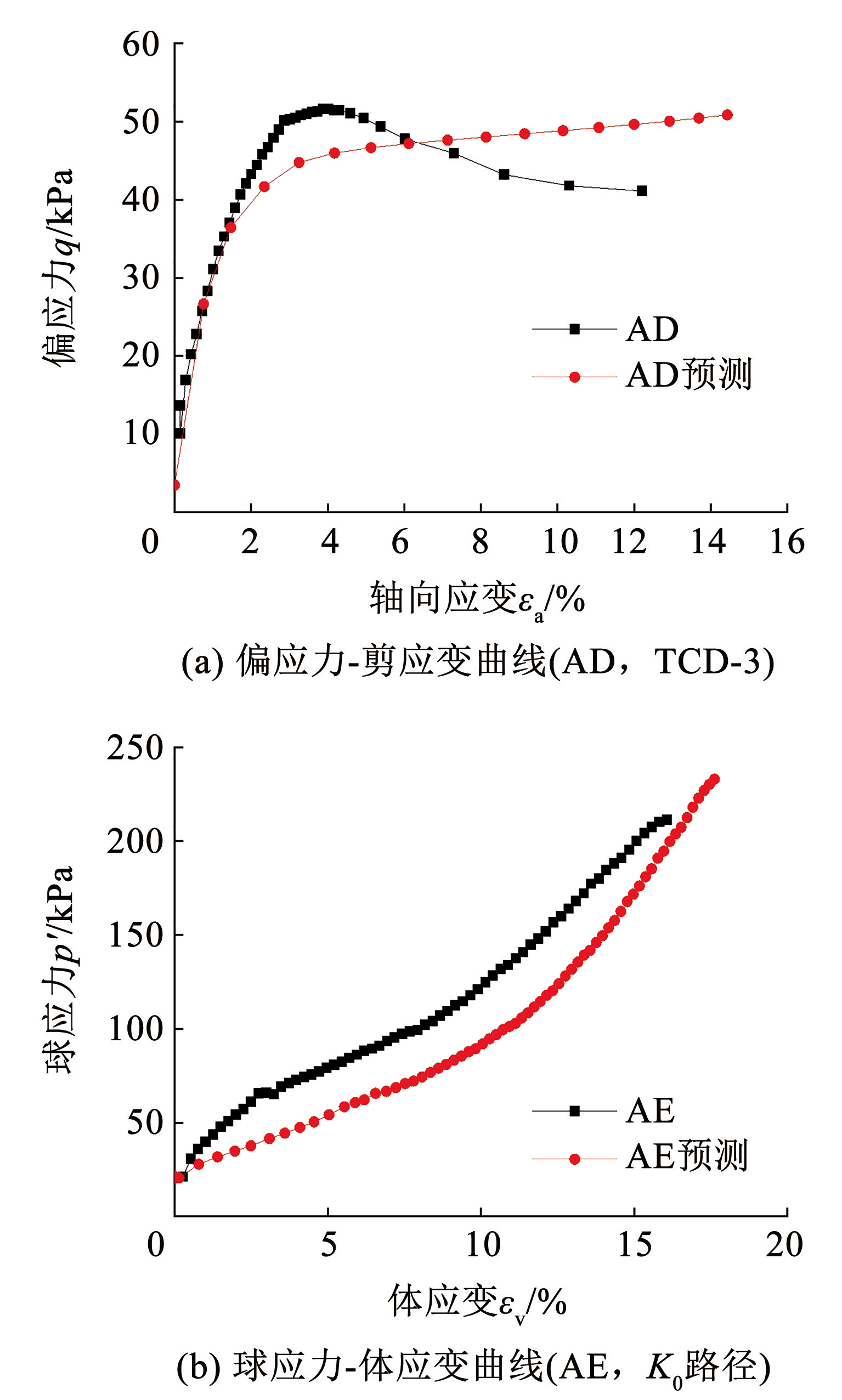
图17连云港软土应力路径试验结果对比

Fig.17Comparison between stress path test data for Lianyungang soft soils

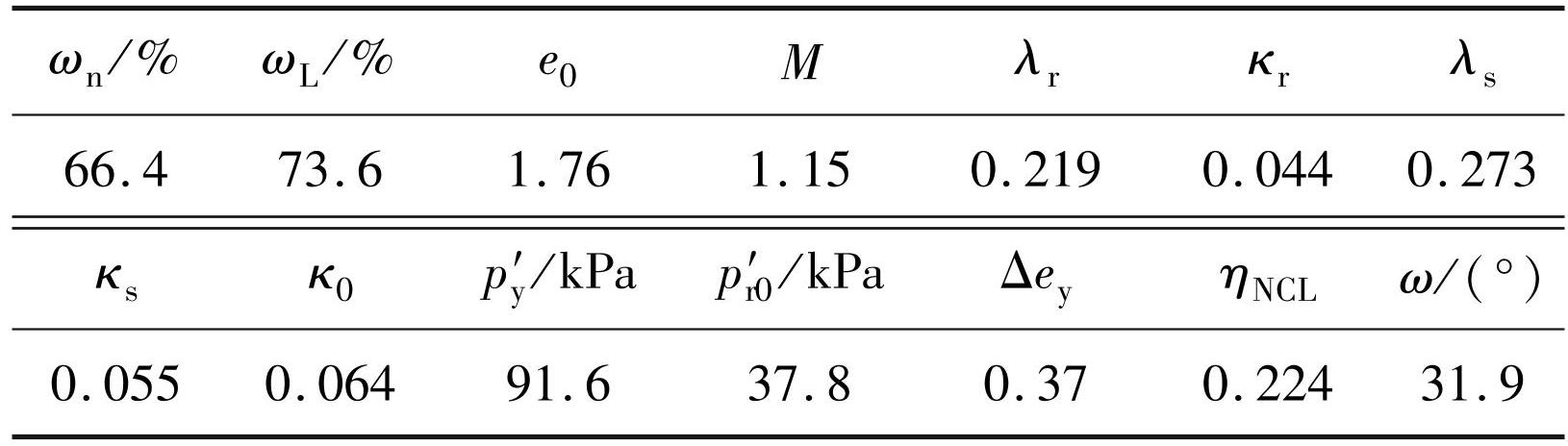
表3连云港软土物理力学指标、结构性和各向异性参数

Tab.3 Physical and mechanical, structural and anisotropic parameters of soft soil in Lianyungang

连云港天然软土应力路径试验的应力-应变曲线^[35]如图17所示（ TCD-3、K₀ 路径）。在轴向加载 TCD-3 路径下（图17（a）），土体的试验应力-应变曲线表现为先上升后下降的应变软化特征，与本构模型的预测结果在加载初期较为一致，后期由于试样出现应变软化现象导致应力-应变曲线下降，因此试验结果与本构模型的预测结果有一定差异，但后期二者的应力-应变曲线发展趋势及偏应力大小大致接近。在 K₀应力路径下（图17（b）），原状软土在体应变达到 3% 时发生屈服，之后土体刚度下降，相同应力增量下土体体应变速率增大，可知本文模型预测的球应力-体应变曲线趋势与试验结果大体相同。

图18土样取自天津滨海新区某地，为海积相软黏土，属于低液限黏土，土样灵敏度为 4.2，属中等灵敏度土。天津软土的基本物理力学指标及结构性和各向异性参数见表4。

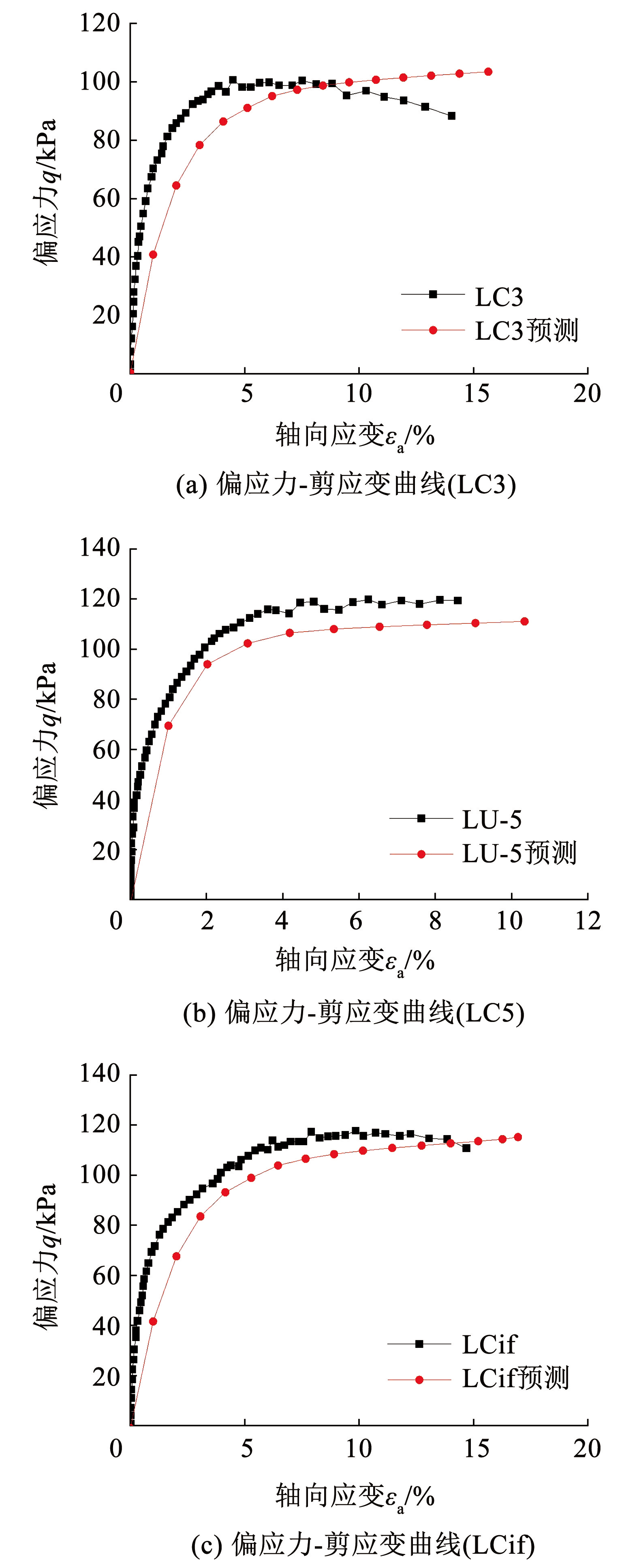
图18天津软土应力路径试验结果对比

Fig.18Comparison between stress path test data for Tianjin soft soils

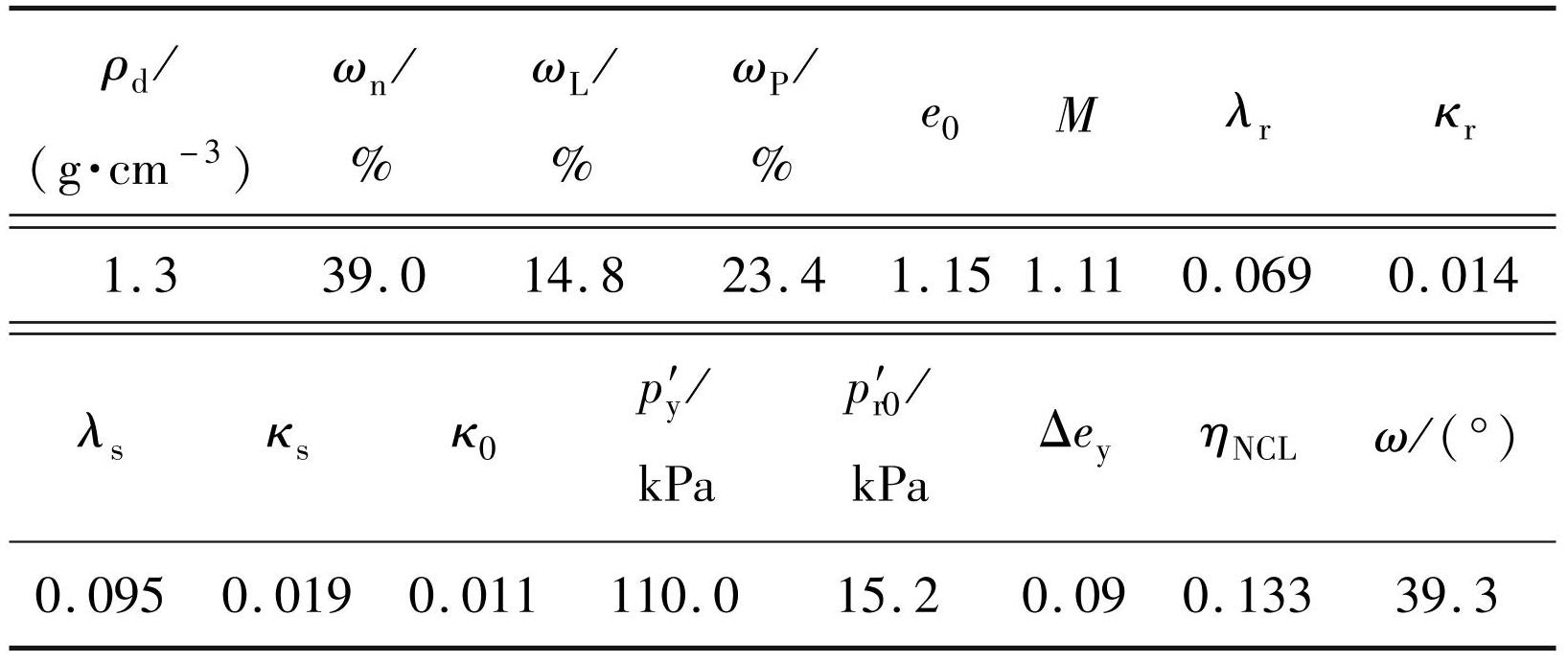
表4天津软土物理力学指标、结构性和各向异性参数

Tab.4 Physical and mechanical, structural and anisotropic parameters of soft soil in Tianjin

天津软土在不同应力路径下的试验结果及模型预测结果^[36]如图18所示（LC 为轴向加载路径，LC3、 LC5、LCif 相应于本文试验的 TCD3、TCD5、TCD∞），可见本文模型对天津软土应力-应变曲线的预测与试验结果大体相同，能够反映天津软土在屈服后应力-应变曲线发展趋于稳定的典型软土特征。

上述结果表明，本文提出的本构模型能够反映结构性对压缩条件下土体刚度的提高以及土的非线性压缩特性。对于不同应力路径下土体的应力-应变特性，本文模型能够反映结构性对土体强度的提高作用，以及结构屈服前后胶结强度逐渐丧失的过程，同时本文模型对轴向加载路径和轴向卸载路径下土体应力应变特性的预测结果与试验结果较为吻合，表明本文模型能够反映不同应力路径下土体的应力应变特性，以及胶结强度对土体抗拉强度的提高作用，证明了本文模型的合理性和有效性。

4 结论

基于湿地湖泊相黏土的结构特征及胶结特性，考虑了结构性和初始各向异性对土体应力应变特性的影响，引入本文提出的胶结强度演化方程建立了湿地湖泊相黏土的胶结结构性和各向异性本构模型，结合室内试验结果进行了模型验证及参数敏感性分析，得到以下主要结论:

1）基于等向压缩和三轴剪切条件下土体胶结强度的变化规律，提出了能够反映压缩、剪切及压缩和剪切共同影响的胶结强度演化规律，并引入到所建立的本构模型中。

2）在修正剑桥模型理论框架下，引入了考虑胶结强度演化、体积应变硬化和剪切应变硬化影响的改进硬化规律，通过对 p′-q 平面进行坐标变换及引入各向异性参数来考虑 K₀固结导致的初始各向异性，建立了湿地湖泊相黏土的胶结结构性和各向异性本构模型。

3）通过一维压缩试验和 K₀固结应力路径试验的验证，表明本文提出的模型能够反映结构性对土体刚度的提高作用和结构性土的非线性压缩特性，能够反映不同应力路径下结构性对土体强度的提高作用，以及加载过程中胶结强度的渐进破损，同时能够反映在轴向卸载路径中胶结强度对土体抗拉强度的提高作用。

4）模型参数的敏感性分析表明，参数 p′_y会改变土体压缩曲线转折时的固结应力，但对结构屈服前后压缩曲线的斜率影响不大; 胶结强度演化参数 k 仅在土体结构屈服前发挥作用，k 的取值越小土体的偏应力 q 越高; 初始胶结强度 p′_r0越高，土体在结构屈服前的强度越大，在土体结构屈服破坏后初始胶结强度 p′_r0对土体的影响消失。

图1湿地湖泊相黏土双对数压缩曲线^[29]

Fig.1Double logarithmic consolidation compression curve of marshy-lacustrine clays

下载: 全尺寸图片

图2湿地湖泊相黏土结构屈服破坏前后微观结构变化^[28]

Fig.2Microstructure for marshy-lacustrine clays before and after structural yield

下载: 全尺寸图片

图3不同塑性剪切应变下土体的临界状态线

Fig.3Critical state lines under different plastic shear strains

下载: 全尺寸图片

图4塑性剪切应变与胶结强度关系

Fig.4Relationship between plastic shear strains and bonding strength

下载: 全尺寸图片

图5土的结构屈服面与胶结强度的演化过程

Fig.5Evolutions of structured yield surface and bonding strength for soils

下载: 全尺寸图片

图6湿地湖泊相黏土胶结结构性和各向异性屈服面

Fig.6Diagram of structured and anisotropic yield surface considering bonding of marshy-lacustrine clay

下载: 全尺寸图片

图7p′_y对一维压缩特性的影响

Fig.7Influences of p′_y on one-dimensional compressive characteristics of marshy-lacustrine clay

下载: 全尺寸图片

图8k 对 TCD3 应力路径下应力-应变曲线的影响

Fig.8Influences of k on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

下载: 全尺寸图片

图9p′_r0对 TCD3 应力路径下应力-应变曲线的影响

Fig.9Influences of p′_r0 on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

下载: 全尺寸图片

图10一维固结压缩试验结果对比

Fig.10Comparison of results for one-dimensional consolidation tests

下载: 全尺寸图片

图11应力路径试验方案示意

Fig.11Schematic diagram of scheme of stress path tests

下载: 全尺寸图片

图12TCD3 应力路径三轴试验结果对比

Fig.12Comparison of results of TCD3 stress path triaxial tests

下载: 全尺寸图片

图13TCD-3 应力路径三轴试验结果对比

Fig.13Comparison of results of TCD-3 stress path triaxial tests

下载: 全尺寸图片

图14TCD∞ 应力路径三轴试验结果对比

Fig.14Comparison of results of TCD∞ stress path triaxial tests

下载: 全尺寸图片

图15TED-3 应力路径三轴试验结果对比

Fig.15Comparison of results of TED-3 stress path triaxial tests

下载: 全尺寸图片

图16TED-∞ 应力路径三轴试验结果对比

Fig.16Comparison of results of TED-∞ stress path triaxial tests

下载: 全尺寸图片

图17连云港软土应力路径试验结果对比

Fig.17Comparison between stress path test data for Lianyungang soft soils

下载: 全尺寸图片

图18天津软土应力路径试验结果对比

Fig.18Comparison between stress path test data for Tianjin soft soils

下载: 全尺寸图片

表1湿地湖泊相黏土的物理力学指标^[28]

下载: 全尺寸图片

表2模拟预测所需的土体模型参数

下载: 全尺寸图片

表3连云港软土物理力学指标、结构性和各向异性参数

下载: 全尺寸图片

表4天津软土物理力学指标、结构性和各向异性参数

下载: 全尺寸图片

图1湿地湖泊相黏土双对数压缩曲线^[29]

Fig.1Double logarithmic consolidation compression curve of marshy-lacustrine clays

图2湿地湖泊相黏土结构屈服破坏前后微观结构变化^[28]

Fig.2Microstructure for marshy-lacustrine clays before and after structural yield

图3不同塑性剪切应变下土体的临界状态线

Fig.3Critical state lines under different plastic shear strains

图4塑性剪切应变与胶结强度关系

Fig.4Relationship between plastic shear strains and bonding strength

图5土的结构屈服面与胶结强度的演化过程

Fig.5Evolutions of structured yield surface and bonding strength for soils

图6湿地湖泊相黏土胶结结构性和各向异性屈服面

Fig.6Diagram of structured and anisotropic yield surface considering bonding of marshy-lacustrine clay

图7p′_y对一维压缩特性的影响

Fig.7Influences of p′_y on one-dimensional compressive characteristics of marshy-lacustrine clay

图8k 对 TCD3 应力路径下应力-应变曲线的影响

Fig.8Influences of k on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

图9p′_r0对 TCD3 应力路径下应力-应变曲线的影响

Fig.9Influences of p′_r0 on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

图10一维固结压缩试验结果对比

Fig.10Comparison of results for one-dimensional consolidation tests

图11应力路径试验方案示意

Fig.11Schematic diagram of scheme of stress path tests

图12TCD3 应力路径三轴试验结果对比

Fig.12Comparison of results of TCD3 stress path triaxial tests

图13TCD-3 应力路径三轴试验结果对比

Fig.13Comparison of results of TCD-3 stress path triaxial tests

图14TCD∞ 应力路径三轴试验结果对比

Fig.14Comparison of results of TCD∞ stress path triaxial tests

图15TED-3 应力路径三轴试验结果对比

Fig.15Comparison of results of TED-3 stress path triaxial tests

图16TED-∞ 应力路径三轴试验结果对比

Fig.16Comparison of results of TED-∞ stress path triaxial tests

图17连云港软土应力路径试验结果对比

Fig.17Comparison between stress path test data for Lianyungang soft soils

图18天津软土应力路径试验结果对比

Fig.18Comparison between stress path test data for Tianjin soft soils

表1湿地湖泊相黏土的物理力学指标^[28]

表2模拟预测所需的土体模型参数

表3连云港软土物理力学指标、结构性和各向异性参数

表4天津软土物理力学指标、结构性和各向异性参数

图1湿地湖泊相黏土双对数压缩曲线^[29]

Fig.1Double logarithmic consolidation compression curve of marshy-lacustrine clays

图2湿地湖泊相黏土结构屈服破坏前后微观结构变化^[28]

Fig.2Microstructure for marshy-lacustrine clays before and after structural yield

图3不同塑性剪切应变下土体的临界状态线

Fig.3Critical state lines under different plastic shear strains

图4塑性剪切应变与胶结强度关系

Fig.4Relationship between plastic shear strains and bonding strength

图5土的结构屈服面与胶结强度的演化过程

Fig.5Evolutions of structured yield surface and bonding strength for soils

图6湿地湖泊相黏土胶结结构性和各向异性屈服面

Fig.6Diagram of structured and anisotropic yield surface considering bonding of marshy-lacustrine clay

图7p′_y对一维压缩特性的影响

Fig.7Influences of p′_y on one-dimensional compressive characteristics of marshy-lacustrine clay

图8k 对 TCD3 应力路径下应力-应变曲线的影响

Fig.8Influences of k on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

图9p′_r0对 TCD3 应力路径下应力-应变曲线的影响

Fig.9Influences of p′_r0 on stress-strain curves of marshy-lacustrine clay on TCD3 stress path

图10一维固结压缩试验结果对比

Fig.10Comparison of results for one-dimensional consolidation tests

图11应力路径试验方案示意

Fig.11Schematic diagram of scheme of stress path tests

图12TCD3 应力路径三轴试验结果对比

Fig.12Comparison of results of TCD3 stress path triaxial tests

图13TCD-3 应力路径三轴试验结果对比

Fig.13Comparison of results of TCD-3 stress path triaxial tests

图14TCD∞ 应力路径三轴试验结果对比

Fig.14Comparison of results of TCD∞ stress path triaxial tests

图15TED-3 应力路径三轴试验结果对比

Fig.15Comparison of results of TED-3 stress path triaxial tests

图16TED-∞ 应力路径三轴试验结果对比

Fig.16Comparison of results of TED-∞ stress path triaxial tests

图17连云港软土应力路径试验结果对比

Fig.17Comparison between stress path test data for Lianyungang soft soils

图18天津软土应力路径试验结果对比

Fig.18Comparison between stress path test data for Tianjin soft soils

表1湿地湖泊相黏土的物理力学指标^[28]

表2模拟预测所需的土体模型参数

表3连云港软土物理力学指标、结构性和各向异性参数

表4天津软土物理力学指标、结构性和各向异性参数

许凤娇, 周德民, 张翼然, 等. 中国湖泊、沼泽湿地的空间分布特征及其变化[J]. 生态学杂志,2014,33(6):1606.XU Fengjiao, ZHOU Demin, ZHANG Yiran,et al. Spatial distribution and dynamics of lake and marsh wetlands in China[J]. Chinese Journal of Ecology,2014,33(6):1606. DOI:10.13292/j.1000-4890.20140327.015

刘春原, 王向会. 衡水湖湿地湖泊相软土研究[M]. 北京: 人民交通出版社,2016. LIU Chunyuan, WANG Xianghui. Study on marshy and lacustrine soft soil in Hengshui Lake[M]. Beijing: China Communications Press,2016

沈珠江. 土体结构性的数学模型———21 世纪土力学的核心问题[J]. 岩土工程学报,1996,18(1):95. SHEN Zhujiang. Mathematical model for soil structure———the core topic of soil mechanics in the 21st century[J]. Chinese Journal of Geotechnical Engineering,1996,18(1):95

VATSALA A, NOVA R, MURTHY B R S. Elastoplastic model for cemented soils[J]. Journal of Geotechnical and Geoenvironmental Engineering,2001,127(8):679. DOI:10.1061/(asce)1090-0241(2001)127:8(679)

BAUDET B A, STALLEBRASS S E. A constitutive model for structured clays[J]. Géotechnique,2004,54(4):269. DOI:10.1680/geot.2004.54.4.269

ZHU E Y, YAO Y P. Structured UH model for clay[J]. Transportation Geotechnics,2015,3:68. DOI:10.1016/j.trgeo.2015.03.003

ROUNANIA M, WOOD D M. A kinematic hardening constitutive model for natural clays with loss of structure[J]. Geotechnique,2000,50(2):153. DOI:10.1680/geot.2000.50.2.153

ASAOKA A, NAKANO M, NODA T. Superloading yield surface concept for highly structured soil behavior[J]. Soils and Foundations,2000,40(2):99. DOI:10.3208/sandf.40.2_99

NAKANO M, NAKAI K, NODA T,et al. Simulation of shear and one-dimentional compression behahior of naturally deposited clays by super/subloading yield surface Cam-clay model[J]. Soil and Foundations,2005,45(1):141. DOI:10.1016/j.soildyn.2004.08.005

王立忠, 沈恺伦. K₀ 固结结构性软黏土的本构模型[J]. 岩土工程学报,2007,29(4):496. WANG Lizhong, SHEN Kailun. A constitutive model of K₀ consolided structured soft clays[J]. Chinese Journal of Geotechnical Engineering,2007,29(4):496

LIU M D, CARTER J P. A structured cam clay model[J]. Canadian Geotechnical Journal,2002,39:1313. DOI:10.1139/T02-069

李吴刚, 杨庆, 刘文化, 等. 黏土的结构性定量化表征及其弹塑性本构模型研究[J]. 岩土工程学报,2022,44(4):678.LI Wugang, YANG Qing, LIU Wenhua,et al. Structured quantitative characterization and elastoplastic constitutive model of clay[J]. Chinese Journal of Geotechnical Engineering,2022,44(4):678. DOI:10.11779/CJGE202204010

沈珠江. 结构性粘土的弹塑性损伤模型[J]. 岩土工程学报,1993,15(3):21. SHEN Zhujiang. An elastoplastic damage model for cemented clays[J]. Chinese Journal of Geotechnical Engineering,1993,15(3):21

沈珠江. 结构性粘土的堆砌体模型[J]. 岩土力学,2000,21(1):1. SHEN Zhujiang. A masonry model for structured clays[J]. Rock and Soil Mechanics,2000,21(1):1

沈珠江. 岩土破损力学: 理想脆弹塑性模型[J]. 岩土工程学报,2003,25(3):253. SHEN Zhujiang. Breakage mechanics for geological materials:an ideal brittle-elasto-plastic model[J]. Chinese Journal of Geotechnical Engineering,2003,25(3):253

刘恩龙, 沈珠江. 结构性土的二元介质模型[J]. 水利学报,2005,36(4):391. LIU Enlong, SHEN Zhujiang. Binary medium model for structured Soils[J]. Journal of Hydraulic Engineering,2005,36(4):391

WHEELER S J, NAATANEN A, KARSTUNEN M,et al. An anisotropic elastoplastic model for soft clays[J]. Canadian Geotechnical Journal,2003,40(2):403. DOI:10.1139/T02-119

魏星, 黄茂松. 天然结构性黏土的各向异性边界面模型[J]. 岩土工程学报,2007,29(8):1225. WEI Xing, HUANG Maosong. Anisotropic bounding surface model for natural structured clays[J]. Chinese Journal of Geotechnical Engineering,2007,29(8):1225

于亚磊, 叶冠林, 熊永林. 上海第4层黏土力学特性的弹塑性本构模拟[J]. 岩土力学,2016,37(9):2541.YU Yalei, YE Guanlin, XIONG Weilin. Elastoplastic constitutive modelling for mechanical behavior of Shanghai 4th layer clay[J]. Rock and Soil Mechanics,2016,37(9):2541. DOI:10.16285/j.rsm.2016.09.014

SUEBSUK J, HORPIBULSUK S, LIU M D. Modified structured cam clay:a generalized critical state model for destructured,naturally structured and artificially structured clays[J]. Computers and Geotechnics,2010,37:956. DOI:10.1016/j.compgeo.2010.08.002

HORPIBULSUK S, LIU M D. Structured cam clay model with cementation effect[J]. Geotechnical Engineering: Journal of Southeast Asian Geotechnical Society,2015,46(1):86

陈波, 孙德安, 金盼. 海相沉积软黏土的弹塑性本构模型研究[J]. 岩土力学,2015,36(3):730.CHEN Bo, SUN Dean, JIN Pan. An elastoplastic constitutive model for marine sedimentary soft clays[J]. Rock and Soil Mechanics,2015,36(3):730. DOI:10.11779/CJGE201712019

孙凯, 陈正林, 路德春. 一种考虑黏聚强度的改良土弹塑性本构模型[J]. 岩土力学,2018,39(5):1589.SUN Kai, CHEN Zhenglin, LU Dechun. An elastoplastic constitutive model incorporating cementation effect of stabilizertreated soils[J]. Rock and Soil Mechanics,2018,39(5):1589. DOI:10.16285/j.rsm.2016.1486

万征, 秋仁东, 宋琛琛. 基于统一硬化参量的原状饱和黏土的结构性本构模型[J]. 岩石力学与工程学报,2019,38(9):1905.WAN Zheng, QIU Rendong, SONG Chenchen. A structural constitutive model of undisturbed saturated clays based on the uniform hardening parameter[J]. Chinese Journal of Rock Mechanics and Engineering,2019,38(9):1905. DOI:10.13722/j.cnki.jrme.2018.1356

万征, 孟达, 宋琛琛, 等. 状态变量相关三维饱和黏土结构性本构模型[J]. 岩石力学与工程学报,2020,39(4):817.WAN Zheng, MENG Da, SONG Chenchen,et al. A threedimensional structural constitutive model of saturated clays related to state variables[J]. Chinese Journal of Rock Mechanics and Engineering,2020,39(4):817. DOI:10.13722/j.cnki.jrme.2019.0729

刘鹏, 丁文其. 双对数压缩曲线在海积软土本构中的应用[J]. 上海交通大学学报,2016,50(11):1706.LIU Peng, DING Wenqi. Application of bi-logarithmic compression curves in modelling of marine soft soil[J]. Journal of Shanghai Jiao Tong University,2016,50(11):1706. DOI:10.16183/j.cnki.jsjtu.2016.11.008

祝恩阳, 李晓强. 胶结结构性土统一硬化模型[J]. 岩土力学,2018,39(1):112.ZHU Enyang, LI Xiaoqiang. A unified hardening model considering bonding in structured soils[J]. Rock and Soil Mechanics,2018,39(1):112. DOI:10.16285/j.rsm.2017.0482

朱楠, 张静娟, 刘春原. 湿地湖泊相黏土应力-应变及屈服特性试验[J]. 哈尔滨工业大学学报,2020,52(11):183.ZHU Nan, ZHANG Jingjuan, LIU Chunyuan. Experimental study on stress-strain behavior and yield characteristics of marshy and lacustrine clay[J]. Journal of Harbin Institute of Technology,2020,52(11):183. DOI:10.11918/201905190

朱楠, 刘春原, 赵献辉, 等. 湿地湖泊相黏土一维固结压缩特性宏微观试验研究[J]. 长江科学院院报,2020,37(2):1.ZHU Nan, LIU Chunyuan, ZHAO Xianhui,et al. Macroscopic and microscopic experimental research on one-dimensional consolidation compressibility of marshy-lacustrine clay[J]. Journal of Yangtze River Scientific Research Institute,2020,37(2):1. DOI:10.11988/ckyyb.20181023

BUTTERFIELD R. A natural compression law for soils[J]. Géotechnique,1979,29(4):469. DOI:10.1680/geot.1979.29.4.469

张先伟, 孔令伟, 郭爱国, 等. 基于SEM和 MIP 试验结构性黏土压缩过程中微观孔隙的变化规律[J]. 岩石力学与工程学报,2012,31(2):406.ZHANG Xianwei, KONG Lingwei, GUO Aiguo. Evolution of microscopic pore of structured clay in compression process based on SEM and MIP test[J]. Chinese Journal of Rock Mechanics and Engineering,2012,31(2):406. DOI:10.3969/j.issn.1000-6915.2012.02.021

COLLINS I F, MUHUNTHAN B. On the relationship between stress-dilatancy,anisotropy,and plastic dissipation for granular materials[J]. Géotechnique,2003,53(7):611. DOI:10.1680/geot.2003.53.7.611

魏汝龙. 正常压密黏土的本构定律[J]. 岩土工程学报,1981,3(3):10. WEI Rulong. Constitutivelaws for normally consolidated clay[J]. Chinese Journal of Geotechnical Engineering,1981,3(3):10

殷杰. 结构性软黏土的修正剑桥模型[J]. 工程力学,2013,30(1):190.YIN Jie. A modified cam clay model for structured soft clays[J]. Engineering Mechanics,2013,30(1):190. DOI:10.6052/j.issn.1000-4750.2011.05.0318

殷杰, 洪振舜, 高玉峰. 天然沉积连云港软黏土的屈服特性[J]. 东南大学学报(自然科学版),2009,39(5):1059.YIN Jie, HONG Zhenshun, GAO Yufeng. Yielding characteristics of natural soft Lianyungang clay[J]. Journal of Southeast University(Natural Science Edition),2009,39(5):1059. DOI:10.3969/j.issn.1001-0505.2009.05.038

熊春发, 孔令伟, 杨爱武. 加荷模式对海积软黏土结构损伤性状的影响分析[J]. 岩土力学,2014,35(7):1892.XIONG Chunfa, KONG Lingwei, YANG Aiwu. Analysis of influence of loading mode on character of structural damage of marine soft clay[J]. Rock and Soil Mechanics,2014,35(7):1892. DOI:10.16285/j.rsm.2014.07.034

1 湿地湖泊相黏土的结构特征及胶结特性

2 胶结结构性和各向异性本构模型

3 本构模型的验证及参数分析

4 结论

友情链接LINKS