欢迎访问《哈尔滨工业大学学报》编辑部网站！

MEMS电热驱动器多场耦合模型及温度特性

doi: 10.11918/202405056

谢海鹏，曹云，孔啸宇，朱恒伯，陈旺生，席占稳

南京理工大学机械工程学院，南京 210094

基金项目: 国家自然科学基金（52475062）

详细信息

作者简介

谢海鹏(2000—)，男，硕士研究生；

席占稳(1963—)，男，研究员，博士生导师

通讯作者

曹云，cy1990@njust.edu.cn

中图分类号: TH122

文献标识码: A

文章编号: 0367-6234(2025)04-0142-09

Multi-field coupling model and temperature characteristics of MEMS electrothermal actuators

XIE Haipeng ， CAO Yun ， KONG Xiaoyu ， ZHU Hengbo ， CHEN Wangsheng ， XI Zhanwen

School of Mechanical Engineering, Nanjing University of Science and Technology, Nanjing 210094 , China

摘要

为研究微小尺度下MEMS电热驱动器的温度特性，考虑空气对驱动器动态热平衡的影响，提出了一种基于空气对流传热的电-热-流-固多场耦合模型。根据能量守恒方程以及气体对流换热和热传导等理论，建立MEMS电热驱动器的电-热-流-固多场耦合模型，并进行了有限元仿真。搭建MEMS电热驱动器温度特性试验平台，将恒定电压激励下的驱动器温度响应试验结果与电-热-流-固多场耦合模型以及传统传热模型仿真结果进行对比分析，结果表明：相较于基于恒定对流换热系数及经验公式的模型，采用电-热-流-固多场耦合模型得到的结果准确性更高，稳态温度分布误差在0.8%~7.6%之间；驱动器各表面的对流换热系数分布不均匀；对流换热系数在上表面、下表面及竖直壁面分别呈现先下降后上升、上升以及先上升后下降的趋势，但在3个特征面上对流换热系数几乎同时达到稳态，此时驱动器温度也达到稳态。基于空气对流换热不均匀特性，所获得的电热驱动器温度特性为MEMS电热驱动器在微机电系统中的应用奠定了基础。

关键词

电热驱动器 / 温度特性 / 对流换热 / 电-热-流-固 / 微机电系统（MEMS）

Abstract

To study the temperature characteristics of MEMS electrothermal actuators at micro-scale, taking into account the influence of air on the dynamic heat balance of the actuator, an electrical-thermal-fluid-solid coupled multi-field model based on air convective heat transfer is proposed. This model is based on the principles of energy conservation along with theories of gas convection and heat conduction. Finite element simulations are conducted to analyze the model. An experimental platform for temperature characterization of MEMS electrothermal actuator is established, and the experimental results of the temperature response of the actuator under constant voltage excitation are compared and analyzed against the simulation results from both the electric-thermal-fluid-solid coupling model and the traditional heat transfer model. The results indicate that compared with the model based on the constant convective heat transfer coefficient and empirical equations, the electric-thermal-fluid-solid coupling model achieves higher accuracy, with the steady-state temperature distribution error ranging between 0.8% and 7.6%. Additionally, the convective heat transfer coefficient varies across different surfaces of the actuator. Specifically it decreases then increases on the upper surface, increases steadily on the lower surface, and increases then decreases on the vertical walls. Despite these variations, the convective heat transfer coefficients on all three characteristic surfaces reach the steady-state almost simultaneously, coinciding with the actuator’s temperature reaching steady state. These findings, based on the uneven characteristics of air convective heat transfer, the obtained temperature characteristics of the electrothermal actuator provide a foundation for the application of MEMS electrothermal actuators in microelectromechanical systems.

Keywords

electrothermal actuator / temperature characterization / convective heat transfer / electro-thermal-fluid-solid / micro-electro-mechanical system (MEMS)

1 V型电热驱动器的多场耦合模型 1.1 MEMS电热驱动器的理论模型 1.1.1 恒定对流换热系数模型及基于经验公式的传热模型 1.1.2 电-热-流-固多场耦合模型 2 MEMS电热驱动器温度特性试验 2.1 红外热成像测量系统 2.2 稳态温度特性 2.3 动态温度特性 2.4 流体场下的对流换热系数分析 3 结论

在微机电系统（micro-electro-mechanical system，MEMS）中，微驱动器承担着将电能转换为可控的机械运动的功能，微驱动器可以分为多种类型，其中包括电热型^[1]、压电型^[2]、静电型^[3]和电磁型^[4]。在多种驱动器之中，电热驱动器因其能够在较低的电压下实现较大的偏转而备受青睐，特别适用于需要在中、低负载下实现较大偏转的应用领域。此外，电热驱动器还具有良好的工艺兼容性、挠度和输出力大等优点，因此被广泛应用于微动开关、微镜^[5]等MEMS器件中。目前，电热驱动器主要分为U型^[6]和V型^[7]驱动器，相比于U型结构，V型电热驱动器的输出力更加稳定，对V型电热驱动器展开研究有助于优化设计^[8]，提高其使用性能。

目前，对微电热驱动器的研究主要集中在建模^[9-10]和应用方面。在微电热驱动器的建模中，最常见的方法是对微电热驱动器解耦建模，分别建立电-热模型和热-力耦合模型。在建立电-热模型时，关键在于如何定义电热驱动器的热边界条件。目前，许多学者针对电热驱动器的传热途径展开研究， Cauchi等^[11]研究表明，在静止空气中运动的电热驱动器，可以合理地忽略驱动器表面的热对流损失。 Ulkir^[12]研究表明，在温度分析中，当驱动器材料的导热系数远大于空气时，可以忽略电热驱动器因对流和辐射损失的热量。Ozsun等^[13]提出并验证了，在微观尺度，且在没有强制对流情况下应将传导作为微电热驱动器实现热平衡的主要方式。但Lin等^[14]研究表明，微电热驱动器不可忽视空气自然对流对温度分布的影响。综上所述，现有针对微电热驱动器的研究在模型构建过程中存在简化或忽略某些关键因素的倾向，如对空气热对流行为的忽略或线性化处理。这些方法未能充分捕捉到空气与微电热驱动器之间的非均匀对流传热特性，从而影响了驱动器温度特性的准确描述。

本文建立了电-热-流-固多场耦合的理论模型，并通过有限元法计算得到了相应的温度响应结果。通过建立实验平台测量静态和动态温度响应特性，将试验数据与理论仿真结果进行了对比分析。结果表明，电-热-流-固多场耦合模型更能准确反映微电热驱动器的实际行为。通过该研究，本文揭示了恒定对流换热系数在实际应用中的不准确性，并指出经验公式在描述微电热驱动器温度特性方面存在局限性。基于电-热-流-固多场耦合模型，进一步地开展了流体作用下，微电热驱动器表面对流换热分析。

1 V型电热驱动器的多场耦合模型

V型电热驱动器是一种以弯曲梁为基础的独特设计，其核心组件包括两个锚点、推杆和横梁，横梁与锚点之间预设角度，驱动器利用横梁的热膨胀弯曲变形实现位移输出。该结构的设计与制造基于成熟的深度反应离子蚀刻（deep reactive ion etching，DRIE）工艺^[15-16]，这使得V型电热驱动器能够以较高的精度和稳定性工作。单个V型电热驱动器的输出力有限，但输出力能够通过增加驱动器数量而实现较为平滑的增长。鉴于此特点，研究中常采用将多个横梁通过推杆连接的方式形成V型阵列电热驱动器。本文聚焦于三横梁V型电热驱动的建模与分析，所选材料是重掺杂单晶硅，结构形式见图1。

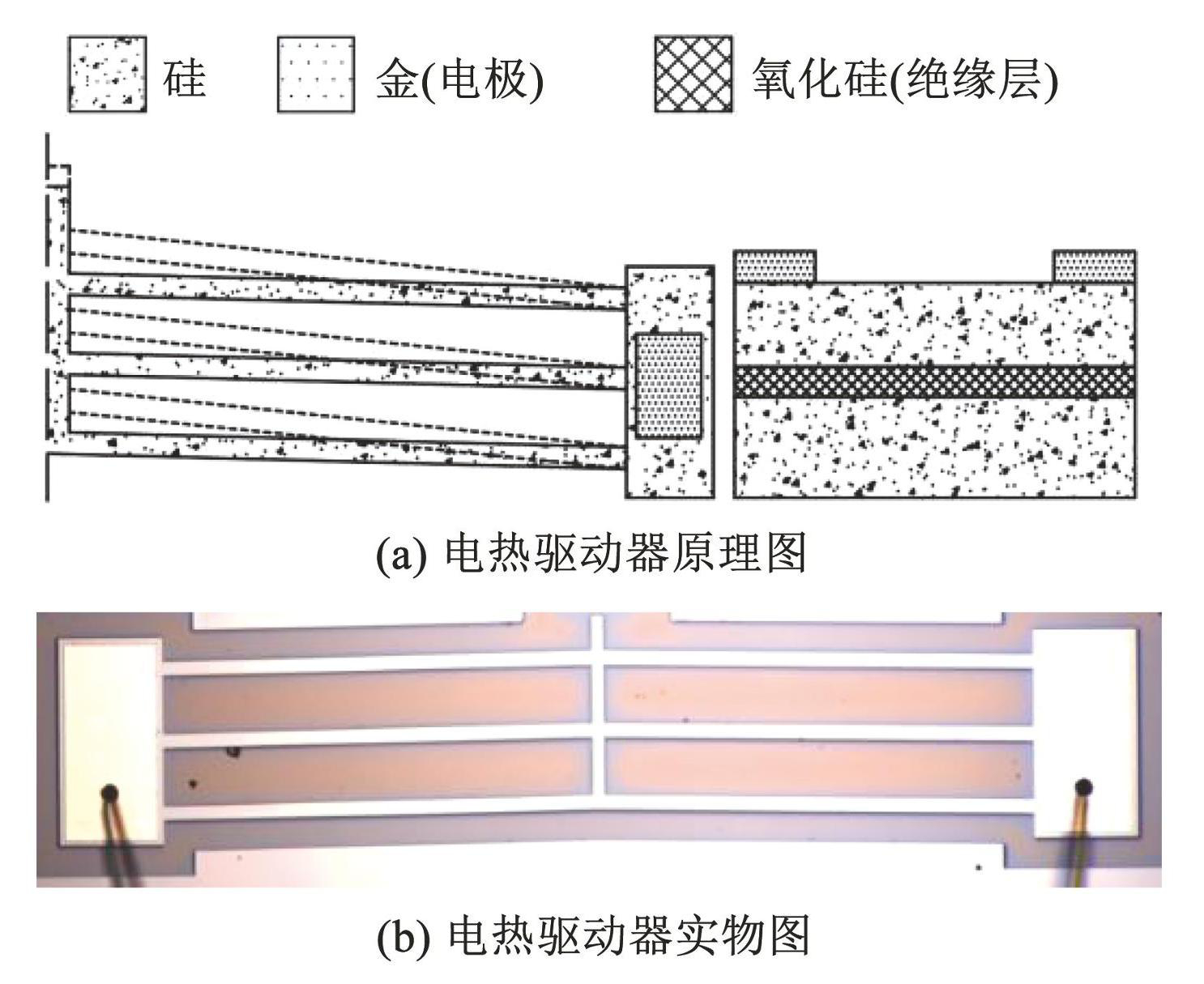
图1V型电热驱动器结构图

Fig.1V-type electrothermal actuator structure

1.1 MEMS电热驱动器的理论模型

微电热驱动器的致动涉及电场、热场、结构场以及流体场等多个物理场的耦合作用^[17]，当施加电压时，通过电流加热微电热驱动器产生热量，从而引发体积膨胀，并最终导致机械形变。在这个过程中，微电热驱动器与锚点、基底之间的热传导以及与周围空气的热对流造成热耗散。现有研究通常假设对流损失的热量遵循定常第3类边界条件，即无论表面温度的空间分布如何，对流系数始终是恒定的。该方法使用的经验对流换热系数往往是从已有试验数据中进行拟合得到的。此方法可能存在以下问题：1）为获取对流换热系数，需要先进行试验收集数据并进行拟合。2）对流换热系数与换热表面的特征长度（如尺寸或形状）紧密相关。不同特征长度下的系数差异显著，宏观尺度下的经验公式可能不完全适合于微尺度^[13]。3）目前微尺度下的自然对流换热研究有限，文献中所提出的经验值并不适用于所有场合。4）空气与微电热驱动器之间的对流换热是不均匀的，将对流系数简化为定值可能会降低所得到的微电热驱动器温度特性结果的准确性。本文首先在恒定对流换热系数模型及基于经验公式的传热模型中分别建立了采用恒定对流换热系数和基于经验公式的传热模型，并针对上述问题，在电-热-流-固多场耦合模型中提出了新的建模方法，即电-热-流-固多场耦合模型。该模型考虑了空气与微电热驱动器之间的不均匀传热过程，将对流损失的热量转换为空气的能量，避免了直接设定对流换热系数的做法。此方法优点在于：1）避免使用经验值进行拟合和设置对流换热系数，从而提高模型预测的准确性。2）提供了研究驱动器对流换热特性的方法，有助于深入了解不同条件下的传热规律。

由于V型电热驱动器阵列在实际应用中显示出了均匀一致的温度分布特性，即每根横梁的温度分布接近，因此将V型电热驱动器阵列的热传导简化为单个V型梁的热传导问题。T_m（x，y，z，t）为驱动器上关于位置（x，y，z）和时间t的温度函数。

根据能量守恒定律，单位时间内微元体内能的增量可表示为

Δ Q = Q_{J} + Q_{Φ} - Q_{air}

(1)

式中：Q_J为微元体产生的焦耳热，Q_Φ为微元体内热传导的净热量，Q_air为微元体与空气热对流产生的热损失。

在某一时间间隔dt产生的热量可表示为

Q_{J} = J^{2} (t) ρ (T) d x d y d z d t

(2)

式中： J（t）为电流密度，由电热驱动器两端激励电压和电阻率共同决定；ρ（T）为单晶硅随温度变化的电阻率。

以微元体x方向为例进行传热分析（见图2），在单位时间内，以热传导的方式流入微元体的热量Q_in和流出微元体的热量Q_out，可以表示为

\{\begin{matrix} Q_{in} = - κ (T) {[\frac{\partial T_{m}}{\partial x}]}_{x} d y d z \\ Q_{out} = - κ (T) {[\frac{\partial T_{m}}{\partial x}]}_{x + d x} d y d z \end{matrix}

(3)

式中：κ（T）为硅的热传导率，是一个随着温度变化的值；T_m为微电热驱动器温度函数T_m（x，y，z，t）的简写形式，由此可得，在dt时间间隔内从x方向进入微元体的净热量可表示为

Δ Φ_{x} d t = \frac{\partial}{\partial x} (κ (T) \frac{\partial T_{m}}{\partial x}) d x d y d z d t

(4)

以此类推可得在dt时间间隔内，微元体y方向和z方向上的净热量可表示为

\{\begin{matrix} Δ Φ_{y} d t = \frac{\partial}{\partial y} (κ (T) \frac{\partial T_{m}}{\partial y}) d x d y d z d t \\ Δ Φ_{z} d t = \frac{\partial}{\partial z} (κ (T) \frac{\partial T_{m}}{\partial z}) d x d y d z d t \end{matrix}

(5)

最终得到通过热传导形式进入微元体的净热量Q_Φ可表示为

Q_{Φ} = κ (T) (\frac{\partial^{2} T_{m}}{\partial x^{2}} + \frac{\partial^{2} T_{m}}{\partial y^{2}} + \frac{\partial^{2} T_{m}}{\partial z^{2}}) d x d y d z d t =

κ (T) \nabla \cdot (\nabla T_{m}) d x d y d z d t

(6)

微元体在dt时间间隔内，内能的增量ΔQ可表示为

Δ Q = ρ_{m} c \frac{\partial T_{m}}{\partial t} d x d y d z d t

(7)

式中： c为单晶硅的比热容，ρ_m为单晶硅的密度。

因此，V型微电热驱动器的瞬态热传导方程可表示为

ρ_{m} c \frac{\partial T_{m}}{\partial t} = J^{2} (t) ρ (T) + κ (T) \nabla \cdot (\nabla T_{m}) d x d y d z d t -

\frac{Q_{air}}{d x d y d z d t}

(8)

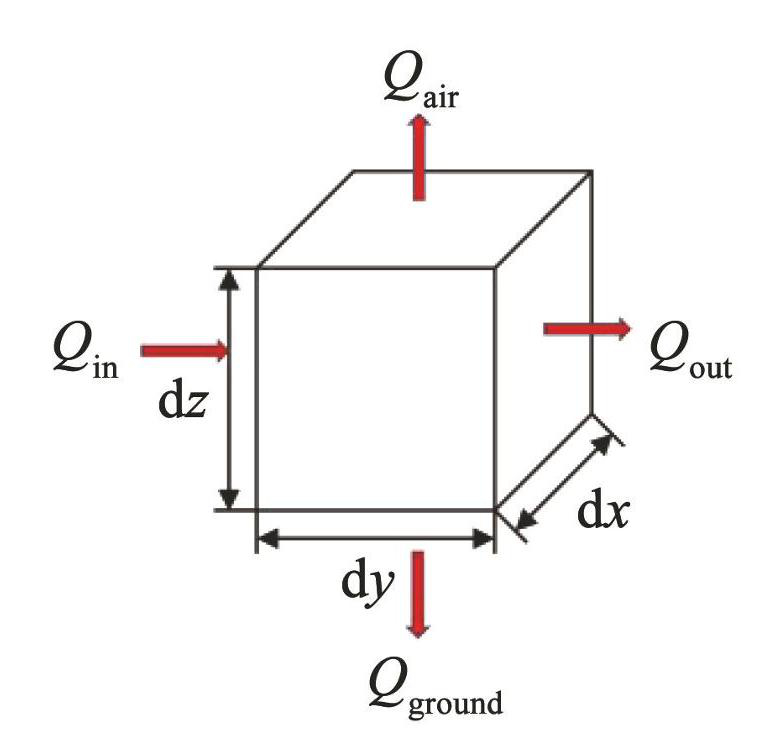
图2微电热驱动器的微元传热示意

Fig.2Heat transfer schematic for micro-electrothermal actuator

1.1.1 恒定对流换热系数模型及基于经验公式的传热模型

对于微电热驱动器与空气之间的对流换热损失，现有研究方法通过设置对流换热系数来模拟微电热驱动器表面的热损失。在建模过程中，考虑微电热驱动器不同表面的热对流损失，其中对流换热损失可以表示为

\{\begin{matrix} Q_{上表面} = κ_{1} (T_{m} - T_{ref}) \frac{d y d z d t}{\cos θ} \\ Q_{下表面} = κ_{2} (T_{m} - T_{ref}) \frac{d x d y d t}{\cos θ} \\ Q_{坚直壁面} = κ_{3} (T_{m} - T_{ref}) \frac{d x d y d t}{\cos θ} \end{matrix}

(9)

式中：κ₁为驱动器上表面的对流换热系数，根据文献设置值为1 350 W/（m²·K）^[14]；κ₂为驱动器下表面的对流换热系数，根据文献设置值为70 W/（m²·K）^[9]，κ₃为驱动器竖直壁面的对流换热系数，根据文献设置值为6 000 W/（m²·K）^[9]。

除了以恒定值设置对流换热系数，部分研究使用对流换热的经验公式代替恒定值。对于大空间下的自然对流，局部表面对流换热系数可以表示为

h = N u \frac{λ}{l}

(10)

式中：Nu为自然对流换热准则关联式，

λ

为空气的传热系数，l为特征长度，电热驱动器的对流换热系数κ₁=h，κ₂=h，κ₃=h。

对于自然对流换热准则关联式Nu^[18]通常采用幂函数形式，表示为

N u = C (G r \cdot P r)^{n} = C R a^{n}

(11)

其中

R a = \frac{g β Δ T H^{3}}{α \cdot ν}

式中：Ra为瑞利数，Gr为格拉晓夫数，C、n为由试验确定的常数，g为重力加速度，β为体积膨胀系数，ΔT为温差，H为特征长度，α为热扩散系数，ν为运动黏度。

针对不同表面的形状和边界条件，需选取不同的系数进行计算，以竖直壁面的对流换热系数为例，竖直壁面对流换热准则关联式为^[18]

N u = {\{0.825 + \frac{0.387 R a_{l_{1}}^{1 / 6}}{{(1 + {(\frac{0.492}{P r})}^{9 / 16})}^{8 / 27}}\}}^{2}, R a < 10^{9}

(12)

综上所述，以对流换热系数建模的电热驱动器瞬态热传导方程可表示为

ρ_{m} c \frac{\partial T_{m}}{\partial t} = J^{2} (t) ρ (T) + κ (T) \nabla \cdot (\nabla T_{m}) d x d y d z d t -

\sum_{i = 1}^{3} κ_{i} \frac{T_{m} - T_{r e f}}{c o s θ d x_{i}}

(13)

初始条件和边界条件为

\{\begin{matrix} T (x, y, z, 0) = T_{ref} \\ T (x, y, z, t) = T_{ref}, y = 0 \\ T (x, y, z, t) = T_{ref}, y = 2 L \end{matrix}

(14)

1.1.2 电-热-流-固多场耦合模型

为提高在流体场下微电热驱动器温度解的准确性，本文针对驱动器所处的流体场进行建模。针对流体，T_a（x，y，z，t）表示流体场内关于空气位置（x，y，z）和时间t的温度表达式，取流体微元进行研究。

微电热驱动器因对流换热损失的热量转换为流体的能量，因此求解流体能量的变化即可得到电热驱动器的热损失。单位质量的微元体总能量包括动能和内能，在单位时间内微元体的总能变化率可表示为^[19]

\frac{\partial (ρ E)}{\partial t} = \frac{\partial}{\partial t} [ρ (e + \frac{1}{2} V^{2})] d x d y d z

(15)

式中ρ为气体密度。

不考虑微元体的辐射换热，通过扩散作用进入微元体的净热流量可以表示为^[19]

Δ Φ_{λ} = - [\frac{\partial}{\partial x} (λ \frac{\partial T_{a}}{\partial x}) + \frac{\partial}{\partial y} (λ \frac{\partial T_{a}}{\partial y}) + \frac{\partial}{\partial z} (λ \frac{\partial T_{a}}{\partial z})] d x d y d z =

- \nabla \cdot (λ \nabla T_{a}) d x d y d z d t

(16)

式中λ为空气的传热系数。

在流体的宏观运动中，气体间通过对流的方式传递的能量可以表示为

- \sum_{i = 1}^{3} \frac{\partial (ρ E u_{i})}{\partial x_{i}} d x d y d z

(17)

流体表面力和体积力对流体做功表现为微元体内动能变化、体积变形时压力p所做的功以及气体流动因摩擦产生的黏性耗散，因此表面力和体积力的做功可以表示为

[ρ \frac{d}{d t} (\frac{1}{2} V^{2}) + \dot{Φ} - p (\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} + \frac{\partial w}{\partial z})] d x d y d z

(18)

式中

\dot{Φ}

为黏性耗散项。

综上所述可得流体单位时间内获得能量的方程为^[19]

\frac{Q_{air}}{d t} = - \nabla \cdot (λ \nabla T_{a}) d x d y d z - \sum_{i = 1}^{3} \frac{\partial (ρ E u_{i})}{\partial x_{i}} d x d y d z +

[ρ \frac{d}{d t} (\frac{1}{2} V^{2}) + \dot{Φ} - p \nabla \cdot V] d x d y d z

(19)

综上所述，流体场下电热驱动器的瞬态热传导方程为

ρ_{m} c \frac{\partial T_{m}}{\partial t} = J^{2} (t) ρ (T) + κ (T) \nabla \cdot (\nabla T_{m}) d x d y d z d t -

\nabla \cdot (λ \nabla T_{a}) d x d y d z - \sum_{i = 1}^{3} \frac{\partial (ρ E u_{i})}{\partial x_{i}} d x d y d z +

[ρ \frac{d}{d t} (\frac{1}{2} V^{2}) + \dot{Φ} - p \nabla \cdot V] d x d y d z

(20)

在求解流体场结果时，仍需同时求解流体的质量守恒和动量守恒方程，其方程如下：

\frac{\partial ρ}{\partial t} + \frac{\partial (ρ u)}{\partial x} + \frac{\partial (ρ v)}{\partial y} + \frac{\partial (ρ w)}{\partial z} = 0

(21)

ρ (\frac{\partial u}{\partial t} + u \cdot \nabla u) = - \nabla p + \nabla \cdot (μ (\nabla u + (\nabla u)^{T})

- \frac{2}{3} μ (\nabla \cdot u) I) + ρ g

(22)

初始条件和边界条件为

\{\begin{matrix} T_{a} (x, y, z, t) = T_{r e f}, t = 0 \\ T_{a} (\infty, t) = T_{r e f} \\ T_{m} (x_{1}, y_{1}, z_{1}, t) = T_{a} (x_{1}, y_{1}, z_{1}, t) \\ T_{m} (x, y, z, 0) = T_{r e f} \\ T_{m} (x, y, z, t) = T_{r e f}, y = 0 \\ T_{m} (x, y, z, t) = T_{ref}, y = 2 L \end{matrix}

(23)

式中：第1项表示流体在初始状态下温度为室温，第2项表示在驱动器壁面温度与紧贴壁面的流体温度相同。

基于上述理论模型建立有限元模型进行求解，建立的有限元模型如图3所示，具体边界条件设置如下

1）对电热驱动器的两个锚点设置为固定约束，固定在基底上；

2）电热驱动器的一个锚点设置为正电位，另一个设置为接地；

3）基底设置为293.15 K的恒定温度；

4）在流体场中，将空气设置为层流状态下的弱可压缩流体，并设置气体重力；

5）对流体场中的流体设置开放边界；

6）在研究电热驱动器的动态特性时，需要与试验电压保持一致，因此需设置与试验相同的电压曲线。

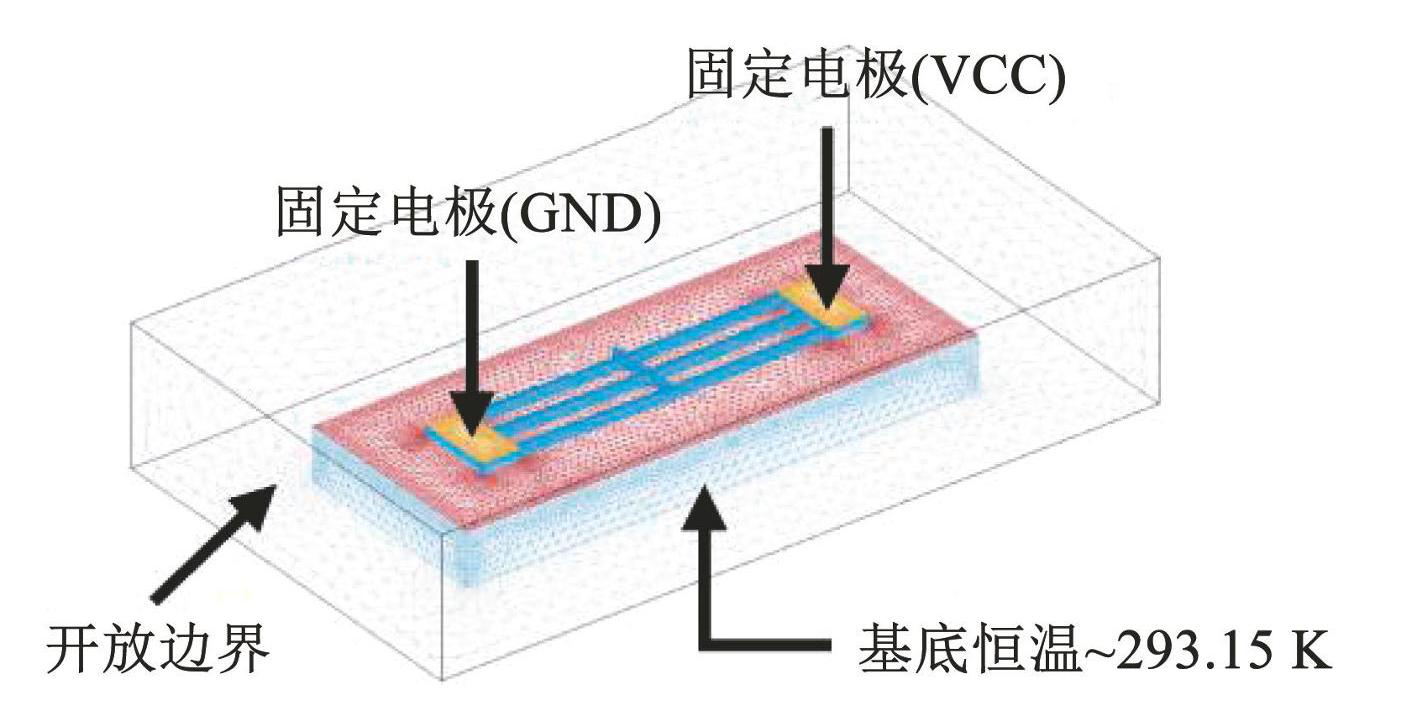
图3V型电热驱动器有限元模型

Fig.3Finite element model of V-type electrothermal actuator

本文所使用的V型电热驱动器尺寸以及该结构采用的重掺杂单晶硅的具体材料参数分别见表1、2。

表1V型电热驱动器尺寸参数

Tab.1 Size parameters of V-shaped electrothermal actuator

表2硅的材料参数^[20]

Tab.2 Material parameters of silicon

掺杂硅的大部分物理特性都取决于温度和掺杂质量分数，其中导热系数、电阻率和热膨胀系数随温度的变化非常复杂，给精确模拟V型微电热驱动器的温度场和结构场带来了困难，因此将上述三者与温度T的关系拟合成如下公式^[21]：

k (T) = 210658 T^{- 1.2747}

(24)

ρ (T) = ρ_{0} (1 + γ (T - 273))

(25)

α (T) = - 4 \times 10^{- 12} T^{2} + 8 \times 10^{- 9} T + 4 \times 10^{- 7}

(26)

式中：ρ₀为室温下的电阻率，γ为硅的温度系数，γ=3×10^-3。

2 MEMS电热驱动器温度特性试验

2.1 红外热成像测量系统

采用红外测温技术测量V型微电热驱动器的温度，搭建微电热驱动器的红外热成像测量系统（见图4）。

图4红外热成像测量系统

Fig.4Infrared thermal imaging measurement system

2.2 稳态温度特性

在8 V电压激励下，V型电热驱动器温度分布如图5所示，温度最高区域出现在中心推杆附近（H附近），最高温度为438℃。在水平方向上，从驱动器中间区域至锚点，热梁上的温度呈现出明显递减的趋势。通过对比图6中V型电热驱动器的稳态温度分布试验结果与仿真曲线发现，试验和3条仿真曲线的分布趋势基本一致。分析电热驱动器中间1 000~2 000 μm区段的温度数据，采用电-热-流-固多场耦合模型所得的数据与试验结果之间的偏差保持在0.8%~7.6%之间，相比之下，使用恒定对流换热系数和基于经验公式模型所获得的数据则在12.7%~18.2%及12.6%~16.8%之间。这些数值上的差异说明电-热-流-固多场耦合模型能更精确地捕捉温度分布的情况。除此之外，在锚点附近的两侧斜梁处，理论预测值与实际测量值之间存在显著偏差，这一现象主要是由两方面原因造成的：1）在模型构建过程中简化了锚点处的传热边界条件，假设锚点处的温度恒定为293.15 K，这种处理导致理论预测的斜梁温度降低，在靠近锚点区域尤为明显。2）在仿真中使用的材料参数无法与真实材料参数完全一致，从而导致仿真温度与试验结果产生偏差。这些误差不仅体现在稳态温度上，还对动态温度特性造成了影响。虽然这些因素对模型结果造成了一定的偏差，但电-热-流-固多场耦合模型相较于恒定对流换热系数模型或基于经验公式的模型，在结果上的误差显著较小。这意味着电-热-流-固多场耦合模型能够更准确地反映V型电热驱动器在流场下的温度分布特性。

图7展示了在不同电压下试验和不同仿真方式电热驱动器中心推杆的稳态温度。从图7中可以看出，虽然所有曲线的变化趋势一致，温度都随电压的增高而增高，但是从误差分析来看，电-热-流-固多场耦合模型的误差最小。

图58 V电压下V型电热驱动器稳态温度热图

Fig.5Steady-state temperature of V-type electrothermal actuator at 8 V

图6电热驱动器横梁温度分布

Fig.6Temperature distribution of electrothermal actuator beam

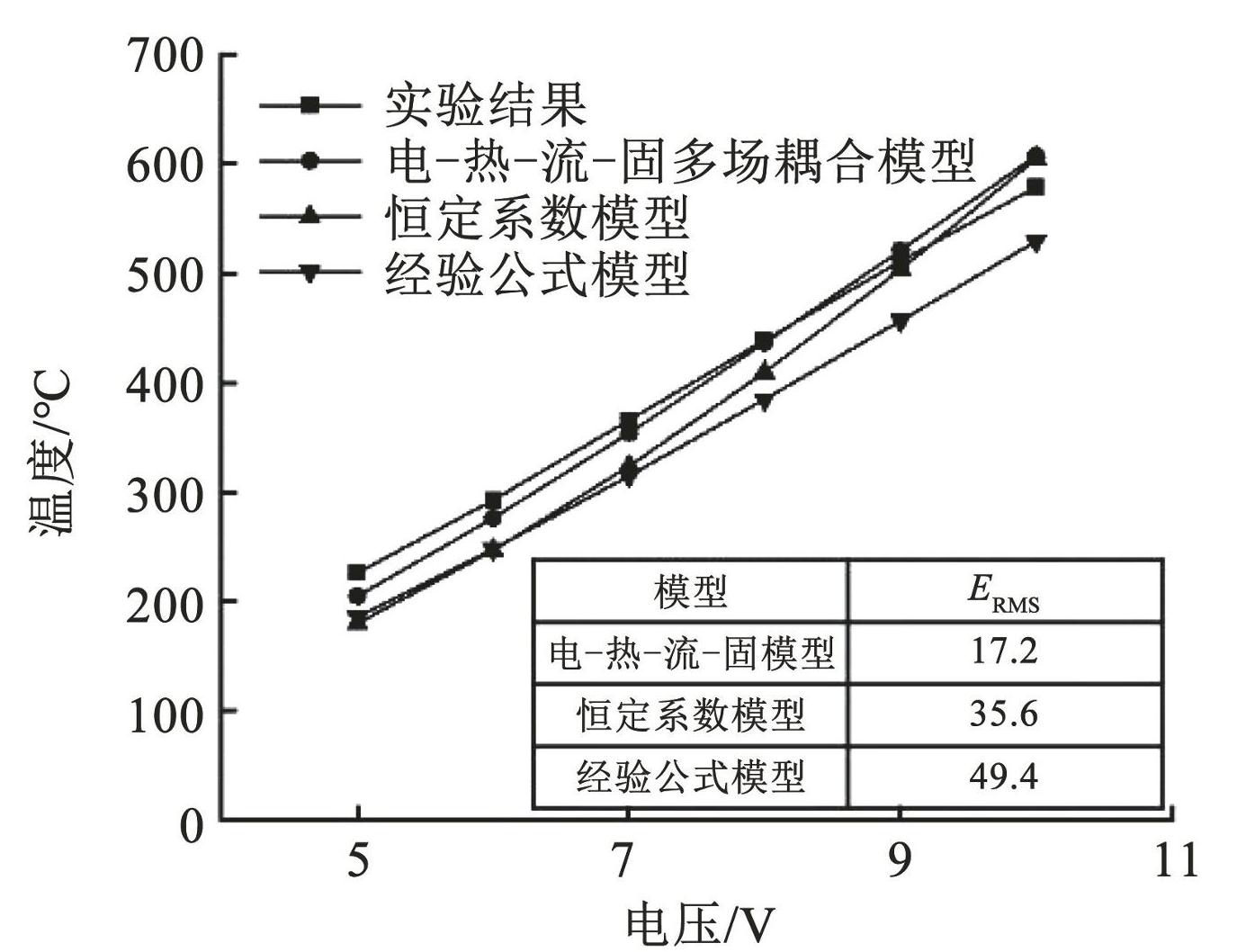
图7不同电压下电热驱动器稳态温度

Fig.7Steady-state temperature of electrothermal actuator at different voltages

2.3 动态温度特性

利用红外热成像测量系统捕捉8 V电压下电热驱动器的动态温度，其动态温度试验和仿真曲线见图8。由于电热驱动器的温度达到稳态所需时间较长，因此定义当动态温度达到最大温度的95%时，可以被认为已经达到稳态条件。通过计算分析得出以下结果：试验温度在t=117 ms时达到稳态，此时温度为416.8℃；电-热-流-固多场耦合模型温度在t=120 ms时达到稳态，此时温度为414.1℃；恒定对流换热系数和基于经验公式的模型分别在t=125 ms和t=110 ms时达到稳态，此时温度分别为389.0℃和365.5℃。从动态温度响应曲线得到，电-热-流-固多场耦合模型的温度上升过程与试验数据更为契合。这表明该耦合模型能够更准确地模拟电热驱动器的动态热响应。

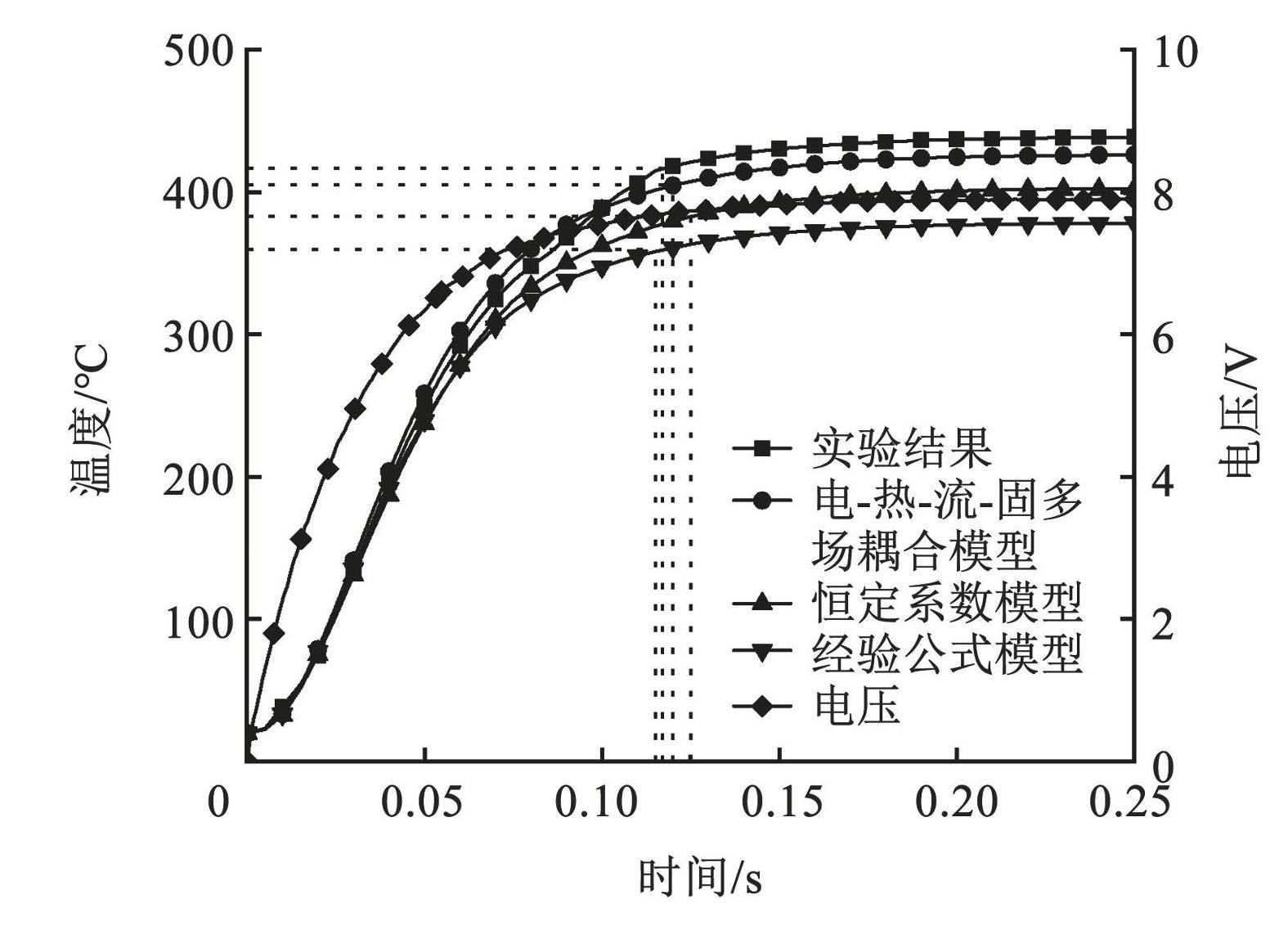
图88 V电压下电热驱动器动态温度响应

Fig.8Dynamic temperature response of electrothermal actuator at 8 V

2.4 流体场下的对流换热系数分析

根据空气的对流换热理论，对流换热系数会随着流体与驱动器的温度发生改变，其一般关系式为^[19]

h = \frac{- {λ \frac{\partial T}{\partial z}|}_{z = 0}}{T_{m} - T_{f}}

(27)

式中：

{\frac{\partial T}{\partial z}|}_{z = 0}

为壁面法线方向上的流体温度变化，λ为空气的传热系数，T_m、T_f分别为固体、流体温度。

基于电-热-流-固多场耦合的有限元模型计算结果，对流体场下电热驱动器的对流换热系数进行分析。驱动器表面对流换热系数分布及平均对流系数随时间变化曲线如图9所示，微电热驱动器的对流换热系数分布呈现出明显的空间不均匀性及随时间动态变化的特点。

图9驱动器表面对流换热系数分布及平均对流系数随时间变化曲线

Fig.9Distribution of convective heat transfer coefficients on the actuator surface and average convective coefficient versus time curve

对于上、下表面，靠近推杆顶端处的对流换热系数呈现出较高的数值，这是由于推杆顶端的温度较高，增强了自然对流换热能力。尽管上、下表面的对流换热系数分布比较相似，但是它们的变化趋势上存在很大差异。上表面与空气间的对流换热在施加电压后立即显著增强，但在20 ms内迅速下降，随后保持缓慢上升逐步趋于稳定；而下表面作为驱动器主要散热面，在整个时间段内对流换热系数逐渐上升，最后趋于稳定。对于垂直壁面，其对流换热系数表现出随时间先上升后下降的趋势，最终趋于平稳，由于传热路径较短，垂直壁面靠近基底处具有较大的对流换热系数。在时间序列上观察到的3个关键表面的对流换热系数几乎同时达到了稳态。这一结果与电热驱动器动态温度响应图（见图8）相吻合，说明当驱动器达到稳态时，其内部温度也达到稳定状态。试验还表明，微电热驱动器的对流换热系数随电压的上升而增大，这一现象是由于电压提升导致表面温度显著上升的结果。

在采用恒定对流换热系数模型时，微电热驱动器各表面的对流换热系数不随时间和温度变化，这一假设导致了两种结果：当恒定值大于实际对流换热系数时，表现为比真实情况下的升温速度更慢；相反，如果实际的对流换热系数随着驱动器温度的上升而增加，则在恒定值下进行计算会缩短驱动器达到稳定状态的时间。这种现象在微电热驱动器横梁的温度分布图（见图6）和动态温度响应图（见图8）中有明显体现。在8 V电压下，微电热驱动器的对流换热系数整体低于设定的恒定值。在横梁的稳态温度分布中，试验结果和通过电-热-流-固多场耦合模型计算得到的温度比使用恒定对流换热系数模型的结果更高。在温度动态响应中，试验和电-热-流-固多场耦合模型得到的温度梯度均大于使用恒定对流换热系数的模型结果。总之，采用恒定对流换热系数模型时，由于未能准确捕捉实际换热系数随时间与温度变化的趋势，因此该模型在描述电热驱动器的温度特性上存在局限性。

基于经验公式的传热模型采用瑞利数（Ra）来评估MEMS电热驱动器周围流场的运动状态，若当流体Ra高于临界值时，热量传递的主要方式是热对流；当Ra低于临界值时，热量传递的主要方式是热传导。由式（13），取重力加速度g为9.8 m/s²，体积膨胀系数β为3.676×10^-3K，ΔT为700 K，特征长度H为10 μm，热扩散系数α为2×10^-5 m²/s，运动黏度

v

为14.8×10^-6 m²/s，计算得到驱动器的Ra约为8.52×10^-2，远小于临界值的10⁹，因此宏观下的临界瑞利数不适用于微尺度。除此之外，一些研究者也对Ra的使用进行了分析。例如，Hickey等^[22]指出，在宏观尺度上Ra对自然对流至关重要，但在微尺度下，Ra并不适用。Ozsun^[13]在研究中提到，在小尺度下惯性力可以忽略不计，如果在微尺度自然对流中使用传统的相关性，实际热量传递将会被低估。Solano等^[23]在研究中对比了宏观尺度和微观尺度的Ra，同样得出了类似结论。

3 结论

1）建立了MEMS电热驱动器的电-热-流-固多物理场耦合模型，并与恒定对流系数模型、基于经验公式模型的仿真结果和试验结果进行对比。在相同加载电压下，电-热-流-固多场耦合模型的稳态温度分布以及动态温度响应与试验结果的一致性更高，稳态温度分布误差在0.8%~7.6%；在不同加载电压下，电-热-流-固多场耦合模型的稳态温度上升曲线均方根误差为17.2，误差最小。

2）在流体场下，电热驱动器各表面的对流换热系数分布不均匀且随时间改变。对流换热系数在上表面呈现先下降后上升的趋势，在下表面呈现上升的趋势，在竖直壁面呈现先上升后下降的趋势。但在3个特征面上，对流换热系数几乎同时达到稳态，此时驱动器温度也达到稳态，并且随着驱动器温度的升高，对流换热系数也随之增加。

图1V型电热驱动器结构图

Fig.1V-type electrothermal actuator structure

下载: 全尺寸图片

图2微电热驱动器的微元传热示意

Fig.2Heat transfer schematic for micro-electrothermal actuator

下载: 全尺寸图片

图3V型电热驱动器有限元模型

Fig.3Finite element model of V-type electrothermal actuator

下载: 全尺寸图片

图4红外热成像测量系统

Fig.4Infrared thermal imaging measurement system

下载: 全尺寸图片

图58 V电压下V型电热驱动器稳态温度热图

Fig.5Steady-state temperature of V-type electrothermal actuator at 8 V

下载: 全尺寸图片

图6电热驱动器横梁温度分布

Fig.6Temperature distribution of electrothermal actuator beam

下载: 全尺寸图片

图7不同电压下电热驱动器稳态温度

Fig.7Steady-state temperature of electrothermal actuator at different voltages

下载: 全尺寸图片

图88 V电压下电热驱动器动态温度响应

Fig.8Dynamic temperature response of electrothermal actuator at 8 V

下载: 全尺寸图片

图9驱动器表面对流换热系数分布及平均对流系数随时间变化曲线

Fig.9Distribution of convective heat transfer coefficients on the actuator surface and average convective coefficient versus time curve

下载: 全尺寸图片

表1V型电热驱动器尺寸参数

下载: 全尺寸图片

表2硅的材料参数^[20]

下载: 全尺寸图片

图1V型电热驱动器结构图

Fig.1V-type electrothermal actuator structure

图2微电热驱动器的微元传热示意

Fig.2Heat transfer schematic for micro-electrothermal actuator

图3V型电热驱动器有限元模型

Fig.3Finite element model of V-type electrothermal actuator

图4红外热成像测量系统

Fig.4Infrared thermal imaging measurement system

图58 V电压下V型电热驱动器稳态温度热图

Fig.5Steady-state temperature of V-type electrothermal actuator at 8 V

图6电热驱动器横梁温度分布

Fig.6Temperature distribution of electrothermal actuator beam

图7不同电压下电热驱动器稳态温度

Fig.7Steady-state temperature of electrothermal actuator at different voltages

图88 V电压下电热驱动器动态温度响应

Fig.8Dynamic temperature response of electrothermal actuator at 8 V

图9驱动器表面对流换热系数分布及平均对流系数随时间变化曲线

Fig.9Distribution of convective heat transfer coefficients on the actuator surface and average convective coefficient versus time curve

表1V型电热驱动器尺寸参数

表2硅的材料参数^[20]

图1V型电热驱动器结构图

Fig.1V-type electrothermal actuator structure

图2微电热驱动器的微元传热示意

Fig.2Heat transfer schematic for micro-electrothermal actuator

图3V型电热驱动器有限元模型

Fig.3Finite element model of V-type electrothermal actuator

图4红外热成像测量系统

Fig.4Infrared thermal imaging measurement system

图58 V电压下V型电热驱动器稳态温度热图

Fig.5Steady-state temperature of V-type electrothermal actuator at 8 V

图6电热驱动器横梁温度分布

Fig.6Temperature distribution of electrothermal actuator beam

图7不同电压下电热驱动器稳态温度

Fig.7Steady-state temperature of electrothermal actuator at different voltages

图88 V电压下电热驱动器动态温度响应

Fig.8Dynamic temperature response of electrothermal actuator at 8 V

图9驱动器表面对流换热系数分布及平均对流系数随时间变化曲线

Fig.9Distribution of convective heat transfer coefficients on the actuator surface and average convective coefficient versus time curve

表1V型电热驱动器尺寸参数

表2硅的材料参数^[20]

陈浩, 曹云, 王新杰, 等. 工艺误差影响下微电热驱动器失效分析[J]. 光学精密工程,2021,29(6):1365.CHEN Hao, CAO Yun, WANG Xinjie,et al. Failure analysis of electro-thermal micro-actuator under effect of process error[J]. Optics and Precision Engineering,2021,29(6):1365. DOI:10.37188/OPE.20212906.1365.

李致富, 黄楠, 钟云, 等. 压电驱动器迟滞非线性的分数阶建模及实验验证[J]. 光学精密工程,2020,28(5):1124. LI Zhifu, HUANG Nan, ZHONG Yun,et al. Fractional order modeling and experimental verification of hysteresis nonlinearities in piezoelectric actuators[J]. Optics and Precision Engineering,2020,28(5):1124. DOI:10.3788/OPE.20202805.1124.

刘加凯. 静电驱动MOEMS保险机构的设计与试验[J]. 光学精密工程,2019,27(2):334. LIU Jiakai. Design and test of electrostatic driving MOEMS arming device[J]. Optics and Precision Engineering,2019,27(2):334. DOI:10.3788/OPE.20192702.0334.

张涛, 吴一辉, 黎海文, 等. 基于MEMS工艺的高能量密度微电磁驱动器[J]. 光学精密工程,2007,15(6):866. ZHANG Tao, WU Yihui, LI Haiwen,et al. Micro electromagnetic actuator with high energy density based on MEMS technology[J]. Optics and Precision Engineering,2007,15(6):866. DOI:10.3321/j.issn:1004-924X.2007.06.011.

章皓. 电热式MEMS微镜驱动控制技术研究[D]. 苏州: 苏州大学,2014. ZHANG Hao. The Research on driving control technology based on electrothermal MEMS micromirror[D]. Suzhou: Soochow University,2014.

卢星帆, 王新杰, 陈浩. U型微电热驱动器理论模型及瞬态位移特性[J]. 哈尔滨工业大学学报,2023,55(1):24. LU Xingfan, WANG Xinjie, CHEN Hao. Theoretical model and transient displacement characteristics of U-shaped electrothermal actuator[J]. Journal of Harbin Institute of Technology,2023,55(1):24. DOI:10.11918/202201086.

李峰, 王新杰, 陈浩. V型电热驱动器的理论建模及位移响应特性[J]. 光学精密工程,2022,30(13):1572. LI Feng, WANG Xinjie, CHEN Hao. Theoretical modeling and displacement response characteristics of V-shaped electrothermal actuator[J]. Optics and Precision Engineering,2022,30(13):1572. DOI:10.37188/OPE.20223013.1572.

DŁUGOSZ, A, JAROSZ P, SCHLIETER T. Optimal design of electrothermal microactuators for many criteria by means of an immune game theory multiobjective algorithm[J]. Applied Sciences,2019,9(21):4654. DOI:10.3390/app9214654.

陈浩, 王新杰, 王炅, 等. V型电热驱动器理论模型及动态特性[J]. 上海交通大学学报,2021,55(10):1263. CHEN Hao, WANG Xinjie, WANG Jiong,et al. Theoretical model and dynamic performance of V-shaped electrothermal actuator[J]. Journal of Shanghai Jiao Tong University,2021,55(10):1263. DOI:10.16183/j.cnki.jsjtu.2020.216.

HUANG Qingan, SHEK LEE N K. Analysis and design of polysilicon thermal flexure actuator[J]. Journal of Micromechanics and Microengineering,1999,9(1):64. DOI:10.1088/0960-1317/9/1/308.

CAUCHI M, GRECH I, MALLIA B,et al. Analytical,numerical and experimental study of a horizontal electrothermal MEMS microgripper for the deformability characterisation of human red blood cells[J]. Micromachines,2018,9(3):108. DOI:10.3390/mi9030108.

ULKIR O. Design and fabrication of an electrothermal MEMS micro-actuator with 3D printing technology[J]. Materials Research Express,2020,7(7):075015. DOI:10.1088/2053-1591/aba8e3.

OZSUN O, ALACA B E, YALCINKAYA A D,et al. On heat transfer at microscale with implications for microactuator design[J]. Journal of Micromechanics and Microengineering,2009,19(4):045020. DOI:10.1088/0960-1317/19/4/045020.

LIN Lin, WU Hao, XUE Liwei,et al. Heat transfer scale effect analysis and parameter measurement of an electrothermal microgripper[J]. Micromachines,2021,12(3):309. DOI:10.3390/mi12030309.

CAO Yun, LIU Haotian, CHEN Hao,et al. Dynamic thermal characterization of MEMS electrothermal actuators in air[J]. IEEE Sensors Journal,2021,21(14):15979. DOI:10.1109/JSEN.2021.3076302.

KONG Xiaoyu, CAO Yun, ZHU Hengbo,et al. A self-latching MEMS optical interrupter with status monitoring for laser initiation system[J]. IEEE Transactions on Electron Devices,2023,70(5):2473. DOI:10.1109/TED.2023.3255159.

SCIBERRAS T, DEMICOLI M, GRECH I,et al. Coupled finite element-finite volume multi-physics analysis of MEMS electrothermal actuators[J]. Micromachines(Basel),2021,13(1):8. DOI:10.3390/mi13010008.

杨世铭, 陶文铨. 传热学[M].4版. 北京: 高等教育出版社,2006. YANG Shiming, TAO Wenquan. Heat transfer[M].4th ed. Beijing: Higher Education Press,2006.

张靖周. 高等传热学[M].2版. 北京: 科学出版社,2015. ZHANG Jingzhou. Advanced heat transfer[M].2nd ed. Beijing: Science Press,2015.

陈浩. 微光路逻辑系统用电热驱动技术研究[D]. 南京: 南京理工大学,2021.CHEN Hao. Study on problems for the electrothermal drive used in the logic micro-system for optical path[D]. Nanjing: Nanjing University of Science and Technology,2021. DOI:10.27241/d.cnki.gnjgu.2021.002324.

CHANG T H, ZHU Yong. A microelectromechanical system for thermomechanical testing of nanostructures[J]. Applied Physics Letters,2013,103(26):263114. DOI:10.1063/1.4858962.

HICKEY R, KUJATH M, HUBBARD T. Heat transfer analysis and optimization of two-beam microelectromechanical thermal actuators[J]. Journal of Vacuum Science Technology A: Vacuum Surfaces,and Films,2002,20(3):971. DOI:10.1116/1.1468654.

SOLANO B, ROLT S, WOOD D. Thermal and mechanical analysis of an SU8 polymeric actuator using infrared thermography[J]. Proceedings of the Institution of Mechanical Engineers, Part C. Journal of Mechanical Engineering Science,2008,222(1):73. DOI:10.1243/09544062jmes676.

1 V型电热驱动器的多场耦合模型

2 MEMS电热驱动器温度特性试验

3 结论

友情链接LINKS