2. 中国空间技术研究院, 100094 北京
2. China Academy of space Technology, 100094 Beijing, China
展开铰链是连接很多空间折展机构的重要部件,展开铰链由于同时具备可动连接、展开、锁定功能,已被广泛应用于太阳翼、大型天线、大型空间支撑臂、可展桁架等航天领域.目前, 展开铰链主要分为储能型、形状记忆材料型和动力展开型,其中由涡卷弹簧驱动的储能型展开铰链因储能元件质量轻、可靠性高而被大量应用.为了确保展开铰链能够可靠展开并锁定,涡卷弹簧的力矩裕度要>1,在这一条件下,铰链展开末端容易产生很大的冲击振动,振动在太空微重力环境下持续很久,可能会危及相关设备的正常工作,甚至会导致系统失效.
在无减速部件展开铰链驱动的航天器研究方面,马尚君等[1]对铰链展开式构型航天器设计及其动力学仿真进行了研究,游斌弟等[2]对卫星太阳阵展开锁紧过程冲击振动进行了研究,张志娟等[3]对太阳翼铰链锁定冲击载荷建模分析方法进行了研究,王晛等[4]进行了太阳翼地面展开锁定动力学仿真分析,陈天智等[5]提出了太阳翼展开铰链展开锁定最大冲击载荷修正方法,谷勇霞等[6]对考虑多间隙时帆板式展开机构动力学进行了分析,Li Junlan等[7]对阻尼摩擦重力等因素对含铰链间隙的展开机构的动力学特性进行了研究.在降低展开铰链锁定冲击的减速部件研究方面,国内外学者研究了在铰链的基础上增加阻尼器以减小冲击,梁小光等[8-9]分析了阻尼器对卫星太阳翼展开铰链锁定冲击力矩的影响等,而且提出了卫星太阳翼阻尼器的参数选定方法.肖应廷等[10]研究黏性阻尼器对减小展开式太阳翼锁定冲击力矩的影响等,Mitter等[11]研究了可调整的大转角阻尼器,蒲海玲等[12]分析了黏滞型阻尼器对太阳翼展开性能的影响,并提出了太阳翼黏滞型阻尼器的可靠性评估方法[13].但适用于高低温、真空等极限环境的阻尼器设计难度过大, 成本高, 重量大,而且有源的阻尼器在太空中工作可靠性不高,因此,设计出无源、重量轻、可靠性好、能适应极限环境的减小冲击的部件具有重要意义.
本文首先介绍了弹簧展开铰链在展开末端产生的冲击问题; 然后从能量的角度提出了解决该问题的途径; 而后针对减小冲击的方法,提出了两种相应的机构设计方案——间歇运动式低冲击铰链机构和耗能型低冲击铰链机构,并对其进行了建模和仿真,以验证机构方案的可行性和检测冲击减小效果; 最后研制了两套低冲击弹簧铰链机构样机,并进行了试验与测试.
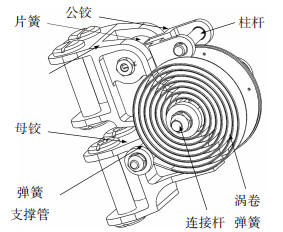
1 弹簧展开铰链及其锁定冲击 1.1 弹簧展开铰链结构由涡卷弹簧驱动的展开铰链包括公铰、母铰、连接杆、涡卷弹簧、锁定杆、柱杆、片簧和弹簧支撑管等[14],如图 1所示.
|
图 1 涡卷弹簧驱动的展开铰链结构 |
公铰和母铰与刚体部件相连(比如太阳翼、卫星天线板或支架),母铰可以围绕连接杆自由转动,涡卷弹簧里端固定在连接杆上,外端通过弹簧支撑管固定在公铰上,片簧、锁定杆和柱杆转接杆组成了锁定装置,片簧一端固定在公铰上,另一端固定在锁定杆上,在涡卷弹簧的驱动下,母铰转动,转到一定位置时与柱杆碰撞,碰撞使母铰反向,此时柱杆滑入母铰的锁定沟槽中,铰链完成锁定.
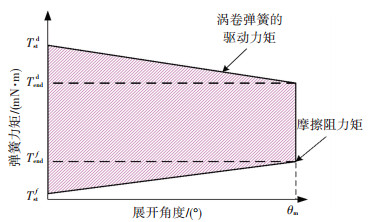
1.2 展开末端锁定冲击根据工程经验,在铰链展开过程中,涡卷弹簧的驱动力矩和摩擦阻力距随展开时间的变化曲线如图 2所示,当铰链展开到位时,设此时弹簧力矩为Tendd,摩擦阻力矩为Tendf,静力矩裕度可以表示为Tendd/Tendf-1≥1[14],由于力矩裕度的存在,展开铰链展开锁定瞬间会产生很大的冲击振动,在某卫星太阳翼地面试验的数据[8]中,最大锁定冲击力矩约120 N·m.例如,卫星天线展开到位时,铰链上的锁定机构工作,使天线的运动突然停止,从而对天线、展开机构、以及卫星上相关设备产生相应的载荷(主要是根部弯矩).过大的冲击载荷可能造成铰链连接部件损坏,甚至导致整个卫星失效.
|
图 2 展开过程中驱动力矩和摩擦阻力的变化曲线 |
铰链展开末端的冲击可以通过展开末端的角速度或者碰撞力矩来衡量,二者的计算过程如下.
1) 角速度计算.设母铰的惯量为Jb,转动角度为θ,最大转角为θm,初始角度为θ0,则母铰的动能可以表示为
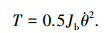
|
根据工程经验, 由于摩擦阻力矩线性增加,采用工程通用的算法[15], 可以把摩擦阻力矩等效成一个线性增大的阻尼,该阻尼的曲线的变化率设为Kf,驱动弹簧的刚度系数为K1, 铰链的等效弹性势能可表示为
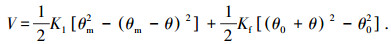
|
代入拉格朗日方程L=T-V得
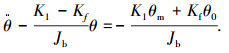
|
初始条件为t=0, θ(0)=0, 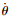

|
在展开铰链展开过程中,展开的角位移一般是确定的,可以看出展开时间和角位移一一对应,因此可以确定展开时间,进而可以带入展开角速度的表达式,得到铰链展开末端母铰的角速度,这里设为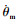
2) 碰撞力矩计算.母铰及其刚体部件和公铰的碰撞是个非线性问题,可以把该问题简化为两个弹性球的碰撞.设Ji(i=1, 2)、θi、Ei、νi、Ri分别为两球的转动惯量、碰撞产生的应变、弹性模量、泊松比和碰撞处的曲率半径.
碰撞力矩可以近似表示为[16]
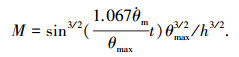
|
(1) |
其中:
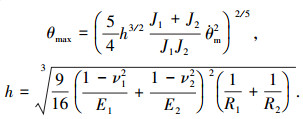
|
由此可以看出,在材料、碰撞处的曲率、惯量一定时,碰撞力矩只与铰链展开末端母铰的角速度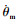
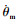
从能量转化的角度,母铰的角速度的二次方正比于涡卷弹簧的驱动力矩和摩擦阻力矩做功之和,设Wd和Wf分别为驱动力矩和摩擦阻力距做功,则
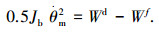
|
在图 2中做功之和表示为阴影的面积,由式(1)可知,母铰的角速度和碰撞力矩正相关,因此,减少图中阴影部分的面积可以有效地减小碰撞力矩.本文提出间歇性运动式和耗能型低冲击展开铰链机构设计方法.
2.1 间歇运动机构法间歇性运动机构可以有效地控制涡卷弹簧的能量释放,常见的例子为由发条驱动的机械钟表.其工作原理为:涡卷弹簧同时驱动铰链展开和间歇性机构的运动,驱动间歇性机构的运动通过锁定可以暂时中断铰链的转动,铰链再输出力或力矩到解锁机构上,然后解除对铰链的锁定,使得铰链由原来的连续转动转化为间歇性转动.
从能量的角度,在间歇性运动机构的作用下,涡卷弹簧的能量间歇性释放,可以使铰链每次仅仅转动一个很小的角度,因此只有最后一个阶段的转动把一部分的能量转化为母铰的动能.如图 3所示,阴影部分的面积表示转化为母铰动能的弹性势能,远小于图 2中的阴影部分面积,因而可以大大降低展开末端母铰的角速度.并且驱动间歇性机构的运动为周期运动,其转动的圈数基本不受限制,因而具有一定的优势.
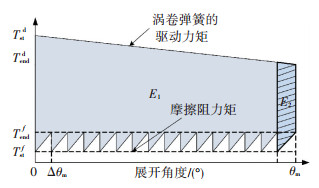
|
图 3 间歇性运动机构作用下弹簧力矩的变化曲线 |
图 3中E1表示未使用间歇性运动机构之前的能量,E2为增加间歇性机构后最后一次冲击的能量,摩擦阻力矩的周期为Δθ,其大小等于间歇性机构擒纵轮的分度.所以系统能量的降低率可以表示为
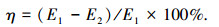
|
(2) |
由式(2)可以看出,系统降低冲击的效果非常显著,达到95%左右.
2.2 耗能机构法耗能机构方案采用在原来铰链的结构基础上,增加一个耗能元件,例如涡卷弹簧,原涡卷弹簧驱动铰链的同时,驱动耗能元件,耗能元件在铰链展开过程中提供阻力,例如一个涡卷弹簧可以提供随展开角度不断增大的阻力,将一部分的能量储存起来.在铰链展开即将达到指定位置时,该耗能元件通过分离机构与铰链和驱动源分离.分离以后,铰链在原驱动涡卷弹簧和摩擦阻力矩的作用下继续展开,直至展开到位, 完成锁定. 图 4为耗能机构法弹簧力矩随着展开角度的变化曲线,相比于图 2,阴影部分的面积减小了一些.但其受到转动角度的限制,其运动被限制在180°之内.
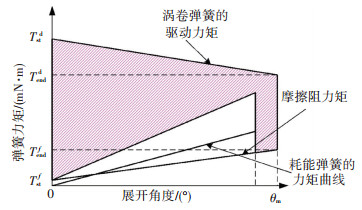
|
图 4 耗能机构作用下弹簧力矩的变化曲线 |
依据前面的设计思路,采用间歇性运动机构方案和耗能机构的方案,研制了两种低冲击铰链机构, 并进行试验验证.
3.1 间歇式低冲击铰链机构及其试验满足前面讨论的运动形式的机构,常见的为擒纵机构.擒纵机构包括擒纵部分和振荡部分,涡卷弹簧同时作用在铰链和擒纵部分上,经过一小角度的转动,擒纵部分通过位形锁定铰链,擒纵部分小的角位移输出一个碰撞力矩,作为振荡部分的输入,振荡部分反馈擒纵部分一个几乎等大的碰撞力矩,解除位形锁定.当铰链转过下一小角度时,擒纵机构会重复以上过程,直到铰链展开到位,结构形式如图 5所示.
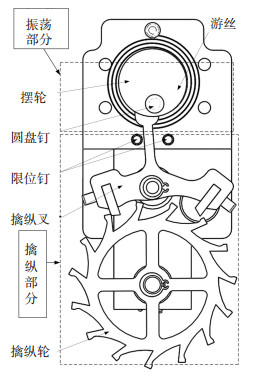
|
图 5 间歇式铰链机构结构 |
擒纵机构可以使铰链间歇性转动,每一小段的运动学分析都可以采用类似自由展开铰链的分析过程,然后通过迭代法求得每一段的末端角速度,该角速度作为下一段的起始角速度,求得的展开末端的角速度通过代入式(1),得到最终的碰撞力矩.
在涡卷弹簧驱动的展开铰链基础上,增加擒纵机构,为了放大铰链的角位移和缩小作用在擒纵机构上的力矩,在擒纵机构和展开铰链之间增加了一对增速齿轮,确定了结构参数,完成了结构设计和三维建模,并对模型进行仿真验证.为简化模型,仿真过程未考虑各处的阻尼,仿真结果如图 6、7所示,以三维模型加工出的样机如图 8所示,图 8中转接机构包含了增速齿轮组,目的是把驱动涡卷弹簧内的力矩转化为施加在增速机构上的力矩,并放大擒纵机构的输入角位移.
|
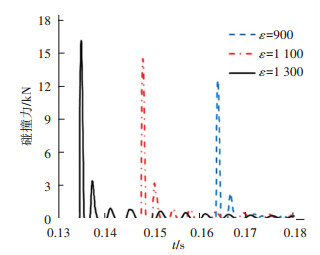
图 6 自由展开铰链的碰撞力仿真[17] |
|
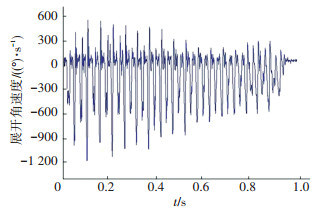
图 7 间歇式铰链机构展开速度曲线 |

|
图 8 间歇式铰链机构原理样机 |
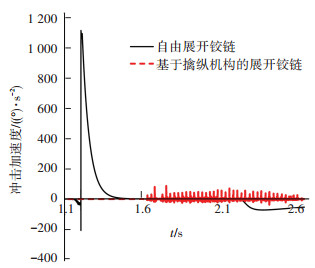
在图 6、7中,ε为涡卷弹簧的预加载力矩(mN·m),不含擒纵机构的自由展开铰链的碰撞力如图 6所示,可以得出自由展开铰链的碰撞力高达1 5764 N,在擒纵机构的作用下,图 9中碰撞力下降到1 250 N,以碰撞力为衡量指标,冲击的减小比例为92.07%.在图 8所示的样机基础上,通过加速度传感器测量冲击加速度,以之来衡量,得到的结果如图 10所示,经过计算也可以得到近似的冲击减小比例.其展开过程的速度曲线如图 7所示.

|
图 9 间歇式铰链机构的碰撞力仿真 |
|
图 10 间歇式铰链机构展开末端角加速度对比 |
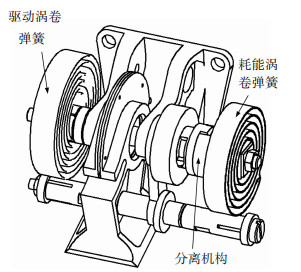
耗能式低冲击铰链机构方案设计如图 11所示,驱动涡卷弹簧和耗能涡卷弹簧分别位于铰链的两侧,前者驱动母铰转动,后者提供一个不断增大的阻力,在展开前、中、后期不断储存能量.为了在展开末期反向力矩涡卷弹簧不作用于铰链,不影响铰链的锁定,在铰链和耗能涡卷弹簧之间增加了一个分离机构,使母铰转到设定的角度时,耗能涡卷弹簧和铰链分离.
|
图 11 基于耗能型机构的展开铰链方案设计 |
图 12是基于耗能机构的展开铰链的样机, 试验台架用于固定铰链,以便于试验和测量.

|
图 12 基于耗能机构的铰链样机图 |
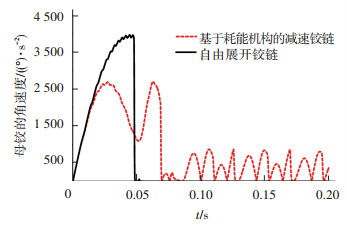
依照图 11的设计方案三维建模,以三维模型进行运动学仿真,以验证方案可行性和测量该方案的减速效果,未考虑摩擦时的仿真结果如图 13所示,自由展开铰链的最大角速度为3 809 (°)/s,基于耗能机构的铰链展开末端的角速度为2 596 (°)/s,减小了31.85%.
|
图 13 耗能式铰链机构仿真 |
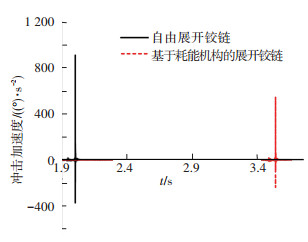
样机测量得到结果见图 14,以冲击加速度为衡量指标,自由展开铰链的最大加速度为899 (°)/s2,基于耗能机构的展开铰链的展开末端加速度为542 (°)/s2,减小了39.71%.
|
图 14 耗能式铰链机构冲击加速度测试 |
1) 为了有效降低弹簧展开铰链锁定冲击问题,首先对铰链展开末端的冲击进行描述,推导出了碰撞力矩和铰链展开末端的角速度关系, 从能量的角度,提出了两种降低铰链锁定冲击的方法.
2) 设计了间歇式和耗能式两种低冲击铰链机构,通过仿真验证了设计的可行性,仿真分析了减小铰链末端冲击的效果,结果表明两种方法可以使铰链冲击分别减小约95%和40%.
3) 研制了两种低冲击铰链机构样机, 进行了展开锁定冲击试验测试,验证了两种低冲击铰链机构的可行性.
| [1] |
马尚军, 刘更, 罗浩. 铰链展开式构型航天器设计及其动力学仿真[J]. 中国空间科学技术, 2010, 12(6): 49-56. |
| [2] |
游斌弟, 王兴贵, 陈军. 卫星太阳阵展开锁紧过程冲击振动[J]. 机械工程学报, 2012, 48(21): 67-76. |
| [3] |
张志娟, 邹元杰, 关晓东. 太阳翼锁定冲击载荷建模分析方法研究[C]//全国结构振动与动力学学术研讨会论文集. 苏州: 中国振动工程学会结构动力学专委, 2011: 281-289.
|
| [4] |
王晛, 陈天智, 柴洪友. 太阳翼地面展开锁定的动力学仿真分析[J]. 航天器工程, 2011, 20(3): 86-92. DOI:10.3969/j.issn.1673-8748.2011.03.014 |
| [5] |
陈天智, 王晛, 柴洪友. 太阳翼展开锁定最大冲击载荷修正方法[J]. 航天器工程, 2011, 20(6): 55-62. DOI:10.3969/j.issn.1673-8748.2011.06.018 |
| [6] |
谷勇霞, 杨天夫, 郭峰. 考虑多间隙的帆板式展开机构动力学分析[J]. 振动、测试与诊断, 2015, 35(1): 36-41. |
| [7] |
LI Junlan, YAN Shaoze, FENG Guo, et al. Effects of damping, friction, gravity, and flexibility on the dynamic performance of a deployable mechanism with clearance[J]. Journal of Mechanical Engineering Science, 2013, 227(8): 1791-1803. DOI:10.1177/0954406212469563 |
| [8] |
梁小光, 陈照波. 阻尼器对卫星太阳翼锁定冲击力矩影响的研究[J]. 噪声与振动控制, 2011, 31(1): 127-130. DOI:10.3969/j.issn.1006-1355-2011.01.027 |
| [9] |
梁小光, 丁竹生, 焦映厚, 等. 卫星太阳翼阻尼器参数选定方法[J]. 哈尔滨工业大学学报, 2011, 43(7): 71-75. |
| [10] |
肖应廷, 廖瑛. 粘性阻尼器对减小展开式太阳翼锁定冲击力矩的研究[C]//系统仿真技术及其应用学术会议论文集. 太原: 中国自动化学会系统仿真专业委员会, 2008: 644-647.
|
| [11] |
MITTER W, ZEMANN J, NITSCHKO T, et al. Adjustable large range rotary deployment damper[C]//Proceedings of 13th European Space Mechanisms and Tribology Symposium. Vienna: European Space Agency, 2009.
|
| [12] |
濮海玲, 王晛, 杨巧龙. 黏滞型阻尼器对太阳翼展开性能的影响分析[J]. 航天器工程, 2013, 22(1): 54-59. DOI:10.3969/j.issn.1673-8748.2013.01.011 |
| [13] |
濮海玲, 刘志全. 王晛太阳翼黏滞阻尼器的可靠性评估方法[J]. 航天器工程, 2013, 22(5): 42-45. DOI:10.3969/j.issn.1673-8748.2013.05.006 |
| [14] |
陈烈民. 航天器结构与机构[M]. 北京: 中国科学技术出版社, 2005.
|
| [15] |
孙京. 太阳翼铰链平面涡卷弹簧参数设计[J]. 航天器工程, 2000, 9(3): 37-43. |
| [16] |
GUO H W, LI Zhongjie, DENG Zongquan, et al. A low-impact deployment hinge based on a novel intermittent mechanism[J]. Applied Mechanics and Materials, 2014, 643: 302-309. DOI:10.4028/www.scientific.net/AMM.643 |
| [17] |
LI Zhongjie, GUO Hongwei, LI Yuchao, et al. A low-impact hinge mechanism based on the lever escapement mechanism[C]//Proceedings of 2014 IFToMM Asian Conference on Mechanism and Machine Science. Tian Jin: IFToMM, 2014.
|
 2016, Vol. 48
2016, Vol. 48


