2. 河北大学 建筑工程学院, 071000 河北 保定;
3. 长城汽车股份有限公司 河北省汽车工程技术研究中心, 071000 河北 保定
2. College of Civil Engineering and Architecture, Hebei University, 071000 Baoding, Hebei, China;
3. Technological Center of Great Wall Automobile Co., Ltd, Hebei Automobile Technology Research center, 071001 Baoding, Hebei, China
噪声、振动与声振粗糙度NVH(noise, vibration & harshness)在汽车研发过程中的重要性越来越引起研究人员的关注.影响NVH的主要因素有发动机、传动系、路面激励及气动噪声等,前3种因素导致的噪声均已有了有效的控制方法,而气动噪声更复杂,目前还没有有效的控制方法,成为影响车内噪声的重要因素[1].
国外学者对气动噪声的基本理论研究开展较早.如英国科学家Lighthill[2]在1952年运用微分方法从流体力学连续性方程和运动方程直接推导出运动气体发声的Lighthill基本方程,建立了声波波动量与流场参量间的直接联系.该方程左边是经典声学波动方程,其他偏离波动方程的项被移至方程的右边,作为气动噪声的声源项,整理后的声源项可以由实验或数值仿真计算得到,然后通过求静止介质中声场的解,便可以把复杂的声学问题转化为流场和声场问题分开处理,这就是著名的声类比的思想[3],但该方程只能处理自由空间内的Lighthill声源项(四极子声源).由于Lighthill方程没有考虑物体边界对声音的影响,1955年Curle[4]在Lighthill基本方程基础上考虑了静止物体边界对声音的影响,导出了更一般的Lighthill方程形式. 1969年Ffowcs-Williams等[5]把Curle方程应用于求解流体中运动物体的发声问题,得出更一般的气动声学方程(简称FW-H方程).应用FW-H方程、计算流体动力学和振动声学仿真的方法[6-7]求解外部流体流经车身表面产生的湍流脉动压力,可以预测和评估气动噪声水平[8].
国内学者对气动噪声的研究要晚于西方国家.近年来, 实验和仿真两方面的研究发现:汽车的后视镜、A柱、前挡风玻璃、进气栅、车顶篷、侧窗、天窗、车轮、底盘和门把手均为气动噪声贡献较大的关键部位.当汽车行驶速度<80 km/h时,气动噪声对车内司乘人员舒适度的影响较小,而当汽车行驶的速度>80 km/h时,尤其在高速路上以120 km/h高速行驶时,气动噪声与车速的六次方成正比[9],传递到车内的气动噪声对司乘人员舒适度的影响较大.对于高速行驶的汽车,车外形成的流场是比较复杂的湍流[10],尤其是后视镜、A柱、车轮、底盘和天线附近的流场比较复杂,压力脉动变化较剧烈,对近场气动噪声的总声压级贡献量较大,而雨刮器和天线的影响相对较小[11].后视镜是气动噪声的主要贡献量之一,在汽车研发阶段,后视镜与车身的合理搭配可以有效降低流体动力和气动噪声.风洞实验和仿真的方法可用于对普通后视镜的压力和速度场的特性进行研究,两种方法均可以把后视镜复杂的湍流流场可视化,真实再现后视镜的流场流动特性,并验证数值仿真方法的可行性.改变后视镜前脸厚度、后脸深度、支架长度与迎风角度可降低后视镜对气动噪声的贡献[12-13].气动噪声实测试验中,由于道路环境背景较为复杂,不易测出后视镜对气动噪声总声压级的贡献; 而数值仿真方法可以较好地模拟后视镜对气动总声压级的贡献.普通后视镜周围的流场是复杂的湍流流场,伴随着剧烈的压力脉动,此脉动是产生气动噪声的主要诱因,合理地改善后视镜的结构可以有效地改善高速行驶汽车外部流场的分布情况,进而可以改善车内的噪声水平[14-15].
综上所述,国内外学者对气动噪声研究中多数文献关注的是后视镜的外部流场的分布,而研究气动噪声经侧窗传递至车内噪声问题的相关文献较少.本文采用Star-CCM+的LES湍流模型[16]计算流场数据和采用声学仿真软件ACTRAN中的FW-H方程相结合的方法开展不同局部特征后视镜对车内外噪声的影响研究.
1 数学控制方程流体的连续性方程为
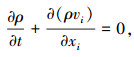
|
动量方程为
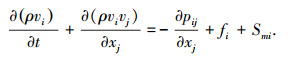
|
由以上两方程可推出Lighthill方程:
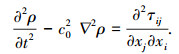
|
(1) |
式中:τij=ρvivj+δij[(p-p0)-c02(ρ-ρ0)].
式(1)只能对四极子声源求解.将该方程推广到求解表面偶极子声源,便成为Lighthill-Curle方程:

|
(2) |
式(2)中的右端第1项为四极子声源项,第2项为偶极子声源项.该方程只能求解运动流体中静止物体表面的噪声.
为求解运动物体与流体相互作用产生声音的问题,将式(2)进一步拓展成更一般的FW-H方程:

|
(3) |
式(3)中的右端第1项为四极子声源项,第2项为表面压力脉动引起的偶极子声源项,第3项为表面加速度引起的单极子声源项.
式(1)~(3)中:ρ为流体的密度,t为时间,c0为均质介质中声音速度,τij为Lighthill应力张量,vi和vj分别为流体速度分量,δij为克劳内克函数,p为流体微元控制体上的压力,ρ0和p0分别为未受扰动时介质的密度和流场压力均值,ρ'和p'分别为流场密度和压力的脉动值,ui为物体运动的速度.
为方便描述,式(2)和(3)中引入了控制面函数f (x, t)(如图 1),控制面上f=0,控制面内f < 0,控制面外f>0.

|
图 1 控制面示意 |
在计算高速行驶汽车的气动噪声时,一般文献只考虑了表面的偶极子声源,而忽略了其它声源项.为了更加准确地反映实际情况,本文对单极子声源、偶极子声源和四极子声源项均进行了考虑,故采用ACTRAN中的FW-H方程(式(3))进行计算.
2 数值计算方法 2.1 模型及计算域本文数值仿真的几何条件与所做风洞实验的几何条件基本相同,整车计算域的长、宽和高分别为车身的12倍、6倍和5倍,边界条件的设定见图 2.

|
图 2 整车的全计算域 |
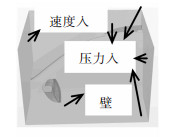
为能准确捕捉到后视镜及其周围的压力脉动并节省计算资源,利用Start-CCM+的LES湍流模型和子域相结合的方法对后视镜和侧窗区域的流场进行计算.子域计算域的长、宽和高分别为后视镜长的6倍、5倍和4倍,边界条件的设定见图 3.
|
图 3 计算子域 |
采用本文的数值仿真方法对图 4所示的3款后视镜进行研究:方案Ⅰ为原状态视镜,方案Ⅱ为一周开槽后视镜,方案Ⅲ为底部凸起而其余部分开槽的后视镜,几何模型中参数D是上镜壳所开沟槽的深度.

|
图 4 后视镜的3种几何模型 |
CFD计算流场的精确程度直接决定着声学软件计算声场的准确度.为提高计算流场精确度和节约计算时间,分别采用全域(1 000万)和子域(300万)两种方法进行.运用定常法计算全域,结果收敛后输出子域控制面上的Table数据作为下一步子域计算的初始条件,然后删除全域网格保留子域,对子域进行网格细化,最后用非定常法和大涡模拟法计算子域流场物理量.在计算流场参量时,运用二阶迎风格式对连续性方程和N-S方程进行离散,算法使用PESIO法.根据奈奎斯特定理,确定流场数据采样样本容量,运用傅里叶变换,将子域计算的瞬态压力脉动的时域数据转换成频域数据,并将其作为ACTRAN中F-WH的声源项,对内场声波的传播进行了计算.
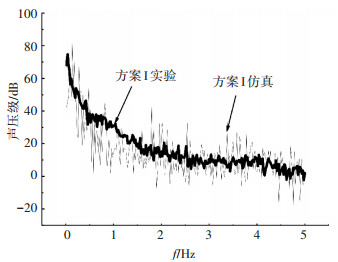
对某SUV整车做了风洞实验.实验时天气干燥,温度为20 ℃,空气的密度为1.293 kg/m3,实验过程中用胶带对某SUV进行全密封.这样只考虑后视镜对整车气动噪声的贡献.在车内主驾驶位及后排左侧座位人工头的左耳和副驾驶位及后排右侧座人工头的右耳均布置了麦克风,来监测气动噪声传至车内的响应,进而评价车内气动噪声的水平. 图 5是方案Ⅰ的数值仿真与实验结果对比曲线,图中的实验曲线是主驾驶位人工头左耳上麦克风监测到的响应曲线.由图 5可知,在500~1 500 Hz频段内仿真结果波动较大, 这是因为玻璃对不同频率的气动噪声隔声量不同,忽略玻璃结构细节及分层,也没有考虑玻璃的滤波作用,故仿真的频谱曲线波动较大.但从图 5可以看出:方案Ⅰ的数值仿真结果与实验结果变化趋势基本一致,说明本数值计算方法在研究汽车气动噪声过程中的正确性、可靠性及可行性.该方法可保证计算结果的合理性,能为后视镜研发设计提供可靠的计算方法.
|
图 5 数值仿真与实验对比 |
汽车高速行驶过程中,气体与汽车产生剧烈的相互作用,后视镜区域是气流变化剧烈的区域,3种方案的后视镜后面和侧窗外侧均有漩涡产生. 3种方案计算条件(边界条件和初始条件)均相同,计算了速度120 km/h行驶的汽车气动噪声问题,并分析了其结果.
气流流经后视镜,产生气体分离和脱落,形成了漩涡,图 6为3种方案的速度矢量图.由图 6可知:方案Ⅰ后视镜后侧与侧窗外前侧流场区是主漩涡区,且有漩涡贴近侧窗;方案Ⅱ后视镜后侧与侧窗外侧流场区均有漩涡,且无漩涡贴近侧窗后;方案Ⅲ后视镜后侧与侧窗外侧流场区均有漩涡,且漩涡偏离侧窗.方案Ⅲ的流场区域中的漩涡比方案Ⅰ和方案Ⅱ偏离侧窗较远,这就减弱了由后视镜产生的湍流压力脉动直接作用在侧窗玻璃上引起的气动噪声,方案Ⅲ的后视镜底部特征凸起将后视镜后侧的漩涡向远离侧窗的方向偏离,故方案Ⅲ能较好地改善流场分布.

|
图 6 后视镜速度矢量图 |
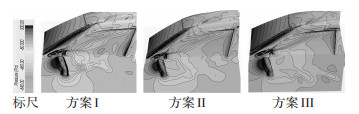
图 7是3种方案压力云图.由图 7可知:方案Ⅰ后视镜后侧与侧窗外前侧等压线较密集,压力梯度变化大,气流速度变化大,气流容易产生分离,致使漩涡生成、脱落、破裂,气流的湍流程度加剧,此区域脉动压力远高于其它部位,且贴近侧窗区域变化更为剧烈;方案Ⅲ后视镜后侧与侧窗外侧等压线较稀疏,压力梯度变化较小,气流分离和再附着程度较小,且湍流区域由侧窗向外偏离,压力脉动要优于其它两种方案.方案Ⅲ后视镜底部特征凸起能较好削弱由后视镜引起湍流脉动压力变化,改善了声源分布,因此是一款较好的后视镜.
|
图 7 后视镜压力云图 |
车外的气动噪声主要由风窗噪声构成,为便于评价噪声分布情况,在车外和侧窗上布置了4个监测点(后视镜正后方、后视镜镜臂上方、前三角窗及驾驶员左耳同高度的侧窗玻璃上),最后一个监测点的声压级频谱曲线如图 8所示.由图 8可以看出:风窗噪声具有较宽的频率范围,属于宽频带噪声,无明显峰值出现,其能量主要分布在低频段,随频率的逐渐增加而逐渐下降,在1 800 Hz以上频率段能量衰减较缓慢,趋于平稳.比较发现3条曲线随频率增加变化趋势基本一致.方案Ⅰ曲线位于曲线族上方,方案Ⅲ的曲线位于曲线族下方且声压级在整个频率段均较小,该方案后视镜底部特征凸起削弱了行驶过程中形成的气动噪声能量,故方案Ⅲ的凸起有较好的降噪功能.

|
图 8 外场测点频谱 |
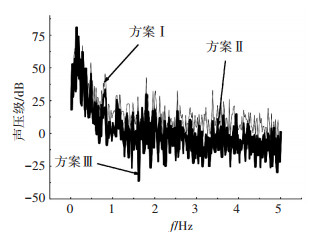
在工程上,评价车内气动噪声水平的高低均在驾驶员左耳布置一个监测点,图 9是驾驶员左耳处监测点的频谱曲线.玻璃对宽频噪声隔声量随频率的变化而改变,由后视镜引起的宽频气动噪声通过车窗玻璃向车内传播时,玻璃的隔声量不同,由于实验时没有考虑玻璃结构细节及分层,也忽略了玻璃的滤波作用,故频谱曲线中波峰较多,但频率在1 800 Hz以上无明显波峰,这是宽频噪声特性.后视镜的基频为40 Hz左右,能量基本集中在低频段,故有图 9的峰值出现,中高频段的能量随频率的增加衰减缓慢,逐渐趋于平稳,方案Ⅲ的底部特征凸起可较好地改善气动噪声经侧窗传递至车内声场的分布,提高了司乘人员乘坐的舒适度.
|
图 9 内场测点频谱 |
1) 采用Star-CCM+和ACTRAN相结合的方法,对某车型三款后视镜进行CFD和声学仿真计算.全域和子域分步计算流场,采用声类比的思想结合计算声场得到的结果与试验结果吻合较好,验证了此数值计算方法的正确性.
2) 汽车以120 km/h的速度行驶时,方案Ⅲ的后视镜底部特征凸起削弱了气流流经后视镜产生压力梯度变化,将车外流场漩涡位置由侧窗向外显著偏离,减少了湍流脉动压力对侧窗的作用,改善了声场的分布,提高了司乘人员的舒适性.
3) 后视镜的基频为40 Hz,决定了气动噪声的能量主要分布在低频段,并随频率逐渐增加而下降,在1 800 Hz以上频率段能量衰减较缓慢,并趋平稳.
4) 本文方法可优化车内声场分布,为汽车研发设计阶段的声学计算提供了一种可靠的计算方法.
| [1] |
NELSON P A, HALLIWELL N A, DOAK P E. Fluid dynamics of flow excited resonance, part Ⅱ:flow acoustic, interaction[J]. Journal of Sound and Vibration, 1983, 91(3): 375-402. DOI:10.1016/0022-460X(83)90287-0 |
| [2] |
LIGHTHILL M J. On sound generated aerodynamically. Ⅰ. general theory[J]. Mathematical and Physical Sciences, 1952, 211(1107): 564-587. DOI:10.1098/rspa.1952.0060 |
| [3] |
LIGHTHILL M J. On sound generated aerodynamically. Ⅱ. turbulence as a source of sound[J]. Mathematical and Physical Sciences, 1954, 222(1148): 1-32. DOI:10.1098/rspa.1954.0049 |
| [4] |
CURLE N. The influence of solid boundaries upon aerodynamic sound[J]. Mathematical and Physical Sciences, Series A, 1955, 231(1187): 505-514. DOI:10.1098/rspa.1955.0191 |
| [5] |
FFOWCS-WILLIAMS F E, HAWKINGS D L. Sound generation by turbulence and surface in arbitrary motion[J]. Mathematical and Physical Sciences, Series A, 1969, 264(1151): 321-342. DOI:10.1098/rsta.1969.0031 |
| [6] |
LOKHANDE B, SOVANI S, XU J. Computational aeroacoustic analysis of a generic side view mirror[C]//Noise and Vibration Conference and Exhibition. Warrendale: SAE, 2003.
|
| [7] |
HOWE M. Theory of Vortex Sound[M]. Cambridge: Cambridge University Press, 2003.
|
| [8] |
MARIE C, YVES D. MICHAEL H, et al. A comparison between the effects of turbulent and acoustic wall pressure fluctuations inside a car[C]//18th AIAA/CEAS Aeroacoustics Conference. Colorado: Springs, 2012: 1-8.
|
| [9] |
BUCHHEIM R, DOBRZYNSKI W, MANKAU H, et al. Vehicle interior noise related to external aerodynamics[J]. International Journal of Vehicle Design, 1982, 3(4): 398-410. |
| [10] |
傅立敏. 汽车空气动力学[M]. 北京: 机械工业出版社, 1998: 103-105.
|
| [11] |
刘龙贵, 谷正气, 张勇, 等. 汽车车身部件气动噪声贡献量数值模拟研究[J]. 科学技术与工程, 2014, 14(10): 90-94. |
| [12] |
李启良. 汽车后视镜非定常流动与气动噪声研究[D]. 上海: 同济大学, 2010: 25-34.
|
| [13] |
李启良, 杨志刚, 陈枫. 汽车后视镜流场的试验与数值研究[J]. 同济大学学报, 2011, 39(7): 1645-1649. |
| [14] |
汪怡平, 谷正气, 杨雪, 等. 微型客车后视镜气动噪声仿真分析与控制[J]. 航空动力学报, 2009, 24(7): 77-1583. |
| [15] |
王毅刚, 杨超, 杨志刚, 等. 汽车外表面气动噪声特性分析[J]. 声学技术, 2014, 33(1): 50-55. |
| [16] |
FELTEN F, FAUTRELLE Y, TERRAIL D, et al. Numerical modeling of electro-gnetically-riven turbulent flows using LES methods[J]. Applied Mathematical Modeling, 2004, 28(1): 15-27. |
 2016, Vol. 48
2016, Vol. 48


