大型设备的备件需求模式一般为间断型,例如重型机械、航空宇航等的维修备件,其价值能达到总库存价值的60%.备件需求模式为间断型时,表现为需求发生随机,需求量波动明显. Johnston给出了间断型需求模式的判别方法:相邻两次需求发生的间隔时间大于1.25倍的观测周期[1].经典的需求预测方法如移动平均法、指数平滑法等对间断需求模式并不适用.因此,根据间断需求模式的特点提出精确的需求预测方法变得尤其重要.关于间断需求预测的研究,最早的有Croston预测方法,该方法分别采用指数平滑法对需求量和需求间隔进行预测[2].针对Croston方法存在有偏估计以及假设需求服从正态分布等问题,出现不少对Croston方法改进的文献[3-4].然而,Croston方法只能计算每期的平均需求. Thomas等[5]引入bootstrap方法对间断需求进行预测,华中生等[6]在此方法基础上加入解释变量的影响,提出IFM预测方法. Bootstrap方法假定需求时间序列存在自相关性难以得到保证,并且只能得到提前期需求分布.智能学习算法被广泛应用到需求预测中,Gutierrez[7]、Kourentzes[8]运用神经网络预测备件需求量,虽然能计算每期的备件需求,但是预测精度并不高.张瑞[9]采用支持向量机预测需求发生时间.此外,时间聚合方法近年来也被应用到间断需求预测中以减小零值及波动性[10],Kourentzes等[11]据此提出ADIDA预测方法,并用实验分析了该方法的预测效果. Babai等[12]用实验分析了时间聚合在间断需求备件库存管理中的作用.但备件需求数据聚合后,不可避免地会丢失一些信息,如观测值减少.
本文提出一种间断需求预测方法,能预测需求发生时间以及需求量值.将实际备件需求时间序列转换为0-1需求发生时间序列,采用神经网络对调制后的0-1需求发生时间序列预测,利用时间聚合方法对实际备件需求时间序列预测,解聚合后得到备件需求预测值.
1 需求发生时间预测 1.1 0-1需求发生时间序列的调制处理为了对需求发生时间进行预测,首先将实际备件需求时间序列X=(x1, x2, …, xn)转换为0-1需求发生时间序列 F =(f1, f2, …, fn).在0-1时间序列中,“0”表示未发生需求,“1”表示发生需求.神经网络具有拟合任意非线性函数及一定的泛化能力,是一种比较成熟的预测模型,由于需求发生时间序列中只含有0和1,不适宜直接用神经网络进行预测,需要将0-1需求发生时间序列转换为连续平滑的序列.
将0-1需求发生时间序列转换为平滑连续的时间序列,可以借鉴数字调制技术,调制是将信号加到载波上,使载波随信号的变化而变化,因此调制后的时间序列依然能够保持原始的数据信息,同时,更加容易被神经网络模型拟合.比较简单的调制方法是幅度调制,即载波幅度随原始信号变化.调制的关键在于载波的设计.原理上,载波波形可以是任意的,由于正弦信号形式简单,通信系统中一般选择正弦信号作为载波.本文对0-1时间序列调制的目的在于使0-1时间序列拓展成一个平滑连续的时间序列,因此对载波的选择根据预测精度而定.选择正弦函数、二次函数、高斯函数以及墨西哥草帽小波函数几个偶函数分别进行试验,通过试验对比分析后,以下面一组数字信号作为载波:
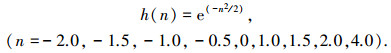
|
预测精度最高.
为减少已调制序列中的零值,用-1代替需求发生时间序列F中的0值,令新的需求发生时间序列为P,那么,已调制序列Y为
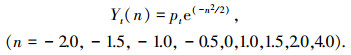
|
将需求发生时间序列F转换为平滑的时间序列Y后,采用神经网络模型外推得到其预测值.由已调制信号分析可知,当ft=1时,Yt(n)>0, (n=-2.0, -1.5, -1.0, -0.5, 0, 1.0, 1.5, 2.0),当ft=0时,Yt(n) < 0, (n=-2.0, -1.5, -1.0, -0.5, 0, 1.0, 1.5, 2.0).因此,可以通过预测值是否>0来判断对应时间是否有需求发生.以完整波形作为神经网络的输入,输出下一个波形的前面两个值Yt+1(n=-2.0)和Yt+1(n=-1.5),由于第一个值Yt+1(n=-2.0)处于两个波形之间的过渡阶段,比较难以正确预测,因此选择第二个值Yt+1(n=-1.5)来判定对应时间段的需求发生预测值ft+1.
当Yt+1(n=-1.5)>0时,ft+1=1;
当Yt+1(n=-1.5) < 0时,ft+1=0.
1.2 0-1需求发生时间序列的预测步骤以下给出0-1需求发生时间序列预测的具体步骤.
Step 1 实际备件需求时间序列X =(x1, x2, …, xn)转换为0-1需求发生时间序列 F =(f1, f2, …, fn);
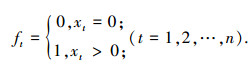
|
为方便后面步骤的调制处理,一般文献中,0-1需求发生时间序列中用0表示没有发生需求; 而在本文中,0值用-1代替,令新的需求发生时间序列为 P, 且;

|
Step 2 对需求发生时间序列进行调制处理,得到已调制序列Yt(n);
Step 3 使用神经网络模型对调制后的序列进行预测得到预测值Yt+1(n=-1.5);
Step 4 将已调制序列的预测值转换为0-1需求发生时间序列的预测值ft+1.

|
在Step 3中,采用应用比较广泛的BP神经网络模型.对只有一个隐层的神经网络,当隐层节点足够多时,就可以以任意精度逼近一个非线性函数[13],因此设计的BP神经网络有3层.输入层节点数和隐层节点数的选取会影响BP网络的预测精度,但目前并没有标准方法来选择这两个参数,只能对多种网络结构进行大量学习实验后确定合适的值.当神经网络的结构比较简单时,这样训练的神经网络具有较好的泛化性.因此,设计隐层节点数为3,这是逼近任意一个复杂的非线性函数相对来说所需要的最小的隐层节点数[14].以整数个载波波形作为输入,每个载波波形中有9个离散点,则输入层节点数为9n,其中,n为正整数.以预测精度为评判标准,对多种输入节点进行大量实验,以此来确定神经网络的输入节点数.输出层节点数为2.
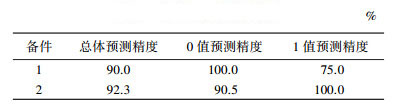
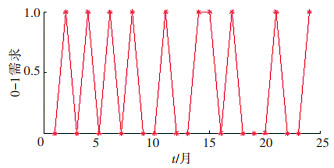
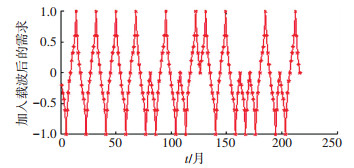
下面通过备件需求实例来介绍需求发生时间的预测.备件需求实验数据有2组,分别来自文献[9, 15],是核电设备的备件需求数据,其信息在3.1节介绍.将实际备件需求时间序列转换为0-1需求发生时间序列,如图 1所示,对其进行调制处理,调制后的时间序列如图 2所示.采用BP神经网络模型对数据进行预测.通过大量实验及比较确定:输入层节点数为27,隐层传递函数为tansig,输出层传递函数为purelin.用总体数据的4/5作为训练数据,1/5作为测试数据,得到备件1、2需求发生时间的预测结果如表 1所示,其中0-1需求发生时间序列的预测精度计算公式在3.2节介绍.
|
图 1 备件1需求发生时间序列 |
|
图 2 备件1调制处理后的时间序列 |
| 表 1 备件1、2预测精度 |
取不同载波形式,备件1、2的0-1需求发生时间序列的预测结果如表 2所示.从表 2预测结果可以看出,当载波选择高斯函数时,预测精度是最高的.取高斯函数中的离散点作为载波时,两个相邻载波的过渡更加平缓,因此,预测值可能更加准确.
| 表 2 不同载波形式的备件预测结果对比 |
间断型备件需求时间序列具有两个特点:需求发生的零星性,即有的时间段上没有需求发生;变化性,即需求量值的起伏波动比较大.基于这两个特点,间断时间序列的预测误差很大.对于间断时间序列,时间聚合是一个有效的预测方法.间断时间序列聚合后,零值减少,方差减小,因此更容易预测.其主要步骤为:
1) 原始数据聚合.时间聚合就是改变观测周期长度,假设实际备件需求时间序列中的观测值为月需求量,当聚合水平为3时,相邻3个月需求量相加得到一个季度需求量.对于聚合水平的选择,一般是通过实验获得一个比较好的数值.
2) 聚合数据预测.实际备件需求时间序列聚合后,不再表现出间断特性,或间断特性不是很明显,因此预测方法可以有多种选择,在本章节仍然采用神经网络对聚合后的时间序列进行预测.
3) 解聚合.对聚合时间序列预测值进行解聚合,即仍使用原始的时间长度作为观测周期长度,例如将季度需求量转换为月需求量.若聚合水平为a,解聚合后得到a个时间段的预测值xt, t=(n+1, n+2, …, n+a).由第1节的预测方法获得0-1需求发生时间序列的预测值ft,t=(n+1, n+2, …, n+a). ft=0表示需求未发生,需求量预测值ft=0. ft=1表示发生需求,假设预测t=(n+1, n+2, …, n+a)时间段中有z个时间段发生需求,通过聚合后的需求量预测值ym平均,可以得到对应时间段需求发生时的需求量预测值x :
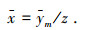
|
下面给出基于时间聚合的预测方法的体算法步骤.
Step 1 设聚合水平为a,实际备件需求时间序列X =(x1, x2, …, xn),计算聚合时间序列Y =(y1, y2, …, ym), m=[n/a],即ym=x(m-1)a+1+x(m-1)a+2+…+xma.
Step 2 用神经网络模型计算Y =(y1, y2, …, ym)的预测值ym+1.已知ym+1对应时间段的0-1需求发生时间序列预测值(fn+1, fn+2, …, fn+a),初始设定z=0,t=n+1.
Step3 判断ft是否为0,如果ft=0, 那么xt=0,如果ft≠0, 那么z=z+1;
Step 4 令t=t+1,如果t≤n+a,则转到Step 3;如果t>n+a,则转到Step 5;
Step 5 令ft中值为1所对应的时间段集合为I={i|fi=1}, i∈{n+1, n+2, …, n+a},则第i期的需求量预测值为xi=ym+1/z.
在运用时间聚合方法对实际备件需求时间序列预测时,还存在这样一个问题,1.2节中0-1需求发生时间的预测是一种单步预测,而本章节的预测方法是一种多步预测.若对需求发生时间也进行多步预测,则预测精度会降低.
为解决这个问题,本文采用一种滚动预测方法,其实质是通过不断更新实际备件需求时间序列来达到单步预测的目的,具体算法如下:
Step 1 初始时刻,设i=0,定义a为聚合水平,n为当前期;
Step 2 获得聚合时间序列的预测值ym+1;
Step 3 对0-1需求发生时间序列进行(a-i)步预测,获得0-1需求发生时间序列的预测值ft,t=(n+1+i, n+2+i, …, n+a);
Step 4 解聚合后获得需求量预测值zt,t=(n+1+i, n+2+i, …, n+a),则(n+i+1)期的需求量预测值为xn+1+i=zn+1+i;
Step 5 获得更新的实际备件需求时间序列;
Step 6 令i=i+1,如果i < a,转到Step 2;如果i≥a,转到Step 7;
Step 7 结束.
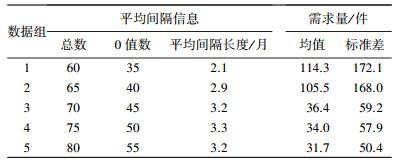
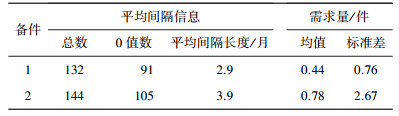
3 实验验证 3.1 实验数据分别采用具有间断形式的时间序列以及备件需求实例对文中预测方法进行验证.间断时间序列样本分为两类:1)通过在三一重工砼活塞的需求数据中随机插入零值来获得间断型需求数据,以不同地区砼活塞的连续型需求数据产生5组间断型需求数据;2)采用2组核电设备关键件的备件需求数据(分别来自文献[9]、[15]).两种实验数据的统计信息如表 3、4所示.
| 表 3 砼活塞需求数据统计信息 |
| 表 4 核电设备备件需求数据统计信息 |
0-1需求发生时间序列的预测精度为
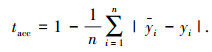
|
根据公式定义,对于i时间段,只有当预测值yi和实际值yi都等于1或者都等于0时,预测结果正确.汇总预测错误的次数,除以总的期数n,可以获得平均需求发生时间的预测精度tacc.
3.2.2 需求量预测误差计算公式需求量的预测误差可以用相对误差来衡量,但是由于某些时间段的需求量为0,为降低分母中出现零值的概率,采用
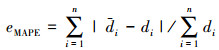
|
作为误差计算公式.式中di为第i期的实际备件需求量,di为第i期的备件需求量预测值.
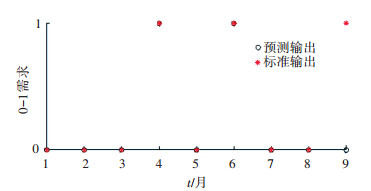
3.3 间断时间序列验证对由砼活塞需求数据所产生的间断时间序列进行预测.间断时间序列转换为0-1序列,对其进行调制处理,采用BP神经网络模型对数据预测.通过大量实验后,经比较确定输入层节点数为27,隐层传递函数为tansig,输出层传递函数为purelin.用总体数据的3/4作为训练数据,剩余1/4作为测试数据,得到数据1的预测结果如图 3所示.
|
图 3 数据1的需求发生预测结果 |
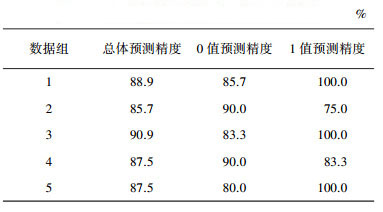
0-1时间序列的预测统计信息如表 5所示,从表 5可以看出,5组数据的需求发生时间的总体预测精度为90%左右,说明该方法具有可行性.
| 表 5 5组数据的需求发生时间预测精度 |
数据1的预测实现过程如下:大量实验后,经比较确定聚合水平为3,神经网络的输入层节点数为3,隐层传递函数为tansig,输出层节点为1,传递函数为purelin.用总数据的3/4作为训练数据,1/4为测试数据,预测结果如图 4所示.

|
图 4 数据1的预测结果 |
其它各组数据的最终预测误差结果见表 6,并与Croston方法的预测误差对比,在相关文献中,一般将Croston方法用于对比实验.
| 表 6 本文方法与Croston方法预测误差比较 |
从表 6可以看出,5组数据的预测误差在60%左右,而Croston方法的预测误差在120%左右.上述结果证明本文提出的预测方法是有效的.
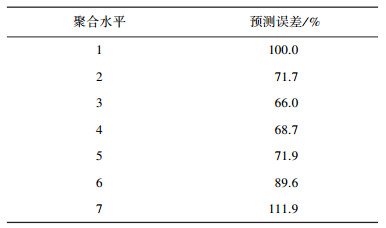
3.4 备件需求实例验证在1.2节中完成了备件1、2中0-1需求发生时间序列的预测,并用图表形式呈现了预测结果.在需求量值的预测实验中,通过实验分析获得聚合水平,表 7给出了不同聚合水平时备件1的需求量预测精度,当聚合水平为3时,预测精度最高,因此,选择备件1的聚合水平为3,同理可获得备件2的聚合水平为3.
| 表 7 不同聚合水平的预测误差对比 |
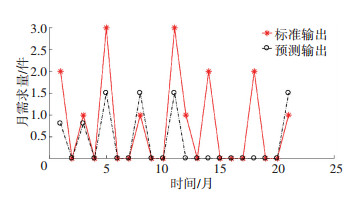
神经网络模型的输入节点数为2,隐层传递函数为tansig,输出层节点数为1,传递函数为purelin.解聚合后其预测值如图 5和图 6所示,从图 5和图 6可以看到,预测值比较接近真实值.
|
图 5 备件1的预测结果 |
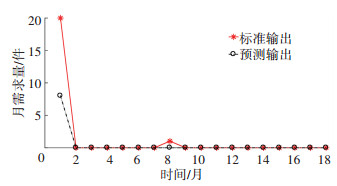
|
图 6 备件2的预测结果 |
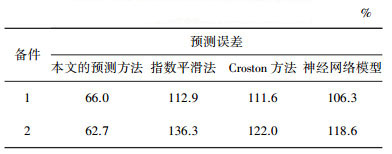
表 8给出了本文提出的方法与指数平滑法、Croston方法以及神经网络方法的预测误差结果比较.
| 表 8 备件需求实例的预测误差对比 |
从表 8中可以看出, 本文所提出的预测方法的预测误差小于其它预测方法,实验对比分析表明本文所提出的预测方法的预测效果更好.
4 结论1) 备件的需求模式一般为间断型,本文通过分析间断模式备件需求时间序列的相关特性,提出了相应的需求预测方法,通过该方法能预测得到需求发生时间以及需求发生时的需求量值.
2) 通过采用间断时间序列和核电设备备件需求实例验证本文所提方法的准确性,预测结果和Croston方法、指数平滑法、神经网络方法对比,实验结果表明本文所提出的方法具有较高的预测精度.
| [1] |
SYNTETOS A A, BOYLAN J E, CROSTON J D. On the categorization of demand patterns[J]. Journal of the Operational Research Society, 2005, 56(5): 495-503. DOI:10.1057/palgrave.jors.2601841 |
| [2] |
CROSTON J D. Forecasting and stock control for intermittent demands[J]. Operational Research Quarterly, 1972, 23(3): 289-304. DOI:10.1057/jors.1972.50 |
| [3] |
BABAI M Z, SYNTETOS A A, TEUNTER R. Empirical heuristics for improving intermittent demand forecasting[J]. Industrial Management & Data Systems, 2013, 113(5): 682-697. |
| [4] |
MUKHOPADHYAY S, SOLIS A O, GUTIERREZ R S. The accuracy of non-traditional versus traditional methods of forecasting lumpy demand[J]. Journal of Forecasting, 2012, 31(8): 721-735. DOI:10.1002/for.v31.8 |
| [5] |
THOMAS W R, CHARLES S N, SCHWARZ H F. A new approach to forecasting intermittent demand for service parts inventories[J]. International Journal of Forecasting, 2004, 20(3): 375-387. DOI:10.1016/S0169-2070(03)00013-X |
| [6] |
HUA Zhongsheng, ZHANG Bin, YANG Jie, et al. A new approach of forecasting intermittent demand for spare parts inventories in the process industries[J]. Journal of the Operational Research Society, 2007, 58(1): 52-61. DOI:10.1057/palgrave.jors.2602119 |
| [7] |
GUTIERREZ R S. Lumpy demand forecasts using neural networks[J]. International Journal of Production Economics, 2008, 111(2): 409-420. DOI:10.1016/j.ijpe.2007.01.007 |
| [8] |
KOURENTZES N. Intermittent demand forecasts with neural networks[J]. International Journal of Production Economics, 2013, 143(1): 198-206. DOI:10.1016/j.ijpe.2013.01.009 |
| [9] |
张瑞. 不常用备件需求预测模型与方法研究[D]. 武汉: 华中科技大学, 2011: 47-62.
|
| [10] |
ALTAY N, LITTERAL L A. Service parts management:demand forecasting and inventory control[M]. London: Springer-Verlag London Limited, 2011: 89-101.
|
| [11] |
KOURENTZES N, SYNTETOS A A, BOYLAN J E, et al. An aggregate-disaggregate intermittent demand approach (ADIDA) to forecasting:an empirical proposition and analysis[J]. Journal of the Operational Research Society, 2011, 62(3): 544-554. DOI:10.1057/jors.2010.32 |
| [12] |
BABAI M Z, MOHAMMAD M A, KONSTANTINOS N. Impact of temporal aggregation on stock control performance of intermittent demand estimators:empirical analysis[J]. Omega, 2012, 40(6): 713-721. DOI:10.1016/j.omega.2011.09.004 |
| [13] |
张立明. 人工神经网络的模型及其应用[M]. 上海: 复旦大学出版社, 1995: 32-36.
|
| [14] |
CHENG X, DING S Q, LEE T H. Geometrical interpretation and architecture selection of MLP[J]. IEEE Transactions on Neural Networks, 2005, 16(1): 84-96. DOI:10.1109/TNN.2004.836197 |
| [15] |
王玮. 集成多SVM的不常用备件需求预测支持系统研究[D]. 武汉: 华中科技大学, 2007: 44-45.
|
| [16] |
LICHMAN M. UCI Machine Learning Repository: Individual family power consumption[DB/OL]. Irvine, CA: University of California, School of Information and Computer Science, 2013[2015-3-6]. http://archive.ics.uci.edu/ml.
|
 2016, Vol. 48
2016, Vol. 48