航天器电源系统中的太阳电池阵作为航天器的主要能量来源,是航天器不可或缺的组成部分.随着航天任务的复杂性不断增加,为了满足航天器更多的功能要求, 太阳电池阵的创新设计显得尤为重要.可展式太阳翼作为主要的太阳电池阵, 广泛应用于各类航天器.
国内外关于可展式太阳翼的结构和机构的研究取得了一系列的成果.邓宗全等[1-2]一直致力于空间折展机构的理论及应用研究;Puig等[3]总结了现有的不同技术在大型可展结构中的应用;张淑杰[4-5]、陈烈民[6-7]等也致力于空间机械可展结构的设计研究和理论分析.但是关于可展式太阳翼基板构型的研究稀少,基板构型与其折展能力之间的关系未得到足够的重视.对于不同基板构型的太阳翼,其压紧与释放机构、展开机构和驱动机构都是针对特定的基板构型而设计的.理解太阳翼基板的构型设计原理, 不仅有助于太阳翼的整体设计,而且有利于简化太阳翼机构,从而可以快速有效地设计出实用的大面积可展式太阳翼,对减轻太阳翼的质量和提高其可靠性具有重要的意义.
日本著名的构造工学专家Miura[8-9]从现实生活中受到启发发明了“三浦折叠”(如图 1所示),该构型已于1995年被应用于卫星上;杨柏翰大学的博士生Zirbel与美国国家航空航天局喷气推进实验室的机械工程师Trease合作完成了基于折纸的新型折叠式太阳电池阵[10-11]的设计(如图 2所示),并即将运用于未来的空间设备上.这些创新均来自于生活灵感及设计经验,没有利用数学方法进行系统地分析.

|
图 1 三浦折叠的过程 |

|
图 2 新型折纸太阳电池阵 |
本文将从几何学和机构构型的角度系统地研究太阳翼基板构型与折展能力之间的关系,给出太阳翼基板构型基本组成单元的概念并找到各基本单元,建立不同基板构型的几何特征约束方程.同时,运用本文提出的理论来分析现有的可展式太阳翼的基板构型,验证该理论的正确性.最后,通过分析新型太阳翼基板构型建立对应的几何模型.
1 太阳翼基板的构型及其折展原理太阳电池阵按构造可分为体装式和可展式[7, 12].体装式太阳电池阵是较早的一种航天器空间电源的形式之一,它是将太阳电池直接连接在航天器本体表面的某些部位上.由于航天器本体表面积有限,所附着的太阳电池数量受到极大限制,从而提供的能量也有限,只能用在功率需求不高的航天器上.可展式太阳电池阵又可分为太阳桨和太阳翼,两者的区别主要在于基板的数量与展开方式不同.一般太阳翼的基板多、面积大、展开复杂.太阳翼还可根据不同的缩展方式,分为折叠式太阳翼和卷式太阳翼.折叠式太阳翼是由多块相互连接的基板组成,在航天器发射时一直处于折叠收拢状态,进入轨道后展开.与折叠式太阳翼不同,卷式太阳翼的收拢方式是把较大面积的基板卷成较小体积,收放在发射火箭侧壁内,到达既定轨道后由地面控制其打开.按照基板抵抗变形的能力不同,可以把太阳电池阵分为3类:刚性基板、半刚性基板和柔性基板的太阳电池阵.
由于太阳翼基板的最终展开形态是平面,因此,以平面为切入点对太阳翼的基板形状和转动副分布特征进行研究,寻找能够展成平面的太阳翼应该具有的几何特征、对基板形状的特定要求以及转动副的分布规律等.要解决上述问题,必须首先找到具备展成平面能力的空间曲面以及该种曲面如何展开可得到平面.可展曲面具备展成平面的能力,在局部上可以与平面建立保长对应,即沿可展曲面的任意一条直母线剪开后可以贴合在一个平面上.下面将详细介绍可展曲面的概念和性质,建立其与太阳翼基板构型的对应关系.
1.1 可展曲面及其与基板构型对应关系可展曲面是一类重要的直纹面,直纹面有一族直母线,若沿它的每一条直母线只有一个切平面,则这种直纹面称为可展曲面.可展曲面只有3种:柱面、锥面和空间曲线的切线曲面.若某曲面是可展曲面,那么必定是由这3种曲面的一种或几种组成; 反之,若某曲面由这3种曲面的一种或几种组成,则该曲面必定能展为平面.可展曲面及其相关定义的数学表示如下.
若曲面S的参数方程表示r(u, v)= a(u)+vb(u),其中b(u)是单位向量,则S是直纹面.如果直纹面满足(a'(u), b(u), b'(u))=0,则该直纹面为可展曲面,其中a'(u)和b'(u)分别为向量a(u)和向量b(u)的切向量,(a'(u), b(u), b'(u))=0表示a'(u)、b(u)和b'(u)的混合积为0.空间曲线Γ= a(u)是可展曲面的准线,b(u)是可展曲面直母线上的单位向量.当b(u)是常向量时,曲面S为柱面,如图 3(a)所示;当a(u)为常向量时,曲面S为锥面,如图 3(b)所示;当a'(u)// b(u)时,曲面S为切线曲面,如图 3(c)所示.

|
图 3 可展曲面分类 |
可展曲面在展开过程中绕其直母线旋转展开成平面,它在绕直母线展开且未展成平面时仍然保持可展曲面的几何特征,即柱面在展开过程中仍然是柱面,锥面仍然是锥面,切线曲面也仍然是切线曲面.从可展曲面参数方程的角度进行分析,对于柱面而言,其直母线的方向向量b(u)为常向量,故柱面上所有的直母线相互平行;对于锥面而言,其参数方程中a(u)是常向量,故锥面上所有直母线交于空间一点;曲线的切线曲面的参数方程中a'(u)// b(u),亦即准线上某点的切线与该点处的直母线平行.
可展曲面在展开成平面的过程中绕直母线旋转展成平面.类比到太阳翼基板构型上,可展曲面代表所有太阳翼基板组成的面,可展曲面上的直母线代表太阳翼基板间的转动副,两直母线之间的曲面代表基板.
太阳翼基板构型主要由基板和基板间的转动副的分布决定.基板间的转动副和基板都可以利用可展曲面的参数方程来表示.确定转动副需要确定转轴方向及其位置.基板间的转动副转轴方向可由可展曲面直母线上的单位矢量b(u)表示,而转动副位置由可展曲面上对应的点r(u, v)= a(u)+vb(u)来描述.单块刚性基板一般为平面,平面可由两条不共线的共面直线来确定,所以对于夹在转动副之间的基板可由两条连接基板的转动副轴线所在直线来确定其位姿,对于只有一条转动副与其相连的基板可由这条转动副轴线所在直线与基板边界所在直线确定其位姿.
1.2 太阳翼基板基本构型分析 1.2.1 卷式柔性太阳翼基板构型如果可展曲面上所有的直母线都作为转动副,对应的太阳翼基板是柔性的,并不存在刚性部分,这种结构在展开且未展成平面的过程时时刻刻都是可展曲面,所以这种结构能展开成平面,它适用于卷式柔性太阳翼. 图 4(a)为简单的柱面型柔性太阳翼基板构型,图 4(b)为简单的锥面型柔性太阳翼基板构型,图 4(c)为渐开线螺旋面型柔性太阳翼基板构型,是切线曲面型柔性太阳翼基板构型的一种.

|
图 4 卷式柔性太阳翼基板构型分类 |
如果在可展曲面上选择有限条直母线当作转动副,对应于太阳翼的基板构型上,相邻直母线之间的曲面代表基板,可展曲面上的直母线则代表基板之间的连接转动副,这种太阳翼基板构型既适用于折叠式刚性太阳翼也适用于折叠式柔性太阳翼.下面针对这种基板构型的不同类型, 阐述其与可展曲面的对应关系和折展原理,同时给出不同太阳翼基板构型对应的几何特征约束方程.
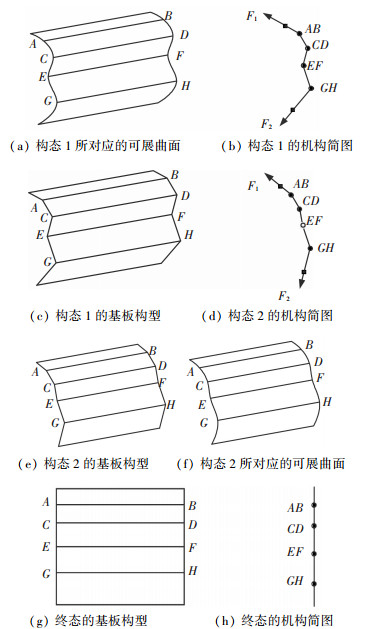
1.2.2.1 柱面型折叠式基板构型分析柱面型折叠式基板构型是将柱面的任意有限条直母线作为转动副且把直母线之间的曲面当做基板形成的太阳翼基板构型,该基板构型任意相邻的两转动副相互平行.下面以柱面上选取的4条直母线作为转动副为例来说明这种基板构型能展开成平面.如图 5(a)所示,4条直母线分别为AB、CD、EF、GH.如果把直母线之间的曲面当作刚体,则其转化成的等效机构如图 5(b)所示.在不改变刚体上连接的运动副相对位置的情况下, 可以把直母线之间曲面换成平面(如图 5(c)所示).在该机构展开成平面的过程中,由于转动副的轴线始终平行(如图 5(d)所示),转动副代表的直母线始终平行(如图 5(e)所示),且从一个柱面上的直母线变成了另一个柱面上的直母线,即从图 5(a)所示的柱面变到图 5(f)所示的柱面,而该柱面能展开成平面,所以该机构的转动副一直处于柱面上,直到展成平面(如图 5(g)所示),图 5(h)为图 5(g)的机构简图.
|
图 5 柱面型折叠式太阳翼基板展开过程 |
下面用数学公式来描述柱面型折叠式基板构型的几何特征.从同一构态的几何特征、不同构态的几何特征和最终构态的几何特征3方面来建立约束方程. ri(uj, vk)表示构态i的第j个转动副轴线上的某点,它的表达式如下:
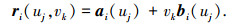
|
式中:bi(uj)为构态i的第j个转动副转轴所在直母线的方向向量,ai(uj)为该转轴所在的直母线与准线交点的位置向量,vk为用来确定转轴上点的位置参数.当i=L时,基板处于终态,即完全展开构态.
对于含有n个转动副的柱面型折叠式基板构型,在同一构态中所有转动副轴线都平行,对应的约束方程为
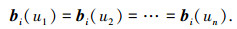
|
在不同构态中基板保持不变形,即在不同构态中任意一条轴线上的任意一点与其相邻转轴上的任意一点距离保持不变,对应的约束方程为
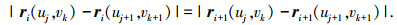
|
对于处于终态的基板构型,它的所有转动副轴线都处于同一平面内,即任意一块基板上的任意一条直线与相邻基板上的任意一条直线共面,对应的约束方程为

|
(1) |
在此说明,同一柱面型折叠式基板构型的边界也处于柱面上,可以把其当做转动副来对待.
如果基板是柔性的,在施加的力合适且机构不处于奇异状态时,外力作用不会导致柔性基板变形.此情况与刚性基板类似,因为在展成平面的过程中机构始终存在自由度.
1.2.2.2 锥面型折叠式基板构型分析锥面型折叠式基板构型是利用锥面的任意有限条直母线作为转动副且把直母线之间的曲面当做基板形成的太阳翼基板构型,该基板构型任意两转动副相交于一点.锥面型折叠式基板构型的分析方法与柱面型相似,它的等效机构的转动副轴线从一个锥面上转变到另一个锥面上,但始终处在锥面上,而锥面能展成平面,所以锥面型折叠式基板构型最终能展成平面.柔性基板和刚性基板都适用于这种基板构型.
下面用数学公式来描述锥面型折叠式基板构型的几何特征.从同一构态的几何特征、不同构态的几何特征和最终构态的几何特征3方面来建立约束方程.对于含有n个转动副的锥面型折叠式基板构型,在同一构态中所有转动副转轴交于一点,对应的约束方程为

|
(2) |
在不同构态中基板保持不变形,即在不同构态中任意一条转动副轴线与其相邻转动副轴线夹角保持不变,对应的约束方程为
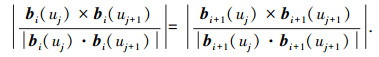
|
(3) |
对于处于终态的基板构型,它的所有转动副轴线都处于同一平面内,即任意一块基板上的任意一条直线与相邻基板上的任意一条直线共面,其对应的约束方程与式(1)相同.
在此说明,同一锥面型折叠式基板构型的边界也处于锥面上,可以把其当做转动副来对待.
1.2.2.3 切线曲面型折叠式基板构型分析柱面型和锥面型基板构型具有共同特点, 即任意相邻的两个转动副轴线始终处于同一个平面内.
利用切线曲面的有限条直母线作为转动副且把直母线之间的曲面当作刚性基板形成的机构.一般情况下,任意选取相邻的两个转动轴不处于同一个平面内,展开过程中不能把所有转动副转到同一平面内,它将最终无法展开成平面.如果直母线之间的曲面是柔性基板,那么只有这些柔性基板变形时,才能使切线曲面所代表的整个太阳翼展成平面.
由上述分析可知,可展曲面仅包括柱面、锥面和切线曲面,基板构型均可由柱面、锥面和切线曲面3类基本单元构成.柔性基板构型可由这3类基板单元和它们之间的组合构成,而刚性折叠式太阳翼基板构型仅有柱面、锥面及柱面锥面组合型这3类.
2 现有太阳翼基板的构型分析可展式太阳翼是现今大部分航天器主要的电力来源,因此,它的设计对航天器至关重要.太阳翼基板的构型又是设计太阳翼展开机构、锁定机构和释放机构等其它机构的基础,这些机构必须针对不同的太阳翼基板构型来设计.由于航天运载器结构尺寸的限制与高运载成本,太阳翼必须具有较高的折展比,以尽可能减轻质量.减小太阳翼质量主要有两条途径:使用较轻的材料和简化太阳翼的结构或机构.在材料选择一定的情况下,优化太阳翼结构显得尤为必要.
下面从太阳翼基板的折展原理并结合基板构型的设计要求来分析现有的可展式太阳翼.在下文提到的折叠式刚性太阳翼基板构型的基板可以是刚性的也可以是柔性的,而折叠式柔性的太阳翼基板构型的基板必须是柔性的,否则不能展开成平面.其原因可以从机构学的角度进行解释:折叠式刚性太阳翼构型可以等效成机构,如果它能展开成平面,说明这种机构在展开成平面的过程中一直存在自由度,而换成柔性基板对这种机构展开过程并不受影响.
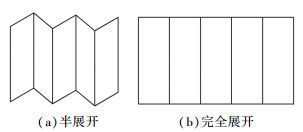
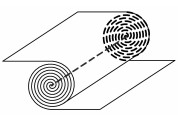
2.1 单柱面型太阳翼基板构型分析单柱面型太阳翼基板构型是由单个柱面直母线为转动副的太阳翼基板构型,主要有单柱面型折叠式刚性太阳翼和单柱面型卷式柔性太阳翼.单柱面型折叠式刚性太阳翼由尺寸相同的矩形基板组成,基板之间由转动副连接,收拢后各个基板能完全贴合在一起,这种构型收拢时体积比较小,展开面积可以较大,但是它有多个自由度,控制复杂,需要锁紧机构和同步机构等其他许多辅助机构. 图 6(a)是其展开过程中的基板构型,这些转动轴一直处于柱面上,图 6(b)是展开后的形状.国际空间站的太阳翼[13]即采用该种基板构型.单柱面型卷式太阳翼的基板是柔性的,其展开过程虽不利于控制,但是收拢后是一个卷起的柱面,具有很大折展比(如图 7所示),可以有效地减小质量,适用于大面积太阳翼.哈勃望远镜的太阳翼[12]就采用了这种基板构型,该构型可利用展开机构使其两边同时伸展成平面.
|
图 6 单柱面折叠式太阳翼基板展开过程 |
|
图 7 哈勃望远镜的太阳翼基板构型 |
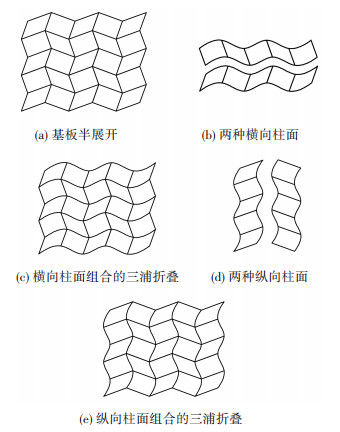
三浦折叠型太阳翼[8-9]是一种多柱面型折叠式太阳翼. 图 8(a)为三浦折叠型太阳翼基板半展开图,可看做是横向的两种柱面组合而成,图 8(b)为两种柱面的形状,图 8(c)为由这两种柱面按照一定的规律组合成的太阳翼基板构型,其转动副始终处于各自柱面上.同时也可以认为它是由两种纵向柱面组合而成,图 8(d)和图 8(e)分别为两种纵向柱面的形状和由这两种柱面组成的太阳翼基板构型.
|
图 8 三浦折叠型太阳翼基板构型 |
这种太阳翼基板构型只有一个自由度,可以不需要同步机构,展开机构能包含展开和同步两种功能,展开控制简单.收拢后各个面贴合在一起,折展比大,适合于各类太阳翼.但该构型也有其缺点,完全展开后收拢会十分困难,这与机构奇异有关.
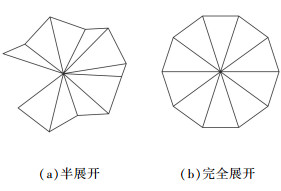
2.3 锥面型太阳翼基板构型分析锥面型折叠式太阳翼一般由尺寸相同的三角形基板组成,有助于收拢时减小体积,增大折展比,柔性基板也适用这种太阳翼基板构型. Ultraflex太阳翼[14]就是采用该种构型,它可以环形展开,图 9(a)为其半展开的形状,它的最终展开图如图 9(b)所示.这种构型适用小面积的太阳翼,同时可作为空间太阳能发电站的基板模块单元.
|
图 9 超柔性太阳翼展开过程示意图 |
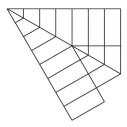
柱面锥面组合型太阳翼基板构型是将多组柱面和锥面的直母线看作转动副形成的基板构型.这是一种新型的太阳翼基板构型[10, 15],由杨柏翰大学和NASA的研究人员通过折纸得到启发研制出来的.这种太阳翼基板构型如图 2所示,它的转动副轴线分布是一种旋转对称图形,由多个锥面和柱面融合在一起形成的太阳翼. 图 10是柱面锥面组合型基板构型的基本旋转图形,该图形的线条在折叠或展开的过程中一直处于锥面和柱面的组合图形上. 图 11为这类太阳翼基板构型的展开过程照片.这种太阳翼基板构型展开过程中基板会发生变形,但可将展开机构包含同步功能,集折叠式和卷式的优点于一身,在收拢或展开的过程中既折叠重合又旋转卷缩,柱面锥面组合型太阳翼的折展比比较大.
|
图 10 基本旋转图形 |

|
图 11 折纸太阳翼的半展开照片 |
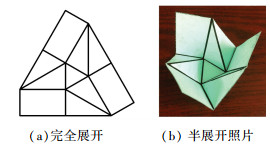
图 11所示的折纸太阳翼基板构型基板会发生变形,针对这个缺点设计一类新型刚性折叠式太阳翼基板构型.它也属于折纸太阳翼基板构型,不仅具备了折纸太阳翼的优点,而且适用于刚性基板和柔性基板. 图 12和图 13为新型刚性折叠式折纸太阳翼基板构型,这两种基板构型分别属于多锥面型基板构型和柱面锥面组合型基板构型,它们收拢时的形状是以中心三角形为底面的三棱柱.通过改变中心正多边形的边数还可设计不同的构型以满足不同需求.
|
图 12 新型多锥面型基板构型 |

|
图 13 新型柱面锥面组合型基板构型 |
图 12中新型多锥面型基板构型所对应的机构是3自由度的闭环过约束机构,选择跟底面正三角形相连的3个直角三角形与正三角形形成的夹角作为分析该基板构型的独立参数.
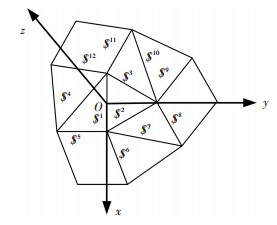
下面将建立多锥面型基板构型的几何模型. 图 14为多锥面型基板构型的半展开分析图,图中$1~ $12代表 12条基板间的转动副.设底面正三角形的边长为2,以它的一条边为x轴,这条边的中点为原点O,过该边相对的顶点和原点的直线为y轴,z轴由右手螺旋法则确定.设β1为左边的直角三角形与底面正三角形的夹角,其他两个的直角三角形与底面相连的3个直角三角形按逆时针分别为β2和β3,其中0≤β1≤π/2,0≤β2≤π/2,0≤β3≤π/2.不难看出, 该基板构型中所有的转动副分布在3个融合的锥面上,锥面的顶点为底面正三角形的3个顶点,转动副轴线$1、$5、$6和$7处于同一个锥面上,转动副轴线$2、$8、$9和$10处于同一个锥面上,转动副轴线$3、$4、$11和$12处于同一个锥面上,其中转动副轴线$1、$2和$3分别同时处在两个不同锥面上.对于分布在同一锥面上的转动副在同一构态中所有转动副转轴都交于一点,即应满足式(2);在不同构态中任意一条转动副轴线与其相邻转动副轴线夹角保持不变,即应满足式(3);处于终态的所有转动副轴线都处于同一平面内,即应满足式(1).通过锥面的参数方程r(u, v)= a(u)+vb(u)结合锥面型折叠式基板几何特征约束方程, 可以确定所有转动副的参数表达式$(u, v)= a(u)+vb(u),转动副参数表达式中包含转动副的位置和转轴的方向信息,其中u是β1、β2和β3的函数,v可取任意值.下面式(4)~(12)是各转动副的参数表达式.
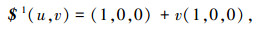
|
(4) |
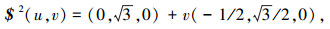
|
(5) |
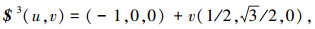
|
(6) |
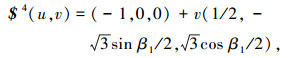
|
(7) |

|
(8) |
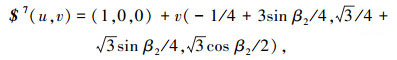
|
(9) |

|
(10) |
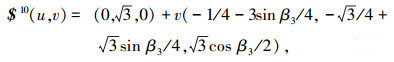
|
(11) |

|
(12) |
|
图 14 新型多锥面型基板构型半展开分析图 |
转动副$6、$9和$12的参数表达式太长,未在文中列出.多锥面型基板构型中的所有基板都连接着至少两条轴线相交的转动副,而转轴副已确定,基板的位姿也将确定,所以所有转动副的参数方程就是该基板构型的几何模型.
4 结论1) 从机构构型角度,把太阳翼基板构型等效成机构来分析折展原理,并建立了不同基板构型的几何特征约束方程.
2) 阐述了太阳翼基板构型均可由柱面、锥面、切线曲面或三者之间的组合演变而来,为太阳翼基板构型创新设计奠定基础.
3) 对现有的太阳翼基板构型进行分类,通过分析现有的太阳翼基板构型验证了它与可展曲面之间的对应关系.
4) 利用可展曲面参数方程和几何特征约束方程建立了新型太阳翼基板构型的几何模型,对太阳翼基板构型建模具有借鉴意义.
| [1] |
邓宗全. 空间折展机构设计[M]. 哈尔滨: 哈尔滨工业大学出版社, 2013.
|
| [2] |
DENG Zongquan, HUANG Hailin, LIU Rongqiang. Synthesis of deployable/foldable single loop mechanisms with revolute joints[J]. Journal of Mechanisms and Robotics, 2011, 3(3): 031006. DOI:10.1115/1.4004029 |
| [3] |
PUIG L, BARTON A, RANDO N. A review on large deployable structures for astrophysics missions[J]. Acta Astronautica, 2010, 67(1): 12-26. |
| [4] |
张淑杰, 李瑞祥, 丁同才. 盘绕式杆状展开机构的设计与力学分析[J]. 力学季刊, 2006(2): 341-347. DOI:10.3969/j.issn.0254-0053.2006.02.025 |
| [5] |
张淑杰, 关富玲, 张京街. 空间可展结构能量节点的设计和动力分析[J]. 工程设计, 2001(2): 53-56. DOI:10.3785/j.issn.1006-754X.2001.02.001 |
| [6] |
袁家军, 陈烈民. 卫星结构设计与分析(下)[M]. 北京: 中国宇航出版社, 2009.
|
| [7] |
陈烈民. 航天器结构与机构[M]. 北京: 中国科学技术出版社, 2005.
|
| [8] |
MIURA K. Method of packaging and deployment of large membranes in space[C]//31st International Conference of Astronautics Federation. Tokyo: IAF, 1980: 1-10.
|
| [9] |
MIURA K. A note on the intrinsic geometry of origami[C]//1st International Conference of Origami Science and Technology. Ferrara: [s. n. ], 1989: 239-249.
|
| [10] |
National Aeronautics and Space Administration. Solar Power Origami-Style[EB/OL]. [2014-08-14]. http://www.nasa.gov/jpl/news/origami-style-solar-power-20140814/.
|
| [11] |
ZIRBEL S A, WILSON M E, MAGLEBY S P, et al. An origami-inspired self-deployable array[C]//ASME 2013 Conference on Smart Materials, Adaptive Structures and Intelligent Systems. Utah: ASME, 2013: 3296.
|
| [12] |
JONE P A, BRIAN R S. Spacecraft solar array technology trends[J]. Aerospace and Electronic Systems, 2011, 26(8): 17-28. DOI:10.1109/MAES.2011.5980605 |
| [13] |
WU S C, GHOFRANIAN S. Anomaly simulation and resolution of International Space Station solar array deployment[C]//Modeling, Simulation, and Verification of Space-based Systems Ⅱ. Bellingham: SPIE, 2005: 38-47.
|
| [14] |
SPENCE B, WHITE S, WILDER N, et al. Next generation ultraflex solar array for NASA's new millennium program space technology 8[C]//IEEE Aerospace Conference. Piscataway: IEEE, 2005: 824-836.
|
| [15] |
ZIRBEL S A, MAGLEBY S P, HOWELL L, et al. Accommodating thickness in origami-based deployable arrays[J]. Journal of Mechanical Design, 2013, 135(11): 103368. |
 2016, Vol. 48
2016, Vol. 48


