2. 汽车仿真与控制国家重点实验室(吉林大学), 130022 长春
2. State Key Laboratory of Automobile Simulation and Control(Jilin University), 130022 Changchun, China
轮式移动机械,如轮式装载机、移动机器人或野外作业车,通常在复杂地形下工作,需要轮式移动机械具有良好的越障性能[1-3].刘昕晖等[4]开发了一种能被动适应复杂地形的轮胎式多功能车,它是一种全地形移动车辆,由前车体和后车体两部分组成,前车体通过能产生横摆和扭转的2自由度铰与后车体连接[4],如图 1所示.相比传统车辆平面运动,2自由度铰接车体车辆能完成复杂的三维运动.

|
图 1 2自由度铰接车体车辆 |
在2自由度铰接车体车辆越障实验中,发现其越障过程中有运动方向偏移现象,需要不断采用方向盘大幅调整运动方向才能使车辆沿预定的路径运动.这种越障运动方向偏移现象使车辆的操控性变得复杂,驾驶员连续不断地操作容易出现失误造成车辆倾翻.为了发挥2自由度铰接车体车辆的使用性能,在环境恶劣崎岖的地形下更好工作,需要研究其无人驾驶时的运动控制,如使其沿直线行驶,完成某项作业任务或者到达某一预定位置.
目前, 国内外有很多关于铰接式车辆的运动控制研究[5-7],其中,Tabatabaei[8]研究了铰接式车辆基于模糊逻辑理论的控制器设计,用于消除铰接式车辆的运动跟踪误差. Bigras等[9]建立了采矿铰接式车辆路径误差的动力学模型,利用中值法将时变非线性系统转化为线性系统,设计了路径的反馈控制. Moon等[10]分析了车辆几何形状、稳定性和安全性,提出了一种新的转向控制算法.上述这些控制方法没有考虑控制输入的饱和现象.在实际工程应用中,考虑到2自由度铰接车体车辆自身结构设计的因素,在运动转向过程中,需要通过液压转向机构进行转向, 控制运动路径.由于液压缸提供的驱动力是有限的,当车轮需要的转向角度过大时,液压缸只能提供恒定的驱动力,输出的转向力矩不能达到计算需要的转向力矩,在控制过程中会导致液压转向机构输出饱和,使实际运动控制路径和理论计算存在偏差.如果车辆在地形起伏比较剧烈的障碍路面运动时,会造成车体运动中实际的倾角比分析计算的大,容易产生倾翻.所以,研究2自由度铰接车体车辆运动控制时,需要考虑到控制输入的饱和现象.
本文首先建立了2自由度铰接车体车辆的越障动力学和运动学模型,然后分析了方程的稳定性和能控性.在考虑控制饱和的情况下,利用反步法设计了控制器,进行2自由度铰接车体车辆运动控制的研究.
1 车辆越障时的动力学方程2自由度铰接车体车辆的前后车体之间的自由度用横摆角θ1和扭转角θ2描述,前车体和后车体之间通过万向铰链连接,车辆转向时,液压缸提供沿O1O2的转向力FO,前车体平面OW1W2转动,前车体传动轴与后车体传动轴夹角即为横摆角θ1;车辆越过左右非对称障碍时,前后车体绕后车体传动轴相对转动产生扭转角θ2,前、后车体驱动力Ff和Fr分别沿前、后车体传动轴指向前.前、后车体质量为mf和mr,前、后车体长度为Lf和Lr,前、后车体瞬心Of和Or在各自轮轴延长线上,由车体转向特性可知,后车体瞬心Of投影到前车体转动平面与前车体转动瞬心Or重合,前、后车体质心在车体投影为Bf和Br,如图 2所示.

|
图 2 2自由度铰接车体车辆运动示意 |
根据车体几何关系,可得
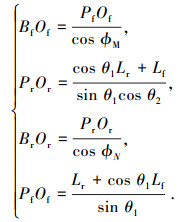
|
(1) |
因为2自由度铰接车体车辆的前后车体为非定常约束,假设作用在车轮上的地面侧向力足够大,车轮运动时无侧滑.牵引力和轮子的滚动阻力的合力在前、后桥中心Pf和Pr点形成两组力和力矩.当前后车体之间的转向铰不动时,作用在Pf和Pr点的力矩和作用在轮子上的地面反作用力矩平衡,整个车体结构可以看作是一个刚体.当转向铰运动时,铰接车运动可以看作是转向铰提供了前后车体之间的相对运动.所以铰接车的运动可以看做是车体的刚体运动和转向铰内部力引起的运动合成.忽略驱动力传递的损耗和液压转向驱动装置的损耗.在动力学模型中,系统输入就是牵引力和前后车体之间的液压转向系统提供的转向力.
当转向铰不运动时,前后车体为绕各自瞬心的刚体运动,则
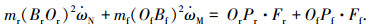
|
(2) |
前、后车体质心在车体上投影Bf和Br到前、后桥中心点Pf和Pr距离≪到瞬心距离,则有cos ϕN≈1,cos ϕM≈1.
前后车体铰接点O加速度为

|
(3) |
前、后车体Pf点和Pr点加速度为
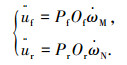
|
(4) |
结合式(1)~(4),可得前、后车体Pf点和Pr点角加速度和加速度为
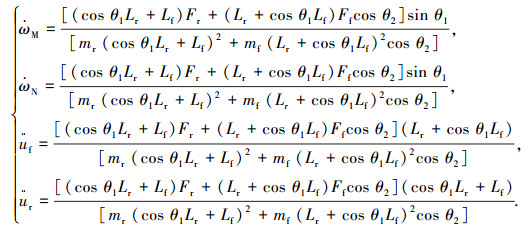
|
(5) |
式中,Ff和Fr是前、后车体的净牵引力(即前、后车体牵引力减去滚动阻力),净引力会使前、后车体在稳态速度上有加减速.
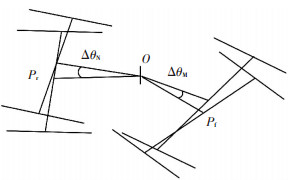
当2自由度铰接车体车辆转向机构转向时,设转向机构的净转向力矩为T0(即转向液压杆输出的转向力矩减去转向阻力矩),转向时示意图如图 3所示.
|
图 3 2自由度铰接车体车辆转向示意 |
转向时,后车体绕Pr点的转向角加速度为
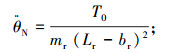
|
(6) |
前车体绕Pf点的转向角加速度为

|
(7) |
式中,bf和br分别为前、后车体质心到前、后桥距离.
式(6)和式(7)相加可得前后车体夹角的角加速度为
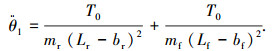
|
(8) |
通过式(5)和式(8),可得前车体角加速度为
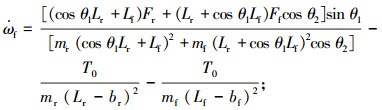
|
(9) |
后车体角加速度为

|
(10) |
综合式(5)和式(8)~(10), 即可得2自由度铰接车体车辆运动时的动力学方程.
2 控制系统的误差动力学方程2自由度铰接车体车辆的非完整约束运动学方程可以用后车体Pr点速度vr,后车体角速度ωr以及前车体相对后车体的角速度rωf描述.给定铰接车期望行驶的直线路径,建立路径坐标系,x轴沿路径,z轴垂直后车体平面,y轴符合右手法则.对于铰接车越障时的直线运动控制,只需要考虑后车体绕z轴的角速度、沿y轴速度和前车体相对后车体的横摆角速度即可,具体为
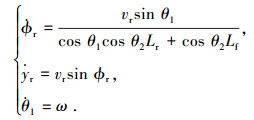
|
(11) |
式中ω为运动学方程控制输入量.
通过控制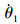
选择状态向量为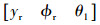
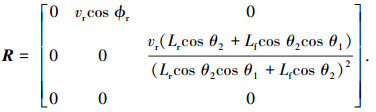
|
其在平衡点的特征根为λ1, 2, 3=0,因此,由线性系统的稳定性判据可知,该系统是临界稳定的.这在实际工程中是不允许的,当系统参数有微小偏移时,其特征值可能变为复平面右半平面的根,必须施加控制.
由控制方程(11)得对应的向量场为
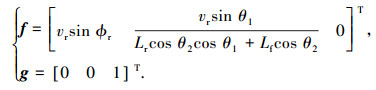
|
通过李括号计算,可得系统能控性矩阵
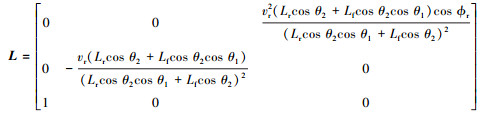
|
因为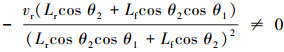

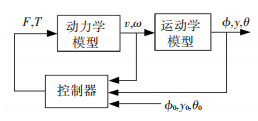
2自由度铰接车体的直线运动控制中,给定车辆的初始值:后车体绕z轴的转角ϕ0、沿y轴偏移量y0和前车体相对后车体的横摆角θ0;采用运动学控制方程确定车辆相应的期望转向角速度ω和期望车速vr.再通过动力学方程采用速度闭环控制律求得对应的牵引力和前后车体转向力矩,直线运动控制系统示意图如图 4所示.
|
图 4 直线运动控制系统 |
直线运动控制中,如果不要求在前进方向上的位置跟踪,运动速度变成动力学方程中的闭环控制.由于发动机输出功率限制,即车辆驱动力FQ是有上限的,期望运动速度vQ需要在车辆许用的范围内.
控制器设计的主要目标是设计控制量ω使系统的状态误差参数[yr ϕr θ1]随着时间的推移趋近于平衡点[0 0 0].考虑到在实际工作中,2自由度铰接车体车辆转向液压机构的输出功率一定,故在转向时,净转向力矩TO有幅值,提供的转向角速度有限制.所以在直线运动控制误差模型中,控制变量需满足上限,则实际的控制输入可以表示为
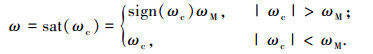
|
式中:sat(ωc)为饱和函数,ωc为控制输入,ωM为控制输入的饱和上限.
令x1=yr,x2=[sin ϕr θ1]T,则式(11)可以表示为
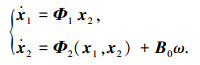
|
(12) |
式中:
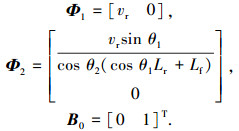
|
根据控制方程(12)的结构形式,采用反步法设计控制器[11],为了考虑输入的饱和现象[12-13],引入虚拟状态变量λ1和λ2, 且
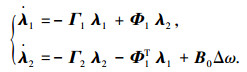
|
(13) |
其中:Δω=ω-ωc,Γ1、Γ2为正定矩阵,虚拟状态变量λ1和λ2的初始值为λ1(0)=0,λ2(0)=0.
引入如下的变换:
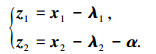
|
(14) |
式中α为虚拟控制.
由式(12)~(14)联立可得
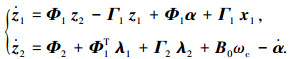
|
(15) |
取虚拟控制如下:
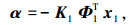
|
其中K1的选择使得

|
为正定矩阵, 则式(15)可写为
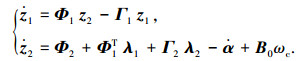
|
(16) |
定义李亚普诺夫函数为
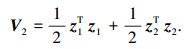
|
(17) |
对式(17)求导,并利用式(16)可得
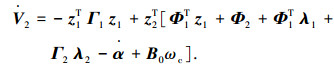
|
(18) |
因此,设计控制输入ωc为
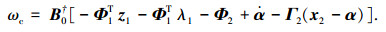
|
式中B0†为B0穆尔-彭罗斯广义逆矩阵.则式(18)可以写为
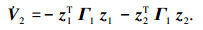
|
因为Γ1、Γ2为正定矩阵,利用LaSalle-Yoshizawa理论可得
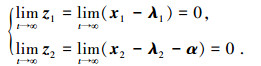
|
为了得到x1、x2的收敛性, 定义关于λ的李亚普诺夫函数为
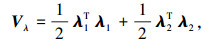
|
(19) |
对式(19)求导可得
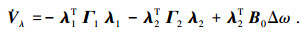
|
(20) |
如果控制输入不饱和,则有Δω=0,利用LaSalle-Yoshizawa理论可以证明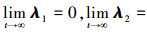
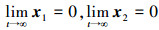
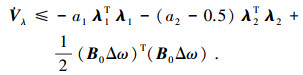
|
(21) |
式中:a1、a2为Γ1、Γ2的最小特征值,并且a2>0.5.对式(21)积分可得
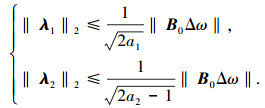
|
(22) |
由式(17)可得
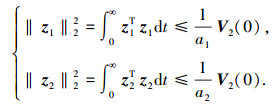
|
(23) |
根据式(14)、式(17)可得
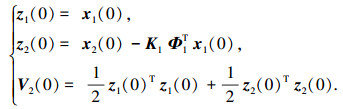
|
(24) |
因此由式(22)~(24)可得
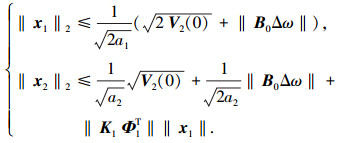
|
(25) |
通过式(25)可知,当a1、a2增大时,控制误差会减小,当足够大时,有t→∞,x1、x2→0,能保证系统的渐进稳定控制.
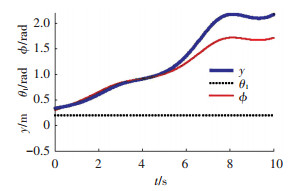
4 仿真分析在2自由度铰接车体车辆越障偏移运动控制中,车体参数取Lr=Lf=1.2 m,br=bf= 0.1 m,mf=5 000 kg,mr=7 000 kg.设初始速度为匀速运动vr=1.67 m/s,系统的初始参数选为:[yr ϕr θ1]=[0.33 m 0.3 rad 0.2 rad],应用matlab中的Simulink模块进行建模仿真分析,没有加入控制算法时, 系统误差随时间变化的曲线见图 5.
|
图 5 未加入控制算法时系统误差随时间变化 |
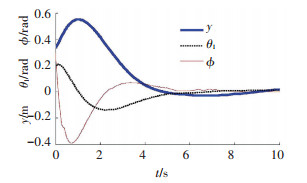
由图 5可知,初始状态车辆运动有微小偏差时,如果不施加控制,即前后车体夹角θ1保持不变,车辆运动时沿y轴向的偏移和后车体进方向的偏角ϕr随时间逐渐增大;在考虑到执行器饱和的情况下,加入抗饱和控制算法后,可得系统误差随时间变化曲线和所需净转向驱动力矩的输出随时间变化曲线如图 6、7所示.
|
图 6 加入抗饱和控制算法后系统误差随时间变化 |

|
图 7 净转向驱动力矩输出随时间变化 |
由图 6和图 7可知,加入设计的抗饱和控制器后,通过前后车体转向液压系统控制前后车体相对角速度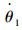
1) 本文对2自由度铰接车体车辆越障偏移控制问题进行了研究.在无控制输入状态下,车辆误差动力学模型是临界稳定的,需要施加控制消除越障偏移误差;在考虑了控制器输入饱和的基础上,应用反步法设计了抗饱和控制器.
2) 数值仿真分析表明,在无控制输入的情况下,当车辆初始运动有微小偏差时,运动偏移误差趋于发散,随着时间的增加,车辆的实际运动路径和期望路径的偏离越来越大.
3) 在采用抗饱和控制算法后,前后车体夹角、后车体进方向的偏角和后车体偏移误差均收敛至0,车辆沿期望的路径运动.
4) 计算了在偏移控制过程中液压转向执行机构的净输出力矩.分析表明, 设计的抗饱和控制器能有效消除越障偏移误差,实现车辆的直线运动控制.
| [1] |
SHIROMA N, ISHIKAWA S. Nonlinear straight path tracking control for an articulated steering type vehicle[C]//ICROS-SICE International Joint Conference. Piscataway: IEEE, 2009: 2206-2211.
|
| [2] |
TATSUYA Y, KOSUKE K, TAKANORI F, et al. Backward path following control of an articulated vehicle[C]//Proceedings of the 2013 IEEE/SICE International Symposium on System Integration. Piscataway: IEEE, 2013: 48-53.
|
| [3] |
BACHA A R. Line detection and lane following for an autonomous mobile robot[D]. Blacksburg: Virginia Polytechnic Institute and State University, 2005.
|
| [4] |
魏巍, 刘昕晖, 陈延礼, 等. 在复杂环境中2自由度轮式铰接车辆的越障能力[J]. 吉林大学学报(工学版), 2011, 41(5): 1201-1209. |
| [5] |
FANG H, FAN R, THUILOT B, et al. Trajectory tracking control of farm vehicles in presence of sliding[J]. Robotics and Autonomous Systems, 2006, 54(10): 828-839. DOI:10.1016/j.robot.2006.04.011 |
| [6] |
WESTON P F, POSTLETH W I. Linear conditioning for systems containing saturating actuators[J]. Automatic, 2000, 36(9): 1347-1354. DOI:10.1016/S0005-1098(00)00044-3 |
| [7] |
HIROSHIMA U, HIGASHI H. Path following control of articulated vehicle by backward driving[C]//International Conference on Control Applications. Piscataway: IEEE, 2002: 421-426.
|
| [8] |
TABATABAEI O. A new desired articulation angle for directional control of articulated vehicles[J]. Proceedings of the Institution of Mechanical Engineers Part K:Journal of Multi-body Dynamics, 2012, 226(4): 298-314. DOI:10.1177/1464419312445426 |
| [9] |
BIGRAS P, PETROV P, WONG T. A LMI approach to feedback path control for an articulated mining vehicle[C]//7th International Conference on Modeling and Simulation of Electric Machines, Converters and Systems. Piscataway: IEEE, 2002: 329-337.
|
| [10] |
MOON K, LEE S H, CHANG S, et al. Method for control of steering angles for articulated vehicles using virtual rigid axles[J]. International Journal of Automotive Technology, 2009, 10(4): 441-449. DOI:10.1007/s12239-009-0050-0 |
| [11] |
ZHOU Jing, WEN Changyun. Adaptive Backstepping Control of Uncertain Systems[M]. Berlin Heidelberg: Springer-Verlag, 2008: 189-197.
|
| [12] |
WESTON P F, POSTLETH W I. Linear conditioning for systems containing saturating actuators[J]. Automatic, 2000, 36(9): 1347-1354. DOI:10.1016/S0005-1098(00)00044-3 |
| [13] |
WU Xiongjun, LIN Zongli. Dynamic anti-windup design in anticipation of actuator saturation[J]. International Journal of Robust and Nonlinear Control, 2012, 24(2): 295-312. |
 2016, Vol. 48
2016, Vol. 48



