2. 车辆传动国家重点实验室(北京理工大学), 100081 北京
2. National Key Lab of Vehicular Transmission, (Beijing Institute of technology), 100081 Beijing, China
混合动力系统从一个稳定状态向另一个稳定状态过渡的过程称为动态响应过程.动态响应过程的协调控制策略是目前混合动力控制研究的热点,清华大学针对没有离合器、制动器状态变化的模式切换过程中,转矩的快速响应及平顺性问题,提出了基于电机转矩补偿的动态转矩协调控制方法[1], 还研究了针对并联式混合动力系统的多动力源协调控制方法[2].重庆大学[3-6]、上海交通大学[7]、吉林大学[8-9]等针对混合动力驱动模式切换过程或换挡过程研究了扭矩协调控制策略.还有研究者将混合动力模式切换系统归类为混杂系统的切换问题, 或通过建立发动机转矩状态观测器及电动机转矩输出补偿方法等对工作模式切换过程的动力源协调控制开展了研究.有些研究者针对特定结构的混合动力系统给出转矩协调控制方法[10-12].
上述研究主要集中于解决模式切换过程中出现的转矩波动问题,对系统整体的动态响应滞后性问题关注较少. Sajjad等[13-14]重点关注了混合动力系统的动态响应过程,将混合动力动态控制问题归结为多变量控制问题,并采用鲁棒控制方法加以解决.北京理工大学[15]提出了机电转矩冲突问题,指出了机电转矩不协调可能造成整个系统失稳的严重后果,并且通过转矩协调系数方法解决该问题.另外,系统的动态响应问题也可以借鉴模式切换过程中协调控制的思想,即采用电机辅助控制,协助响应性能较慢的发动机工作,进而实现改善动态过程车辆性能的目的.
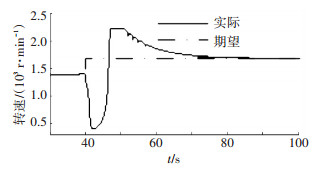
混联式混合动力系统由于其特殊的多功率流耦合特性,在其动态响应过程中,多功率流的交互作用与动态特性的影响更为显著.例如车辆在混合驱动模式下,从15 km/h向25 km/h过渡的过程中,发动机、电机的转速转矩值都应该发生变化.以发动机转速为例,在车辆15 km/h车速时,发动机经过优化策略得到的转速为1 382 r/min,在25 km/h车速时,发动机速度为1 676 r/min.发动机需要在这一过程中提高转速,理想的调速状态如图 1所示,车辆在40 s时开始速度变化,发动机转速在40 s时立即由1 382 r/min变为1 676 r/min.但实际的动态响应过程并非如此,图 1为未加入协调控制时的发动机转速响应过程,从图 1中可以看出,发动机转速要经历40 s左右的时间才能从1 382 r/min变为1 676 r/min,而且,这一过程中,发动机转速相对1 676 r/min有很大的偏差,这样的偏差直接导致了这40 s内系统性能的恶化.本文的目的为缩短动态响应时间,减小动态响应过程中各状态量相对于目标状态量的波动量.
|
图 1 发动机转速期望、实际动态响应 |
本文针对混联式混合动力汽车的结构特点,在当前模式下对其运行工况发生变化时系统各状态量的变化进行协调控制,提出模式内多动力协调控制算法.利用系统耦合关系,采用B电机转矩补偿的方法补偿了电机A及发动机协调控制过程中的动力损失,提高了段内状态变化的速度,减小了动态响应过程中状态点相对稳态优化点的波动.通过仿真对该协调算法进行了验证.
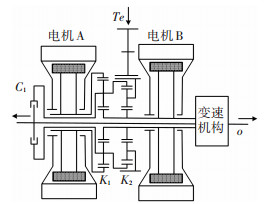
1 混合动力汽车动力系统结构本文研究的混联式混合动力系统的行星机构有行星架、齿圈、太阳轮3个自由端,分别连接混合动力系统的发动机、电动机(即图 2中电机B)、发电机(即图 2中电机A)3个功率部件,3个动力源输出动力,经行星机构耦合,由输出轴o输出,驱动整车运行.
|
图 2 混联式混合动力系统结构耦合方案 |
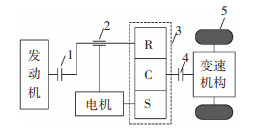
相对于电机的快速响应特性,发动机响应较慢,调速较慢,制约了整个系统动态响应过程中状态变化的速度.如图 3所示,为了辅助发动机调速,需要减小发动机的负载,即减小第2个行星机构上的內部力矩.第1个行星机构的行星架与第2个行星机构的齿圈相连,因此,也需要减小第1个行星机构的內部力矩,可以通过减小电机A的转矩来实现.两个行星机构的內部力矩减小,导致两个太阳轮上的力矩相应减小,太阳轮与输出轴相连,为了保证输出轴上的力矩不变,可通过增大电机B的转矩来实现.
|
1—单向离合器; 2—湿式离合器; 3—行星齿轮机;4—换挡离合器;5—车轮 图 3 某并联式混合动力结构方案 |
在国内代表性的协调控制[1-9]研究中,所针对的研究对象多为并联式结构,不具备在当前模式下协调控制(主要指协同调速)的能力.以杜波的研究对象(图 3)为例[4],在混合驱动模式下,欲辅助发动机调速,行星机构的内部力矩需减小,行星机构的行星架与输出轴相连,导致输出轴力矩减小,没有自由的动力源可以补充损失的力矩,因此,不能减小行星机构的内部力矩,即无法实现辅助发动机调速的功能,但其电机补偿发动机转矩保证输出转矩稳定的思想非常值得借鉴.
本文针对车辆动态响应过程中, 各动力源响应滞后性问题,应用电机A转矩控制,并采用专家PID算法设计其控制器(简称电机A专家PID控制),辅助发动机动态调速; 由此导致发动机控制器本身的控制输出作用降低的问题,采用发动机虚拟速差控制,抵消了自身控制输出作用降低的问题; 电机A、发动机的协调控制又导致了系统输出轴转矩波动的问题,采用电机B基于模型的补偿控制降低了输出轴的转矩波动; 结合3个动力源的协调控制,提出动态响应过程中的多动力协调控制的策略.
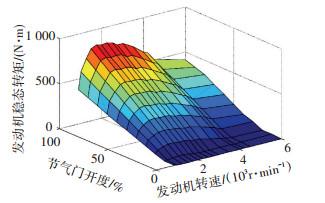
2 系统动力学模型建立 2.1 发动机模型协调控制发生在发动机状态动态变化的过程中.对电机参与协调情况下的发动机调速过程进行仿真, 需要建立发动机的动态模型.发动机是一个高度非线性系统,运行机理非常复杂,难以用理论模型来准确描述其运动状态,可以参考杜波[5]模式切换转矩协调控制中发动机的模型进行建模.在发动机稳态试验数据基础上(如图 4所示),采用多项式拟合的方法建立发动机稳态数值模型,并用一阶惯性环节对发动机稳态转矩进行修正,以表征其动态特性,进而获得发动机转矩值.本文所使用发动机为转速控制发动机,建立发动机模型中,输入为实际转速与目标转速之间的差值,输出为发动机转矩:
|
图 4 发动机稳态转矩数值模型 |

|
(1) |
式中: Te为发动机动态输出转矩,τe为发动机转矩响应的时间常数,ne为发动机的转速,Δne为发动机实际转速与目标转速的转速差,f为发动机转矩在发动机当前转速约束的条件下与发动机转速偏差之间的函数关系.
2.2 电机模型与发动机建模过程类似,电机依旧需要建立动态模型.电机A、电机B和转向电机的建模方法相同,这里以电机A为例进行介绍.电机模型包括机械和电气两部分,其中机械部分与发动机的建模方法类似.电机可以分别在4个象限工作,需要利用其发电和电动状态下的外特性对其目标转矩进行限制;本文电机采用转矩控制,电机转矩响应很快,可以利用时间常数较小的一阶惯性环节来近似表示其动态特性.
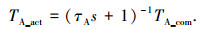
|
式中: TA_act为电机实际转矩,τA为电机转矩响应时间常数,TA_com为电机目标转矩.
电机的电气部分可以等效为可控电流源,这里利用SimpowerSystem模块来建立其电气模型.由于电动机和发电机的效率计算方法不同,因此先根据电机实际转速和转矩的乘积来判断其工作状态,再计算其需求功率或者发电功率,最后由实际功率值除以母线电压即可得到电流源的电流.
2.3 耦合机构模型耦合机构由行星机构、离合器、制动器组成,利用Simdriveline的现有模块进行建模,并对其具体参数进行设置.其中增加了若干组转矩传感器和转速传感器,用于检测操纵元件的工作状态,便于仿真分析.离合器和制动器采用油压控制,其工作状态由控制策略决定.
电机B协调控制算法中会用到系统的动态模型,根据行星机构转速转矩关系、等效转动惯量关系以及行星机构耦合关系,可以得到系统的动态模型:
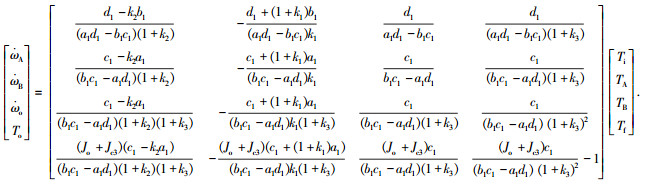
|
(2) |
式中:
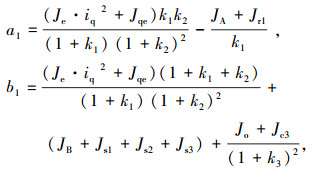
|
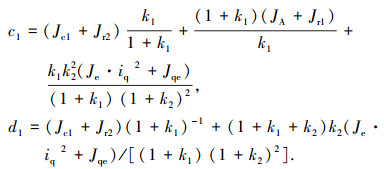
|
式中: 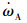
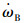
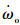
如第一节所述,当发动机转速需要升高时,可以通过降低电机A转矩,增大电机B转矩来实现.同理,发动机转速需要减小时,可以通过增大电机A转矩,减小电机B转矩来实现.但是,电机的转矩变化也会对发动机自身转速调节机制产生影响,为了抵消这一影响,采用发动机虚拟速差控制弥补发动机自身转速调节的损失.电机A和发动机转矩变动,会导致系统输出转矩波动,为了减少这一波动,采用基于模型的转矩补偿控制调节电机B的转矩,实现减小输出转矩波动的目的.电机A、B以及发动机三者的控制作用相互影响,依据各自的控制目标,协调三者之间的矛盾关系,制定多动力源协调控制策略.协调控制算法的流程图如图 5所示.
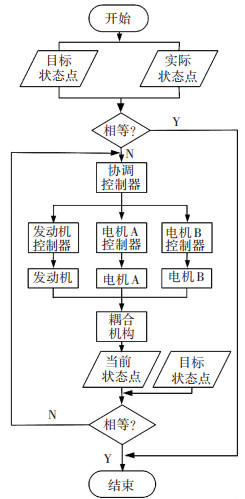
|
图 5 段内协调控制流程图 |
为了缩短发动机和电机向其目标转速转矩变化过程,并保持两者经过系统合成后的输出转矩波动尽可能小.可以利用电机动态响应快的特性来弥补发动机对其转矩控制指令响应慢的不足.
通过功率耦合机构耦合特性分析,混联式混合动力系统各功率部件转矩与转速满足一定的稳态约束关系,即
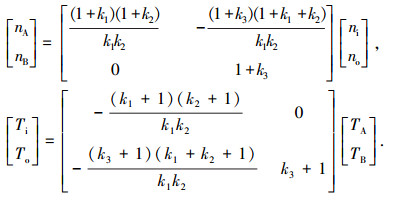
|
(3) |
式中: nA为发电机转速;nB为电动机转速;ni为功率耦合机构输入转速,等于发动机转速;no为功率耦合机构输出转速;k为行星排特性参数.
电机A协调目的为减小自身转矩值,辅助发动机调速.由式(2)第4行可知,电机A的转矩对输出轴上的转矩影响不大,在电机B不超出自身限制时(图 6),可以由电机B来补充损失.由式(3)可知,电机转矩与发动机转矩方向相同时,可以促进发动机调速, 但是,在低速模式下,电机A处于发电状态,出于对母线电流冲击的影响,电机A的转矩尽量不要反向.

|
图 6 电机B额定特性 |
电机A转矩的控制策略:采用专家PID控制算法,对电机稳态目标值进行修正, 可以克服PID控制参数单一的缺点,基于协调过程中的各状态的变化规律,分区段、分结构的协调控制整个系统.
令e(k)表示当前采样时刻的发动机转速误差值,e(k-1)、e(k-2)分别表示前1个和前两个采样时刻的发动机转速误差值,则有
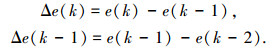
|
根据误差及其变化,分5种情况设计控制器.
1) 当|e(k)|>300 r/min时,说明误差的绝对值已经很大.不论误差变化趋势如何,都应采用控制器最大输出,以达到迅速调整误差,使误差绝对值以最大速度减小.此时相当于开环控制, 输出为
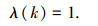
|
2) 当e(k)Δe(k)≥0时,说明误差在朝误差绝对值增大方向变化,或误差为常数值,未发生变化.此时,如果|e(k)|>200 r/min, 说明误差也较大,可考虑由控制器实施较强的控制作用,以达到扭转误差绝对值朝减小方向变化,并迅速减小误差的绝对值,输出为

|
此时,如果|e(k)| < 200 r/min,则说明尽管误差朝绝对值增大方向变化,但误差绝对值本身并不很大,可以实施一般的控制作用,只要扭转误差的变化趋势,使其朝误差绝对值减小方向变化,输出为
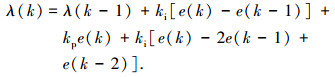
|
3) 当e(k)Δe(k) < 0, Δe(k)Δe(k-1)>0或者e=0时,说明误差的绝对值朝减小的方向变化,或者已经达到平衡状态.此时,可考虑变为电机A目标转矩.输出为
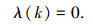
|
4) 当e(k)Δe(k) < 0, Δe(k)Δe(k-1) < 0时,说明误差处于极值状态.如果此时误差的绝对值较大,即|e(k)|≥200 r/min,可考虑实施较强的控制作用,输出为

|
如果此时误差的绝对值较小,即|e(k)| < 200 r/min,考虑实施较弱的控制作用,输出为
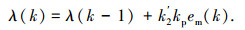
|
在各种情况下电机A的控制转矩为

|
式中: λ(k)为电机协调控制器中当前采样时刻电机A转矩的修整系数,λ(k-1)、λ(k-2)分别表示前1个和前两个采样时刻的电机A转矩的修整系数;k1′、k2′为系数输出的调节系数;kp、ki、kd为修整系数控制的PID系数,经过反复方阵调整,其值为k1′=1.50, k2′=1.05, kp=0.002 0, ki=0.002 1, kd=0.000 5;em(k)为误差的第k个极值; TA_稳为电机A的稳态目标值,TA(k)为当前采样时刻电机A的控制量.
在上述策略上再加上限制,可构成电机A协调控制算法:
当λ(k)>1时,取λ(k)=1.
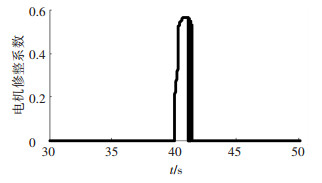
车辆从15~25 km/h运行的过程中,电机A的修整系数λ的取值如图 7所示.图中车辆从40 s开始进入动态响应的状态变化阶段.
|
图 7 电机A修整系数 |
通常发动机控制器只采集发动机目标转速与发动机实际转速的差值,不采集电机转矩,发动机转速偏差经过发动机控制器,得出发动机的参考转矩值,通过发动机转矩的增大或减小,实现调节发动机转速的目的.这里存在如下问题:发动机控制器并不接收负载(电机转矩)信号,电机为了协调发动机转速的变化,会通过改变自身转矩的大小来调节负载转矩,进而实现辅助调速的目的,电机调节对发动机调速有促进的作用,发动机通过转速偏差的变化来解读这一促进作用,会在一定程度上降低发动机控制器本身的控制输出作用.为了避免出现这一现象,需要对发动机进行调节.本文采用发动机虚拟速差控制来解决这一问题.虚拟速差是指对发动机控制器要接受的速差进行处理,乘以相应的调节系数,得到虚拟转速偏差,发送给发动机控制器,增强发动机自身的调节作用.
发动机的转矩响应较慢,对于转速的突然变化,发动机很难快速给出快速的响应.同时,大的转速差将导致大的转矩输出,在下一时刻转速偏差变小时,控制转矩依旧很大,造成超调的不良影响.因此,发动机转矩协调控制中,对发动机接收的虚拟转速差进行处理时,应当保证其尽量复现实际转速差的变化,不应该引入额外的冲击.可采用基于规则的平滑的速差修整系数对实际速差进行修整,得到虚拟速差,发送给发动机控制器.
发动机转速差修整系数采用理查德S形函数曲线,如图 8所示, 取值为
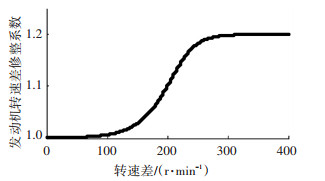
|
图 8 发动机转速差修整系数曲线 |
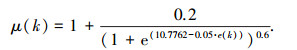
|
式中μ(k)表示当前采样时刻的发动机转速差修整系数.发动机控制器实际接受的速差为
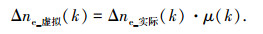
|
上述电机A、发动机的协调控制会导致动态响应过程中输出轴上的转矩波动,需要协调控制电机B来解决这一问题.
电机B协调控制的作用是保证系统输出转矩平稳,借鉴模式切换过程中电机补偿发动机转矩缺失的思想[4], 耦合机构输出轴上的需求转矩减去发动机、电机传递过来的转矩即为电机B的转矩值.但是,耦合机构输出轴上由发动机和电机B传递的转矩值无法采集,需要在线对发动机转矩、电机A转矩进行观测,然后通过系统的数学模型,推算出输出轴上二者传递而来的转矩值.由式(2)第4行可得电机B的转矩控制量为:
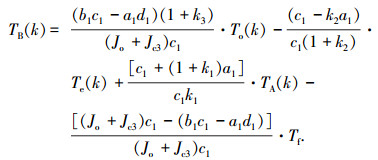
|
式中: TB(k)为电机B在当前采样时刻的控制量;To(k)为当前采样时刻的系统需求输出转矩值,由加速踏板位置、当前车速、系统最大输出功率共同决定;Te(k)为当前采样时刻发动机的转矩值,由式(1)发动机的动态模型得到;Tf为整车负载转矩等效到耦合机构输出轴上的阻力矩,其值大小在路面坡度平稳、车速缓慢的情况下视为常值.
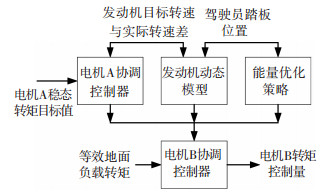
电机B的协调控制方法如图 9所示.
|
图 9 电机B协调控制方法示意 |
为验证本文所建立的控制策略,根据传动系统动力学模型,在MATLAB/Simulink中建立混合动力汽车的动力学仿真模型,进行仿真分析.车辆动态响应过程的时间较长,为了比较清晰地描述模式内动态响应,本文仿真过程描述车速从15~25 km/h过程中系统内部的变化.
图 10(a)、(b)分别为不采用协调控制策略和采用协调控制策略两种情况下,车辆行驶工况变化时各个动力源的转速状态.
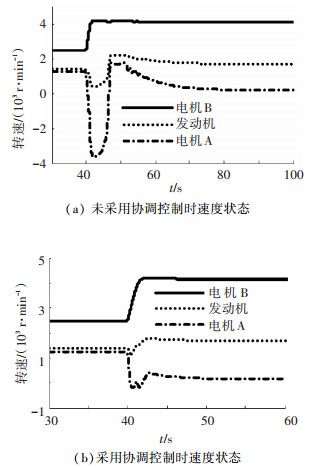
|
图 10 动力源转速状态 |
图 10(a)中,车辆在40 s时开始状态变化,发动机、电机有了新目标转速转矩点,经过40 s左右的时间,发动机和电机的转速都到达了目标的转速值.在变化的过程中,电机A、B的转速发生了大范围的变化,偏离给定的状态点很远,会造成经优化得到的性能指标大幅变差的不良影响.如果车辆不经常处于状态变换的工况,那么系统动力源的转速只有在相对较短的状态变换过程时偏离给定点,这样造成的优化目标恶化的程度有限.如果车辆的状态变换频繁,系统不断地处于状态变换的工况,各动力源的转速会一直处于偏离给定目标值较大的状态,将会对系统需要优化的性能产生较大程度的不良影响.由于系统自身响应特性的限制,状态变换只能是一个过程,不可能瞬间完成,因此状态变换引起的性能指标恶化必不可少,尤其是在工况变换频繁的环境里.如果状态变换的过程可以缩短,而且该过程中各个状态量与目标值的偏差又不是很大,则可以有效地降低工况变换过程中的性能指标损失.相对于图(a),加入协调控制的图(b)中状态变换时间短了46.19%,相对于无协调控制,有协调控制情况下发动机转速偏差减少54.48%, 电机A转速偏差减少59.57%, 电机B转速偏差增加7.28%(计算方法为二者累积的偏差的平方和之差除以未加入协调控制的累积偏差和).协调控制的效果明显优于无协调控制的效果.
图 11(a)、(b)分别为不采用协调控制策略和采用协调控制策略两种情况下车辆行驶工况变化时,各个动力源的转矩状态. 图 11(a)中电机A的转矩快速到达目标值,发动机、电机B的转矩经历了较长的时间以及较大的波动才到达目标值,如上所述,会对优化性能造成较大的不利影响.其中,相对于图 11(a),图 11(b)中发动机转矩波动减小47.86%,电机A转矩波动减小42.02%,电机B转矩波动增加18.14%.电机B因为要补偿发动机和电机A协调控制的损失,转矩波动有所增加,但增加的幅度远比发动机和电机A减小的幅度小.证明了电机B在其转矩范围内可以完成对输出转矩的补偿作用.
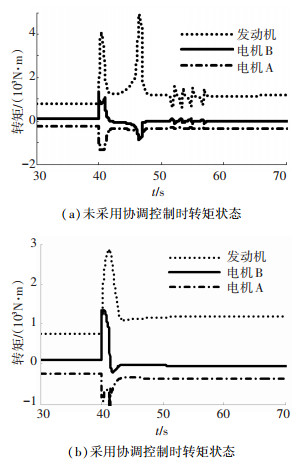
|
图 11 动力源转矩状态 |
图 12(a)、(b)分别为采用协调控制策略和不采用协调控制策略两种情况下车辆行驶工况变化时,车辆的冲击度变化状态.对比两图可以看出,图 12(a)中的冲击度相对于图 12(b)有一定的改善,但改善程度有限.主要原因有二,一是车辆突然加速时必然存在冲击度的出现,而且驾驶员模型的非智能操作也对此产生的一定的影响.二是考虑到建模与实际系统的差距,本文用于控制器设计的数学模型与用于仿真的simulink模型存在刻意的不一致.这样,经过传动效率以及延迟的影响,B电机协调控制算法得出的转矩并不能精确的等于需要补偿的转矩,所以对车辆冲击度的改善不明显.解决的办法是准确估计输出轴上的转矩,由实际需求转矩减去输出轴转矩即为B电机应该额外补偿的转矩.相对于图 12(a),图 12(b)中的冲击度下降21.86%.
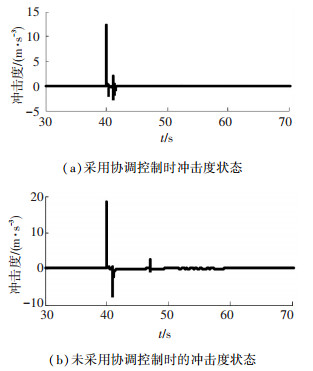
|
图 12 车辆冲击度状态 |
图 13为只加入电机协调控制的转速转矩状态,对比图 10、11,此时的控制效果介于二者之间,说明发动机协调控制对控制需要的结果可以产生有利的影响.
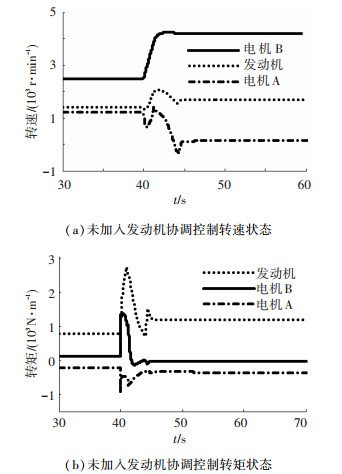
|
图 13 只加入电机协调控制的转速转矩状态 |
1) 电机A采用专家PID协调控制,一定程度上克服了PID控制参数单一性的缺点,根据不同的发动机转速差协调控制电机A的转矩,实现了辅助发动机调速的目的.
2) 发动机采用虚拟速差协调控制,增大发动机控制器接收的速差反馈信号,加强了发动机自身的调速效果,实现了发动机自身主动快速调速的目的.
3) 电机B采用基于模型的输出转矩补偿控制,在电机A辅助发动机调速的同时,补偿电机A以及发动机的转矩损失,保证输出转矩的需求量,在一定程度上降低了系统的冲击度.
| [1] |
李孟海, 罗禹贡, 杨殿阁, 等. 基于模型匹配控制的PHEV动态协调控制方法[J]. 汽车工程, 2007, 29(3): 203-207. DOI:10.3321/j.issn:1000-680X.2007.03.007 |
| [2] |
童毅. 并联式混合动力系统动态协调控制问题的研究[D]. 北京: 清华大学, 2004.
|
| [3] |
杜波, 秦大同, 段志辉, 等. 新型并联式混合动力汽车模式切换协调控制[J]. 中国机械工程, 2011, 23(6): 739-744. |
| [4] |
杜波, 秦大同, 段志辉, 等. 新型混合动力汽车动力切换动态过程分析[J]. 汽车工程, 2011, 33(12): 1018-1023. |
| [5] |
杜波, 秦大同, 段志辉. HEV多领域物理建模与模式切换控制仿真系统[J]. 仿真学报, 2013, 25(7): 1668-1674. |
| [6] |
WEI Hanbing, QIN Datong, CHEN Shujiang. Multiple-objective stochastic optimal control strategy for the fuel consumption and emissions of full hybrid electric vehicle[J]. Automotive Engineering, 2014, 36(8): 923-928. |
| [7] |
WANG Lei, ZHANG Yong, SHU Jie, et al. Coordinated control for a series-parallel hybrid electric bus during EV/HEV mode transition[J]. WSEAS Transactions on Circuit and Systems, 2012, 6(11): 198-209. |
| [8] |
冀尔聪. 并联式混合动力汽车模式切换中的协调控制问题研究[D]. 长春: 吉林大学, 2006.
|
| [9] |
PENG Silun, YAN Yunbing. Steady-state model research of nine degrees of freedom for electric vehicle with motorized wheels[C]//International Conference on Digital Manufacturing & Automation. Changsha: ICDMA, 2010: 415-418.
|
| [10] |
KOPRUBAIS K, WESTERVELT E, RIZZONI G. Toward the systematic design of controllers for smooth hybrid electric vehicle mode change[C]//Proceedings of the 2007 American Control Conference. New York: AACC, 2007: 2985-2990.
|
| [11] |
ROY I, ROBERT D. Engine torque ripple cancellation with an integrated starter alternator in a hybrid electric vehicle:implementation and control[J]. IEEE Transactions on Industry Application, 2003, 96(6): 1765-1774. |
| [12] |
AKIHIRO K, TETSUYA A, SHOICHI S. Driving force control of a parallel-series hybrid system[J]. JSAE Review, 1999(20): 337-341. |
| [13] |
SAIJAD F, FRANCIS A. The role and use of robust multivariable control in hybrid electric vehicle energy management-Part Ⅰ: an overview[C]//IEEE International Conference on Control Applications. Dubrovnik: CCA, 2012: 303-309.
|
| [14] |
SAIJAD F, FRANCIS A. The role and use of robust multivariable control in hybrid electric vehicle energy management-part Ⅱ: application[C]//IEEE International Conference on Control Applications. Dubrovnik: CCA, 2012: 317-322.
|
| [15] |
WANG Weida, HAN Lijin, XIANG Changle, et al. Synthetical efficiency-based optimization for the power distribution of power-split hybrid electric vehicles[J]. Chinese Journal of Mechanical Engineering, 2014, 27(1): 58-68. DOI:10.3901/CJME.2014.01.058 |
 2016, Vol. 48
2016, Vol. 48


