2. 东京大学 生产技术研究所, 153-8505 东京
2. Institute of Industrial Science, The University of Tokyo, 153-8505 Tokyo, Japan
作为半自动驾驶控制系统,自适应巡航控制系统(adaptive cruise control,简称ACC)广泛安装于现代车辆上,它不但具有传统的定速巡航功能,而且可以利用车载传感器感知前方的行驶环境,自动地调整车速,以保持一个安全的车间距行驶.通过代替驾驶员进行决策,汽车ACC系统不仅能减轻驾驶员的精神负担,而且能有效减少由于驾驶员的失误引起的交通事故,以及改善乘坐舒适性和交通流等,因而近年来得到了国内外学者的广泛关注[1-2].
目前ACC系统的控制设计主要采用分层结构[3]:上层控制系统根据车载传感器检测到的前方行驶环境决定车辆的期望纵向加速度,下层控制器通过控制相应的油门和刹车使得汽车最终表现出来的实际加速度和上层得到的期望加速度一致,而如何选取ACC的上层控制策略是实现ACC系统功能的关键[2]. PID控制、模糊控制、LQR控制等传统控制方法都在ACC系统中得到了广泛的应用[4-6],但这些控制方法大多以距离控制为主要目标,即考虑安全性而忽略舒适性,而据美国高速公路管理局调查,乘坐舒适性往往是人们考虑安装ACC系统最重要的原因[7].
在车辆跟车时,安全性与舒适性往往是矛盾的关系.过高的安全性意味着大的车辆减速度,这会造成乘客的不适; 而过高的舒适性则会使车辆不能及时在危险工况下停车,而造成事故.本文基于模型预测控制算法,建立一种考虑安全性与舒适性的多目标自适应巡航系统上层控制算法,协调ACC系统跟车时安全性与舒适性目标,并且通过引入误差补偿项来提高系统的鲁棒性; 针对线性模型预测控制(MPC)算法本身采用硬约束容易导致因约束上下界不可超越而无优化解问题,采用向量约束管理法,通过向量化松弛因子,对不同硬约束采取不同比例的软化使系统可解.
1 ACC系统车间纵向运动学模型在进行ACC控制策略设计时,上层控制器是针对驾驶行为的控制,下层控制器是针对油门刹车机械特性的控制,本文在设计时,下层控制器的设计采用文献[6]方法,为模型匹配鲁棒下位控制器,这里不再赘述.为对ACC上层控制策略进行设计,需对ACC车辆及前车的相互纵向运动学特性进行建模.
根据图 1中ACC系统的本车与前车之间的相互纵向运动学特性,可得到如下关系式:
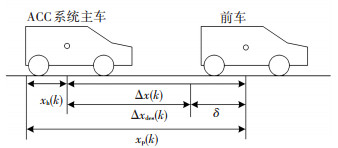
|
图 1 汽车ACC系统的纵向运动学示意 |
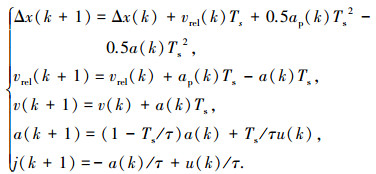
|
(1) |
式中:Δx(k)为两车车间距,vrel(k)为两车相对速度,v(k)、a(k)、j(k)分别为本车速度、本车加速度、本车加速度变化率,u(k)为ACC系统的上层控制输入,ap(k)为前车加速度,Ts为ACC系统的采样周期,τ为ACC系统中采用一阶惯性环节作为理想下位控制对象的时间常数[8].
根据式(1),选取两车间距、本车速度、两车相对速度、本车加速度、本车加速度变化率作为状态变量,x(k)=Δx(k), v(k), vrel(k), a(k), j(k)Τ,并把前车加速度视作ACC系统的扰动w(k),得到如式(2)离散状态方程模型,该模型充分考虑前车加速度干扰,能更全面反映系统的动态演化规律,提高模型的精度和可靠性,且引入加速度和加速度变化率,有利于ACC系统多目标控制需求的设计:
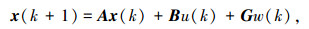
|
(2) |
系统矩阵为

|
虽然ACC系统本身是一个舒适性系统,但安全性是其最基本也是最重要的控制目的,为保证ACC系统在车辆整个行驶过程中的安全性,必须对实际车间距进行严格约束:
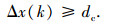
|
式中: dc为最小安全间距,包括一个车身长和一个固定的距离.
对于跟车控制,ACC系统的最终目标是使两车实际车间距趋近于间距策略计算出的期望跟车间距,本车车速趋近于前车速度,即两车处于相对静止的状态:
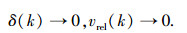
|
式中, δ(k)为间距策略计算出的车间距与实际车间距差值.
关于舒适性,Moon等[9]通过大量试验分析指出,ACC汽车加速度和加速度变化率越小,乘坐舒适度就越高,因此本文通过优化行驶过程中的加速度以及加速度变化率的绝对值,来提高ACC系统的乘坐舒适性,即目标为
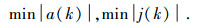
|
综上建立优化性能指标模型:
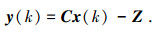
|
式中:
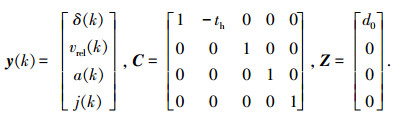
|
其中: th为恒定车头时距(constant time headway, 简称CTH)策略的车间时距离,d0为CTH策略的最小安全间距[10].
为了保证ACC在跟车模式下平稳跟车,引入指数衰减函数[11]作为待优化性能向量的参考轨迹yref,沿着参考轨迹yref,性能向量y中的各分量将平滑趋近于0,平滑系统的响应曲线如下:

|
其中:
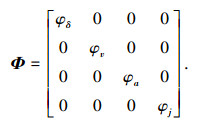
|
式中: φδ、φv、φa、φj分别对应状态量δ、vrel、a、j的参考轨迹系数,取值均在0~1.
2.2 鲁棒跟车预测模型设计实际上,因车辆参数测量误差、参数时变、未建模动态和外部干扰等因素,跟车系统动力学模型不可避免存在模型不确定性. Garcia等[12]指出,无约束线性模型预测控制(MPC)的鲁棒性等价于线性最优控制方法,因此,MPC本身对模型失配不具备良好的鲁棒性.当模型不确定性较大时,跟车预测模型存在较大的预测误差,不能准确反映跟车系统的实际特性.此时,车辆MPC系统的控制误差增大,不仅会削弱跟踪性能,甚至可能使系统丧失多目标协调控制功能.
为提高MPC鲁棒性,提高系统对模型误差和外部干扰的抵抗能力.基于反馈校正法,引入误差修正项ex(k),建立如下MPC鲁棒性控制算法:
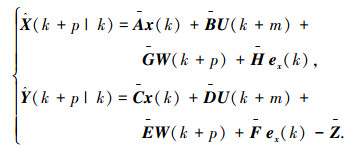
|
(3) |
其中:
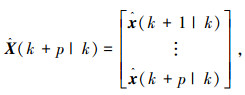
|
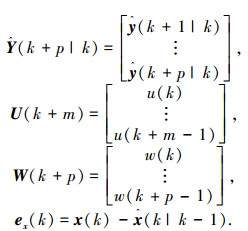
|
式中:p为预测时域,m为控制时域,且m≤p,u(k), u(k+1), u(k+2), …, u(k+m-1)为控制序列,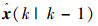
通过引入误差项,补偿模型失配造成的预测误差,提高其预测精度,系统预测矩阵如下:
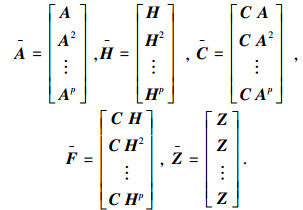
|
式中: H=diag(h1, h2, …, hm)为校正矩阵,满足0 < hi < 1, i=1:m;

|
在MPC的框架下,将车辆ACC系统行驶过程中需要优化的多个性能指标以加权的方式写成如下的性能指标函数:
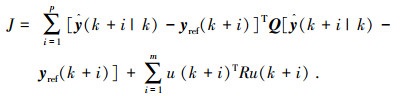
|
(4) |
式中: Q和R为权系数,Q=diag(qδ, qv, qa, qj);u为控制量阵.
Q是分别对车间距、相对速度、加速度及冲击度的加权,由于本文综合考虑舒适性与安全性,故取相同权值,R的选取影响控制量,随着控制指标对控制消耗能量重视程度的降低,相应控制器控制下系统的跟踪能力增强,同时控制量即车辆加速度的幅度也会增大.
2.3 基于向量约束管理法的求解可行域扩展设计MPC采用硬约束容易导致因约束上下界不可超越而无优化解问题,为此,采用向量约束管理法解决非可解问题[12],即:当控制输入或系统输出超出约束范围时,采用向量松弛因子法,对所有硬约束分别进行松弛化,扩大约束的上下界,消除硬约束的强制性,保证预测优化问题可解.
由2.2节目标值,确定系统硬约束为

|
(5) |
MPC性能指标中,约束集包括纵向乘坐舒适性标准、驾驶员期望跟踪误差范围和跟车安全性条件,三者均为硬约束.前两者反映了驾驶员乘坐舒适性要求和驾驶员对跟踪误差的容许程度,后者用于保证跟车过程的安全性.对于前两者,稍微扩大约束条件的上下界,仅仅弱化舒适性程度和跟踪性能,不影响ACC的正常工作; 但是对于跟车安全性约束,降低其下界,则意味着可能发生追尾碰撞事故,不适合采用软约束.因此本文仅对前两者的约束松弛化,而不处理与跟车安全性相关的约束.考虑到本文主要考虑舒适性,这里仍把冲击度作为硬约束,对式(5)松弛化处理如下:
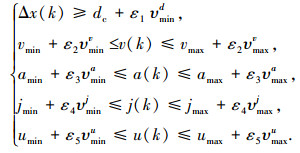
|
(6) |
式中: ε1、ε2、ε3、ε4、ε5称为松弛因子,满足ε1=ε4=0,ε2≥0,ε3≥0,ε5≥0;υmind、υminv、υminj、υmina、υminu为式(5)中硬约束下界的松弛系数,满足υmind≤0,υminv≤0,υmina≤0,υminj≤0,υminu≤0;υmaxv、υmaxa、υmaxj、υmaxu为式(5)中硬约束上界的松弛系数,满足υmaxv≥0,υmaxa≥0,υmaxj≥0,υmaxu≥0.
松弛系数用于反映松弛因子对不同变量以及变量各分量的松弛程度.向量式松弛因子可使式(5)硬约束不同比例增大或减小,保证了各个约束变化不受干涉.
将式(3)代入式(6),可得到约束条件的矩阵形式:
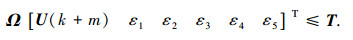
|
式中:
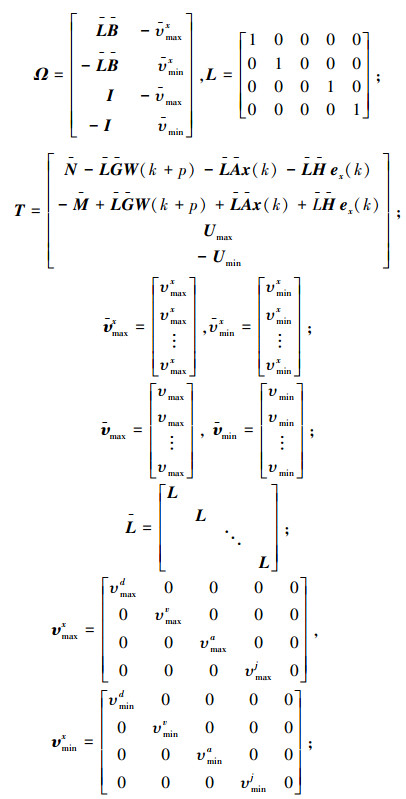
|
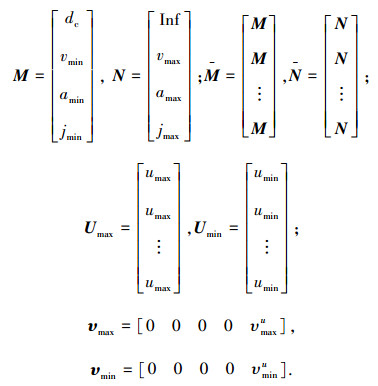
|
为避免约束上下界被松弛因子无限扩大,失去约束不等式对系统输入输出的限制作用,通常将松弛因子的2范数融于代价函数,对松弛因子进行惩罚.为此,定义一种带松弛因子的代价函数:
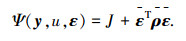
|
(7) |
其中:
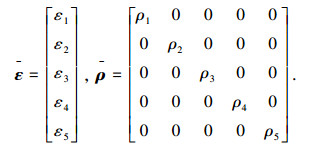
|
式中: J为2.2节所定义的性能指标函数,ρ1、ρ2、ρ3、ρ4、ρ5为各松弛因子的权系数.
将式(3)、式(4)代入式(7),可在MPC框架下,将多目标鲁棒跟车ACC系统的上层控制算法最终转化为如下形式的带约束的在线二次优化问题:
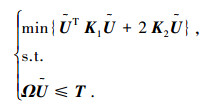
|
(8) |
式中:
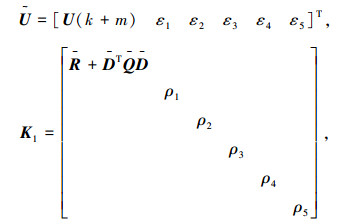
|

|
上述预测优化问题中,当系统输入输出不满足I/O硬约束时,滚动时域优化求解会自动增大松弛因子,扩展I/O软约束的范围,保证u(k+i|k)的最优解存在.代价函数中,松弛因子的二次项限制的增大,惩罚软约束的松弛程度,使闭环系统自动在求解可行性和约束松弛程度之间寻找平衡点.惩罚系数越大,松弛因子扩展约束范围的能力越弱; 反之,能力增强.同一松弛因子下,松弛系数越大或分系数越大,对相应变量或变量分量的松弛程度越大,反之越小.
另外,自适应巡航过程中,若车间距离接近跟车安全性条件的边界时,因控制输入量为软约束,预测优化问题(式(8))可自动降低期望加速度的下界,采用大制动强度减速,以减弱车间距离接近安全车距的速度,避免追尾碰撞事故.这说明,不对跟车安全性约束松弛化,对保障跟车安全性是有利的,而且因期望加速度软约束的存在,不会导致非求解问题.
在每一个采样时刻,ACC系统通过车载传感器检测得到当前的行驶环境信息.首先, 对未来状态进行预测,并进行反馈校正; 然后, 通过在线优化相应的多目标性能指标,求取对应的数学规划得到控制序列,并将第一个值附加于控制系统,在下个采样时刻重复该操作.
3 仿真分析为验证提出的多目标鲁棒跟车自适应巡航控制算法,利用MATLAB/SIMULINK进行仿真,与文献[13]所采用的LQR上层控制算法进行对比.前车工况为先减速、后加速再匀速行驶,仿真参数取为:
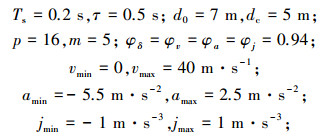
|
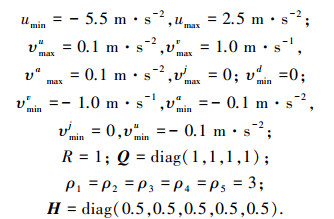
|
|
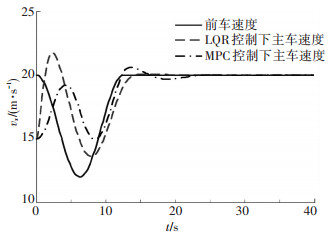
图 2 跟车模式下速度变化曲线 |
|
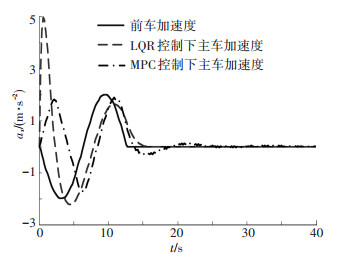
图 3 跟车模式下加速度变化曲线 |
|
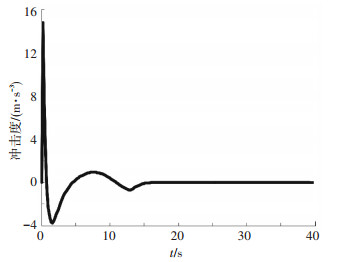
图 4 LQR控制器下主车冲击度变化曲线 |
|
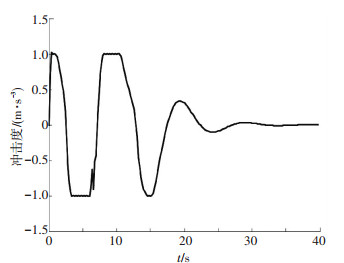
图 5 MPC控制器下主车冲击度变化曲线 |
|
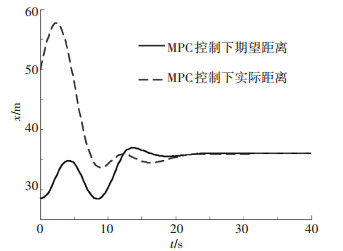
图 6 跟车模式下车间距变化曲线 |
由图 2、3可见,LQR控制器下的ACC系统会出现较大的速度变化及较大的加速度. 图 3中,大约在0.7 s左右,主车加速度达到约5 m/s2峰值,这是因为LQR控制无法对控制目标进行限制,这正是LQR控制的缺点,过大的加速度会给驾驶员带来强烈的不舒适感,违背跟车目的;本文所设计的多目标MPC控制算法可以实现较为平稳的跟车,加速度最大值没有超过2 m/s2,保证了车辆跟车的舒适性.与LQR控制器相比,MPC控制器有一定延时性,即不能快速地跟随前车,但这符合跟车模式下保证舒适性的要求.
由图 4、5可见, 主车冲击度变化更进一步说明所设计的多目标鲁棒MPC控制算法优势,由于对冲击度采取硬约束处理,使冲击度始终保持在舒适性要求范围内.仿真结果表明,本文设计的MPC控制算法能使主车冲击度保持在[-2 m·s-3,2 m·s-3],而LQR控制器下ACC系统主车冲击度,在0.5 s左右甚至达到了15 m/s3,这会引起驾驶员的极度不适.
由图 6可见,所设计的MPC控制算法能使实际车间距较为平滑地收敛到期望车间距,从而实现平稳舒适跟车目的.
4 结论1) 建立一种考虑前车加速度干扰的ACC系统纵向动力学控制模型,全面反映系统的动态演化规律,提高模型的精度和可靠性.
2) 设计了一种考虑ACC系统安全性和舒适性的多目标MPC控制算法,引入修正项提高控制系统的鲁棒性.
3) 采用向量约束管理法来解决MPC硬约束造成的控制系统无解问题,所设计的控制算法,兼顾了安全性和舒适性要求,实现ACC系统跟车目的.
| [1] |
RAZA H, LOANNOU P. Vehicle following control design for automated highway systems[J]. IEEE Trans on Control Systems, 1996, 16(6): 43-60. DOI:10.1109/MCS.1996.546270 |
| [2] |
VAHIDI A, ESKANDARIAN A. Research advances in intelligent collision avoidance and adaptive cruise control[J]. Intelligent IEEE Trans on Transportation Systems, 2003, 4(3): 143-153. DOI:10.1109/TITS.2003.821292 |
| [3] |
RAJAMANI R. Vehicle dynamics and control[M]. Second Edition. Heidelberg: Springer Science & Business Media, 2011.
|
| [4] |
ZHANG J, IOANNOU P A. Longitudinal control of heavy trucks in mixed traffic:environmental and fuel economy considerations[J]. IEEE Transactions on Intelligent Transportation Systems, 2006, 7(1): 92-104. DOI:10.1109/TITS.2006.869597 |
| [5] |
NARANJO J E, GONZÁLEZ C, REVIEJO J, et al. Adaptive fuzzy control for inter-vehicle gap keeping[J]. IEEE Transactions on Intelligent Trans Systems, 2003, 4(3): 132-142. DOI:10.1109/TITS.2003.821294 |
| [6] |
侯德藻, 高锋, 李克强, 等. 基于模型匹配方法的汽车主动避撞下位控制系统[J]. 汽车工程, 2003(4): 399-402. DOI:10.3321/j.issn:1000-680X.2003.04.022 |
| [7] |
JENNESS J W, LERNER N D, MAZOR S, et al. Use of advanced in-vehicle technology by young and older early adopters[R]//Survey Results on Adaptive Cruise Control Systems. Washington, DC: National Highway Traffic Safety Administration, 2008.
|
| [8] |
MARTINEZ J J, de CANUDAS W C. A safe longitudinal control for adaptive cruise control and stop-and-go scenarios[J]. IEEE Transactions on Control Systems Technology, 2007, 15(2): 246-258. DOI:10.1109/TCST.2006.886432 |
| [9] |
MOON S, YI K. Human driving data-based design of a vehicle adaptive cruise control algorithm[J]. Vehicle System Dynamics, 2008, 46(8): 661-690. DOI:10.1080/00423110701576130 |
| [10] |
SWARROP D, HEDRICK J K, CHIEN C C, et al. A comparison of spacing and headway control laws for automatically controlled vehicles[J]. Vehicle Sytem Dynamics, 1994, 23: 597-625. DOI:10.1080/00423119408969077 |
| [11] |
LUO L, LIU H, LI P, et al. Model predictive control for adaptive cruise control with multi-objectives:comfort, fuel-economy, safety and car-following[J]. Journal of Zhejiang University-SCIENCE A(Applied Physics & Engineering), 2010, 11(3): 191-201. |
| [12] |
GARCIA C, PRETT D. Model predictive control:Theory and practice-A Survey[J]. Automatica, 1989, 25(3): 335-348. DOI:10.1016/0005-1098(89)90002-2 |
| [13] |
李朋, 魏民祥, 侯晓利. 自适应巡航控制系统的建模与联合仿真[J]. 汽车工程, 2012(7): 622-626. DOI:10.3969/j.issn.1000-680X.2012.07.013 |
 2016, Vol. 48
2016, Vol. 48


