随着核电系统、输油管道系统等随机退化系统的安全性受到越来越多的重视,目前随机退化系统维护建模问题已成为工业界和学术界关注的焦点.
在进行系统视情维修建模时,通常需要根据系统的退化特征采用科学合理的方法对系统的状态变化过程进行描述.针对随机退化系统,许多学者[1-3]利用随机过程对系统的退化过程进行描述,并在此基础上提出视情维修策略.目前, 文献中基于随机过程的退化模型主要分为3类:连续退化模型、随机冲击模型及多竞争风险模型.连续退化模型通常采用Markov决策过程、Gamma过程等对系统的退化过程进行描述.文献[4]利用Markov决策过程对系统状态退化过程进行描述.文献[5]通过对检测间隔时间和维护策略联合优化,建立了半Markov决策模型.文献[6]和[7]运用Gamma过程对系统随机退化过程进行建模.随机冲击模型[8-9]主要是针对受随机冲击影响的系统,通常采用Poisson过程来建模.文献[10]和[11]分别运用Poisson过程对受随机冲击影响的系统进行建模研究.考虑到系统在工作过程中退化路径并不是唯一的,一些学者提出了多竞争风险模型.该类模型最常见的是DTS (degradation-threshold-shock)模型.文献[12]首次对DTS模型进行了分析.文献[13]在退化过程和冲击过程相互独立的假设之下,采用DTS模型对系统退化过程进行建模.文献[14]通过引入加性和乘性退化模型,针对带随机退化和随机冲击的单部件系统,提出了不完全维护策略.文献[15]针对单机可修系统,建立了随机退化和随机冲击竞争失效模型.上述文献中所建立的系统退化模型均假设系统一旦启动就立即开始退化,这对某些具有多阶段退化特征的情况并不适用,例如点蚀过程、裂纹产生与生长过程等.此外,该类模型通常假设系统的退化过程是平稳的,并不考虑环境变化对系统退化过程的影响,这与实际有一定的差距.
本文通过引入环境影响因子来描述环境变化对系统退化过程的影响,针对具有两退化阶段的随机退化系统,建立了基于随机过程的带有随机突变的两阶段退化模型,并在此基础上构建了视情维护模型.
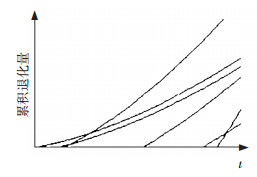
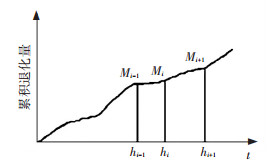
1 退化过程建模任何系统都具有一定的自愈能力,使其在开始运行的一段时间内保持全新状态.随着系统工作时间的增加以及外部环境变化的影响,系统自愈能力逐渐下降,系统中某些点或区域开始退化.将系统中最初开始退化的点或区域称为退化点,则系统的退化过程可分为退化点的产生和生长两个过程.系统并不是孤立存在的,系统在运行过程中必然要受到周围环境的影响.例如,湿度及酸碱度等因素对管道腐蚀过程的影响.本文考虑环境变化对系统退化过程的影响,对两阶段退化系统的退化过程进行分析.用Mi表示系统中第i个退化点的退化过程,hi表示第i次环境变化,系统的退化过程及第i个退化点的生长过程如图 1和图 2所示.
|
图 1 系统退化过程 |
|
图 2 退化点生长过程 |
为有效描述问题,做如下假设:1)系统不可修,每次对系统的维护都对系统进行更换;2)t时刻系统的退化状态可由周期性检测完全获得,且数据可靠;3)环境变化对退化点产生过程的影响为ρi(i=0, 1, 2, …),对退化点生长过程的影响为qi(i=0, 1, 2, …);4)环境一旦发生变化,可立刻被观察到.
由于环境变化具有随机性.假设在时间t上,环境变化的次数服从强度因子为λh的泊松过程,环境变化发生的时间序列为Sh,则第i次环境变化的时刻为Shi, Sh0=0. {Nh(t), t≥0}为一计数过程且有Nh(t)=max{i|Shi≤t, i=0, 1, 2, …},则在[0, t]内,环境变化n次的概率可以表示为
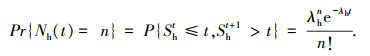
|
引入环境变化系数φ(φ∈{-1, 1})来表示环境恶化或改善,即,当φ=-1时,表示环境改善,一定程度减缓系统的退化;当φ=1时,表示环境的恶化,加快系统的退化.
根据文献[16],采用非齐次泊松过程(no-homogeneous Poisson Process NHPP)对退化点的产生过程进行建模. N={N(t), t≥0}为一计数过程,表示t时刻退化点的数目.假设在时间t上退化点的数目N(t)服从以λ(t)=λtδ-1为强度因子的NHPP,时间段[0, t]内退化点的数目为E[N(t)],则时间区间[t1, t2]内产生n个退化点的概率为
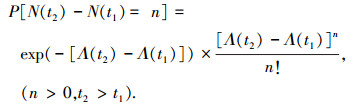
|
由于环境变化对退化点产生过程的影响,在相同的时间内,系统内产生的退化点的数目发生变化,假设

|
因此有
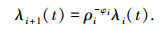
|
令P[N(t1), N(t2), n]=P{N(t2)-N(t2)=n},t时刻产生退化点数目的均值为
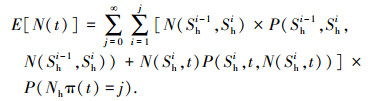
|
则t时刻,系统内产生n个退化点的概率为
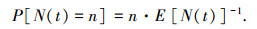
|
根据文献[16],采用非定态伽马过程(non-stationary gamma process)对退化点的生长过程进行建模.令αi(t)=αitqi,由于受环境变化的影响,变化前后退化点的退化速率发生变化,本文引入环境变化系数及环境影响因子进行描述,即α′i(t)/βi′=qi-φiαi(t)/βi,用di(t)表示t时刻第i个退化点的退化量,则其概率密度函数为
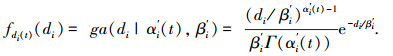
|
其中αi′(t)和βi′分别为Gamma分布的形状参数和尺度参数.由积分可得其分布函数为
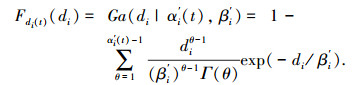
|
在周期性检测策略下,对系统的退化过程进行建模.当第n个检测周期到达时,退化点i的退化量为Di(nδ).假设退化点i的产生时间为ti0, 到达第n个检测周期时,已经历过Nhi(nδ)次环境变化,冲击发生的时刻为Sihj,且Sih0=ti0.可得
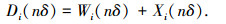
|
(1) |
式中:Wi(nδ)表示退化点在n次冲击作用后产生的损伤累计,Xi(nδ)表示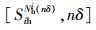

|
(2) |
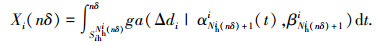
|
(3) |
将式(2)和(3)代入式(1)可得

|
假设Gai(n)(x)为Δdi(Sihj-1, Sihj)的n重卷积,即有
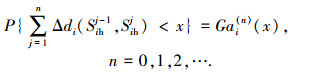
|
Gai(n)(x)可以通过Laplace变换来进行求解.假设Gai* (θ)是Gai(x)的Laplace变换公式,则有
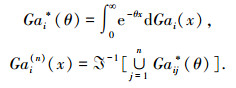
|
式中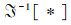
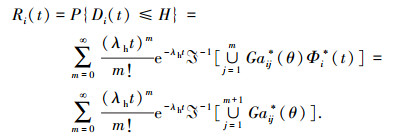
|
式中: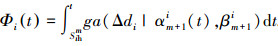
假设t时刻,系统内存在n个退化点,系统的退化量由退化情况最严重的退化点的退化量来表示,即有
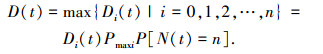
|
式中:
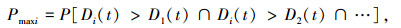
|
则t时刻系统的可靠度为
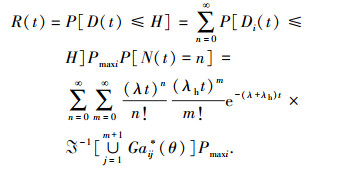
|
假设系统允许的最大退化量为hf,当系统退化量一旦达到hf,系统发生突发性故障,系统立即停机,此时对系统进行故障替换;当系统退化量达到hcm时,系统发生潜在失效,潜在失效不能被立即发现,此时系统仍可以继续运行,直到下一个检测周期到达.在第n个检测周期,系统发生潜在失效,此时对系统进行修复性维护,则其概率为

|
系统在运行过程中出现突发故障的概率为
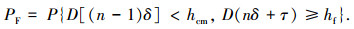
|
(4) |
由式(4)可得到t时刻系统进行维护的概率为
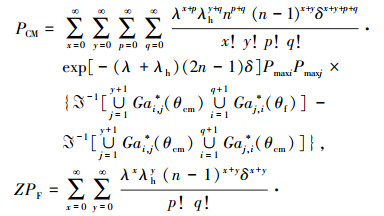
|
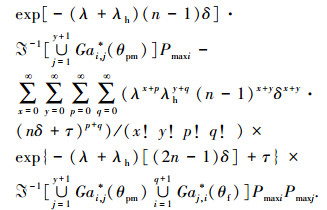
|
每次维护结束记为一个维护周期,cin为每次检测的检测成本,ccm为每次修复性维护的成本,cf为每次故障性维护的成本,且有ccm < cf,则有期望维护成本:
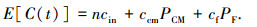
|
C(t)表示系统在时间t内产生的维修成本,由更新定理可得单位维修成本:
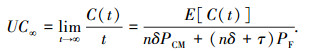
|
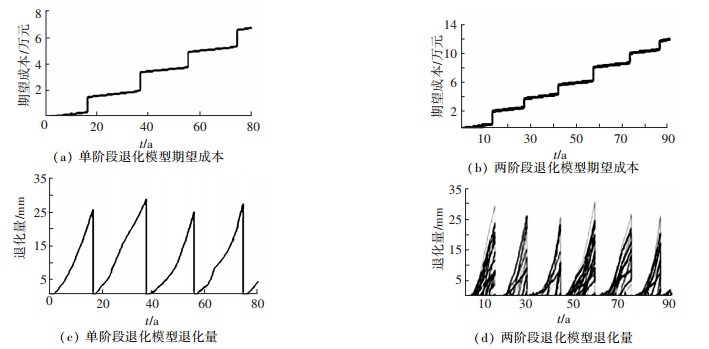
核电系统中的蒸汽发生器传热管工作环境复杂多变,其腐蚀过程可分为腐蚀点的萌发和点蚀坑深的增长两个过程,可采用非齐次Poisson分布和非定态Gamma分布对其进行描述[16].假设管道壁厚为df=3.0 mm的传热管,当某一腐蚀坑深度达到3.0 mm时,整个管道立即失效;当某一腐蚀坑深度达到2.5 mm时,对管道进行替换.管道故障后的维护成本为cf=18 000元,管道达到替换阈值时,对其进行替换的成本为ccm=12 000元,每次检测的成本cin=200元.为了简化计算,假设所有的退化点产生后,在不受环境变化影响的情况下其退化率相同.各参数设置如下α0=5,β0=8,q=1.6,λ0=0.08,δ=0.5年.经过Monte-Carlo仿真,对单阶段与两阶段退化模型下管道的维护成本和退化水平进行分析,可得到图 3、4.

|
图 3 λh=0时期望成本与退化量随时间的变化趋势 |
|
图 4 λh=8时期望成本与退化量随时间的变化趋势 |
由图 3和图 4对比可知, 在λh=0和λh=8时,管道的维护成本随时间逐渐增加,同时呈阶梯式增长.由于每次对管道检测都会产生一定的检测费用,因此维护成本以一定的速率逐渐增加,而当管道达到维护阈值对管道进行维护时,会产生相应的维护成本,此时维护成本增长较快.由图 3(c)、(d)和图 4(c)、(d)可以看出,单阶段退化模型中,管道从0时刻就开始退化,而两阶段退化模型中,在系统运行一段时间后,管道内产生退化点,此时管道开始退化,并且在退化过程中不断有新的退化点产生并持续增长.由图 3和图 4中还可以看出,管道中不断产生新的退化点,且t时刻管道系统的退化情况并不由最早产生的退化点的退化情况决定,而是由该时刻退化情况最严重的退化点决定.根据模型可知, 退化点的生长过程服从非定态Gamma分布,且受环境变化的影响,因此各退化点生长过程具有一定的随机性.在某一时刻,产生较晚的退化点的退化情况可能比产生较早的退化点的退化情况更严重.对λh=0和λh=8时整个管道退化速率进行了分析, 由图 3和图 4中系统退化曲线坡度的变化可知,当λh=0时,管道的退化过程相对比较平稳;当λh=8时,管道内各退化点的退化速率随时间发生变化.
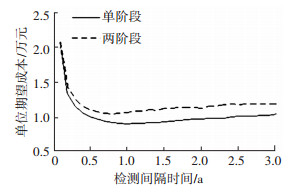
对单阶段和两阶段退化模型的维护成本率进行分析,得如图 5所示曲线.
|
图 5 期望成本与检测间隔时间关系曲线 |
由图 5可知,无论单阶段还是两阶段退化模型,期望成本率随检测间隔时间的增加,呈现出先减小后增加的趋势,并且总体上两阶段退化模型下系统的期望成本率高于单阶段退化模型下系统的期望成本率.对于单阶段退化模型,管道从0时刻就开始退化,但在退化过程中,整个管道的退化情况由唯一的退化过程来描述,而对于两阶段退化模型,在t时刻,系统的退化情况由已产生的退化点中退化最严重退化点的退化情况来决定.根据图 3和图 4分析,各退化点退化量的增长具有随机性,系统中较晚产生的退化点的退化情况可能比系统中最初产生的退化点的退化情况更严重,这使得在两阶段退化情况下,系统总的退化速率比单阶段模型下系统的退化速率大,相应的维护成本率也比单阶段退化情况下的维护成本高.
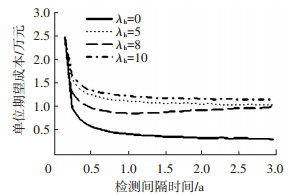
由于系统在退化过程中还受到环境变化的影响,在不同的环境变化情况下,对系统的期望成本率进行分析,可得到图 6和图 7.
|
图 6 单阶段退化系统期望成本率与检测间隔时间关系曲线 |
|
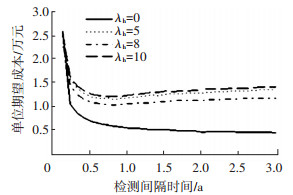
图 7 两阶段退化系统期望成本率与检测间隔时间关系曲线 |
由图 6和图 7可知,随着检测周期的增大,单阶段退化管道和两阶段退化管道的期望成本都呈现出先减小后增大的特点.因此,可以得到使成本最低的检测间隔时间,即每条曲线的最低点所对应的检测间隔时间.当检测间隔时间一定时,分析了对环境变化因子对成本的影响.分析结果表明, 单阶段退化模型和两阶段退化模型中,期望成本并不随λh的增大而增大.在该试验中,随着λh的增大,期望成本先增大后减小再增大.由于系统退化受系统内因及环境变化的影响,当系统退化的随机性与环境变化的随机性相互作用,内外因对系统退化的影响减弱时,系统的退化率减小,最终表现为维护成本降低.相反当内外因对系统退化的影响加强时,系统的退化率增加,系统的维护成本增加.
取检测间隔时间为0.7年,分别对单阶段退化系统与两阶段退化系统的寿命分布受环境变化因素影响情况进行分析.采用Bootstrap估计法对管道的寿命分布及95%置信区间进行估计,结果如图 8和图 9所示.
|
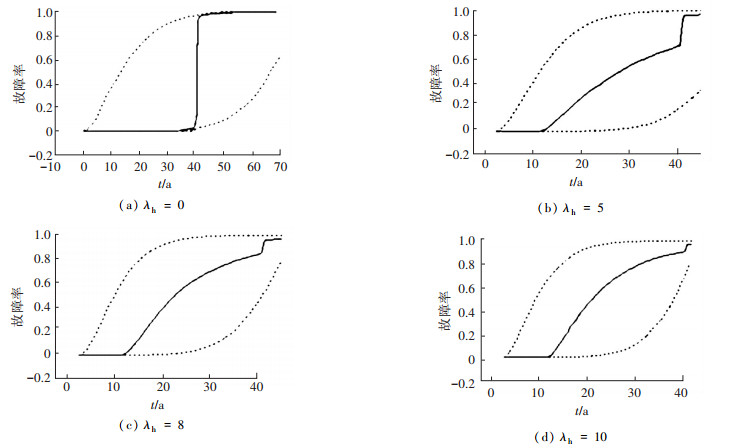
图 8 单阶段退化系统寿命概率分布及其95%置信区间的估计 |
|
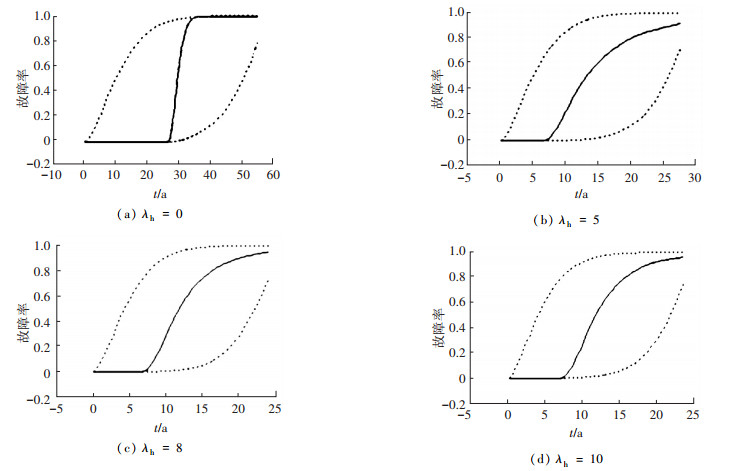
图 9 两阶段退化系统寿命概率分布及其95%置信区间估计 |
由图 8和图 9可知,当管道所处相同环境条件下时,单阶段退化模型下管道的寿命明显比两阶段退化情况下的管道寿命要长,这与图 3、图 4呈现出的特点是一致的.由此可知, 运用单阶段退化模型来对该类系统退化情况进行预测时,没有充分考虑系统内其他退化点的退化情况,并不能准确的描述系统的退化情况,可能会造成对系统退化情况的乐观估计.对于单阶段或两阶段退化情况下,随着环境变动性的增加,管道的寿命分布范围也增大,且随着λh的增加,管道的寿命呈缩短趋势.对于受环境影响较大的系统来讲,外部环境的变动性直接影响到系统寿命,对系统退化情况的合理预测以及有效的检测和维护措施是保证系统正常运行的重要手段.
4 结论1) 对退化系统的维护,通常将系统的退化过程看作是一个单阶段的随机退化过程,并且系统的退化路径也是唯一的.本文针对具有两阶段退化的系统建立了两阶段退化系统视情维修模型,可为该类系统的维护决策问题提供有效的解决方法;
2) 本文在建立两阶段退化模型时进一步考虑环境变化对系统退化过程的影响, 这对减少由于对系统退化情况估计不准造成的不合理维护及保证系统安全运行具有重要意义;
3) 本文结合Bootstrap法得到的退化系统寿命分布的95%置信区间,可以为实际系统的检修以及维护方案的制定提供有价值的信息.
| [1] |
HONG H P, ZHOU W, ZHANG S, et al. Optimal condition-based maintenance decisions for systems with dependent stochastic degradation of components[J]. Reliability Engineering & System Safety, 2014, 121(1): 276-288. |
| [2] |
陶红玉, 周炳海. 基于随机过程的风力机状态维护建模[J]. 计算机集成制造系统, 2014, 20(6): 1416-1423. |
| [3] |
XIANG Y, FENG Q M, COIT D W. Accelerated burn-in and condition-based maintenance for n-subpopulations subject to stochastic degradation[J]. ⅡE Transactions Institute of Industrial Engineers, 2014, 46(10): 1093-1106. |
| [4] |
SOPIE B M. A preventive maintenance policy with sequential checking procedure for a Markov deteriorating system[J]. European Journal of Operational Research, 2002, 142(3): 548-576. DOI:10.1016/S0377-2217(01)00310-1 |
| [5] |
CHEN D, TRIVEDI K S. Optimization for condition-based maintenance with semi-Markov decision process[J]. Reliability engineering & system safety, 2005, 90(1): 25-29. |
| [6] |
CHENG T, PANDEY M D. An accurate analysis of maintenance cost of structures experiencing stochastic degradation[J]. Structure and Infrastructure Engineering, 2012, 8(4): 329-339. DOI:10.1080/15732479.2011.563088 |
| [7] |
GRALL F M A. Monitoring and condition-based maintenance with abrupt change in a system's deterioration rate[J]. International Journal of Systems Science, 2013, 44(10): 1-12. |
| [8] |
PERSONA A, PHAM H, SGARBOSSA F. Age replacement policy in a random environment using system ability[J]. International Journal of Systems Science, 2010, 41(11): 1383-1397. DOI:10.1080/00207720903353617 |
| [9] |
SHEU S H, LI S H, CHANG C C. A generalised maintenance policy with age-dependent minimal repair cost for a system subject to shocks under periodic overhaul[J]. International Journal of Systems Science, 2012, 43(6): 1007-1013. DOI:10.1080/00207720802645220 |
| [10] |
ESARY J D, MARSHALL A W. Shock models and wear processes[J]. The Annals of Probability, 1973, 1(4): 627-649. DOI:10.1214/aop/1176996891 |
| [11] |
Van der WEIDER J A M, PANDEY M D. Stochastic analysis of shock process and modeling of condition-based maintenance[J]. Reliability Engineering & System Safety, 2011, 96(6): 619-626. |
| [12] |
LEMOINE A J, WENOCUR M L. On failure modeling[J]. Naval Research Logistics Quarterly, 1985, 32(3): 497-508. DOI:10.1002/(ISSN)1931-9193 |
| [13] |
DELOUX E, CASTANIER B, BERENGUER C. Predictive maintenance policy for a gradually deteriorating system subject to stress[J]. Reliability Engineering & System Safety, 2009, 94(2): 418-431. |
| [14] |
WANG Y, PHAM H. Imperfect preventive maintenance policies for two-process cumulative damage model of degradation and random shocks[J]. International Journal of System Assurance Engineering and Management, 2011, 2(1): 66-77. DOI:10.1007/s13198-011-0055-8 |
| [15] |
HUYNK K T, CASTRO I T, BARROS A, et al. Modeling age-based maintenance strategies with minimal repairs for systems subject to competing failure modes due to degradation and shocks[J]. European Journal of Operational Research, 2012, 218(1): 140-151. DOI:10.1016/j.ejor.2011.10.025 |
| [16] |
ZHOU Binghai, ZHAI Ziqing. Failure probabilistic analysis of steam generator heat-transfer tubing with pitting corrosion[J]. Engineering Failure Analysis, 2011, 18(5): 1333-1340. DOI:10.1016/j.engfailanal.2011.03.022 |
 2016, Vol. 48
2016, Vol. 48


