在注重能源与环境可持续发展的今天,如何高效地将低品位的工业余热热能转换为高品位的机械能或电能越来越受到关注.研究对余热的利用需要同时考虑余热的数量和质量[1].目前, 评价余热利用的指标主要包括热平衡分析法、㶲分析法和能级分析法[2].热平衡分析法和㶲分析法分别以热力学第一和第二定律为理论基础,从量和质的角度评价对热能的利用.利用低品位热源进行发电的研究目前主要集中在有机朗肯循环[3-5]和以氨水为工质的卡林纳循环[6-11],由于部分有机工质价格昂贵且对环境的破坏作用, 使有机朗肯循环的应用受到限制,而采用价格低廉自然工质的卡林纳循环自从1983年被Kalina[6]提出以来就受到国内外学者的广泛关注. Zhang等[12]对卡林纳循环相关研究进行了较详细的综述;Bombarda等[13]对卡林纳循环和有机朗肯循环的性能进行了对比分析,得出了在输出净功相同的情况下,卡林纳循环需要更高的蒸发压力和温度;Zhang等[14]从㶲分析的角度对有机朗肯循环进行了分析,得出了循环在给定初始条件下的卡林纳循环的最佳蒸发参数;Nag等[15]以㶲效率作为评价指标分析了卡林纳循环的性能,研究了透平进口浓度对㶲效率的影响规律并对系统中各设备的㶲损失进行了分析计算;Singh等[16]从㶲分析的角度对卡林纳循环进行分析评价,得出卡林纳循环在给定透平进口压力的条件下存在最佳工作浓度.
本文主要选取动力回收效率和㶲效率作为评价指标, 对氨水朗肯热电循环与卡林纳发电循环组合系统(AWKRC)进行性能分析,并对系统运行不同的循环流程时各个设备的㶲损失进行计算分析,以指导和改进优化循环特性.
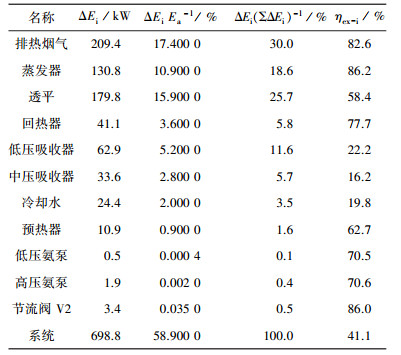
1 AWKRC组合系统介绍AWKRC组合系统的原理是根据氨水混合工质朗肯循环不仅蒸发过程具有较大的温度变化,而且因为其浓度不变,所以其冷凝过程也同样有较大的温度变化,因此可以在采暖季用于加热采暖水. AWKRC组合系统包括非采暖季运行的卡林纳循环如图 1(a)和采暖季运行的氨水朗肯循环如图 1(b).卡林纳循环和氨水朗肯循环之间的转化是通过三通阀开启的方向实现的(实际应用时两个对应的三通阀也可以用1个四通阀代替),在转换过程中除了供暖侧设备外,在系统内部无需添加任何设备.
|
E—蒸发器; T—透平; R—回热器; A1—低压吸收器(冷凝器); A2—中压吸收器; P1—低压泵; P2—高压泵; S—分离器; PH—预热器 图 1 氨水工质卡林纳循环和朗肯循环组合循环流程 |
在非采暖季运行的卡林纳循环见图 1(a),卡林纳循环流程主要包括高压、中压和低压3个部分.低压部分:透平T出口的乏汽(状态点16)在回热器R被冷却到状态18, 进入低压吸收器A1并被分离器S出口的稀溶液(状态点7)吸收,形成基本溶液(状态点1,浓度为xb).中压部分:低压吸收器A1出口的基本溶液被低压氨泵P1升压(状态点2),然后氨水基本溶液分成两路,一部分(点3)进入回热器R中冷却透平出口乏汽,而自身被加热到两相状态(点5)进入分离器S中实现气液分离过程,分离后的稀溶液(点5′)经过预热器PH冷却后在阀V2中节流,进入低压吸收器A1喷淋在管束上,吸收自回热器R来的透平乏汽,而分离器S出口的富氨气体则流入到中压吸收器A2, 被另外一路氨水基本溶液(点8)吸收,形成循环的工作溶液(点10,浓度为xw).高压部分:中压吸收器A2出口的工作溶液(点10)经过高压氨泵P2的升压成为高压流体(点11),首先进入预热器PH被分离器出口的稀溶液预热到状态12,然后在蒸发器E中被余热热源加热到过热状态15(点13和14分别为泡点和露点),进入透平T膨胀作功,最后透平出口的低压乏汽16再经回热器冷却后返回低压吸收器,完成循环.
在采暖季运行的氨水朗肯循环见图 1(b),氨水朗肯循环的运行参数是在卡林纳循环对应的高压和中压之间,所以不必使用低压泵,低压吸收器A1此时为冷凝器,其出口溶液(点1)经过高压泵P2加压到蒸发压力(点11),在回热器R中被透平乏汽预热,预热后的氨水溶液(点12)在蒸发器E中被余热源加热至过热状态15,然后进入透平T中膨胀作功,透平乏汽在回热器R中冷却后(点18)进入冷凝器,释放的热量被冷却水带走,凝结为液体(点1),完成循环.与卡林纳循环相比,氨水朗肯循环的透平乏汽的压力和温度较高,即使经过回热器释放一部分热量用于预热进入蒸发器的溶液,回热器出口湿蒸汽(点18)的温度仍然较高,可以使逆流式冷凝器中的冷却水温度升高到集中采暖要求的90 ℃.采暖水的回水(40 ℃)进入冷却塔进一步降温至15 ℃后,再进入冷凝器(低压吸收器A1).
2 AWKRC系统热力学分析模型考虑余热源为烟气,在蒸发器中的进、出口温度分别为th1和th4时,热源释放的显热热量为
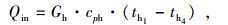
|
而热源最大可能释放的热量为
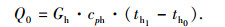
|
(1) |
式中,th0为热源允许排放温度的最低值,本文取为120 ℃.当热源排放温度低于此值时,可能会对传热设备造成低温腐蚀.该温度值的选取并不影响循环性能的定性分析比较.
循环过程中系统透平做功为

|
工质泵消耗功为
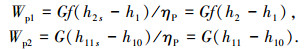
|
式中: ηT、ηP分别为透平和工质泵的等熵效率,分别取为70%和60%,卡林纳循环运行时的工质泵有两台;而氨水朗肯循环只运行高压泵,且h10=h1.
冬季按氨水朗肯循环时,系统采暖供热量为

|
式中:tc2、tc3分别为采暖供、回水温度,分别取tc2=90 ℃和tc3=40 ℃; 考虑到冷却水温度的季节性变化,卡林纳循环和氨水朗肯循环运行时冷却水进口温度分别取为tc1=25 ℃和15 ℃.
余热热源具有的总㶲为
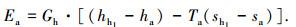
|
(2) |
式中下标“h1”和“a”分别为热源进口温度状态和环境温度下的状态,卡林纳循环和氨水朗肯循环运行时环境温度分别取为Ta=298.15 K和288.15 K.
热水获得余热的热水㶲为
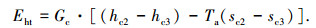
|
循环热效率ηth为输出净功与蒸发器中余热热源释放热量的比值,动力回收效率η0为输出净功与余热热源可能释放的最大热量之比值.由于较高的循环热效率可能是建立在较高的余热排放温度基础上的,所获得的热量可能较少,所以动力回收效率更能体现给定参数的余热动力回收系统的作功能力.
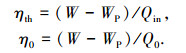
|
当系统按氨水朗肯循环运行时,输出的能量不仅有电能而且有供热量,而动力回收效率只考虑了系统对外输出净功的大小,因而有局限性.由于电能和热能的能级不同,本文以热泵的平均热力系数Ohpav来平衡电能和热能的品位,取Ohpav为5.定义综合动力回收效率为
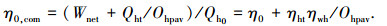
|
系统㶲效率为
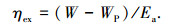
|
按氨水朗肯循环运行时,除了透平做功部分的动力㶲效率外,系统产生的采暖热水也可以得到热水㶲效率为
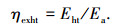
|
氨水朗肯循环的总㶲效率是动力㶲效率和热水㶲效率之和,即
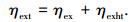
|
对各设备进行㶲分析计算时,设备的㶲损ΔEi是该设备进口㶲值与出口㶲值之差;设备的㶲效率ηex-i是设备出口㶲与进口㶲之比;设备的㶲损系数ΔEi/Ea是各设备的㶲损与余热源的总㶲之比值;而设备的㶲损百分比ΔEi/ΣΔEi则是各设备的㶲损与系统中所有设备㶲损之和的比值.
3 结果与讨论 3.1 卡林纳循环热源温度与最佳浓度的匹配关系在分析外界条件对系统性能的影响规律时,取卡林纳循环的循环倍率(低压吸收器出口流量与工作溶液流量的比值) f=3.5, 且在其他状态参数变化时使其保持不变.当外界热源温度变化时,卡林纳循环的工作浓度xw和基本浓度xb受到一定的限制,影响工作溶液浓度的限制条件主要是保证透平的进口压力维持在一定范围内, 使系统工作稳定,本文选取的工作浓度分别是0.50、0.55和0.60,而当确定了工作浓度后,基本溶液浓度的制约因素主要是保证透平背压为正压(高于大气压)和回热器中的传热端差条件. Hua等[9]指出,存在最佳工作浓度和基本浓度的匹配关系.本文作者进一步的详细计算表明:上述工作浓度和基本浓度的最佳匹配关系随热源温度的变化而有所变化,即当热源温度升高时,对应于某个工作浓度的基本浓度最佳值亦有所增加,如图 2所示.
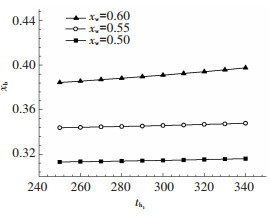
|
图 2 工作浓度在不同热源温度条件下的最佳匹配基本浓度 |
在组合系统由卡林纳循环转换为氨水朗肯循环时,流体循环工作管线主要是工作溶液的管线,所以其工作溶液浓度接近于卡林纳循环的工作浓度xw.本文将两者取相同值.
3.2 蒸发器工质过热度对循环系统性能的影响及过热度的确定以卡林纳循环为例,当热源温度一定时,影响卡林纳循环性能的另一个主要因素是蒸发器中工质的过热度.从图 2中可以看出:当热源温度th1=300 ℃、工作浓度xw=0.50的条件下,与之相匹配的基本浓度xb=0.314 4,在保证蒸发器工质与热源的传热端差为20 K的条件下,过热度Δtr对系统动力回收效率和㶲效率的影响见图 3(a).由图 3(a)可见,在其他条件确定且在最优的状态下,蒸发器中工质的过热度对系统的动力回收效率和㶲效率的影响都存在最优值且同时达到最优状态.因为在热源进口温度和环境温度确定的条件下,无论是式(1)中热源最大可能释放的热量Q0还是式(2)中余热源的总㶲Ea已经确定不变,此时影响动力回收效率或㶲效率的因素只有循环净功的大小,所以两者将同时达到最佳状态.而循环热效率则不然,因为由式(1)确定的热源释放的热量Qin将随着排烟温度而变化,所以循环热效率并不能完全反映余热动力回收系统的效率.
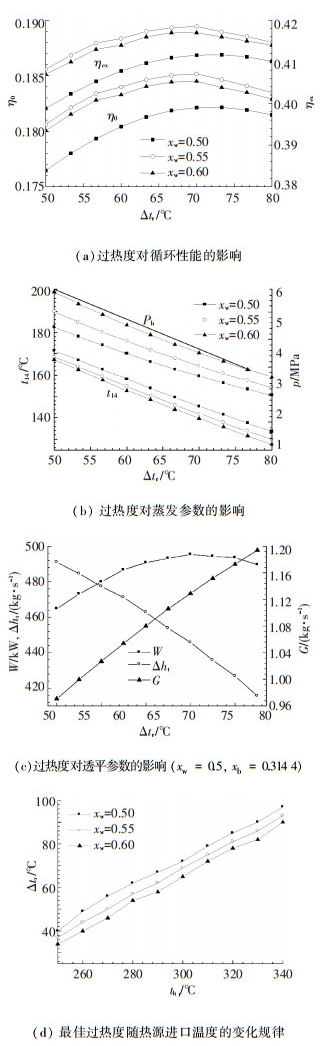
|
图 3 th1=300 ℃, tc1=25 ℃时过热度对卡林纳循环性能的影响及过热度的确定 |
因为余热源的进口温度和蒸发器的端差在计算前已经确定,所以工质在蒸发器中的出口温度也是确定的.在过热度增加的过程中,导致露点温度t14降低,如图 3(b),因为氨水溶液的露点状态参数是与溶液的温度和浓度相关,而工作溶液浓度在此分析过程中是不变的,露点温度的降低将引起蒸发压力即循环系统高压ph的降低和泡点温度的降低,从而导致热源排烟温度降低,因而对系统输入热量增加;但另一方面, 系统工质吸热平均温度的降低将使得循环热效率也有所降低,所以在相反作用的两方面因素影响下,存在最佳的过热度,或者是最佳的蒸发压力.从另一个角度,由图 3(c)可见,透平焓降和透平流量随过热度的变化趋势相反,蒸发器过热度的增加会使得工质焓降减少而透平流量有所增加,而透平输出净功正比于透平流量和焓降的乘积,所以这两方面相反的作用也导致透平输出净功在随过热度的变化过程中存在最佳值. 图 3(d)显示了不同的热源温度和工作浓度对应的最佳过热度的取值.由图可见,最佳过热度随着热源温度的升高而呈线性增大,最佳过热度的变化大约是热源温度变化的一半;最佳过热度随着工作浓度的增大而下降,在工作浓度为0.50~0.60内,工作浓度每变化0.01,最佳过热度的对应变化大约是1 K.
以上讨论虽然是针对卡林纳循环,但热源与氨水混合工质蒸发过程的匹配关系对于氨水朗肯循环也同样适用,上述最佳过热度的分析成果也可用于氨水朗肯循环.
3.3 冷热源进口温度对系统性能的影响规律 3.3.1 热源进口温度对系统性能的影响在热源进口温度th1变化时,对应于不同的工作浓度,按最佳匹配取相对应的基本浓度和最佳过热度. 图 4(a)和图 4(b)分别显示了在不同的工作浓度条件下热源进口温度对卡林纳循环和氨水朗肯循环动力回收效率和㶲效率的影响规律.在按氨水朗肯循环运行时,评价指标有动力回收效率η0、综合动力回收效率η0com、动力㶲效率ηex和包括热水㶲的综合㶲效率ηext.
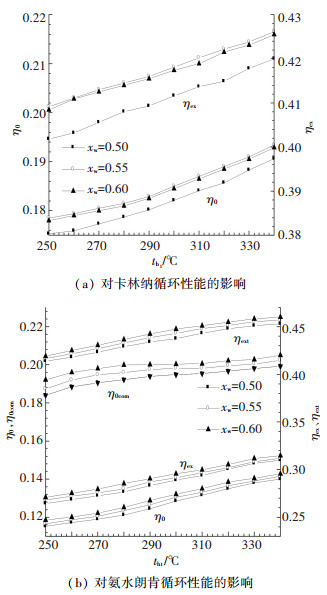
|
图 4 热源温度对系统性能的影响规律 |
由图 4(a)可见,在不同的工作浓度条件下,卡林纳循环的动力回收效率和㶲效率都随着热源温度的升高而增大,而工作浓度由0.5变化到0.55时动力回收效率和㶲效率都是上升的,由0.55变化到0.6时动力回收效率和㶲效率都略有下降.由图 4(b)可见,氨水朗肯循环的动力回收效率和㶲效率性能随热源温度的变化规律与卡林纳循环的相似,即都随着热源温度的升高而增大;但工作浓度的影响则与卡林纳循环有所区别,在工作浓度由0.5变化到0.6范围内,工作浓度的升高对氨水朗肯循环的动力回收效率和㶲效率都是上升的.当热源温度为300 ℃,卡林纳循环和氨水朗肯循环的冷源温度分别为25 ℃、15 ℃时,卡林纳循环的动力回收效率和㶲效率分别为18.2%和41.1%;而氨水朗肯循环的动力回收效率、综合动力回收效率、动力㶲效率和综合㶲效率分别为14.6%、19.6%、33.1%和46.5%.
3.3.2 冷却水进口温度对系统性能的影响在热源进口温度一定条件下,冷却水进口温度tc1对系统的性能也有较大影响,图 5各图分别显示了冷却水进口温度在不同的工作浓度条件下对卡林纳循环和氨水朗肯循环的动力回收效率和循环㶲效率的影响规律.从图 5可以看出,在热源进口温度不变的情况下,冷却水进口温度的升高对系统性能不利.由于冷却水温度直接决定了透平背压的大小,当冷却水温度升高之后,使得透平背压升高,从而使透平焓降降低,作功能力减少,导致系统性能的下降.对于卡林纳循环,当工作浓度由0.50变化到0.55时动力回收效率和㶲效率都是上升的; 由0.55变化到0.60时动力回收效率和㶲效率都略有下降.而对于氨水朗肯循环,当工作浓度由0.50变化到0.60时,氨水朗肯循环的动力回收效率和㶲效率都是上升的.
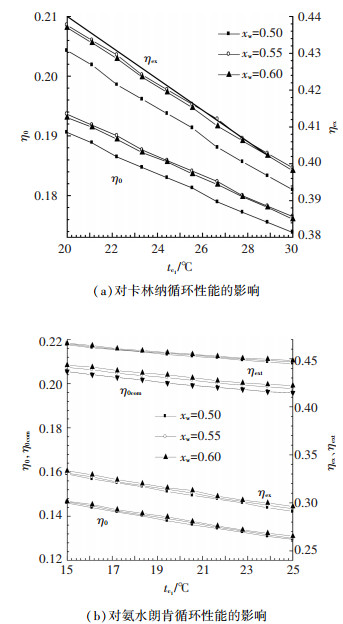
|
图 5 冷源进口温度对循环系统性能的影响规律 |
取热源温度th1=300 ℃,蒸发器工质与热源的传热端差为20 K,蒸发器过热度Δtr=70 K,卡林纳循环时冷源温度tc1=25 ℃,而冬季氨水朗肯循环时冷却水温度取tc1=15 ℃,热水供暖温度为90 ℃,卡林纳循环和氨水朗肯循环的工作浓度均取0.50,卡林纳循环对应的基本浓度为0.314 4.在此条件下卡林纳循环和氨水朗肯循环及其各个设备的㶲损失、㶲效率以及㶲损系数(设备㶲损占总㶲损的份额)如表 1和2所示.此时,卡林纳循环的动力回收效率和㶲效率分别为18.2%、41.1%,氨水朗肯循环的动力回收效率为14.6%,其发电㶲效率为33.1%,总㶲效率可达到46.5%,其中热水㶲效率为13.4%,而当热水供暖温度降低为70 ℃时,热水㶲效率降低到8.7%.由此可见,提高热水供暖温度有利于提高氨水朗肯循环的热水㶲效率,此时冷凝器需要保证是逆流传热.
| 表 1 卡林纳循环各设备㶲分析结果 |
| 表 2 氨水朗肯循环各设备㶲分析结果 |
由表 1、2可见,两种循环中排烟㶲损失均占总㶲损的30%以上.蒸发器和透平的㶲损失之和占整个卡林纳循环系统㶲损失的40%左右,其原因主要是因为考虑到余热源为烟气,蒸发器中的传热过程需要比其他传热过程选择更大的节点温差.透平的㶲损失较大是因为透平的等熵膨胀效率取为0.7,也就是有30%的等熵焓降将耗散为热量.
由于氨水朗肯循环透平排汽温度较高,回热器热侧流体的出口温度也仍然较高,可以满足在逆流式冷凝器中将冷却水加热到供暖热水的条件.同时由于在冷凝器变温冷凝过程中与冷却水之间还是具有较大的传热温差,导致氨水朗肯循环冷凝器中的㶲损所占份额较大,达到了14.5%.
图 6的2个分图分别显示了卡林纳循环和氨水朗肯循环的㶲流分析,可以更好地描述各个设备之间㶲损与热源输入㶲量的对比关系.
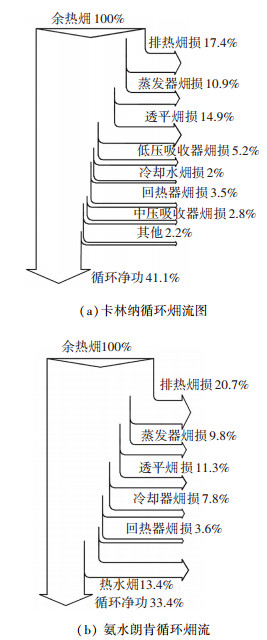
|
图 6 氨水组合系统㶲流图 |
针对以上对氨水组合系统的㶲效率分析和各个设备的㶲损情况,在热源温度为300 ℃、卡林纳循环和氨水朗肯循环的冷却水进口温度分别为25 ℃和15 ℃、工作浓度取为0.50的条件下,AWKRC系统中蒸发器和冷凝器的传热过程曲线如图 7所示.其中横坐标中的Q0是余热源最大可能释放的热量(即排放到120 ℃时所释放的热量).
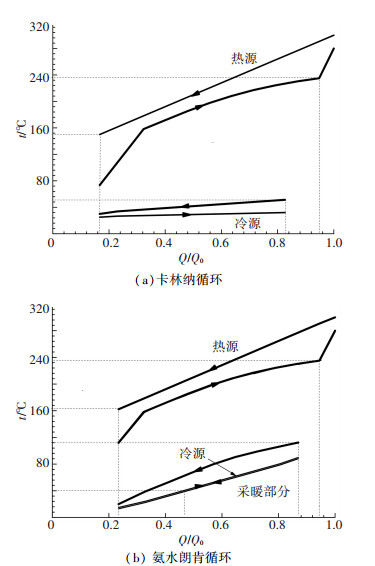
|
图 7 卡林纳循环和氨水朗肯循环工质与热源与冷源的传热曲线 |
1) 卡林纳循环和氨水朗肯循环都存在蒸发器出口工质最佳过热度,使动力回收效率和㶲效率两者同时达到最优.
2) 热源进口温度的升高和冷源进口温度的降低均使卡林纳循环和氨水朗肯循环的动力回收效率和㶲效率增大.在给定的热源进口温度和冷源进口温度条件下,卡林纳循环工质的工作浓度由0.50变化到0.55时动力回收效率和㶲效率都是上升的;由0.55变化到0.60时两者都略有下降.而对于氨水朗肯循环,当工作浓度由0.50变化到0.60时,工作浓度的升高使动力回收效率和㶲效率均有所增大.
3) 在热源进口温度300 ℃,卡林纳循环和氨水朗肯循环冷却水进口温度分别取25 ℃和15 ℃,热水供暖温度为90 ℃,工质工作浓度为0.50,循环其他参数均取最佳值时,卡林纳循环的动力回收效率和㶲效率分别为18.2%和41.1%;氨水朗肯循环的动力回收效率、综合动力回收效率、动力㶲效率和综合㶲效率分别为14.6%、19.6%、33.1%和46.5%.
| [1] |
AL-RABGHI O M, BEIRUTTY M, AKYURT M, et al. Recovery and utilization of waste heat[J]. Heat Recovery Systems and CHP, 1993, 13(5): 463-470. DOI:10.1016/0890-4332(93)90047-Y |
| [2] |
蔡九菊, 王建军, 陈春霞, 等. 钢铁企业余热资源回收与利用[J]. 钢铁, 2007, 42(6): 5-8. |
| [3] |
朱江, 鹿院卫, 马重芳, 等. 低温地热有机朗肯循环(ORC)工质选择[J]. 可再生能源, 2009, 27(2): 76-79. DOI:10.3969/j.issn.1671-5292.2009.02.020 |
| [4] |
RADERMACHER R. Thermodynamic and heat transfer implications of working fluid mixtures in Rankine cycle[J]. International Journal Heat Fluid Flow, 1989, 10(2): 90-102. DOI:10.1016/0142-727X(89)90001-5 |
| [5] |
SALEH B, KOGLBAUER G, WENDLAND M, et al. Working fluids for low-temperature organic Rankine cycle[J]. Energy, 2007, 32(7): 1210-1221. DOI:10.1016/j.energy.2006.07.001 |
| [6] |
KALINA A I. Combine-cycle system with novel bottoming cycle[J]. Journal of Engineering for Gas Turbine and Power, 1984, 106(4): 737-742. DOI:10.1115/1.3239632 |
| [7] |
陈亚平. 改进型卡列纳循环的热力学分析[J]. 东南大学学报, 1989, 19(4): 52-59. |
| [8] |
陈亚平. 简化型卡列纳循环的热力学分析[J]. 热力发电, 1997, 47(4): 20-23. |
| [9] |
HUA Junye, CHEN Yaping, WANG Yaodong, et al. Thermodynamic analysis of ammonia-water power/chilling cogeneration cycle with low-grade waster heat[J]. Applied Thermal Engineering, 2014, 64(1/2): 483-490. |
| [10] |
HUA Junye, CHEN Yaping, LIU Huajin, et al. Thermodynamic analysis of simplified dual-pressure ammonia-water absorption power cycle[J]. Journal of Cent South University, 2012, 19(3): 797-802. DOI:10.1007/s11771-012-1074-6 |
| [11] |
HUA Junye, CHEN Yaping, WU Jiafeng. Thermal performance of a modified ammonia-water power cycle for reclaiming mid/low-grade waste heat[J]. Energy Conversion and Management, 2014, 85: 453-459. DOI:10.1016/j.enconman.2014.05.102 |
| [12] |
ZHANG Xinxin, MAO Gang, ZHANG Ying. A review of research on the Kalina cycle[J]. Renewable and Sustainable Energy Reviews, 2012, 16(7): 5309-5318. DOI:10.1016/j.rser.2012.05.040 |
| [13] |
BOMBARDA P, INVERNIZZI C M, PIETRA C. Heat recovery from Diesel engines:A thermodynamic comparison between Kalina and ORC cycles[J]. Applied Thermal Engineering, 2010, 30(2/3): 212-219. |
| [14] |
ZHANG Junhui, LIU Juanfang, CHEN Qinghua. Optimal evaporating temperature and exergy analysis for Organic Rankine cycle[J]. CIESC Journal, 2013, 64(3): 820-826. |
| [15] |
NAG P K, GUPTA A. V. S. S. K. S. Exergy analysis of the Kalina cycle[J]. Applied Thermal Engineering, 1998, 18(6): 427-439.
|
| [16] |
SINGH O K, KAUSHIK S C. Energy and exergy analysis and optimization of Kalina cycle coupled with a coal fired steam power plant[J]. Applied Thermal Engineering, 2013, 51(1/2): 787-800. |
 2016, Vol. 48
2016, Vol. 48