2. 东北大学科技产业集团有限公司, 110819 沈阳
2. Northeastern University Science & Technology Industry Co., LTD., 110819 Shenyang, China
钢铁企业高炉煤气(BFG)、焦炉煤气(COG)和转炉煤气(LDG)是企业重要的二次能源,其中,高炉煤气的产生量大且广泛应用于钢铁生产过程,如热风炉、焦炉、加热炉和电厂锅炉等的加热[1].近年来,随着节能减排工作的开展,钢铁企业高炉煤气得到了有效利用,放散率逐年下降.但在实际生产中,由于高炉煤气是炼铁的副产品,其产生量和消耗量均随高炉等设备生产工况的变化而变化,煤气供需关系时刻处于不平衡状态,煤气放散等现象仍然存在,造成能源浪费和环境污染,严重时威胁设备的安全运行[2-3],因此,有效地预测高炉煤气的动态供需关系,提前做出调整预案,对钢铁企业提高煤气利用率,降低煤气放散有重要意义.目前,国内外对钢铁企业副产品煤气的预测与调度开展了大量的研究工作,文献[4-5]为克服预测煤气柜柜位问题,建立时间序列预测模型,解决传统理论模型不能正确反映工艺特点和处理突发事件延迟的问题,显著减少预测误差.目前, BP神经网络在高炉煤气的机理预测上得到广泛应用,但是在实际生产中并不能完全提供所需求的数据源,距在线运行有较大差距[6-8].很多学者基于参数优化建立的最小二乘支持向量机(Least squares support vector machine, Lssvm)预测模型,对高炉、转炉煤气柜和高炉煤气发生量进行预测,取得较好效果[9-12],但这些模型没有考虑设备实际运行工况对煤气产生量和消耗量的影响.
本文根据钢铁企业高炉煤气供需特性,深入探究煤气时间序列预测规律,应用小波分析与Lssvm相结合的方法建立高炉煤气产生量、消耗量预测模型,研究高炉生产工况与煤气产生量之间的关系,以准确、及时得到高炉煤气产生量、消耗量数据,为优化调度提供依据.
1 高炉煤气动态预测模型 1.1 小波分析小波分析是工程信号的一种处理手段,广泛应用于图像处理、地理勘测、医学等多个领域[13].本文将对高炉煤气产生量1 500个历史数据进行分离,用小波分析方法得出煤气量趋势数据,把“信号”的粗糙部分提取出来
采用小波滤波器进行一维多尺度分解,其分解函数为[13-14]

|
式中:φJ, k(t)为尺度函数,cJ, k为尺度系数;ψm, k(t)为小波函数,dm, k为小波系数.
设原始时间序列采集样本为A0(n)={c0(n)|n=1, 2, …, l}.其中,n和c0(n)分别是时间序列A0(n)中样本数据的顺序编号和煤气量数据.在任何小波函数f(t)∈L2(R)位于V0空间中,都可以根据分辨率为2-N的低频部分和2-J(1≤J≤N)的高频部分完全重构,其分解空间关系如下:

|
式中:Vi(i≥1)为低频数据空间, Wj(j≥1)为高频数据空间.
对连续采集煤气量A0(n)时间序列进行小波多尺度一维分解,其实质就是把采集到的煤气量分为趋势数据Di(n)和波动数据Ai(n),即“信号”里的低频部分和高频部分,低频部分是煤气量的趋势数据,主要描述煤气量的发展趋势;而高频部分是煤气量的波动数据,包含了煤气量的扰动和噪声信息.根据实际需要,可以对所得到的低频数据进行再分解,但不能超过输入样本数为N的log2N层.
1.2 向量空间重构向量空间重构是时间序列预测中的首要步骤,重构后影响到模型的建立和预测精度,其主要问题是时延τ和嵌入维数m的确定.对于确定的时间序列,都会存在一个最优的τ和m[15].利用迭代求逆法建立Lssvm预测模型.首先由小波分解后得到低频数据,即趋势煤气量数据Di(n)={ci(n)|n=1, 2, …, l}组成训练样本集:

|
最终确立输入输出
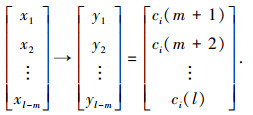
|
式中:xi∈Rm, xi、yi分别是模型样本学习的输入值与输出值.
1.3 模型建立根据结构风险最小化原则,考虑样本学习逼近误差ε,Lssvm优化目标表示为[16]

|
式中:ω、b为权值向量和偏差系数, ε为样本误差, ξi、ξi*为引入的松弛变量, γ(γ>0)为正则化系数.
上式求解过程转化为二次规划问题,引入乘子ai(ai≥0),建立Lagrange方程求解,得

|
式中:参数由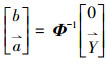
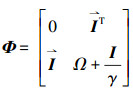

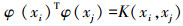

在建立模型过程中,需要实时更新数据,即当新一组训练样本(xi+l, yi+l), i, j∈[1, N]进入到训练集时,采用窗口平移化方法,移除(xl-N, yl-N)数据,并计算模型预测误差:
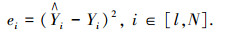
|
式中:ei为第i个预测值误差平方, 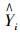
得到误差更新权重: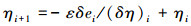
根据上述公式推导,建立高炉煤气动态预测模型,其具体过程如下:
1) 确立初始样本采样周期l、向量空间变换样本维数m以及模型中其它参数;
2) 输入煤气产生量和消耗量值A0(n)={c0(n)|n=1, 2, …, l},利用小波分析方法,提取低频“信号”Di(n)={ci(n)|n=1, 2, …, l};
3) 建立Lssvm输入矩阵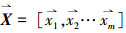
4) 当数据集(xi, yi), i∈(l, l+N)进入训练集时,排除之前N个数据,加入上次预测误差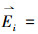
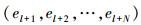

|
图 1 高炉煤气动态预测模型流程图 |
由以上4个步骤建立的高炉煤气产生量与消耗量动态预测模型,充分考虑时间序列的不确定性对高炉煤气预测的影响,建立具有自我修正和时序更新能力的模型,从而可以预测煤气大幅度波动下的煤气量数据,即只要是样本数据能够时刻更新,预测模型都会针对样本数据进行及时调整,根据预测误差对训练数据进行合理化加权修改.这样,不仅能够保证模型的预测精度,而且可以对时刻变化的数据进行预测,以达到对设备变工况下煤气产生量、消耗量进行有效预测.
2 模型验证及效果分析 2.1 实际生产数据的验证本文以某钢铁厂一座3 200 m3高炉的煤气产生量和相应的热风炉煤气消耗量数据作为样本数据,时间频率为5 min(每隔5 min采集一次数据),分别以1 500个连续时间点作为样本数据,对未来8 h,即96个样本点进行预测.
应用小波分析方法对煤气产生量的历史数据进行处理.将煤气产生量的历史数据分解为波动数据和趋势数据,见图 2,分别为历史煤气产生量数据(图 2(a))、波动数据(图 2(b))和趋势数据(图 2(c)).为说明小波分析对预测模型精度提升的有效性,本文将随机选取高炉煤气产生量数据7 500 min(1 500个样本点)进行小波分析及Lssvm预测,并且与未进行小波分析样本数据进行对比.由上节分析可知,原始数据含有大量的“噪声”数据,模型在学习样本数据时,误差达到2.04%,虽然模型可以预测出煤气产生量的发展趋势,但预测精度很不理想,绝对平均误差5.62%、最大误差30.14%、最小误差0.16%,而采用小波分析后的Lssvm预测,预测精度明显提升,绝对平均误差2.77%,最大预测误差10.12%,最小预测误差0.07%,如图 3所示.

|
图 2 高炉煤气产生量及小波分析后的波动数据、趋势数据 |

|
图 3 小波分析前后Lssvm预测效果对比 |
为说明建立的Updata_Lssvm预测模型的优劣,这里与其他3种预测模型进行对比分析,分别为1)原始Lssvm预测,即无参数寻优的Lssvm预测模型;2)BP神经网络预测;3)遗传参数寻优的GALssvm预测,核函数均选取高斯径向基核函数.
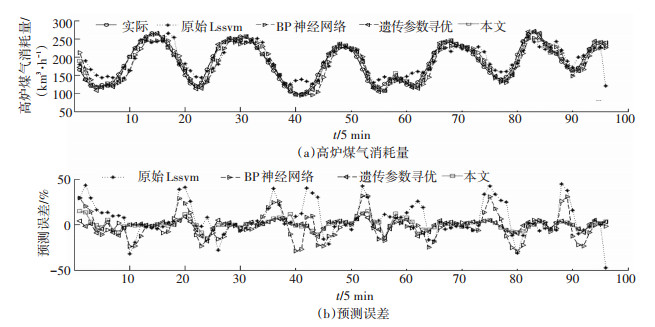
本文都将采用平均绝对误差、最大误差、最小误差以及是否有自我修正和自我更新能力作为评判模型好坏的标准. 图 4为高炉煤气产生量480 min(96个样本点)预测效果图.图中的预测曲线依次为处理后的实际数据曲线(data)、原始Lssvm预测曲线(pro_Lssvm)、BP神经网络预测曲线(pro_BP)、遗传参数寻优的GALssvm预测曲线(pro_GALssvm)以及本文所建立Updata_Lssvm预测曲线.从图中可以看出,pro_GALssvm预测模型与本文所建立的模型预测精度较好,pro_Lssvm和pro_BP次之. pro_Lssvm和pro_BP在20和40个样本点附近出现较大误差.而且在热风炉高炉煤气消耗量预测效果图(图 5)中也可以看出本文模型与pro_GALssvm预测精度较好,pro_Lssvm和pro_BP预测模型在整个预测过程中均存在大范围的波动.

|
图 4 不同预测模型高炉煤气产生量480 min预测效果 |
|
图 5 不同预测模型热风炉高炉煤气消耗量480 min预测效果 |
表 1为预测模型参数及误差分析表,由表 1可见,本文所建立模型的预测精度最高.无参数优化的Lssvm预测误差大,学习样本数据过程较慢,建模不具有稀疏性,对样本数据要求平缓无拐点,而且当参数选取不当时,会出现无法计算等缺点. BP神经网络预测不仅预测效果差,而且预测时间长,通过梯度下降法确定网络权值过程中容易陷入局部极小值点.而基于遗传算法的GALssvm预测模型预测结果虽然较好,但参数选取固定,只能适应固定预测样本,难以确立预测结果与实际值之间的关系,不具备模型自我修正与良好的适应性,即参数选取取决于训练样本维数,并且参数优化以预测均方差为目标,训练过程中很可能会出现拟合不当现象.而本文根据Lssvm特性,首先应用小波分析对初始数据做出处理,得到Lssvm适应的学习预测样本,大大降低了随机与波动数据对预测模型的影响,而且采用样本更新方法,根据预测误差对模型进行修正,使得模型具有自我修正和更新能力.
| 表 1 预测模型参数及误差分析 |
由以上分析可知,本文所建立的模型解决了样本数据的随机性且保证了预测精度,具有模型自我修正和数据更新功能,能够解决变工况下煤气产生量和消耗量预测问题.
3 结论1) 本文基于对大量生产数据的分析,研究了高炉变工况下高炉煤气产生量和热风炉高炉煤气消耗量预测问题.对大量含有随机“噪声”的实际生产数据,应用小波分析将煤气产生量数据分解为波动数据和趋势数据,提取出对Lssvm预测模型有良好学习和预测效果的预测数据,并与小波分析前数据相比,其绝对平均误差降低到2.77%.
2) 结合高炉实际运行工况,对传统Lssvm预测模型进行改进,通过预测误差与模型存在的联系,建立具有时序更新和自我修正功能的Update_Lssvm预测模型,有效解决了高炉煤气产生量与消耗量预测不具有自适应能力的问题.
3) 与其它预测模型相比,本模型预测精度显著提高,其中,高炉煤气产生量预测精度达到1.55%,热风炉高炉煤气消耗量预测精度达到4.23%,完全符合实际应用的需要,为高炉煤气优化调度提供了理论依据.
| [1] |
HE Feng, ZHANG Qingzhi, LEI Jiasu, et al. Energy efficiency and productivity change of China's iron and steel industry:Accounting for undesirable outputs[J]. Energy Policy, 2013(54): 204-213. |
| [2] |
LARSSON M, WANG Chuan, DAHL J. Development of a method for analysing energy, environmental and economic efficiency for an integrated steel plant[J]. Appl Therm Eng, 2006, 26(13): 1353-1361. DOI:10.1016/j.applthermaleng.2005.05.025 |
| [3] |
SUN Wenqiang, CAI Jiuju, SONG Junz. Plant-wide supply-demand forecast and optimization of byproduct gas system in steel plant[J]. Journal of Iron and Steel Research (International), 2013(9): 1-7. |
| [4] |
JEONG C Y, CHU Y H, HAN C H, et al. Gas holder level control based on time-series analysis and process heuristics[J]. Korean J Chem Eng, 2011, 28(1): 16-21. DOI:10.1007/s11814-010-0340-2 |
| [5] |
KONG Haining, QI Ershi, LI Hui, et al. An MILP model for optimization of byproduct gases in the integrated iron and steel plant[J]. Applied Energy, 2010, 6(87): 2156-2163. |
| [6] |
张琦, 谷延良, 提威, 等. 钢铁企业高炉煤气供需预测模型及应用[J]. 东北大学学报(自然科学版), 2010, 31(12): 1737-1740. |
| [7] |
肖冬峰, 杨春节, 宋执环. 基于改进BP网络的高炉煤气发生量预测模型[J]. 浙江大学学报(工学版), 2012, 36(11): 2103-2107. DOI:10.3785/j.issn.1008-973X.2012.11.024 |
| [8] |
邱东, 陈爽, 仝彩霞, 等. 钢铁企业高炉煤气平衡与综合优化[J]. 计算机技术与发展, 2009, 19(3): 196-199. DOI:10.3969/j.issn.1673-629X.2009.03.052 |
| [9] |
刘颖, 赵珺, 王伟, 等. 基于数据的改进回声状态网络在高炉煤气发生量预测中的应用[J]. 自动化学报, 2009, 35(6): 731-738. |
| [10] |
HAN Zhongyang, LIU Ying, ZHAO Jun, et al. Real time prediction for converter gas tank levels based on multi-output least square support vector regressor[J]. Control Engineering Practice, 2012(20): 1400-1409. |
| [11] |
ZHANG Xiaoping, ZHAO Jun, WANG Wei, et al. An optimal method for prediction and adjustment on by product gas holder in steel industry[J]. Expert Systems with Applications, 2011(38): 4588-4599. |
| [12] |
张晓平, 赵珺, 王伟, 等. 基于最小二乘支持向量机的焦炉煤气柜位预测模型及应用[J]. 控制与决策, 2010, 25(8): 1178-1183. |
| [13] |
彭玉华. 小波变换与工程应用[M]. 北京: 科学出版社, 1999: 2, 13-58.
|
| [14] |
RAMIREZA A M, LECUMBERRIA P, GÓMEZ M, et al. Frailty assessment based on wavelet analysis during quiet standing balance test[J]. Journal of Biomechanics, 2011(44): 2213-2220. |
| [15] |
LIU Jiang, CHEN Jiapin, JIANG Shan, et al. Online LSSVM for function estimation and classification[J]. Joumal of University of Science and Technology, 2003, 10(5): 73-77. |
| [16] |
THISSEN U, BRAKEL R V, WEIJER de A P, et al. Using support vector machines for time series prediction[J]. Chemometrics and Intelligent Laboratory Systems, 2003(69): 35-49. |
 2016, Vol. 48
2016, Vol. 48



