2. 车辆传动国家重点实验室(北京理工大学), 100081 北京
2. National Key Lab of Vehicular Transmission(Beijing Institute of Technology), 100081 Beijing, China
传统液力变矩器叶栅设计方法为基于一维束流理论的环量分配法和等角变换法.雷雨龙等[1]对传统等动量矩设计方法进行改进,提出动量矩不等分配法进行叶片设计并对不同分配方案进行比较.叶片曲率变化较大时,此设计方法易出现较大扭曲,使设计出来的叶片制造困难.王健等[2]对叶型进行分层堆叠成型,在给定叶片角度及厚度规律的基础上,利用等角变换将叶片展开图映射到三维空间中构造三维叶片.使用此方法设计叶片时,设计参数过多[3],导致优化改型比较困难.刘冀察[4]提出将儒科夫斯基型线应用到液力变矩器叶片设计中的想法,提出必须进行尾部厚度处理之后才能将儒氏型线应用到液力变矩器叶片设计中.
美国、德国、日本、韩国等汽车工业发达的国家,已经形成了一套完整的三维集成设计系统[5-6],其叶轮机械叶栅造型方法主要分曲面造型法、曲线堆叠法和反设计法.曲面造型法是直接利用三维曲面进行叶片造型的方法,采用的曲面主要有直纹面、贝塞尔曲面和非均匀有理B样条曲面[7-8,];曲线堆叠法是将三维空间曲面分解为曲线进行构造的方法,主要有标准叶型函数法、叶片骨线加厚度分布构造法和吸力面压力面构造法3种[9-10];反设计法是由给定的流场状态参数分布反求出叶型几何的方法,主要有二维反设计法和三维反设计法[11].
随着计算能力的提高及计算流体动力学(CFD)技术的发展,三维流场仿真可以应用到叶栅系统设计中.新型的液力变矩器三维流动设计对三维叶片造型提出了新的要求[12-13].理想的叶片构型方法应尽量满足以下3点要求:1)型线灵活容易调整,具有较好的适应性及鲁棒性;2)约束条件可以灵活地处理,工艺及形状约束易于施加;3)设计变量尽可能少.
叶栅几何描述方法十分重要,关系到后续计算过程的效率高低和叶栅综合性能的优劣[14].儒科夫斯基型线具有如下优点:1)全叶型可解析,精度高,便于CAD中应用;2)曲率连续, 没有突变,流线光滑;3)控制参数少,只需两参数即可进行叶型构造.
本文探索将儒科夫斯基型线用于液力变矩器导轮叶片设计的方法,首先, 简化了儒科夫斯基型线表达式,并在其基础上进行尾缘加厚处理; 随后, 利用该型线对已有液力变矩器导轮叶片进行拟合,并利用CFD对其性能进行计算并与实验结果进行对比; 最后, 在CFD仿真基础上利用遗传算法对儒氏导轮液力变矩器进行优化,验证了儒科夫斯基型线导轮设计的可行性和实用性.
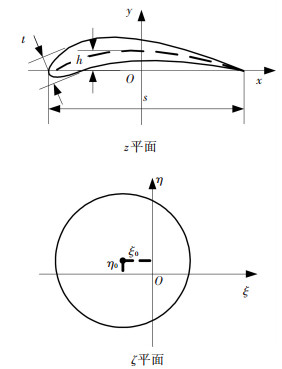
1 儒科夫斯基型线概述儒科夫斯基变换是保角变换中一个十分重要的变换函数,在研究理想流体平面势流运动中,应用该变换可以将复杂的绕翼型流动变换为简单的绕圆柱流动.由圆柱流动ζ平面向型线z平面的儒可夫斯基变换解析函数具有如下形式:
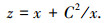
|
式中常数C为实数.
如图 1所示,对ζ平面中圆心位于第二象限的圆进行儒科夫斯基保角变换,即可得到z平面中的儒科夫斯基型线.其中ζ平面中圆心与虚轴(η轴)的距离与型线厚度(t)有关,圆心与实轴(ξ轴)的距离与型线的弯度(h)有关,弦长(s)与实数C有关,儒科夫斯基型线的表达式为
|
图 1 儒科夫斯基变换 |

|
式中:δ=t/s,称为相对厚度; ε=h/s,称为相对弯度; yc为型线相对于弦长的量纲一的纵坐标; xc为型线相对于弦长的量纲一的横坐标.式中:±前表达式为型线中弧线,取正号时表示上型线,取负号时表示下型线.对该式关于ε进行泰勒级数展开并进行坐标变换,忽略3次以上高阶量后得[15]
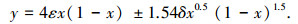
|
(1) |
式(1)为弦长s=1、前缘在原点处的型线,且中弧线最大弯度为ε,最大厚度为δ.
由图 1可知,用式(1)设计的叶片型线具有尖尾缘,而液力变矩器导轮往往是铸造成型,而尖锐的尾缘无法铸造,所以必须对该方法进行改进.文献[12]中提出加一个厚度项来构造光滑尾缘儒科夫斯基型线的方法,表达式为
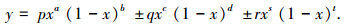
|
(2) |
式中:上型线为式中“±”均取“+”; 下型线为式中“±”均取“-”; p为控制型线中弧线弯度项; q为控制型线厚度项; r为控制尾部加厚项,为主要控制参数,且一般有r < q,s≥d,t≈c,各系数均为正数; a、b、c、d、s、t为微调参数,可以调节型线头部和尾部的收缩、升降等.经过对一系列导轮叶片进行统计研究表明,r取值0.05~0.10,s取值2~3,t取值0.2~0.5.
2 儒氏型线导轮叶片设计及拟合儒科夫斯基型线具有钝头前缘,比纯粹圆弧更为合理,特别适合于大头导轮叶片的构型.对单元儒科夫斯基型线进行旋转、缩放,即可获得需要的导轮平面叶型,最后,利用多圆柱面投影将二维叶片型线投影到三维,进行叶片三维实体的构造.
如图 2,对单元儒科夫斯基型线进行旋转,可得到相应姿态的“单元导轮型线”,再对此型线进行缩放即可得到导轮型线.导轮型线的姿态由旋转角(β)决定.
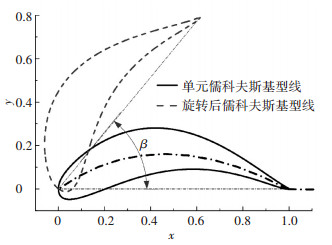
|
图 2 旋转单元儒科夫斯基型线 |
为验证儒氏型线是否能对已有叶片进行表达,对初始导轮型线作逆向旋转、缩放处理,可获得“单元导轮型线”,随后可用儒氏型线对其进行拟合.设获得的原始“单元导轮型线”上、下型线离散点为(xi, yi),i=1, …, n, n为离散点数量.上型线φs和下型线φd的表达式为
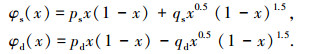
|
式中:ps、qs、pd、qd为待求系数.根据最小二乘法原则,所求系数应使误差平方和最小,即
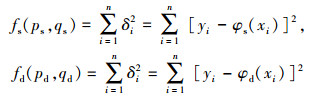
|
取极小值.由极值定理,可得以下求解方程组:
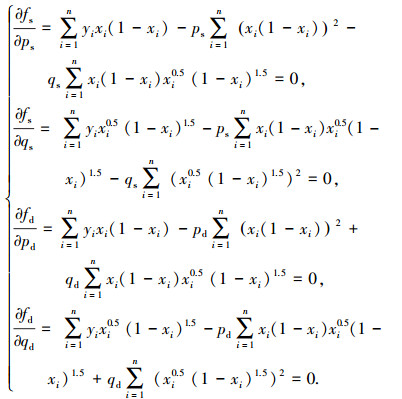
|
由以上方程组可解出最小二乘法拟合的儒科夫斯基型线弯度和厚度系数,同时,利用光滑尾缘儒科夫斯基型线的表达式(式(2))对其进行尾缘光滑修正,获得拟合后导轮内、外环曲线.选取D265、D315及D400 3组液力变矩器导轮叶片,利用儒氏型线对其内、外环型线进行拟合,将拟合结果与原始型线进行对比,结果见图 3~5.
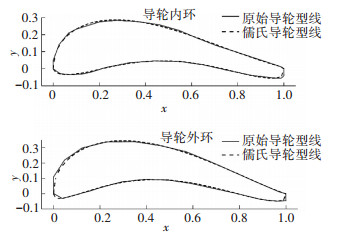
|
图 3 D265液力变矩器导轮型线拟合结果 |
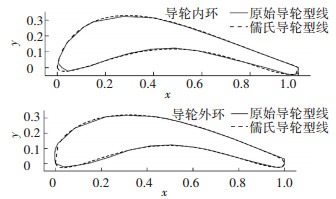
|
图 4 D315液力变矩器导轮型线拟合结果 |

|
图 5 D400液力变矩器导轮型线拟合结果 |
由图 3~5可知,D265导轮叶片头部较大,弯度较小;D315导轮叶片弯度较大;D400导轮叶片具有较大弯度,但是叶片较狭长,头部较平.拟合结果对比可知,拟合误差主要出现在叶片首、尾部.其中D400内环导轮型线用儒科夫斯基型线拟合时在头部出现最大误差,误差绝对值在0.015以下.以上所有导轮儒氏型线拟合误差均方根在0.008以内,标准偏差在0.007以内,拟合结果证明儒氏型线对不同特征导轮叶片均能较精确的表达.
3 儒氏型线导轮叶片三维造型及性能预测选取有效直径为400 mm的D400型液力变矩器为原型,利用多圆柱面投影法对儒科夫斯基型线进行三维映射,得到三维导轮叶片并与原始叶片进行对比(见图 6),由图 6可知,儒科夫斯基型线对原始导轮有较好的拟合效果.

|
图 6 三维导轮叶片对比 |
采用全流道模型,在网格独立性分析基础上,利用非结构网格对流道进行空间离散,单个叶轮网格数约为300万,计算模型总网格数为900万.利用剪应力输运方程(SST)模型,对儒科夫斯基导轮液力变矩器进行牵引工况下(i=0~0.8)三维流场计算,其计算模型如图 7.将原始液力变矩器及儒氏导轮液力变矩器计算结果进行对比, 结果见图 8及图 9.

|
图 7 液力变矩器全流道CFD计算模型 |
|
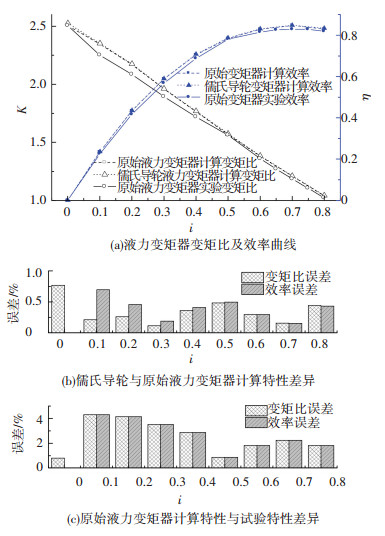
图 8 变矩比及效率计算结果对比 |
|
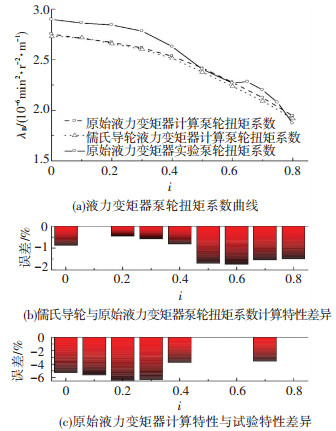
图 9 泵轮扭矩系数计算结果对比 |
图 8、9中误差柱状图为原始液力变矩器与儒氏导轮液力变矩器计算结果的误差,同时原始液力变矩器实验数据及误差也在曲线图中给出.由原始液力变矩器与儒氏导轮液力变矩器计算结果对比可知,儒氏导轮变矩比及效率的计算结果与原始液力变矩器吻合度较高,特性曲线几乎重合(见图 8(a)),儒氏导轮液力变矩器计算数值要比原始稍高,但误差均在1%以内(见图 8(b));儒氏导轮计算泵轮扭矩系数较原始导轮小(见图 9(a)),但误差也在2%以内(见图 9(b)),误差主要出现在高速比区域.由于D400导轮叶片内环型线头部较平,用儒氏叶型对其拟合时在头部出现较大误差(图 5),内环处导轮头部的差异是导致计算结果误差的主要因素.同时,原始液力变矩器的实验特性也在图中显示,两种CFD计算结果与实验结果较吻合,效率与变矩比误差在5%以内(见图 8(c)),泵轮扭矩系数误差在6.5%以内(见图 9(c)),验证了全流道CFD计算的准确性.
4 基于遗传算法的液力变矩器导轮叶片优化利用程序实现儒氏导轮叶片的参数化生成,采用批处理、脚本文件实现液力变矩器三维流场仿真过程的自动化,搭建基于三维流场仿真的液力变矩器设计计算平台[16],为缩短优化周期,采用周期性稳态CFD计算作为特性预测手段来优化叶栅参数.选取内环旋转角(βin)、外环旋转角(βout)、内环弯度pin、外环弯度pout、内环厚度qin、外环厚度qout作为设计变量,最高效率(ηmax)及泵轮起动力矩系数(λB0)指标作为目标函数,起动变矩比(K0)作为约束,建立导轮六变量多目标优化模型:

|
采用基于存档的小种群遗传算法(AMGA)对儒氏导轮液力变矩器进行多目标优化. AMGA算法采用较大的外部存档保留精英解,可使用小种群获得大量非劣解,从而减少适应值评估次数,降低计算量,其采用拥挤距离算法保证解的多样性,同时利用惩罚函数对约束进行处理,具有较强的全局搜索能力[17].
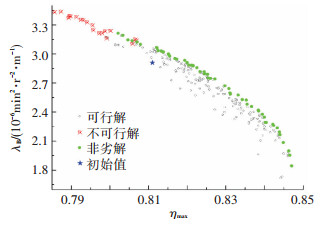
利用AMGA算法直接在自动化液力变矩器设计计算平台上寻优,共计算280个样本点,其中获得256个可行解,62个非劣解. 图 10给出优化后的结果与初始值的对比.由图 10可知,优化后,液力变矩器获得一系列的非劣解,设计人员可以根据实际需要在这些设计中进行权衡、选择.
|
图 10 多目标优化结果 |
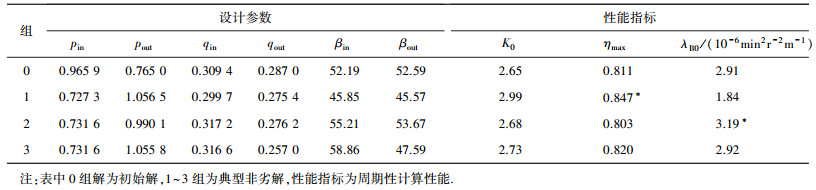
表 1中1~3为选取的3组典型非劣解,0组为初始解.由表 1可知,经过优化后,设计人员可以在一系列不同性能的液力变矩器中进行选择,其中No.1解具有较高的效率,但是其能容较低;No.2解以牺牲经济性为代价提高了功率密度;No.3解综合了效率及功率密度两项指标,虽然单项指标并非最优,但是经过优化后液力变矩器动力性及经济性较初始解有所的提高.
| 表 1 三组典型非劣解 |
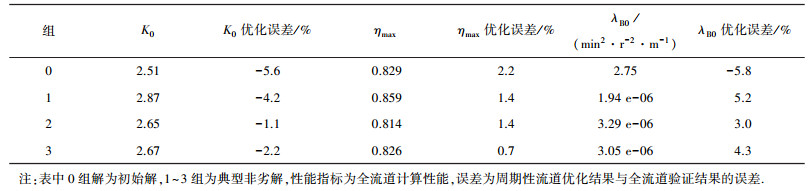
周期性稳态流场计算速度虽然快,但精度相对较低,为提高设计精度,利用全流道CFD模型对优化结果进行验证,得到精确的优化后液力变矩器特性及误差(见表 2),其误差值为周期性流道优化结果与全流道模型计算结果.由表 2可知,利用儒科夫斯基导轮,结合CFD仿真,可以对原型液力变矩器进行有效优化.
| 表 2 优化结果全流道模型验证 |
1) 通过变换并加入尾部加厚项处理, 可以使儒科夫斯基型线适应液力变矩器导轮叶片设计的需要.
2) 型线误差及CFD计算误差结果表明,儒氏型线能够精确表达原始导轮.
3) 编制了参数化儒科夫斯基型线导轮叶片设计程序,并结合自动化液力变矩器三维流场设计分析平台,利用遗传算法对儒氏导轮进行优化.优化结果表明No.3与原型在各性能指标上均有所提高,同时获得了不同性能的非劣解可满足不同使用需求,验证了儒氏型线应用于液力变矩器导轮叶片设计的实用性.
4) 传统的叶片造型方法一般需要至少25个参数对叶片进行表达[18],而儒氏导轮只需要6个参数即可对型线进行完整表达,大大减少了设计变量,从而缩减了设计周期.
5) 对厚度项进行处理后,儒科夫斯基型线也可能应用于液力变矩器涡轮及泵轮的叶片设计,该应用仍有待进一步研究.
| [1] |
雷雨龙, 王健, 胡延辉, 等. 液力变矩器叶栅动量矩分配规律[J]. 吉林大学学报(工学版), 2009, 39(4): 880-884. |
| [2] |
王健, 葛安林, 雷雨龙, 等. 液力变矩器叶片三维成型法及其性能分析[J]. 吉林大学学报(工学版), 2007, 37(1): 43-47. |
| [3] |
魏巍, 刘城, 闫清东. 柔性扁平循环圆液力元件叶栅系统设计方法[J]. 农业机械学报, 2011, 42(4): 33-37. |
| [4] |
刘冀察. 儒科夫斯基翼型用于液力变矩器叶型设计的研究[J]. 工程机械, 2003(1): 22-24. |
| [5] |
KYOUNG S, KYUSUP K, JAEIN P. Development of the integrated process for torque converter design and analysis[C]//Proceedings of 2008 SAE World Congress. Detroit: SAE International, 2008: 0785.
|
| [6] |
ABE H, MASAAKI T, AKIO M. Development of super ultra flat torque converter with multi plate lock-up clutch[J]. SAE Int J Engines, 2009, 2(1): 48-55. DOI:10.4271/2009-01-0141 |
| [7] |
HAZEN F, ABDEL H. Incorporation of sweep in a transonic fan design using a 3D blade-row geometry package intended for aero-structural-manufacturing optimization[D]. Monterey: Naval Postgraduate School, 1997: 32-35.
|
| [8] |
ROSSGATTERER M, JUTTLER B, KAPL M. Medial design of blades for hydroelectric turbines and ship propellers[J]. Computers & Graphics, 2013, 36(5): 434-444. |
| [9] |
OZHAN O, IBRAHIM S. Multi-objective aerodynamic optimization of axial turbine blades using a novel multilevel genetic alorithm[J]. Journal of Turbomachinery, 2010, 132(1): 0411009-1. |
| [10] |
DAMIR V, ZELJAN L, IGOR P. Computational procedure for optimum shape design based on chained bezier surfaces parameterization[J]. Engineering Applications of Artificial Intelligence, 2012, 25(3): 648-667. DOI:10.1016/j.engappai.2011.11.007 |
| [11] |
MAHDI N, FARZAD P. Optimization of a seven-stage centrifugal compressor by using a Quasi-3D inverse desigh method[J]. Journal of Mechanical Science and Technology, 2013, 27(11): 3319-3330. DOI:10.1007/s12206-013-0854-8 |
| [12] |
GEORGIA K, SOTIRIOS S, IOANNIS N. A software tool for parametric design of turbomachinery blades[J]. Advances in Engineering Software, 2009, 40(1): 41-51. DOI:10.1016/j.advengsoft.2008.03.008 |
| [13] |
YAN Qingdong, LIU Cheng, WEI Wei. Numerical simulation of the flow field of a flat torque converter[J]. Journal of Beijing Institute of Technology, 2012, 21(3): 309-314. |
| [14] |
DERKSEN W, TIM R. Bezier-PARSEC:An optimized aerofoil parameterization for design[J]. Advances in Engineering Software, 2010, 41(7): 923-930. |
| [15] |
姜海波, 赵云鹏. 基于中弧线-厚度函数的翼型形状解析构造法[J]. 图学学报, 2013, 34(1): 50-54. DOI:10.3969/j.issn.2095-302X.2013.01.008 |
| [16] |
刘城, 潘鑫, 闫清东, 等. 基于DOE及RSM的液力变矩器叶片数对性能的影响及优化[J]. 北京理工大学学报, 2012, 32(7): 689-693. DOI:10.3969/j.issn.1001-0645.2012.07.008 |
| [17] |
SANTOSH T, PATRICK K. AMGA: an archive-based micro genetic algorithm for multi-objective optimization[C]//Proceedings of 2008 Genetic and Evolutionary Computation Conference. Atlanta: Computer Science Curriculum Press, 2008: 729-736.
|
| [18] |
魏巍, 闫清东. 液力变矩器叶栅系统样条拟合参数设计体系[J]. 农业机械学报, 2009, 40(2): 22-26. |
 2016, Vol. 48
2016, Vol. 48