张拉整体结构是由多个离散的受压构件和一组连续的受拉构件形成的空间稳定索杆体系[1-2].无论任何形式的外力作用在张拉整体结构上,结构里的构件都只需抵抗轴向力[3].张拉整体结构在移动机器人[4]、可展天线[5-6]、智能传感器[7]等领域都得以应用,加州大学的Skelton等[8-10]首先对张拉整体质量进行研究,开辟出一条张拉整体研究的新途径.目前, 国内较少涉及张拉整体质量研究.张拉整体结构质量减轻将会减小控制它所需要的能量,大大提高利用效率和结构性能,张拉整体轻质化研究将会是这一结构的关注重点.张拉整体轻质化研究需要一个系统的优化设计方法.桁架优化通常选取节点坐标和构件横截面积为优化参数,得到桁架结构的最小质量和优化形状[11].与桁架的优化相比,张拉整体结构是一类特殊的索杆结构,在优化过程不仅要保持结构预应力稳定平衡,而且结构节点位置不能发生改变.
本文以圆柱形张拉整体结构为研究对象,在任意给定的一组外力的情况下,选取构件力密度和横截面积为设计参数,以结构力平衡为约束,对圆柱形张拉整体结构最小质量进行优化,综合考虑压杆的两种失效模式, 设计结构的临界最小质量.在给定外力和考虑有效替代空间的情况下,设计三维T型杆自相似迭代结构替换压杆, 从而进一步减轻结构质量.
1 圆柱形张拉整体结构的构型图 1为一个折纸结构.下面就以它为基础构建一个张拉整体结构.把此结构表面的顶点作为所有构建结构的节点.在它棱的位置放置绳,不相邻的节点以杆相连,每个节点上放置两根杆,杆构件按照螺旋形状分布.为了增加结构的稳定性和刚度,这里采用了类似于DNA结构的反向双螺旋形式来布置杆组形式,所形成的结构如图 2所示.

|
图 1 空间折纸模型 |

|
图 2 双螺旋圆柱形张拉整体模型 |
设此结构的第i个节点坐标为
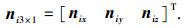
|
此结构的节点都分布于圆柱体表面,设圆柱体的高度为h,其截面半径为r.所有节点都分布于互相平行的水平面上,每层的节点数都相同.最底层为第1层,依次排序,设每层的节点数为k,节点i所在的层编号为c,结构中节点的总数为a.为描述方便, 对其各个节点进行编号, 按节点的编号,编排压杆和拉索的序号.则第i个节点的坐标为

|
系统的节点矩阵为

|
设系统中有q根杆,p根索,整个系统的杆向量矩阵和索向量矩阵可表示为
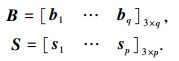
|
式中: bi(i=1, …, q)为第i根杆所对应的杆向量,sj(j=1, …, p)为第j根索所对应的索向量.
为了建立构件矩阵和节点矩阵关系,需要构建连接矩阵,其具体构建方法为:连接矩阵的一行代表系统的一个节点与系统所有构件的关系(起点“-1”、终点“1”、无关“0”).矩阵的一列代表系统的一个构件与系统所有节点之间的关系(起点“-1”、终点“1”、无关“0”).因为任一构件(第i个构件)只与其两个端点连接的节点有关,所以定义连接矩阵第i列元素时,代表该构件起始节点位置的矩阵元素为-1,终止节点位置的矩阵元素为1,其余与该构件无关的节点位置处的矩阵元素为0.按照这样的方法,分别构建系统的杆构件连接矩阵CBT和索构件连接矩阵CST.
构件矩阵、节点矩阵和连接矩阵的关系为
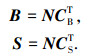
|
各构件的长度也可以通过上述关系式计算获得.
2 静力平衡方程定义作用于节点的外力矩阵为

|
其中: 
定义索构件的内力矩阵为

|
定义杆构件的内力矩阵为

|
索构件和杆构件的力密度分别为
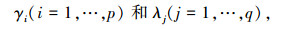
|
则系统的内力矩阵可表示为
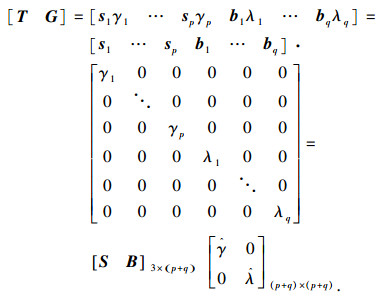
|
式中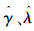
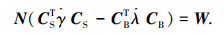
|
由于此结构中各构件只受到轴向力的作用,并且杆构件受到压力的作用,索构件受到拉力的作用.结构中的杆构件是两端具有弹性支撑的压杆, 而当支撑刚度超过屈曲失稳阀值时, 杆的屈曲荷载与两端刚性支撑铰支杆相同[14].两端铰支压杆主要有两种失效形式:一种是材料可能会屈服失效,即杆材料在外力作用下发生塑性变形;另一种是杆可能会发生弯曲变形,即实体杆达到其临界荷载, 造成压杆的屈曲破坏.而索构件由于拉力的作用,其失效形式为屈服失效.综合考虑压杆的两种失效形式,设计此结构的临界最小质量.当压杆的材料属性和长度固定时,结构的临界最小质量跟节点坐标位置、连接矩阵及外力有关.根据这一思想,结构的质量表达式为如下两种情况:
1) 当压杆的失效临界状态为弯曲失稳时,

|
(1) |
2) 当压杆的失效临界状态为屈服时,
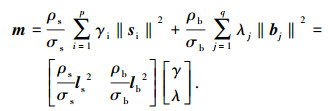
|
(2) |
式中: σb是杆材料的屈服应力,ρb为杆材料的质量密度; σs是索材料的屈服应力,ρs为索材料的质量密度; E为杆的弹性模量; ls、lb分别为索和杆的长度.
分别以式(1)和(2)为目标函数,力密度为自变量,以力平衡方程为约束,此时对应的优化模型为[15]

|
由线性规划算法进行优化分析,即可求出两种情况下最优的构件力密度.
设第i个压杆的长度为li,当压杆的失效临界状态为弯曲失稳时,其优化力密度为λib,计算压杆横截面半径rmin b为
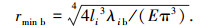
|
(3) |
当压杆的失效临界状态为屈服时,其优化力密度为λiy,计算压杆横截面半径:
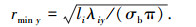
|
(4) |
临界质量圆柱形张拉整体结构中压杆的横截面半径为r=max(rmin b rmin y),则所设计的结构中压杆的失效临界状态即为rmin b、rmin y中最大的情况,其质量为这个结构的临界最小质量.
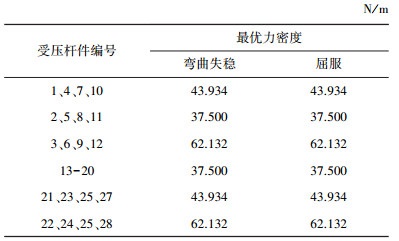
4 力密度优化仿真分析取L=1 m、r=1 m、k=4、c=6的圆柱形张拉整体结构,为了方便,索和杆的材料属性相同,弹性模量E为206 GPa,质量密度ρ为7.862×103 kg/m3,材料的屈服应力σ为690 MPa, 结构受到垂直向下的力F为100 N.根据图 3流程图和优化模型及算法,用matlab编程计算,即可得到各构件的最优力密度,压杆的失效临界状态为弯曲失稳以及屈服时,杆构件的力密度计算结果如表 1所示.

|
图 3 临界最小质量流程 |
| 表 1 弯曲失稳及屈服时杆的最优力密度 |
观察发现两种情况下压杆的力密度值相同,双螺旋圆柱形张拉整体结构中共有2种杆,其杆长分别为
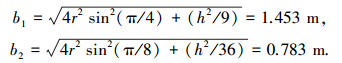
|
压杆共有3种轴向力,分别以杆1、2、3为研究对象,计算两种失效临界状态的横截面半径.
由式(3)、(4)可知
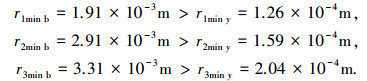
|
由此可知设计此结构的临界最小质量采用的失效临界状态为压杆弯曲失稳.此时结构共有3种受力情况压杆,横截面积不同,但有两种长度.力密度优化后的结构临界质量为m=1.033 9 kg.
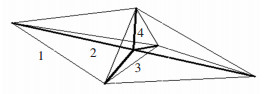
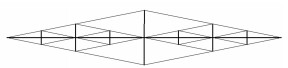
5 三维T型杆自相似迭代设计由材料力学[16]可知,对于压杆,减小其支撑间距,就可以提高其抗失稳的能力.这里采用三维T型杆对压杆进行替代,以增加其抗失稳能力,减小构件质量.三维T型杆单元结构如图 4所示.由图可知,T型杆中共有9条索,分为两类:斜拉索s1和圆周索s2;含有5根细长压杆,分为两类:水平杆l1和竖直杆lv1.索s1和压杆l1的夹角为α.合理设计三维T型杆单元的构型,就可以用其替换压杆来达到减小质量的目的.同理,利用多个三维T型杆单元进行进一步替代,也就是自相似迭代,就可以达到进一步减轻压杆质量的目的. 图 5是迭代4次的三维T型杆结构.
|
1—斜拉索s1; 2—水平杆l1; 3—圆周索s2; 4—竖直杆lv1 图 4 三维T型杆单元模型 |
|
图 5 自相似迭代3次三维T型杆结构正视图 |
由文献[8]可知,三维T型杆自相似迭代设计时所涉及的3个设计参数为:ε≤0.5,表示杆、索的材料性能对质量的影响; 三维T型杆中的夹角α表示三维T型杆的构型对对质量的影响; 最优迭代次数n*,表示迭代次数对质量的影响.
各设计参数的计算公式如下:
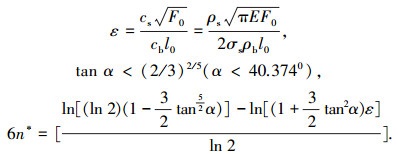
|
(5) |
式中: n*四舍五入取最靠近右侧表达式的整数值,所有三维T型单元都用等角度αi=α设计. F0为压杆轴向压力,l0为压杆的杆长.
5.1 有效替代空间在对三维张拉整体结构中的压杆进行三维T型杆自相似迭代替换时,还要考虑压杆所处整个系统中的空间大小,在对杆进行替换的过程中可能会出现三维T单元中的构件与结构中其他的构件发生干涉的情况.为了避免干涉,需求得以下两个边界:1)压杆与压杆空间相交构件夹角的最小角度; 2)三维T单元的斜拉索s1与压杆空间相异构(距离较近的构件)相交时三维T单元的夹角.
现假设三维张拉整体结构中的某一压杆需进行三维T型杆替换来减小质量.设这一压杆为杆l,其起点节点坐标为nq,终点节点坐标为nz,压杆的位置矢量为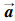
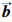
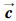
压杆与压杆空间相交构件的夹角通式为
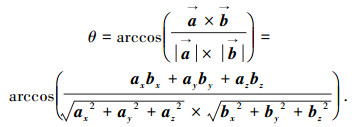
|
(6) |
三维T单元的斜拉索s1与压杆空间相异构件(距离较近的构件)相交时,压杆l的中点空间坐标为
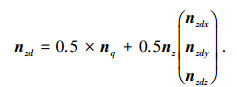
|
两点nq和nc连线的向量为
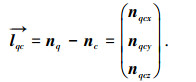
|
相异构件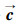
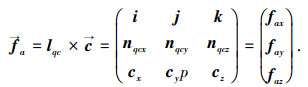
|
杆l的中点nzd到上述平面的距离为
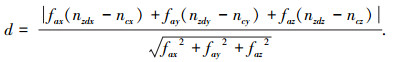
|
此时该情况边界条件下的夹角为
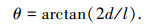
|
(7) |
对于这样的某一压杆需要求i+j个夹角,取其最小的夹角为边界夹角:
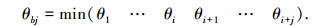
|
(8) |
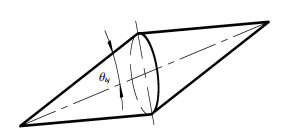
这时压杆所处整个系统中不发生干涉的有效替代空间为夹角为θbj的相对圆锥体,如图 6所示.
|
图 6 有效替代空间 |
在对压杆进行三维T型杆自相似迭代替换来减轻质量时,三维T型杆的夹角α不仅要满足设计参数α < 40.374°,还要使三维T型杆处于不发生干涉的相.对圆锥体空间内,即α < θbj.则三维T型杆的夹角α的选择需满足:
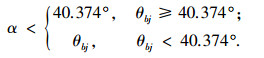
|
则替代后张拉整体结构总质量为
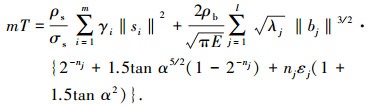
|
(9) |
利用前面计算的结构杆长和力密度,由式(5)计算每个杆的ε值.经计算可知,所有的杆的ε值都<0.5,故此结构可以通过三维T单元迭代替换减轻质量.
由于此圆柱形张拉整体结构存在两个螺旋方向,每个方向联接方式相同,旋向相反,并且结构在水平截面圆周上4等分,在竖直方向上5等分来布置节点位置.因此,此结构具有很好的对称性和规律性.所以只需考虑中间长杆的有效替代空间即可.选择杆15为研究对象,杆15连接起点节点10和终点节点19, 与这一压杆相交的构件有18个,相交于起点10的有9个构件,相交于终点19的有9个构件,由于联接方式相同,故只考虑起点节点10相交的构件即可,共有8根索和1根压杆,与这一压杆空间相异的构件(距离较近的构件)有2根索,根据式(6)、(7)、(8)计算这10个夹角可得整个系统中压杆不发生干涉的边界夹角θbj为16.58°.
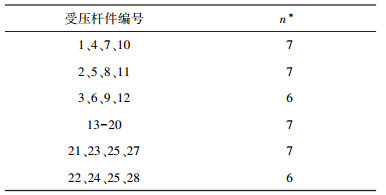
由式(8)、(9)可知,式(9)是关于夹角α的增函数,α越大,替代后的总质量越大,所以尽量选择较小的夹角,这里选择tan α=0.2(α=11.31° < 16.58°)作为三维T型杆的夹角,计算系统中每根压杆的最优迭代次数n*结果见表 2.
| 表 2 杆的最优迭代次数n*值 |
利用分析获得的夹角α、最优迭代数目n*、原始杆杆长及材料属性值,根据图 3相同流程,用matlab编程计算三维T型杆迭代替换n*次后圆柱形双螺旋张拉整体系统的质量m′=0.330 5 kg,

|
则替代后的结构质量只有替代前系统质量的32%.由式(1)和(9)比较可知,该质量减轻的方法不是通过改变材料属性实现的,而是通过自相似迭代结构进一步减小压杆横截面积实现的.
6 结论1) 本文给出了一种有效的张拉整体结构构型方法,通过建立节点矩阵和连接矩阵,快速得到圆柱形张拉整体结构的杆、索向量矩阵,这比通过节点坐标和构件长度建立杆系结构的方法更方便有效.
2) 给定一组外力的情况下,详细地给出了圆柱形张拉整体结构最小质量优化的过程和方法,该最小质量优化方法避免了传统杆系优化结果无法保持张拉整体结构预应力稳定平衡和节点位置不变的弊端.
3) 最小质量优化过程中,详细地介绍了压杆的失效模式,讨论了临界质量圆柱形张拉整体结构中压杆的横截面半径的选择方法,并得到了临界最小质量.
4) 在获得临界质量圆柱形张拉整体结构的基础上,通过引进三维T型杆自相似迭代结构,进一步给出了设计一个质量更轻的张拉整体结构的详细过程和方法,提出了有效替代空间的概念,并给出了有效空间的计算方法.
| [1] |
FULLER R B. Tensile-integrity structures: US3063521A[P]. 1962-11-13[2015-01-15]. http://patft.uspto.gov/.
|
| [2] |
刘锡良, 陈志华. 一种新型空间结构——张拉整体体系[J]. 土木工程学报, 1995, 28(4): 52-57. |
| [3] |
MOTTO R. Tensegrity structural systems for the future[M]. London: Kogan Page Science, 2003: 14-135.
|
| [4] |
PUAL C, ROBERTS J W, LIPSON H, et al. Gait production in a tensegrity based robot[C]//the 2005 International Conference on Advanced Robots. Seattle: IEEE, 2005: 216-222.
|
| [5] |
TIBERT A G, PELLGRINO S. Deployable tensegrity reflectors for small satellites[J]. Spacecraft and Rockets, 2002, 39(5): 701-709. DOI:10.2514/2.3867 |
| [6] |
TIBERT A G. Deployable tensegrity structures for space applications[D]. Stockholm: Royal Institute of Technology, 2002.
|
| [7] |
江洁, 李团结. 张拉整体结构振动最优控制的作动器优化配置[J]. 西安电子科技大学学报, 2014, 41(1): 170-175. DOI:10.3969/j.issn.1001-2400.2014.01.030 |
| [8] |
SKELTON R E, de OLVERIRA M C. Tensegrity Systems[M]. New Yorks: Spriger, 2010: 73-128.
|
| [9] |
NAGASE K, SKELTON R E. Minimal mass design of tensegrity structures[C]//Sensors and Smart Structures Technologies for Civil, Mechanical and Aerospace Systems. San Diego: SPIE, 2014: 1-14.
|
| [10] |
SKELTON R E, FRATERNALIB F, CARPENTIERIB G, et al. Minimum mass design of tensegrity bridges with parametric architecture and multiscale complexity[J]. Mechanics Research Communications, 2014, 58: 124-132. DOI:10.1016/j.mechrescom.2013.10.017 |
| [11] |
陈芸. 基于遗传算法的桁架形状优化及最小质量设计[J]. 南京工业大学学报(自然科学版), 2006, 28(6): 32-36. DOI:10.3969/j.issn.1671-7627.2006.06.008 |
| [12] |
PELLEGRIN S, CALLADINE C R. Matrix analysis of statically and kinematically indeterminate frameworks[J]. International Journal of Solid & Structures, 1986, 22: 409-428. |
| [13] |
KANGWAI R D, GUEST S D. Symmetry-adapted equilibrium matrices[J]. International Journal of Solid & Structures, 2000, 37: 1525-1548. |
| [14] |
罗尧治, 年有增, 符刚. 基于压杆失稳的张拉整体结构极限承载力[J]. 空间结构, 2004, 10(1): 7-11. DOI:10.3969/j.issn.1006-6578.2004.01.002 |
| [15] |
ZHANG J Y, OHSAKI M. Adaptive force density method for form finding problem oftensegrity structures[J]. International Journal of Solid & Structures, 2006, 43: 5658-5673. |
| [16] |
张功学. 材料力学[M]. 北京: 西安电子科技大学出版, 2008: 173-184.
|
 2016, Vol. 48
2016, Vol. 48