波浪能是蕴藏在海水中的可再生能源,波浪能相对其他形式的海洋能源,具有开发方便、装置廉价、小巧的优点.全球可利用的波浪能达到25亿kW,相当于目前世界发电装机容量的2倍[1-5].波浪能的转换包括三级转换[6]:一级转换为波浪能的采集过程,从波浪中吸收能量转换为其他形式的能量,波能采集装置主要有振荡水柱式[7]、点吸式[8-11]、摆式[12]等; 二级转换承担定向、增速、稳速的作用; 三级转换实现机械能到电能的转换.
近年来,国内外学者对不同形式的波能装置做了大量的实验和数值计算.郑雄波等[13]基于频域线性波理论和势流理论对一种双浮体波浪能装置的水动力系数和能量吸收进行了分析.王晓明等[14-15]基于势流理论对一种摇荡波能装置的重心位置和吃水与能量吸收的关系进行了研究. Ronald等[16]基于频域线性波理论对圆柱体波能装置的运动性能和能量吸收进行了研究.史宏达等[17]基于自由面VOF方法建立二维数值水池,对一种振荡水柱式波能装置进行了研究. Yi等[18]运用基于时域平均的NS方程的CFD方法对一种双浮体波能装置进行了模拟. 2013年,哈尔滨工程大学成功对一种通过液压发电的波浪能装置进行了实验,并运用CFD方法对该波能装置进行了全面的时域数值模拟[19].
国内外对波浪能装置的研究多是基于频域线性波理论和势流理论,忽略了流体的黏性效应,而本文的CFD方法的优势在于考虑了流体的黏性效应,能够对复杂形状的浮子进行多自由度的时域模拟,直观地反映出浮子运动时物理量的时历变化,也能够得出计算域内每个时间节点的流场信息.
1 力学模型本文的波浪能装置中浮子如图 1(a)所示,两个浮子呈反对称布置,并与箱体连接,浮子可以在随箱体运动的同时绕箱体轴向转动,波浪推动浮子做纵摇和垂荡运动,浮子与箱体的相对运动带动动力输出系统PTO做功,实现了波浪能的吸收与转化.针对该波浪能装置,取单独一个浮子进行研究,将运动简化为浮子质心的平动和整体绕质心轴线的转动,即垂荡和纵摇运动. 图 1(a)为浮子的实验模型,(b)为浮子的CFD计算模型及详细尺寸,(c)为浮子在波浪中运动示意图.
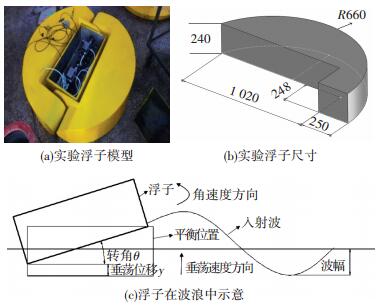
|
图 1 浮子模型和几何尺寸(单位:mm) |
浮子有纵摇和垂荡两个自由度,纵摇和垂荡都可以进行能量输出,根据本文所运用的CFD方法可将纵摇和垂荡的力学模型表示为

|
(1) |
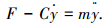
|
(2) |
其中:

|
F和M是ANSYS 15.0 CFX软件中可直接得到的物理量,即流体在浮子表面压力积分的总和,包含了波浪的激振力(力矩)、波浪阻尼力(力矩)和静水回复力(力矩).式中:M为波浪对浮子的总力矩,N·m;θ为纵摇幅值,(°);J为转动惯量,kg·m2;ΔJ为附加转动惯量,kg·m2;N为纵摇PTO阻尼系数,Ns/m;N0为与水相关的纵摇阻尼系数,Ns/m;V为浮子排水量,m3;h为稳心高,m;Mθ为纵摇激振力矩,N·m; 纵摇运动及力矩沿z轴方向. F为波浪对浮子的总垂荡力,N;y为垂荡幅值,m;m为质量,kg;λ为附加质量,kg;C为垂荡PTO阻尼系数,Ns/m;C0为与水相关的垂荡阻尼系数,Ns/m;ρ为水的密度,kg/m3;g为重力加速度,m/s2;s为水线面面积,m2;K为锚链弹性系数,N/m;Fb为垂荡激振力,N.垂荡运动及力的方向沿y轴方向.
根据式(1)、(2)可知,控制浮子运动最直接的方法就是改变N和C的大小,N和C也是影响浮子能量吸收的重要因素,本文通过改变N和C研究了浮子的运动规律和能量吸收的变化.
俘获宽度比是衡量浮子能量吸收性能的重要指标,俘获宽度比η可按式(3)计算:

|
(3) |

|
(4) |
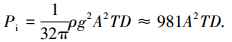
|
式中:η为装置的俘获宽度比; Pa为浮子平均吸收功率,W; Pi为浮子宽度内的波浪平均功率,W; t2-t1为浮体运动时长, s; C为PTO机械阻尼系数,Ns/m;A为波高, m; T为波浪周期,s; D为浮子直径,m; v为浮子运动速度,m/s.
2 流体模型利用CFX软件,基于连续性方程、N-S方程和k-ω湍流模型对计算域内的网格节点进行迭代求解.运用CFD方法对图 1(b)中的浮子进行三维时域模拟,选取计算域为16 m×5 m×5 m,网格划分及边界条件的设置如图 2.浮子域内采用非结构网格,浮子域外采用结构网格,在波长方向上保证每个波长内有100-150个网格,波高方向上保证每个波高内有40-50网格,计算域的总网格数目在30万左右.网格划分如图 2(a)所示.

|
图 2 计算域和浮子的网格划分及尺寸 |
边界条件的设置模拟真实实验条件,图 2(b)为水池中浮子和波浪示意图,造波板、水池池壁、池底和浮子的边界条件设置为wall,模拟真实水池壁面,保证流体不可穿透;如图 2(c)所示,水池顶端和末端设置为Opening,保证与外界有流体交换,维持域内压力平衡,x轴负方向为波浪前进方向,y轴为波高方向,z轴垂直于xy平面,为水池宽度方向.造波板位于x=0处,浮子位于距造波板6 m处.生成的波浪与实验中波况一致,波高分为0.10 m和0.15 m,周期为1.6~3.0 s的规则波.根据波浪周期选取计算时间步长为0.1 s.
3 CFD模拟结果与实验对比分析按照上述CFX的模拟方法,模拟了浮子在波高为0.10 m和0.15 m,周期为1.6~3.0 s的波浪上的纵摇幅值, 并与实验值对比.实验中在浮子上安装有角位移传感器,可以得出不同时刻的浮子转角,选取4种不同波况,将计算值与实验值的浮子纵摇角进行对比, 结果见图 3.
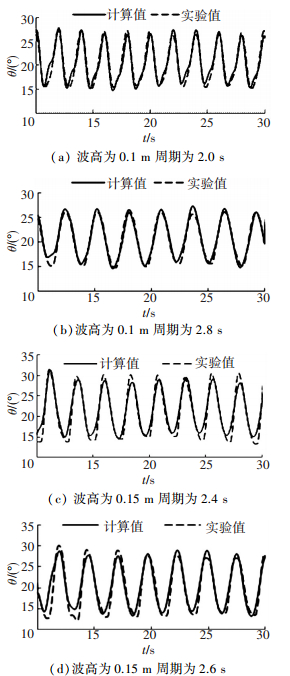
|
图 3 不同波况下浮子纵摇角的计算值与实验值对比 |
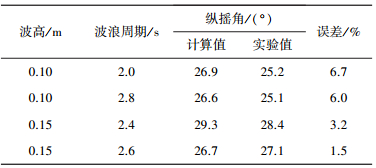
图 3为浮子在不同波况中历时20 s的纵摇运动,可以看出,不同波况下浮子的纵摇角也不相同.图(a)和图(b)中波高较小,其纵摇角在27°左右.图(c)和图(d)中波高较大,其纵摇角最大幅值约30°. 表 1中列出了4种波况下的浮子运动20 s内幅值的平均值.
| 表 1 浮子纵摇角的计算值和实验值对比的误差 |
从表 1中可以看出,计算值与实验值的浮子纵摇角相差不大,在波高较小时,计算值与实验值的误差在6%左右;波高较大时,计算值与实验值的误差在2%左右.
从图 3中可以看出, 两条曲线趋势一致,能够很好地吻合在一起.由表 1可知,计算值与实验值误差都在允许范围内,说明了利用该方法模拟浮子纵摇运动的准确性;由于本实验没有对浮子的垂荡运动进行数据采集,故选取与此相关的其它实验进行对比,对垂荡运动的模拟请参考文献[19].综上所述, 利用CFD方法模拟波能装置运动是可行的.
4 不同自由度对浮子运动及能量吸收的影响波浪中的能量分为势能和动能两部分,势能和动能相等,浮子的垂荡运动主要吸收了波浪的势能,而纵摇主要吸收了波浪的动能.浮子对波浪能量的吸收率不仅与自身尺度和质量分布有关,还与运动情况有关,本文研究了不同质量分布对浮子运动的影响,以及浮子处于不同自由度时能量吸收的影响.
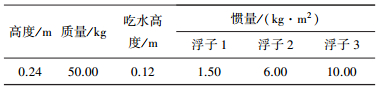
浮子在大小和形状确定后,质量也相对确定.但不同的质量分布,对旋转轴的惯量也不同,保证相同的质量,选取3种不同惯量的浮子,具体参数如表 2所示.
| 表 2 浮子基本参数 |
浮子做单自由度垂荡运动时,运动幅值与质量有关,与惯量无关.对于表 2中质量50 kg的浮子,选取波浪周期范围为1~3 s的规则波,对浮子的垂荡运动进行CFD模拟,将模拟结果转化为频域值,如图 4所示,RAO为浮子的运动幅值(从最低点到最高点)与波高之比, 记为r.
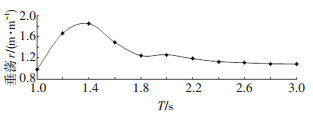
|
图 4 浮子的垂荡RAO曲线 |
从图 4可以看出,浮子的垂荡r值先增大后减小,在波浪周期为1.4 s时出现最大值,浮子的垂荡共振周期为1.4 s,在波浪周期较大时,浮子的垂荡r略>1,这表明浮子在远大于其自身固有周期的波浪中垂荡时,其垂荡幅值与波幅几乎相等.
在浮子垂荡共振周期下,浮子的垂荡幅值和速度最大,其能量输出也相应较高.取浮子垂荡PTO阻尼系数为10~1 500 Ns/m,在共振周期下的垂荡速度和俘获宽度比曲线如图 5.
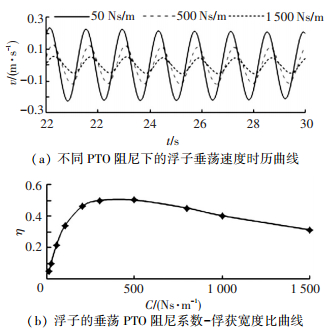
|
图 5 浮子垂荡速度时历曲线和垂荡PTO阻尼系数-俘获宽度比曲线 |
从图 5(a)中可以看出,浮子的垂荡速度曲线呈周期性变化,大小与波浪周期一致,在垂荡PTO阻尼系数为50 Ns/m时,浮子的垂荡速度最大,PTO阻尼增大至1 500 Ns/m时,其垂荡速度最小,约为阻尼系数为50 Ns/m时的20%.这表明垂荡PTO的阻尼越大,浮子的垂荡速度越小.
从图 5(b)中可以看出,垂荡PTO阻尼从10增大至1 500 Ns/m时,俘获宽度比先增大后减小,在PTO垂荡阻尼系数为500 Ns/m时俘获宽度比最大值为0.5.根据式(4)可知,瞬时功率越大,浮子的平均功率越大,而PTO阻尼系数越大,速度越小,故平均功率存在最大值.
4.2 纵摇运动浮子做纵摇运动时,重心位于水线面附近,初始时刻其浮心在水线面下距底部0.06 m,重心与浮心距离为0.06 m.选取不同质量分布(即不同惯量)的3种浮子(见表 2),对其进行纵摇CFD模拟.其中浮子1的波浪周期范围为1.0~2.4 s,浮子2和3的波浪周期为1.4~4.0 s.得出浮子1~3的纵摇RAO曲线如6所示.
从图 6可以看出,随着波浪周期的增大,3种浮子的纵摇RAO曲线都是先增大后减小,对于不同惯量的浮子,固有周期不同.惯量为1.5 kg·m2的浮子,固有周期为1.2 s;惯量为6.0 kg·m2的浮子,固有周期为2.8 s;惯量为10 kg·m2的浮子,固有周期为3.2 s;惯量越大,固有周期越大.
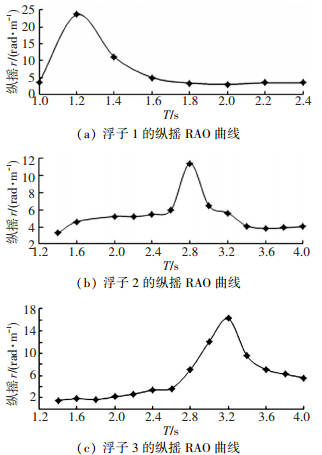
|
图 6 不同浮子的纵摇RAO曲线 |
在3种浮子的共振周期下,加入不同的纵摇PTO阻尼,得出纵摇PTO阻尼与纵摇速度和俘获宽度比曲线如图 7所示.

|
图 7 浮子纵摇速度时历曲线和纵摇PTO阻尼系数-俘获宽度比曲线 |
图 7(a)为浮子1在不同纵摇PTO阻尼系数下的纵摇速度时历曲线,可以看出,纵摇PTO的阻尼越大,纵摇速度幅值越小,这是由于PTO阻尼越大,浮子克服PTO做功越多,其自身摇荡的动能就越小.
从图 7(b)~(d)中可以看出,随着纵摇PTO阻尼系数的增大,俘获宽度比先增大后减小,在最佳纵摇PTO阻尼下出现最大值,该规律与垂荡运动时相同.惯量较小的浮子1最佳纵摇PTO阻尼系数为2 Nms/rad,该阻尼系数下的俘获宽度比为0.747.惯量较大的浮子2和浮子3的最佳纵摇PTO阻尼系数为8 Nms/rad,俘获宽度比仅为0.032和0.039.浮子2和3的惯量为浮子1的4倍和6.7倍,而俘获宽度比仅为浮子1的4.3%和5.2%.这是由于浮子1所处的波浪周期为1.2 s,半波长约为1.1 m,而浮子2和3所处波浪的半波长约为6 m和8 m,浮子在波长方向的尺度为0.66 m,与周期为1.2 s的半波长最为接近,波浪提供给浮子1较大的力矩,使其有较大的纵摇速度和能量吸收.
4.3 垂荡加纵摇运动上述研究为单自由度的垂荡和纵摇运动,在真实海况中,浮子是垂荡和纵摇两个自由度并存,并且垂荡和纵摇在能量吸收中可以相互影响,本节研究浮子具有两个自由度时,其运动和俘获宽度比的变化.浮子1~3运动曲线如图 8所示(A为波高).

|
图 8 浮子垂荡位移和纵摇角时历曲线 |
从图 8(a)中可以看出,浮子在仅做垂荡运动时,其垂荡幅值大于浮子具有两个自由度时的垂荡幅值;在具有两个自由度时,3种浮子的垂荡位移曲线基本重合,这说明惯量对浮子的垂荡幅值几乎无影响.从图 8(b)(c)(d)中可以看出,浮子仅做纵摇运动时,其纵摇幅值大于具有两个自由度时的纵摇幅值;浮子2和3的中纵摇幅值相差最为明显.通过对浮子垂荡和纵摇幅值的对比可以得出,浮子做单自由度运动时的运动幅值要大于两自由度时的运动幅值.
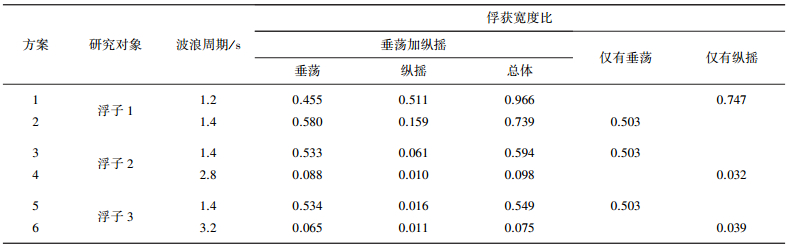
将3种浮子在不同自由度下的俘获宽度比进行对比,取每个浮子的垂荡和纵摇两个共振周期作为给定波况,研究浮子具有单自由度和两自由度时的能量吸收变化,结果见表 3.
| 表 3 不同浮子在不同自由度下的俘获宽度比 |
浮子1的垂荡固有周期为1.4 s,垂荡PTO最佳阻尼系数为500 Ns/m,纵摇固有周期为1.2 s,纵摇PTO最佳阻尼系数为2 Nms/rad.取最佳垂荡和纵摇PTO阻尼系数分别在垂荡和纵摇固有周期下模拟浮子的运动,即为方案1和2.将6种方案下的浮子进行模拟,得出俘获宽度比如表 3所示.
通过方案1中不同自由度对比可以得出,浮子1处于纵摇共振周期1.2 s时,浮子具有两个自由度的俘获宽度比为0.966,较只有纵摇时的俘获宽度比0.747时高.通过方案2对比可以得出,浮子1处于垂荡共振周期1.4 s时,浮子具有两个自由度的俘获宽度比为0.739,较只有垂荡时的俘获宽度比0.503时高.这说明浮子具有两个自由度时的总俘获宽度比要比单自由度时高.该规律在浮子2和3上也得到了验证.
将方案2、3和5对比可知,浮子具有两个自由度时垂荡俘获宽度比比单自由度时高;将方案1、4和6对比可知,浮子具有两个自由度时纵摇俘获宽度比比单自由度时低.这说明两个自由度在能量吸收上可以相互影响.这是由于浮子处于不同自由度运动时,其浸深和角度都会受到影响.例如,浮子仅有垂荡时,自身只有平动而无转动,当有垂荡和纵摇两个自由度时,浮子在垂荡的同时要有一定的转动,直观上浮子的姿态更适应波面的变化,会使周围流场产生变化,进而影响其能量吸收.
将3个浮子的垂荡固有周期和纵摇固有周期对比得出,浮子1的垂荡固有周期与纵摇固有周期最接近,俘获宽度比最高.表明对于具有两个自由度的浮子,两个自由度的固有周期接近更有利于能量的吸收.
4.4 流场分析为了更加直观全面地研究浮子不同自由度对浮子运动的影响,从流场的角度出发,研究处于不同自由度的浮子在流场上的区别.选取浮子处于接近波峰,但垂荡位移和纵摇角仍继续增大的时刻,对该时刻流场进行分析,分别将单自由度运动与两自由度运动的涡量场进行对比, 结果如图 9、10所示.
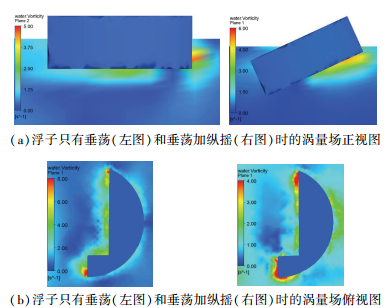
|
图 9 浮子垂荡单自由度和垂荡纵摇双自由度时涡量场对比 |
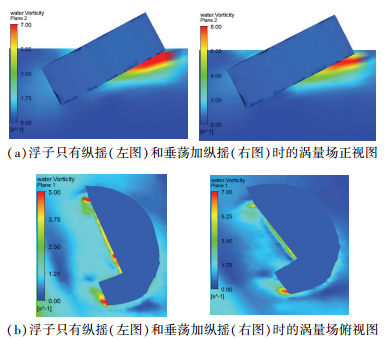
|
图 10 浮子纵摇单自由度和垂荡纵摇双自由度时涡量场对比 |
图 9为浮子在垂荡共振周期1.4 s时的涡量分布云图,将浮子做垂荡单自由度运动和垂荡加纵摇双自由度运动时的流场对比,从图 9(a)可以看出,浮子仅有垂荡时(左图)的涡量分布在浮子下方和迎浪面上,浮子双自由度运动(右图)的涡量分布在浮子下方浸深较小处.从图 9(b)可以看出,两种情况下,涡量区分布几乎相同,平均分布在浮子远离拐角的直边上,在交界线处,涡量区和涡量强度较大.通过将图(b)中左右两图对比可知,浮子在做垂荡运动时,其周围涡量在0~8 s-1,在交界线处约为8 s-1;浮子在做垂荡加纵摇运动时,其涡量在0~4 s-1,涡量最大处在浮子背浪面的交界线处,这说明浮子在做双自由度运动时,其周围流体涡量较小,使其自身能量耗散较小,能够更加充分地吸收外界能量.
图 10为浮子在纵摇周期为1.2 s时的涡量分布云图,从图 10(a)可以看出,两种情况下浮子周围流场的涡量分布几乎相同,都是位于浮子下方靠近波面处.从图 10(b)可以看出,涡量最大处位于交界线附近,浮子仅有纵摇时涡量分布区域要比两自由度时大.浮子仅有纵摇运动时浸深变化较大,而浮子有垂荡和纵摇双自由度时,其自身位置和角度能更好地适应波面高度和角度的变化,其周围流体的涡量分布和强度要小,自身能量较大,说明其在波浪中获能较多.
5 结论1) 对于单自由度垂荡运动的浮子,其垂荡速度随着垂荡PTO阻尼的增加而减小,其俘获宽度比随着垂荡PTO阻尼系数的增加先增加后减少,垂荡时俘获宽度比存在最佳垂荡PTO阻尼系数.
2) 对于单自由度纵摇运动的浮子,不同惯量的浮子其纵摇固有周期不同,惯量越大,固有周期越大;纵摇时俘获宽度比存在最佳纵摇PTO阻尼系数.
3) 对于双自由度运动的浮子,其总俘获宽度比要比单自由度运动时高,且两个自由度在浮子的能量吸收上可以相互影响.双自由度运动的浮子在流场上与单自由度运动时不同,从涡量分布和涡量强度对比上可以看出,具有垂荡和纵摇运动的浮子对周围流体的影响较小,自身能量耗散较小.
| [1] |
GORDON R. Forecasting ocean wave energy:Tests of time-series models[J]. Ocean Engineering, 2009, 36(5): 348-356. DOI:10.1016/j.oceaneng.2009.01.003 |
| [2] |
BYUNG H C, DONG S Y, SHIN Y P, et al. Modeling and control of a 75 kW class variable liquid-column oscillator for highly efficient wave energy converter[J]. Ocean Engineering, 2011, 38(2): 436-443. |
| [3] |
GORDON R. Integrating wave energy into the power grid:Simulation and forecasting[J]. Ocean Engineering, 2013, 73(15): 168-178. |
| [4] |
MANABU T, TOSHIAKI S, YOICHI K, et al. Wells turbine with end plates for wave energy conversion[J]. Ocean Engineering, 2007, 34(11): 1791-1795. |
| [5] |
訚耀保. 海洋波浪能量综合利用[M]. 上海: 上海科学技术出版社, 2011.
|
| [6] |
张登霞. 双浮子海浪发电装置参数分析以及结构优化设计[D]. 河北: 燕山大学, 2001.
|
| [7] |
刘臻. 岸式振荡水柱波能发电装置的试验及数值模拟研究[D]. 山东: 中国海洋大学, 2008.
|
| [8] |
苏永玲, 谢晶, 葛茂泉. 振荡浮子式波浪能转换装置研究[J]. 上海水产大学学报, 2003, 12(4): 338-342. |
| [9] |
HEE C L. Optimum design of a sloping-wall-type wave absorber placed in a sinusoidal propagating wave[J]. Ocean Engineering, 2014, 88(15): 588-597. |
| [10] |
ADRIANA M F, NUNO F. Finite depth effects on the wave energy resource and the energy captured by a point absorber[J]. Ocean Engineering, 2013, 67(15): 13-26. |
| [11] |
CASKA A J, FINNIGAN T D. Hydrodynamic characteristics of a cylindrical bottom-pivoted wave energy absorber[J]. Ocean Engineering, 2008, 35(1): 6-16. DOI:10.1016/j.oceaneng.2007.06.006 |
| [12] |
任建莉, 钟英杰, 张雪梅, 等. 海洋波能发电的现状与前景[J]. 浙江工业大学学报, 2006, 34(1): 69-73. DOI:10.3969/j.issn.1006-4303.2006.01.018 |
| [13] |
郑雄波, 张亮, 马勇. 双浮体波浪能装置的水动力计算与能量转换特性分析[J]. 科技导报, 2014, 32(19): 26-30. DOI:10.3981/j.issn.1000-7857.2014.19.003 |
| [14] |
王晓明, 尚建忠, 张志雄. 吃水深度对双浮体波浪能转换装置影响分析[J]. 太阳能学报, 2013, 34(7): 1264-1270. DOI:10.3969/j.issn.0254-0096.2013.07.025 |
| [15] |
王晓明, 尚建忠, 张志雄. 双浮体波浪能转换装置中重心布置对波浪能吸收影响分析[J]. 国防科技大学学报, 2013, 35(4): 56-61. DOI:10.3969/j.issn.1001-2486.2013.04.011 |
| [16] |
COCHET C, YEUNG R W. Dynamic analysis and configuration design of a two-component wave-energy absorber[C]//Proceedings of 31st International Conference on Ocean, Offshore and Arctic Engineering. New York: American Society of Mechanical Engineers, 2012: 631-640.
|
| [17] |
史宏达, 李海锋, 刘臻. 基于VOF模型的OWC气室波浪场数值分析[J]. 中国海洋大学学报, 2009, 39(3): 526-530. |
| [18] |
YI H Y, YE L. Reynolds-averaged navier-stokes simulation of the heave performance of a two-body floating-point absorber wave energy system[J]. Computers & Fluids, 2013, 73: 104-114. |
| [19] |
国威, 张亮, 郑雄波, 等. 基于CFD的波浪能转换装置水动力性能分析[J]. 华中科技大学学报, 2014, 42(7): 22-26. |
 2016, Vol. 48
2016, Vol. 48