近几年,国内外对微动磨损的分析和预测研究得比较多[1-2], 对微动疲劳的研究也越来越多[3-6]. Houghton等[7]针对航空花键副提出了一种综合磨损实验法, 并对其在循环交变载荷下的微动疲劳寿命进行了预估. Ratsimba等[8]对花键副的微动磨损提出了一种预测方法, 并进行了验证, 认为少量润滑油情况下的磨损情况要比不加润滑的好, 最后利用Archard模型计算了磨损深度.Leen等[9]对航空花键副在过载扭矩下的微动疲劳寿命进行了预估. Limmer等[10]则提出了一种实验和数值相互综合的方法预测花键副疲劳行为.国内有学者对构件的微动疲劳行为进行了预测[11-14], 但针对具体花键副的比较少, 且无论国内还是国外,目前基本都是单独对微动磨损和微动疲劳进行研究, 关于二者在微动作用中的界限和关系还比较模糊, 微动疲劳预估寿命方法也不够完善.
本文在假设微动过程中微动磨损与微动疲劳共同作用的情况下, 针对某型机主减速器花键副的微动损伤机理进行了研究.对国内外现有的微动疲劳预测方法进行了分析, 在传统SWT法预估疲劳寿命的基础上, 忽略疲劳发生的位置和方向,提出了新的损伤累积计算方法.以某航空花键副为研究对象,在给定工况下预估了其微动磨损疲劳寿命, 对如何预防花键副微动疲劳进行了讨论分析, 为维修和设计花键副提供更准确的数值基础.
1 花键副微动损伤机理航空花键副有浮动式和定心式两种.本文主要针对定心式花键副进行分析.定心式航空花键副由于变形引起的微小振动, 使得其在交变循环载荷下主要的磨损方式为微动磨损.微动初期, 内、外花键副参与接触的接触副表面局部地区发生擦伤和塑性变形, 接触表面观测不到萌生的裂纹.随后, 内、外花键副两接触面直接接触, 加上温度变化, 发生黏着效应, 使得该运动副局部接触区域表面和次表面产生黏着磨损.由黏着磨损产生磨损碎片及落入联接件中的外来磨料(灰尘、润滑油中夹杂的杂质颗粒等), 同时, 塑性变形导致接触表面的局部位置产生强冷硬化, 材料变脆, 导致大颗粒材料剥离或者撕裂, 并堆积形成磨粒磨损.随着花键副工作载荷循环次数增加, 在伴有轻微表面磨损行为的情况下, 擦伤的划痕逐渐连接成片, 在与该接触表面夹角<30°的边缘处萌生微裂纹, 并且裂纹随着微动作用生长.在花键副工作早期不会产生扩展性的裂纹, 微裂纹的相对位置逐渐靠向接触表面中心.同时, 新氧化膜的形成产生氧化磨损.随着微动过程的进行, 接触的键齿上磨蚀坑的尺寸也在增大, 逐渐发生大的应力集中, 导致微动磨损形成的大凹坑底部产生了扩展性裂纹.随着载荷循环次数继续增加, 在微动和外载荷共同作用下, 位移幅值增大, 已萌生的裂纹沿着与花键齿接触面成一定角度的方向进行扩展, 当以这个角度扩展到一定深度后突然改变方向, 沿着垂直于接触表面的方向进行扩展, 直至花键副键齿断裂失效, 花键副寿命终止.整个过程是一个复杂且发展的过程, 因此, 以此机理为基础对花键副寿命进行预测, 得到的花键副寿命也能从时间上一定程度地说明花键副的损伤机理过程.
2 花键副微动磨损疲劳预测模型 2.1 微动疲劳预测方法有学者认为微动疲劳是一种表面损伤现象, 另有学者认为微动疲劳是一种复合疲劳现象; 部分学者认为降低滑移幅值可以提高微动疲劳强度, 另一部分却认为滑移幅值的增加使得表面磨损将欲产生裂纹位置的材料磨损, 在一定程度上可以抑制裂纹产生, 反而提高了微动疲劳寿命.学者们观点不统一, 导致目前还没有非常成熟通用的微动疲劳预测方法.
Nowell等[15]在Ruiz临界值的基础上提出了著名的表面损伤参数, 即Ruiz损伤参数:
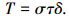
|
式中:T为Ruiz损伤参数, σ为平行于接触表面的最大拉应力, τ为界面上的剪切应力, δ为两接触面间的相对滑移幅值.Nowell认为, 当该损伤参数达到一个临界值时, 此处即产生裂纹.但这种方法只能对裂纹位置进行大概预估, 且临界值的选取是凭经验, 因此Vidner等[16]提出了修正的Ruiz微动疲劳损伤参数:
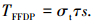
|
式中: TFFDP为修正的Ruiz微动疲劳损伤参数, σt为切向正应力, τ为界面上的剪切应力, s为两接触面间的相对滑移幅值.Vidner认为, 微动表面损伤产生的裂纹的扩展是由切向正应力决定的, 该方法虽然能有效地预测微动疲劳裂纹的位置, 但他们认为的拉伸裂纹为微动损伤裂纹主导模式的思想不被有些学者所认同, 因此, 在疲劳寿命预估方面还是具有局限性.
潘容等[17]对Jin等[18]提出的MSSR参数法进行了介绍和分析计算, 并对MSSR参数法进行了修正, 提出了NMSSR法:

|
式中:nMSSR为修正的MSSR参数, Δτmax为最大剪切应力, m为材料参数, RT为最大剪切应力和平均剪切应力的比, Δσn, mavD为正应力的幅值, A、B、C、D为常数, 其具体值见参考文献[17].用修正后的MSSR法所预测的微动疲劳寿命集中在2倍误差带以内, 结果优于修正前的MSSR法.但该方法不能体现出零件的材料特性, 不具有通用性, 而且仅仅得到与疲劳寿命之间的模糊定性.
Fatemi等[19]提出了最大剪切应变幅值和最大正应力都作用在最大剪切应变平面上的FS参数法:
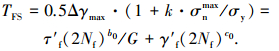
|
式中: TFS为FS损伤参数, k为趋于1的材料常数, σy为材料屈服强度, τ′f为剪切疲劳强度系数, G为剪切模量, b0为剪切疲劳强度指数, γ′f为剪切疲劳延性系数, c0为剪切疲劳延性指数, Nf为产生裂纹时的循环次数.该方法虽然考虑了零件的材料特性, 但是对裂纹形式的定义不全面, 与实际情况误差较大, 因此, 综合FD参数法及FS参数法, Shen等[20]提出了以下方法:
拉伸型裂纹占主导的微动疲劳预测参数为
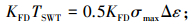
|
剪切型裂纹占主导的微动疲劳预测参数为

|
式中:Δε为一个周期内同一平面的最大正应变和最小正应变的差, σmax为该平面上的最大正应力, KFD为微动磨损作用系数, Δγmax为最大剪切应变幅值, σnmax为作用在最大剪切应变平面上的最大正应力, σy为材料的屈服强度, k为常数, 其具体值参考文献[21].该方法对拉伸型裂纹占主导的微动疲劳预测及剪切型裂纹占主导的微动疲劳预测均给出了准确的评估参数, 能更有针对性地对不同裂纹形式的疲劳进行预测.
2.2 微动磨损疲劳预测方法在微动疲劳预测方面, 目前用的较多的还是由Smith等[21]提出的临界平面参数法(SWT):

|
(1) |
式中:TSWT为临界平面损伤参数, Δε为一个周期内同一平面的最大正应变和最小正应变的差, σmax为该平面上的最大正应力, σ′f为疲劳强度系数, b为疲劳强度指数, ε′f为疲劳延性系数, c为疲劳延性指数, Nf为产生一定裂纹时的循环次数.SWT法与其他方法相比, 能更好地预测微动疲劳行为.
只考虑微动磨损作用预测微动疲劳寿命时, 采用的损伤累积模型为[22]:
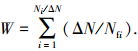
|
式中:W为累积损伤, Nfi为第i个磨损增量ΔN下产生裂纹时的循环次数.该模型只是进行简单的叠加, 认为每一个磨损循环下对应的疲劳寿命均相等, 不符合实际情况, 也不能准确地反映微动磨损作用对微动疲劳寿命的影响.
本文以Achard模型[23]计算磨损量的思路为基础, 在ANSYS中计算出第i个磨损增量ΔN时对应的最大正应力σmaxi和应变范围值Δεi, 利用式(1)计算对应失效循环次数Nfi.
其Achard模型方程为
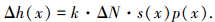
|
式中: Δh(x)为x点的磨损量增量; k为材料磨损系数, 一般由磨损实验测得; s(x)为x点的相对滑移距离; p(x)为x点的接触应力.
计算该应力和应变时对应的失效循环次数Nfi, 若ΔN < Nfi, 则未发生失效, 继续下一个磨损循环增量下对应的最大应力和应变范围值, 并重复上述Nfi的计算过程, 再次比较磨损循环增量与失效循环次数的大小, 直到当第n个磨损循环增量时ΔN>Nfn, 认为产生裂纹, 机构失效.由于考虑到微动磨损作用, 当计算每一次磨损循环增量时, 节点位置和模型都要进行更新, 应力应变也都发生变化, 产生的磨损将欲产生裂纹位置的材料磨损, 抑制了裂纹的产生; 因此, 当进入下一个磨损循环增量时, 对于计算疲劳寿命, 只对上一次的磨损循环增量进行累积, 而不对上一个磨损循环增量下应力和应变范围对应的失效循环次数Nfi进行累积.最终得考虑微动磨损作用下的微动疲劳寿命为
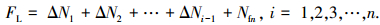
|
其中,

|
计算流程如图 1所示.
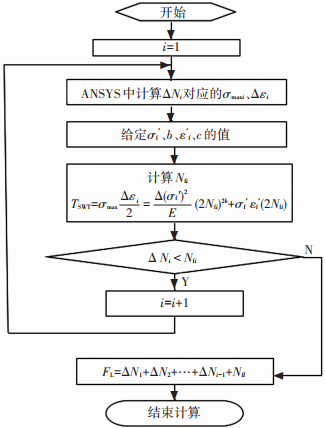
|
图 1 花键副微动疲劳寿命计算流程 |
鉴于本文采用临界平面的方法计算疲劳损伤, 需要对循环周期下给定的一个平面和另一个平面之间是如何相互作用产生损伤做出假设.其中一种方法是针对每个磨损循环增量都计算临界平面SWT值, 并对这种计算结果进行累积, 忽略该临界平面随着磨损作用的方向改变; 另一种方法是针对每个磨损循环增量计算每个平面方向上的SWT值, 将每个平面上的损伤增量进行累积.后一种方法虽然计算结果准确、精密, 但是计算量大, 需要存储每个磨损增量下每个单元重心36个平面上的损伤[23].因此, 本文计算疲劳寿命时, 假设该临界平面的方向在磨损作用下不发生任何变化.
3 花键副微动磨损疲劳预测 3.1 花键副应力及应变计算航空花键副承载形式比较复杂, 其所受扭矩一个主循环伴随多个次循环, 在利用有限元仿真计算正应力及应变时, 需要将一个次循环周期内的扭矩值离散为q个载荷步Tj(j=1, 2, …, q), 然后进行瞬态动力学分析.所受力矩为
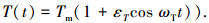
|
式中:Tm为外激励扭矩均值; εT为外激励扭矩的幅值波动系数, 取0.1;ωT为系统角速度; n为系统转速; ωT=2πn/60, 则一个次循环周期为τ=60/n.
对模型施加完约束后进行加载.选择外花键内圆柱面上的所有节点并施加Y方向的力Fj:
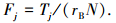
|
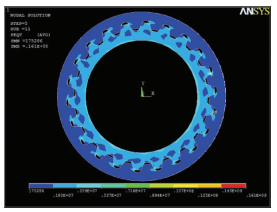
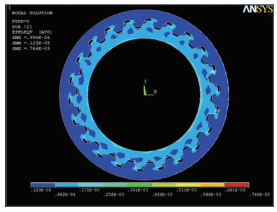
式中:rB为外花键内孔半径, rB=0.8d/2;d为外花键分度圆直径; N为外花键内孔圆柱面上所有节点数; 系统输入功率P=1 015 kW, 转速n=5 915 r/min, 齿数z=22, m=2.5 mm, 压力角为20°, q=5.求解得到的应力应变如图 2~3所示.(篇幅所限只给出第5载荷步的结果)
|
图 2 花键副正应力云图 |
|
图 3 花键副应变云图 |
从图 2、3中可以看出, 花键副22对齿均匀承载, 第5个载荷步时最大正应力为16.1 MPa, 最大应变为0.766×10-3, 最小应变为0.123×10-5.
3.2 花键副微动磨损疲劳寿命预测取ΔN=1×106, 根据2.2节建立的微动磨损疲劳寿命预测方法及3.1节中ANSYS计算出的每个载荷步在第i个磨损循环增量ΔN时对应的最大正应力σmaxij和应变范围值Δεij, 将每个载荷步的最大正应力σmaxij进行叠加, 得到花键副在第i个磨损循环增量ΔN时对应的最大正应力:
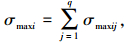
|
同时, 得出每个载荷步在第i个增量ΔN时对应的应变范围值为
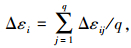
|
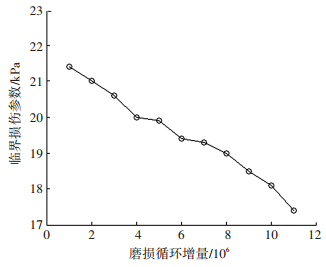
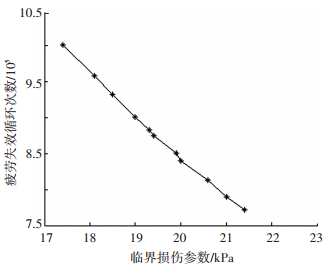
则得到花键副在每个磨损循环增量ΔN时对应的最大正应力和应变幅值, 即得到对应的SWT值, 如图 4所示.再根据SWT参数法计算出每个磨损循环增量下的疲劳裂纹产生时的循环次数, 如图 5所示.其中的各种材料常数见文献[24].
|
图 4 每个磨损循环增量对应的SWT值 |
|
图 5 临界损伤参数与微动磨损疲劳失效循环次数的关系 |
从图 4、5中可看出, 当第11个磨损循环增量时, 花键副发生疲劳失效, 失效时该磨损循环增量下对应的疲劳失效次数为1 000 589.随着工作循环次数的增加, 花键副SWT值减小; 疲劳失效循环次数随着应力应变的增大即SWT值的增大而减小.该花键副疲劳寿命为
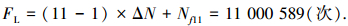
|
1) SWT法在计算花键副疲劳寿命时更具有通用性和普遍性.在第11个磨损循环增量时花键副发生疲劳失效, 失效时该磨损循环增量下对应的疲劳失效次数为1 000 589次.随着工作循环次数的增加花键副SWT值减小, 疲劳失效循环次数随着应力应变的增大即SWT值的增大而减小.
2) 提出的损伤累积模型能较准确地反映微动磨损对微动疲劳的作用, 为花键副的设计和维修提供了准确的数值基础.
3) 以上研究未考虑键齿之间的齿侧间隙.实际花键齿间是存在齿侧间隙的,一个键齿失效会引起实际啮合齿对数发生变化,且并非一个键齿失效就会导致各个花键副疲劳失效;因此, 为了得到更为精确的花键副微动磨损疲劳失效寿命, 后续会对这一问题进一步进行分析研究.
| [1] |
MCCOLL I R, DING J, LEEN S B. Finite element simulation and experimental validation of fretting wear[J]. Wear, 2004, 256(24): 1114-1127. |
| [2] |
DING J, LEEN S B, MCCOLL I R. The effect of slip regime on fretting wear-induced stress evolution[J]. International Journal of Fatigue, 2004, 26(12): 521-531. |
| [3] |
HILLS D A, MUGADU A. An overview of progress in the study of fretting fatigue[J]. The Journal of Strain Analysis for Engineering Design, 2002, 37(9): 591-601. |
| [4] |
BANERJEE N, HILLS D A. Analysis of stick-slip and contact-edge behaviour in a simplified fretting fatigue test[J]. The Journal of Strain Analysis for Engineering Design, 2006, 41(10): 183-192. |
| [5] |
NAKAZAWA K, MARUYAMA N, HANAWA T. Effect of contact pressure on fretting fatigue of austenitic stainless steel[J]. Tribology International, 2003, 36(3): 79-85. |
| [6] |
SUM W S, WILLIAMS E J, LEEN S B. Finite element, critical-plane, fatigue life prediction of simple and complex contact configurations[J]. International Journal of Fatigue, 2005, 27(20): 403-416. |
| [7] |
HOUGHTON D, WAVISH P M, WILLIAMS E J, et al. Multiaxial fretting fatigue testing and prediction for splined couplings[J]. International Journal of Fatigue, 2009, 31(9): 1805-1815. |
| [8] |
RATSIMBA C H H, MCCOLL I R, WILLIAMS E J, et al. Measurement, analysis and prediction of fretting wear damage in a representative aeroengine spline coupling[J]. Wear, 2004, 257(32): 1193-1206. |
| [9] |
LEEN S B, MCCOLL I R, RATSIMBA C H H, et al. Fatigue life prediction for a barrelled spline coupling under torque overload[J]. Journal of Aerospace Engineering, 2003, 217(8): 123-141. |
| [10] |
LIMMER L, NOWELL D, HILLS D A. A combined testing and modelling approach to the prediction of the fretting fatigue performance of splined shafts[J]. Journal of Aerospace Engineering, 2001, 215(13): 105-112. |
| [11] |
陶峰, 欧阳祖行, 刘正埙. 微动疲劳寿命的估算方法研究[J]. 机械设计与制造工程, 2011, 30(6): 5-7. |
| [12] |
沈明学, 彭金方, 郑健峰, 等. 微动疲劳研究进展[J]. 材料工程, 2010, 12(10): 86-91. |
| [13] |
何明鉴. 微动磨损疲劳——燕尾联结应力分布及裂纹位置预测[J]. 航空动力学报, 1989, 4(3): 205-208. |
| [14] |
赵家绪, 于洋, 赖祖涵. 高频微动磨损疲劳试验的设计与实践[J]. 物理测试, 1991, 5(2): 1-5. |
| [15] |
NOWELL D, HILLS D A. Crack initiation criteria in fretting fatigue[J]. Wear, 1990, 136(35): 329-343. |
| [16] |
VIDNER J, LEIDICH E. Enhanced Ruiz criterion for the evaluation of crack initiation in contact subjected to fretting fatigue[J]. Int J Fatigue, 2007, 29(12): 2040-2049. |
| [17] |
潘容, 古远兴. 微动疲劳寿命预测方法研究[J]. 燃气涡轮试验与研究, 2009, 22(2): 13-17. DOI:10.3969/j.issn.1672-2620.2009.02.003 |
| [18] |
JIN O, MALL S. Effects of slip on fretting behavior:experiments and analyses[J]. Wear, 2004, 256(21): 671-684. |
| [19] |
FATEMI A, KURATH P. Multiaxial fatigue life predictions under the influence of mean-stresses[J]. J Eng Mater Technol, 1988, 110(4): 380-388. DOI:10.1115/1.3226066 |
| [20] |
SHEN L J, LOHRENGEL A, SCHÄFER G. Plain-fretting fatigue competition and prediction in spline shaft-hub connection[J]. International Journal of Fatigue, 2013, 52(38): 68-81. |
| [21] |
SMITH K N, WATSON P, TOPPER T H. A stress-strain function for the fatigue of metals[J]. J Mater JMLSA, 1970, 5(1): 767-778. |
| [22] |
SOCIE D. Multiaxial fatigue damage models[J]. J Eng Mater Technol, 1987, 109(4): 293-299. DOI:10.1115/1.3225980 |
| [23] |
MADGE J J, LEEN S B, SHIPWAY P H. The critical role of fretting wear in the analysis of fretting fatigue[J]. Wear, 2007, 263(50): 542-551. |
| [24] |
MADGE J J, LEEN S B, MCCOLL I R, et al. Contact-evolution based prediction of fretting fatigue life:Effect of slip amplitude[J]. Wear, 2007, 262(7): 1159-1170. |
 2016, Vol. 48
2016, Vol. 48


