2. 先进制造国家重点实验室(西安交通大学), 710049 西安;
3. 中石油长庆油田公司油气工艺研究院, 710018 西安
2. State Key Laboratory for Manufacturing System(Xi'an Jiaotong University), 710049 Xi'an, China;
3. Oil & Gas Technology Institute, Changqing Oil Field Company, 710018 Xi'an, China
端面齿联轴器作为重型燃气轮机、航空涡轮发动机等高参数转子系统(高能量、高速度、高稳定性)[1]的连接与传扭重要部件[2],对转子系统高能量、大扭矩传递过程和复杂工况下的稳定运行起关键性作用.由于自身结构的复杂性和工况条件限制,国内外只有少数学者对端面齿联轴器的刚度特性进行了研究,较深入的研究主要采用接触力学理论、磨损理论并考虑棘轮效应等作为理论基础,辅以有限元分析获得定性定量结论加以验证[2-6],但研究工作并不完备.目前的研究主要考虑外部载荷(轴向或剪切方向)、预紧力状态、结构变形、楔形接触面的滑移、磨损等多个因素(物理量)的影响.这些因素与端面齿的刚度特性密切相关,许多重要参数的物理特征受刚度特性影响、支配甚至存在相互映射和数学解析关系,而目前针对端面齿刚度特性的直接研究较少,所以理论研究工作需要进一步完善与发展.由于重型燃机服役条件极其恶劣并受端面齿结构制约,直接进行端面齿各项性能测试非常困难,导致理论研究缺少有效的试验数据支撑,这是导致研究工作不完备的客观条件.
端面齿联轴器的重要特征是通过周向或中心拉杆螺栓对轮盘进行紧固连接,多个螺栓的预紧状态对结构部件刚度的影响非常大.早期的螺栓连接刚度分析以预紧条件下平行弹簧模型为基础[7],但对端面齿联轴器而言该模型过于简单.当外部负载引起构件额外变形时,文献[8]提出一种新的解析模型来补偿传统模型的不足,文献[9-10]进一步发展了该新模型,但当构件外形变化或受到不对称外载荷时,该模型并不适用[11-13].大量研究表明外部荷载对联轴器的连接刚度[14-17]存在影响.普通联轴器只受螺栓预紧力的作用,可不考虑外载荷的影响.但端面齿联轴器由于其结构特殊性,当螺栓预紧之后,会导致被夹紧轮盘承受一个额外载荷,从而发生不同于普通联轴器变形的额外变形,进而引起连接刚度发生非线性变化.
本文对重型燃机所采用端面齿联轴器的结构变形与刚度特性进行了系统分析和参数化建模,端面齿的接触应力、扭转刚度、压缩刚度等重要参数可通过刚度分析模型求解得到,有效支持端面齿联轴器的行为状态分析.基于测试手段进行结构刚度分析是端面齿联轴器结构完整性研究的重要内容,由于直接进行端面齿各项性能测试非常困难,考虑到拉杆螺栓体积较大,从测试的“结构适应性”而言,其性能参数如螺栓预紧力和螺栓刚度可直接测试获取,本文构建的刚度分析模型建立了螺栓与端面齿在工作环境下存在的潜在联系,为端面齿联轴器测试研究提供了有效的方法.基于所建立的刚度分析模型, 对端面齿联轴器的螺栓预紧过程中各个结构部件的变形和刚度变化规律进行了研究.
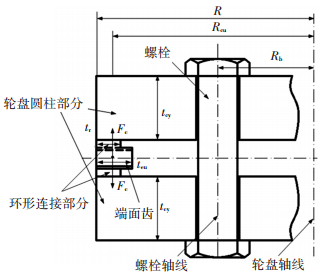
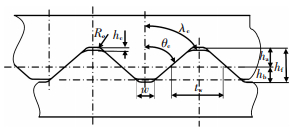
1 端面齿联轴器刚度特性分析与参数化建模本文选择重型燃机所采用双轮盘端面齿联轴器结构进行刚度特性分析和参数化建模.该结构联轴器主要由3部分组成:24个端面齿、圆柱体以及中间环形连接部分(如图 1).由于连接结构共有24个端面齿和6根螺栓,因此单根螺栓承受预紧力是单个端面齿所承受载荷的4倍.端面齿的几何外形如图 2所示.
|
图 1 端面齿联轴器的半截面 |
|
图 2 端面齿截面 |
分析图 1联轴器结构的刚度特性,需对整体结构各构件的变形(压缩、扭转)进行分析,围绕模型表征参数化和模型参数可识别的研究出发点,本文在受力分析的基础上, 根据经验公式对联轴器各构件的变形情况进行了系统分析和参数化建模;因为所建立分析模型的表达式力学关系和物理意义明确,所以便于测试研究.
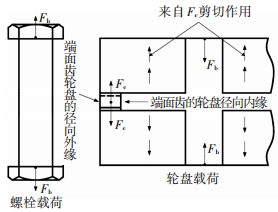
根据图 3,端面齿所受载荷对轮盘圆柱部分的作用可作为外载进行处理,由于端面齿载荷中心点与螺栓的预紧载荷中心不在同一直线,导致整个结构存在附加弯矩,该弯矩使得轮盘圆柱和端面齿均产生扭转变形,进而对连接结构的刚度产生影响.同时必须注意到,端面齿所受载荷并不是等效传递给轮盘圆柱,而是以剪切作用方式进行传递.如图 4,该载荷导致轮盘圆柱部分的压缩变形可表述为
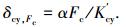
|
(1) |

|
图 3 端面齿联轴器结构变形 |
|
图 4 由端面齿接触载荷转化的剪切载荷示意图 |
式中:α表示比例因子,体现了端面齿载荷对连接结构产生压缩变形的效率;Kcy′为轮盘圆柱的等效刚度,由经验公式可表述为:Kcy′=πE(ds2-dw2)/(8tcy).
轮盘圆柱和端面齿在承载方向的扭转变形使得圆柱部分和端面齿的原有结构刚度发生了变化,并且呈现出非线性的特征,圆柱部分的扭转变形可表述为
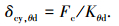
|
(2) |
式中: Kθd为圆柱部分的等效扭转刚度,可看出随Kθd增加将导致轮盘圆柱整体变形变小.
端面齿环形部分对连接结构的整体变形有影响,根据文献[8],环形连接部分在燃机实际工作时能起到缓解冲击振动的作用,其压缩变形为
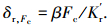
|
式中:β为比例因子;Kr′为环形部分的等效刚度,且Kr′=ArE/tr,Ar为环形部分径向横截面积.
进一步分析端面齿自身变形对联轴器刚度的影响.端面齿自身变形同时受齿面接触压力和端面齿自身扭转的影响,而端面齿自身扭转与螺栓夹紧载荷存在联系,端面齿扭转角度随螺栓夹紧载荷的增加而增加,求解端面齿联轴器的等效刚度必须和螺栓的夹紧载荷相联系.由有限元分析可知,在螺栓加载初期,端面齿的接触压力逐渐增加,端面齿接触面为滑移或近接触状态.与此同时,端面齿开始发生扭转变形,使得端面齿接触面积减小,再加上端面齿的扭转,使得端面齿的等效压缩刚度发生了变化.随着螺栓载荷进一步增加,端面齿部分接触面的接触状态变成了粘连,而近接触部分也逐渐消失.因此,将端面齿压缩变形δcu, Fpc与端面齿接触状态及接触压力建立如下联系:

|
(3) |
式中:Fpc表示端面齿的总体接触力;Kcu表示端面齿的刚度,可表述为
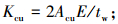
|
(4) |
Acu为端面齿接触面有效面积,可表征为Fb或端面齿接触压力的函数,即
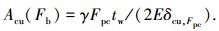
|
(5) |
根据图 3,δ′cu, Fpc通过有限元分析可直接获得,则δcu, Fpc可表述为

|
(6) |
式中θcu为螺栓加载过程中端面齿的扭转角度.
由受力平衡关系可知:Kbδb=Kdδd,δd为轮盘整体的压缩变形量,可描述为
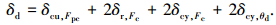
|
Kd表示轮盘的整体轴向等效刚度,可定义为
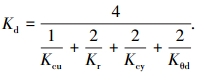
|
式中:Kr=βKr′,Kcy=αKcy′.求解方程(3)~(6),可得

|
(7) |
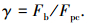
|
(8) |
当螺栓载荷或端面齿接触面摩擦系数足够大时,端面齿接触面会趋于整体粘连状态,此时端面齿接触面的等效接触面积将不会发生变化,当端面齿体积足够小以及齿数足够多时会发生这种情况[6].本文并不考虑这种情况,由于重型燃机端面齿体积相对较大,单个齿面所承受载荷相对更小,因此端面齿接触面之间始终保持着非整体粘连状态.
上述分析主要集中在结构变形上,而结构部件刚度及比例因子需要进一步推导.相关刚度和变形参数都可通过有限元或经验方法获得.根据式(1),比例因子α可通过有限元分析所获得的δcy, θd计算得到:

|
同样方法可用来得到比例因子β:
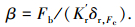
|
同样,根据有限元分析得到图 3中δcy, θd′和θcu后,Kθd可由式(2)和(6)得到,γ、Acu可由式(7)和(8)得到,而Kcu可由式(4)和(5)推导得到.
为增加分析模型的独立性及工程实用性,将模型中需通过有限元确定的系数,包括Kcu、Kr、Kθd、Kcy等进一步进行独立分析.将刚度系数与螺栓预紧力Fb和联轴器结构参数联系起来,构建多项式函数表达式,记为

|
式中:

|
Fbij表示第i个预紧力的j次方;Z是多项式系数矩阵,为联轴器结构参数(如端面齿结构或螺栓结构)所构成的多项式函数矩阵,表示为
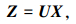
|

|
式中:xij为第i个元素的第j次方,表示联轴器特定结构下的尺寸;U为多项式系数矩阵,对其求解可得到不同尺寸、不同预紧力下联轴器各部件的刚度矩阵为
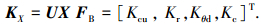
|
由此,联轴器整体轴向刚度KD可重新表达为
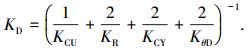
|
式中:KCU、KR、KθD、KCY分别表示经多项式拟合处理后Kcu、Kr、Kθd、Kcy的表达形式.求解KD可预测实际端面齿联轴器的力与变形的关系.
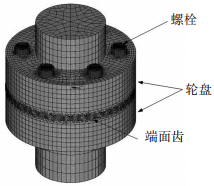
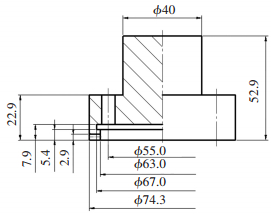
2 有限元建模对建立的刚度分析模型通过有限元方法和实验进行验证.有限元模型采用商用软件Ansys建立,如图 5.模型中螺栓头采用了简化模型,即不包含螺纹.单元类型采用8节点轴对称体单元185.设定建模材料为弹性且各向同性,杨氏模量为209 GPa.有限元模型中有6根螺栓,24个端面齿,几何尺寸见图 6.
|
图 5 端面齿联轴器有限元建模 |
|
图 6 模型几何尺寸(mm) |
由于环形连接部分相对于端面齿及圆柱部分属于薄壁结构件,该部分网格密度与质量对分析结果影响较大,因此对该部分网格进行了加密处理,并确保网格划分质量的合法性(单元节点不能是其它单元的内部节点)、相容性(单元须在区域内部,不可落入外部)、协调性(相邻单元的自由度相互匹配)、良好过渡性(单元之间过渡平稳)和网格划分一致性(单元节点只能与单元节点相连,不能与相邻单元中间节点相连,相邻单元公共边具有相同的节点数).经过上述处理所建立有限元模型总共有12 243个网格节点,15 955个八节点三维实体单元.
通过接触耦合对来模拟接触条件,分别是螺母和轮盘表面之间的接触、两个轮盘端面齿之间的接触和螺栓头和轮盘表面之间的接触,各接触面摩擦因数设为0.2,接触目标单元选用Targe170,接触单元选用Conta174,并考虑了接触对目标面和接触面对应节点的相互匹配.
模型边界条件的施加包括两个步骤:为保证模型不出现刚体位移,对一端进行全约束,另一端设置为自由端,如图 5; 施加螺栓预紧载荷,施加方法如图 7,通过试错法不断调整螺栓头与螺母之间的建模距离ΔlT来确定所需预紧载荷Fb大小.

|
图 7 螺栓预紧力的确定方法 |
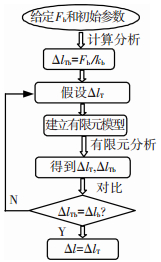
具体过程如图 8所示:1)给定预紧载荷Fb,以及螺栓弹性模型E、横截面积A和有效长度l等初始参数;2)计算螺栓拉伸刚度kb(kb= EA/L),确定给定Fb下的螺栓伸长量Δlb;3)假设一个ΔlT初值,通过有限元计算提取Fb以及螺栓伸长量ΔlTb;4)对比Δlb与ΔlTb,若不相等调整ΔlT大小,直到二者相等为止;5)当Δlb与ΔlTb相等时,预紧力设定值即为实际螺栓预紧力大小.
|
图 8 螺栓预紧力确定流程 |
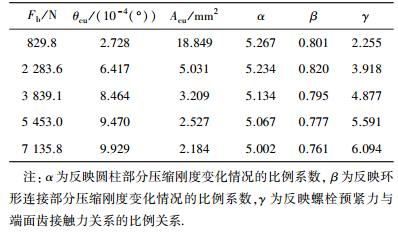
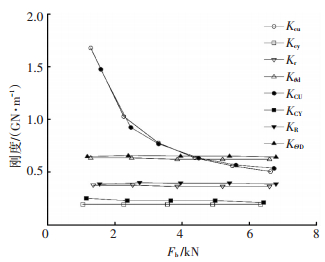
表 1计算结果表明,端面齿扭转角θcu随预紧载荷Fb的增加而增加,其他比例系数随Fb的增加而降低.由图 9可知,联轴器各部件刚度特性有所区别,端面齿压缩刚度Kcu随Fb的变化比较明显,而其它部件刚度随Fb的增大略微减小.由于轮盘圆柱部分扭转变形,使得端面齿在联轴器预紧后存在向轮盘径向外方向翻转的趋势,而端面齿与环形连接部分形成的凹陷使得端面齿产生向内方向的扭转.相对而言,端面齿向内方向扭转的可能性更大,因此θcu随Fb的增加而增加,Kcu随Fb的增加而降低.
| 表 1 分析模型计算结果 |
|
图 9 端面齿联轴器各部件刚度的变化 |
端面齿扭转使其有效接触面积Acu随预紧力Fb的增加而明显减小,因此端面齿的平均压缩量增加,在总接触力不变的情况下,Kcu随扭转角θcu的增加而降低.在螺栓预紧加载初期,由于端面齿顶端局部变形比较严重,导致整体压缩变形较大,而预紧加载后期,整个端面齿表现为平稳受载,压缩刚度也逐渐缓和.
比例系数α反映了圆柱部分压缩刚度Kcy的变化情况,可发现随着螺栓预紧力Fb的增加,比例系数α(表 1)及压缩刚度Kcy(图 9)呈现缓慢衰减状态,或者认为圆柱部分的压缩刚度逐渐减小.由前面的分析可知,圆柱部分的扭转变形在螺栓预紧过程中逐渐变化,该变形是导致Kcy减小的主要原因;或可认为当圆柱部分发生扭转变形时,同样的预紧力会在圆柱部分压缩方向产生更大的压缩变形,反映在刚度值求解结果上呈现减小趋势.
比例系数β反映了环形连接部分压缩刚度Kr的变化情况,可发现随着螺栓预紧力Fb的增加, 比例系数β及压缩刚度Kr呈现缓慢的衰减状态,可认为环形连接部分压缩变形有所增加.环形连接部分压缩变形量受端面齿和圆柱部分扭转变形的影响很大,当两者的扭转逐渐增加时,环形连接部分的局部压缩变形量明显增加,因此总体变形量也较其受到平稳压缩时变形量更大.
比例系数γ反映了螺栓预紧力与端面齿接触力的关系.由分析结果可知, 比例因子γ随着预紧力的增加而增加,或者也可认为端面齿的接触力随着预紧力的增加其增加的速率放缓.端面齿总的接触力是其接触应力的反映,根据有限元分析结果,端面齿总接触力很大程度上由端面齿顶端的局部接触应力所决定.在预紧加载的初始阶段,端面齿顶端的局部接触应力变化较大,而到加载后期(预紧力较大),其局部接触应力变化逐渐缓慢.
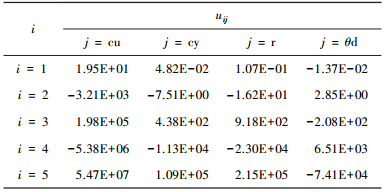
由图 9可知,经多项式拟合函数处理后的刚度值KCU、KR、KθD、KCY与Kcu、Kr、Kθd、Kcy非常接近,误差在5%以内.多项式系数矩阵U的元素值uij见表 2.
| 表 2 μij计算结果 |
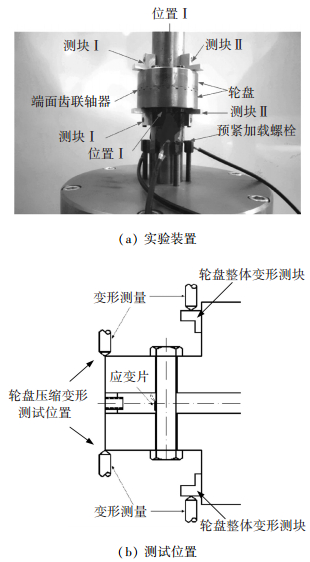
本文设计了一个多轴液压紧固系统, 对刚度分析模型进行有效性验证,如图 10(a)所示.该装置能保证六根螺栓同时预紧且各螺栓预紧载荷相互偏差在±2.5%以内.实验螺栓采用45#材料,螺栓总长51 mm,有效工作长度43 mm,螺纹部分长15 mm,螺栓头直径8.88 mm,螺栓杆直径5.78 mm.实验前各螺栓螺母经热循环炉加热至300 ℃后置于空气进行冷却,以消除残余应力,经超声振动仪去除表面磨屑,以保证螺纹表面光洁度.
|
图 10 实验测试装置 |
测试位置如图 10(b)所示.各实验螺栓贴有应变片,沿轴向方向,可测量螺栓受载之后的轴向应变,通过换算可获得各螺栓预紧力大小,对各预紧力取均值即可得到加载过程螺栓的预紧力大小.同时,在螺栓预紧后采用螺旋测微仪对整个轮盘的变形量δd以及δd′进行测量. δd′为除去轮盘圆柱扭转量后的整体变形量,表达式为

|
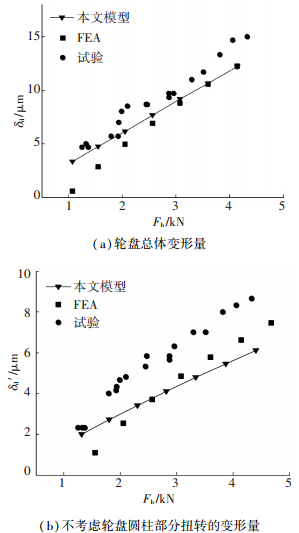
测试设备采用日本横河应变仪(型号MX100),应变仪输入端与应变片引线端相连并进行温度补偿.采样数据通过网络数据线与PC相连进行传输,采样频率1 Hz.实验过程中对六根螺栓的轴向应变进行同时采集(换算得到螺栓预紧力大小),同时对轮盘变形δd以及δd′进行测量,得到了多组端面齿联轴器螺栓预紧力与轮盘结构变形量的关系,如图 11所示.
|
图 11 试验及仿真结果对比 |
由图 11可知, 轮盘变形δd与δd′随螺栓预紧载荷Fb的增大而增加,二者变化规律相似,且与Fb呈线性关系.对比图 11 (a)和图 11 (b)可知,轮盘圆柱部分存在一个扭转变形,大小约为轮盘整体压缩变形量的一半.本文刚度分析模型计算结果与FEA结果和实验结果对比较为理想,特别是整体变形量δd.而造成δd′ 存在差异的原因主要在有限元模型的网格密度上,通过加密端面齿联轴器有限元建模网格,该问题可以得到改善.如前所述,环形连接部分由于其薄壁结构特征,有限元分析时对该部分网格不断进行加密处理,发现在保证网格质量的情况下逐渐加密网格使得端面齿及圆柱部分扭转变形量的预测值不断得到改善,从而逐渐改善了有限元模型的计算精度;同时发现当网格加密到一定程度后有限元分析结果变化不大,同时对计算机处理能力提出了要求,因此在保证计算精度的情况下对网格数量进行了控制.
5 结论1) 建立了一种端面齿联轴器刚度分析参数化模型,联轴器各部件的扭转角、压缩刚度、扭转刚度等重要参数可通过该模型求解得到,为端面齿联轴器行为分析提供了完备的刚度数据支持,弥补了传统研究的不足.
2) 解决了端面齿联轴器现有测试手段存在的结构受限难题:基于参数化模型构建测试方法,联轴器的结构变形和刚度数据可直接测试获得,使得复杂工况下端面齿联轴器的性能测试具有“结构适应性”.
3) 通过仿真分析和实验发现:螺栓预紧过程中端面齿及圆柱部分存在不同程度的扭转,导致联轴器各部件刚度特性各有区别; 端面齿压缩刚度随预紧力增大明显增大,其他部件刚度略微减小.由于该扭转的存在, 使得端面齿联轴器在结构变形、刚度变化规律、各接触面接触应力及接触状态等特征上不同于一般联轴器.
4) 本文刚度特性分析仅考虑了螺栓预紧载荷,对于其它形式载荷,如联轴器受到扭转及弯曲等载荷并没有进行分析,但该分析模型对其它形式载荷仍具有效性.
| [1] |
席文奎, 陈润霖, 张宏涛, 等. 高参数转子系统通流力的系统表征及协同设计研究[J]. 西安交通大学学报(自然科学版), 2013, 47(01): 52-56. |
| [2] |
JIANG X J, ZHANG Y Y, YUAN S X. Analysis of the contact stresses in curvic couplings of gas turbine in a blade-off event[J]. Strength Material, 2012, 44(5): 539-550. DOI:10.1007/s11223-012-9412-3 |
| [3] |
YUAN S X, ZHANG Y Y, ZHANG Y C, et al. Stress distribution and contact status analysis of a bolted rotor with curvic couplings[J]. Journal of Mechanical Engineering Science, 2010, 224(9): 1815-1829. DOI:10.1243/09544062JMES1853 |
| [4] |
PEDERSEN N L, PEDERSEN P. Stiffness analysis and improvement of bolt-plate contact assemblies[J]. Mechanics Based Design of Structures and Machines, 2008, 36(1): 47-66. DOI:10.1080/15397730701735749 |
| [5] |
RICHARDSON I J, HYDE T M, BECKER A A, et al. A three-dimensional finite element investigation of the bolt stresses in an aero-engine curvic coupling under a blade release condition[J]. Journal of Aerospace Engineering, 2000, 214(4): 231-245. |
| [6] |
RICHARDSON I J, HYDE T M, BECKER A A, et al. A validation of the three-dimensional finite element contact method for use with curvic couplings by comparing predictions with photoelastic test data[J]. Journal of Aerospace Engineering, 2002, 216(2): 63-75. |
| [7] |
MOTOSH N. Determination of joint stiffness in bolted connections[J]. Journal of Engineering for Industry, Transactions of the ASME, 1976, 98 Ser B(3): 858-861. |
| [8] |
ZHANG O. New analytical model of bolted joints[J]. Journal of Mechanical Design, Transactions of the ASME, 2004, 126(4): 721-728. DOI:10.1115/1.1760777 |
| [9] |
ZHANG O. Discussions on behavior of bolted joints in tension[J]. Journal of Mechanical Design, Transactions of the ASME, 2005, 127(3): 506-510. DOI:10.1115/1.1867513 |
| [10] |
LIU S G, MA Y H, ZHANG D Y, et al. Studies on dynamic characteristics of the joint in the aero-engine rotor system[J]. Mechanical Systems and Signal Processing, 2007, 29: 120-136. |
| [11] |
KIM J, YOON J C, KANG B S. Finite element analysis and modeling of structure with bolted joints[J]. Applied Mathematical Modelling, 2007, 31(5): 895-911. DOI:10.1016/j.apm.2006.03.020 |
| [12] |
BOUZID A H, NECHACHE A. The modelling of bolted flange joints used with disc springs and tube spacers to reduce relaxation[J]. International Journal of Pressure Vessels and Piping, 2010, 87(12): 730-736. DOI:10.1016/j.ijpvp.2010.09.001 |
| [13] |
BOUZID A H, HICHEM G. A new approach to model bolted flange joints with full face gaskets[J]. Journal of Pressure Vessel Technology, Transactions of the ASME, 2011, 133: 021203-021209. DOI:10.1115/1.4001920 |
| [14] |
KWIATHOWSKI J K, WINNICKI L A, KRZYSPIAK A. Stress analysis of bolted tensile end plate connections[J]. Rozprawy Inzynierskie, 1986, 34(1/2): 113-117. |
| [15] |
LEHNHOFF T F, KO K I, MCKAY M L. Member stiffness and contact pressure distribution of bolted joints[J]. Journal of Mechanical Design, Transactions of the ASME, 1994, 116(2): 550-557. DOI:10.1115/1.2919413 |
| [16] |
LEHNHOFF T F, BUNYARD B A. Effects of bolt threads on the stiffness of bolted joints[J]. Journal of Pressure Vessel Technology, Transactions of the ASME, 2001, 123(2): 161-165. DOI:10.1115/1.1319504 |
| [17] |
NASSAR S A, YANG X J, GANDHAM S V T, et al. Nonlinear deformation behavior of clamped bolted joints under a separating service load[J]. Journal of Pressure Vessel Technology, Transactions of the ASME, 2011, 133(2): 0210011-0210019. |
 2016, Vol. 48
2016, Vol. 48