2. 武汉理工大学 理学院, 430070 武汉
2. School of Science, Wuhan University of Technology, 430070 Wuhan, China
复合材料的广泛应用,在很大程度上取决于复合材料的成型制造技术.采用先进制造技术可以降低复合材料构件成本,保障产品质量,提高生产效率.自动铺丝技术是在20世纪70年代提出来的,旨在克服缠绕技术周期性、稳定性和非架空的特点给复杂构件的成型带来的不便及自动铺带必须沿自然路径进行铺放的限制.它综合了自动铺带技术和纤维缠绕技术的优点,将多股预浸丝束集成一条宽度可变的预浸带后自动按照一定线型铺到构件表面,可实现复杂、甚至带窗口构件的铺放生产,在大型、超大型复合结构部件的成型制造中具有极大的优越性[1-3].自动铺放线型规划过程是一个环节多、影响因素多、涉及面广的复杂过程.尤其是复杂构件曲面,需同时考虑构件曲面几何结构、原材料间和铺层力学性能的耦合关系.线型反映了丝束在构件曲面上的排布形式,决定了构件的复合材料结构和性能,也是铺丝运动规划、自动NC编程以及轨迹仿真模拟的重要依据.最近,Fayazbakhsh和Croft等[4-5]将自动铺放过程中出现的丝束离缝和重叠等缺陷分布作为变量,研究了其对制品力学性能的影响;Beakou等[6]研究了铺放过程中压紧力、预浸丝束黏性、铺放速度和丝束回弹等对丝束局部曲皱的影响,建立了曲面上丝束不屈皱的铺放路径的最小弯曲半径的数学模型;Gürdal等[7-11]提出了用变刚度方法进行复合材料层压结构铺层顺序的优化.这些研究工作为铺放线型规划提供了一定的理论依据.在铺放路径规划方面,Lewis等[12]首先提出了自然路径规划法来保证自动铺放过程中预浸带整体变形最小.此后,国内外学者基于此算法从精度和效率上进行了不断的改进.胡翠玲和罗海燕等[13-14]将复杂曲面三角网格化,采用测地线构造原理求解了该曲面上自然铺放路径.该方法计算简便,适用于较规则构件曲面. Shirinzadeh等[15-16]对复杂曲面上纤维铺放路径规划进行了研究,解决了纤维在多个方向上实现连续排布和转向排布的问题,并提出了能实现曲面上纤维均匀排布的铺放路径算法SCAR.韩振宇和邵忠喜等[17-18]为研究纤维铺放路径规划和优化算法,在分析与某一参考线成固定角度规划法和等距偏置法的基础上,提出了纤维带铺放丝束数量计算方法.该规划算法主要涉及到构件曲面特征和刚度要求,未考虑到沿规划路径进行铺放时预浸料可能产生的变形对构件结构强度的影响.李俊斐等[19]及熊文磊等[20]分析了铺放过程中预浸料产生畸变的原因及影响路径可铺放性的因素,提出了使路径能够保证预浸料良好可铺放性的同时又满足构件的强度分布要求的自调节路径规划算法.文献[12-20]对铺放路径规划做了大量的工作,但在考虑影响规划过程的因素方面侧重点有所不同.
本文从构件曲面外形、丝束变形和铺层力学方向对铺放路径规划过程的影响入手,引入丝束最小弯曲半径、铺放方向容许偏角控制系数和最大重叠系数, 将铺放路径看作网格化曲面上的空间曲线,应用曲面微分几何和空间解析几何理论求解,提出一种复杂曲面工程实用的铺放线型规划方法.
1 铺放路径工艺性铺放路径是空间曲面上的曲线.如图 1,C为曲面S上过点P的一条曲线,kn、kg、n和τ分别为曲面上曲线在P点的法曲率、测地曲率、单位法曲率向量和单位测地曲率向量,t和k分别为曲线在P点单位切向量和主法向量,s为弧长参数.根据微分几何理论,曲面上曲线测地曲率和法曲率为
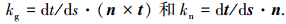
|
由于丝束带很薄(0.125~0.200 mm),kn不会对丝束的铺放工艺性产生影响,而kg的存在会使丝束在幅宽方向产生侧弯进而影响其可铺性.对于曲面上丝束的变形,熊文磊等[20]已作详细分析,并得到了曲面上宽度为w的丝束微元内侧纤维的压缩应变为ε=-2w/(2/kg+w).一定宽度丝束发生极限变形时,其变形程度可用最小侧弯半径ρmin来表示,即丝束铺放侧弯过程中,丝束中心的测地曲率半径ρg(ρg=1/kg)必须大于ρmin,否则丝束会产生局部屈皱,将大大影响固化构件的力学性能.丝束不产生曲皱的条件为压缩应变的绝对值|ε|≤|εmax|(εmax为铺放材料容许压缩应变),令ε=εmax,则单丝束最小相对侧弯半径:ρmin=-w(εmax-1+0.5).对于丝束数为n和宽度为n·w的丝束带,当其铺放路径的测地曲率不为零时,丝束带内侧的曲率最大,所以只要保证内侧丝束不产生屈皱就能使丝束具有良好的可铺放性.内侧丝束产生极限变形时,丝束带的最小侧弯半径为
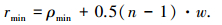
|

|
图 1 曲面上曲线的曲率 |
复合材料结构中预浸丝束是主要承载材料,有限宽丝束只有在不发生曲皱的情况下才能承受最大载荷.曲面上kg为0的曲线是测地线,沿测地线方向铺放时丝束不发生变形,所以测地线方向是丝束平整铺放的理想方向.在复杂轮廓构件的曲面上难以推导出铺放路径的精确数学模型,因此采用近似的方法将构件曲面离散为若干三角面片.丝束的平整铺放路径是由网格面上若干条测地线所构成.如图 2,一条测地线可表示为网格上点的序列P1、P2、…、PV、…(下标V表示铺放路径上离散点的序号),其中PV是网格的顶点或者是边上的一个点,但大多数情况是网格棱边上的点.在这里若不考虑点PV-1和PV是网格内点的情况,则可通过将网格棱边上点与网格顶点统一作为网格顶点来处理.具体的做法是将棱边上的点与此点相邻的网格顶点相连,这样铺放路径上的一系列的点都可看作为曲面网格顶点.

|
图 2 丝束当前路径点的法曲率 |
测地线的变化只能沿着曲面的法向方向,而不能在切平面上“左右”偏移.这样,在点PV的微邻域内,测地线是逼近曲面沿给定方向的法截线.因此点PV处的法向量nPV和两个切向量PV-1PV、PVPG是共面的,则有
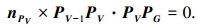
|
一般情况下,PV点处单位法向量nPV可用通过与此点相邻的三角面片的法向量做凸组合来近似替代.将交于该顶点的所有三角网格的法向量进行重心加权平均[21]:
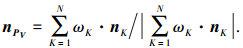
|
在这里重心权重
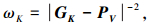
|
式中:重心GK=∑VJ∈fKVJ/3,fK为顶点PV相邻三角形面片,VJ为fK上顶点,N为顶点PV相邻三角形面片数.
在已知各三角面片顶点以及点PV-1和点PV的情况下,根据上述共面条件易于求解点PG.点PG即是铺放路径测地方向上的点,向量PVPG的方向表示路径在点PV处测地线的铺放方向.
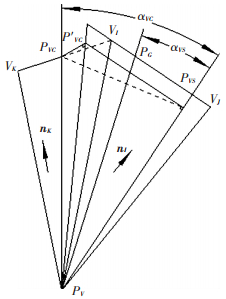
1.2 力学铺放方向及偏角计算复合材料构件的铺层是一种可设计的材料结构,其主要承载材料为纤维,为了使材料的性能得到最大的发挥,铺放路径上任一点的切向量必须满足一定的铺层力学方向要求,而这一方向往往与测地线的铺放方向存在一个偏离角度.如图 3,路径上点PV处力学方向为所要计算的向量PVPVS的方向,其与已知参照向量PVPVC方向的夹角为αVC,与测地线方向PVPG的偏角为αVS.依据图形几何变换原理,在平面内任一单位向量P绕该平面单位向量n旋转θ后得到新的单位向量为
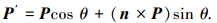
|
(1) |
|
图 3 丝束当前路径点力学铺放方向 |
其中, 逆时针旋转θ>0,顺时针θ<0.下面来计算向量PVPVS和αVS,图中下标I、J、K和L为网格顶点编号.
1) 当〈PVPVC, PVVI〉≥αVC,式中〈〉为向量夹角求取运算符时,向量PVPVC与PVPVS同在单位法向量为nK三角面片PVVIVK内,令
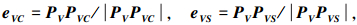
|
由式(1)有
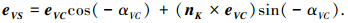
|
2) 当〈PVPVC, PVVI〉<αVC时,向量PVPVC与PVPVS不在1个三角面片内,若PVPVS在单位法向量为nI三角面片PVVIVJ内(在其它面片内计算方法一样),向量PVPVC投影到三角面片PVVIVJ内的向量为PVP′VC, 设向量PVPVC与三角面片PVVIVJ的倾角为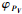

令
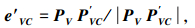
|
则有
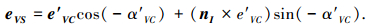
|
根据以上分析,在曲面上可以计算出丝束力学路径在点PV处的力学铺放方向PVPVS,其相对于测地线铺放方向的偏角为αVS=〈PVPG, PVPVS〉.
1.3 材料容许的铺放方向与偏角计算预浸丝束有一定的幅宽限制,复合材料构件不能完全按照铺层理想的纤维方向进行铺放,被铺丝束会产生屈皱或撕裂.根据微分几何理论,曲面上曲线在某点有限邻域内的测地曲率半径是此曲线投影到该点处的切平面上的弧长半径,并且影响被铺丝束变形程度的主要因素是铺放路径在该点处的测地曲率kg,存在这样的rg,满足rg≥rmin时,铺放路径在曲面上是可铺的.此时的铺放方向相对于测地线铺放方向存在一个偏离角,如图 4, 在网格曲面上铺放路径PV-1PV投影到点PV处的切平面上的线段PV-1TPV近似为半径为rPV-1测地弧线段.由于网格边长rPV-1,在切平面上从点PV-1T到点PV的转角为
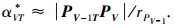
|
|
图 4 曲面上点、线在切平面上投影 |
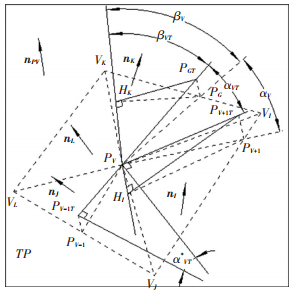
向量PVPGT和PVPV+1T的方向分别为铺放路径在点PV处的测地线方向PVPG和与该方向偏角为αV的铺放方向PVPV+1在切平面上的投影.向量PVPGT与PV-1TPV位于同一直线,且所夹αVT*的两边分别垂直于直线PVPGT和PVPV+1T,则有αV的投影:αVT=αVT*.
向量PVPG和PVPV+1的位置可在同一个三角面片或不在三角面片内.设切平面与三角面片PVVKVI和PVVIVJ的夹角分别为γK=〈nK, nPV〉和γI=〈nI, nPV〉, 与它们的交线分别为PVHK和PVHI,PGHK⊥PVHK,PGHI⊥PV+1HI,直线PVHK与PVHI可不在同一直线上,其单位方向向量分别设为lK和lI, lK=nPV×nK, lI=nPV×nI.直线PVHK与PVPGT的夹角βVT=〈lK, PVPGT〉, 在切平面上将向量lK绕单位向量nPV旋转θ=-βVT-αVT,则有
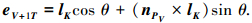
|
式中: eV+1T=PVPV+1T/|PVPV+1T|,则可求出向量PVPV+1T,∠PV+1TPVHI=〈lI, PVPV+1T〉. ∠PV+1PVHI为向量lI与PVPV+1T的夹角〈lI, PVPV+1〉, 将向量PVVI投影到切平面得到的向量为PVVIT, 则:∠PGTPVVIT=〈PVPGT, PVVIT〉.
1) 当αVT≤∠PGTPVVIT时,向量PVPG和PVPV+1的位置在同一个三角面片PVVKVI内、上,依立体解析几何理论有
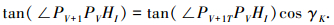
|
在三角面片PVVKVI上将向量lI绕单位向量nK旋转θ=-∠PV+1PVHI, 无论网格曲面是凸曲面还是凹曲面,都有
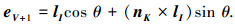
|
其中eV+1=PVPV+1/|PVPV+1|.
2) 当αVT>∠PGTPVVIT时,向量PVPG和PVPV+1的位置不在同一个三角面片内,若向量PVPV+1在三角面片PVVIVJ内(在其它面片内计算方法一样).依立体解析几何理论有
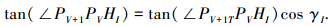
|
在三角面片PVVIVJ上将向量lI绕单位向量nI旋转θ=-∠PV+1PVHI,则有
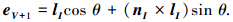
|
根据以上分析,丝束在点PV处的可行铺放方向PVPV+1及其与测地线铺放方向PVPG的偏角αV=〈PVPG, PVPV+1〉可以求出.同时,当rPV-1=rmin时,可得到丝束材料在点PV处的容许偏角αVmax.在实际工程中,丝束的容许铺放方向与力学铺放方向必在测地线铺放方向的同侧,不在同侧的铺放方向及其偏角的计算方法与在同侧相同,不再赘述.
2 铺放线型规划铺放线型规划内容包括铺放路径规划和覆盖性分析.规定曲面线型由上向下,从左向右进行规划,沿铺放方向用当前铺放丝束带的左侧丝束去拼接上一相邻线型段右侧丝束,原则上要求当前丝束带幅宽最大.以开曲面为研究对象,总体过程:在待铺曲面上确定当前线型段的参考点,以此参考点在该曲面上向垂直于该点的力学方向右侧偏移半个丝束带宽得到路径规划基点,并计算出该点的力学方向;再以力学方向为目标同时兼顾丝束的可铺性确定当前路径及其铺放终点,更新待铺曲面边界;在待铺曲面边界上选取下一条线型段的参考点,以此参考点按上述类似的方法从左向右遍历整个曲面,从而得到完整铺放线型.
2.1 铺放路径规划在路径规划过程中同时兼顾铺层力学方向和丝束的可铺性的影响,通过利用丝束的有限变形,使复合材料结构中纤维承载能力得到充分发挥.
2.1.1 路径规划方法一般曲面上路径规划基点的初始方向是铺层力学设计要求的方向,但当按照基点和初始方向生成整根铺放路径时,得到路径上任意点的力学铺放方向和测地线铺放方向往往是不一致的.因此,在满足构件整体结构性能的前提下,提出一种实用的路径规划方法.定义力学铺放方向偏角与容许偏角的比例控制系数为
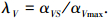
|
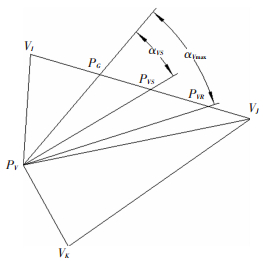
λV反映了路径当前点处铺层力学的设计方向超出材料容许形变的程度.规划过程中每步依靠当前λV的值来确定当前路径点的合理铺放方向,再根据所规划的铺放方向来计算下一路径点PV+1.如图 5.
|
图 5 力学铺放方向偏角与材料容许偏角 |
1) 当λV∈[0, 1],在丝束容许变形范围内,按路径当前点的力学铺放方向进行铺放,铺放质量良好,能够满足构件整体结构性能要求,此时实际铺放方向PVPV+1为力学铺放方向PVPVS.
2) 当λV∈(1, λ](λ为铺放工艺性的协调参数,它表示力学铺放方向超出材料容许形变程度的可接受值,可根据构件曲面外形、制造精度要求和丝束规格等铺放路径工艺设计原则综合确定),将实际铺放方向PVPV+1取为材料容许的铺放方向PVPVR.
3) 当λV∈(λ, ∞),铺放路径当前点的力学方向超出材料容许形变程度的可接受值,按照现有的曲面外形和丝宽以及铺层力学方向的要求不能规划出当前路径点PV处合理的铺放方向,此时,可通过综合考虑各影响因素,采用更窄的丝束进行铺放,或局部修改铺层设计来微调力学铺放方向.
铺放路径基点P0的方向与力学方向一致,因此在网格化曲面上,易于计算出路径上与其相邻点P1,当前点PV的铺放方向及下一路径点PV+1的计算过程如下:
1) 对相交于点PV的三角面片的法向量做凸组合来计算出该点处单位法向量nPV; 根据向量PV-1PV, 应用测地线的法截面算法,求出路径的测地线铺放方向PVPG及点PG.
2) 根据给定的参照向量PVPVC, 应用图形变换原理和空间解析几何理论计算出点PV处力学铺放方向PVPVS及该方向与PVPG的夹角αVS.
3) 在点PV的切平面上,已知丝束最小侧弯半径rmin,求出从PV-1的投影点到PV的近似转角,此角度为点PV的铺放方向PVPVR相对于向量PVPG的容许偏角αVmax在切平面上的投影.
4) 根据相交于点PV的各线段间的几何关系,计算出PVPV+1所在的三角面片与切平面交线的单位方向向量;再根据图形变换原理和立体解析几何理论,求出向量PVPVR及其相对于向量PVPG的偏角αVmax.
5) 计算λV的值和确定下一路径点PV+1
① λV∈[0, 1],点PV的铺放方向PVPV+1取向量PVPVS的方向,点PV+1为向量PVPVS所表示的直线与点PV邻域内的网格边的交点;
② λV∈(1, λ],点PV的铺放方向PVPV+1取向量PVPVR的方向,点PV+1为向量PVPVR所表示的直线与点PV邻域内的网格边的交点;
③ λV∈(λ, ∞),点PV处不能计算出合理的铺放方向,计算结束.
6) 重复步骤1)~5),计算出点PV+1的铺放方向及其相邻待规划点,直到构件边界,或在某点处力学铺放方向的偏角与材料容许的偏角间的比值大于λ,计算终止.连接P0、P1、…、PV、…,构成铺放路径.
2.1.2 路径规划验证以某自由曲面铺放路径规划为例进行验证,在CATIA中将曲面模型网格化,转化为STL文件,将其导入到VC++中进行模型重构,再对上述规划过程进行编程.给定预浸丝束的最小侧弯半径rmin=3 000 mm,铺放工艺性的协调参数λ=1.5,铺层力学的设计方向为30°,基点的铺放方向与力学方向重合.
图 6为测地线铺放路径、30°力学铺放路径和实际规划的铺放路径示意图,从图 6可以看出,开始时力学路径与测地路径比较接近,随曲面上路径点的曲率变化,二者分离,规划所得到的路径在这两条路径中间且靠近前者的一侧.从仿真结果来看,达到了铺放路径规划的目标,验证了所规划路径的合理性.

|
图 6 铺放路径规划算法验证 |
对于复杂构件曲面,不能保证相邻铺丝路径间的距离总是恒定值,若以相同的丝束数目进行铺放就会出现丝束带间离缝或重叠.覆盖性分析内容包括线型规划的初始参考点(线或面)、边界处理和丝束增减位置计算.
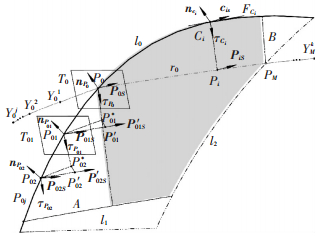
2.2.1 线型规划的初始参考点线型规划的初始参考点位于曲面边界上,要求沿铺放方向的左侧无待铺区域,是线型的左极限点.如图 7,曲面边界由曲线l0、l1、l2构成,沿顺时针方向遍历整个边界,采用定步长δ来求得线型的初始参考点Ci(N=[s/δ],[]为取整运算符,s为曲面边界周长,i∈[1, N]).点Ci处的法向量和力学方向分别为nCi和Ci S,过该点法向量为τCi的平面为FCi,其中τCi=nCi×CiS.在点Ci的领域内选取m个考查点Ci1、Ci2、…、Cim,分别判断这些点在平面FCi的左侧或右侧.若所有考查点都位于该平面的右侧,则认为点Ci为铺放丝束带的左极限点,同时将该点作为线型规划的初始参考点.通过此方法求得的参考点可能有多个,但是求解线型的最终结果相同.
|
图 7 初始参考点与边界处理 |
求得初始参考点Ci后,在被铺曲面上将该点向垂直于CiS方向右侧偏移半个丝束带宽,得到当前铺放路径的基点Pi.如图 7,点Pi在待铺曲面内,计算出该点的力学方向Pi S.若按2.1节铺放路径规划方法只能得到路径PiPM(点PM为边界上的铺放路径终点).为了求得完整的铺放路径,还需以点Pi向PiS的反方向来求得另一路径P0Pi(点P0为边界上的铺放路径起始点),然后将这两段路径连接重构,组成一条完整的铺放路径.反方向求解路径方法与上述类似,在这里不再赘述.
以点P0为起始点,以点PM为终点进行铺放时,所得铺放区域在点P0和PM处出现漏铺的情况,如图 7区域A和B.为了能够铺满这两个区域,必须将该路径向曲面外延伸.具体过程如下:以区域A铺满为例,求解第一个延伸点Y01.待铺曲面上点P0的法向量为nP0,力学方向为P0S,令τP0=P0S×nP0,过点P0作待铺曲面的切平面T0.曲面上点P0处的丝束带沿其宽度方向的测地线长度可近似为在该切平面上的带宽,因此在T0平面上将点P0沿τP0方向平移单丝宽得到点P01*后,再将点P01*沿nP0反方向投影到曲面上得到点P01′,点P01′可近似为点P0右相邻丝束路径点.再按照2.1节铺放路径规划的方法,以点P01′向P01S′反方向求得边界上的点P01,连接点P01和P01*构成直线,将该直线沿τP0的反方向平移使得点P01*与点P0重合,将点P01对应的点Y01看作为铺放路径的外延伸点.然后求解第二个延伸点Y02,将点P01在该点的切平面T01沿τP01方向平移单丝宽得到点P02*后,求解点Y02的方法与点Y01相同.重复以上步骤,将路径不断向外延伸,直到下列情况停止延伸:1)延伸点Y0j右侧丝束数目为最大出丝数(总出丝n为偶数时,j=n/2;n为奇数时,j=(n+1)/2). 2)当将计算过程的点P0j+1*沿nP0j反方向投影时,在曲面上找不到对应点.连接点P0、Y01、…、Y0j构成当前路径的延伸线.在区域B铺满的条件下,铺放路径的延伸点的求解方法与区域A类似,只是求解过程中所涉及的方向与区域A相反.连接点Y0j…Y01、P0…PM…YMk组成当前铺放路径r0,保证了区域A和B能够被铺满.更新当前铺放路径和待铺区域边界,并以点Y0j(r0对应的铺放右边界上第一个点)作为规划下一铺放路径r1的参考点.确定了规划参考点后,r1的求解过程与r0类似,依次求得待铺曲面所有其它铺放路径.
2.2.3 增丝和减丝位置计算覆盖性的目的是合理地分布丝束增/减位置,减小丝束带间离缝或重叠.在这里引用重叠系数f(丝束带间重叠部分宽度与单丝宽的比值),最大重叠系数定义为fmax.为了确定丝束增/减位置,对于铺放路径上每个点都要计算出其对应的丝束数目.
如图 8,待铺区域边界点C为当前铺放路径的参考点,求得的铺放路径为r,规划起始点(基点)P、铺放起始点P0和终点PM,同时确定路径延伸点Y0j和YMk(n为偶数时,j, k∈[1, n/2];n为奇数时,j, k∈[1, (n+1)/2]).铺丝头沿路径r从点Y0j到YMk进行铺放,可将路径分为3段进行覆盖性分析. (1)铺丝头进入待铺曲面时,在点Y0j对应的P0j进行增丝操作;走出待铺曲面,在点YMk对应的PMk进行减丝操作. (2)铺丝头在待铺曲面时,要计算出丝束数目来判断丝束的增/减.
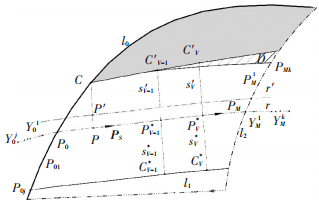
|
图 8 丝束增减位置计算 |
铺放头左侧丝束增/减的判断:当前路径点PV沿垂直于该点铺放方向左侧作测地线与边界线的交点为CV′,计算出测地线弧长为sV′,则左侧丝束的数目为
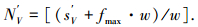
|
式中:[]为取整运逄符.判断NV′与上一规划点的左侧丝束数目NV-1′的关系.若两者相等,则左侧丝束数不变;若前者大于后者,则增丝;若前者小于后者,则减丝.
当NV′>N′(N′为左侧最大出丝数)相邻铺放路径的丝束带间出现离缝(图中D区),则当前路径无效.此时,为了保证左侧丝束控制在最大出丝范围内,应将规划基点P向左回退单丝宽所得到的点P′作为新的基点,以此参考点重新规划出新的铺放路径r′,再从新的铺放起始点开始计算左侧出丝数目.若当前的左侧出丝数目仍>N′,则点P继续回退,直到空缺铺满或点P′与C重合.当点P′与C重合时仍有空缺未铺满,则当前铺放路径无效,此时需要重新确定待铺曲面路径规划的参考点,其方法与求解线型初始参考点的方法类似,得到的参考点不能与点C重合.接下来再规划出新的铺放路径,继续进行覆盖性分析,直到整个曲面满铺.
铺放头右侧丝束增/减的判断:铺丝头右侧最大出丝数与左侧相等.将当前路径点PV沿垂直于该点铺放方向右侧作测地线,如果该测地线向右延伸碰不到待铺曲面边界,则该测地线的长度sV*最大长度为N′w,并计算出终点CV*;若碰到边界,则计算出sV*和交点CV*.此时点CV*为当前路径点PV处铺丝头的极右出丝点.再计算出右侧丝束的数目NV*=[(sV*+fmax·w)/w], 判断其与上一规划点的左侧丝束数目NV-1*的关系.右侧丝束增/减的判断与左侧相同,不再叙述.当前路径对应的所有铺丝头极右出丝点依次连接而构成的曲线作为下一铺放路径对应的左边界.
2.2.4 线型规划验证在铺放路径验证的基础上,给定单丝宽为5 mm、满丝数目为6根和fmax=0.5,进行线型规划算法验证. 图 9中,粗实线表示铺放路径,其两侧阴影区域表示丝束带覆盖范围.两相邻路径间颜色较深的区域为丝束重叠部分,而白色部分为丝束带间的间隙.从图 9中可看出,该曲面的铺放过程中丝束数目有增有减,铺放路径向曲面外延伸.
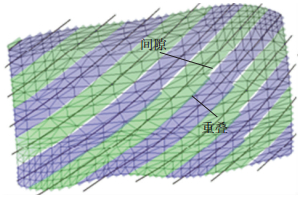
|
图 9 铺放线型规划效果 |
由于受到构建曲面外形、丝束变形能力和铺层力学方向等因素的制约,在实际铺放过程中就要求增/减丝束.一方面,对于丝束带间的拼接,在合理的位置增/减丝束有助于提高铺放效率和节约成本;另一方面,铺放路径向外延伸使得构件曲面边界能够铺满, 减少了构件的后加工和原材料成本.根据以上分析和结合线型规划结果,表明了这种规划方法的有效性.
3 结论1) 复杂曲面的铺放路径难以用精确的数学模型来表示,本文将曲面进行网格化处理,应用曲面微分几何和空间解析几何理论进行分析计算,给出了丝束变形能力和铺层方向约束条件下,能够均匀铺满整个曲面的线型规划方法.
2) 该线型规划算法引入了丝束最小弯曲半径、铺放方向容许偏角控制系数和最大重叠系数,很好地考虑了预浸丝束在铺放过程中的形变适应能力、铺放制品的铺层力学要求和规划结果中丝束增减位置分布的要求.该规划方法能充分利用丝束的有限变形,发挥纤维的承载能力,改善构件铺放质量, 提高铺放效率和节约成本.
3) 仿真结果表明,该线型规划能协调处理力学方向和测地线方向不一致的情况,能根据重叠系数要求进行合理的丝束增减处理,为解决自动铺放制造的实际工程应用提供了一定的理论支持.
| [1] |
史耀耀, 阎龙, 杨开平. 先进复合材料带缠绕、带铺放成型技术[J]. 航空制造技术, 2010(17): 32-36. DOI:10.3969/j.issn.1671-833X.2010.17.003 |
| [2] |
肖军, 李勇, 李建龙. 自动铺放技术在大型飞机复合材料结构件制造中的应用[J]. 航空制造技术, 2008(1): 50-53. DOI:10.3969/j.issn.1671-833X.2008.01.009 |
| [3] |
GRANT G G. Fiber placement process utilization within the worldwide aerospace industry[J]. SAMPE Journal, 2000, 36(4): 7-12. |
| [4] |
FAYAZBAKHSH K, NIK M A, PASINI D, et al. Defect layer method to capture effect of gaps and overlaps in variable stiffness laminates made by Automated Fiber Placement[J]. Composite Structures, 2013, 97(3): 245-251. |
| [5] |
CROFT K, LESSARD L, PASINI D, et al. Experimental study of the effect of automated fiber placement induced defects on performance of composite laminates[J]. Composites:Part A, 2011, 42(5): 484-491. DOI:10.1016/j.compositesa.2011.01.007 |
| [6] |
BEAKOU A, CANO MJ, CAMA B L, et al. Modelling slit tape buckling during automated prepreg manufacturing:A local approach[J]. Composite Structures, 2011, 93(10): 2628-2635. DOI:10.1016/j.compstruct.2011.04.030 |
| [7] |
GÜRDAL Z, OLMEDO R. In-plane response of laminates with spatially varying fiber orientations:variable stiffness concept[J]. AAIA Journal, 1993, 31(4): 751-758. DOI:10.2514/3.11613 |
| [8] |
OLMEDO R, GÜRDAL Z. Buckling response of laminates with spatially varying fiber orientations[C]//Proccedings of the 34th AAIA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference. La Jolla: AAIA Press, 1993: 2261-2269.
|
| [9] |
GHIASI H, FAYAZBAKHSH K, PASINI D, et al. Optimum stacking sequence design of composite materials. Part Ⅱ:Variable stiffness design[J]. Composite Structures, 2010, 93(1): 1-13.. DOI:10.1016/j.compstruct.2010.06.001 |
| [10] |
HALE R D, MOON R, LIM K, et al. Integrated design and analysis tools for reduced weight, affordable fiber steered composites[R]. Lawrence: university of Kansas, 2004.
|
| [11] |
IJSSELMUIDEN S T, ABDALLA M M, GÜRDAL Z. Optimization of variable-stiffness panels for maximum buckling load using lamination parameters[J]. AIAA Journal, 2010, 48(1): 134-143. DOI:10.2514/1.42490 |
| [12] |
LEWIS H W, ROMERO J E. Composite tape placement apparatus with natural path generation means: 4696707[P]. 1987-09-29[2014-09-28]. http://www.freepatentsonline.com/4696707.pdf.
|
| [13] |
胡翠玲, 肖军, 李勇, 等. 复合材料自动铺带技术研究(Ⅰ):自然路径特性分析及算法[J]. 宇航材料工艺, 2007(1): 40-43. DOI:10.3969/j.issn.1007-2330.2007.01.010 |
| [14] |
罗海燕, 李勇, 肖军, 等. 复合材料自动铺带技术研究:曲面铺带轨迹算法[J]. 航空学报, 2009, 30(9): 1782-1786. DOI:10.3321/j.issn:1000-6893.2009.09.034 |
| [15] |
SHIRINZADEH B, ALICI G, FOONG C W, et al. Fabrication process of open surfaces by robotic fibre placement[J]. Robotics and Computerk-Integrated Manufacturing, 2004, 20(1): 17-28. DOI:10.1016/S0736-5845(03)00050-4 |
| [16] |
SHIRINZADEH B, CASSIDY G, OETOMO D, et al. Trajectory generation for open-contoured structures in robotic fiber placement[J]. Robotics and Computer-Integrated Manufacturing, 2007, 21(6): 380-394. |
| [17] |
韩振宇, 邵忠喜, 富宏亚, 等. S型进气道纤维铺放轨迹网格化生成[J]. 航空制造技术, 2009(19): 72-78. DOI:10.3969/j.issn.1671-833X.2009.19.015 |
| [18] |
邵忠喜, 富宏亚, 韩振宇, 等. S形进气道纤维铺放轨迹规划和优化方法[J]. 宇航学报, 2010, 31(3): 855-861. DOI:10.3873/j.issn.1000-1328.2010.03.038 |
| [19] |
李俊斐, 王显峰, 肖军. 开孔曲面自动铺放轨迹规划算法研究[J]. 航空学报, 2013, 34(7): 1716-1723. |
| [20] |
熊文磊, 肖军, 王显峰, 等. 基于网格化曲面的自适应自动铺放轨迹算法[J]. 航空学报, 2013, 34(2): 434-441. |
| [21] |
神会存, 李建华, 周来水. 三角网格模型顶点法矢与离散曲率计算[J]. 计算机工程与应用, 2005, 41(26): 12-15. DOI:10.3321/j.issn:1002-8331.2005.26.004 |
 2016, Vol. 48
2016, Vol. 48


