凸度仪是目前热轧板带横向厚度分布常用的检测仪器,测量方法为:在板带宽度方向上均匀布置数百个厚度测量点,并对各个离散的厚度检测数据进行曲线拟合[1].实际生产中,一般很少在线检测铝板带的横向厚度分布,未考虑其对冷轧板形的影响;然而,终轧板带横向厚度分布与板形(板凸度和平直度)直接相关,并且板形具有遗传性,后续冷轧无法纠正其板形,造成冷轧板形的质量差.因此,随着对板带冷轧和热轧产品质量要求的提高,对热轧板带横向厚度分布的预测与控制,具有重要的理论意义和工程应用价值.
终轧道次板带横向厚度分布受多种因素的影响,如工作辊弯辊、工作辊温度、轧辊倾斜等,并且具有较强的非线性、时变性以及相互耦合等特点.按照传统理论建立的数学模型很难对其进行准确的预测.目前,神经网络在轧制板形模式识别[2~4]、板带温度预测[5]以及板形预测与控制领域有了广泛的应用[6~8].现有的板形预测模型均以实际测得的板形偏差值[9~10]或工作辊凸度[11]为模型的输入向量之一;然而,受实际情况的限制,工作辊的凸度很难实现在线测量,理论计算模型误差较大;板形在线检测设备投资大,测量精度受多种因素的影响.在板形控制领域,神经网络主要是用来对工作辊弯辊、轧辊倾斜与轧制力等板形调控手段进行控制[12~15],而很少用于热轧板带工作辊分段冷却的控制.
为解决上述问题,本文根据某厂二辊可逆热轧机的轧制环境,建立了符合实际生产需要的终轧板带横向厚度分布的自适应(PSO)-BP神经网络预测模型,并将预测模型用于板带横向厚度分布控制系统的反馈环节,在设定合理的轧制力、轧制速度等轧制因素前提下,对工作辊分段冷却系统进行调节,最终通过现场试验验证了该模型的准确性.
1 自适应PSO-BP神经网络模型 1.1 PSO-BP网络模型BP网络应用广泛,但是该算法对初始的权值和阈值敏感,容易陷入局部最优.而PSO作为一种智能优化算法,其收敛速度快, 鲁棒性高, 全局搜索能力强,已得到了广泛应用[16].因此,本文选用PSO-BP混合算法训练神经网络.
利用一定样本数据,对神经网络进行训练,首先使用PSO算法优化神经网络所有的权值和阈值并作为PSO算法的解,以系统的平均误差E作为PSO的目标函数,当目标函数达到预先给定值或者达到最大迭代次数时,PSO算法终止,然后使用BP算法继续训练.这样提高了神经网络的学习能力,以及增强了神经网络的泛化性能和预测能力.系统的平均误差为
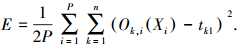
|
式中:tk1为训练样本1在第k个输出端的期望输出.
BP神经网络隐含层的激励函数f为logistic函数,网络的预测输出为

|
式中:wjk为连接权值,bk为阈值.
1.2 网络自适应结构调整神经网络拓扑结构中,输入节点与输出节点是由问题本身决定的,而隐含层节点数的选择目前还没有准确的计算公式.为了找到合适的隐含层节点数,最好的方法就是网络在学习过程中,能够自组织地选择合适的结构[9].
通过设定隐含层节点删除与合并条件,使网络在训练的过程中能够自主地判断节点数.设zj是隐含层节点j在学习第i个样本的输出,P为训练样本数,则
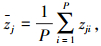
|
样本分散度为
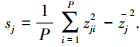
|
当sj过小时,表明隐含层节点j的输出变化以及对网络的学习作用都很小,可以删除此节点.
两个隐含层节点之间的相关系数rjh的计算公式如下:
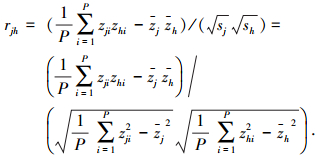
|
如果rjh过大,说明隐含层节点j和h的功能重合度较大,需要将两个节点合并.
1.3 自适应PSO-BP网络算法流程首先, 设计一个基本的网络结构,确定其输入输出节点数,并且输入训练样本;然后, 优化网络自身的结构; 最后, 用优化的结构进行样本的训练及预测.网络结构优化的流程如图 1所示.网络算法的具体步骤如下:
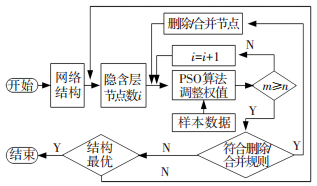
|
图 1 神经网络结构自适应流程 |
1) 根据实际情况设定输入输出节点数、训练的目标误差、迭代步数以及一个初始的隐含层节点数i.
2) 输入样本数据,用PSO算法修改网络的权值;判断迭代步数m是否超过规定的步数n,若没有超过迭代步数,则增加一个隐含节点继续学习;若超出迭代步数,转到3).
3) 判断是否符合删除或合并条件,符合则删除或合并节点,然后返回到2);否则转到4).
4) 判断当前网络结构是否是最优的,若此时网络达到学习精度的最小规模,则网络优化过程结束,转到5);否则返回1).
5) 网络结构优化结束后,开始对网络进行训练与预测.
2 板带横向厚度分布的预测模型对于二辊可逆热轧机而言,由于板带凸度没有外部补偿(即工作辊为平辊,无弯辊力),影响板带横向厚度分布的主要因素是工作辊的热凸度、轧制力引起的挠度、轧制速度和工作辊磨损.神经网络模型的结构为一个输入层、一个输出层和一个隐含层,其中,输入的向量为轧制力F、轧制速度v、工作辊温度Tj(Tj为与板厚测量点一一对应的工作辊表面温度)和工作辊磨损C;输出向量为终轧板带厚度Hj;隐含层节点数通过上述网络的自调整学习过程获得,设定网络的训练次数为1 000.样本数据来源于宽660 mm的热轧3004铝合金板带,除去距板带边缘<18 mm的部分,剩余部分均匀取13个点作为板厚测量点,即j=13.工作辊磨损通过离线计算模型得出;工作辊表面温度利用自主研发的温度测量系统测得,经验证温度测量误差为±1 ℃;板厚值为轧后板带的厚度,利用千分尺测量得出.对于一种材料的板带,只需训练一次神经网络,即只需测量用于样本数据的板厚值,网络模型训练完成后,轧制过程中的板带厚度可通过工作辊表面温度测量值以及其他相关轧制参数预测得出.
为了提高神经网络的泛化能力,选取稳态轧制时终轧道次的轧制数据作为神经网络的训练样本,选取60组数据作为神经网络的样本值,其中45组数据为训练样本,剩余15组数据为测试样本.
3 网络测试和结果分析在使用神经网络进行预测前,首先, 要通过训练网络使其具有联想记忆和预测能力; 然后, 将训练完成的网络预测模型作为文件存储,需要时可以调用该文件对未训练的样本进行预测.任意选取两组(a,b)板带横向厚度分布的预测值与实际值,见图 2.由图 2可知, 预测板带横向厚度分布规律与实际分布相同;两组数据中所有预测点的平均绝对误差分别为2.5、4.1 μm.为进一步说明预测模型的可靠性,对60组样本数据的预测误差进行统计,各点厚度的预测误差均在±10 μm内,平均绝对误差为3.6 μm,并且误差在±4 μm范围内占87.1%.
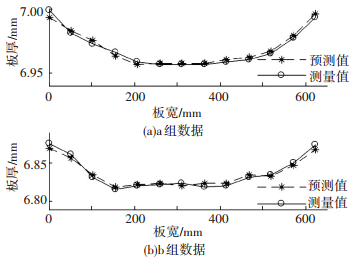
|
图 2 板厚网络预测与实际值 |
图 3为板带中间点厚度预测值的误差,误差在±5 μm内,平均绝对误差为2.8 μm.经分析可知:与板带边缘部分相比,板带中部的预测精度较高,预测值较稳定.
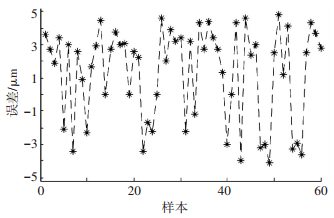
|
图 3 预测误差 |
由于热精轧板带较薄,可忽略宽展,终轧板带横向厚度分布与板形(板凸度和平直度)直接相关,所以可用终轧道次出口板带横向厚度分布来反馈控制板形.对于二辊可逆热轧机而言,板厚控制手段主要有调整轧制力和工作辊的分段冷却,其中轧制力的调整需要改变工作辊的辊缝值,由此导致板带出口厚度和其他轧制参数发生变化,其调整过程不稳定;并且在轧制前,根据轧制工艺已设定了合理的工作辊空载辊缝.因此,轧制过程控制板带横向厚度分布的主要手段为工作辊的分段冷却.
为了提高控制系统的响应速度,离线完成神经网络的训练过程,并存储于热轧生产线的计算机中.使用轧制过程参数,利用已存储的神经网络预测模型来反应板带的轧制状态,并且结合分段冷却技术对板带横向厚度分布进行调节.如图 4所示,其主要步骤为:首先利用工作辊温度在线测量系统对工作辊表面温度进行测量,然后将k时刻的温度值(Ti(k))以及其他轧制参数输入到神经网络预测模型中,对比各点板厚预测值(Hi(k))与实际目标值(ri),再经模糊控制器得出各冷却区段对应的冷却液的实际调节量(ui(k)),最终通过冷却系统控制工作辊轴向温度分布,达到调节板带横向厚度分布的目的.

|
图 4 预测神经网络控制系统流程图 |
该厂的热轧产品用于冷轧产品的原材料,即需要中凸值为0.02~0.04 mm的板带断面形状,板带厚度误差要求为±0.3 mm.据此,将图 4所示控制系统用于热轧板带横向厚度分布的控制,随机选取5卷终轧板带进行测量,如图 5所示,板带中凸值在0.023~0.035 mm,且横向厚度分布均匀.
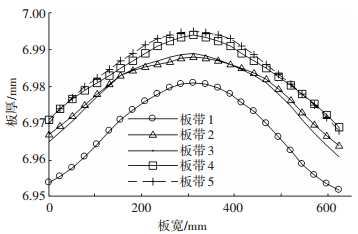
|
图 5 热轧板带横向厚度分布 |
经统计,稳态轧制下(即去除板带头尾部分)板带厚度的绝对误差在15 μm以内的频率为79%,绝对误差在30 μm内的频率为90%,稳态轧制时板带中部的平均厚度误差为10.3 μm.未使用该系统前,二辊可逆热轧机稳态轧制时,板厚误差绝对值在30 μm以内的频率仅为37%, 轧制板带的断面形状为凹型、平型,且板带横向厚度分布不规则,造成轧后板带为不合格产品.使用预测神经网络控制系统前后结果对比表明:系统运行稳定,说明本文方法能够有效地改善热轧板带的质量.
5 结论1) PSO-BP混合神经网络算法,克服了BP网络对网络初始权值和阈值敏感的缺点,避免网络得到局部最优解;网络自适应结构,使网络在学习过程中能够自组织地寻求最优的隐含层节点数,提高了网络收敛速度和预测精度.
2) 自适应PSO-BP神经网络预测模型的精度高,终轧道次板带厚度预测的平均绝对误差为3.6 μm,满足对终轧板厚控制的要求;此神经网络预测模型,在预测误差范围内可以代替凸度仪,减少设备投入.
3) 离线训练完成的神经网络,用于板带厚度控制的反馈环节,这一方法为热轧板带厚度的预测以及分段冷却技术的应用提供了较为广阔的应用前景.
| [1] |
刘华, 顾廷权, 缪明华. 带钢断面形状检测与特征参数识别方法[J]. 钢铁研究学报, 2012, 24(2): 59-62. |
| [2] |
刘建, 王益群, 孙福, 等. 基于粒子群理论的板形模糊模式识别方法[J]. 机械工程学报, 2008, 44(1): 173-178. DOI:10.3321/j.issn:0577-6686.2008.01.030 |
| [3] |
任海鹏, 刘丁, 郑岗. 一种基于遗传算法的板形模式识别方法[J]. 重型机械, 2002(3): 9-12. DOI:10.3969/j.issn.1001-196X.2002.03.003 |
| [4] |
JIA Chunyu, SHAN Xiuying, LIU Hongmin, et al. Fuzzy neural model for flatness pattern recognition[J]. Journal of Iron and Steel Research, International, 2008, 15(6): 33-38. DOI:10.1016/S1006-706X(08)60262-9 |
| [5] |
LAURINEN P, RONIBG J. An adaptive neural network model for predicting the post roughing mill temperature of steel slabs in the reheating furnace[J]. Journal of Materials Processing Technology, 2005, 168(3): 423-430. DOI:10.1016/j.jmatprotec.2004.12.002 |
| [6] |
SHIM M, LEE K Y, LEE D S. Intelligent controller design for the flatness control in cold rolling process[C]//Proceedings of the 40th IEEE Conf on Decision and Control. Orlando: IEEE, 2001: 2720-2725.
|
| [7] |
刘建昌, 王柱. 基于神经网络模式识别的板形模糊控制器[J]. 东北大学学报(自然科学版), 2005, 26(8): 718-721. DOI:10.3321/j.issn:1005-3026.2005.08.002 |
| [8] |
BARRIOS J A, TORRES-ALVARADO M, CAVAZOS A. Neural fuzzy and Grey-Box modelling of entry temperature prediction in a hot strip mill[J]. Expert Systems with Application, 2012, 39(3): 3374-3384. DOI:10.1016/j.eswa.2011.09.025 |
| [9] |
贾春玉, 单修迎, 牛召平. 自调整动态神经网络模型及其在带材板形预测中的应用[J]. 钢铁研究学报, 2006, 18(12): 50-53. DOI:10.3321/j.issn:1001-0963.2006.12.013 |
| [10] |
JIA Chunyu, LIU Hongmin, ZHOU Huifeng. Fuzzy control system of hydraulic roll bending based on genetic neural network[J]. Journal of Iron and Steel Research, 2005, 12(3): 22-27. |
| [11] |
王海勇. 铝板带热精轧横向厚度分布神经网络建模与板形控制[D]. 长沙: 中南大学, 2012: 42-44.
|
| [12] |
SON J S, LEE D M, KIM I S, et al. A study on on-line learning neural network for prediction for rolling force in hot-rolling mill[J]. Journal of Materials Processing Technology, 2005, 164-165: 1612-1617. DOI:10.1016/j.jmatprotec.2005.01.009 |
| [13] |
SIKDAR S, KUMARI S. Neural network model of the profile of hot-rolled strip[J]. The International Journal of Advanced Manufacturing Technology, 2009, 42(5): 450-462. |
| [14] |
刘建昌, 陈莹莹, 张瑞友. 基于PSO-BP网络板形智能控制器[J]. 控制理论与应用, 2007, 24(4): 674-678. |
| [15] |
XU Liang, LI Zhangying, SONG Yuzhi, et al. Prediction of ship roll based on second diagonal recurrent neural network[J]. Scientific Journal of Control Engineering, 2013, 3(3): 106-110. |
| [16] |
GUDISE V G, ven AYAGAMOORTHY K. Comparison of particle swarm optimization and back propagation as training algorithms for neural networks[C]//Proceedings of the 2003 IEEE on Swarm Intelligence Symposium (SIS' 03). Indianapolis: IEEE, 2003: 110-117.
|
 2016, Vol. 48
2016, Vol. 48


