通常把飞行速度大于5 Ma的飞行器称为高超声速飞行器,由于其高速度、高机动性、大飞行包线等优势,因而具有重要的民用、军事价值和战略意义.一般说来,高超声速飞行器主要分为两种类型:1)火箭基高超声速飞行器,也称为无动力再入高超声速飞行器.这类高超声速飞行器本身不具备动力装置,而是借助火箭助推器将其投送到预定的速度和高度,然后利用自身的动能、重力势能以及气动舵面、反作用力喷气等装置按照预定的轨迹滑翔到最终目标,例如: 洛克希德·马丁公司的高超声速技术飞行器(hypersonic technology vehicle,HTV)[1]、美国陆军的先进高超声速武器(advanced hypersonic weapon,AHW)[2].2)采用吸气式超燃冲压发动机作为动力的高超声速飞行器,简称吸气式高超声速飞行器.超燃冲压发动机可以在高超声速飞行的状态下,使碳氢或液氢燃料和吸入的空气在超声速燃烧室内进行充分地燃烧.相比于常规的火箭发动机,超燃冲压发动机不需要携带额外的氧化剂,进而有效地提升飞行器的载荷比.同时,超燃冲压发动机的机械结构极其简单,具有较低的生产成本和良好的可靠性.但由于超燃冲压发动机在低速(一般小于3.0Ma)是无法启动的,因此,这类高超声速飞行器往往采用超燃冲压发动机与火箭发动机或涡轮喷气发动机组合的方式,以实现大范围的全包线飞行[3].吸气式高超声速飞行器正得到美国、俄罗斯、英国、中国等国家的高度重视,也是本文介绍的对象.具有代表性的吸气式高超声速飞行器有: 美国航空航天局的X-43A[4]、波音公司的X-51A[5]、俄罗斯的“鹰”试验飞行器、英国的“Shyfe”验证机、印度的“Avatar”空天飞机[2].
吸气式高超声速飞行器的研制是一项尖端、复杂、多学科的工程,其涉及到高超声速飞行动力学、超声速燃烧技术、热传导理论及热防护材料、飞行器导航、制导与控制等多个学科[6-10].为了适应高速度、高动压的飞行环境,许多先进的设计理念和制造工艺被应用到吸气式高超声速飞行器的研制.例如: 扁平细长的机身设计增加了飞行器的升阻比;轻质复合材料的应用提升了系统的防热性能以及有效载荷比;机身-发动机一体化构型可以产生适于超燃冲压发动机工作的进气工况.然而,这些先进的技术也会给吸气式高超声速飞行器的控制带来一些不期望的特性如图 1所示.例如: 细长的外形设计和轻质材料的应用使得飞行器的机身具有更大的挠性,在高超声速飞行过程中极易激发弹性模态,引起机体的震动;由于超燃冲压发动机整合在机身下方,因此发动机的推力会产生一个附加的抬头力矩,增加了执行机构的负担;与此同时,超燃冲压发动机的进气、排气也会对飞行器的升力、阻力和俯仰力矩产生严重的扰动.值得指出的是,超燃冲压发动机对于飞行动压、进气条件以及燃空比有着相对苛刻的要求,不当的工况会引发所谓的热阻现象,进而导致发动机无法正常工作.可见,吸气式高超声速飞行器相比于普通的飞行器而言,具有更强的非线性、更复杂的耦合、更严重的弹性振动以及更严格的控制约束[11-13].

|
图 1 吸气式高超声速飞行器控制的难点 Figure 1 Difficulties in the control of air-breathing hypersonic vehicles |
除了吸气式高超声速飞行器本身的特点,高速、高动压的飞行环境也会产生一些不利的因素.大的飞行包线使得飞行器的飞行环境发生剧烈的变化,又由于高超声速气动热、气动力的某些机理尚未明确,因此,目前建立的动力学模型仅适用于某一特定的工作范围,并且具有很大的不确定性.高动压的飞行环境使得飞行器的执行机构(例如: 气动舵面)表现出一定的非线性特性,甚至可能出现部分或者完全失效.同时,对于一些必要的飞行状态(例如: 攻角、侧滑角)很难采用已有常规的手段进行精确测量,例如: 空速管、惯性导航系统、嵌入式的大气数据传感器[14].可见,吸气式高超声速飞行器控制器的设计是极具挑战性的.
本文根据国内外近期相关的成果以及作者的研究,针对吸气式高超声速飞行器的控制问题进行阐述,并基于作者的认知,进一步总结了控制器设计环节所面临的一些实际问题.
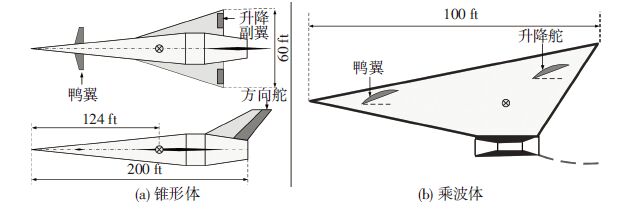
1 吸气式高超声速飞行器模型概述本文主要对于吸气式高超声速飞行器建模的发展做简要的概述和总结.在高超声速飞行过程中,飞行器的几何构型对于飞行特性起着决定性的作用.目前,常见的高超声速飞行器的几何构型主要有带翼锥形体构型(winged-cone hypersonic vehicle,如图 2(a)所示)和乘波体构型(wave-rider hypersonic vehicle,如图 2(b)所示).锥形体构型的机身主体是一个轴对称的几何体,由前段(圆锥体)、中段(圆柱体)、后段(圆台)3部分组成,具有大升阻比、大细长比、大后掠角以及小展弦比等特点,是一种比较成熟的高超声速飞行器构型.乘波体构型已经被证明是实现高超声速飞行的最优方案,其独特的几何外形可使飞行器不需要额外的机翼来产生升力,而是利用压缩升力和激波升力进行高超声速飞行.目前,以超燃冲压发动机作为动力的高超声速飞行器绝大部分采用乘波体构型.其他的高超声速飞行器构型还有翼身融合体 (wing-body hypersonic vehicle)、升力体(lifting-body hypersonic vehicle)等.
|
图 2 两种常见的高超声速飞行器构型 Figure 2 Two common configurations of air-breathing hypersonic vehicles |
由于吸气式高超声速飞行器具有非常复杂的非线性、耦合以及不确定性,对其建立精准的数学模型是极为困难的,因此,目前相关建模的研究主要集中于纵向、刚体动力学建模[15-17].Chavez等[18]首次采用牛顿碰撞理论建立了可分析的超燃冲压发动机以及吸气式高超声速飞行器的数学模型. Shaughnessy等[19]利用风洞实验测量气动力、力矩系数在不同攻角、速度和气动舵偏角下的数值,为一类带翼锥形体构型的高超声速飞行器建立了纵向刚体运动模型.Marrison等[20]进一步在特定平衡点处得到其简化的拟合形式,这个模型在早期的高超声速飞行控制中得到了广泛的应用[21].近期,Bolender等[22]利用斜波理论和普朗特-迈耶扩张理论对于文献[18]的工作进行了发展和改进,构建了一类乘波体构型的高超声速飞行器的纵向弹性体运动模型.该模型可以很好地捕捉到超燃冲压发动机、空气动力学、结构动力学之间的关系.Parker等[23]进一步利用多项式拟合的方法对于文献[22]提出的模型进行简化处理,得到了面向控制器设计的吸气式高超声速飞行器模型(control-oriented model,COM).为方便后文的阐述,以下总结了几种具有代表性的数学模型.
1.1 锥形体纵向运动拟合模型锥形体构型的高超声速飞行器(如图 2(a)所示)的纵向运动刚体动力学方程为[20]
| $\left\{ \begin{array}{*{35}{l}} \dot{V}=\frac{T\cos \alpha -D}{m}-g\sin \gamma , \\ \dot{h}=V\sin \gamma , \\ \dot{\gamma }=\frac{L+T\cos \alpha }{mV}-\frac{g\cos \gamma }{V}, \\ \dot{\alpha }=Q-\dot{\gamma }, \\ \dot{Q}=\frac{{{M}_{yy}}}{{{I}_{yy}}}. \\ \end{array} \right.$ | (1) |
其中推力T、升力L、阻力D、俯仰力矩Myy有如下表达式:
| $\left\{ \begin{array}{*{35}{l}} T=\bar{q}S{{C}_{T}}\left( \alpha ,M,\delta T \right), \\ L=\bar{q}S{{C}_{L}}\left( \alpha ,M \right), \\ D=\bar{q}S{{C}_{D}}\left( \alpha ,M \right), \\ {{M}_{yy}}=\bar{q}S\bar{c}\left[ {{C}_{M}}\left( \alpha \right)+{{C}_{M}}\left( {{\delta }_{e}} \right)+{{C}_{M}}\left( Q \right) \right]. \\ \end{array} \right.$ | (2) |
式中: g为重力加速度常数;m为飞行器的质量;Iyy为飞行器的转动惯量;q为表动压;S为机身的参考面积;c为参考长度;M为飞行马赫数.相关的空气动力/力矩系数可以通过如下拟合公式得到:
| $\left\{ {\begin{array}{*{20}{l}} {{C_L}\left( {\alpha ,M} \right) = \alpha \left( {0.493 + 1.91/M} \right),} \\ \begin{gathered} {C_D}\left( {\alpha ,M} \right) = 0.0082\left( {171{\alpha ^2} + 1.15\alpha + 1} \right) \times \hfill \\ \left( {0.0012{M^2} - 0.054M + 1} \right) \hfill \\ \end{gathered} \\ \begin{gathered} {C_T}\left( {\alpha ,M,\delta T} \right) = 0.0105\left[ {1 - 164{{\left( {\alpha - {\alpha _0}} \right)}^2}} \right]. \hfill \\ \left( {1 + 17/M} \right)\left\{ {\begin{array}{*{20}{l}} {1.15\delta T,{\text{if }}\delta T{\text{ < }}1} \\ {1 + 0.15\delta T,{\text{if }}\delta T \geqslant 1} \end{array},} \right. \hfill \\ \end{gathered} \\ {{C_M}\left( \alpha \right) = {{10}^{ - 4}} \times \left( {0.06 - {{\text{e}}^{ - M/3}}} \right) \cdot \left( { - 6565{\alpha ^2} + 6875\alpha + 1} \right),} \\ \begin{gathered} {C_M}\left( Q \right) = cQ/\left( {2V} \right)\left( { - 0.025M + 1.37} \right) \cdot \hfill \\ \left( { - 6.83{\alpha ^2} + 0.303\alpha - 0.23} \right) \hfill \\ \end{gathered} \\ {{C_M}\left( {{\delta _e}} \right) = 0.0292\left( {{\delta _e} - \alpha } \right).} \end{array}} \right.$ | (3) |
式中α0为平衡点处的攻角值.上述吸气式高超声速飞行器的数学模型(1)~(3)包含5个刚体飞行状态量: 速度V、高度h、飞行航迹角γ、飞行攻角α、俯仰角速率Q;两个控制输入量: 燃料节流阀控制量δT、升降舵偏转角δe.该模型并没有考虑机身的弹性模态、超燃冲压发动机与机身之间的耦合以及气动舵偏转角对于气动力(升力和阻力)的影响,因此对于吸气式高超声速飞行器动态特性的描述十分有限.即便如此,其数学表达式仍是十分复杂的.
1.2 乘波体纵向运动拟合模型乘波体构型的高超声速飞行器的纵向运动刚体动力学方程与式(1)是相同的,其弹性体模型具有如下表达式(仅为一种简单的表达形式,详见文献[23-24]):
| ${{{\ddot{\eta }}}_{i}}=-2{{\xi }_{i}}{{\omega }_{i}}{{{\dot{\eta }}}_{i}}-{{\omega }_{i}}^{2}{{\eta }_{i}}+{{N}_{i}},\left( i=1,2,3 \right).$ | (4) |
式中: 0<ξi<1,ωi>0为常数.推力T、升力L、阻力D、俯仰力矩Myy以及广义力Ni可以通过如下多项式拟合得到:
| $\left\{ {\begin{array}{*{20}{l}} \begin{gathered} T = \bar qS\left[ {\left( {C_{T,\Phi }^3{\alpha ^3} + C_{T,\Phi }^2{\alpha ^2} + C_{T,\Phi }^1\alpha + C_{T,\Phi }^0} \right)\Phi + } \right. \hfill \\ \left. {C_T^3{\alpha ^3} + C_T^2{\alpha ^2} + C_T^1\alpha + C_T^0 + C_T^\eta \eta } \right] \hfill \\ \end{gathered} \\ {L = \bar qS\left[ {C_L^\alpha \alpha + C_L^{{\delta _e}}{\delta _e} + C_L^{{\delta _c}}{\delta _c} + C_L^0 + C_L^\eta \eta } \right]} \\ \begin{gathered} D{\text{ = }}\left[ {\bar qSC_D^{{\alpha ^2}}{\alpha ^2} + C_D^\alpha \alpha + C_D^{\delta _e^2}\delta _e^2 + C_D^{{\delta _e}}{\delta _e} + } \right. \hfill \\ \left. {C_D^{\delta _c^2}\delta _c^2 + C_D^{{\delta _c}}{\delta _c} + C_D^0 + C_D^\eta \eta } \right] \hfill \\ \end{gathered} \\ \begin{gathered} {M_{yy}} = {z_T}T + \bar q\bar cS\left[ {C_M^{{\alpha ^2}}{\alpha ^2} + C_M^\alpha \alpha + C_M^{{\delta _e}}{\delta _e} + } \right. \hfill \\ \left. {C_M^{{\delta _c}}{\delta _c} + C_M^0 + C_M^\eta \eta } \right] \hfill \\ \end{gathered} \\ {{N_i} = \bar qS\left[ {N_i^{{\alpha ^2}}{\alpha ^2} + N_i^\alpha \alpha + N_i^{{\delta _e}}{\delta _e} + N_i^{{\delta _c}}{\delta _c} + N_i^0 + N_i^\eta \eta } \right].} \end{array}} \right.$ | (5) |
式中:C**、N**分别为力、力矩的拟合系数.上述吸气式高超声速飞行器的数学模型(1),(4),(5)包含5个刚体飞行状态量为速度V、高度h、飞行航迹角γ、飞行攻角α以及俯仰角速率Q;6个弹性模态状态量为η=[η1 ${\dot{\eta }}$1 η2 ${\dot{\eta }}$2 η3 ${\dot{\eta }}$3]T;3个控制输入量为燃空比(即燃料与空气的混合比)Φ、鸭翼及升降舵的偏转角δc、δe.该模型充分地反映出吸气式高超声速飞行器复杂的飞行动力学特性,例如: 推力和俯仰力矩之间的耦合zTT,弹性模态对于刚体动力学的影响CTηη、CLηη、CDηη、CMηη,以及非最小相位特性CLδeδe、CDδe2δe2+CDδeδe等[23].
1.3 线性参数变化系统模型基于乘波体纵向运动拟合模型,文献[25]进一步推导出与之对应的线性变参数模型(linear parameter-varying model,LPVM),该模型可以应用于增益调度控制 (gain-scheduling control,GSC) 或者基于线性不等式的鲁棒控制 (LMI-based robust control,LMI-BRC) 等,其表达式具有如下线性形式:
| $\left\{ \begin{array}{*{35}{l}} \begin{align} & \left[ \begin{array}{*{35}{l}} {\dot{x}} \\ {\dot{\eta }} \\ \end{array} \right]=\left[ \begin{matrix} {{A}_{11}}\left( \theta ,\mu \right) & {{A}_{12}}\left( \theta ,\mu \right) \\ {{A}_{21}}\left( \theta ,\mu \right) & {{A}_{22}}\left( \theta ,\mu \right) \\ \end{matrix} \right]\left[ \begin{array}{*{35}{l}} x \\ \eta \\ \end{array} \right]+ \\ & \left[ \begin{array}{*{35}{l}} {{B}_{1}}\left( \theta ,\mu \right) \\ {{B}_{2}}\left( \theta ,\mu \right) \\ \end{array} \right]u+\left[ \begin{array}{*{35}{l}} {{P}_{1}}\left( \theta ,\mu \right) \\ {{P}_{2}}\left( \theta ,\mu \right) \\ \end{array} \right], \\ \end{align} \\ \text{y=}C\left( \mu \right)\left[ \begin{array}{*{35}{l}} x \\ \eta \\ \end{array} \right]. \\ \end{array} \right.$ | (6) |
式中: x=[V h γ α Q]T为刚体运动的状态向量;η为乘波体纵向运动拟合模型中定义的弹性模态的状态向量;θ=θV,h为调整输出(即飞行速度V和飞行高度h)的函数;μ为与燃料消耗有关的慢变参数.由于模型(6)中的相关函数系数Aijθ,μ、Biθ,μ、Piθ,μ、Cμ具有较为繁琐的表达形式,这里不再赘述,可以参阅文献[25].
1.4 六自由度模型利用动力学基本原理,可以推导出吸气式高超声速飞行器的六自由度模型(6 degrees of freedom model,6-DOFM)如下:
| $^{e}\dot{p}={{R}_{\text{eb}}}\upsilon ,{{{\dot{R}}}_{\text{eb}}}={{R}_{\text{eb}}}S\left( \omega \right)$ | (7) |
| $\begin{align} & m\dot{\upsilon }+m\dot{\omega }\times {{r}_{g}}=-m\omega \times \left( \omega \times {{r}_{g}}+\upsilon \right)+ \\ & {{F}_{\text{grav}}}+{{F}_{\text{A,base}}}+{{F}_{\text{A, }\!\!\delta\!\!\text{ }}}+{{F}_{\text{T}}} \\ \end{align}$ | (8) |
| $\begin{align} & J\dot{\omega }+m{{r}_{g}}\times \dot{\upsilon }=-\omega \times J\omega -m{{r}_{g}}\times \omega \times \upsilon + \\ & {{M}_{\text{A,base}}}+{{M}_{\text{A, }\delta \text{ }}}+{{M}_{\text{T}}}, \\ \end{align}$ | (9) |
| $\dot{u}={{f}_{\text{act}}}\left( u,{{u}_{c}} \right).$ | (10) |
式中: ep为飞行器质心在地面固定坐标系下的分量(假设飞行器的质心与体坐标系原点重合);Reb∈SO(3)为体坐标系到地面固定坐标系的旋转矩阵;υ为飞行速度在体坐标系下的分量;ω为飞行器角速度在体坐标系下的分量;Fgrav为重力;FA,base、MA,base分别为基本的空气动力、力矩;FA,δ、MA,δ分别为气动舵面产生的控制(附加)力、力矩;FT、MT分别为推力以及推力产生的附加力矩,其他变量的定义详见文献[26].方程(10)用来描述控制指令uc到实际执行输出u的动态特性.
需要说明的是,模型(7)~(10)仅给出了高超声速飞行器六自由度运动模型的整体框架,相关的力/力矩表达式还需要进行复杂的近似拟合处理,所得到的拟合模型具有极其复杂的形式,因此,该六自由度模型常被用作控制算法的计算机仿真验证模型.通过进行必要的假设(如惯量矩阵J为对角阵)并且合理地忽略一些耦合(如忽略气动舵面产生的附加阻力),可以得到面向控制器设计的六自由度运动模型.例如,文献[26]进一步采用克里金法(kriging method)和最小二乘法(least square method)对于气动力/力矩进行拟合,拟合后的模型可用于制导律、控制器的设计.
本文概述了高超声速飞行器控制中常用的4种数学模型,实际的控制器设计不仅仅局限于这些模型,例如将要介绍的精确线性化模型以及T-S模糊模型.可以看出,锥形体、乘波体模型均为描述高超声速飞行器纵向运动的非线性模型,反映了高超声速飞行的本质属性,但其表达形式十分复杂.而线性变参数模型以及以下将要给出的反馈线性化模型、T-S模糊模型则是在上述两种非线性模型的基础上,采用一定的模型处理方法而得到的具有一定线性形式的高超声速飞行器模型,这类模型虽然易于控制器设计,但仍有一定的不足,例如: 反馈线性化模型完全抵消了原系统的非线性,T-S模糊模型的建立则需要具备充分的经验.六自由度模型仅仅给出了基本的运动学、动力学方程以及执行机构的非线性,具体的力、力矩还需要大量的理论分析及风洞试验进行确定.表 1对各个模型的特点及用途进行了简要的总结.值得指出的是,目前大部分对于吸气式高超声速飞行器控制的研究局限于纵向运动,并且忽略弹性模态(4),仅对刚体动力学(1)进行控制系统的设计.即便如此,所要考虑的数学模型仍是十分复杂的,往往需要结合多种线性、非线性控制理论来进行控制器的综合设计.
| 表 1 吸气式高超声速飞行器模型总结 Table 1 A summary on the models of air-breathing hypersonic vehicles |
一般来说,在实施高超声速飞行器控制器设计之前,首先需要对其复杂的数学模型进行预处理,然后利用适当的控制方法进行控制器的设计.本文以高超声速飞行器模型的处理手段为分类准则,阐述了3大类控制构型: 基于线性化模型的控制、基于非线性模型的反向递推控制以及基于T-S模糊模型的控制.进而可以利用以上3种构型并结合不同的控制方法进行控制器的设计,最后举例说明了两种被广泛应用的控制方法: 自适应控制与滑模变结构控制.
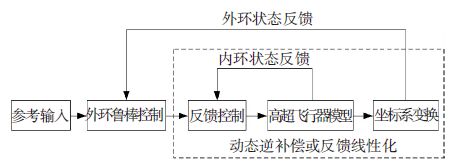
2.1 模型线性化控制模型线性化控制的基本思想为: 首先采用一定的手段,将吸气式高超声速飞行器的非线性模型进行线性化处理,然后利用适当的控制理论对于得到的线性模型进行控制器设计,最终的控制器由模型线性化部分和线性模型控制律组成,如图 3所示.虽然平衡点处小偏差线性化方法也可以应用于高超声速飞行器模型,但是对于大范围的机动来说,采用这种方法并不适用.
|
图 3 高超声速飞行器模型线性化控制的基本结构 Figure 3 Structure of the linearized model-based control for air-breathing hypersonic vehicles |
在高超声速飞行控制中,常用的线性化手段主要有动态逆补偿(dynamic inverse compensation,DIC)和反馈线性化(feedback linearization,FL).动态逆补偿的基本思想是设计一个逆系统来抵消系统中的非线性动态,进而得到相应的伪线性系统.反馈线性化则利用微分几何理论和Lie导数等工具,对于满足一定条件的系统模型通过反馈控制实现输入-输出解耦,在特定的坐标系下,原非线性模型可以转化为具有标准形式的线性模型.
例如,文献[23]首先对于乘波体纵向运动拟合模型进行如下假设:
1) 忽略模型中的弹性模态(4)以及其与刚体模型之间的耦合CTηη、CLηη、CDηη、CMηη;
2) 鸭翼的偏转抵消了升降舵偏角对于升力的影响,并且忽略升降舵产生的附加阻力,进而系统是最小相位的;
3) 通过增加执行机构动态:
然后利用坐标进行变换:
z=[V LfV Lf2V γ Lfγ Lf2γ]T,
以及反馈控制律:
| $\left[ \begin{array}{*{35}{l}} {{\Phi }_{c}} \\ {{\delta }_{e}} \\ \end{array} \right]={{\left[ \begin{matrix} {{L}_{{{\Phi }_{c}}}}L_{f}^{2}V & {{L}_{{{\delta }_{e}}}}L_{f}^{2}V \\ {{L}_{{{\Phi }_{c}}}}L_{f}^{2}\gamma & {{L}_{{{\delta }_{e}}}}L_{f}^{2}\gamma \\ \end{matrix} \right]}^{-1}}\left[ \begin{array}{*{35}{l}} {{u}_{V}}-L_{f}^{3}V \\ {{u}_{\gamma }}-L_{f}^{3}\gamma \\ \end{array} \right],$ |
实现了输入-输出的完全解耦: V(3)=uV,γ(3)=uγ,其中,符号LXiY表示相应的Lie导数运算,μV、μγ分别为新的控制输入.并且,原非线性模型在新坐标系下的表达式为线性能控能观标准型,即实现了模型的精确线性化.
动态逆补偿和反馈线性化都面临一个共同的问题[28]: 由于吸气式高超声速飞行器模型的非线性部分并不能精确已知,即存在建模的不确定性[29],因此,在模型线性化过程中必然会产生相应的逆误差或反馈误差.这就要求所设计的控制器在保证控制精度的同时,还需具备一定的鲁棒性来克服线性化误差.针对具有一定不确定性的吸气式高超声速飞行器模型,文献[30]采用鲁棒反馈线性化方法推导出一种面向控制的线性不确定性模型(control-oriented linearized uncertainty model,CLUM):
| $\left\{ \begin{array}{*{35}{l}} \dot{x}=Ax+Bv+\sum\limits_{j=1}^{2}{{{C}_{j}}{{\xi }_{j}}\left( t \right)}, \\ {{z}_{j}}={{K}_{j}}x+{{C}_{j}}v. \\ \end{array} \right.\left( j=1,2 \right)$ | (11) |
式中: χ为飞行状态向量(包括刚体、弹性体状态);v为新定义的控制输入向量;zj为不确定性输出;
模型线性化控制方法在吸气式高超声速飞行器控制领域已有较为广泛的应用.文献[21]利用动态逆补偿将高超声速飞行器模型进行线性化,针对建模存在的参数不确定性,利用随机鲁棒控制理论进行反馈控制律的设计;文献[30]基于鲁棒反馈线性化模型(11)设计了极大-极小线性二次型输出跟踪鲁棒控制器;文献[31]利用反馈线性化和线性二次型高斯调节器,实现了具有弹性模态和输入耦合的吸气式高超声速飞行器的跟踪控制;文献[32]首先对可能存在执行机构故障的吸气式高超声速飞行器模型进行反馈线性化,并得到其线性模型,然后利用滑模观测器设计自适应控制律来实现飞行速度、高度的精确跟踪,并具备一定的容错能力.
模型线性化控制方法的主要优势在于克服了高超声速飞行器模型的复杂性,同时,可以将成熟的线性控制理论引入到高超声速飞行器的控制问题当中.需要指出的是,基于模型线性化的控制方法主要存在两点不足: 1) 为了使吸气式高超声速飞行器模型满足精确线性化条件,需要适当地增加动态并忽略一些非线性特征及弱耦合项;2) 线性化过程抵消了一些有益的非线性,造成执行机构效能的浪费.可见,模型线性化方法虽然简化了控制器的设计,但实际的应用仍有诸多制约.因此,更为广泛、有效的方法是直接针对吸气式高超声速飞行器的非线性模型进行控制器的设计,例如将要介绍的反向递推法.
2.2 反向递推控制反向递推法(back-stepping)是一种应用广泛的基于Lyapunov函数的非线性综合设计方法.该方法首先将系统分为若干个串联的子系统,然后从包含输出的子系统到包含输入的子系统依次设计虚拟控制律,并最终得到执行机构的控制指令[33].由于反向递推法可以在每一步充分地考虑系统的非线性,并且设计过程自然地保持了系统的稳定性,因此,在吸气式高超声速飞行器控制领域应用较为广泛.
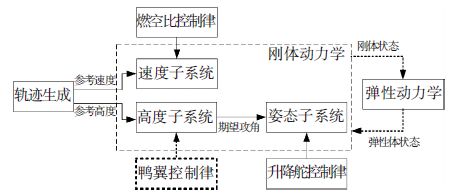
对于吸气式高超声速飞行器纵向运动的刚体动力学模型(1),本文可以将其拆分成3个子系统: 速度子系统 (第1个动态方程)、高度子系统 (第2和第3个动态方程)、姿态子系统 (第4和第5个动态方程),如图 4所示,然后依次对这3个子系统采用适当的非线性理论进行控制律的设计.反向递推法的标准设计步骤在许多文献及教材中均有详细的介绍,这里不再赘述.需要说明的是,虽然鸭翼的引入消除了系统的非最小相位特性、进而简化了控制器的设计难度,但是增加了飞行器机构的复杂性以及热防护系统的负担,因此,有些控制方法采用非线性理论来克服系统的非最小相位特性[34].另外,吸气式高超声速飞行器的弹性动力学(4)与刚体动力学(1)之间是相互耦合的,但目前的控制器设计很少考虑到机体的弹性模态,比较普遍的处理方法是将其对于刚体动力学的影响等价为满足特定条件的外界扰动.
|
图 4 高超声速飞行器反向递推法控制的基本结构 Figure 4 Structure of the back-stepping design for air-breathing hypersonic vehicles |
基于上述构型,很多非线性控制理论可以应用于子系统控制律的设计.针对吸气式高超声速飞行器模型中的弹性模态和参数不确定性,文献[24]采用反向递推和自适应控制理论进行鲁棒控制器的设计,并证明了可以通过选择适当的控制参数来实现输出的渐进跟踪以及对于弹性模态的抑制;文献[34]结合自适应控制理论、小增益参数和反向递推设计方法,仅利用燃空比和升降舵作为系统输入,实现了输出的跟踪控制,克服了吸气式高超声速飞行器的非最小相位特性;文献[35]针对非匹配不确定扰动采用反向递推与非线性扰动观测器相结合的方法,为吸气式高超声速飞行器设计了追踪控制器;文献[36]利用自适应动态面与反向递推的设计方法,克服了执行机构的约束和不确定性.实际上,反向递推法还可以与其他非线性理论相结合进行控制器设计,例如: 神经网络控制[37-38],但限于篇幅限制这里不再列举.
反向递推法设计的优势在于可以充分考虑高超声速飞行器模型的动态特性: 在抵消有害非线性的同时,将一些有利于系统稳定的非线性加以利用,进而减少了所设计的高超声速飞行控制器的保守性.但反向递推法相对于其他方法而言,其设计过程略显繁琐.尤其当设计的步数较多时,对于虚拟控制的高阶求导会生成大量的分析计算,所得到的控制律形式也极为复杂[33].这个问题可以通过利用指令滤波器[39]或者其他形式的微分器加以解决[40].
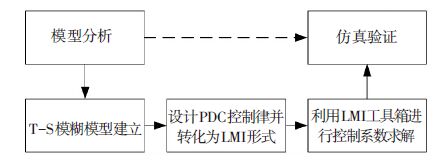
2.3 T-S模糊控制除了动态逆补偿和反馈线性化,设计者还可以采用一些智能控制理论来充分逼近模型的动态特性,从而避免了繁杂的非线性分析,例如神经网络控制、模糊控制等.这里着重阐述一种比较成熟的智能控制方法: T-S模糊控制(Takagi-Sugeno fuzzy control,T-S FC).T-S模糊控制的基本思想是: 首先通过一定的模糊规则将吸气式高超声速飞行器的非线性模型近似为一系列线性子系统的加权形式,即T-S模糊建模,然后利用并行分布补偿(parallel-distributed compensation,PDC)原理设计并得到最终的控制律.采用T-S模糊控制的非线性系统的稳定性可以利用线性矩阵不等式(linear matrix inequality,LMI)等工具加以证明,如图 5所示.以文献[41]为例,说明吸气式高超声速飞行器T-S模糊建模的方法.
|
图 5 高超声速飞行器T-S模糊控制器的设计步骤 Figure 5 Design steps of the T-S fuzzy controller for air-breathing hypersonic vehicles |
首先,注意到速度V和攻角α对于乘波体纵向运动拟合模型有重要影响,本文将V和α作为两个前提变量,并定义模糊子集: S={Small,Middle,Big}和模糊隶属函数(以V为例):
If V≥VM,
| $\text{then}\left\{ \begin{array}{*{35}{l}} {{h}_{S}}\left( V \right)=0, \\ {{h}_{M}}\left( V \right)=1-{{h}_{B}}(V), \\ {{h}_{B}}\left( V \right)=\text{exp}\{-3.5\times {{10}^{-12}}|V\left( t \right)-{{V}_{B}}{{|}^{4}}\}, \\ \end{array} \right.$ |
If V<VM,
| $\text{then}\left\{ \begin{array}{*{35}{l}} {{h}_{\text{S}}}\left( V \right)=\text{exp}\{-3.5\times {{10}^{-12}}|V\left( t \right)-{{V}_{S}}{{|}^{4}}\}, \\ {{h}_{\text{M}}}\left( V \right)=1-{{h}_{B}}(V), \\ {{h}_{\text{B}}}\left( V \right)=0. \\ \end{array} \right.$ |
式中: VS、VB、VM分别为速度在可行域的下界(Small)、上界(Big)和一个平衡点(Middle);攻角的隶属度函数也有类似的形式.
然后,得到如下9(32)条模糊规则:
Rule (i): If V is Small (or Middle or Big), α is Small (or Middle or Big),then:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}={{A}_{i}}x+{{B}_{i}}u, \\ y=Cx. \\ \end{array} \right.$ |
式中: i=1,2,…,9;x、u分别为系统状态向量、输入向量;Ai、Bi分别可以通过特定的算法得到;C为输出矩阵.从而吸气式高超声速飞行器T-S模糊模型具有如下形式:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}={{A}_{h}}x+{{B}_{h}}u, \\ y=Cx. \\ \end{array} \right.$ | (12) |
式中:
在得到T-S模糊模型(12)之后,本文可以采用并行分布补偿的方法进行控制器设计,并应用线性矩阵不等式工具求解使闭环系统满足稳定性条件以及特定性能指标的控制参数,限于篇幅这里不再赘述.利用上述T-S模糊控制方法,文献[41]为吸气式高超声速飞行器设计了保性能控制器,即: 在实现输出跟踪的同时,还满足了一定的性能指标,最终控制器参数满足的条件以线性矩阵不等式的形式给出,可以利用标准的数学软件(如Matlab的LMI工具箱)进行求解;文献[42]考虑了执行机构和传感器出现故障的情形,采用T-S模糊控制方法设计了容错控制器;文献[43]将滑模变结构控制理论与T-S模糊建模相结合,进一步考虑了执行机构的饱和、死区等非线性特性;文献[44]利用T-S模糊控制实现了吸气式高超声速飞行器的动态输出反馈控制.
基于T-S模糊模型的控制器设计的优势在于可以利用简单的线性形式去逼近高超声速飞行器复杂的飞行动态,甚至可以考虑机身的弹性动力学(需要说明的是,精确线性化方法目前还难以考虑高超声速飞行器的弹性模态),同时也有较为成熟的理论去证明闭环系统的稳定性.T-S模糊建模虽然简化了控制器的设计过程,但也存在不足: 1)随着模糊规则的增加,系统的设计过程会变得更加复杂;2)隶属函数的选取需要一定的经验;3)T-S模糊控制方法通常只能给出满足稳定性和性能指标的控制器参数的充分条件.
2.4 自适应控制和滑模变结构控制以上总结了3种高超声速飞行器常用的控制构型: 模型线性化、反向递推以及T-S模糊控制.基于此,许多控制理论可以与之相结合进行控制器的设计.这里主要介绍两种广泛应用的控制方法: 自适应控制和滑模变结构控制.
2.4.1 自适应控制由于吸气式高超声速飞行器的模型参数存在严重的不确定性,因此,自适应理论在飞行控制中有着较为广泛的应用,主要体现在两个方面: 1) 不确定参数的辨识. 2) 自适应跟踪控制.参数辨识是高超声速飞行器研究领域的一个重要课题,例如: X-43A在飞行试验的最后阶段进行了一系列的机动飞行,进而成功地辨识出特定的未知参数,为进一步分析高超声速飞行的动态特性以及设计高性能的控制器获取了必要的条件.但参数辨识问题不是本文研究的重点,因此,以下主要对于自适应跟踪控制问题进行阐述.
由于自适应控制对系统不确定性(尤其是参数不确定性)具有强大的处理能力,因此,在吸气式高超声速飞行器跟踪控制中已有着广泛的应用,例如文献[24, 27, 34, 45-46].以反向递推方法中的速度子系统(如图 4所示)为例,简要说明自适应控制的设计过程.
考虑速度动态方程(1) 以及推力T、阻力D的拟合方程(5),并假设:
1) 推力和阻力表达式中的拟合系数为未知的常值;
2) 气动舵(鸭翼、副翼)和弹性模态对于动力学方程(1)的影响可以等价为一个具有上界的未知扰|d(t)|≤D,D>0为未知的上界;
3) 执行机构(燃空比)部分失效: Φ=κΦc,其中,Φc为控制指令,0<κ≤κ≤1为未知的失效系数.
首先将跟踪误差${\tilde{V}}$=V-Vr的动态方程改写成如下线性参数化形式:
| $\dot{\tilde{V}}=\psi _{1}^{\text{T}}{{\theta }_{1}}{{\Phi }_{c}}+\psi _{2}^{\text{T}}{{\theta }_{2}}-g\sin \gamma -{{{\dot{V}}}_{r}}+d\left( t \right),$ | (13) |
其中Vr为速度参考轨迹,并且
| $\left\{ \begin{array}{*{35}{l}} {{\theta }_{1}}={{\left[ \kappa C_{T,\Phi }^{3}\text{ }\kappa C_{T,\Phi }^{2}\text{ }\kappa C_{T,\Phi }^{1}\text{ }\kappa C_{T,\Phi }^{0} \right]}^{\text{T}}}, \\ {{\Psi }_{1}}=\left( \bar{q}S\cos \text{ }\alpha /m \right)\times {{\left[ {{\alpha }^{3}}\text{ }{{\alpha }^{2}}\text{ }\alpha \text{ }1 \right]}^{\text{T}}}, \\ {{\theta }_{2}}={{\left[ C_{T}^{3}\text{ }C_{T}^{2}\text{ }C_{T}^{1}\text{ }C_{T}^{0}\text{ }C_{D}^{{{\alpha }^{2}}}\text{ }C_{D}^{{{\alpha }^{1}}}\text{ }C_{D}^{0} \right]}^{\text{T}}}, \\ {{\Psi }_{2}}=\left( \bar{q}S/m \right)\times {{\left[ {{\alpha }^{3}}\cos \alpha \text{ }{{\alpha }^{2}}\cos \alpha \text{ }\alpha \cos \alpha \text{ }\cos \alpha \text{ }{{\alpha }^{2}}\text{ }\alpha \text{ }1 \right]}^{\text{T}}}, \\ \end{array} \right.$ |
对于线性参数化方程(13),可以设计控制律:
| ${{\Phi }_{c}}=\frac{1}{\Psi _{1}^{\text{T}}{{{\hat{\theta }}}_{1}}}\left[ -{{k}_{V}}\tilde{V}-\Psi _{2}^{\text{T}}{{{\hat{\theta }}}_{2}}+g\sin \gamma +{{{\dot{V}}}_{r}}-\hat{D}\ sgn \left( {\tilde{V}} \right) \right],$ |
和自适应律:
| $\left\{ \begin{array}{*{35}{l}} \dot{\hat{\theta }}=\text{proj}\left( {{\Gamma }_{1}}{{\Psi }_{1}}{{\Phi }_{c}}\tilde{V} \right), \\ \dot{\hat{\theta }}=\text{proj}\left( {{\Gamma }_{2}}{{\Psi }_{2}}\tilde{V} \right), \\ \dot{\hat{D}}={{\sigma }_{D}}\left| {\tilde{V}} \right|. \\ \end{array} \right.$ |
式中: sgn(·)为符号函数;proj(·)为投影函数;kV>0,Γ1>0,Γ2>0,σD>0.选取Lyapunov函数:
| $W=\frac{1}{2}\left( {{{\tilde{V}}}^{2}}+{{\left\| {{{\tilde{\theta }}}_{1}} \right\|}_{\Gamma _{1}^{-1}}}+{{\left\| {{{\tilde{\theta }}}_{2}} \right\|}_{\Gamma _{2}^{-1}}}+\sigma _{D}^{-1}{{{\tilde{D}}}^{2}} \right),$ |
并对W求取一阶导数,容易得到
由上述例子可以看出,自适应控制的优势在于可以很好地处理高超声速飞行器的参数不确定性,这也是高超声速飞行控制中所面临的重要的问题之一,另外,由于自适应控制方法具有强大的在线估计能力,其也可用于高超声速飞行器的参数辨识、故障检测与处理等问题,是目前应用最为广泛的高超声速飞行控制手段.但需要说明的是: 1) 自适应跟踪控制器中的估计参数一般并不收敛到其真实值,这是由于输入信号的“持续激励”条件[47]在实际的跟踪控制问题中是无法满足的(例如,一般会设定比较平缓的参考轨迹Vr,以避免剧烈的机动飞行);2) 除了参数不确定性,还需进一步考虑其他的约束条件,例如: 燃空比的上、下限、气动舵的最大偏转角、终端约束、高超声速飞行走廊(hypersonic corridor)等.
2.4.2 滑模变结构控制由于滑模变结构控制对于系统的不确定性、外界扰动具有较强的鲁棒性,因此在理论和工程中都有着较为广泛的应用,例如,滑模观测器、滑模微分器、机器人控制、航天器姿态控制等.同样,滑模变结构理论也可应用于吸气式高超声速飞行器的控制问题.滑模控制器的设计主要分为两步[48]: 1) 设计滑模面函数s(t),使得被控系统在滑模面s(t)=0上的运动满足预期的性能指标(收敛率,稳态误差等). 2) 设计趋近律u(t),使原系统的状态可以在有限时间内到达滑动面.滑模变结构控制已在吸气式高超声速飞行器控制领域有着广泛的应用,例如文献[49-54].
一般来说,直接针对高超声速飞行器复杂的非线性模型进行滑模面、趋近律的设计是非常困难的,因此需要对于非线性模型进行预处理.例如,针对具有特定不确定性及外界扰动的吸气式高超声速飞行器模型,利用模型线性化控制中的假设并对跟踪输出(即速度V和高度h)反复地进行求导运算,可以得到如下形式的表达式:
| $\left[ \begin{array}{*{35}{l}} {{V}^{\left( 3 \right)}} \\ {{h}^{\left( 4 \right)}} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} {{f}_{V}} \\ {{f}_{h}} \\ \end{array} \right]+\left[ \begin{array}{*{35}{l}} {{g}_{V}} \\ {{g}_{h}} \\ \end{array} \right]u+\left[ \begin{matrix} \Delta V \\ \Delta h \\ \end{matrix} \right]\text{ }.$ | (14) |
式中: fV、fh、gV、gh分别为确定的函数,控制矩阵G=[gVT ghT]T是可逆的;ΔV、Δh分别为满足一定条件的集中扰动项.针对模型(14),可以采用标准的滑模变结构设计方法来实现输出的跟踪控制,这里不再赘述.然而,模型可线性化的假设是十分苛刻的,实际的应用必然存在局限性.因此,以下着重介绍一种基于T-S模糊建模的滑模变结构控制器设计方法.
首先,对于具有参数不确定性和扰动项的吸气式高超声速飞行器模型进行T-S模糊建模.利用与T-S模糊控制相同的模糊集合与隶属度函数,定义如下9(32)条模糊规则:
Rule (i): If V is Small (or Middle or Big),α is Small (or Middle or Big),then:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}=\left( {{A}_{i}}+\Delta {{A}_{i}} \right)x+{{B}_{i}}u+{{D}_{i}}\omega \left( t \right), \\ y=Cx. \\ \end{array} \right.$ |
式中:i=1,2,…,9;x、u分别为系统状态向量、输入向量;Ai、ΔAi、Bi、Di分别可以通过特定的算法得到;ΔAi为状态矩阵Ai的参数不确定性;C为输出矩阵;ω(t)为不确定的外界扰动以及未建模的非线性.进而得到T-S模糊模型:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}=\left( {{A}_{h}}+\Delta {{A}_{h}} \right)x+{{B}_{h}}u+{{D}_{h}}\omega \left( t \right), \\ y=Cx. \\ \end{array} \right.$ |
式中:
然后,对应每个模糊规则定义如下参考模型:
Rule (i): If V is Small (or Middle or Big),α is Small (or Middle or Big),then:
| ${{{\dot{x}}}_{m}}={{A}_{mi}}{{x}_{m}}+{{B}_{mi}}r\left( t \right).$ |
式中: xm为参考模型状态;r(t)为已知的参考输入;Ami是Hurwitz的.进一步,定义跟踪误差e=x-xm,并设计如下形式的积分型滑模面函数:
Rule (i): If V is Small (or Middle or Big),α is Small (or Middle or Big),then:
| ${{s}_{i}}\left( t \right)={{G}_{i}}\left\{ \left[ e\left( t \right)-e\left( {{t}_{0}} \right) \right]-\int_{{{t}_{0}}}^{t}{\left[ {{A}_{mi}}e\left( \tau \right)+{{B}_{i}}{{K}_{i}}e\left( \tau \right) \right]\text{d}\tau } \right\}.$ |
式中: Gi∈R2×7,Ki∈R2×7为需要设计的常值矩阵.因此,整个系统的滑模面函数可以表示为
| $s\left( t \right)=\sum\limits_{i=1}^{9}{{{h}_{i}}{{s}_{i}}\left( t \right),}$ |
可以证明,通过设计参数Gi与Ki,当被控系统在滑模面s(t)=0上运动时,相应的跟踪误差e(t)满足特定的H∞性能指标.
最后,设计者需要设计适当的控制律,以驱动系统的状态在有限时间内到达滑模面s(t)=0.文献[43]给出了一种自适应控制律,由于篇幅限制这里不再赘述.
以上给出了基于T-S模糊建模的滑模变结构控制器的设计方法.滑模变结构控制方法的优势在于对高超声速飞行过程中的强扰动、强不确定性具有优异的鲁棒性,并且通过滑模面的设计可以保证一定的飞行性能指标,这是一般的控制方法所不具备的优势.需要指出的是: 1) 滑模面s(t)=0的性质很大程度上决定了闭环系统的控制效果,本文可以通过设计特殊的滑模面来提高系统的性能,例如,通过构造终端滑模面(terminal sliding mode surface,TSMS)可以实现输出的有限时间跟踪控制;2) 滑模变结构控制中的趋近控制律往往是不连续(由符号函数引起),产生所谓的“抖振”现象,另外,终端滑模变结构控制还会产生奇异现象,这些在控制器的设计环节都是需要进一步考虑并克服的.
本文主要阐述了吸气式高超声速飞行器3种常见的控制构型: 基于模型线性化的设计方法、反向递推设计方法、T-S模糊控制方法,并举例说明自适应控制、滑模变结构控制在高超声速飞行控制领域的应用.总的来说,模型线性化方法虽然简化了控制器设计,却忽略了吸气式高超声速飞行器的一些重要非线性(如非最小相位特性),限制了其在实际工程中的应用;反向递推法和T-S模糊控制方法虽然设计步骤略显繁琐,但具有强大的非线性处理能力和良好的控制性能,因此也是目前比较主流的设计方法;自适应控制可以有效地处理飞行器建模产生的不确定性,在实际的飞行试验中(如X-43A,HIFiRE项目等)已有应用;而滑模变结构控制具有较强的鲁棒性和适应性,并且可以达到优异的控制性能(如有限时间收敛),其应用前景十分广阔.当然,吸气式高超声速飞行器的控制方法远不止这些,例如,神经网络控制(neural networks control,NNC),轨迹线性化控制(trajectory linearization control,TLC),线性变参数控制(linear parameter varying control,LPVC)等.无论采用何种方法进行控制器的设计,都需要充分考虑实际系统自身的特点,因此,以下将进一步讨论吸气式高超声速飞行器控制中需要解决的实际问题.
3 吸气式高超声速飞行器控制面临的问题 3.1 执行机构的非线性针对吸气式高超声速飞行器气动舵面的饱和、死区等非线性的控制器设计已经获得较多的关注,例如: 文献[36-37, 39, 43, 55-56].实际的执行机构还可能存在一些更为复杂的动态非线性特性,这里着重介绍两种常见的、但未在高超声速飞行控制中充分考虑的非线性特性: 齿隙非线性和延迟特性.
气动舵面的机械连接以及伺服机构的电气特性会产生齿隙非线性(backlash nonlinearity).齿隙非线性的数学描述为[57]
| ${{\dot{u}}_{0}}\left( t \right)=\left\{ \begin{array}{*{35}{l}} {{{\dot{u}}}_{1}}\left( t \right), & \text{if }{{{\dot{u}}}_{1}}\left( t \right)\text{0}\wedge {{u}_{0}}\left( t \right)\text{=}{{\text{K}}_{\text{B}}}{{u}_{1}}\left( t \right)-{{\text{B}}_{\text{r}}}\text{, } \\ {} & \text{if }{{{\dot{u}}}_{1}}\left( t \right)\text{0}\wedge {{u}_{0}}\left( t \right)\text{=}{{\text{K}}_{\text{B}}}{{u}_{1}}\left( t \right)-{{\text{B}}_{\text{1}}}\text{, } \\ 0, & \text{otherwise}\text{.} \\ \end{array} \right.$ | (15) |
式中:uI、uO分别为齿隙非线性的输入和输出;KB>0,Br>0,Bl>0为未知常数.由表达式(15)可以看出: 齿隙特性是控制输入及其导数的函数,因此,对这类非线性执行机构进行理论分析以及控制器设计会更为复杂.
齿隙非线性特性(15)可以写成如下线性形式:
| ${{u}_{0}}={{\text{K}}_{\text{B}}}{{u}_{1}}+{{d}_{\text{B}}}\left( t \right),$ |
式中dB(t)为残差项.一般情况下的齿隙效应均无法进行准确测量,因此执行机构失效系数KB与残差dB(t)通常是未知的,进一步可以证明dB(t)具有常值上界.对于以上形式的处理方法,可以结合自适应控制进行处理,具体过程可参考文献[58].
另外一种更为有效的方法是利用逆补偿的思想建立如下齿隙逆补函数(inverse backlash function):
| ${{u}_{1}}=BI\left( {{u}_{0}} \right)=\frac{1}{{{K}_{\text{B}}}}{{u}_{0}}+{{B}_{r}}{{x}_{r}}\left( {{{\dot{u}}}_{0}} \right)+{{B}_{1}}{{x}_{1}}\left( {{{\dot{u}}}_{0}} \right),$ |
其中:
| ${{x}_{r}}\left( {{{\dot{u}}}_{0}} \right)=\frac{{{e}^{k{{{\dot{u}}}_{0}}}}}{{{e}^{k{{{\dot{u}}}_{0}}}}+{{e}^{-k{{{\dot{u}}}_{0}}}}},{{x}_{1}}\left( {{{\dot{u}}}_{0}} \right)=\frac{{{e}^{-k{{{\dot{u}}}_{0}}}}}{{{e}^{k{{{\dot{u}}}_{0}}}}+{{e}^{-k{{{\dot{u}}}_{0}}}}}.$ |
考虑到在实际系统中,参数KB、Br以及Bl是难以进行准确测量的,因此实际的逆输入uI可以设计为
| ${{u}_{1}}=\widehat{BI}\left( {{u}^{'}}_{0} \right)=\frac{1}{{{{\hat{K}}}_{\text{B}}}}\left[ {{u}^{'}}_{0}+\widehat{{{K}_{\text{B}}}{{B}_{\text{r}}}}{{x}_{r}}\left( {{{\dot{u}}}^{'}}_{0} \right)+\widehat{{{K}_{\text{B}}}{{B}_{\text{1}}}}{{x}_{1}}\left( {{{\dot{u}}}^{'}}_{0} \right) \right],$ |
其中: 上标“^”代表对应的估计值,uO′为实际的控制输入,即
| ${{u}^{'}}_{0}={{{\hat{K}}}_{\text{B}}}{{u}_{1}}-\widehat{{{K}_{\text{B}}}{{B}_{\text{r}}}}{{x}_{r}}\left( {{{\dot{u}}}^{'}}_{0} \right)-\widehat{{{K}_{\text{B}}}{{B}_{\text{1}}}}{{x}_{1}}\left( {{{\dot{u}}}^{'}}_{0} \right),$ |
可以证明,理想控制输入uO与实际控制输入uO′之间的差异Δu=uO-uO′是有界的[57].同样,齿隙逆补偿方法可以与自适应控制相结合,设计控制律和自适应律实现输出的跟踪控制.
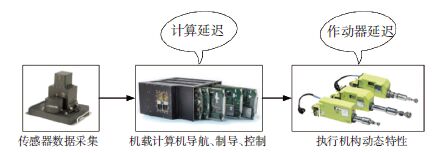
另一种需要考虑的非线性是执行机构的延迟特性,此处仅作简要的说明.由于机载计算机有限的处理速度和执行机构的动态特性,从采集导航数据、机载计算机计算并发出控制指令到作动器实际的控制效果,必然会有一定的延迟,如图 6所示.虽然这些延迟在普通低速飞行器的控制器设计中是可以忽略不计的,但是对于至少以5 Ma巡航的高超声速飞行器来说,0.1 s的执行机构延迟就可能产生近200 m的位置测量误差,这对于高性能的飞行控制是不被允许的.
|
图 6 高超声速飞行控制中的延迟特性 Figure 6 Delays in the hypersonic flight control |
另外,由于延迟特性会引起的控制指令与实际控制输出之间传递函数的相位移动,进而导致控制指令的失效.例如,由于燃料泵的延迟特性,超燃冲压发动机的燃流量指令Φc与实际燃流量Φ之间的传递函数可以表示为
| $\frac{\Phi \left( s \right)}{{{\Phi }_{c}}\left( s \right)}=\frac{{{\omega }^{2}}{{e}^{-\tau s}}}{{{s}^{2}}+2\xi \omega s+{{\omega }^{2}}}.$ |
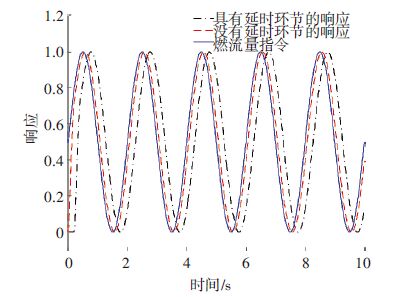
式中: ξ=0.7,ω=20 rad/s,延迟特性常数假设为τ=0.2 s.如果利用上述环节来响应正弦燃流量指令: Φc=0.5 sin(πt)+0.5,其输出结果如图 7所示.可以看出,具有延迟特性的环节,实际的燃流量与燃流量指令有着较大的误差,并且这一误差将会随着燃流量指令频率的增加而进一步增大.为了克服延迟效应,可以利用时滞系统控制理论进行高超声速飞行器控制器的设计,另外,所设计的控制律形式要尽量精简,以减少机载计算机在处理数据的耗时.例如,文献[59]已经证明: 采用文献[33]中经典的自适应反向递推设计方法可以实现一类带有输入时滞特性的线性系统的输出跟踪,且不受最小相位条件的约束,因此,针对于吸气式高超声速飞行器执行机构的延迟问题,可以利用其线性化模型设计飞行控制器.
|
图 7 延迟特性对于燃流量指令响应的影响 Figure 7 Effects of delay on the response of fuel equivalency ratio command |
控制系统的故障可分为3种情形: 执行机构故障、传感器故障以及组件故障[60].吸气式高超声速飞行器的气动舵面工作在高温、高动压的恶劣环境下,很可能出现执行机构部分失效甚至全部失效的情形,因此,所设计的控制器还需要具备一定的容错控制能力[61].一般来说,容错控制主要分为两类: 1)利用设计控制器的鲁棒性来克服执行机构失效;2)通过引入故障的检测机制来确定故障发生的位置和程度,进而采用一定的处理机制进行克服.
对于吸气式高超声速飞行器容错控制的研究主要集中于第1类,即: 通过设计具有强鲁棒性或者自适应能力的控制器来保证在执行机构、传感器等出现故障时仍能达到一定的性能指标.例如: 文献[62]利用动态面反步法对于一类带有舵面冗余的高超声速飞行器设计了容错控制器,实现了在部分舵面卡死情况下的指令跟踪控制;文献[63]利用扰动观测器增强型的反步法为高超声速飞行器设计了跟踪控制器,并通过引入指令滤波器和辅助系统实现了飞行控制系统对于执行机构幅值、速度约束的鲁棒性;文献[64]通过在标准的动态逆控制器中引入故障观测器,使得飞行控制系统能够适应一类突变的故障,而对于其他类型的故障,则利用支持向量机进行在线补偿;文献[42]利用T-S模糊控制的方法考虑了执行机构部分失效的情形,并保证了闭环系统的渐近稳定性;文献[65-66]设计了自适应容错控制器,使得在执行机构部分失效的情况下仍能实现有限时间的输出跟踪;文献[67]利用反馈线性化模型设计了自适应控制器,在升降舵卡死的情况下保证系统的稳定性,并利用高增益观测器实现了输出反馈控制;文献[68]利用神经网络估计执行机构故障对系统产生的影响,进而利用带有指令预处理机制的反向递推法设计了控制器;对于传感器出现故障也有相关的研究[42, 69],其中,文献[42]基于T-S模糊模型考虑了如下传感器故障:
| ${{\zeta }^{'}}\left( t \right)={{F}_{\text{s}}}\zeta \left( t \right).$ |
式中: ζ(t)为可测量的真实值;ζ(t)′为测量值;Fs=diag{fsi}为传感器测量矩阵并满足:
| ${{f}_{\text{sil}}}\le {{f}_{\text{si}}}\le {{f}_{\text{sih}}}<\infty ,$ |
式中fsih、fsil分别为测量值的上界和下界.显然,如果fsil=fsih=0,则代表测量信号完全丢失;如果fsil=fsih=1,则代表传感器没有故障.基于此,文献[42]利用并行分布补偿原理及线性矩阵不等式工具设计了模糊线性反馈控制器,并实现了输出的跟踪.此外,还有许多相关的研究成果限于篇幅无法详细列举说明.
3.3 多目标控制大多数已有控制器设计的目标为: 实现高超声速飞行器输出(速度、高度)的渐进跟踪以及系统状态的收敛或有界.近期,一些研究成果利用终端滑模变结构控制技术(terminal sliding mode control,TSMC)实现了有限时间精确跟踪,即: 跟踪误差可以在特定有限的时间内收敛到零,并保持对于外界扰动的鲁棒性.然而,仅仅实现对于输出的跟踪是远远不够的,还需要针对于多个性能指标进行控制系统的综合设计.
对于吸气式高超声速飞行器的控制系统,设计者还需要进一步考虑系统的动态性能指标.恶劣的动态性能将严重危害吸气式高超声速飞行器的正常工作,例如: 剧烈的超调或震荡很容易激发机身的弹性模态;对于未来可能的载人高超声速飞行器,还需进一步考虑飞行过程中的舒适度、最大过载等性能指标.近几年,已有相关的控制理论和方法在控制器的设计中考虑系统动态性能的指标.例如,文献[70-71] 通过引入性能函数(performance function) ρ(t)以及误差变换e(t)=ρ(t)s(ε),首先将常规的控制误差et转化为新的误差变量ε(t),然后通过控制ε(t)的有界来保证e(t)满足预定的最小收敛率及最大超调量,从而使控制系统满足预定的动态性能指标.
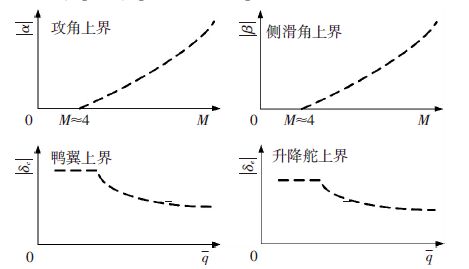
另外,对于吸气式高超声速飞行器来说,某些约束必须严格地进行限制,这主要体现在超燃冲压发动机的工作条件.一般来说,为了满足发动机的进气条件,飞行攻角α和侧滑角β的上界近似与飞行马赫数有以下关系[72] (如图 8所示):
| $\begin{align} & \left| \alpha \right|\le {{K}_{\alpha }}{{M}_{\infty }}+{{B}_{\alpha }},{{M}_{\infty }}\ge 4, \\ & \left| \beta \right|\le {{K}_{\alpha }}{{M}_{\infty }}+{{B}_{\alpha }},{{M}_{\infty }}\ge 4. \\ \end{align}$ |
|
图 8 攻角、侧滑角以及气动舵偏转角的约束 Figure 8 Constraints on angle of attack,angle of sideslip and deflection angles of aerodynamic control surfaces |
式中:Kα>0,Bα>0,Kβ>0,Bβ>0为特定常数,并且4Kα+Bα≈0,4Kβ+Bβ≈0.由此可见,随着马赫数的不断降低,攻角和侧滑角的约束越来越严格(尤其在M∞=4附近),这对于吸气式高超声速飞行器的减速机动控制具有极大的挑战性.与此同时,由于高超声速飞行会产生严重的气动热,因此对于飞行器本身的热防护措施是及其苛刻的.从另一角度来说,如果设计的控制器能够充分地考虑相关方面的约束,如合理的热流量、动压变化范围等,则会在很大程度上减轻热防护系统的设计压力,这就需要在飞行过程中严格地限制气动舵的偏转角为
| $\left| {{\delta }_{c}} \right|\le {{{\bar{\delta }}}_{c}}\left( {\bar{q}} \right),\left| {{\delta }_{e}} \right|\le {{{\bar{\delta }}}_{e}}\left( {\bar{q}} \right),$ |
式中δc(q)、δe(q)是与动压q有关的函数.
根据上述讨论,可以将吸气式高超声速飞行器的控制指标分为两类: 1) 软指标(soft objective),其中包括系统的跟踪特性(例如: 跟踪误差、趋近速度、调整时间)、 飞行舒适度、 过载等;2) 硬指标(hard objective),其中包括执行机构的限制、飞行姿态的约束(例如: 最大攻角及侧滑角)等.在实际的控制系统中,各个控制指标往往无法同时满足.例如: 对于攻角α的约束会制约航迹角γ,使其无法跟踪控制指令γc,进而产生较大的高度跟踪误差.在两个或多个指标发生冲突的情况下,可以将控制系统的设计目标转化为带有约束条件的最优控制问题: 设计控制律u,在满足硬指标的前提下,使得特定的综合性能指标函数J(x,u)达到极值,即
u=argminJ(x,u),s.t.(x,u)∈Ωhard,
其中Ωhard为硬指标确定的可行域. 一般来说,对于该类问题的求解是十分困难的.近期,文献[73]通过引入控制Barrier函数(control barrier function,CBF)的概念,利用二次规划解决了一类多目标控制问题.但是在吸气式高超声速飞行器控制领域还没有相关方面的研究,是一个具有实际意义的研究方向.
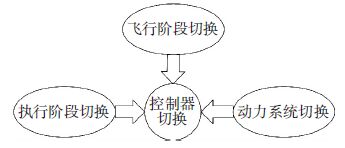
3.4 切换控制吸气式高超声速飞行器还涉及相关的模式切换,主要包括: 飞行模式的切换、动力系统的切换以及执行机构的切换,如图 9所示.目前对于吸气式高超声速飞行器控制的研究主要集中在巡航段,但实际的飞行任务或者机动过程必然要经历上升段和下降段.由于飞行器在各个飞行阶段的动态特性是不尽相同的,仅依靠单一的控制律很难统一地实现每个飞行段的控制指标,因此,往往需要设计不同的控制器参数、结构来适应不同的飞行阶段.另一方面,超燃冲压发动机在低马赫数(一般M∞<4)是难以启动的,一般需要与其他动力装置进行组合以实现全包线的飞行.例如: X-43A的飞行实验就采用飞马座火箭将其助推到特定的速度、高度,进而点燃超燃冲压发动机以维持高超声速飞行,对于X-43A与助推器分离的稳定性问题,NASA的研究人员[74]做了大量的分析和验证.另外,在某些大机动飞行过程中,需要执行机构提供充足的控制力、力矩.但由于气动舵(主要考虑升降舵)需要克服推力产生的抬头力矩,并且过大的舵偏角在高超声速飞行中会产生严重气动热和附加阻力,因此其控制裕度是十分有限的.基于上述原因,吸气式高超声速飞行器通常采用气动舵面与反作用力控制系统(reaction control system,RCS)组合的方式来提供足够的机动能力,即: 执行机构可能发生切换.
|
图 9 高超声速飞行中的控制器切换问题 Figure 9 Switching control problem in the hypersonic flight |
由此可见,对于大机动、大飞行包线的高超声速飞行来说,单一的控制参数、控制结构往往难以满足预定的控制指标.因此,需要针对不同的情形设计切换控制系统,并能够对于闭环系统的稳定性及性能进行充分地分析,而这也是目前吸气式高超声速飞行器控制的一个重要的研究方向.采用近似线性化的方法,设计者可以将具有参数或结构变化的吸气式高超声速飞行器控制问题表述成一类多模型切换控制问题:
| $\left\{ \begin{array}{*{35}{l}} \dot{x}=A\left( \lambda \right)x+B\left( \lambda \right)u, \\ y=Cx. \\ \end{array} \right.$ |
式中:u=[Φ δACS δRCS]T;δACS为气动舵输入;δRCS为反作用力控制输入; {A(λ),B(λ)|λ=1,2,…,N}为切换系统矩阵的集合,λ=λ(x)为系统的切换信号,λ=i表示系统(A(i),B(i),C)被激活.对于上述多模型切换控制问题已有较为成熟的理论[75-76],但是切换时刻的控制指令往往具有较大的幅值,甚至超出了实际作动器的执行能力,这就需要在控制器的设计中进一步考虑平滑切换问题(可以结合最优控制、模糊控制等理论).此外,如何推导出标准的切换模型、并使其能够充分地逼近真实的飞行动态,进而设计高性能的控制器,仍是今后研究的一个努力方向.
3.5 制导与控制的一体化设计众所周知,飞行器的制导与控制是紧密相连的.由于飞行系统的复杂性,制导子系统与控制子系统的设计往往是分开进行的.虽然这种模块化设计思想在工程实际中证明是有效的,但并不是最优的设计方案: 1) 为了简化设计过程,控制(制导)模块的设计忽略了其与制导(控制)模块之间的弱耦合,因此,整合后的制导/控制系统往往会出现不匹配的情形,需要进行大量繁琐的验证、修正工作;2) 制导/控制系统的模块化设计往往具有一定的保守性,并且在理论上难以保证闭环系统的稳定性.这就促使设计者进行制导/控制系统的一体化设计,即: 在整体上把握制导、控制之间的耦合、约束,同时完成制导律与控制律的全部设计指标.
虽然制导/控制一体化的设计思想在20世纪80年代就已出现[77],但由于各个通道之间的严重耦合(如飞行器的纵向运动与横向运动),目前大部分的研究成果仅仅局限于单通道的制导/控制一体化设计.许多控制方法已成功应用到一体化设计,例如: 最优控制方法[77]、反向递推控制方法[78]、滑模变结构控制方法[79]、H∞控制方法[80]等.但这些研究成果对于以快速机动为目标的高超声速飞行器来说是远远不够的.由于高超声速飞行器需要大幅度的横向机动,各个通道之间往往具有严重的耦合.在这种情况下,单通道一体化设计方法难以保证整个飞行系统的稳定性.此外,无法利用一些有益的耦合项来进一步提高系统的控制性能.目前,已有一些研究成果对于多通道耦合的制导/控制一体化设计进行了一些探索,例如: 非线性次优控制方法[81-82]、反馈线性化控制方法[83]、分块反向递推控制方法[84]等.
另一个制约制导/控制一体化设计的因素是飞行过程中的各种约束.如多目标控制部分所述,由于系统状态、执行机构存在特定的约束,内环控制系统往往无法精确跟踪外环制导系统产生的控制指令,进而产生执行机构的饱和(气动舵)或者失效(超燃冲压发动机),严重地危害了系统的稳定性.带有约束的制导/控制一体化设计方面的研究目前还是比较少的,而对于吸气式高超声速飞行器来说是一个具有实际意义的研究课题.
本文总结了吸气式高超声速飞行器控制系统设计中亟待解决的几个问题.实际高超声速飞行控制系统设计所面临的问题远不止这些,例如: 吸气式高超声速飞行器的细长外形、薄壁结构以及轻质复合材料使其具有比普通飞行器更为明显的弹性模态,但限于篇幅和作者的能力很难全部涉猎.值得说明的是,虽然飞行控制仅仅是整个高超声速飞行器工程中的一个子系统,但却是至关重要的.这是因为控制系统的设计还需要慎重考虑其与导航、制导子系统之间的融合,并能充分满足其他分系统(如飞行器结构、推进系统、热防护系统)的需求[2],如图 10所示.可见,吸气式高超声速飞行器控制系统的设计是一个涉及多学科的综合问题,仍有许多问题需要进一步解决.

|
图 10 控制系统与各系统之间的关系 Figure 10 Relationship between the control subsystem and other subsystems |
由于吸气式高超声速飞行器独特、复杂的飞行动态特性,对其设计具有鲁棒性、可靠性、高性能的控制器是非常具有挑战性的.本文着重阐述了吸气式高超声速飞行器控制系统的设计方法: 模型线性化方法、反向递推法、T-S模糊控制方法、自适应和滑模变结构控制方法,进而总结了实际控制器设计过程中需要克服的若干问题.限于文章篇幅和作者能力,所提及的研究方法和控制问题是十分有限的.但有一点可以肯定,对于吸气式高超声速飞行器控制系统的设计需要兼顾各个子系统,这样所设计的控制器才具有实际的应用价值,同时也是今后高超声速飞行器控制领域的努力方向.
| [1] |
WEEKS D, WALKER S, SACKHEIM R. Small satellites and the DARPA/Air Force FALCON program[J].
Acta Astronautica,2005, 57 (2-8) : 469-477.
DOI: 10.1016/j.actaastro.2005.03.058 ( 0) 0)
|
| [2] |
李惠峰.
高超声速飞行器制导与控制技术[M]. 北京: 中国宇航出版社, 2012 .
( 0) 0)
|
| [3] |
RODRIGUEZ A, DICKESON J, CIFDALOZ O, et al. Modeling and control of scramjet-powered hypersonic vehicles: challenges, trends, and tradeoffs[C]// AIAA Guidance, Navigation and Control Conference and Exhibit. Honolulu: AIAA, 2008.
( 0) 0)
|
| [4] |
VOLAND R, HUEBNER L, MCCLINTON C. X-43A hypersonic vehicle technology development[J].
Acta Astronautica,2006, 59 (1-5) : 181-191.
DOI: 10.1016/j.actaastro.2006.02.021 ( 0) 0)
|
| [5] |
HANK J M, MURPHY J S, MUTZMAN R C. The X-51A scramjet engine flight demonstration program[C]// Proceedings of the 15th AIAA International Space Planes and Hypersonic Systems and Technologies Conference. Dayton: AIAA, 2008.
( 0) 0)
|
| [6] |
崔尔杰. 近空间飞行器研究发展现状及关键技术问题[J].
力学进展,2009, 39 (6) : 658-673.
CUI Erjie. Research statutes, development trends and key technical problems of near space flying vehicles[J]. Advances in Mechanics,2009, 39 (6) : 658-673. (  0) 0)
|
| [7] |
孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J].
自动化学报,2013, 39 (11) : 1901-1913.
DOI: 10.3724/SP.J.1004.2013.01901 SUN Changyin, MU Chaoxu, YU Yao. Some control problems for near space hypersonic vehicles[J]. ACTA Automatica Sinica,2013, 39 (11) : 1901-1913. DOI: 10.3724/SP.J.1004.2013.01901 (  0) 0)
|
| [8] |
黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J].
控制理论与应用,2011, 28 (10) : 1496-1505.
HUANG Lin, DUAN Zhisheng, YANG Jianying. Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications,2011, 28 (10) : 1496-1505. (  0) 0)
|
| [9] |
黄长强, 国海峰, 丁达理. 高超声速滑翔飞行器轨迹优化与制导综述[J].
宇航学报,2014, 35 (4) : 369-379.
DOI: 10.3873/j.issn.1000-1328.2014.04.001 HUANG Changqiang, GUO Haifeng, DING Dali. A survey of trajectory optimization and guidance for hypersonic gliding vehicle[J]. Journal of Astronautics,2014, 35 (4) : 369-379. DOI: 10.3873/j.issn.1000-1328.2014.04.001 (  0) 0)
|
| [10] |
叶友达. 高超声速空气动力学研究进展与趋势[J].
科学通报,2015, 60 (12) : 1095-1103.
DOI: 10.1360/N972014-01180 YE Youda. Advances and prospects in hypersonic aerodynamics[J]. Chinese Science Bulletin,2015, 60 (12) : 1095-1103. DOI: 10.1360/N972014-01180 (  0) 0)
|
| [11] |
吴宏鑫, 孟斌. 高超声速飞行器控制研究综述[J].
力学进展,2009, 39 (6) : 756-765.
DOI: 10.3321/j.issn:1000-0992.2009.06.013 WU Hongxin, MENG Bin. Review on the control of hypersonic flight vehicles[J]. Advances in Mechanics,2009, 39 (6) : 756-765. DOI: 10.3321/j.issn:1000-0992.2009.06.013 (  0) 0)
|
| [12] |
XU Bin, SHI Zhongke. An overview on flight dynamics and control approaches for hypersonic vehicles[J].
Science China Information Sciences,2015, 58 (7) : 1-19.
DOI: 10.1007/s11432-014-5273-7 ( 0) 0)
|
| [13] |
王文博, 范国超, 许承东. 临近空间高超声速飞行器制导与控制技术研究综述[J].
战术导弹技术,2013 (6) : 32-36.
DOI: 10.16358/j.issn.1009-1300.2015.06.06 WANG Wenbo, FAN Guochao, XU Chengdong. Survey of the guidance and control for near-space hypersonic vehicle[J]. Tactical Missile Technology,2013 (6) : 32-36. DOI: 10.16358/j.issn.1009-1300.2015.06.06 (  0) 0)
|
| [14] |
王鹏, 金鑫, 张卫民. FADS系统在尖楔前体高超声速飞行器中的应用[J].
中国科学:物理学力学天文,2013, 43 (9) : 1105-1110.
DOI: 10.1360/132012-314 WANG Peng, JIN Xin, ZHANG Weimin. Application of FADS system in hypersonic flight vehicles with sharp wedged fore-bodies[J]. SCIENTIA SINICA: Physica, Mechanica & Astronomica,2013, 43 (9) : 1105-1110. DOI: 10.1360/132012-314 (  0) 0)
|
| [15] |
华如豪, 叶正寅. 吸气式高超声速飞行器多学科动力学建模[J].
航空学报,2015, 36 (1) : 346-356.
DOI: 10.7527/S1000-6893.2014.0243 HUA Ruhao, YE Zhengyin. Multidisciplinary dynamics modeling and analysis of a generic hypersonic vehicle[J]. Acta Aeronautica ET Astronautica Sinica,2015, 36 (1) : 346-356. DOI: 10.7527/S1000-6893.2014.0243 (  0) 0)
|
| [16] |
杨超, 许赟, 谢长川. 高超声速飞行器气动弹性力学研究综述[J].
航空学报,2010, 31 (1) : 1-11.
YANG Chao, XU Yun, XIE Changchuan. Review of studies on aeroelasticity of hypersonic vehicles[J]. Acta Aeronautica ET Astronautica Sinica,2010, 31 (1) : 1-11. (  0) 0)
|
| [17] |
李惠峰, 肖进, 张冉. 高超声速飞行器刚体/弹性体耦合动力学建模[J].
北京航空航天大学学报,2012, 38 (2) : 160-165.
LI Huifeng, XIAO Jin, ZHANG Ran. Hypersonic vehicle rigid/elastic coupled dynamic modeling[J]. Journal of Beijing University of Aeronautics and Astronautics,2012, 38 (2) : 160-165. (  0) 0)
|
| [18] |
CHAVEZ F R, SCHMIDT D K. Analytical aeropropulsive/aeroelastic hypersonic-vehicle model with dynamic analysis[J].
Journal of Guidance, Control, and Dynamics,1994, 17 (6) : 1308-1319.
DOI: 10.2514/3.21349 ( 0) 0)
|
| [19] |
SHAUGHNESSY J, PINCKNEY S, MCMINN J, et al. Hypersonic vehicle simulation model: winged-coneconfiguration[R]. Langley: NASA Langley Research Center, 1990.
( 0) 0)
|
| [20] |
MARRISON C I, STENGEL R F. Design of robust control systems for a hypersonic aircraft[J].
Journal of Guidance, Control, and Dynamics,1998, 21 (1) : 58-63.
DOI: 10.2514/2.4197 ( 0) 0)
|
| [21] |
WANG Qian, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J].
Journal of Guidance, Control, and Dynamics,2000, 23 (4) : 577-585.
DOI: 10.2514/2.4580 ( 0) 0)
|
| [22] |
BOLENDER M A, DOMAN D B. Nonlinear longitudinal dynamical model of an air-breathing hypersonic vehicle[J].
Journal of Spacecraft and Rockets,2007, 44 (2) : 374-387.
DOI: 10.2514/1.23370 ( 0) 0)
|
| [23] |
PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J].
Journal of Guidance, Control, and Dynamics,2007, 30 (3) : 856-869.
DOI: 10.2514/1.27830 ( 0) 0)
|
| [24] |
FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible airbreathing hypersonic vehicles[J].
Journal of Guidance, Control, and Dynamics,2009, 32 (2) : 402-417.
DOI: 10.2514/1.39210 ( 0) 0)
|
| [25] |
SIGTHORSSON D O, SERRANI A. Development of linear parameter-varying models of hypersonic airbreathing vehicles[C]//AIAA Guidance, Navigation, and Control Conference. Chicago: AIAA, 2009. DOI: 10.2514/6.2009-6282.
( 0) 0)
|
| [26] |
SHAKIBA M, SERRANI A. Control oriented modeling of 6-DOF hypersonic vehicle dynamics[C]//AIAA Guidance, Navigation, and Control Conference. Portland: AIAA, 2011. DOI:10.2514/6.2011-6227.
( 0) 0)
|
| [27] |
SERRANI A, BOLENDER M A. A nonlinear adaptive reconfigurable controller for a generic 6-DOF hypersonic vehicle model[C]//American Control Conference. Portland, OR: IEEE, 2014: 1384-1389. DOI: 10.1109/ACC.2014.6858885.
( 0) 0)
|
| [28] |
方洋旺, 柴栋, 毛东辉, 等. 吸气式高超声速飞行器制导与控制研究现状及发展趋势[J].
航空学报,2014, 35 (7) : 1776-1786.
DOI: 10.7527/S1000-6893.2014.0021 FANG Yangwang, CHAI Dong, MAO Donghui, et al. Status and development trend of the guidance and control for air-breathing hypersonic vehicle[J]. Acta Aeronautica ET Astronautica Sinica,2014, 35 (7) : 1776-1786. DOI: 10.7527/S1000-6893.2014.0021 (  0) 0)
|
| [29] |
曾开春, 向锦武. 高超声速飞行器飞行动力学特性不确定分析[J].
航空学报,2013, 34 (4) : 798-808.
DOI: 10.7527/S1000-6893.2013.0139 Zeng Kaichun, XIANG Jinwu. Uncertainty analysis of flight dynamic characteristics for hypersonic vehicles[J]. Acta Aeronautica ET Astronautica Sinica,2013, 34 (4) : 798-808. DOI: 10.7527/S1000-6893.2013.0139 (  0) 0)
|
| [30] |
REHMAN O, PETERSEN I, FIDAN B. Feedback linearization-based robust nonlinear control design for hypersonic flight vehicles[J].
Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,2012, 227 (1) : 3-11.
DOI: 10.1177/0959651812447722 ( 0) 0)
|
| [31] |
REHMAN O, FIDAN B, PETERSEN I. Robust control system design for an uncertain nonlinear system using minmax LQG design method[J].
Asian Journal of Control,2014, 16 (4) : 1029-1041.
DOI: 10.1002/asjc.777 ( 0) 0)
|
| [32] |
GAO Gang, WANG Jinzhi. Observer-based fault-tolerant control for an air-breathing hypersonic vehicle model[J].
Nonlinear Dynamics,2014, 76 (1) : 409-430.
DOI: 10.1007/s11071-013-1135-x ( 0) 0)
|
| [33] |
KRSTIC M, KANELLAKOPOULOS I, KOKOTOVIC P.
Nonlinear and adaptive control design[M]. New York: Wiley, 1995 .
( 0) 0)
|
| [34] |
FIORENTINI L, SERRANI A. Nonlinear adaptive control design for non-minimum phase hypersonic vehicle models with minimal control authority[C]// Proceedings of the 48th IEEE Conference on Decision and Control. Shanghai: IEEE, 2009: 1405-1410. DOI:10.1109/CDC.2009.5400744
( 0) 0)
|
| [35] |
SUN Haibin, LI Shihua, YANG Jun, et al. Non-linear disturbance observer-based back-stepping control for airbreathing hypersonic vehicles with mismatched disturbances[J].
IET Control Theory & Application,2014, 8 (17) : 1852-1865.
DOI: 10.1049/iet-cta.2013.0821 ( 0) 0)
|
| [36] |
ZONG Qun, WANG Fang, TIAN Bailing, et al. Robust adaptive dynamic surface control design for a flexible air-breathing hypersonic vehicle with input constraints and uncertainty[J].
Nonlinear Dynamics,2014, 78 (1) : 289-315.
DOI: 10.1007/s11071-014-1440-z ( 0) 0)
|
| [37] |
XU Bin. Robust adaptive neural control of flexible hypersonic flight vehicle with dead-zone input nonlinearity[J].
Nonlinear Dynamics,2015, 80 (3) : 1509-1520.
DOI: 10.1007/s11071-015-1958-8 ( 0) 0)
|
| [38] |
XU Bin, YANG Chenguang, PAN Yongping. Global neural dynamic surface tracking control of strict-feedback systems with application to hypersonic flight vehicle[J].
IEEE Transactions on Neural Networks and Learning Systems,2015, 26 (10) : 2563-2575.
DOI: 10.1109/TNNLS.2015.2456972 ( 0) 0)
|
| [39] |
XU Bin, WANG Shixing, GAO Daoxiang, et al. Command filter based robust nonlinear control of hypersonic aircraft with magnitude constraints on states and actuators[J].
Journal of Intelligent & Robotic Systems,2014, 73 (1) : 233-247.
DOI: 10.1007/s10846-013-9941-4 ( 0) 0)
|
| [40] |
FARRELL J, POLYCARPOU M, SHARMA M, et al. Command filtered backstepping[J].
IEEE Transactions on Automatic Control,2009, 54 (6) : 1391-1395.
DOI: 10.1109/TAC.2009.2015562 ( 0) 0)
|
| [41] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Fuzzy guaranteed cost tracking control for a flexible air-breathing hypersonic vehicle[J].
IET Control Theory & Application,2012, 6 (9) : 1238-1249.
DOI: 10.1049/iet-cta.2011.0065 ( 0) 0)
|
| [42] |
HU Xiaoxiang, GAO Huijun, KARIMI H R, et al. Fuzzy reliable tracking control for flexible air-breathing hypersonic vehicles[J].
International Journal of Fuzzy Systems,2011, 13 (4) : 323-334.
( 0) 0)
|
| [43] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Adaptive fuzzy integral sliding mode control for flexible air-breathing hypersonic vehicles subject to input nonlinearity[J].
Journal of Aerospace Engineering,2013, 26 (4) : 721-734.
DOI: 10.1061/(ASCE)AS.1943-5525.0000193 ( 0) 0)
|
| [44] |
HU Xiaoxiang, WU Ligang, HU Changhua, et al. Dynamic output feedback control of a flexible air-breathing hypersonic vehicle via T-S fuzzy approach[J].
International Journal of Systems Science,2014, 45 (8) : 1740-1756.
DOI: 10.1080/00207721.2012.749547 ( 0) 0)
|
| [45] |
BROCANELLI M, GUNBATAR Y, SERRANI A, et al. Robust control for unstart recovery in hypersonic vehicles[C]//AIAA Guidance, Navigation, and Control Conference. Minneapolis: AIAA, 2012. DOI:10.2514/6.2012-4698.
( 0) 0)
|
| [46] |
WIESE D P, ANNASWAMY A M, MUSE J A, et al. Adaptive control of a generic hypersonic vehicle[C]//AIAA Guidance, Navigation, and Control Conference. Boston: AIAA, 2013. DOI:10.2514/6.2013-4514.
( 0) 0)
|
| [47] |
IOANNOU P, FIDAN B.
Adaptive control tutorial[M]. Philadelphia: SIAM, 2006 .
( 0) 0)
|
| [48] |
WU Ligang, SHI Peng, SU Xiaojie.
Sliding mode control of uncertain parameter-switching hybrid systems[M]. London: Wiley, 2014 .
( 0) 0)
|
| [49] |
WANG Na, YAO Xiuming, LI Wenshuo. Nonlinear disturbance observer-based sliding mode control for flexible airbreathing hypersonic vehicles[J].
Mathematical Problems in Engineering,2015, 2015 : 1-15.
DOI: 10.1155/2015/675659 ( 0) 0)
|
| [50] |
CHENG Xianlei, TANG Guojian, WANG Peng, et al. Predictive sliding mode control for attitude tracking of hypersonic vehicles using fuzzy disturbance observer[J]. Mathematical Problems in Engineering. DOI:10.1155/2015/727162.
( 0) 0)
|
| [51] |
WANG Jianmin, WU Yunjie, DONG Xiaomeng. Recursive terminal sliding mode control for hypersonic flight vehicle with sliding mode disturbance observer[J].
Nonlinear Dynamics,2015, 81 (3) : 1489-1510.
DOI: 10.1007/s11071-015-2083-4 ( 0) 0)
|
| [52] |
SHAO Xingling, WANG Honglun. Sliding mode based trajectory linearization control for hypersonic reentry vehicle via extended disturbance observer[J].
ISA Transactions,2014, 53 (6) : 1771-1786.
DOI: 10.1016/j.isatra.2014.09.021 ( 0) 0)
|
| [53] |
WANG Jie, ZONG Qun, SU Rui, et al. Continuous high order sliding mode controller design for a flexible air-breathing hypersonic vehicle[J].
ISA Transactions,2014, 53 (3) : 690-698.
DOI: 10.1016/j.isatra.2014.01.002 ( 0) 0)
|
| [54] |
WANG Peng, TANG Guojian, WU Jie. Sliding mode decoupling control of a generic hypersonic vehicle based on parametric commands[J].
Science China Information Sciences,2015, 58 (5) : 1-14.
DOI: 10.1007/s11432-014-5122-8 ( 0) 0)
|
| [55] |
CHEN Mou, WU Qinxian, JIANG Changsheng, et al. Guaranteed transient performance based control with input saturation for near space vehicles[J].
Science China Information Sciences,2014, 57 (5) : 1-12.
DOI: 10.1007/s11432-013-4883-9 ( 0) 0)
|
| [56] |
AN Hao, LIU Jianxing, WANG Changhong, et al. Disturbance observer-based antiwindup control for air-breathing hypersonic vehicles[J].
IEEE Transactions on Industrial Electronics,2016, 63 (5) : 3038-3049.
DOI: 10.1109/TIE.2016.2516498 ( 0) 0)
|
| [57] |
ZHOU Jing, WEN Changyun.
Adaptive backstepping control of uncertain systems: nonsmooth nonlinearities[M]. Berlin Heidelberg: Springer-Verlag, 2008 .
( 0) 0)
|
| [58] |
ZHOU Jing, WEN Changyun, ZHANG Ying. Adaptive backstepping control of a class of uncertain nonlinear systems with unknown backlash-like hysteresis[J].
IEEE Transactions on Automatic Control,2004, 49 (10) : 1751-1759.
DOI: 10.1109/TAC.2004.835398 ( 0) 0)
|
| [59] |
ZHOU Jing, WEN Changyun. Adaptive backstepping control of uncertain systems with unknown input time-delay[J].
Automatica,2009, 45 (6) : 1415-1422.
DOI: 10.1016/j.automatica.2009.01.012 ( 0) 0)
|
| [60] |
GAO Zhiwei, CECATI C, DING S X. A survey of fault diagnosis and fault-tolerant techniques-Part I: Fault diagnosis with model-based and signal-based approaches[J].
IEEE Transactions on Industrial Electronics,2015, 62 (6) : 3757-3767.
DOI: 10.1109/TIE.2015.2417501 ( 0) 0)
|
| [61] |
钱佳淞, 齐瑞云, 姜斌. 高超声速飞行器再入容错制导技术综述[J].
飞行力学,2015, 33 (5) : 390-394.
QIAN Jiasong, QI Ruiyun, JIANG Bin. Review of reentry fault-tolerant guidance technology on hypersonic vehicles[J]. Flight Dynamics,2015, 33 (5) : 390-394. (  0) 0)
|
| [62] |
黄宇海, 齐瑞云, 姜斌, 等. 基于动态面backstepping控制的高超声速飞行器自适应故障补偿设计[J].
中国科学技术大学学报,2012, 42 (9) : 768-774.
DOI: 10.3969/j.issn.0253-2778.2012.09.011 HUANG Yuhai, QI Ruiyun, JIANG Bin, et al. Adaptive failure compensation design for hypersonic vehicles based on dynamic surface backstepping control[J]. Journal of University of Science and Technology of China,2012, 42 (9) : 768-774. DOI: 10.3969/j.issn.0253-2778.2012.09.011 (  0) 0)
|
| [63] |
AN Hao, LIU Jianxing, WANG Changhong, et al. Approximate back-stepping fault-tolerant control of the flexible air-breathing hypersonic vehicles[J].
IEEE/ASME Transactions on Mechatronics,2016, 21 (3) : 1680-1691.
DOI: 10.1109/TMECH.2015.2507186 ( 0) 0)
|
| [64] |
CHEN Fuyang, WANG Zheng, TAO Gang, et al. Robust adaptive fault-tolerant control for hypersonic flight vehicles with multiple faults[J].
Journal of Aerospace Engineering,2015, 28 (4) : 04014111.
DOI: 10.1061/(ASCE)AS.1943-5525.0000449 ( 0) 0)
|
| [65] |
WANG Jie, ZONG Qun, HE Xiao, et al. Adaptive finite-time control for a flexible hypersonic vehicle with actuator fault[J].
Mathematical Problems in Engineering,2013, 2013 : 920796.
DOI: 10.1155/2013/920796 ( 0) 0)
|
| [66] |
JI Yuehui, ZHOU Hailiang, ZONG Qun. Adaptive active fault-tolerant control of generic hypersonic flight vehicles[J].
Proceedings of the Institution of Mechanical Engineers, Part I: Journal of Systems and Control Engineering,2015, 229 (2) : 130-138.
DOI: 10.1177/0959651814552809 ( 0) 0)
|
| [67] |
HE Jingjing, QIN Ruiyun, JIANG Bin, et al. Adaptive output feedback fault-tolerant control design for hypersonic flight vehicles[J].
Journal of the Franklin Institute,2015, 352 (5) : 1811-1835.
DOI: 10.1016/j.jfranklin.2015.01.016 ( 0) 0)
|
| [68] |
FU Wenxing, WANG Yuji, ZHU Supeng, et al. Neural adaptive control of hypersonic aircraft with actuator fault using randomly assigned nodes[J].
Neurocomputing,2016, 174 (Part B, 22) : 1070-1076.
DOI: 10.1016/j.neucom.2015.10.023 ( 0) 0)
|
| [69] |
GAO Zhifeng, LIN Jinxing, CAO Teng. Robust fault tolerant tracking control design for a linearized hypersonic vehicle with sensor fault[J].
International Journal of Control, Automation and Systems,2015, 13 (3) : 672-679.
DOI: 10.1007/s12555-014-0169-2 ( 0) 0)
|
| [70] |
BECHLIOULIS C P, ROVITHAKIS G A. Robust adaptive control of feedback linearizable MIMO nonlinear systems with prescribed performance[J].
IEEE Transactions on Automatic Control,2008, 53 (9) : 2090-2099.
DOI: 10.1109/TAC.2008.929402 ( 0) 0)
|
| [71] |
BECHLIOULIS C P, ROVITHAKIS G A. Adaptive control with guaranteed transient and steady state tracking error bounds for strict feedback systems[J].
IEEE Transactions on Automatic Control,2009, 45 (2) : 532-538.
DOI: 10.1016/j.automatica.2008.08.012 ( 0) 0)
|
| [72] |
BOLENDER M, WILKIN H, JACOBSEN L, et al. Flight dynamics of a hypersonic vehicle during inlet unstart[C]//Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference. Bremen: AIAA, 2009. DOI:10.2514/6.2009-7292.
( 0) 0)
|
| [73] |
AMES A D, GRIZZLE J W, TABUADA P. Control barrier function based quadratic programs with application to adaptive cruise control[C]//Proceedings of the IEEE 53rd Annual Conference on Decision and Control. Los Angeles, CA: IEEE Compendex, 2014: 6271-6278. DOI:10.1109/CDC.2014.7040372.
( 0) 0)
|
| [74] |
PEEBLES C.
Road to Mach 10: lessons learned from the X-43A flight research program[M]. Reston: AIAA, 2008 .
( 0) 0)
|
| [75] |
LIBERZON D.
Switching in systems and control[M]. New York: Springer Science & Business Media, 2003 .
( 0) 0)
|
| [76] |
SUN Z, GE S.
Switched linear systems-control and design[M]. Berlin: Springer Science & Business Media, 2004 .
( 0) 0)
|
| [77] |
WILLIAMS D, RICHMAN J, FRIEDLAND B. Design of an integrated strapdown guidance and control system for a tactical missile[C]. Guidance and Control Conference. Gatlinburg: AIAA, 1983. DOI:10.2514/6.1983-2169.
( 0) 0)
|
| [78] |
SHARMA M, RICHARDS N. Adaptive, integrated guidance and control for missile interceptors[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit. Providence: AIAA, 2004. DOI:10.2514/6.2004-4880.
( 0) 0)
|
| [79] |
SHIMA T, IDAN M, GOLAN O. Sliding mode control for integrated missile autopilot guidance[J].
Journal of Guidance, Control, and Dynamics,2006, 29 (2) : 250-260.
DOI: 10.2514/1.14951 ( 0) 0)
|
| [80] |
GUO Jianguo, ZHOU Jun. Integrated guidance-control system design based on H∞ control[C]//Proceedings of the 2010 International Conference on Electrical and Control Engineering. Wuhan: IEEE, 2010: 1204-1207. DOI:10.1109/iCECE.2010.300.
( 0) 0)
|
| [81] |
VADDI S S, MENON P K, OHLMEYER E J. Numerical SDRE approach for missile integrated guidance control[J].
Journal of Guidance, Control, and Dynamics,2009, 32 (2) : 699-703.
DOI: 10.2514/1.34291 ( 0) 0)
|
| [82] |
XIN Min, BALAKRISHNAN S N, OHLMEYER E J. Integrated guidance and control of missiles with θ-D method[J].
IEEE Transactions on Control Systems Technology,2006, 14 (6) : 981-992.
DOI: 10.1109/TCST.2006.876903 ( 0) 0)
|
| [83] |
尹永鑫, 杨明, 王子才. 导弹三维制导控制一体化设计[J].
电机与控制学报,2010, 14 (3) : 87-91.
DOI: 10.3969/j.issn.1007-449X.2010.03.016 YIN Yongxin, YANG Ming, WANG Zicai. Three-dimensional guidance and control for missile[J]. Electric Machines and Control,2010, 14 (3) : 87-91. DOI: 10.3969/j.issn.1007-449X.2010.03.016 (  0) 0)
|
| [84] |
KIM B, CALISE A, SATTIGERI R. Adaptive, integrated guidance and control design for line-of-sight based formation flight[J].
Journal of Guidance, Control, and Dynamics,2007, 30 (5) : 1386-1398.
DOI: 10.2514/1.27758 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


