航天器的外热流是航天器在太空接受的主要热源,是影响航天器温度的主要因素之一[1].航天器在设计、发射、运行阶段均需要计算其外热流.有学者研究表明,各类型航天器(例如轨道空间相机[2]和外露式星载光电设备[3])的外热流计算结果,都是其热分析的基本数据;一旦外热流参数取值存在偏差,则会造成温度计算结果与测控结果出现偏差[4].
外热流研究包括:推导并验证外热流分析所需轨道参数的计算公式[5],分析特定轨道下航天器的各项外热流或总外热流受轨道参数的影响[6-7],以及进行空间热环境综合监测的实验[8].在外热流计算中,六面体航天器简化模型较为常用.宁献文等[9]通过合理简化推导了倾斜轨道六面体航天器极端外热流的解析模型,并利用Nevada软件证实了六面体航天器理论模型计算的有效性;徐向华等[10]建立了三轴稳定的六面体航天器外热流模型,推导了圆形太阳同步轨道卫星的外热流公式,分析了航天器表面外热流受太阳阳光与轨道面的夹角(β)和航天器在轨位置的影响.
本文将分析国际空间站(international space station,ISS)站载设备的外热流:计算ISS轨道外热流分析所需的轨道参数;利用简化六面体航天器外热流计算公式分析ISS各区域的总外热流变化规律;并以阿尔法磁谱仪(alpha magnetic spectrometer,AMS)为ISS站载设备代表,分析ISS站载设备外热流的影响因素.
1 国际空间站站载设备ISS站载设备随ISS在低地球圆形轨道上飞行(轨道高度约370~460 km[11]),因此,ISS的轨道外热流是站载设备外热流的主体,但二者并不完全相等.站载设备的外热流除了受到ISS轨道外热流的影响外,还受到ISS部件和操作的次要影响.
本文以AMS作为ISS站载设备的代表,分析ISS站载设备外热流的影响因素.AMS项目是大型空间高能粒子探测实验研究.2011年5月19日,AMS设备被安装在ISS右舷侧,进行长期(约20 a)宇宙线探测任务[12].目前,AMS合作组已发表的结果有:0.5~350 GeV宇宙射线正电子分数[12],0.5~500 GeV宇宙射线正电子分数[13],宇宙射线中电子与正电子通量[14]以及1.0~1.8 TeV宇宙射线质子通量[15].在热控制方面,AMS热控团队[16-17]进行了测控数据观测并分析了ISS右舷主散热板、β等对该仪器温度的影响.通过分析AMS外热流的影响因素,可总结类似空间站站载设备的热特性并运用于未来站载设备的热设计中.
2 国际空间站轨道参数ISS轨道参数是计算ISS轨道外热流的基础.涉及轨道参数的计算为:轨道周期τ0、太阳阳光与轨道面的夹角β、ISS在地球阴影区的持续时间τsh和受晒因子τ*.
2.1 轨道周期假设ISS轨道高度h保持370.4 km,其轨道周期τ0可根据开普勒第三定律求解:
| $\frac{{{a}^{3}}}{\tau _{0}^{2}}=\frac{GM}{4{{\pi }^{2}}}.$ | (1) |
式中:a为轨道半径,a=h+Re;Re为地球赤道半径,6.378 14×103 km;G为引力常量,6.674 28×10-11 Nm2/kg2;M为地球质量,5.98×1024 kg.当ISS轨道高度h=370.4 km时,ISS的轨道周期为91.8 min.
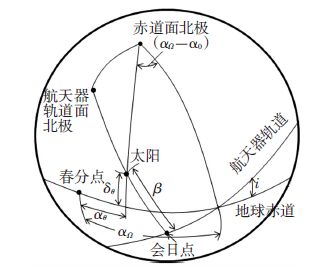
2.2 太阳阳光与轨道面的夹角β是太阳阳光与轨道面的夹角,是航天器热环境的重要参数.当太阳直射北半球时,从图 1的球面三角关系可得:
| $sin\beta =\cos i\sin {{\delta }_{\theta }}+\sin i\cos {{\delta }_{\theta }}\sin \left( {{\alpha }_{\Omega }}-{{\alpha }_{\theta }} \right).$ | (2) |
式中:i为航天器轨道倾角;δθ为太阳赤纬,αθ为太阳赤经,两者可根据给定日期从天文年历表中查出;αΩ为轨道升交点赤经.计算中假定1 d内的太阳赤经αθ、太阳赤纬δθ保持不变.根据ISS轨道倾角i=51°[11]可计算出β范围为-75.50°~+74.43°(近似为-75°~+75°).
|
图 1 阳光与轨道面夹角计算中的球面三角关系示意 Figure 1 Schematic view of β calculation in spherical coordinate system |
ISS在轨运行可能进入地球的阴影区域,在地球阴影区的持续时间τsh内,ISS接受不到太阳直接辐射和地球反照辐射,因此,地球阴影区对ISS的外热流有重要的影响.假定:1)地球的阴影为圆柱体,其直径等于地球的直径;2)太阳光为平行光,不考虑太阳半阴影影响;3)忽略在一个轨道周期内太阳位置的变化(通过计算,在一个轨道周期(91.8 min)内β的变化为[0.003°,0.31°],可引起平均总外热流的最大误差为2.23 W/m2,是相同工况下该表面平均总外热流(111.52 W/m2)的2%,且不影响文中对总外热流变化规律的分析.因此,本文中忽略太阳位置在一个轨道周期内的变化),且认为轨道是闭合的,则根据图 2的几何关系,ISS在地球阴影区的持续时间τsh满足:
| ${{\tau }_{\text{sh}}}=\frac{{{\theta }_{E}}{{\tau }_{0}}}{2\pi }=\frac{\left( {{\theta }_{e}}-{{\theta }_{i}} \right){{\tau }_{0}}}{2\pi },$ | (3) |

|
图 2 地球阴影在圆形轨道内的投影 Figure 2 Projection of the earth shadow on circular orbit |
式中θe、θi分别为航天器与会日点的角距θ在90°~270°范围内满足下式的解
| $\cos \theta =\frac{\pm \sqrt{1-{{\left( {{R}_{e}}/a \right)}^{2}}}}{\cos \beta },$ | (4) |
由此可知,当a≥Recsc β时,即当|β|>70.965°时,ISS不进入地球阴影区.ISS的受晒因子τ*是ISS在一个轨道周期内受到太阳照射的时间与轨道周期的比值,即
| ${{\tau }_{*}}=\frac{{{\tau }_{0}}-{{\tau }_{\text{sh}}}}{{{\tau }_{0}}}.$ | (5) |
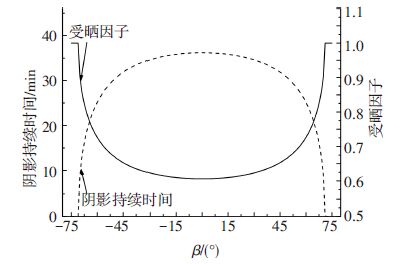
在ISS的β范围[-75°,+75°]内,通过上述公式可计算阴影持续时间τsh和受晒因子τ*随β的变化曲线(见图 3).在ISS所处的低地球轨道上,当β>70.965°时,ISS轨道无阴影区(τsh=0且τ*=1);当β≤70.965°时,ISS受地球阴影区的影响:ISS在阴影区的持续时间与β成反比关系,而受晒因子与β成正比关系.当β=0°时,ISS在一个轨道周期里的阴影持续时间最长(36.19 min),而受晒因子最小(0.61).
|
图 3 ISS所在轨道的阴影持续时间和受晒因子随β的变化 Figure 3 Time duration of the earth shadow and the sun illuminated factor on the ISS orbit vs. β |
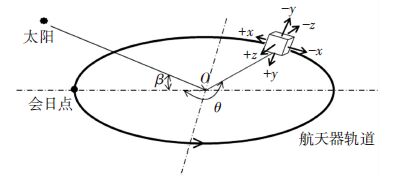
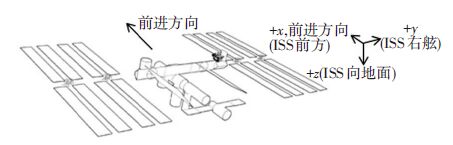
在ISS轨道上,外热流主要包括太阳辐射热流q1、地球对太阳光的反照热流q2和地球红外辐射热流q3.本文中使用简化六面体航天器(见图 4)的6个表面代表ISS正常飞行姿态下ISS各区域(见图 5),分析在ISS正常飞行姿态下ISS各区域的外热流变化规律.
|
图 4 简化六面体航天器在轨示意 Figure 4 Schematic view of simplified hexahedral in orbit |
|
图 5 ISS正常飞行姿态下ISS区域与简化六面体航天器表面的对应关系示意 Figure 5 Schematic view of the relationship between the ISS areas and the simplified hexahedral surfaces with the ISS normal flight attitude |
为了计算各表面的太阳光线入射角,需要采用球面坐标系(见图 4).该球面坐标系的中心为地心,主平面为航天器轨道面,原点为轨道会日点,由此可知各表面、太阳和航天器的球面法线坐标(经度α,纬度δ)(见表 1),则各表面所接收的太阳辐射热流q1可计算为
| ${{q}_{1}}=S\max \left( \cos {{\beta }_{s}},0 \right).$ | (6) |
其中:S为太阳常数,计算中采用其平均值1 367 W/m2;βs为阳光和受照面法线方向的夹角,其余弦值可由下式计算:
| $\cos {{\beta }_{s}}=\sin \delta \sin \beta +\cos \delta \cos \beta \cos \alpha ,$ | (7) |
由此可计算各表面或位置的βs余弦值(见表 1).
| 表 1 各表面或位置的法线坐标以及βs余弦值 Table 1 Normal coordinate of the ISS surfaces or locations and cosine value of βs |
地球反照是指地球对太阳辐射的反射作用.地球反照受地球表面环境的影响较大,不同区域内反照率差别明显.对于无特殊条件下的航天器表面可使用下式近似计算地球反照角系数为
| ${{\varphi }_{2}}={{\varphi }_{3}}\cos \Phi .$ | (8) |
式中:φ3为该表面的地球红外辐射角系数;Φ为相角,cos Φ=cos θcos β.因此,地球反照热流q2计算式可近似为
| ${{q}_{2}}={{\varphi }_{3}}S\rho \max \left( 0,\cos \Phi \right)={{\varphi }_{3}}S\rho \max \left( 0,\cos \theta \cos \beta \right).$ | (9) |
式中ρ为地球反照率,取为0.3.
3.3 地球红外辐射热流地球红外辐射EIR,是指太阳投射到地球上的辐射能被地球吸收后,以红外辐射能的形式向太空排散.本文假定地球在轨运行处于热平衡状态,且地球为均匀辐射体,EIR恒为246.05 W/m2,则各表面地球红外辐射热流q3的计算公式为
| ${{q}_{3}}={{\varphi }_{3}}{{E}_{\text{IR}}}.$ | (10) |
式中,φ3为该表面的地球红外辐射角系数,可采用表 2计算.
| 表 2 各表面的地球红外辐射角系数计算公式 Table 2 Equations of the angular coefficient of the IR from earth for the ISS areas |
ISS的总外热流Σq是太阳辐射热流q1、地球反照热流q2和地球红外辐射热流q3的总和,即轨道环境对ISS热影响的总和.由上述外热流计算公式可知,对于确定的轨道高度,各表面的地球红外辐射热流可以近似当作恒定值,但各表面的地球反照热流和太阳辐射热流则随着航天器在轨位置的变化而不断变化.因此,本文重点结合简化六面体航天器(见图 4)的外热流计算结果,分析ISS正常飞行姿态下(见图 5)ISS各区域总外热流随β和θ变化的规律.
3.4.1 各表面平均总外热流随β变化的规律平均总外热流(Σq)average是总外热流在一个轨道周期内的均值.各表面的平均总外热流随β变化的规律如图 6所示.ISS向地面的平均总外热流约为350 W/m2,受β变化的影响较小.ISS前、后方的平均总外热流在相同β下相等,β=0°时最大(401.61 W/m2),随着|β|增大而缓慢下降,|β|=75°时最小(195.57 W/m2).ISS向太空面的平均总外热流随β的变化规律与ISS前、后方类似,β=0°时最大(437.23 W/m2),β=75°时最小(113.44 W/m2).ISS左、右舷平均总外热流对β变化敏感,不同β下其数值差异较大;当β>+20°时,ISS左舷平均总外热流将高于其他表面,且随着β的增大而明显增大,当|β|=+75°时达到最大(1 403.00 W/m2);当β<-20°时,ISS右舷平均总外热流将高于其他表面,且随着β的减小而明显增大,当β=-75°时达到最大(1 403.00 W/m2).

|
图 6 各表面平均总外热流随β的变化 Figure 6 Orbit-averaged total external flux density vs. β on the ISS areas |
由上述分析可知,β=0°和β=±75°是外热流的极端工况条件,且鉴于β为负值时航天器外热流变化规律与正值时类似,以下仅分析β=0°和β=+75°下各表面的总外热流随θ变化的规律.
当β=0°时,各表面总外热流随θ的变化如图 7所示.在不同θ角度下,外热流值最大可达1 445.23 W/m2(ISS前、后方),最小为0 W/m2(ISS向太空面).ISS左、右舷总外热流随θ变化规律一致.在一个θ周期内,ISS向太空面的总外热流最大值与最小值差可达1 367 W/m2,ISS前、后方的总外热流最大值与最小值差可达1 372.36W/m2,尤其当ISS进出地球阴影区时ISS前、后方总外热流变化剧烈.

|
图 7 当β=0°时各表面总外热流随θ的变化 Figure 7 Total external flux density vs. θ on the ISS areas at β=0° |
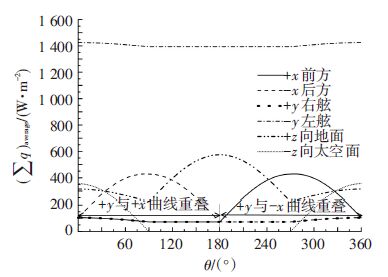
当β=+75°时,各表面总外热流随θ的变化如图 8所示.ISS不进入地球阴影区,此时ISS轨道为全日照轨道.在不同θ角度下,外热流值最大可达1 424.50 W/m2(ISS左舷),最小为0 W/m2(ISS向太空面).ISS左舷总外热流远大于其他表面总外热流,且在一个θ周期内其总外热流变化较小,最大值与最小值差仅为31.44 W/m2.
|
图 8 当β=+75°时各表面总外热流随θ的变化 Figure 8 Total external flux density vs. θ on the ISS areas at β=+75° |
站载设备的总外热流除了受到ISS轨道外热流的影响外,还在一定程度上受到ISS部件及操作的影响.ISS主要部件有左、右舷太阳能电池板和左、右舷主散热板等可转动部件,桁架、服务模块和实验台架等固定部件(见图 9);ISS的主要操作是指ISS对左、右舷太阳能电池板、左、右舷主散热板和ISS飞行姿态的操作.本文以AMS作为站载设备的代表,通过Thermal Desktop软件建立AMS热模型,基于蒙特卡洛方法计算AMS的外热流,该AMS热模型中包含了来自ISS的热影响.以下将结合AMS温度规律研究[16-17]中的AMS热控重点区域(AMS左舷、前方和后方),利用AMS外热流数值模拟结果,分析ISS固定部件、转动部件操作和飞行姿态操作对AMS外热流的影响.

|
图 9 ISS主要部件示意(图片来源:美国宇航局) Figure 9 ISS main components (credit by NASA) |
ISS固定部件对AMS外热流的影响主要表现在红外辐射、遮挡与反射轨道外热流等方面.
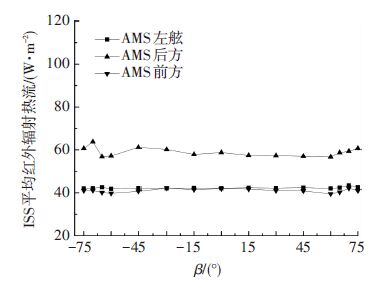
4.1.1 红外辐射图 10为AMS左舷、前、后方受到ISS平均红外辐射热流随β的变化,可见在不同β下AMS的3个面受到的ISS平均红外辐射热流都较为稳定.保持这种稳定状态的主要原因是:1)ISS固定部件和AMS之间有稳定的几何关系;2)对ISS固定部件的温度控制限制了其红外辐射强度.
|
图 10 AMS的ISS平均红外辐射热流随β的变化 Figure 10 Orbit-averaged IR density from the ISS vs. β on the AMS areas |
ISS的固定部件还有可能遮挡与反射轨道外热流,由于固定部件和AMS之间具有稳定的几何关系,因此可认为其对轨道外热流的遮挡与反射在相同轨道条件下保持不变.
4.2 ISS可转动部件操作对AMS外热流的影响根据AMS热控记录和学者研究[16-17],ISS右舷主散热板和左舷太阳能电池板操作对AMS有重要热影响,详见文献[16-17],以β=+75°为例,分析各项操作对AMS外热流的影响.
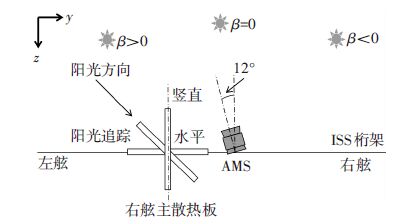
4.2.1 右舷主散热板ISS右舷主散热板(starboard main radiator,SMR)靠近AMS左舷(见图 11).文献[16]指出SMR角度变化可明显改变AMS左舷的外热流.图 11所示为3种具有代表性的SMR操作状态:水平、竖直和阳光追踪.其中阳光追踪是指SMR始终与阳光方向保持平行,以避免阳光照射散热面.
|
图 11 ISS右舷主散热板操作示意 Figure 11 Schematic view of operations of the ISS SMR |
当β=+75°时,在不同SMR工况下AMS左舷总外热流随θ的变化如图 12所示.AMS左舷总外热流在SMR水平和阳光追踪两种工况下的变化基本一致,而竖直工况下的变化则与之存在明显差异.在SMR竖直工况下,SMR对阳光的遮挡减少了AMS左舷的太阳辐射热流(当0°<θ<60°、135°<θ<165°、315°<θ<360°时),使得AMS左舷总外热流显著低于SMR水平和阳光追踪工况,其最大差值可达1 257.57 W/m2(θ=30°时).

|
图 12 ISS右舷主散热板不同工况下AMS左舷总外热流随θ的变化(β=+75°) Figure 12 Total external flux density vs. θ with different SMR angles on the AMS port area at β=+75° |
ISS太阳能电池板离AMS相对较远(见图 9).通常,太阳能电池板处于自动追踪阳光的状态(如图 13),以获得最大的有效太阳辐射来满足ISS电力需求.但在AMS运行期间,为了给某个ISS站载设备降温,当β≥+70°时左舷太阳能电池板(port solar arrays,PSA)始终被锁定于280°(如图 13).这一操作也改变了部分AMS区域的外热流.

|
图 13 ISS左舷太阳能电池板操作示意 Figure 13 Schematic view of operations of the ISS PSA |
当β=+75°时,不同PSA工况下AMS左舷总外热流随θ的变化如图 14所示.当0°<θ<30°或315°<θ<360°时,PSA被锁定于280°导致PSA遮挡阳光,使得AMS左舷总外热流低于同θ角度PSA自动追踪阳光工况下数值.因为PSA遮挡效果随θ变化而变化,导致AMS左舷总外热流数值也随之波动.当θ=0°(即θ=360°)时,AMS左舷总外热流降幅最大,下降1 176.72 W/m2.

|
图 14 ISS左舷太阳能电池板不同工况下AMS左舷总外热流随θ的变化(β=+75°) Figure 14 Total external flux density vs. θ with different PSA operations on the AMS port area at β=+75° |
通常,ISS长期处于正常飞行姿态,如图 15(a)所示.为了进行飞船对接、宇航员舱外行走等活动,需对ISS进行短期飞行姿态调整,其中采取正、负侧边飞行姿态较为频繁.ISS飞行姿态的改变使ISS区域与简化六面体航天器表面对应关系随之发生变化.在正常飞行姿态下(见图 15(a)),ISS左、右舷与简化六面体航天器-y、+y面对应;而在正侧边飞行姿态下(见图 15(b)),ISS前、后方与简化六面体航天器-y、+y面对应.以β=+75°为例,分析ISS飞行姿态操作对AMS外热流的影响.

|
图 15 不同飞行姿态下ISS区域与简化六面体航天器表面的对应关系示意 Figure 15 Schematic view of the relationship between the ISS areas and the simplified hexahedral surfaces with different ISS flight attitudes |
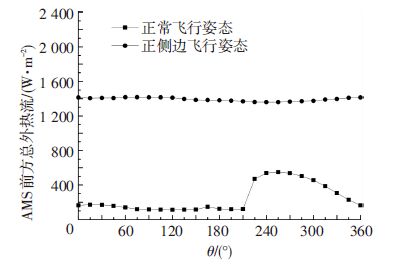
当β=+75°时,上述两种ISS飞行姿态下AMS前方总外热流随θ的变化如图 16所示.
|
图 16 在ISS不同飞行姿态下AMS前方总外热流随θ的变化(β=+75°) Figure 16 Total external flux density vs. θ with different ISS flight attitudes on the AMS ram area at β=+75° |
若ISS姿态从正常飞行调整到正侧边飞行,则AMS前方总外热流将明显增高:θ=105°时增加量最大,为1 302.23 W/m2;θ=255°时增加量最小,为809.15 W/m2.并且,AMS前方总外热流在姿态调整后的变化规律不同于调整前,调整后的数值更为稳定(平均为1 391.92 W/m2).此时,本文中基于ISS正常飞行姿态下的外热流变化规律将不再适用于调整后的正侧边飞行姿态.
5 结 论1) ISS的轨道外热流受β和θ变化的影响明显,极端工作条件主要发生在ISS进出地球阴影区、β零值和最值时.
2) ISS的固定部件对AMS的红外辐射热流较为稳定,对各项外热流的遮挡和反射在相同轨道参数下不变.
3) 在ISS操作中,右舷主散热板和左舷太阳能电池板的操作可改变AMS外热流,ISS正常飞行姿态下的AMS外热流变化规律不适用于ISS正侧边飞行姿态.
| [1] |
侯增祺, 胡金刚.
航天器热控制技术——原理及其应用[M]. 北京: 中国科学技术出版社, 2008 .
( 0) 0)
|
| [2] |
邓桂俊, 武克用. 太阳同步圆形轨道空间相机太阳辐射外热流的计算[J].
光学精密工程,1997, 5 (6) : 107-112.
DENG Guijun, WU Keyong. Calculation on space external thermal flow of sun for space camera in sun synchronous round orbit[J]. Optics and Precision Engineering,1997, 5 (6) : 107-112. (  0) 0)
|
| [3] |
孙创, 夏新林, 董士奎, 等. 外露式星载光电设备在轨热分析[J].
宇航学报,2009, 30 (2) : 775-779.
DOI: 10.3873/j.issn.1000-1328.2009.02.065 SUN Chuang, XIA Xinlin, DONG Shikui, et al. Thermal analysis for exposed photoelectric instrument on satellite[J]. Journal of Astronautics,2009, 30 (2) : 775-779. DOI: 10.3873/j.issn.1000-1328.2009.02.065 (  0) 0)
|
| [4] |
钟奇, 文耀普, 李国强. 近地热环境参数对航天器温度影响浅析[J].
航天器工程,2007, 16 (3) : 74-77.
DOI: 10.3969/j.issn.1673-8748.2007.03.014 ZHONG Qi, WEN Yaopu, LI Guoqiang. Influences of near-earth thermal environment parameters on spacecraft temperature: a first review[J]. Spacecraft Engineering,2007, 16 (3) : 74-77. DOI: 10.3969/j.issn.1673-8748.2007.03.014 (  0) 0)
|
| [5] |
李万林. 卫星空间外热流轨道参数ψ0,Ω0和ω0计算[J].
中国空间科学技术,1993 (6) : 58-61.
LI Wanlin. Calculation of orbital parameters ψ0, Ω0 and ω0 used for calculating space heat flux[J]. Chinese Space Science and Technology,1993 (6) : 58-61. (  0) 0)
|
| [6] |
徐向华, 任建勋, 梁新刚. 近地倾斜轨道航天器在轨热辐射分析[J].
太阳能学报,2004, 25 (5) : 717-721.
DOI: 10.3321/j.issn:0254-0096.2004.05.031 XU Xianghua, REN Jianxun, LIANG Xingang. Thermal radiation analysis of spacecraft on inclined near-earth orbit[J]. ACTA Energiae Solaris Sinica,2004, 25 (5) : 717-721. DOI: 10.3321/j.issn:0254-0096.2004.05.031 (  0) 0)
|
| [7] |
吴晓迪, 孙云辉, 李秩. 太阳同步轨道卫星空间热流分析[J].
激光与红外,2015, 45 (7) : 805-808.
DOI: 10.3969/j.issn.1001-5078.2015.07.015 WU Xiaodi, SUN Yunhui, LI Zhi. Spatial heat flux analysis of a satellite in the sun-synchronous orbit[J]. Laser & Infrared,2015, 45 (7) : 805-808. DOI: 10.3969/j.issn.1001-5078.2015.07.015 (  0) 0)
|
| [8] |
谭沧海, 潘增富, 钟奇, 等. 一种空间热环境综合监测仪的设计[J].
宇航学报,2014, 35 (5) : 604-610.
DOI: 10.3873/j.issn.1000-1328.2014.05.015 TAN Canghai, PAN Zengfu, ZHONG Qi, et al. Design of space thermal environment monitoring instrument[J]. Journal of Astronautics,2014, 35 (5) : 604-610. DOI: 10.3873/j.issn.1000-1328.2014.05.015 (  0) 0)
|
| [9] |
宁献文, 张加迅, 江海, 等. 倾斜轨道六面体卫星极端外热流解析模型[J].
宇航学报,2008, 29 (3) : 754-759.
DOI: 10.3873/j.issn.1000-1328.2008.03.004 NING Xianwen, ZHANG Jiaxun, JIANG Hai, et al. Extreme external heat flux analytical model for inclined-orbit hexahedral satellite[J]. Journal of Astronautics,2008, 29 (3) : 754-759. DOI: 10.3873/j.issn.1000-1328.2008.03.004 (  0) 0)
|
| [10] |
徐向华, 程雪涛, 梁新刚. 圆形太阳同步轨道卫星的空间热环境分析[J].
宇航学报,2012, 33 (3) : 399-404.
DOI: 10.3873/j.issn.1000-1328.2012.03.018 XU Xianghua, CHENG Xuetao, LIANG Xingang. Analysis on space thermal environment for circular sun-synchronous orbit[J]. Journal of Astronautics,2012, 33 (3) : 399-404. DOI: 10.3873/j.issn.1000-1328.2012.03.018 (  0) 0)
|
| [11] |
KITMACHER G H.
Reference guide to the international space station[M]. Burlington: CreateSpace Independent Publishing Platform, 2010 .
( 0) 0)
|
| [12] |
AGUILARM, ALBERTI G, ALPAT B, et al. First result from the Alpha Magnetic Spectrometer on the International Space Station: Precision Measurement of the Positron Fraction in Primary Cosmic Rays of 0.5-350 GeV[J].
Physical Review Letters,2003, 220 (25) : 141102.
DOI: 10.1103/PhysRevLett.110.141102 ( 0) 0)
|
| [13] |
ACCARDO L, AGUILARM, AISA D, et al. High statistics measurement of the positron fraction in primary cosmic rays of 0.5-500 GeV with the alpha magnetic spectrometer on the international space station[J].
Physical Review Letters,2014, 113 (12) : 121101.
DOI: 10.1103/PhysRevLett.113.121101 ( 0) 0)
|
| [14] |
AGUILARM, AISA D, ALVINO A, et al. Electron and positron fluxes in primary cosmic rays measured with the alpha magnetic spectrometer on the international space station[J].
Physical Review Letters,2014, 113 (12) : 121102.
DOI: 10.1103/PhysRevLett.113.121102 ( 0) 0)
|
| [15] |
AGUILARM, AISA D, ALPAT B, et al. Precision measurement of the proton flux in primary cosmic rays from rigidity 1 GV to 1.8 TV with the alpha magnetic spectrometer on the international space station[J].
Physical Review Letters,2015, 114 (17) : 171103.
DOI: 10.1103/PhysRevLett.114.171103 ( 0) 0)
|
| [16] |
WANG Kun, SUN Qie, SONG Lipeng, et al. Investigations on the temperature warnings of the Alpha Magnetic Spectrometer on the International Space Station[J].
Nuclear Instruments and Methods in Physics Research A: Accelerators, Spectrometers, Detectors and Associated Equipment,2015 (791) : 69-79.
DOI: 10.1016/j.nima.2015.04.021 ( 0) 0)
|
| [17] |
WANG Kun, LI Jinbo, CUI Zheng, et al. Operations of the thermal control system for Alpha Magnetic Spectrometer electronics following the beta angle of the International Space Station[J].
Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment,2014 (767) : 235-244.
DOI: 10.1016/j.nima.2014.08.010 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


