从20世纪后期开始,世界各国开展的深空探测活动日益频繁,探测目标的选择更具有挑战性,逐步转向小行星、火星等地外天体;探测方式也不断更新,从无人探测逐步向载人探测发展.美国国家航空航天局(NASA)于1989年发射了“Galileo号”探测器执行木星探测任务,在飞往木星的途中访问了Gaspra和Ida两颗主带小行星,揭开了小行星探测的序幕[1].此后,美国于1996年发射的“尼尔号”探测器也对Eros小行星进行了绕飞探测并成功着陆[2-3];日本于2003年发射的“隼鸟号”探测器成功实现了对Itokawa小行星的采样返回探测任务[4];中国的“嫦娥号”探测器于2012年成功实现了对Toutatis小行星的飞越探测[5-6].迄今为止,人类已经进行了多次无人小行星探测任务,但是无人探测始终具有局限性,任务的灵活性、有效性、可靠性均不如载人探测,很难对小行星进行深层次的科学探测.因此,载人小行星探测是解决这些问题的有效途径.
在小行星探测转移轨道设计方面,Mccue等[7]对任意两个非共面椭圆轨道之间的转移问题进行了研究,在已知转移轨道的始末位置和飞行时间的情况下,应用两脉冲转移轨道的设计方式,得到发射-到达所需的总ΔV,再通过不断地改变转移轨道的始末位置和飞行时间,获得相应的很多组发射-到达总ΔV,将所得到的发射-到达总ΔV的大小根据发射-到达日期的对应关系绘制成等高线图,即“总ΔV的等高图”,就可以寻找出最优两脉冲转移轨道的发射-到达窗口,得到初步确定的转移轨道;文献[7]最初将研究的转移轨道设计方法仅应用于以地球为中心的不同高度的轨道之间,Hulkower等[8-9]在此研究基础上,将该方法应用于太阳系内不同行星间的转移轨道设计中,为以后转移轨道优化算法的提出奠定了设计基础;Lau[10]对近地小行星的可探测性进行了分析,并对近地小行星的可探测性进行了排序;任远等[11]融合了状态转移矩阵与古典变分理论,推导了两脉冲转移轨道的性能指标对可调参数的解析偏导数,并基于此方法提出了一种快速的两脉冲轨道转移优化算法;崔平远等[12]系统地研究中国开展小行星探测任务中候选目标星的筛选方法和星际转移轨道设计方案,利用最优两脉冲转移方法,对Ivar小行星等典型小行星的交会轨道进行设计分析,给出了全局最优两脉冲交会轨道的设计参数;乔栋等[13]针对星际转移发射机会搜索问题,基于主矢量原理,提出了在转移时间固定的情况下,根据主矢量的变化情况寻找中间脉冲,搜索潜在的最优多脉冲转移发射机会,应用于多脉冲转移领域.
本文在上述研究工作的基础上,结合载人小行星探测严格的时间约束条件的同时,对单次脉冲大小进行约束,并通过序列二次规划算法进行轨道优化,对从地球停泊轨道到小行星绕飞轨道之间的往返转移轨道进行了设计与优化,该方法发射-到达窗口搜索速度明显高于绘制能量等高图.
1 载人小行星探测两脉冲轨道方案不同于载人月球探测,载人小行星探测是真正进入深空领域、脱离地球引力影响的长期性行星际飞行任务,这种任务经历是登月任务所不能取代的.从飞行距离、任务时间、任务难度而言,在载人探月、探火星、探小行星这3类任务中,载人小行星探测任务的规模居中,因此可作为载人登月和载人登火星任务之间的过渡,为载人登火星任务奠定基础.
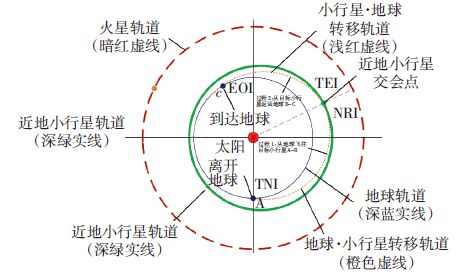
考虑未来载人深空探测任务飞行时间、运载能力、推进系统技术成熟度等约束,基于两脉冲的转移轨道方案设计仍然是载人小行星探测任务的重要选择,该轨道方案主要过程如图 1所示.首先,在地球停泊轨道对载人深空探测器组合体施加一个加速脉冲TNI(trans-NEO injection),使其进入地球-小行星Earth-Asteroid(E-A)的星际转移轨道,在接近目标小行星时,施加一个减速脉冲NRI(NEO rendezvous insertion),使载人深空探测器组合体环绕小行星伴飞,并开展星表科学探测;完成星表探测后,对探测器组合体施加一个加速脉冲TEI(trans-Earth injection),脱离目标小行星绕飞轨道,进入小行星-地球Asteroid-Earth(A-E)星际转移轨道,在探测器组合体到达地球停泊轨道附近时,施加减速脉冲EOI(Earth orbit injection)进入环地轨道.
|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 1 载人小行星探测两脉冲往返转移轨道方案描述 Figure 1 The program of two-impulse round-trip transfer trajectory for manned asteroid exploration |
两脉冲转移轨道的设计关键是求解Gauss问题[14],如果已知飞行器的始、末位置矢量(R0,Rf)、飞行时间t和飞行方向(顺行、逆行),就可以确定连接R0与Rf的转移轨道,即确定飞行器的始、末速度矢量(v0,vf).
在二体引力场中,飞行器的位置和速度矢量可以表示为:
| $\begin{align} & {{r}_{2}}=f\cdot {{r}_{1}}+g\cdot {{v}_{1}}, \\ & {{v}_{2}}=\dot{f}\cdot {{r}_{1}}+\dot{g}\cdot {{v}_{1}}. \\ \end{align}$ | (1) |
式中:r1、r2分别为飞行器初始、末端位置,km;v1、v2分别为飞行器初始、末端速度矢量,km/s;f、f·、g、g·分别满足下列方程:
| $f=1-\frac{{{r}_{2}}}{p}\left( 1-\cos \theta \right)=1-\frac{a}{{{r}_{1}}}\left( 1-\cos \Delta E \right),$ | (2) |
| $g=\frac{{{r}_{1}}{{r}_{2}}\sin \theta }{\sqrt{\mu p}}=t-\sqrt{\frac{{{a}^{3}}}{\mu }}\left( \Delta E-\sin \Delta E \right),$ | (3) |
| $\dot{f}=\sqrt{\frac{\mu }{p}}\tan \frac{\theta }{2}\left( \frac{1-\cos \theta }{p}-\frac{1}{{{r}_{1}}}-\frac{2}{{{r}_{2}}} \right)=\frac{\sqrt{\mu a}}{{{r}_{1}}{{r}_{2}}}\sin \Delta E,$ | (4) |
| $\dot{g}=1-\frac{{{r}_{1}}}{p}\left( 1-\cos \theta \right)=1-\frac{a}{{{r}_{2}}}\left( 1-\cos \Delta E \right).$ | (5) |
式中:a为转移轨道半长轴,km;ΔE为近心点角距的变化,(°);θ为r1与r2的夹角,(°);μ为引力常数;p为半正焦弦,p=h2/μ,其中h为角动量的模值,h=|r×v|,本文中p可以表示为
| $p=\frac{{{r}_{1}}{{r}_{2}}\left( 1-\cos \theta \right)}{{{r}_{1}}+{{r}_{2}}-2\sqrt{{{r}_{1}}{{r}_{2}}}\cos \frac{\theta }{2}\cos \frac{\Delta E}{2}}.$ | (6) |
对式(6)进行迭代计算,就可以求得Gauss问题的解.定义k=r1r2(1-cos θ),l=r1+r2,m=r1r2(1+cosθ),则轨道半长轴a可以表示为
| $a=\frac{mkp}{\left( 2m-{{l}^{2}} \right){{p}^{2}}+2klp-{{k}^{2}}}.$ | (7) |
飞行时间t可以表示为
| $t=g+\sqrt{\frac{{{a}^{3}}}{\mu }}\left( \Delta E-\sin \Delta E \right),$ | (8) |
由式(1)~(8)可以得出
| ${{v}_{1}}=\frac{{{r}_{2}}-f\cdot {{r}_{1}}}{g},$ | (9) |
| ${{v}_{2}}=\frac{\dot{g}\cdot {{r}_{2}}-{{r}_{1}}}{g}.$ | (10) |
由式(9)~(10)可以看出,Gauss问题的求解过程可以简化为对标量f、${\dot{f}}$、g、${\dot{g}}$进行计算,求得速度矢量v1、v2.
载人探测任务对发射机会的搜索有严格的约束条件,时间约束是其中重要的轨道约束条件之一.假设地球发射时刻为T0,到达小行星时刻为T1,离开小行星时刻为T2,返回到地球的时刻为T3,则轨道设计参数可以写成X=[T0,T1,T2,T3]T,探测轨道需要满足以下时间约束:
10 d≤T1-T0≤160 d,
0d≤T2-T1≤20 d,
10 d≤T3-T2≤160 d,
0 d≤T3-T0≤340 d.
根据以上针对交会类探测任务提出的各项约束条件,相应的搜索和优化的目标函数可定义为
| $J\left( X \right)=\Delta {{V}_{1}}+\Delta {{V}_{2}}+\Delta {{V}_{3}}+\Delta {{V}_{4}}\to \min .$ | (11) |
式中:ΔV1、ΔV2、ΔV3、ΔV4分别为T0、T1、T2、T3时刻施加的速度脉冲.相应地,各转移阶段所需施加的脉冲计算式如下:
| $\begin{align} & \Delta {{V}_{1}}=\sqrt{{{\left\| {{v}_{S}}\left( {{T}_{0}} \right)-{{v}_{\text{E}}}\left( {{T}_{0}} \right) \right\|}^{2}}+2{{\mu }_{\text{E}}}/\left( {{R}_{\text{E}}}+h \right)}- \\ & \sqrt{{{\mu }_{\text{E}}}/\left( {{R}_{\text{E}}}+h \right)}, \\ & \Delta {{V}_{2}}=\sqrt{{{\left\| {{v}_{S}}\left( {{T}_{1}} \right)-{{\upsilon }_{\text{A}}}\left( {{T}_{1}} \right) \right\|}^{2}}}, \\ & \Delta {{V}_{3}}=\sqrt{{{\left\| {{v}_{S}}\left( {{T}_{2}} \right)-{{v}_{\text{A}}}\left( {{T}_{2}} \right) \right\|}^{2}}}, \\ & \Delta {{V}_{4}}=\sqrt{{{\left\| {{v}_{S}}\left( {{T}_{3}} \right)-{{v}_{\text{E}}}\left( {{T}_{3}} \right) \right\|}^{2}}+2{{\mu }_{\text{E}}}/\left( {{R}_{\text{E}}}+h \right)}- \\ & \sqrt{{{\mu }_{\text{E}}}/\left( {{R}_{\text{E}}}+h \right)}. \\ \end{align}$ | (12) |
式中:μE为地球引力常数;RE为地球的平均半径,km;h为地球停泊轨道高度,km;vS为探测器的日心速度矢量,km/s;vE为地球的日心速度矢量,km/s;vA为小行星的日心速度矢量,km/s.
速度脉冲满足的任务约束条件为
| $\Delta {{V}_{1}}\le A,\Delta {{V}_{2}}\le B,\Delta {{V}_{3}}\le C,\Delta {{V}_{4}}\le D.$ | (13) |
对于载人小行星探测任务,考虑到宇航员所能承受的最大过载能力,一般情况下A、B、C、D的大小都不超过5,并且越小越好.
3 两脉冲往返转移轨道优化利用序列二次规划算法(sequential quadratic programming,SQP)对初步设计的两脉冲轨道进行进一步优化[15].SQP方法是求解带约束优化问题的高效方法,该方法的核心思想是:在进行每一步迭代时,都求解一个二次规划子问题,以此来确立一个下降方向,通过减少价值函数来取得步长,重复上述步骤就可以求出原问题的解.应用牛顿-拉格朗日法求解该问题的基本原理如下:
| $\left\{ \begin{array}{*{35}{l}} \min f\left( x \right), \\ \text{s}\text{.t}\text{.}{{h}_{i}}\left( x \right)=0,i\in E=1\left\{ 1,\cdots ,l \right\}. \\ \end{array} \right.$ |
式中,f(x)、hi(x)都是二阶连续可微的实函数.记h(x)=(h1(x),…,hl(x))T,则该问题的拉格朗日函数为
| $L\left( x,\mu \right)=f\left( x \right)-\sum\limits_{i=1}^{l}{{{\mu }_{i}}{{h}_{i}}\left( x \right)}=f\left( x \right)-{{\mu }^{\text{T}}}h\left( x \right),$ |
式中μ=(μ1,…,μl)T为拉格朗日乘子向量.约束函数h(x)的梯度矩阵为
| $\nabla h\left( x \right)=\left[ \nabla {{h}_{1}}\left( x \right),\cdots ,\nabla {{h}_{l}}\left( x \right) \right],$ |
则h(x)的Jacobi矩阵为A(x)=$\nabla $h(x)T,根据式(13)的KT(kuhn-tucker)条件,可以得到如下方程组
| $\nabla L\left( x,\mu \right)=\left[ \begin{array}{*{35}{l}} {{\nabla }_{x}}L\left( x,\mu \right) \\ {{\nabla }_{\mu }}L\left( x,\mu \right) \\ \end{array} \right]=\left[ \begin{matrix} \nabla f\left( x \right)-A{{\left( x \right)}^{\text{T}}}\mu \\ -h\left( x \right) \\ \end{matrix} \right]=0.$ | (14) |
用牛顿法求解上述非线性方程组(14),记函数$\nabla $L(x,μ)的Jacobi矩阵为
| $N\left( x,\mu \right)=\left[ \begin{array}{*{35}{l}} W\left( x,\mu \right) & -A{{\left( x \right)}^{\text{T}}} \\ -A\left( x \right) & 0 \\ \end{array} \right],$ | (15) |
其中
| $W\left( x,\mu \right)=\nabla _{xx}^{2}L\left( x,\mu \right)={{\nabla }^{2}}f\left( x \right)-\sum\limits_{i=1}^{l}{{{\mu }_{i}}{{\nabla }^{2}}{{h}_{i}}\left( x \right)},$ |
是L(x,μ)函数关于x的Hesse阵,式(15)也被称为KT矩阵.给定点zk=(xk,μk)的牛顿法迭代格式为
zk+1=zk+pk,
式中pk=(dk,vk)满足线性方程组:
| $N\left( {{x}_{k}},{{u}_{k}} \right){{p}_{k}}=-\nabla L\left( {{x}_{k}},{{u}_{k}} \right),$ |
即
| $\left[ \begin{matrix} W\left( {{x}_{k}},{{u}_{k}} \right) & -A{{\left( {{x}_{k}} \right)}^{\text{T}}} \\ -A\left( {{x}_{k}} \right) & 0 \\ \end{matrix} \right]\left[ \begin{matrix} {{d}_{k}} \\ {{v}_{k}} \\ \end{matrix} \right]=\left[ \begin{matrix} -\nabla f\left( {{x}_{k}} \right)+A{{\left( {{x}_{k}} \right)}^{\text{T}}}{{\mu }_{k}} \\ h\left( {{x}_{k}} \right) \\ \end{matrix} \right].$ | (16) |
只要矩阵A(xk)行满秩且W(xk,uk)是正定的,方程组(16)的系数矩阵是非奇异的,且该方程有唯一解.由于KT条件(14)是拉格朗日函数稳定点的条件,所以通常把基于求解方程(14)的优化方法称为拉格朗日法.如果用牛顿法求解该方程组,则根据牛顿法的性质,该方法具有局部二次收敛性质.
本文定义的寻优变量T=[tl,tA]T,其中tl为发射时间,tA为到达时间,则待优化的目标函数表示为式(11)所示.下面应用该方法对以下算例进行轨道优化设计.
4 仿真算例与分析根据载人小行星探测任务中,候选目标星的选星准则,综合考虑目标小行星的类型、轨道特性、绝对星等、自旋周期、发射窗口等约束条件[16-17],本文选取Nereus小行星(编号4660)作为载人小行星探测目标星.Nereus小行星的类型为Apollo小行星,直径约为330 m,公转周期为1.82 a,自转周期为15.1 h.在日心黄道坐标系下,历元2 457 000.5(2014-12-09T0)Nereus小行星的基本轨道参数,见表 1.
| 表 1 Nereus基本轨道参数 Table 1 The esential orbit parameters of Nereus Asteroid |
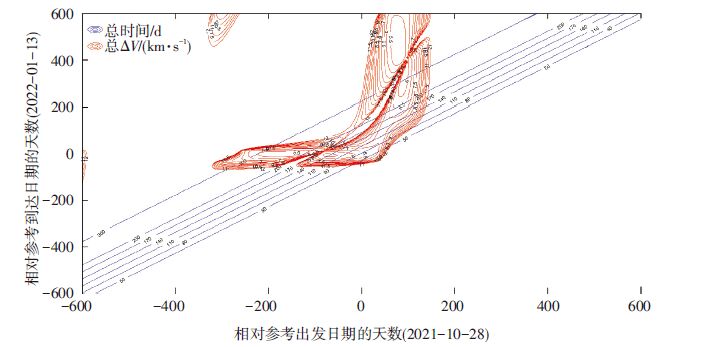
根据发射时间约束条件,可以计算出E-A段和A-E段的发射-到达总ΔV与飞行时间关系图,分别如图 2、3所示. 根据图 2、3,可初步得到地球到Nereus小行星的往返轨道初步设计参数(见表 2),其中停留星表时间14 d.
|
图 2 探测Nereus小行星E-A段总ΔV与飞行时间关系曲线 Figure 2 The total ΔV of E-Astage for Nereus Asteroid exploration with fight time |

|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 3 探测Nereus小行星A-E段总ΔV与飞行时间关系曲线 Figure 3 The total ΔV of A-E stage for Nereus Asteroid exploration with fight time |
| 表 2 地球到Nereus小行星(E-A-E)轨道方案初步设计参数 Table 2 The preliminary design parameters of transfer trajectory between Earth and Nereus Asteroid (E-A-E) |
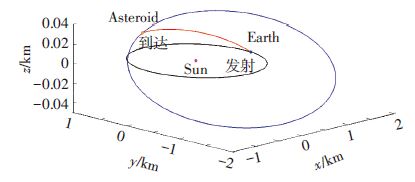
通过进一步轨道优化,设计出从地球停泊轨道飞往小行星绕飞轨道的日心转移轨道,如图 4所示,图中黑色为地球运行轨道,蓝色为小行星运行轨道,红色为日心转移轨道.
|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 4 E-A段日心转移轨道 Figure 4 The transfer trajectory of E-A stage |
表 3具体给出了J2000地心平赤道春分点坐标系下E-A段的优化轨道设计参数.探测器组合体2021年8月17日从地球停泊轨道出发,施加的加速脉冲ΔV1为3.256 766 862 km/s,到达小行星绕飞轨道的时间为2022年1月1日,施加的减速脉冲ΔV2为3.585 633 071 km/s,E-A段最优两脉冲转移轨道的总ΔV=6.842 399 933 km/s,整个E-A段优化转移飞行时间为136.826 265 d.
| 表 3 E-A段两脉冲转移轨道优化参数 Table 3 The optimal parameters of two-impulse transfer trajectory of E-A stage |
表 3中,vx、vy、vz分别为探测器的速度v在x、y、z轴的分量;vmag为探测器速度的模值大小,即
|
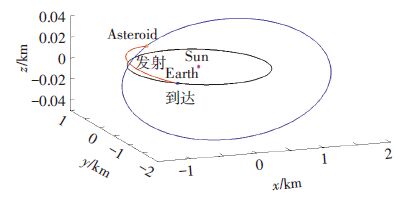
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 5 A-E段日心转移轨道 Figure 5 The transfer trajectory of A-E stage |
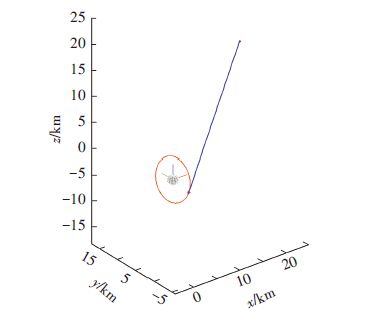
图 4,5给出的最优两脉冲转移轨道是地球停泊轨道与小行星绕飞轨道(轨道高度500 m)之间的转移轨道.图 6为以地球为中心的A-E段转移轨道,中心体为地球,红色为地球停泊轨道,蓝色为日心转移轨道,其中x、y、z轴为探测器与日心间的距离;图 7为以小行星为中心的A-E段转移轨道,中心体为小行星,红色为小行星绕飞轨道,蓝色为日心转移轨道,其中x、y、z轴为探测器与日心间的距离.通过图 6,7可以更为清楚地看到地球停泊轨道与小行星绕飞轨道附近的转移轨道情况.

|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 6 A-E段以地球为中心的转移轨道 Figure 6 The geocentric view of transfer trajectory of A-E stage |
|
注:彩图见电子版(http://hit.alljournals.cn) (2016年第10期) 图 7 A-E段以小行星为中心的转移轨道 Figure 7 The asteroid view of transfer trajectory of A-E stage |
表 4具体给出了J2000地心平赤道春分点坐标系下A-E段的优化轨道设计参数.探测器组合体2022年1月9日从小行星绕飞轨道出发,施加的加速脉冲ΔV3为4.417 889 104 km/s,到达地球停泊轨道的时间为2022年1月1日,施加的减速脉冲ΔV4为3.356 902 452 km/s,E-A段最优两脉冲转移轨道的总ΔV=7.774 791 556 km/s,整个E-A段优化转移飞行时间为160.689 203 d.
| 表 4 A-E段两脉冲转移轨道优化参数 Table 4 The optimal parameters of two-impulse transfer trajectory of A-E stage |
表 4中参数定义与表 3中相同.至此,A-E段转移任务结束.对目标小行星Nereus的整个载人飞行探测过程可以看出,整个任务的时间约束在307 d以内,其中包含在小行星表面进行9 d的科学探测,整个任务的总能量小于15 km/s.
对于载人小行星探测,转移轨道的设计部分是具有多约束条件的轨道设计,初步设计中通过能量等高线图得到的局部最优解,虽然总的速度增量较小,仅为13.739 0km/s,但是出发到达小行星后施加的脉冲ΔV2(5.258 7 km/s)和返回时从小行星出发施加的脉冲ΔV3(6.237 5 km/s)过大,严重超出宇航员能承受的最大过载.因此,在轨道优化阶段,对单次脉冲大小进行控制,在单次脉冲不超过5 km/s的约束条件下进行优化设计,最终得到符合各项约束条件的转移轨道设计参数,总的速度增量ΔV为14.617 2 km/s,单次施加脉冲最大的ΔV3为4.417 9 km/s,总体设计合理可行.
5 结 語本文针对星际转移轨道设计中发射窗口的搜索问题,结合发射-到达约束条件,通过对星历的计算和Gauss问题的求解,得到了初始转移轨道参数.利用序列二次规划算进行了轨道优化,仿真结果证明该方法收敛性好、计算效率高、边界搜索能力强,是一种有效的轨道优化方法.
| [1] |
D’AMARIO L A, BYRNES D V. Interplanetary trajectory design for the Galileo mission[C]//AIAA 21st Aerospace Sciences Meeting. Reno, NV: AIAA, 1983:10-13. DOI:10.2514/6.1983-99.
( 0) 0)
|
| [2] |
MCADAMS J V. Postlaunch contingency trajectories for the near-earth asteroid rendezvous mission[J].
Journal of Guidance, Control, and Dynamics,1997, 20 (4) : 819-823.
DOI: 10.2514/2.4118 ( 0) 0)
|
| [3] |
PEROZZI E, ROSSI A, VALSECCHI G B. Basic targeting strategies for rendezvous and flyby missions to the near-Earth asteroids[J].
Planetary and Space Science,2001, 49 (1) : 3-22.
DOI: 10.1016/S0032-0633(00)00124-0. ( 0) 0)
|
| [4] |
KAWAGUCHI J, FUJIWARA A, UESUGI T. Hayabusa-Its technology and science accomplishment summary and Hayabusa-2[J].
Acta Astronautica,2008, 62 (10/11) : 639-647.
DOI: 10.1016/j.actaastro.2008.01.028 ( 0) 0)
|
| [5] |
乔栋, 黄江川, 崔平远, 等. 嫦娥二号卫星飞越 Toutatis 小行星转移轨道设计[J].
中国科学:技术科学,2013, 43 (5) : 487-492.
DOI: 10.1360/092013-231 ( 0) 0)
|
| [6] |
ZHU Menghua, FA Wenze, HUANG Jiangchuan, et al. Morphology of asteroid (4179) Toutatis as imaged by Chang′e-2 spacecraft[J].
Geophysical, Research Latter,2014, 41 (2) : 328-333.
DOI: 10.1002/2013GL058914 ( 0) 0)
|
| [7] |
MCCUE G A, BENDER D F. Optimum transfers between nearly tangent orbits[J].
Journal of the Astronautical Sciences,1966, 13 : 72.
( 0) 0)
|
| [8] |
HULKOWER N D, LAU C O, BENDER D F. Optimum two-impulse transfers for preliminary interplanetary trajectory design[J].
Journal of Guidance, Control, and Dynamics,1984, 7 (4) : 458-461.
DOI: 10.2514/3.19878 ( 0) 0)
|
| [9] |
HULKOWER N D, ROSS D J. Missions to the asteroid anteros and the space of true anomalies[J].
Acta Astronautica,1983, 10 (3) : 42-47.
DOI: 10.1016/0094-5765(83)90032-2 ( 0) 0)
|
| [10] |
LAU C O. Accessibility of Near-Earth Asteroids[J].
Journal of Guidance, Control, and Dynamics,1987, 10 (3) : 225-232.
DOI: 10.2514/3.20207 ( 0) 0)
|
| [11] |
任远, 崔平远, 栾恩杰. 最优两脉冲行星际轨道转移优化算法[J].
航空学报,2007, 28 (6) : 1307-1310.
REN Yuan, CUI Pingyuan, LUAN Enjie. Interplanetary optimum two-impulse transfer trajectories[J]. ACTA Aeronautica ET Astronautica Sinica,2007, 28 (6) : 1307-1310. (  0) 0)
|
| [12] |
崔平远, 乔栋, 崔祜涛, 等. 小行星探测目标选择与转移轨道方案设计[J].
中国科学:技术科学,2010, 40 (6) : 677-685.
DOI: 10.1007/s11431-010-0007-6 ( 0) 0)
|
| [13] |
乔栋, 崔平远, 尚海滨. 星际探测多脉冲转移发射机会搜索方法研究[J].
北京理工大学学报,2010, 30 (3) : 275-278.
DOI: 10.15918/j.tbit1001-0645.2010.03.008 QIAO Dong, CUI Pingyuan, SHANG Haibin. Searching launch opportunity of multiple impulsive transfer for interplanetary mission[J]. Transactions of Beijing Institute of Technology,2010, 30 (3) : 275-278. DOI: 10.15918/j.tbit1001-0645.2010.03.008 (  0) 0)
|
| [14] |
乔栋. 深空探测转移轨道设计方法研究及在小天体探测中的应用[D]. 哈尔滨: 哈尔滨工业大学, 2007.
QIAO Dong. Study of transfer trajectory design method for deep space exploration and application to small body exploration[D]. Harbin: Harbin Institute of Technology, 2007. (  0) 0)
|
| [15] |
BVSKENS C, MAURER H. SQP-methods for solving optimal control problems with control and state constraints: adjoint variables, sensitivity analysis and real-time control[J].
Journal of Computational and Applied Mathematics,2000, 120 (1/2) : 85-108.
DOI: 10.1016/S0377-0427(00)00305-8 ( 0) 0)
|
| [16] |
CUI Pingyuan, QIAO Dong, CUI Hutao, et al. Target selection and transfer trajectories design for exploring asteroid mission[J].
Science China Technological Sciences,2010, 53 (4) : 1150-1158.
DOI: 10.1007/s11431-010-0007-6 ( 0) 0)
|
| [17] |
王悦, 刘欢, 王开强, 等. 载人探测小行星的目标星选择[J].
航天器工程,2012, 21 (6) : 30-36.
WANG Yue, LIU Huan, WANG Kaiqiang, et al. Target selection for Human exploration of Asteroid[J]. Spacecraft Engineering,2012, 21 (6) : 30-36. (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


