随着纳米卫星、小卫星的应用与推广,卫星系统的测点设置受到体积的限制,卫星系统的故障检测、诊断只能利用较少的观测变量.广泛使用的闭环控制使得航天器的早期故障难以被检测[1].航天器长期在失重、高低温交变等恶劣的环境中运行,早期故障容易恶化,最终导致系统部件失效,进而产生灾难性的后果[2],因此,早期故障检测能够帮助卫星提早隔离故障部件,合理规划卫星任务,降低运行成本.
针对飞轮的故障检测问题,目前研究主要集中在各种观测器的设计.利用观测器能精确的识别、检测飞轮的故障参数,但数学公式的推导、证明非常复杂.例如:基于迭代学习型的观测器[3]能通过自主迭代学习算法精确的估计飞轮的故障.正交匹配追踪算法[4](OPM)能够用于追踪飞轮系统的瞬时故障和缓变故障.自适应的神经元参数估计方法[5]能够利用飞轮系统多个输入、输出量对非线性系统建模,并检测、分离飞轮系统的故障.未知输入观测器[6]通过分析残差向量的变化对飞轮的传感器以及系统的故障参数进行检测、分离.基于扩展卡尔曼滤波的动量轮故障检测方法[7]将动量轮的物理模型参数扩展为状态空间的状态量,实现飞轮物理参数的实时跟踪与检测.基于自适应观测器与扩张状态观测器的综合观测器[8]能在执行器输出量不可得的限制条件下实现故障检测,并获得飞轮的真实输出估计.自适应的神经模糊推理系统[9](ANFIS)能够利用系统观测变量的输入、输出与信号指令等数据来估计飞轮的物理参数,从而检测飞轮系统的故障.算法的收敛性是上述模型设计的关键问题,建模精度会影响算法的收敛性.对无法精确建模的物理系统,基于数据分析[10]的故障检测方法能避免物理建模,根据观测数据,利用概率推理实现航天器的故障检测、诊断.
针对物理建模或者参数获取存在困难的复杂系统,本文从观测数据出发,进行故障检测,避免物理建模;上述的故障检测方法要求多个观测变量,而本文只需要一个观测变量.利用所有变量进行故障检测将增加航天器系统的操作与维护成本.基于符号动力学[11-13]的模型能够简单、快速的提取系统的非线性特征,因此,基于符号动力学的单变量故障检测方法能简单、快速的提取飞轮的非线性特征,而字符映射使得该方法能够快速处理大量的观测数据,适合卫星实时在线故障检测.且字符映射能够降低系统噪声的影响,使得本文算法能够更加容易检测飞轮的微弱故障.基于上述原因,本文建立飞轮系统的Simulink仿真模型,设置两种故障并采集相应的电流信号,利用符号动力学模型构建电流信号的状态转移矩阵,并计算健康状态的字符概率距离,通过设定的阈值检测飞轮系统的故障.
1 飞轮模型常见的飞轮系统故障类型[14]主要有:轴承卡死、轴承性能异常、电机不转、电机性能下降、壳体与轮体组件异常等几类故障模式.按照故障变化的快慢可以划分为缓变故障与突变故障.而早期故障一般都是一类缓变故障,随着时间推移慢慢影响飞轮的性能,本文为了模拟早期故障,调整故障参数,产生一组不同故障幅值的故障数据.主要有电机增益变小故障与摩擦力力矩增大故障.
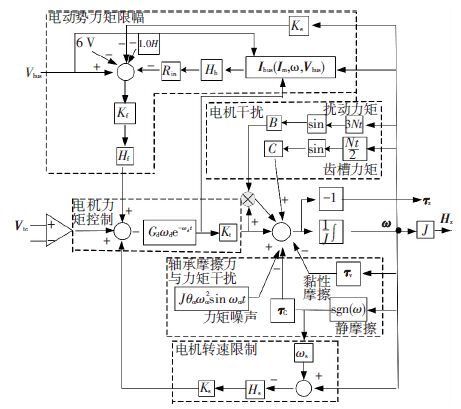
1.1 飞轮模型根据文献[15]给出的ITHACO-A型飞轮的数学模型,建立基于Simulink的飞轮高精度开环系统仿真模型,如图 1所示.
|
图 1 飞轮高精度开环系统仿真模型 Figure 1 High accurate simulation model of flywheel |
图 1中的相关参数介绍如下:Vtc为等效的直流电动机驱动控制力矩,主要是电压控制;Gd为电机驱动增益;ωd为驱动带宽;Im为电机电流;Kt为电机转动系数;Ke为电机电动势反馈系数;Ibus为母线电流;Vbus为母线电压;Rin为输入电阻;Kf为电压反馈增益;τv为滑动摩擦力矩;τC为静摩擦力矩,也叫库伦摩擦力矩;τz为控制力矩;J为飞轮转动惯量;θα为力矩噪声引起的角误差;ωα为高通噪声滤波器频率;ωs为转速限制阈值;Ks为转速限制增益系数;ω为飞轮的实时转速.
1.2 动量轮开环系统的数学模型根据图 1的仿真模块,建立飞轮开环系统的状态空间模型为
| $\left[ \begin{matrix} {{{\dot{I}}}_{m}} \\ {\dot{\omega }} \\ \end{matrix} \right]=\left[ \begin{matrix} {{G}_{\text{d}}}{{\omega }_{\text{d}}}\left[ {{\psi }_{1}}\left( {{I}_{m}},\omega \right)-{{\psi }_{3}}\left( \omega \right) \right]-{{\omega }_{d}}{{I}_{m}} \\ \frac{1}{J}\left[ {{K}_{t}}{{I}_{m}}-{{\tau }_{C}}{{\psi }_{2}}\left( \omega \right)-{{\tau }_{v}}\omega \right] \\ \end{matrix} \right]+\left[ \begin{matrix} {{G}_{\text{d}}}{{\omega }_{\text{d}}} \\ 0 \\ \end{matrix} \right]{{V}_{\text{tc}}},$ | (1) |
| ${{\tau }_{\text{z}}}={{k}_{\text{t}}}{{I}_{m}}.$ | (2) |
式中:ψ1(Im,ω)、ψ2(ω)、ψ3(ω)分别描述了电动势力矩限制、轴承摩擦力与力矩干扰、电机转速限制这3个非线性模块.飞轮仿真模型的参数设置见表 1.
| 表 1 飞轮参数 Table 1 Flywheel parameters |
式(1),(2)反映了飞轮在姿态控制过程中,电流与系统状态的关系密切,系统的闭环控制必然引起电流的变化,通过分析电流的变化规律能够发现系统的早期故障特征.因此,本文主要分析的信号是飞轮的电流信号.
2 非线性系统的特征提取针对非线性系统,其动态特征提取主要通过相平面分析、小扰动线性化、仿真分析等方法完成,主要从非线性方程中提取动态系统的固有模式.例如:平衡点的个数、自持振荡现象.而从非线性系统的观测数据进行非线性分析,主要通过信号处理的方法完成特征提取.利用信号处理的技术提取非线性系统的固有模式.一般可分为:
1) 信号预处理.主要是对样本数据进行降噪,利用时域、频域或者时频域的分析方法对数据进行降噪处理.
2) 相空间重构技术. 基于采样定理,利用时间延迟变量来重构状态向量为
x(n)=[y(n),y(n+T),…,y(n+(dE-1)T)].
式中: T为时间延迟变量,dE为相空间的维度.
3) 信号分类. 信号分类与识别主要依据系统的不变量.这类不变量具有吸引子的性质,这类不变量并不局限于某一特殊的相轨迹.在非线性问题中主要有两类不变量:分形维数与李雅普洛夫指数.
4) 建模与预测. 主要是确定动态模型的参数,判断参数是否与不变量(李雅普洛夫指数与分形维数)一致.
上述3个步骤主要是分析随机系统,并提取随机系统的自由度或者复杂度,从而用最简单的结构去表示随机系统的基本特征或者固有模式.最后步骤是利用基本特征定义系统行为,并用于判断系统的异常状态或者早期故障.
在非线性系统中,慢变参数能缓慢的改变非线性系统的长周期变化规律.符号动力学方法利用提取时间序列的长周期特征实现早期故障检测,符号化映射能实现信号降噪.字符序列的统计量能同时分析信号的长周期与短周期变化细节.利用D阶马尔科夫过程定义字母符号序列的固有模式,提取非线性系统的周期性特征.因此,基于符号动力学的特征提取方法能够简单、快速的处理非线性系统的数据,并提取非线性系统的周期性特征,避免了复杂的非线性方程求解.
2.1 非线性系统的符号化映射假设一个连续随机系统的物理过程可以利用如下方程表示:
| $\frac{\text{d}x\left( t \right)}{\text{d}t}=f\left( x\left( t \right),\theta \left( {{t}_{s}} \right) \right);x\left( 0 \right)={{x}_{0}}.$ | (3) |
式中:t∈0,∞为快速变化的时间;ts为慢速变化的时间;x∈Rn为相空间的状态向量;θ∈Rl为式(3)关系式中的缓慢变化的(慢变)参数,系统的微弱故障可能由此参数引起,这里定义为早期故障.实际问题中的函数关系式有可能由于未知参数、非参数的不确定性以及噪声的影响,很难获取准确的表达式,从而导致早期故障难以被检测,但是通过对系统产生的时间序列进行分析,可以学习系统中存在的行为(寻找时间序列中存在的不变量).系统状态可以由一组时间序列表示,在式(3)中的相空间就可以通过一组区间(网格)划分为不同的子区间.这类闭合子区间为:B≡{B0,…,Bm-1},这里假设有m个子区间,且满足Bj∩Bk=∅,∀j≠k.第i时刻的信号序列所对应的字符区间B是由字符sij表示,即:当对应的信号序列x0(ti)∈Bj时,则信号序列在i时刻所对应的字符为sij,因此,对于一段时间内的信号序列x0有如下变换:
| ${{x}_{0}}\to {{s}_{i1}}{{s}_{i2}}{{s}_{i3}}\cdots {{s}_{ik}}\cdots .$ | (4) |
最终,通过字符集合把一个时间序列信号分割为不同的子区间序列,每个子区间通过一个字母表示,如式(4)所示,这种映射也叫动态系统符号化映射.使得一个连续随机的时间序列通过字母符号化进行离散变换,变成一组不同字母组合的符号序列.
时间序列数据通过子区间进行分割,相空间的信号由于离散而丢失一部分系统信息.这类丢失的信息可能是测量噪声、误差或者初始条件引起的变异信息.但字母组合能够保留系统的主要特征,例如,相轨迹的周期性和吸引子等特征.
2.2 字符序列的特征提取针对一串连续的符号序列,需要定义这串序列的变化规律,通常有两种机器学习方法[16],主要有ε机器学习和D阶马尔科夫机器学习方法.本文选择D阶马尔科夫机器学习方法提取符号序列的固有特征的主要原因是利用D阶马尔科夫链描述系统的状态演变过程会使得符号序列的特征向量具有相同的维度,从而使得异常程度或者故障程度的计算相对简单.
考虑一组字符串序列包含了系统的某一规律(周期性),D阶马尔科夫机器学习方法可以定义系统的有效状态(周期性转移的有效状态).某一周期内的字符串组合的长度看作D∈N,且字符的独立不重复组合定义如下:
q(D,s)={SD∈S:SD=s}.
在字符序列中存在独立不重复的字符串排列组合,其对应的集合Q(D)代表符号动力学特征提取的有效状态,且不同状态的组合个数记为|Q(D)|=|A|D,而|A|表示字符的个数.有效状态的转移概率如下:
| ${{\pi }_{jk}}=P\left( s\in {{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftarrow}$}}{S}}}^{1}}|{{q}_{j}}\in Q,\left( s,{{q}_{j}} \right)\to {{q}_{k}} \right),\sum\limits_{k}{{{\pi }_{jk}}=1,}$ | (5) |
其中,状态转移的概率计算公式如下:
| ${{\pi }_{jk}}=\frac{P\left( {{s}_{{{i}_{1}}}}\cdots {{s}_{{{i}_{D}}}}s \right)}{P\left( {{s}_{{{i}_{1}}}}\cdots {{s}_{{{i}_{D}}}} \right)}\approx \frac{N\left( {{s}_{{{i}_{1}}}}\cdots {{s}_{{{i}_{D}}}}s \right)}{N\left( {{s}_{{{i}_{1}}}}\cdots {{s}_{{{i}_{D}}}} \right)}.$ | (6) |
状态转移概率是有效状态qj=si1…siD向有效状态qk=si1…siDs转移而出现的可能性.
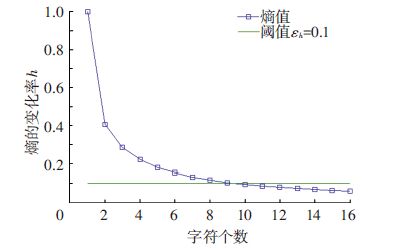
2.3 字符个数的确定符号个数的选择对于符号动力学系统建模至关重要,最优的字符个数能够帮助符号动力学模型更准确地提取系统的非线性特征,同时有效地降低噪声的干扰;较少的字符个数导致系统特征的细节丢失,但是太多的字符个数会导致信息冗余,且浪费计算资源.本文采用一种基于熵值变化率的指标来确定字符个数,使得字符个数取值达到最优,如图 2所示.
| $H\left( k \right)=-\sum\limits_{i=1}^{i=k}{{{p}_{i}}}{{\log }_{2}}{{p}_{i}}.$ | (7) |
|
图 2 基于熵值变化率的字符个数选择 Figure 2 Selection of number of symbols from change in entropy |
式中:pi为字符si出现的概率,且有H(1)=0.通过熵的变化率h(k)选择合理的字符个数[17],即
| $h\left( k \right)\triangleq H\left( k \right)-H\left( k-1 \right),\forall k\ge 2.$ | (8) |
h是一个量纲一的变量,从图 2中可以看出:熵值的变化率会随着字符个数的增加单调递减,表明字符个数的增加会降低熵值的变化率.虽然较低的熵值变化率使得模型能够更加准确的提取系统的微弱变化,但同时会增加故障检测的计算量.微弱故障检测能力与模型的计算量需要平衡,最优的字符个数才能够使算法的性能最优.因此,字符个数的选择应该使得熵值变化率相对较小,且用较少的字符.本文设置熵值变化率的阈值为εh=0.1,相应的字符个数为9.
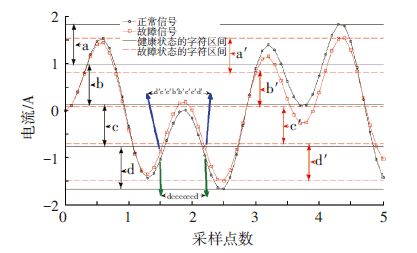
2.4 字符序列的故障检测原理分析假设电流信号服从杜芬方程的变化规律,且字符个数选取4.则字符a、b、c、d分别代表了正常信号的字符区间,而a′、b′、c′、d′则分别代表了故障信号的字符区间.故障参数θ能够引起电流信号幅值、周期的微弱变化,从而导致故障信号的字符区间发生变异,与故障对应的电流字符序列会重新组合.
例如:在图 3中,选取某一段电流信号.根据式(4),将健康状态的电流数据转换为对应的字符序列“dccccccd”,而故障状态的电流数据转换为对应的字符序列“d′c′c′b′b′c′c′d′”.字符序列已经重新组合.因此,重新组合的字符序列能够反映电流信号的故障.
|
图 3 字符序列的重新组合 Figure 3 The recombination of symbol sequence |
虽然状态转移矩阵能够定义系统的行为,但是健康与故障状态下的差异性难以通过状态转移矩阵的计算加以区分.而状态转移矩阵中具有单位值的概率特征向量能够代表系统的固有特征.因此,本文用向量的距离代替两个矩阵的距离.实际信号由于噪声干扰以及系统动态变化的影响,不同时间段的样本所对应的字符概率特征向量肯定存在一定的差异性,健康状态的字符概率特征向量之间的差异性需要定义一个合理的阈值.待测状态的字符概率特征向量在该范围内变化视为正常,否则故障.通过下式就能合理反映不同健康状态之间的差异.
δ=‖pT-pH‖.
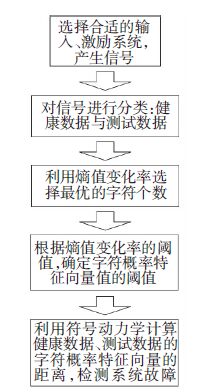
式中:pH为健康数据的字符概率特征向量(symbol probability vector) ;pT为测试数据的字符概率特征向量;δ反映了健康数据与测试数据之间的字符概率距离.因此,飞轮系统的符号动力学故障检测方法的流程如图 4所示.
|
图 4 飞轮系统的符号动力学故障检测流程 Figure 4 The fault detection of flywheel system based on symbolic dynamic filter |
Step 1 非线性系统的输入会引起系统状态的改变,不同的激励信号使得系统的正常特征产生较大的波动.结合式(1)、(2),利用Simulink仿真模型获取飞轮系统在指定工作状态下的电流信号序列集合.
Step 2 信号分类.主要是调整故障参数幅值,当故障偏差幅值取零时,假定为系统健康数据;当故障偏差幅值增大时,假定为测试数据.
Step 3 状态转移矩阵通过式(6)获取,式(7)计算状态转移矩阵的熵,式(8)计算状态转移矩阵的熵值相对于字符个数的变化率.根据图 2确定最优的字符个数.
Step 4 字符概率特征向量的阈值能反映健康状态的扰动范围.式(9)能够反映两个字符概率特征向量之间的距离.简称字符概率距离.而这种距离是基于状态转移矩阵的熵,它的大小与系统噪声有一定的关系.因此,阈值设置应参考熵率的取值.
Step 5 利用式(10)实现飞轮系统的故障检测,当δ大于阈值时,飞轮系统出现故障;否则,飞轮系统正常.
由于字符概率距离是一种向量的距离,本文选择余弦的反函数,描述健康字符概率特征向量与故障字符概率特征向量之间的距离,计算公式如下:
| $M=\arccos \left( \frac{\left\langle {{p}_{\text{F}}},{{p}_{\text{H}}} \right\rangle }{{{\left\| {{p}_{\text{F}}} \right\|}_{2}}{{\left\| {{p}_{\text{H}}} \right\|}_{2}}} \right).$ | (9) |
式中,〈x,y〉是向量x与y的内积,而 ‖x‖2是向量x的欧拉距离.与传统的欧拉距离相比,利用向量夹角的反余弦值能准确、直观地反映微弱故障与正常状态之间的差异性.距离指标M反映了故障信号序列的长周期偏离正常信号序列的严重程度.
对多个正常状态的时间序列(健康数据样本集合)进行符号化映射,能够得到一系列字符概率距离.这个距离反映了正常状态偏离期望状态的程度.对字符概率特征向量距离的集合进行分析,取最大值作为该指标的阈值.当新获取的测试数据属于正常状态时,满足下式所定义的条件.否则,测试数据为故障数据.
| $M\le {{M}_{\varepsilon }}.$ | (10) |
M是量纲一的变量.然而,系统噪声使得健康数据在一定范围内波动.字符概率距离的阈值Mε与系统内部参数变化无关,阈值设置应该考虑系统噪声的影响.这种不确定性导致字符概率距离存在一定的波动.字符个数越少,符号动力学模型的降噪能力越强,对应的字符概率阈值越小;而字符个数越多,符号动力学模型的降噪能力变弱,对应的字符概率阈值越大.参考熵值的变化率,这里选择Mε=0.1.
3 飞轮系统的故障检测小卫星由于体积的限制,只能布置少量的系统观测点,卫星系统中重要的部件至少有一个状态观测变量,这类重要的观测量包含系统的早期故障特征.工程中常见的故障检测方法是单变量阈值检测方法,单变量故障检测具有简单、快速的优点,数据存储少,实时性强,适用于星载计算机,能够完成卫星实时在线的故障检测、诊断.
符号动力学[18]能用于非线性系统的异常检测或者早期故障的预测分析.符号动力学[19]计算简单、快速,对数据量要求小,能够有效分析复杂非线性系统的变化规律.而飞轮的控制方程也可以看作一个非线性方程,电流信号就能反映飞轮系统的动态变化过程.
飞轮的转速始终通过电流驱动,当飞轮系统出现故障时,飞轮转速会产生异常扰动,但闭环控制会通过电流的增加或者减少实现目标转速的扰动补偿.因此,卫星动量轮的异常检测主要针对飞轮的电流信号.本文的指定工作状态:小卫星在姿态保持过程中,为了抵抗空间干扰力矩的作用,卫星利用飞轮的动量矩交换实现卫星姿态的保持,飞轮转速将围绕目标转速波动.飞轮的电流能够反映系统的异常扰动.此过程中设置了飞轮电机增益变小与飞轮摩擦力力矩增大的故障.为了体现微弱故障检测能力,仿真给出了5个不同故障幅值的故障数据.
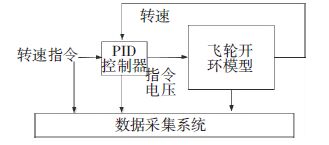
飞轮闭环系统为一个速度反馈系统(图 5),确保目标转速的鲁棒性,但同时增加故障检测的难度.系统包括:飞轮开环模型、飞轮转速PID控制器和飞轮数据采集系统.
|
图 5 飞轮闭环系统框图 Figure 5 Block diagram of the closed system with flywheel system |
飞轮转速控制器的(PID)参数设置:比例系数0.1、积分系数0.1、微分系数0.1;系统仿真过程中,电机电流、飞轮转速的初始值取0,其他对应的物理参数选取无故障时相应的取值;仿真系统的步长0.01 s,仿真时间为400 s,故障发生时间是200 s,一次采样40 000点.
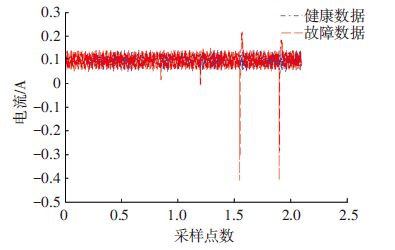
3.1 电机增益变小故障如图 6所示,第1段数据为飞轮电流的健康数据,飞轮的电机增益变小故障仿真5次,一共有6个观测数据,为对比分析,6段数据放在同一图中.电机增益参数的故障幅值为健康取值的比例分别为:1.00、0.99、0.95、0.90、0.70、0.50,对应的故障参数偏差幅值分别为:0、0.01、0.05、0.10、0.30、0.50.由于飞轮在健康状态下存在一定的动态调整过程,使得电流信号存在一个阶跃变化,而为了检测幅值更小的故障,需要消除这类正常扰动的影响.因此,符号动力学模型只分析电流从50~400 s之间的数据,即相对稳定的数据.采样点数为35 000,6段数据共有210 000个点.
根据图 6所示,第1、2段数据的差异性非常微弱,难以区分.主要是噪声力矩使得电流信号存在正常的波动范围,故障引起的波动与噪声引起的波动相差微弱,导致两种状态难以区分;而第5、6段的数据明显超出了电流正常的波动范围,但是通过闭环控制的调整,电流又回到正常的波动范围.因此,随着故障偏差幅值的增加,在故障初期的电流阶跃扰动越来越明显,但又快速回到正常波动范围,使得故障状态与正常状态难以区分.
|
图 6 电机增益变小故障的飞轮电流 Figure 6 The current of flywheel under the motor gain decrease fault |
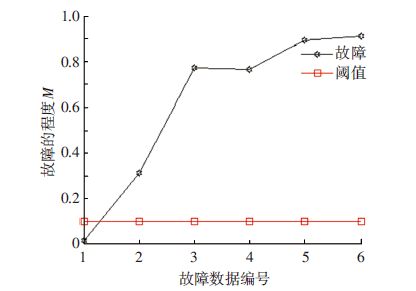
根据飞轮系统符号动力学故障检测模型的流程图(图 4),计算健康状态与故障状态的字符概率距离,具体的计算结果如图 7所示. 随着故障偏差幅值的增加,对应的字符概率距离变大.由于第5、6段数据的故障差异性更加明显,导致对应的字符概率距离比其余故障的字符概率距离大.
|
图 7 电机增益故障的检测结果 Figure 7 The fault detection of the motor gain decrease fault |
基于扩展卡尔曼滤波[7]的故障检测方法将飞轮的故障检测视为系统参数辨识与跟踪问题.为便于计算,将式(1)表示为线性离散状态空间的时变形式.在物理建模的过程中忽略飞轮系统的3个非线性函数,并将飞轮的非线性函数简化为
| $\left\{ \begin{array}{*{35}{l}} \dot{X}\left( t \right)=FX\left( t \right)+BU\left( t \right), \\ Y\left( t \right)=X\left( t \right). \\ \end{array} \right.$ | (11) |
| $F=\left[ \begin{matrix} -\frac{{{R}_{\text{A}}}}{{{L}_{\text{A}}}} & -\frac{\Psi }{{{L}_{A}}} \\ \frac{\Psi }{J} & -\frac{{{M}_{\text{f}}}}{J} \\ \end{matrix} \right].$ | (12) |
式(12)中给出了飞轮系统的物理参数与系数矩阵的对应关系.飞轮故障检测的目标是识别矩阵系数F中的物理参数.电机增益变小的故障相当于磁通量变小的故障.图 8是飞轮增益变小故障的检测结果,在图 8中,可以看到物理参数的取值通过飞轮的3个变量可以得到实时跟踪.故障偏差幅值设为0.1.

|
图 8 扩展卡尔曼滤波算法的故障检测结果 Figure 8 The fault detection by Extended Kalman Filter algorithm |
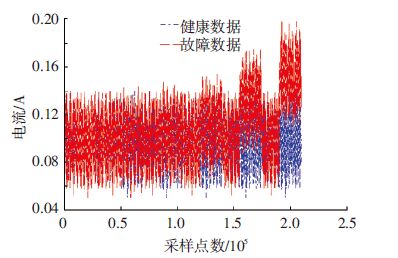
如图 9所示,第1段数据为飞轮电流的健康数据,飞轮的电机增益故障采集了5次,一共有6个观测数据,为对比分析,将6段数据放在同一图中.电机摩擦力力矩参数的故障幅值为健康取值的比例分别为:1.00、1.01、1.05、1.10、1.30、1.50,对应的故障参数偏差幅值分别为:0、0.01、0.05、0.10、0.30、0.50.由于飞轮在健康状态下存在动态调整过程,使得电流信号存在一个阶跃变化,而为了检测幅值更小的故障,需要消除这类正常扰动的影响.因此,符号动力学模型只分析电流从50~400 s之间的数据,即相对稳定的数据.采样点数为35 000.6段数据共有210 000个点.
根据图 10所示,第2、3、4段数据与第1段数据的差异性非常的微弱,难以区分.对比图 9与图 6的电流变化,电机增益变小故障直接影响飞轮电流,而摩擦力矩增大故障是通过转速变化间接影响飞轮电流.当故障幅值足够大时,电机电流超出了健康状态的波动范围.闭环控制为了抑制摩擦力力矩增大故障的影响,飞轮只能增加电流输出.因此,摩擦力矩增大故障能够显著的增加飞轮系统的能耗,对系统危害更大.从图 9的第6、7段数据可以看到:异常扰动的电流不能回到正常的波动范围.随着故障偏差幅值的增加,电流的扰动幅值增加.故障状态与正常状态之间的差异性更明显.
|
图 9 摩擦力力矩增大故障的飞轮电流 Figure 9 The current of flywheel in the motor friction increase fault |
根据飞轮系统符号动力学故障检测模型的流程图(图 4),计算健康状态与故障状态的字符概率距离,具体的计算结果如图 10所示. 随着故障偏差幅值的增加,对应的字符概率距离变大.

|
图 10 摩擦力力矩故障的检测结果 Figure 10 The current of flywheel in the motor friction increase fault |
对比图 7与图 10的字符概率距离,都超出了阈值控制线 Mε=0.1,本文所提的方法能够检测飞轮的微弱故障或者早期故障.此外,早期故障的物理模型难以获取,而相关的观测数据却容易得到,对于实际问题中的早期故障,基于数据的方法比基于模型的方法更适合早期故障检测的研究.
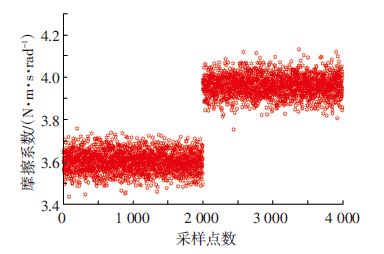
摩擦力矩增大的故障相当于摩擦力矩系数增大的故障,图 11是飞轮系统摩擦力力矩增大故障的检测结果,故障偏差幅值设为0.1.图 8的故障检测结果要比图 11的故障检测结果更准确,主要原因是噪声方差使得摩擦力矩参数估计值的方差变大.
|
图 11 扩展卡尔曼滤波算法的故障检测结果 Figure 11 The fault detection by Extended Kalman Filter algorithm |
将该方法与本文方法进行对比:首先,对比变量个数,该方法需要飞轮转速、指令电压、飞轮电流3个观测量,而本文方法只需飞轮系统的电流信号.其次,本文方法只关注飞轮的数据特征,而基于模型的方法注重算法的收敛度与精度分析,推导过程严密,在建模过程中需要忽略飞轮状态方程的3个非线性项.因此,当求解的物理方程变为更复杂的非线性方程时,求解过程会遇到较大的困难.最后,系统状态方程的精确表达式在实际工程中很难精确获取,而系统中变量的观测数据相对容易获取,工程应用性强.且本文算法的可移植性强,能够用于卫星其他部件的故障检测.
4 结 论1) 本文提出了一种基于字符概率特征向量的故障检测方法.与基于模型的故障检测方法对比分析,本文只需要单一变量的观察数据进行故障检测,单变量故障检测能够减少观测点的设置,降低卫星系统的维护成本,且工程数据获取比模型参数获取相对容易.
2) 本文算法是从数据中学习系统的行为,描述待测样本偏离学习样本的程度.因此,本文算法能够避免复杂的数学建模,工程中易于实施.且算法的降噪能力强,具有可移植性、数据处理量大.本文算法具有简单、快速的优点,适合星上实时的故障检测.
| [1] |
周东华, 刘洋, 何潇. 闭环系统故障诊断技术综述[J].
自动化学报,2013, 39 (11) : 1933-1943.
DOI: 10.3724/SP.J.1004.2013.01933 ZHOU Donghua, LIU Yang, HE Xiao. Review on fault diagnosis techniques for closed-loop systems[J]. ACTA Automatica Sinica,2013, 39 (11) : 1933-1943. DOI: 10.3724/SP.J.1004.2013.01933 (  0) 0)
|
| [2] |
CHANDOLA V, BANERJEE A, KUMAR V. Anomaly detection: A survey[J].
ACM Computing Surveys (CSUR),2009, 41 (3) : 1-58.
DOI: 10.1145/1541880.1541882 ( 0) 0)
|
| [3] |
ZHANG Aihua, HU Qinglei, ZHANG Youmin. Observer-based attitude control for satellite under actuator fault[J].
Journal of Guidance, Control, and Dynamics,2015, 38 (4) : 806-811.
DOI: 10.2514/1.G000625 ( 0) 0)
|
| [4] |
WANG Zhenhua, SHEN Yi, ZHANG Xiaolei, et al. Fault diagnosis for satellite attitude control systems with four flywheels[J].
Journal of Dynamic Systems, Measurement, and Control,2014, 136 (4) : 0410161-0410164.
DOI: 10.1115/1.4026515 ( 0) 0)
|
| [5] |
SOBHANI-TEHRANI E, TALEBI H A, KHORASANI K. Hybrid fault diagnosis of nonlinear systems using neural parameter estimators[J].
Neural Networks,2014, 50 : 12-32.
DOI: 10.1016/j.neunet.2013.10.005 ( 0) 0)
|
| [6] |
曲春娣, 张洪钺. 卫星动量轮闭环系统的UIO双观测器故障诊断[J].
航天控制,2005, 23 (6) : 66-71.
DOI: 10.3969/j.issn.1006-3242.2005.06.016 QU Chundi, ZHANG Hongyue. The fault diagnosis of momentum close-loop system used in satellite based on the UIO double observers[J]. Aerospace Control,2005, 23 (6) : 66-71. DOI: 10.3969/j.issn.1006-3242.2005.06.016 (  0) 0)
|
| [7] |
李知周, 张锐, 朱振才, 等. 基于扩展卡尔曼滤波的动量轮故障检测方法[J].
航空学报,2010, 31 (8) : 1614-1621.
LI Zhizhou, ZHANG Rui, ZHU Zhencai, et al. Extended Kalman filter-based fault detection for momentum wheel[J]. ACTA Aeronautica et Astronautica Sinica,2010, 31 (8) : 1614-1621. (  0) 0)
|
| [8] |
岑朝辉, 魏蛟龙, 蒋睿, 等. 基于综合观测器的执行器过程故障量精确诊断[J].
宇航学报,2011, 32 (6) : 1318-1326.
DOI: 10.3873/j.issn.1000-1328.2011.06.018 CEN Zhaohui, WEI Jiaolong, JIANG Rui, et al. Accurate diagnosis on process fault parameters of nonlinear actuator based on adaptive observer and extended state observer[J]. Journal of Astronautics,2011, 32 (6) : 1318-1326. DOI: 10.3873/j.issn.1000-1328.2011.06.018 (  0) 0)
|
| [9] |
BELLALI B, HAZZAB A, BOUSSERHANE I K, et al. Parameter estimation for fault diagnosis in nonlinear systems by ANFIS[J].
Procedia Engineering,2012, 29 : 2016-2021.
DOI: 10.1016/j.proeng.2012.01.254 ( 0) 0)
|
| [10] |
沈毅, 张攸磊, 王振华. 基于EMD和有向因子图的航天器故障诊断[J].
哈尔滨工业大学学报,2013, 45 (1) : 19-24.
SHEN Yi, ZHANG Xiaolei, WANG Zhenhua. Spacecraft fault diagnosis based on empirical mode decomposition and directed factor graph[J]. Journal of Harbin Institute of Technology,2013, 45 (1) : 19-24. (  0) 0)
|
| [11] |
BAHRAMPOUR S, RAY A, SARKAR S, et al. Performance comparison of feature extraction algorithms for target detection and classification[J].
Pattern Recognition Letters,2013, 34 (16) : 2126-2134.
DOI: 10.1016/j.patrec.2013.06.021 ( 0) 0)
|
| [12] |
陈冲, 丁炯, 张宏, 等. 累积放电模型及其符号动力学研究[J].
物理学报,2013, 62 (14) : 49-55.
DOI: 10.7498/aps.62.140502 CHEN Chong, DING Jiong, ZHANG Hong, et al. Study of an integrate-and-discharge model with symbolic dynamics[J]. Acta Physica Sinica,2013, 62 (14) : 49-55. DOI: 10.7498/aps.62.140502 (  0) 0)
|
| [13] |
王松岭, 许小刚, 刘锦廉, 等. 基于符号动力学信息熵与改进神经网络的风机故障诊断研究[J].
华北电力大学学报(自然科学版),2013, 40 (4) : 51-58.
DOI: 10.3969/j.ISSN.1007-2691.2013.04.09 WANG Songling, XU Xiaogang, LIU Jinlian, et al. Fault diagnosis of fan based on symbolic dynamics entropy and improved neural network[J]. Journal of North China Electric Power University,2013, 40 (4) : 51-58. DOI: 10.3969/j.ISSN.1007-2691.2013.04.09 (  0) 0)
|
| [14] |
厉海涛, 金光, 周经伦, 等. 动量轮在轨状态可靠性贝叶斯网络建模与评估[J].
航空学报,2009, 30 (6) : 1084-1089.
DOI: 10.3321/j.issn:1000-6893.2009.06.019 LI Haitao, JIN Guang, ZHOU Jinglun, et al. Bayesian network reliability modeling and assessment of momentum wheel on orbit[J]. ACTA Aeronautica et Astronautica Sinica,2009, 30 (6) : 1084-1089. DOI: 10.3321/j.issn:1000-6893.2009.06.019 (  0) 0)
|
| [15] |
ZHAO Shuping, KHORASANI K. A recurrent neural network based fault diagnosis scheme for a satellite[C]//Proceedings of the 33rd Annual Conference of the IEEE Industrial Electronics Society, IECON. Taipei: IEEE Computer Society, 2007: 2660-2665. DOI:10.1109/IECON.2007.4459995.
( 0) 0)
|
| [16] |
SHALIZI C R, SHALIZI K L, CRUTCHFIELD J P. An algorithm for pattern discovery in time series[R/OL]. (2002-10-29)[2002-11-27]. http://arxiv.org/abs/cs/0210025.
( 0) 0)
|
| [17] |
RAJAGOPALAN V, RAY A. Symbolic time series analysis via wavelet-based partitioning[J].
Signal Processing,2006, 86 (11) : 3309-3320.
DOI: 10.1016/j.sigpro.2006.01.014 ( 0) 0)
|
| [18] |
RAJAGOPALAN V, CHAKRABORTY S, RAY A. Estimation of slowly varying parameters in nonlinear systems via symbolic dynamic filtering[J].
Signal Processing,2008, 88 (2) : 339-348.
DOI: 10.1016/j.sigpro.2007.08.007 ( 0) 0)
|
| [19] |
李洪伟, 周云龙, 任素龙, 等. 符号动力学信息熵在气液两相流型电导信号分析中的应用[J].
化工学报,2012, 63 (11) : 3486-3492.
DOI: 10.3969/j.issn.0438-1157.2012.11.015 LI Hongwei, ZHOU Yunlong, REN Sulong, et al. Application of conductance signals analysis of gas-liquid two-phase flow patterns based on symbolic dynamics entropy[J]. CIESC Journal,2012, 63 (11) : 3486-3492. DOI: 10.3969/j.issn.0438-1157.2012.11.015 (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48


