随着人类迈向太空步伐的加速,深空探测任务变得也越发频繁,积极地进行太空探索与开发的时代也随着航天等相关领域的各种技术的进步而慢慢到来.月球作为离地球最近的一个天体,自然而然成为了人类离开地球、迈向深空的首个开发目标.众所周知,以“阿波罗”系列为典型代表的月球探测飞行器由于技术复杂、成本高昂、不可重复使用等缺点,早在上世纪70年代就已经退出了历史舞台.为了建立月球基地,需要研制出能够实现较大运载能力、可重复使用、节省能量的地月运输工具来实现地月之间大规模的物资转移(对于建立月球基地,就需要从地球向月球运送大量的水、食品、科考器材等,同时需要从月球向地球运送大量的宝贵的月球采样的样品以及其他物质).
基于此想法,学者大胆地提出了两种构想,一种构想是以TUI公司的Robert[1-2]为代表的研究团队于1980年首次提出的一种动量交换/电动绳系卫星推进系统(momentum-exchange/electrodynamic reboost tethers,MXER).MXER采用动量交换原理,结合电动绳系变轨原理进行载荷转移.该系统一次只能转移一个载荷,并且在转移载荷的过程中,母星系统的轨道参数由于动量(或能量)的损失将发生较大变化,因此需要采用电动绳原理进行轨道的调整与恢复.另一种基于动量交换原理进行载荷运输的绳系卫星系统概念是英国Glasgow大学的Cartmell[3-4]等于1996年首次提出的驱动型动量交换绳系卫星(motorized momentum exchange tether,MMET).MMET不同于MXER,MXER主要实现载荷与母星之间的动量交换以完成载荷的轨道转移,而MMET将母星置于系统质心处,而由两根等长的系绳分别连接两套相同的抓捕系统.这样,MMET就能更加合理地利用两个载荷之间的能量转移,在不消耗母星能量的前提下同时实现其中一个载荷升轨、另一个载荷降轨的目的.
在此后近20年的研究历程中,Cartmell及其研究团队继续对MMET广泛地开展研究.Ziegler等[5-6]通过将系绳简化为刚性杆模型对MMET动力学进行了研究,同时也针对性地开展了一些地面模拟试验.在文献[5-6]研究的基础上,Chen等[7-9]将系绳的柔性特性加入到MMET动力学模型的建立过程中,并对柔性动力学进行了初步的仿真分析,其研究成果标志着MMET动力学的研究向更实际的情况靠近.此外,Murray等[10-11]对基于MMET的地月转移系统中的月球跟踪轨道进行了研究.结果表明,如果月球轨道的升交点(或降交点)能够被准确地跟踪,则MMET通过适时发送载荷使得载荷与月球同时到达该点,并保证载荷能够被月球影响球捕获.
近来,齐乃明等[12-13]在上述研究基础上对MMET进行了进一步的研究.首先,对载荷的两种地月转移方式(MMET方式以及传统脉冲方式)进行了能量对比分析.研究结果表明,相同条件下,采用MMET进行载荷的地月转移所需的能量比采用传统脉冲变轨方式进行载荷地月转移所需的能量要少.其次,将结构偏差(即系绳长度存在偏差以及载荷质量存在偏差)、锥形绳的概念引入到MMET之中[13-15],分析了结构偏差对母星轨道参数、姿态参数的影响,并分析了锥形绳对母星轨道、姿态以及系统能量的影响.
综上所述,文献[5-6]在处理系统势能时,采用了离散处理方法,该方法的精度取决于离散程度,而且在求解动力学方程时略显复杂.本文在不影响系统模型精度的情况下,采用泰勒展开的方式对连续地月载荷转移系统(continuous cislunar payload transfer system,CCPTS)的势能进行了相应简化.首先,在考虑系绳柔性之后,对比分析系绳柔性对CCPTS的轨道参数、姿态参数的影响;其次,通过对柔性模型与刚性杆模型的对比分析,揭示重力梯度力矩的存在以及对CCPTS姿态及轨道参数的影响; 最后,分析系绳初始旋转角速度、系绳长度对系绳纵向、横向振动量的影响.通过设置不同的系绳初始旋转角速度以及不同的系绳长度,对比分析系绳初始旋转角速度以及系绳长度对系绳横向、纵向振型函数的振动幅值、振动周期的影响.
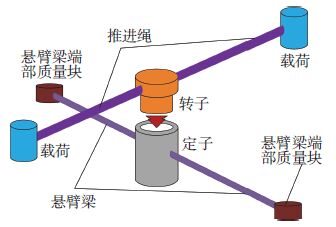
1 连续地月物质转移系统概念本文所研究的连续地月物质转移系统(简称CCPTS)包括两套长期驻轨的子系统,一套子系统运行于地球某椭圆轨道上,称为驻地载荷转移系统;另一套子系统运行于月球某椭圆轨道上,称为驻月载荷转移系统.两套系统工作原理相似,如图 1所示给出了CCPTS的示意图.
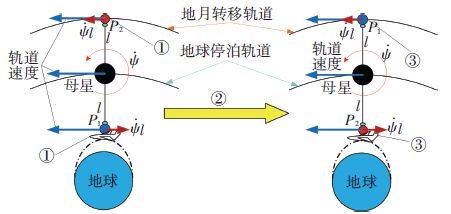
由图 1可知,CCPTS由以下几部分组成:母星系统(包括控制系统以及定子与转子)、推进绳(与母星转子部分相连,由转子的旋转带动系绳的旋转,从而改变末端载荷的轨道速度和方向)、抓捕机构、悬臂梁平衡系统(该系统与驱动系统的定子部分相连,主要控制CCPTS的旋转面的朝向稳定与平衡)组成.当考虑系绳柔性时,CCPTS进行载荷交换并实现地月转移的全过程的示意,如图 2所示.图 2中,l为系绳长度,ψ·为系绳旋转角速度.该过程主要将由月球飞向地球的载荷P2送到地面,同时将由地球运往月球的载荷P1送入到地月转移轨道.该过程包括3个子过程:①空天飞机等运输工具将载荷P1运送到低地球轨道、并与CCPTS此时处于低轨端的抓捕机构实现交会对接,同时,来自月球的载荷P2也实现与CCPTS此时处于高轨端的抓捕机构实现交会对接.这两个子过程必须同时进行,以保证对接前后母星的轨道参数不发生较大变化;②当CCPTS的系绳两端抓捕机构成功实现对载荷P1、P2的捕获之后,首先,CCPTS的轨道参数会发生一些微小变化,需要调整CCPTS的轨道参数;其次,系绳两端的载荷P1、P2要想实现各自的归宿(P1进入正确的地月转移轨道,P2落入低地球轨道与空天飞行器对接并最终落回地面),CCPTS驱动系统就必须提供合适的驱动力矩,当系统经过n+1/2个调整周期(即系统回到轨道近地点,同时载荷P1、P2的位置互换)之后,CCPTS无论是系绳展长方向还是抓捕机构末端速度等都必须符合地月转移要求并同时做好载荷分离准备;③当载荷P1与此时处于高轨的CCPTS的抓捕机构实现分离的瞬间,载荷P2也同处于低轨的抓捕机构实现分离,并由刚好到达该处的空天飞行器接收带回地面.
|
图 2 CCPTS进行载荷转移过程示意 Figure 2 Schematic of transferring payload by CCPTS |
|
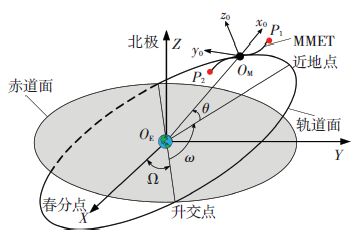
图 3 惯性坐标系与轨道坐标系 Figure 3 Inertia coordinate and orbit coordinate |
同理,处于月球轨道的转移系统—Lunavator的工作机制类似于CCPTS,不同的是,当Lunavator运行到其轨道近月点时,母星两端的系绳的长度刚好等于此时的近月点高度,其作用是方便地将载荷放置在月球表面或从月球表面抓取载荷.
2 连续地月转移系统二维柔性动力学模型 2.1 坐标系定义在进行动力学模型建立之前,需要定义如下几个坐标系:
1) 惯性坐标系OEXYZ.坐标原点OE为地球质心,OEX轴指向春分点,OEY轴位于地球赤道面内并垂直于OEX,OEZ轴与OEX轴、OEY轴构成右手系并指向地球北极,3个轴方向上的单位矢量分别为I、J及K.
2) 轨道坐标系OMxoyozo.原点定义在CCPTS质心OM处,OMxo轴位于轨道面内,由地心指向CCPTS质心方向,OMyo轴垂直于OMxo并位于轨道平面内,OMzo与OMxo、OMyo构成右手坐标系,3个轴方向上的单位矢量分别为ro、θo及no;惯性系与运动系如图 3所示.图 3中ω为近地点幅角,θ为真近角,Ω为升交点赤经.
3) 轨道面坐标系OEX-rY-rZ-r.坐标原点位于地心,OEX-r轴指向CCPTS轨道近地点(perigee)方向,OEY-r轴位于轨道平面内垂直于OEX-r(位于CCPTS运行方向一侧),OEZ-r轴与OEX-r、OEY-r构成右手坐标系,3个轴方向上的单位矢量分别为i、j及k.
4) 体轴坐标系OMxbybzb.OMxb由低轨载荷(lower payload)指向高轨载荷(upper payload),OMyb位于轨道面内,垂直于OMxb,OMzb轴与OMxb、OMyb构成右手坐标系.3个轴方向上的单位矢量分别为ib、jb及kb;轨道面坐标系与体轴系的几何关系如图 4所示,图 4中R为母星矢径,ψ为俯仰角,OM为母星.

|
图 4 CCPTS在轨道面坐标系下的示意 Figure 4 Schematic of CCPTS in orbital plane coordinate |
CCPTS质心运行在以地球为中心的椭圆轨道上,半长轴为a,离心率为e,轨道倾角为i,并对系统做出如下假设:
1) 系绳旋转面与轨道面夹角为零;
2) 忽略第三体引力以及地球扁率等扰动因素对系统的影响.
假设系绳距母星任意一点x处由于系绳柔性而产生的形变在体轴系下的分量为:xb方向(即纵向)形变为u(x,t),yb方向(即横向)形变为v(x,t).系绳形变在体坐标系下的相对位置关系,如图 5所示.

|
图 5 系绳形变在体坐标系下相对位置关系 Figure 5 Relative position of tether deformation in body frame |
由于系绳纵向与横向形变均可以表达为时间与空间的函数,因此由Bubnov-Galerkin方法,在一阶模态近似情况下,得到系绳的纵向与横向形变为[9]
| $u\left( x,t \right)=sin\left( \frac{\pi }{l}x \right){{q}_{1}}\left( t \right),$ | (1) |
| $v\left( x,t \right)=sin\left( \frac{\pi }{l}x \right){{q}_{2}}\left( t \right).$ | (2) |
式中,q1(t)、q2(t)分别为系绳纵向、横向振型函数.
由图 4可以得到载荷P1、P2在轨道面坐标系中的坐标分量表达式为
| ${{x}_{{{P}_{1}}}}=Rcos~\theta +lcos\left( \psi +\theta \right),$ | (3) |
| ${{y}_{{{P}_{1}}}}=Rsin~\theta +lsin\left( \psi +\theta \right);$ | (4) |
| ${{x}_{{{P}_{2}}}}=Rcos~\theta -lcos\left( \psi +\theta \right),$ | (5) |
| ${{y}_{{{P}_{2}}}}=Rsin~\theta -lcos\left( \psi +\theta \right).$ | (6) |
母星在轨道面坐标系下的分量可以表示成
| ${{x}_{M}}=Rcos~\theta ,$ | (7) |
| ${{y}_{M}}=Rsin~\theta .$ | (8) |
为了求得变形绳在轨道面坐标系下的坐标分量,先将体坐标系分量(x+u,v,0)通过坐标变换转到与轨道面坐标系平行的坐标系OMX′Y′中,得
| $\left[ \begin{matrix} X\prime \\ Y\prime \\ Z\prime \\ \end{matrix} \right]~=\left[ \begin{matrix} cos\left( \psi +\theta \right) & -sin\left( \psi +\theta \right) & 0 \\ sin\left( \psi +\theta \right) & cos\left( \psi +\theta \right) & 0 \\ 0 & 0 & 1 \\ \end{matrix} \right]\left[ \begin{matrix} x+u \\ v \\ 0 \\ \end{matrix} \right].$ |
然后将坐标系OMX′Y′的原点平移到地心,得到轨道面坐标系中的变形绳的坐标分量:
| ${{x}_{{{T}_{1}}}}=Rcos~\theta +\left( u+x \right)cos\left( \psi +\theta \right)-vsin\left( \psi +\theta \right),$ | (9) |
| ${{y}_{{{T}_{1}}}}=Rsin~\theta +\left( u+x \right)sin\left( \psi +\theta \right)+vcos\left( \psi +\theta \right);$ | (10) |
| ${{x}_{{{T}_{2}}}}=Rcos~\theta -\left( u+x \right)cos\left( \psi +\theta \right)+vsin\left( \psi +\theta \right),$ | (11) |
| ${{y}_{{{T}_{2}}}}=Rsin~\theta -\left( u+x \right)sin\left( \psi +\theta \right)-vcos\left( \psi +\theta \right)$ | (12) |
CCPTS的平动动能,由动力学知识,系统平动动能Ttrans的表达式可以表示为
| $\begin{align} & {{T}_{trans}}=\frac{1}{2}[{{m}_{M}}({{{\dot{x}}}^{2}}_{M}+{{{\dot{y}}}^{2}}_{M})+{{m}_{P}}({{{\dot{x}}}^{2}}_{{{P}_{1}}}+{{{\dot{y}}}^{2}}_{{{P}_{1}}}+{{{\dot{x}}}^{2}}_{{{P}_{2}}}+{{{\dot{y}}}^{2}}_{{{P}_{2}}})+ \\ & \rho Al({{{\dot{x}}}^{2}}_{{{T}_{1}}}+{{{\dot{y}}}^{2}}_{{{T}_{1}}}+{{{\dot{x}}}^{2}}_{{{T}_{2}}}+{{{\dot{y}}}^{2}}_{{{T}_{2}}})] \\ \end{align}$ |
式中:mM为母星质量;mP为载荷质量;ρ为系绳质量密度;A为系绳横截面积.
二维模型中,系统的转动动能Trot的表达式为
| ${{T}_{rot}}=\frac{1}{2}{{I}_{z}}{{\omega }_{z}}^{2}$ |
式中:Iz为CCPTS相对于z轴的转动惯量;ωz为相对于z轴的转动角速度.假设载荷P1、P2、母星OM以及系绳T1、T2均为圆柱体,各自的尺寸半径为(rP,rM,rT),载荷及母星的尺寸高度为(hP,hM),由此得到CCPTS转动动能为
| ${{T}_{rot}}=\frac{1}{2}{{I}_{z}}{{\left( \dot{\psi }+\dot{\theta } \right)}^{2}},$ |
其中,
| $~{{I}_{z}}=\frac{1}{2}{{m}_{M}}{{r}^{2}}_{M}+{{m}_{P}}({{r}^{2}}_{P}+2{{L}^{2}})+12\rho Al{{r}^{2}}_{T}+56\rho A{{l}^{3}}.$ |
联立式(3)~(8)得到CCPTS载荷与母星的动能表达式为
| ${{T}_{P,M}}=({{m}_{P}}+\frac{1}{2}{{m}_{M}})({{\dot{R}}^{2}}+{{R}^{2}}{{\dot{\theta }}^{2}})+\frac{1}{2}{{I}_{PM}}{{\left( \dot{\psi }+\dot{\theta } \right)}^{2}}.$ | (13) |
式中IPM为载荷P1、P2以及母星OM关于CCPTS质心的转动惯量,其具体表达式为
| ${{I}_{PM}}={{m}_{P}}{{r}^{2}}_{P}+12{{m}_{M}}{{r}^{2}}_{M}+2{{m}_{P}}{{l}^{2}}.~$ |
结合式(9)~(12),得系绳的平动和转动动能为
| $\begin{align} & {{T}_{T}}=\rho Al+[({{{\dot{R}}}^{2}}+{{R}^{2}}{{{\dot{\theta }}}^{2}})+({{{\dot{q}}}^{2}}_{1}+{{{\dot{q}}}^{2}}_{2})/2+({{q}_{1}}{{{\dot{q}}}_{2}}-{{{\dot{q}}}_{1}}{{q}_{2}}+ \\ & 2l-{{{\dot{q}}}_{2}})\left( \dot{\theta }+\dot{\psi } \right)\left] +12 \right[{{I}_{T}}+\rho Al(4l-{{q}_{1}}+{{q}^{2}}_{1}+ \\ & {{q}^{2}}_{2})]{{\left( \dot{\theta }+\dot{\psi } \right)}^{2}}. \\ \end{align}$ | (14) |
式中,
| ${{I}_{T}}=\rho Al\left( \frac{5}{6}{{l}^{2}}+\frac{1}{2}{{r}^{2}}_{T} \right).$ |
由于系统由母星、系绳及载荷组成,且考虑系绳存在弹性变形,因此,系统势能除重力势能之外还包括系绳形变产生的弹性势能.在满足动力学研究的前提下,为了简化分析,略去x/R、l/R二次以上的项,由图 4可以得到系统的重力势能为
| ${{V}_{G}}=-m\frac{\mu }{R}+\frac{\mu {{I}_{P}}_{M}}{{{R}^{3}}}(1-3co{{s}^{2}}\psi ).$ | (15) |
式中:m=mM+2mP+2ρAl,表示CCPTS总质量,μ为地球引力场数.同时,由系绳的弹性形变产生的弹性势能为
| $~{{V}_{E}}=\frac{1}{2}{{\int }_{0}}^{l}EA{{\varepsilon }_{T}}^{2}dx.$ | (16) |
式中,εT为系绳总应变.系绳拉力T与系绳弹性模量E、系绳横截面积A以及应变εE存在如下关系:
| $T=EA{{\varepsilon }_{T}}={{T}_{0}}+EA{{\varepsilon }_{E}}.$ | (17) |
式中,T0为系绳不受外力(重力之外的力)情况下,来自于CCPTS离心力作用在系绳上的拉力,εE表示系绳的形变导致的实际应力,各自的表达式为
| ${{T}_{0}}=\left( {{m}_{P}}l+\frac{1}{2}\rho A{{l}^{2}} \right){{{\dot{\psi }}}^{2}},$ | (18) |
| ${{\varepsilon }_{E}}=u\prime +\frac{1}{2}v{{\prime }^{2}}(1-u\prime +u{{\prime }^{2}})-\frac{1}{8}v{{\prime }^{4}}+\frac{5}{8}u{{\prime }^{4}}+\cdots .$ | (19) |
式中,“u′、v′”分别为“u、v”对x的导数.
联立式(1)~(2)、(16)~(19)得到两系绳总的弹性势能为
| $\begin{align} & {{V}_{E}}={{T}_{0}}\frac{{{\pi }^{4}}}{{{l}^{3}}}\left[ \frac{{{l}^{2}}{{q}^{2}}_{2}}{2{{\pi }^{2}}}+\frac{3{{q}^{2}}_{1}{{q}^{2}}_{2}}{8}-\frac{3{{q}^{4}}_{2}}{32}+\frac{15{{q}^{4}}_{1}}{32} \right]+ \\ & \frac{l{{T}^{2}}_{0}}{EA}+\frac{{{\pi }^{2}}EA{{q}^{2}}_{1}}{2l}+\frac{3{{\pi }^{4}}EA{{q}^{4}}_{2}}{32{{l}^{3}}}-\frac{3{{\pi }^{4}}EA{{q}^{2}}_{1}{{q}^{2}}_{2}}{8{{l}^{3}}}. \\ \end{align}$ | (20) |
联立式(13)~(15)、(20)得Lagrange函数L~的表达式为
| $\tilde{L}={{T}_{P,M}}+{{T}_{T}}-{{V}_{G}}-{{V}_{E}}.$ |
采用Lagrange方法建立CCPTS柔性动力学模型.选择(R,θ,ψ,q1,q2)作为系统广义坐标,相应的广义力为(0,0,τ,0,0),由拉格朗日函数,可得
| $\frac{~d}{~dt}\left( \frac{\partial \tilde{L}}{\partial {{{\dot{q}}}_{i}}} \right)-\frac{\partial \tilde{L}}{\partial {{q}_{i}}}={{Q}_{i}},~$ |
得到以下二维柔性动力学方程:
| $\begin{align} & \ddot{R}-R{{{\dot{\theta }}}^{2}}+\frac{\mu }{{{R}^{2}}}+\frac{3\mu {{I}_{PT}}}{2m{{R}^{4}}}\left( 3co{{s}^{2}}\psi -1 \right)=0, \\ & {{{\ddot{q}}}_{1}}-{{q}_{2}}\left( \ddot{\theta }+\ddot{\psi } \right)-2{{{\dot{q}}}_{2}}\left( \dot{\theta }+\dot{\psi } \right)-(2\bar{l}+{{q}_{1}}){{\left( \dot{\psi }+\dot{\theta } \right)}^{2}}+ \\ & \frac{3({{T}_{0}}-EA){{q}^{2}}_{2}{{q}_{1}}}{4\rho A{{{\bar{l}}}^{4}}}+\frac{15{{T}_{0}}{{q}^{3}}_{1}}{8\rho A{{{\bar{l}}}^{4}}}+\frac{EA{{q}_{1}}}{\rho A{{{\bar{l}}}^{2}}}=0, \\ & m(2R\dot{R}\dot{\theta }+{{R}^{2}}\ddot{\theta })+[\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tilde{I}}+\rho Al(4\bar{l}{{q}_{1}}+{{q}^{2}}_{1}+{{q}^{2}}_{2})]\left( \ddot{\psi }+\ddot{\theta } \right)+ \\ & \rho Al[{{q}_{1}}{{{\ddot{q}}}_{2}}-{{{\ddot{q}}}_{1}}{{q}_{2}}+2\bar{l}{{{\ddot{q}}}_{2}}+(4\bar{l}{{{\dot{q}}}_{1}}+2{{q}_{1}}{{{\dot{q}}}_{1}}+2{{q}_{2}}{{{\dot{q}}}_{2}})\cdot \\ & \left( \dot{\theta }+\dot{\psi } \right)]=0, \\ & {{{\ddot{q}}}_{2}}+({{q}_{1}}+2\bar{l})\left( \ddot{\theta }+\ddot{\psi } \right)-{{q}_{2}}{{\left( \dot{\psi }+\dot{\theta } \right)}^{2}}+\frac{{{T}_{0}}{{q}_{2}}}{\rho A{{{\bar{l}}}^{2}}}+ \\ & \frac{3\left( EA-{{T}_{0}} \right){{q}^{3}}_{2}}{8\rho A{{{\bar{l}}}^{4}}}+2{{{\dot{q}}}_{1}}\left( \dot{\theta }+\dot{\psi } \right)+\frac{3\left( {{T}_{0}}-EA \right){{q}^{2}}_{1}{{q}_{2}}}{4\rho A{{{\bar{l}}}^{4}}}=0, \\ & [\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tilde{I}}+\rho Al(4\bar{l}{{q}_{1}}+{{q}^{2}}_{1}+{{q}^{2}}_{2})]\left( \ddot{\theta }+\ddot{\psi } \right)- \\ & 12{{\left( {{m}_{P}}l+\frac{1}{2}\rho A{{l}^{2}} \right)}^{2}}\frac{l{{{\dot{\psi }}}^{2}}\ddot{\psi }}{EA}+\rho Al[{{q}_{1}}{{{\ddot{q}}}_{2}}-{{{\ddot{q}}}_{1}}{{q}_{2}}+ \\ & 2\bar{l}{{{\ddot{q}}}_{2}}+(4\bar{l}{{{\dot{q}}}_{1}}+2{{q}_{1}}{{{\dot{q}}}_{1}}+2{{q}_{2}}{{{\dot{q}}}_{2}})\left( \dot{\theta }+\dot{\psi } \right)]- \\ & \pi \left( {{m}_{P}}l+\frac{1}{2}\rho A{{l}^{2}} \right)\left[ \frac{{{q}^{2}}_{2}}{l}+\frac{3{{q}^{2}}_{1}{{q}^{2}}_{2}}{4{{{\bar{l}}}^{3}}}-\frac{3{{q}^{4}}_{2}}{16{{{\bar{l}}}^{3}}}+\frac{15{{q}^{4}}_{1}}{16{{{\bar{l}}}^{3}}} \right]\ddot{\psi }+ \\ & 3\frac{\mu {{I}_{PT}}}{{{R}^{3}}}sin\left( 2\psi \right)-\pi \left( {{m}_{P}}l+\frac{1}{2}\rho A{{l}^{2}} \right)\left[ \frac{2{{q}_{2}}{{{\dot{q}}}_{2}}}{l} \right.+ \\ & \left. \frac{3({{q}_{1}}{{{\dot{q}}}_{1}}{{q}^{2}}_{2}+{{q}_{2}}{{{\dot{q}}}_{2}}{{q}^{2}}_{1})}{2{{{\bar{l}}}^{3}}}-\frac{3{{q}^{3}}_{2}{{{\dot{q}}}_{2}}}{4{{{\bar{l}}}^{3}}}+\frac{15{{q}^{3}}_{1}{{{\dot{q}}}_{1}}}{4{{{\bar{l}}}^{3}}} \right]\dot{\psi }=\tau . \\ \end{align}$ |
式中:
| $\begin{align} & {{{\tilde{I}}}_{PT}}={{m}_{P}}l+\frac{1}{2}\rho A{{l}^{2}}, \\ & \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{\tilde{I}}=\frac{1}{2}{{m}_{M}}{{r}^{2}}_{M}+{{m}_{P}}{{r}^{2}}_{P}+2{{m}_{P}}{{l}^{2}}+\frac{1}{2}\rho Al{{r}^{2}}_{T}+\frac{5}{6}\rho A{{l}^{3}}. \\ \end{align}$ |
系统参数见表 1,仿真时间取为60 000 s.
| 表 1 CCPTS参数 Table 1 Parameters of CCPTS |
仿真初始条件及各广义坐标初值如下:
| $\begin{align} & R\left( 0 \right)=6.728\times {{10}^{6}}~m,\text{ }\dot{R}\left( 0 \right)=0~m/s, \\ & \theta \left( 0 \right)=0~rad,\text{ }\dot{\theta }\left( 0 \right)=0.001\text{ }26~rad/s, \\ & \psi \left( 0 \right)=0~rad, \\ & \dot{\psi }\left( 0 \right)=0.087\text{ }3~rad/s,{{q}_{1}}\left( 0 \right)={{q}_{2}}\left( 0 \right)=0~m, \\ & {{{\dot{q}}}_{1}}\left( 0 \right)={{{\dot{q}}}_{2}}\left( 0 \right)=0~m/s. \\ \end{align}$ |
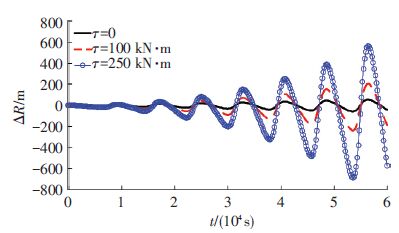
图 6给出了不同外力矩作用下,CCPTS的二维柔性模型与二维刚性模型的矢径偏差ΔR随时间的变化关系.由图 6可知,当外力矩τ=0时,由于系绳柔性所造成的母星质心偏差的变化幅值随时间逐渐增加.此外,随着外力矩的增加,ΔR的幅值也随之线性增加,说明CCPTS的姿态运动与轨道运动存在一定程度的耦合作用.
|
图 6 CCPTS母星质心矢径偏差ΔR时间变化关系 Figure 6 Time history of ΔR of CCPTS's chief satellite |
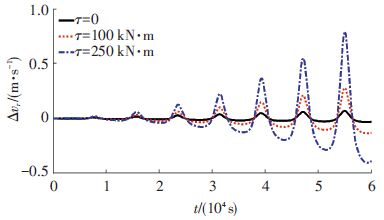
图 7、8给出了不同外力矩作用下母星径向速度偏差
| $\begin{align} & \Delta R\approx \frac{pesin~\theta }{{{\left( 1+ecos~\theta \right)}^{2}}}\Delta \theta , \\ & \Delta \dot{R}\approx e\sqrt{\frac{\mu }{p}}cos~\theta \cdot \Delta \theta . \\ \end{align}$ |
式中:p为半正交弦,Δθ=θflexible-θrigid.结合图 6~8可知,Δθ与ΔR、
|
图 7
母星径向速度偏差 |

|
图 8 CCPTS真近角偏差Δθ随时间变化关系 Figure 8 Time history of Δθ of CCPTS's true anomaly |
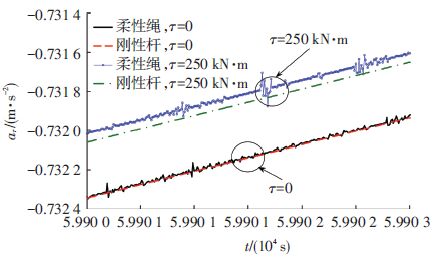
图 9给出了系绳为柔性绳与刚性杆两种情况下质心径向加速度
|
图 9 CCPTS质心径向加速度${\ddot{R}}$随时间变化关系 Figure 9 Time history of the detail view of ${\ddot{R}}$ |
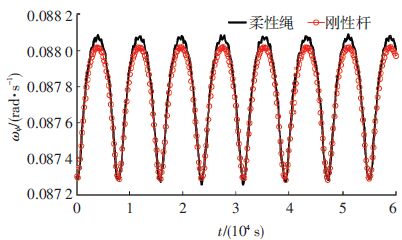
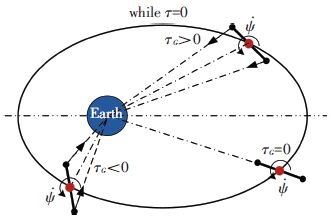
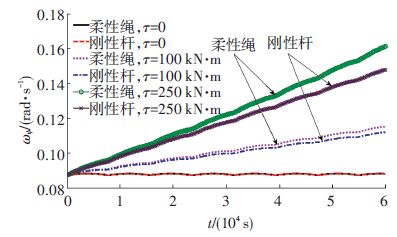
图 10给出了外力矩为零时系绳俯仰角速度ψ·(=ωψ)随时间的变化关系.由图 10可知,当母星位于近地点时,系绳俯仰角速度达到最小值0.087 3 rad/s,当母星位于远地点时,系绳俯仰角速度达到最大值(对于柔性绳,ψ·max=0.088 1 rad/s,对于刚性杆,${\dot{\psi }}$max=0.088 0 rad/s).究其原因,是由于重力梯度力矩τG作用的结果.当母星位于近地点时,系绳受到的重力梯度力矩幅值达到最大值,系绳的旋转角加速度幅值也达到最大.当母星位于远地点时,系绳所受到的重力梯度力矩幅值最小.系绳受到的重力梯度力矩的正负关系如图 11所示.当τG<0时,系绳的旋转运动受到阻碍,系绳角速度将减小.当τG>0时,系绳的旋转运动受到促进作用,系绳角速度将增加.当外力矩不为零时,随着外力矩的增加,系绳所受到的微弱的重力梯度力矩的周期性影响将逐渐减弱,${\dot{\psi }}$的变化规律逐渐从周期性变化变成近似线性增加的趋势,如图 12所示.
|
图 10 τ=0,系绳俯仰角速度ωψ随时间变化关系 Figure 10 Time history of pitch angular velocity ωψ of tether with τ=0 |
|
图 11 不同外力矩对系绳俯仰角速度的影响重力梯度力矩在轨道不同位置、不同姿态所对应的正负关系 Figure 11 The positive and negative relationship of the gravity gradient torque with different position and different attitude in the parking orbit |
|
图 12 不同外力矩对系绳俯仰角速度的影响 Figure 12 Impact of external torque on pitch angular velocity |
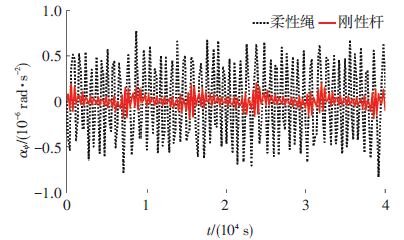
图 13给出了外力矩为零时系绳俯仰角加速度${\ddot{\psi }}$随时间的变化关系.由图 13可知,当不考虑系绳柔性时,因系绳重力梯度力矩所产生的系绳旋转角加速度${\ddot{\psi }}$在[-1.840,1.804](×10-6 rad/s2)之间剧烈振荡,当考虑系绳横向和纵向振动时,系绳旋转角加速度的振荡幅值介于[-7.881,7.746](×10-6 rad/s2)之间,并且呈现良好的周期性变化规律,各自振荡周期与系绳绕母星旋转周期相同.
|
图 13 τ=0,CCPTS系绳俯仰角加速度随时间变化关系 Figure 13 Time history of pitch angular acceleration ${\ddot{\psi }}$ of tether with τ=0 |
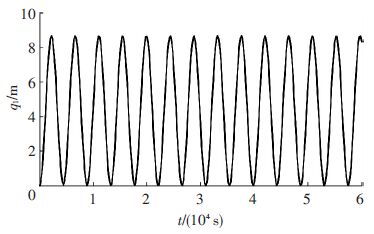
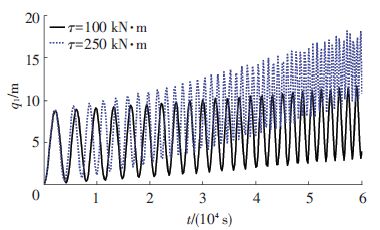
图 14、15给出了τ=0、τ≠0两种情况下系绳纵向振动量q1(x)随时间的变化关系.由图 14可知,当外力矩为零时,系绳纵向振形函数q1(x)随时间呈现周期性变化关系,纵向最大振动量为8.683 m,振荡周期为4 400 s(对应的振荡频率为2.272 7×10-4/s).由图 15可以看出,当外力矩不为零时,系绳纵向振动函数q1(x)的振动幅值随时间逐渐增加,而且振荡周期逐渐减小,振荡频率逐渐增加,外力矩越大,纵向振动量增加越快.
|
图 14 τ=0,CCPTS系绳纵向振动量q1随时间变化关系 Figure 14 Time history of tether's longitudinal vibration displacement q1 with τ=0 |
|
图 15 τ≠0,CCPTS系绳纵向振动量q1随时间变化关系 Figure 15 Time history of tether's longitudinal vibration displacement q1 with τ≠0 |
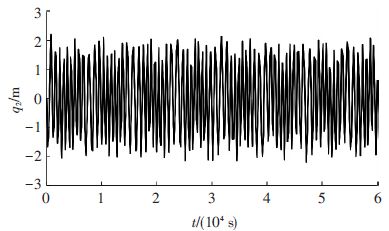
图 16、17给出了不同外力矩作用下,系绳横向振型函数(或横向振动量)q2随时间的变化关系.由图 16可知,当外力矩为零时,系绳横向振型函数q2随时间进行周期性振荡,振荡幅值介于[-2.144,2.103]m之间.当外力矩不为零时,系绳横向振动函数不再随时间呈周期性变化关系,振荡幅值随时间呈现小幅衰减趋势.
|
图 16 τ=0,CCPTS系绳横向振动量q2随时间变化关系 Figure 16 Time history of tether's transverse vibration displacement q2 with τ=0 |
|
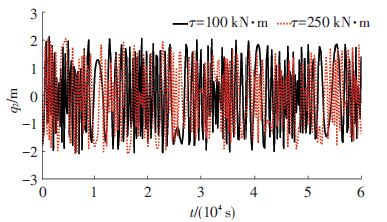
图 17 τ≠0,CCPTS系绳横向振动量q2随时间变化关系 Figure 17 Time history of tether's transverse vibration displacement q2 with τ≠0 |
表 2给出了系绳旋转角速度取不同初值且外力矩为零时,系绳纵向振动量随时间的变化关系.当系绳旋转角速度较小时,系绳在旋转过程中所受到的离心力较小.随着系绳初始旋转角速度的增加,系绳所受到的离心力随之增加,结果导致系绳纵向振动量也随之增加,振荡周期逐渐缩短.相比于系绳初始旋转角速度对系绳纵向振动量的影响,当${\dot{\psi }}$(0)=0.001 rad/s时,系绳横向振动量随时间呈现不规律变化,振荡幅值介于[-41.41,41.16]m之间.随着系绳俯仰角速度初值的增加,系绳横向振动量q2的振动幅值逐渐减小,并且振荡周期减小.由此说明,随着系绳俯仰角速度的增加,系绳在纵向的张紧程度加剧,结果导致系绳在横向的振动量减小.
| 表 2 系绳初始俯仰角速度对系绳纵向、横向振动量的影响 Table 2 Relations between the magnitudes of tether's longitudinal and transverse vibration displacements and initial pitch angular velocity |
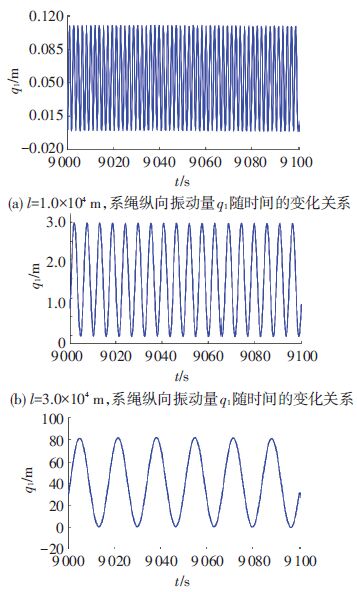
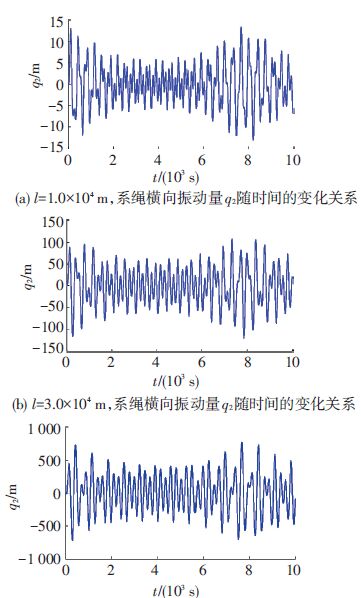
图 18(a)~(c)给出了系绳长度对系绳纵向振动量q1的影响,此时,取系绳的旋转角速度初值ψ·(0)=0.008 73 rad/s,外力矩为零,其他参数同上.由图 18可知,随着系绳长度的增加,系绳纵向振型函数q1的振动幅值呈指数增加,同时,系绳的纵向振形函数的振动周期随之逐渐地近似等比例增加(1.849 1 s→5.529 4 s→16.600 0 s).图 19(a)~(c)给出了系绳长度对系绳横向振动量q2的影响.对比可知,系绳长度的增加引起了系绳横向振动量q2的振动幅值的非线性增加,然而,对于横向振动周期而言,却没有明显的增加趋势(143 s→205 s→232 s).
|
图 18 不同系绳长度对系绳纵向振动量q1的影响 Figure 18 Impact of different tether length on tether's longitudinal vibration displacement q1 |
|
图 19 不同系绳长度对系绳横向振动量q2的影响 Figure 19 Impact of different tether length on tether's transverse vibration displacement q2 |
表 3给出了不同系绳长度与系绳纵向、横向振动幅值的关系.由表 3可知,随着系绳长度的增加,系绳纵向、横向振动幅值均非线性增加.由此说明,系绳的长度对系绳的稳定性影响明显.
| 表 3 系绳长度对系绳纵向、横向振动量的影响 Table 3 Relations between the magnitudes of tether's longitudinal and transverse vibration displacements and tether length |
1) 系绳的柔性对轨道参数R、θ有一定的影响,同时外力矩的大小也将改变系绳柔性对CCPTS轨道、姿态参数的影响程度.由于系绳纵向、横向振动方向与母星径向加速度方向往复变化,母星径向加速度、真近角加速度出现“毛刺”现象.
2) 由于系绳长度不可忽略,因此,CCPTS存在重力梯度力矩,并且对系绳的旋转运动产生了一定程度的影响,相比于重力梯度力矩对刚性杆模型的影响,该影响对柔性绳较大.
3) 系绳初始角速度以及系绳长度对系绳纵向、横向振动量均产生了较大影响.随着系绳初始旋转角速度的增加,系绳纵向振动量急剧增加、振动周期缩短,系绳横向振动量幅值逐渐减小、振动周期亦缩短;系绳长度的增加导致了系绳纵向、横向振动幅值的非线性指数增加,系绳纵向振动周期近似等比例增加,横向周期增加不明显.
| [1] |
ROBERT P H, Chauncey U. Cislunar tether transport system[J].
Journal of Spacecraft and Rockets,2000, 37 (2) : 177-186.
DOI: 10.2514/2.3564 ( 0) 0)
|
| [2] |
ROBERTP H. Commercial development of a tether transport system[C]// 36th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit. Huntsville, AL: AIAA, 2000. DOI:10.2514/6.2000-3842.
( 0) 0)
|
| [3] |
CARTMELL M P. Generating velocity increments by means of a spinning motorised tether[C]//34th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit. Cleveland, OH: AIAA, 1998. DOI:10.2514/6.1998-3739.
( 0) 0)
|
| [4] |
CARTMELLM P, MCKENZIE D J. A review of space tether research[J].
Progress in Aerospace Science,2008, 44 (1) : 1-21.
DOI: 10.1016/j.paerosci.2007.08.002 ( 0) 0)
|
| [5] |
ZIEGLER S W. The rigid body dynamic of tethers in space [D]. UK: University of Glasgow, 2003.
( 0) 0)
|
| [6] |
ZIEGLERS W, CARTMELL M P. Using motorized tethers for payload orbital transfer[J].
Journal of Spacecraft and Rockets,2001, 38 (6) : 904-913.
( 0) 0)
|
| [7] |
CHEN Yi. Dynamical modelling of a flexible motorised momentum exchange tether and hybrid fuzzy sliding mode control for spin-up [D]. Glasgow: University of Glasgow, 2010.
( 0) 0)
|
| [8] |
CHEN Yi, CARTMELL M P. Hybrid fuzzy sliding mode control for motorised space tether spin-up when coupled with axial and torsional oscillation[J].
Astrophys and Space Science,2010, 326 (1) : 105-118.
DOI: 10.1007/s10509-009-0212-6 ( 0) 0)
|
| [9] |
ISMAIL N A. The dynamics of a flexible Motorised Momentum Exchange Tether (MMET) [D]. UK: University of Glasgow, 2012.
( 0) 0)
|
| [10] |
MURRAY C. Continuous Earth-moon payload exchange using motorized tethers with associated dynamics[D]. UK: University of Glasgow, 2011.
( 0) 0)
|
| [11] |
MURRAY C, CARTMELL M P. Moon-tracking orbits using motorized tethers for continuous Earth-moon payload exchanges[J].
Journal of Guidance, Control and Dynamics,2013, 36 (2) : 567-576.
DOI: 10.2514/1.56248 ( 0) 0)
|
| [12] |
阳勇, 齐乃明, 黄盘兴, 等. 连续地月转移系统动力学研究与能量分析[J].
航空学报,2015, 36 (6) : 2005-2015.
DOI: 10.7527/S1000-6893.2015.0061 YANG Yong, QI Naiming, HUANG Panxing, et al. Dynamics and energy analysis of continuous cislunar transfer system[J]. Acta Aeronautica ET Astronautica Sinica,2015, 36 (6) : 2005-2015. DOI: 10.7527/S1000-6893.2015.0061 (  0) 0)
|
| [13] |
QI Naiming, YANG Yong, ZHAO Jun, et al. Effects of asymmetries on the dynamics of motorized momentum exchange tether and payloads injection precision [D]. [S.l.]: International Journal of Aerospace Engineering, 2015: 1-13. DOI: 10.1155/2015/468482.
( 0) 0)
|
| [14] |
齐乃明, 阳勇, 黄盘兴, 等. 结构偏差对二维连续地月载荷转移系统动力学影响[J].
北京航空航天大学学报,2015, 41 (11) : 2000-2009.
DOI: 10.13700/j.bh.1001-5965.2014.0730 QI Naiming, YANG Yong, HUANG Panxing, et al. Two dimensional dynamics of continuous cislunar payload transfer system considering structural deviation effect[J]. Journal of Beijing University of Aeronautics and Astronautics,2015, 41 (11) : 2000-2009. DOI: 10.13700/j.bh.1001-5965.2014.0730 (  0) 0)
|
| [15] |
YANG Yong, QI Naiming, LIU Yanfang, et al. Influence of tapered tether on cislunar payload transmission system and energy analysis[J].
Aerospace Science and Technology,2015, 46 : 210-220.
DOI: 10.1016/j.ast.2015.07.004 ( 0) 0)
|
| [16] |
刘暾, 赵钧.
空间飞行器动力学[M]. 哈尔滨: 哈尔滨工业大学出版社, 2003 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48

 , 阳勇, 赵钧, 孙启龙, 林海奇
, 阳勇, 赵钧, 孙启龙, 林海奇