入水过程是指运动体以一定的初速度从空气中撞击并穿越气水界面进入水中的过程.当射弹以较高的速度入水形成空泡时,入水空泡的内部不仅含有空气,而且含有由于空化作用形成的水蒸汽,同时射弹头部也会承受较大的冲击载荷.高速射弹在入水时形成的空泡形态和冲击阻力与射弹的头型关系密切.
入水问题的研究最早开始于19世纪末期,Worthington等[1]对球形体垂直入水进行了实验研究,分析了该过程中的液体喷溅和空泡演化等现象.进入 20世纪中叶,May等[2-5]针对球形体垂直入水进行了系列实验,探究了其入水的阻力系数、附加质量和表面特性,其中文献[5]还针对轴对称体诸如锥形、球形、圆盘等航行体开展了垂直入水实验研究,取得了这些形状航行体入水的流体动力等实验数据.与此同时,针对高速航行体入水问题,展开了相关的研究,Lundstrom等[6]开展了速度处于800~1 070 m/s的穿甲弹入水实验研究,在基于对空泡形成和溃灭现象的观测研究之上得到了穿甲弹入水的流体动力特性,基于此研究,文献[6]提出了空泡半径的预测公式.近年来,Paryshev[7]针对水下运动体高速运动的空泡问题展开了系列理论研究,发展了入水运动体的空泡理论.Weiland等[8]通过将枪管放入水中,研究射弹入水的空泡形成机理,得到了超空化发展的临界时间尺度.
国内学者也开展了一些相关研究,何春涛等[9]针对锥头圆柱体进行了2~56 m/s的垂直和倾斜入水实验,得到了该系列速度下的航行体入水空泡形成发展的规律.魏卓慧等[10]利用附加质量法对截锥头航行体垂直入水的冲击载荷进行了计算,得到了入水深度与截锥参数的关系.胡平超等[11]对航行体入水展开三维数值模拟,研究分析了阻力系数等流体动力系数的变化规律.马庆鹏等[12]针对不同锥角的锥头射弹垂直高速入水展开了数值模拟,得到了射弹锥角对入水空泡形态及流体动力的影响.
射弹的头型对入水空泡形态和射弹流体动力有较大的影响,本文针对127°锥角圆柱体射弹100 m/s垂直入水过程进行了数值模拟,并与基于能量守恒原理计算的理论结果进行了了对比,验证了本文数值模拟方法的有效性.在此基础上,开展了不同头型射弹垂直入水的二维数值模拟研究,分析了射弹头型对高速射弹垂直入水空泡演化、射弹流体动力及弹道特性的影响.
1 数学模型 1.1 基本控制方程文献[13]中提到,当航行体入水速度低于700 m/s时,水的可压缩性可以忽略不计.故本文的数值模拟假设流体不可压缩,忽略流体高速运动的热效应,对于入水过程产生的多相流使用VOF模型进行模拟.VOF模型将多相流体简化为密度可以变化的单相介质,并用体积分数表示不同相的构成.本文涉及水、水蒸汽、空气三相,它们的体积分数满足如下关系式:
| ${{\alpha }_{l}}+{{\alpha }_{v}}+{{\alpha }_{g}}=1,$ |
式中,αl,αv,αg分别为水相、水蒸汽相和气相的体积分数.
混合相的连续性方程为
| $\frac{\partial {{\rho }_{m}}}{\partial t}+\frac{\partial }{\partial {{x}_{i}}}\left( {{\rho }_{m}}{{v}_{i}} \right)=0.$ |
混合相的运动方程为
| $\begin{align} & \frac{\partial }{\partial {{x}_{j}}}\left( {{\rho }_{m}}{{v}_{i}} \right)+\frac{\partial }{\partial {{x}_{j}}}\left( {{\rho }_{m}}{{v}_{i}}{{v}_{j}} \right)= \\ & -\frac{\partial p}{\partial {{x}_{i}}}\frac{\partial }{\partial {{x}_{i}}}\left[ \left( {{\mu }_{m}}+{{\mu }_{t}} \right)\left( \frac{\partial {{v}_{i}}}{\partial {{x}_{j}}}+\frac{\partial {{v}_{j}}}{\partial {{x}_{i}}} \right) \right] \\ \end{align}$ |
式中:vi为速度分量;ρm=1-αg-αvρl+αgρg+αvρv为混合相的密度;μm=1-αg-αvμl+αgμg+αvμv为混合相的动力黏度;μt=ρmCμk2/ε为湍流黏性系数.
1.2 湍流与空化模型射弹高速入水的过程中,将引发随机性较强的湍流,本文选用SST k-ω湍流模型[14]来模拟入水过程中的湍流现象.它的两个输运方程如下:
| $\begin{align} & \frac{\partial }{\partial t}\left( \rho k \right)+\frac{\partial }{\partial {{x}_{i}}}\left( \rho k{{v}_{i}} \right)= \\ & P-{{\beta }^{*}}\rho \omega k+\frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +{{\sigma }_{k}}{{\mu }_{t}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]+{{P}_{kb}}, \\ & \frac{\partial }{\partial t}\left( \rho \omega \right)+\frac{\partial }{\partial {{x}_{j}}}\left( \rho \omega {{v}_{j}} \right)=\alpha \frac{\omega }{k}P-\beta \rho {{\omega }^{2}}+ \\ & \frac{\partial }{\partial {{x}_{j}}}\left[ \left( \mu +{{\sigma }_{k}}{{\mu }_{t}} \right)\frac{\partial k}{\partial {{x}_{j}}} \right]2\rho \left( 1-{{F}_{1}} \right){{\sigma }_{\omega 2}}\frac{1}{\omega }\frac{\partial k}{\partial {{x}_{j}}}\frac{\partial \omega }{\partial {{x}_{j}}}+{{P}_{\omega }}, \\ \end{align}$ |
其中,湍流动力黏度的控制方程为
| ${{\mu }_{t}}=\frac{\rho {{a}_{1}}k}{max\left( {{a}_{1}}\omega ,\Omega {{F}_{2}} \right)}.$ |
式中:${{a}_{1}}=0.31;\Omega =\sqrt{2{{W}_{ij}}{{W}_{ij}}}$为剪切应变的不变测度;F2=tanharg22为混合函数.其中Wij和arg2的表达式分别为
| $\begin{align} & {{W}_{ij}}=\frac{1}{2}\left( \frac{\partial {{v}_{i}}}{\partial {{x}_{j}}}-\frac{\partial {{v}_{j}}}{\partial {{x}_{i}}} \right), \\ & ar{{g}_{2}}=max\left( \frac{2\sqrt{k}}{{{\beta }^{*}}\omega d},\frac{500\nu }{{{d}^{2}}\omega } \right). \\ \end{align}$ |
模型中F1的表达式为
| $\begin{align} & {{F}_{1}}=tanhar{{g}^{4}}_{1}, \\ & ar{{g}_{1}}=min\left[ max\left( \frac{\sqrt{k}}{{{\beta }^{*}}\omega d},\frac{500\nu }{{{d}^{2}}\omega } \right),\frac{4\rho {{\sigma }_{\omega 2}}k}{C{{D}_{k\omega }}{{d}^{2}}} \right], \\ & C{{D}_{k\omega }}=max\left( 2\rho {{\sigma }_{\omega 2}}\frac{1}{\omega }\frac{\partial k}{\partial {{x}_{j}}}\frac{\partial \omega }{\partial {{x}_{j}}},{{10}^{-20}} \right). \\ \end{align}$ |
式中:ν=μ/ρ 为流体的运动黏度;d为流场中质点距离最近壁面的距离;CDkω为湍流交叉扩散项.
在引发湍流的同时,入水过程将伴随液相的空化,本文应用Schnerr and Sauer空化模型[15]对空化现象进行模拟,其控制方程如下:
| $\begin{align} & \frac{\partial {{\alpha }_{v}}}{\partial t}+\frac{\partial }{\partial {{x}_{i}}}\left( {{\alpha }_{v}}{{v}_{i}} \right)={{F}_{vap}}\frac{2{{\alpha }_{nuc}}\left( 1-{{\alpha }_{v}} \right){{\rho }_{v}}}{{{R}_{B}}}\sqrt{\frac{2}{3}\frac{{{p}_{v}}-p}{{{\rho }_{l}}}}- \\ & {{F}_{cond}}\frac{3{{\alpha }_{v}}{{\rho }_{v}}}{{{R}_{B}}}\sqrt{\frac{2}{3}\frac{p-{{p}_{v}}}{{{\rho }_{l}}}}. \\ \end{align}$ |
式中:RB=1×10-6 m为空化气核半径;αnuc=5×10-4为不可凝结气体的体积分数;Fvap=50 和Fcond=0.001为经验常数.
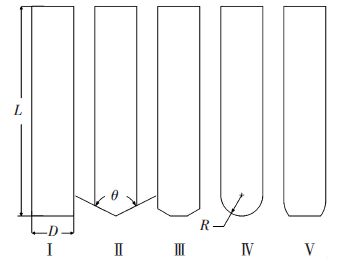
2 数值计算 2.1 计算模型及边界条件本文针对如图 1所示的5种头型的射弹开展数值模拟研究,射弹总长度L=50 mm,射弹柱段直径D=10 mm,锥头模型Ⅱ的锥角θ=127°,球头模型Ⅳ球头半径R=D/2.由于本文涉及的模型均为轴对称体,故采用二维轴对称模型进行计算.为保证计算结果的可对比性,不同头型射弹的质量均取为0.01 kg.截锥头模型Ⅲ与截球头模型Ⅴ分别与模型Ⅱ、Ⅳ有相同的锥角和球半径,模型Ⅲ与模型Ⅴ头部高度为模型Ⅱ、Ⅳ的3/4.
|
图 1 射弹模型及其参数 Figure 1 Models of projectile and their parameters |
初始计算域及网格划分如图 2所示,取射弹对称轴为x轴,计算域的宽度方向为y轴.本文的计算采用动计算域方法,该方法把整个计算域均设置为动网格区域,并定义其刚体运动规律,随着运动的发展,计算域沿运动方向不断扩大,故本文的初始计算域水域相对空气域要小一些.计算域顶端、侧面为压力出口,计算域底端为压力入口,它们的压力值及液相体积分数通过自定义函数进行指定.为保证计算的准确性,计算域的网格划分均采用四边形结构网格.弹体前后2D、径向7D范围内进行渐进加密,加密区近壁面第1层网格高度为5×10-6 m,加密区外围的网格稍稀疏.

|
图 2 初始计算域和流场网格示意 Figure 2 Initial simulation domain and mesh |
本文对流体控制方程的离散方法选用有限体积法,对离散方程组进行耦合求解从而采用PISO算法,用PRESTO!格式对压力场的进行离散,动量方程的求解使用了二阶迎风格式,采用Geo-Reconstruct格式对各相体积分数进行求解.
3 数值计算方法验证文献[13]提供了一种基于能量守恒原理的入水空泡发展的计算方法,该原理给出了计算射弹入水的速度和空泡半径公式分别为
| $\frac{d{{v}_{p}}}{dt}=g-\frac{{{\rho }_{l}}{{A}_{0}}{{C}_{dx}}{{v}^{2}}_{p}}{2m}.$ |
式中:vp为入水的瞬时速度;ρl为水的密度;A0为射弹的截面积;Cdx为阻力系数.
| $~a\left( x \right)=\sqrt{{{\left[ A\left( x \right) \right]}^{2}}-{{[Ax-Bxt-{{t}_{b}}]}^{2}}}+D/2.$ |
式中:$~{{[Ax]}^{2}}=\frac{1}{\pi {{p}_{g}}}{{\left[ \frac{d{{E}_{p}}}{d{{x}_{b}}} \right]}_{\xi }};{{\left[ Bx \right]}^{2}}=\frac{{{p}_{g}}}{N{{\rho }_{l}}};{{p}_{g}}$为空泡内部压力高于饱和蒸气压的差值;N=lnΩ/a,它的取值一般在15~30之间,对于本文的亚音速问题,可以取15进行求解;D为射弹柱状体直径.
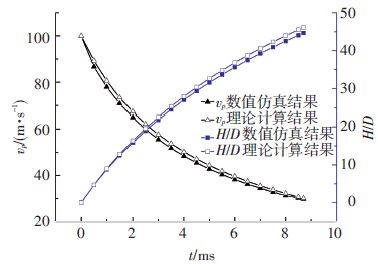
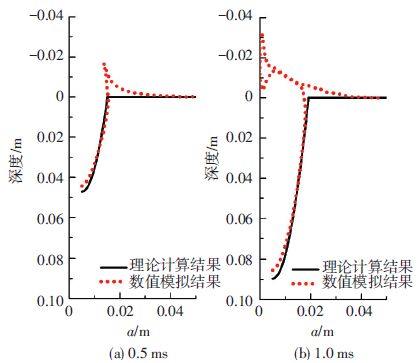
针对锥头射弹(模型Ⅱ)以100 m/s的速度垂直入水过程,分别进行了数值模拟和基于能量守恒原理的理论计算,得到的射弹入水速度与深度的数值结果与理论结果对比如图 3所示,0.5,1.0 ms时刻空泡形态的数值结果与理论结果的对比如图 4所示.图中,理论求解和数值求解得到的相关参数差异很小,可以看出本文的数值模拟方法有很高的准确性,能够比较有效地模拟高速射弹垂直入水过程的空泡演化过程和弹道特性.
|
图 3 入水速度与深度数值结果与理论结果的对比 Figure 3 Comparison of analytical and numerical results of water-entry velocity and depth |
|
图 4 0.5,1.0 ms时刻空泡形态数值结果与理论结果的对比 Figure 4 Comparison of analytical and numerical cavity shapes at time 0.5,1.0 ms |
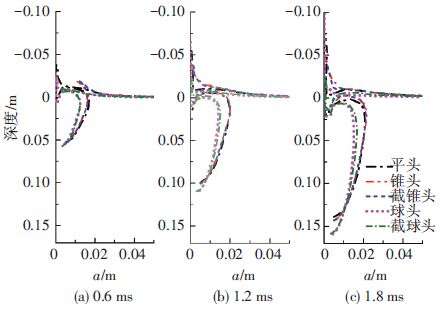
图 5为射弹入水不同时刻的空泡形态对比.从图 5中可以看到,在同一时刻,球头和截球头射弹形成的空泡形态基本一致,平头、锥头和截锥头形成的空泡形态近似一致,而且球头和截球头射弹形成的空泡半径小于其他3种头型.这是由于球头和截球头射弹头部与弹身结合处过渡光滑,空化程度较低.在空泡发生表面闭合之后,在闭合处会出现尾部射流,其中球头射弹由于航行速度较高,因此形成的尾部射流最高.另外,球头和截球头射弹形成空泡的起始位置小于弹身半径,表明其入水空泡将头部包裹了一部分,故其在入水后期具有较小的阻力系数.其余的3种头型空泡则只包裹了弹身.
|
图 5 入水0.6,1.2,1.8 ms时刻空泡形态对比 Figure 5 Comparison of cavity shapes at time 0.6,1.2,1.8 ms |
表 1给出了不同头型射弹入水空泡表面闭合的时间以及闭合时的量纲一的入水深度.其中,截球头射弹由于入水初期速度衰减过快并且空泡半径小,在空泡闭合之前,回流撞击到了射弹尾部,故没有准确的空泡闭合时间.平头射弹速度衰减快,造成的尾部回流速度高,最先发生表面闭合,球头射弹空泡半径小,其闭合时间也较早,锥头和截锥头的闭合则发生在最后.
| 表 1 不同头型射弹空泡表面闭合时间及深度 Table 1 Cavity surface closure time and depth of projectiles |
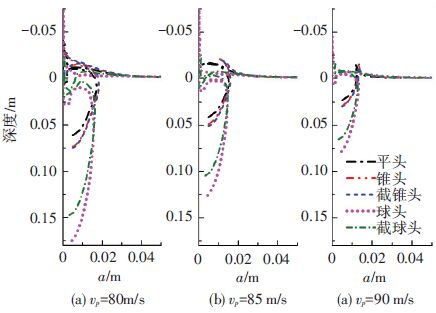
图 6分别给出了入水不同瞬时速度条件下5种头型射弹形成的空泡形态对比.在同一瞬时速度处,平头、锥头和截锥头射弹的最大空泡半径大于球头和截球头射弹.这是因为非流线型头型更有利于形成低压区,从而提高空化程度.
|
图 6 入水80,85,90 m/s瞬时速度空泡形态对比 Figure 6 Comparison of cavity shapes at velocity 80,85,90 m/s |
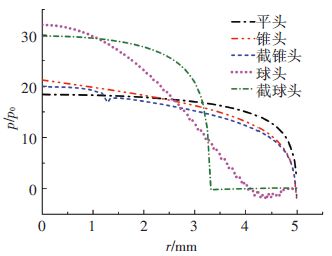
头部是射弹承受压力最大的位置,也是入水阻力的主要来源.图 7给出了入水2 ms时刻不同头型头部母线处的压力系数分布.平头头部压力系数分布相对而言比较均匀,锥头和截锥头的压力系数变化趋势较为一致,球头和截球头头部压力变化较大,对头部材料的抗剪切能力要求较高.在顶点处,各头型射弹压力系数均较高,球头与截球头达到了30倍大气压左右,其余3种头型为20倍大气压,这造成的较强的冲击载荷对射弹结构有较大的影响.截球头和截锥头在其头型截断处压力有较大的变化,这是由于该处流体流速高,相应产生了低压.
|
图 7 入水2 ms时刻头部母线压力系数分布 Figure 7 Pressure of projectiles’ head generatrix at time 2 ms |
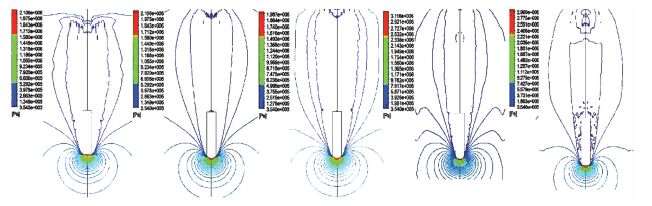
图 8给出了入水2 ms时刻不同头型射弹空泡附近的压力等值线图,图 8中压力等值线的最低值设置为饱和蒸汽压,从图 8中可以看出,不同头型压力的分布趋势是较为一致的,最大压力均集中在头部顶点处.此时,空泡都已经完成了表面闭合,故低于饱和蒸汽压的低压区域正好是空泡区域.
|
图 8 入水2 ms时刻流场的压力等值线图 Figure 8 Contour of pressure at time 2 ms |
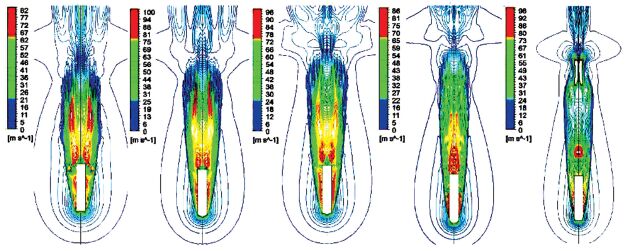
头型对射弹入水的速度场也有较明显的影响,图 9给出了入水2 ms时刻不同头型射弹的速度等值线图.对于不同的头型,高速区都是空泡内部的气相区域.
|
图 9 入水2 ms时刻流场的速度等值线图 Figure 9 Contour of velocity at time 2 ms |
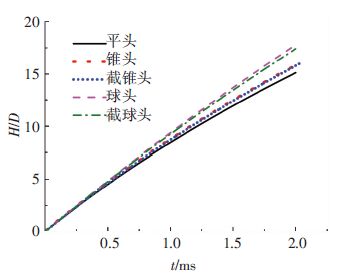
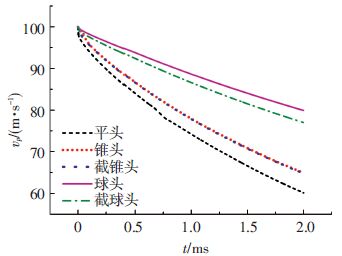
图 10,11分别给出了不同头型射弹入水深度与速度随时间的变化曲线.由图 10,11可见,不同头型射弹入水深度与速度的变化趋势是一致的,入水初期阻力值较大,射弹速度均有较明显的衰减.在同一时刻,入水深度随平头、截锥头、锥头、截球头、球头的次序递增,而速度按相同的次序递减,说明头部流线型越好,入水速度衰减越慢,入水深度增加越快.锥头与截锥头射弹由于入水过程阻力相当,入水速度与深度相差很小.
|
图 10 量纲一的入水深度对比 Figure 10 Comparison of non-dimensional depth of waterentry |
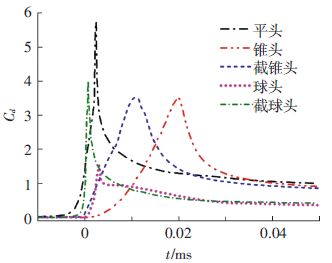
图 12给出了入水初期不同头型射弹的阻力系数变化曲线.
|
图 11 入水速度对比 Figure 11 Comparison of velocity of waterentry |
|
图 12 入水初期阻力系数 Figure 12 Initial drag coffecients of waterentry |
由图 12可见,射弹入水初期会产生较高的阻力系数峰值,其中平头射弹由于其撞击水面的面积最大,故峰值最高达到了5.5以上,之后依次是截球头、截锥头、锥头、球头.截锥头与锥头射弹从头部到弹身的过渡较缓,阻力系数峰值相比其他3种头型射弹有一定的延后.
5 结 论1) 头型对入水空泡的形态和表面闭合时间有较大的影响,平头射弹始终具有较大的空泡半径,截球头和球头射弹形成的空泡半径小.表面闭合时刻从早到晚顺序为:平头、球头、锥头、截锥头.
2) 高速射弹头型承受的压力值均比较大,对其头部的抗冲击性能要求较高,同时球头和截球头射弹头部各区域压差大,对其头部剪切强度要求亦较高.
3) 高速射弹入水过程中,流场的低压区和高速区是气态介质体积分数较大的空泡区域.不同头型射弹入水的速度衰减和深度趋势相同,射弹头部流线型越好,入水速度衰减越慢,入水深度增加越快.阻力系数峰值按平头、截球头、截锥头、锥头、球头的次序递减.
| [1] |
WORTHINGTON A M, COLE R S. Impact with a liquid surface studied by the aid of instantaneous photography[J].
Philosophical Transactions of the Royal Society,1900, 194 (A) : 175-199.
( 0) 0)
|
| [2] |
MAY A, WOODHULL J C. Drag coefficients of steel spheres entering water vertically[J].
Journal of Applied Physics,1948, 9 (2) : 127-139.
DOI: 10.1063/1.1715027 ( 0) 0)
|
| [3] |
MAY A, WOODHULL J C. The virtual mass of a sphere entering water vertically[J].
Journal of Applied Physics,1950, 21 (12) : 1285-1289.
DOI: 10.1063/1.1699592 ( 0) 0)
|
| [4] |
MAY A. Effect of surface condition of a sphere on its water-entry cavity[J].
Journal of Applied Physics,1951, 22 (10) : 1219-1222.
DOI: 10.1063/1.1699831 ( 0) 0)
|
| [5] |
MAY A. Vertical entry of missiles into water[J].
Journal of Applied Physics,1952, 23 (12) : 1362-1372.
DOI: 10.1063/1.1702076 ( 0) 0)
|
| [6] |
LUNDSTROM E A, FUNG W K. Fluid dynamic analysis of hydraulic ram. AD031644 [R]. Washington. DC: Joint Technical Coordinating Group for Aircraft Survivability,1976.
( 0) 0)
|
| [7] |
PARYSHEV E V. Approximate mathematical models in high-speed hydrodynamics[J].
Journal of Engineering Mathematics,2006, 55 : 41-64.
DOI: 10.1007/s10665-005-9026-x ( 0) 0)
|
| [8] |
WEILAND C, VLACHOS P P. Time-scale for critical growth of partial and supercavitation development over impulsively translating projectiles[J].
International Journal of Multiphase Flow,2012, 38 (1) : 73-86.
DOI: 10.1016/j.ijmultiphaseflow.2011.08.012 ( 0) 0)
|
| [9] |
何春涛, 王聪, 魏英杰, 等. 圆柱体垂直入水空泡形态试验研究[J].
北京航空航天大学学报,2012, 38 (11) : 1542-1546.
HE Chuntao, WANG Cong, WEI Yingjie, et al. Vertical water entry cavity of cylinder body[J]. Journal of Beijing University of Aeronautics and Astronautics,2012, 38 (11) : 1542-1546. (  0) 0)
|
| [10] |
魏卓慧, 王树山, 马峰. 刚性截锥形弹体入水冲击载荷[J].
兵工学报,2010, 31 (S1) : 118-120.
( 0) 0)
|
| [11] |
胡平超, 张宇文, 袁绪龙. 航行器垂直入水空泡特性与流体动力研究[J].
计算机仿真,2011, 28 (6) : 5-8.
DOI: 10.3969/j.issn.1006-9348.2011.06.002 HU Pingchao, ZHANG Yuwen, YUAN Xulong. Research on cavitation and hydrodynamic of vertical water-entry for supercavitating vehicles[J]. Computer Simulation,2011, 28 (6) : 5-8. DOI: 10.3969/j.issn.1006-9348.2011.06.002 (  0) 0)
|
| [12] |
马庆鹏, 魏英杰, 王聪, 等. 不同头型运动体高速入水空泡数值模拟[J].
哈尔滨工业大学学报,2014, 40 (11) : 24-29.
MA Qingpeng, WEI Yingjie, WANG Cong, et al. Numerical simulation of high-speed water entry cavity of cylinders[J]. Journal of Harbin Institute of Technology,2014, 40 (11) : 24-29. (  0) 0)
|
| [13] |
LEE M, LONGORIA R G, WILSON D E. Cavity dynamics in high-speed water entry[J].
Physics of Fluids,1997, 9 (3) : 540-550.
DOI: 10.1063/1.869472 ( 0) 0)
|
| [14] |
MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J].
AIAA Journal,1994, 32 (8) : 1598-1605.
( 0) 0)
|
| [15] |
SCHNERR G H, SAUER J. Physical and numerical modeling of unsteady cavitation dynamics[C]//Proceedings of the 4th International Conference on Multiphase Flow. New Orleans: [s.n.], 2001.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


