在鲁棒控制领域中,传统方法如H∞方法或μ综合方法设计的控制器尽管能够达到鲁棒性指标要求,但是在控制器设计完成以前通常难以准确预知其结构和复杂程度,例如文献[1]就指出了H∞控制器存在的阶次过高难以实现的问题.另一方面,经典PID控制方法实现过程简单,但仅能考虑单通道鲁棒性指标,不能有效保证MIMO系统的鲁棒性能,无法满足新一代导弹的极限飞行特性要求.在本文中,考虑把经典控制与现代鲁棒控制两者各自的优势结合起来,形成经典设计满足H∞鲁棒性指标的综合设计方法——定结构H∞控制,并将其应用到导弹驾驶仪的设计之中.
文献[2]给出了定结构H∞控制方法最初的设计思想,它来源于基于Hermite-Biehler理论的H∞-PID控制器设计理论,在该理论中提出了采用线性优化的方法来设计鲁棒PID控制器.该方法的不足之处是在确定微分和积分增益之前必须首先确定比例增益,无法同时得到所有的控制参数.文献[3-4]介绍了近年来为解决这一问题相继发表的有关研究成果,同时,在文献[5-6]中,分别提出了基于线性矩阵不等式(LMI)的解决方法.然而上述方法仍然没有解决控制器同时满足多种控制指标和约束的问题.
本文提出了一种基于梯度修正粒子群优化的定结构H∞控制器设计方法,基本思路是采用带约束条件的粒子群优化算法对定结构H∞控制器(如鲁棒PID控制器)进行自动优化并得到MIMO系统的控制参数,使得所设计的控制系统在满足时域指标的同时满足H∞鲁棒性指标.文献[7-8]给出了粒子群优化算法(PSO)的最初版本,它是一种全局优化算法,目前已发展成为一种通用的优化算法,并被广泛应用于多目标优化、神经系统训练和决策支持等各领域,相关应用成果如文献[9-11]所述.相对于其他算法,PSO算法具有算法结构简单、计算量和内存占用小、对目标函数没有诸如线性、可微、凸集要求等优点.在标准PSO算法提出后,大量的改进算法相继提出,如文献[11-12]给出了带等式与不等式约束条件的PSO优化算法的相关研究成果.基于此,本文采用了一种基于梯度修正策略的约束PSO优化算法,并将其应用到导弹定结构H∞鲁棒控制器的设计中.
1 问题描述考察由式(1)描述的线性模型闭环控制系统∑[x]:
| $\left[ \begin{matrix} z \\ y \\ \end{matrix} \right]=G\left( s \right)\left[ \frac{w}{u} \right],u=K\left( s;x \right)y.$ | (1) |
其带扰动与不确定性的控制结构如图 1所示.其中G(s)为控制对象模型,K(s;x)为定结构H∞控制器,x为控制器设计变量;z、y分别为控制输出和传感器输出向量;d、w、u分别为控制扰动输入、传感器扰动输入和控制输入向量;Δ(s)为模型不确定性并满足‖Δ(s)‖∞<1;w2为权函数.

|
图 1 闭环控制系统 Figure 1 Closed-loop control system |
将闭环控制系统标称部分和不确定部分分离后可由图 2所示的简化模型描述.
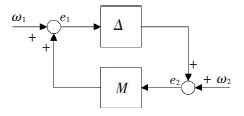
|
图 2 小增益定理 Figure 2 Small gain theorem |
依据文献[13]中的小增益定理,图 2所示的闭环控制系统内稳定的充分必要条件是‖Δ(s)‖∞<1当且仅当‖wT(s)T(s;x)‖∞≤1,其中T(s;x)为补灵敏度函数.
设传递函数L(s;x)=G(s)
| $T\left( s;x \right)=\frac{L\left( s;x \right)}{1+L\left( s;x \right)}.$ |
同时,定义灵敏度函数S(s)为
| $S\left( s;x \right)=\frac{1}{1+L(s;x)},$ |
则系统的标称性能定义为
| $\|{{w}_{S}}\left( s \right)S\left( s;x \right){{\|}_{\infty }}\le 1,$ |
式中wS(s)为灵敏度函数权函数.
鲁棒性能定义为
| $\|{{w}_{S}}\left( s \right)S\left( s;x \right)+{{w}_{T}}\left( s \right)T\left( s;x \right){{\|}_{\infty }}\le 1.$ | (2) |
在定结构控制器的所有类型中,可以将PID控制器看作定结构控制器中的一种,如以标准PID控制器为例,其控制律表达式为
| $K\left( s;x \right)={{k}_{p}}\left( x \right)+\frac{{{k}_{i}}\left( x \right)}{s}+\frac{{{k}_{d}}\left( x \right)s}{1+Ts}.$ | (3) |
式中:kp、ki、kd分别为比例系数、积分系数和微分系数;T为滤波器时间常数.在本文中,所要解决的问题即为如何找到定结构控制器—如以式(3)所示的标准PID控制器的参数kp、ki、kd使得闭环控制系统的性能满足式(2)所示的鲁棒性能指标.
2 导弹定结构控制导弹的定结构控制器可以有各种形式,如姿态控制器、迎角控制器和过载控制器等,每种控制器依据控制对象本身的特性和控制需求还可以细分为更多的定结构回路控制结构.不失一般性,本文以经典雷声(raytheon)驾驶仪控制结构为例,其中俯仰通道和偏航通道的控制结构相同,如图 3,4所示.

|
图 3 俯仰/偏航通道控制结构 Figure 3 Pitch/yaw channel control structure |

|
图 4 滚转通道控制结构 Figure 4 Roll channel control structure |
在图 3,4中,Az、Azm分别为法向过载输出信号和法向过载给定信号;θ为俯仰角;q为俯仰角速率;Ay、Aym分别为侧向过载输出信号和侧向过载给定信号;ψ为偏航角;r为偏航角速率;φ、φm分别为滚转角输出信号和滚转角给定信号;p为滚转角速率.在俯仰/偏航通道中,3个回路分别为角速率阻尼回路,俯仰角/偏航角增稳回路和过载控制回路,并在过载回路中采用积分校正以消除静差.滚转通道以滚转角控制回路为外回路,内回路采用滚转角速率改善其阻尼特性.三通道控制律的表达式为
| $~{{\delta }_{e}}=\left( {{k}_{e1}}+\frac{{{k}_{e}}_{2}}{s} \right)\left( {{A}_{z}}-{{A}_{zm}} \right)+{{k}_{e3}}\theta +{{k}_{e4}}q,$ | (4) |
| ${{\delta }_{r}}=\left( {{k}_{r1}}+\frac{{{k}_{r2}}}{s} \right)\left( {{A}_{y}}-{{A}_{ym}} \right)+{{k}_{r3}}\psi +{{k}_{r4}}r,$ | (5) |
| ${{\delta }_{a}}={{k}_{a1}}\left( \varphi -{{\varphi }_{m}} \right)+{{k}_{a2}}p.$ | (6) |
在导弹驾驶仪的设计指标中,除了鲁棒性指标,通常还有一些时域指标如上升时间、超调量、稳态误差等需要在设计时一并考虑.样例导弹对阶跃信号的过载和滚转响应性能指标见表 1.
| 表 1 时域性能指标要求 Table 1 Time domain performance index |
在闭环控制系统的时域性能指标表达方式中,最常见的有误差绝对值积分(IAE)、误差平方积分(ISE)和带时间权重的误差平方积分(ISTE)等,如
| $\begin{align} & IAE={{\int }^{\infty }}_{0}e(t)dt, \\ & ISE={{\int }^{\infty }}_{0}{{e}^{2}}(t)dt, \\ & ITSE={{\int }^{\infty }}_{0}t{{e}^{2}}(t)dt. \\ \end{align}$ |
式中,IAE和ISE的不足之处在于采用这两个指标的控制系统超调较小但稳态时间较长,其原因在于在所有时间范围内对误差采用了同样的要求,这一点并不合理.ISTE克服了这一弱点,但同样不能保证鲁棒性要求.因此,在本文中,性能指标函数J同时采用了时域指标ITSE和式(2)所示的鲁棒性指标,如
| $~J=\|{{w}_{S}}\left( s \right)S\left( s;x \right)+{{w}_{T}}\left( s \right)T\left( s;x \right){{\|}_{\infty }}+\int _{0}^{\infty }t{{e}^{2}}(t)dt,$ | (7) |
该性能指标函数同时兼顾了时域响应性能和混合灵敏度H∞鲁棒性能,同时为了保证系统是在稳定的前提下达到上述指标,取下式作为其约束条件:
| $Re{{\lambda }_{max}}(\sum \left[ x \right])<0,$ | (8) |
式中,λmax(∑[x])为闭环系统∑[x]的最大极点,因此式(8)保证了满足性能指标要求的闭环系统所有极点均在复平面虚轴的左边.
3 粒子群优化算法粒子群优化算法(particle swarm optimization,PSO)是一种通过模拟鸟类群体行为进行建模与仿真研究而发展起来的一种基于群体协作的随机搜索算法,属于群体智能搜索算法的一种.由于粒子群优化算法其算法本身结构简单,并在多种复杂优化问题的应用中表现优异,近年来引起了越来越多的关注.
3.1 标准PSO算法在PSO算法中,每一个优化问题的解作为一只单个的鸟,或称为粒子,粒子的属性包括其位置x和速度v.每个粒子在多维空间中依据个体经验和群体中其他粒子的经验来动态调整自身移动的轨迹与速度.在每一时刻k,第i个粒子xi=(xi1,xi2,…,xin)∈Rn依据以下公式对位置和速度进行调整:
| ${{x}^{k+1}}_{i,d}={{x}^{k}}_{i,d}+{{v}^{k+1}}_{i,d},$ | (9) |
| $\begin{align} & {{x}^{k+1}}_{i,d}=\left\{ \begin{matrix} -{{x}_{max}},d,\text{ }{{x}^{k+1}}_{i,d}<-{{x}_{max}},d; \\ {{x}_{max}},d,\text{ }{{x}^{k+1}}_{i,d}>{{x}_{max}},d; \\ {{x}^{k+1}}_{i,d},~others. \\ \end{matrix} \right. \\ & {{v}^{k+1}}_{i,d}=\omega {{v}^{k}}_{i,d}+{{c}_{1}}{{\zeta }^{k}}_{1}\left( {{p}^{k}}_{i,d}-{{x}^{k}}_{i,d} \right)+{{c}_{2}}{{\zeta }^{k}}_{2}\left( {{g}^{k}}_{i,d}-{{x}^{k}}_{i,d} \right), \\ \end{align}$ | (10) |
式中:xki,d为粒子i在第k步中的d维位置,xmax,d为粒子运动的最远位置;vki,d 为粒子i在第k步中的d维速度,vmax,d为粒子在d维的最大速度,粒子的运动被设定为不能超过此最大速度;pki,d为粒子个体的当前最优值; gki,d为粒子群体的当前最优值;c1为粒子个体认知加速常数,c2为群体认知加速常数,参数c1和c2分别代表了个体自身行为和群体行为对个体影响的大小; ζ1、ζ2 是介于[0,1]之间的随机数;ω为惯性系数,代表了粒子的运动惯性,按照运动惯性随进化代数逐渐减小的原则,其表达式为
| $~w={{w}_{max}}-({{w}_{max}}-{{w}_{min}})\frac{k}{{{k}_{max}}}.$ |
式中:wmax、wmin分别为w的最大值与最小值;kmax为最大进化代数.
3.2 约束PSO算法粒子群算法最初是作为一种非约束优化算法被提出的,然而在工程实践中有相当多的应用属于要求满足一定约束条件下的最优化问题.本文采用了一种基于梯度修正策略的新型约束优化方法,该方法的思想来源于利用运动微分量(梯度)对运动趋势进行预测的方法,文献[15-16]给出了该梯度预测技术的应用情况.
具有不等式约束条件的优化问题(最小值)可以描述为
| $Minimize~f\left( x \right),$ |
满足
| $\begin{matrix} {{g}_{j}}\left( x \right)\le 0, & j=1,\ldots ,q; \\ {{l}_{i}}\le {{x}_{j}}\le {{u}_{i}}, & i=1,\ldots ,n. \\ \end{matrix}$ |
式中:x为一维设计向量;li、lj分别为其下界和上界;g为不等式约束条件.
梯度修正PSO算法的步骤如下.
1) 定义约束违反变量Δv为
| $\Delta v=min\left\{ 0,-g\left( x \right) \right\}.$ | (11) |
2) 约束函数变化率变量∇xv可以表示为
| $\nabla v\approx \frac{1}{e}\cdot g({{x}_{i}}+e)-g({{x}_{i}}),\forall i=1,\ldots ,n.$ |
式中e为用于扰动的小量.且约束违反量Δv与粒子位置变化量Δx具有如下关系:
| $\Delta v={{\nabla }_{x}}v\times \Delta x\Rightarrow \Delta x={{({{\nabla }_{x}}v)}^{-1}}\times \Delta v.$ | (12) |
3) 当∇xv不可逆时,计算∇xv的伪逆(∇xv)+用于取代式(12)中的(∇xv)-1.
4) 违反约束条件的粒子位置更新公式可以表示为
| $~{{x}^{k+1}}={{x}^{k}}+\Delta x={{x}^{k}}+{{\nabla }_{x}}{{v}^{-1}}\times \Delta v\approx {{x}^{k}}+{{\nabla }_{x}}{{v}^{+}}\times \Delta v.~$ |
5) 重复步骤1)~4),直到违反约束条件的粒子被拉回到满足约束条件的解空间中.
从梯度修正法的执行步骤可以看出,算法直接利用了粒子的移动趋势信息对其进行修正,相比于罚函数法,并没有增加新的算法参数,过程较为简洁并且易于实现.将上述梯度修正算法与标准PSO优化算法相融合成为梯度修正PSO算法,在初始化和每次粒子位置更新时调用梯度修正算法对不满足约束条件的解进行修正,使其满足约束条件要求,具体步骤为:
1) 确定粒子种群数量N和优化最大代数kmax;
2) 在粒子的取值范围内初始化粒子种群每个每一个粒子的位置和速度;
3) 判断每个粒子的位置是否违反约束条件,如违反则调用梯度修正法将其拉回到满足约束条件的区域;
4) 计算每一个粒子的目标函数值;
5) 计算每个粒子的个体最优值 pki,d 和当前粒子种群最优值gki,d,如粒子当前值优于pki,d,则将粒子当前值设置为pki,d,如全部粒子当前值中有优于gki,d的粒子,则将该粒子当前值设置为gki,d;
6) 判断当前最优值是否满足性能指标停止条件或达到最大优化代数,如满足二者之一即停止算法并转到步骤8);
7) 依据式(9),(10)更新每个粒子的位置并转到步骤3);
8) 输出最优粒子的位置和对应的性能指标值.
梯度修正法与标准粒子群算法的差异在于增加了对约束条件的处理环节,即粒子位置与约束条件关系的判断和修正,代价是运行算法所需时间的增加.
4 算例仿真与分析 4.1 算法性能测试当前,优化算法的优劣尚不能从理论上进行证明,只能通过测试函数的实测结果来进行比较.为验证将梯度修正策略应用于约束粒子群优化的验证将梯度修正策略应用于约束粒子群优化的实际效果,表 2采用3个标准测试函数(G4、G8、G12)来对其性能进行全面测试与验证,这3个测试函数在约束优化算法的性能测试中被广泛采用,其函数定义和说明可详见文献[17].测试程序在Matlab7.8环境下运行,采用一台Intel 双核2.4 GHz CPU,内存为2 G字节.每个任务运行30次,进化代数为1 000或性能指标全部达到.同时为了与其他算法进行对比,本文选择了文献[18-20]中介绍的其他3种常见约束优化算法:同态图法 (HM)、随机排序法(SR)以及协同进化法(CR).这3种算法的稳定性很高,常用来与新提出的算法进行性能比较.在进行比较分析时,梯度修正粒子群算法参数取为:粒子数量为30;粒子维数依测试函数;粒子最大移动速度vmax,d=xmax,d/2;学习因子c1=2,c2=2;惯性系数最大与最小值wmax=0.9,wmin=0.4;最大搜索代数为1 000.
| 表 2 4种约束优化算法测试结果 Table 2 Four constrained optimization algorithms test results |
比较结果见表 2.从测试结果可以看出梯度修正PSO算法在处理带约束的优化问题中具有良好的性能,明显优于与之比较的HM、SR和CR3种算法.梯度修正PSO算法对测试函数获得的最优值与其他3种算法相当,平均搜索效率高于上述算法.在测试函数G4中,其最差优化结果也好于算法HM.从优化时间来看,4种算法也基本相当.测试结果表明,梯度修正粒子群算法具有良好性能,用于导弹定结构控制器设计是完全适合的.
4.2 仿真验证目前,战术导弹工程上多采用基于多工作点线性化模型的控制律设计,六自由度非线性模型验证的方法.本文以文献[21]中的样例导弹线性化模型为设计对象,该样例导弹在15 000 m高度、0.9 Ma、40°攻角下的特征工作点俯仰/偏航状态方程为
| $\begin{align} & ~\left[ \begin{array}{*{35}{l}} {\dot{u}} \\ {\dot{w}} \\ {\dot{q}} \\ {\dot{v}} \\ {\dot{r}} \\ \end{array} \right]=\left[ \begin{array}{*{35}{l}} -0.099\text{ }31 & -0.019\text{ }20 & -20.290 & 190\text{ }0.018\text{ }00 & -20.290\text{ }19 \\ -0.047\text{ }87 & -0.688\text{ }73 & 234.204\text{ }817 & -0.089\text{ }97 & 0 \\ -0.116\text{ }69 & -0.275\text{ }33 & -5.587\text{ }227 & -0.012\text{ }13 & 0 \\ 0.189\text{ }22 & -0.034\text{ }71 & 0 & -0.670\text{ }48 & -234.204\text{ }81 \\ -0.038\text{ }20 & 0.025\text{ }21 & 0 & 0.047\text{ }61 & -1.587\text{ }22 \\ \end{array} \right]\text{ }\cdot \left[ \begin{array}{*{35}{l}} u \\ w \\ q \\ v \\ r \\ \end{array} \right]+ \\ & \left[ \begin{array}{*{35}{l}} 0.149\text{ }33 & \text{ }0.149\text{ }33 \\ -2.058\text{ }67 & 0.180\text{ }70 \\ -3.977\text{ }95 & 0.175\text{ }13 \\ -0.060\text{ }70 & 3.158\text{ }67 \\ 0.055\text{ }13 & -2.977\text{ }95 \\ \end{array} \right]\cdot \left[ \begin{matrix} {{\delta }_{e}} \\ {{\delta }_{r}} \\ \end{matrix} \right]. \\ \end{align}$ |
俯仰/偏航输出方程为
| $\begin{align} & \left[ \begin{matrix} {{A}_{z}} \\ q \\ {{A}_{y}} \\ r \\ \end{matrix} \right]=\left[ \begin{array}{*{35}{l}} -0.167\text{ }10 & -2.028\text{ }05 & -3.823\text{ }94 & -1.256\text{ }49 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0.408\text{ }76 & -0.463\text{ }14 & 2.003\text{ }90 & -1.531\text{ }80 & 1.934\text{ }04 \\ 0 & 0 & 0 & 0 & 1 \\ \end{array} \right].\left[ \begin{array}{*{35}{l}} u \\ w \\ q \\ v \\ r \\ \end{array} \right]+ \\ & \left[ \begin{array}{*{35}{l}} -3.464\text{ }98 & -0.134\text{ }57 \\ 0 & 0 \\ -0.317 & 2\text{ }2.313\text{ }38 \\ 0 & 0 \\ \end{array} \right].\left[ \begin{matrix} {{\delta }_{e}} \\ {{\delta }_{r}} \\ \end{matrix} \right]. \\ \end{align}$ |
式中:u、v、w分别为弹体轴纵向、侧向和法向速度;q、r为俯仰角速率和偏航角速率,姿态由角速率积分得到;Az、Ay分别为法向和侧向过载,δe、δr分别为等效升降舵和方向舵偏角.
滚转状态方程为
| $\left[ \begin{matrix} {\dot{p}} \\ {\dot{\varphi }} \\ \end{matrix} \right]=\left[ \begin{matrix} -0.867\text{ }639 & 0 \\ 1 & 0 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} p \\ \varphi \\ \end{matrix} \right]+\left[ \begin{matrix} -67.434\text{ }369 \\ 0 \\ \end{matrix} \right]\cdot {{\delta }_{a}}.$ |
滚转输出方程为
| $\left[ \begin{matrix} p \\ \varphi \\ \end{matrix} \right]=\left[ \begin{matrix} 57.295\text{ }78 & 0 \\ 0 & 57.295\text{ }78 \\ \end{matrix} \right]\cdot \left[ \begin{matrix} p \\ \varphi \\ \end{matrix} \right]+\left[ \begin{matrix} 0 \\ 0 \\ \end{matrix} \right]\cdot {{\delta }_{a}}.$ |
式中:φ、p分别为滚转角和滚转角速率;δa为等效副翼舵偏角.
为保证控制器各项参数均为正值,缩小搜索空间的范围,式(4)~(6)所示的控制器可以改写为
| $\begin{align} & {{\delta }_{e}}=({{10}^{{{x}_{e1}}}}+\frac{{{10}^{{{x}_{e2}}}}}{s})({{A}_{z}}-{{A}_{zm}})+{{10}^{{{x}_{e3}}}}\theta +{{10}^{{{x}_{e4}}}}q, \\ & {{\delta }_{r}}=({{10}^{{{x}_{r1}}}}+\frac{{{10}^{{{x}_{r2}}}}}{s})({{A}_{y}}-{{A}_{ym}})+{{10}^{{{x}_{r3}}}}\psi +{{10}^{{{x}_{r4}}}}r, \\ & {{\delta }_{a}}={{10}^{{{x}_{a1}}}}(\varphi -{{\varphi }_{m}})+{{10}^{{{x}_{a2}}}}p. \\ \end{align}$ |
则
| $\begin{array}{*{35}{l}} \left( {{x}_{e1}}{{x}_{e2}}{{x}_{e3}}{{x}_{e4}} \right)= \\ \left( lo{{g}_{10}}{{k}_{e1}}lo{{g}_{10}}{{k}_{e2}}lo{{g}_{10}}{{k}_{e3}}lo{{g}_{10}}{{k}_{e4}} \right), \\ \left( {{x}_{r1}}{{x}_{r2}}{{x}_{r3}}{{x}_{r4}} \right)= \\ \left( lo{{g}_{10}}{{k}_{r1}}lo{{g}_{10}}{{k}_{r2}}lo{{g}_{10}}{{k}_{r3}}lo{{g}_{10}}{{k}_{r4}} \right), \\ \left( {{x}_{a1}}{{x}_{a2}} \right)=\left( lo{{g}_{10}}{{k}_{a1}}lo{{g}_{10}}{{k}_{a2}} \right). \\ \end{array}$ |
因此,待搜寻参数的范围Δf可以表示为
| $\begin{align} & {{\Delta }_{fe}}:=\{\left( {{x}_{e1}},{{x}_{e2}},{{x}_{e3}},{{x}_{e4}} \right)\in {{R}^{4}}: \\ & {{x}_{e1}}>0,{{x}_{e2}}>0,{{x}_{e3}}>0,{{x}_{e4}}>0\}, \\ & {{\Delta }_{fr}}:=\text{ }\{\left( {{x}_{r1}},{{x}_{r2}},{{x}_{r3}},{{x}_{r4}} \right)\in {{R}^{4}}:{{x}_{r1}}>0, \\ & {{x}_{r2}}>0,{{x}_{r3}}>0,{{x}_{r4}}>0\}, \\ & {{\Delta }_{fa}}:=\left\{ \left( {{x}_{a1}}{{x}_{a2}} \right)\in {{R}^{3}}:{{x}_{a1}}>0,{{x}_{a2}}>0 \right\}. \\ \end{align}$ |
样例导弹的定结构鲁棒控制问题即为在满足式(8)约束的条件下寻找优化参数
样例导弹法向和侧向通道的特性非常相似,可以采用相同的控制结构,并且为降低问题的复杂性,本文认为控制参数也相同.同时滚转通道控制结构较为简单,只有两个控制参数,因此这里仅给出俯仰/偏航通道应用梯度修正PSO算法进行定结构H∞控制器的设计过程.对滚转通道可以采用相同的方法进行控制器设计.在设计完成后,控制器的验证则针对三通道模型进行.
在采用混合灵敏度H∞设计方法时,权函数的选择是关键问题之一.灵敏度函数S(s;x)的幅值与闭环系统的指令跟踪和抗干扰能力直接相关,而补灵敏度函数T(s;x)决定了系统的鲁棒稳定性.相应的,权函数wS(s)和wT(s)应分别反映对这两个函数的形状要求.由于命令信号和干扰信号的频率较低,因此在低频段,在保证闭环系统鲁棒稳定的前提下,S(s;x)必须尽量小,即wS(s)的幅值应尽量大,以使系统取得良好的命令跟踪能力和抗干扰能力;而系统的测量噪声一般随频率的增大而增大,因此要求在高频段T(s;x)较小,即wT(s)的幅值应尽量大,以抑制测量噪声的不利影响.综合考虑上述因素,灵敏度和补灵敏度权函数分别取为
| $\begin{align} & {{w}_{S}}\left( s \right)=\frac{0.1\left( s+50 \right)}{s+0.001}\cdot {{I}_{2}}, \\ & {{w}_{T}}\left( s \right)=\frac{s+10}{13}\cdot {{I}_{2}}. \\ \end{align}$ |
由于导弹的定结构H∞控制器的设计问题相对于测试函数而言要复杂得多,计算量也大很多,依据多轮设计与仿真的经验,此时梯度修正PSO算法的参数可以取为:粒子数量为100; 粒子维数为4; 粒子最大移动速度:vmax,d=xmax,d/2,i=1,…,4;学习因子 c1=2,c2=2;惯性系数最大与最小值 wmax=0.9,wmin=0.4;最大搜索代数为400; 终止条件达到最大代数.
采用如式(7)~(8)的性能指标函数和约束条件,俯仰/偏航通道性能指标函数收敛性曲线如图 5所示.

|
图 5 俯仰/偏航通道性能指标函数收敛性曲线 Figure 5 Pitch/yaw channel performance index function convergence curve |
从图 5可以看出,性能指标函数表现出良好的收敛特性,粒子在经历到250代以后性能指标函数已趋于稳定,程序运行环境与前述算法测试环境相同,整个优化过程时间约为587 s.
此时灵敏度函数和补灵敏度函数如图 6~8所示.由图 6~8可知,灵敏度函数S(s;x)曲线总在wS-1(s)函数的曲线以下,同时补灵敏度函数T(s;x)的曲线也处于w-1T(s)函数的曲线下方,鲁棒性能函数曲线一直在1以下,这表明所设计的定结构H∞控制器满足定理1条件中的鲁棒性能要求.

|
图 6 灵敏度函数 Figure 6 Sensitivity function |
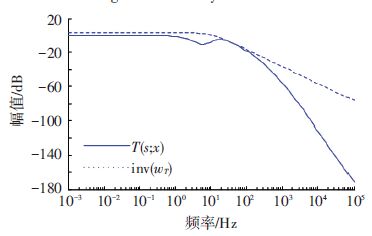
|
图 7 补灵敏度函数 Figure 7 Complementary sensitivity function |

|
图 8 鲁棒性能函数 Figure 8 Robust performance function |
样例导弹按照BTT控制方式,在法向和滚转通道同时给以阶跃激励信号,这样可以有效激励出通道间的耦合特性,对三通道模型的仿真结果如图 9所示.图 9中分别给出了法向与滚转通道的阶跃响应以及侧向通道的零过载响应.各通道的时域性能指标见表 3.从三通道联合仿真的结果可以看出,法向和滚转通道的阶跃响应达到了表 1要求的性能指标要求,并且通道间耦合作用仅引起很小的侧向过载,符合BTT控制的要求.

|
图 9 三通道标称仿真结果 Figure 9 3 channel nominal simulation results |
| 表 3 三通道阶跃响应性能 Table 3 3 channel step response performance |
在图 1所示的闭环控制系统中,摄动量分别取为:模型不确定性权函数依照文献[21]选取;加速度计噪声取为1%;角速率陀螺噪声取为0.1%;角度陀螺噪声取为 1%.在输入信号、模型不确定性和噪声同时作用下系统的响应如图 10所示(20次),可知系统在摄动下的性能仍然满足表 1所示的性能指标,从而验证了系统的鲁棒性能.
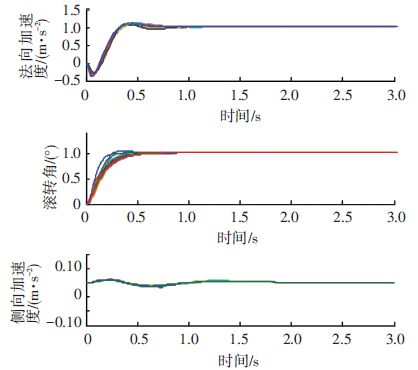
|
图 10 三通道摄动仿真结果 Figure 10 3 channel perturbed simulation results |
1) 本文提出了一种导弹定结构控制器的新型设计架构,在该架构中,采用了一种基于梯度修正策略的约束粒子群优化算法,通过自动优化的方法来设计导弹定结构控制器,使得设计结果在满足多种时域指标的同时还满足H∞鲁棒性指标,克服了传统经典控制器设计方法的不足.
2) 通过典型测试函数的测试并与其他约束优化算法进行对比,表明了梯度修正粒子群算法在解决约束优化问题中的优越性.以三通道导弹数学模型为控制对象,采用该算法设计了定结构H∞控制器并对其时域和鲁棒性能进行了分析,结果各项性能指标满足要求,从而验证了算法的有效性.
| [1] |
郑建华, 杨涤.
鲁棒控制理论在倾斜转弯导弹中的应用[M]. 北京: 国防工业出版社, 2001 .
ZHENG Jianhua, YANG Di. Robust control theory in the application of bank missile[M]. Beijing: national defence industry press, 2001 . (  0) 0)
|
| [2] |
HO M. Synthesis of H∞ PID controllers: A parametric approach[J].
Automatica,2003, 39 (6) : 1069-1075.
DOI: 10.1016/S0005-1098(03)00078-5 ( 0) 0)
|
| [3] |
SEDLACZEK K, EBERHARD P. Using augmented Lagrangian particle swarm optimization for constrained problems in engineering[J].
Structural and Multidisciplinary Optimization,2006, 32 (4) : 277-286.
DOI: 10.1007/s00158-006-0032-z ( 0) 0)
|
| [4] |
MARUTA I, SUGIE T, KIM T, et al. Identification of piecewise affine systems via distributed particle swarm optimization[C]//Proceedings of the 18th IFAC World Congress. Milano, Italy: IFAC Secretariat, 2011. DOI:10.3182/20110828-6-IT-1002.02438.
( 0) 0)
|
| [5] |
SHIMOMUR T, FUJII T. Multiobjective control via successive over-bounding of quadratic terms[J].
International Journal of Robust and Nonlinear Control,2005, 15 (8) : 363-381.
DOI: 10.1002/rnc.997 ( 0) 0)
|
| [6] |
SAEKI M. Fixed structure PID controller design for standard H∞ control problem[J].
Automatica,2006, 42 (1) : 93-100.
DOI: 10.1016/j.automatica.2005.07.006 ( 0) 0)
|
| [7] |
KENNEDY J, EBERHART R. Particle Swarm Optimization[C]//Proceedings of the IEEE International Conference on Neural Networks. Perth, WA: IEEE, 1995:1942-1948. DOI:10.1109/ICNN.1995.488968.
( 0) 0)
|
| [8] |
KENNEDY J, EBERHART R C.
Swarm Intelligence[M]. San Francisco, CA: Morgan Kaufmann, 2001 .
( 0) 0)
|
| [9] |
杨希祥, 降振宇, 张为华. 基于粒子群优化的固体运载火箭上升段弹道优化设计研究[J].
宇航学报,2010, 31 (5) : 1304-1309.
DOI: 10.3873/j.issn.1000-1328.2010.05.008 YANG Xixiang, JIANG Zhenyu, ZHANG Weihua. Solid rocket based on particle swarm optimization on the ballistic optimization design research[J]. Journal of Aerospace,2010, 31 (5) : 1304-1309. DOI: 10.3873/j.issn.1000-1328.2010.05.008 (  0) 0)
|
| [10] |
傅阳光, 周成平, 丁明跃. 基于混合量子粒子优化算法的三维航迹规划群[J].
宇航学报,2010, 31 (12) : 2657-2664.
DOI: 10.3873/j.issn.1000-1328.2010.12.006 FU Yangguang, ZHOU Chengping, DING Mingyue. Quantum particle swarm optimization algorithm based on hybrid 3D path planning[J]. Journal of Aerospace,2010, 31 (12) : 2657-2664. DOI: 10.3873/j.issn.1000-1328.2010.12.006 (  0) 0)
|
| [11] |
AFSHAR M H. Large scale reservoir operation by constrained particle swarm optimization algorithms[J].
Journal of Hydro-environment Research,2012, 6 (1) : 75-87.
DOI: 10.1016/j.jher.2011.04.003 ( 0) 0)
|
| [12] |
JANSEN P W, PEREZ R E. Constrained structural design optimization via a parallel augmented Lagrangian particle swarm optimization approach[J].
Computers and Structures,2011, 89 (13/14) : 1352-1366.
DOI: 10.1016/j.compstruc.2011.03.011 ( 0) 0)
|
| [13] |
ZHOU Kemin, DOYLE J, GLOVER K, et al.
Robust and optimal control[M]. [s.l.]: Prentice Hall, 1996 .
( 0) 0)
|
| [14] |
BLANCHINI F, LEPSCHY A, MINANI S, et al. Characterization of PID and lead/lag compensators satisfying given H∞ specifications[J].
IEEE Transactions on Automatic Control,2004, 49 (5) : 736-740.
DOI: 10.1109/TAC.2004.825961 ( 0) 0)
|
| [15] |
CHOOTINAN P, CHEN A. Constraint handling in genetic algorithms using a gradient-based repair method[J].
Computers and Operations Research,2006, 33 (8) : 2263-2281.
DOI: 10.1016/j.cor.2005.02.002 ( 0) 0)
|
| [16] |
ZAHARA E, KAO H T. Hybrid nelder-mead simplex search and particle swarm optimization for constrained engineering design problems[J].
Expert Systems with Applications,2009, 36 (2) : 3880-3886.
DOI: 10.1016/j.eswa.2008.02.039 ( 0) 0)
|
| [17] |
HE Qie, WANG Ling. A hybrid particle swarm optimization with a feasibility-based rule for constrained optimization[J].
Applied Mathematics and Computation,2007, 186 (2) : 1407-1422.
DOI: 10.1016/j.amc.2006.07.134 ( 0) 0)
|
| [18] |
KOZIEL S, MICHALEWICZ Z. Evolutionary algorithms, homomorphous mappings, and constrained parameter optimization[J].
Evolutionary Computation,1999, 7 (1) : 19-44.
DOI: 10.1162/evco.1999.7.1.19 ( 0) 0)
|
| [19] |
RUNARSSON T P, YAO Xin. Stochastic ranking for constrained evolutionary optimization[J].
IEEE Transactions on Evolutionary Computation,2000, 4 (3) : 284-294.
DOI: 10.1109/4235.873238 ( 0) 0)
|
| [20] |
COELLO C A C, BECERRA R A. Efficient evolutionary optimization through the use of a cultural algorithm[J].
Engineering Optimization,2004, 36 (2) : 219-236.
DOI: 10.1080/03052150410001647966 ( 0) 0)
|
| [21] |
ZANG Yuejin.
Air-to-air mu integrated controller design and research. Nanjing:Nanjing University of Aeronautics and Astronautics[M]. 2012 .
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


