柔性弹箭动力学建模通常采用基于能量原理的拉格朗日法建立封闭的柔性弹箭气动弹性和飞行力学方程组,在小攻角和小变形条件下,对弹体弹性变形和大运动进行耦合[1-6].其中,对弹箭振动特性和气动力参数的准确获取是柔性弹道计算和稳定性分析的关键.线性多体系统传递矩阵法特别适合于解决线性多体系统振动特性、正交性、动力响应等问题[7],兼具方便建模,计算速度快和精度高的优点.计算流体力学(CFD)方法可以很好的预测复杂几何体的气动特性参数和流体流动现象[8-11],但是如果将其应用到整个的封闭方程里则计算量太大,计算周期长,不利于快速计算和通过系统方程进行理论分析.而基于气动力系数导数的气动力计算方法则在小变形和小攻角范围内可以兼顾精度高和计算简单的特点.
本文采用多体系统传递矩阵法和CFD与经验公式相结合的方法,分别计算了火箭弹的振动特性和气动力系数导数,在此基础上计算弯曲火箭弹沿轴向单位长度气动力系数分布,并通过CFD方法对该方法的精度进行了验证.
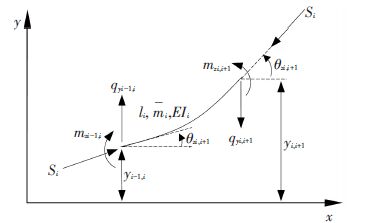
1 模型建立 1.1 火箭弹结构建模随着长细比的增加,弹体的抗弯刚度和横向振动的固有频率降低,弹体的横向弯曲为影响飞行力学的主要因素,因此大长细比火箭弹可看作自由-自由非均质Euler-Bernoulli梁[3, 12-13].如图 1所示,非均质梁进一步简化为N段均质梁依次连接而成[7],第i段梁的输入端和输出端在物理坐标下的状态矢量为Zi-1,i和Zi,i+1,其中Zi-1,i=[yi-1,iθzi-1,imzi-1,iqyi-1,i]T.如图 2所示,yi-1,i、θzi-1,i、mzi-1,i和qyi-1,i分别为物理坐标系下梁输入端的位移、转动角度、所受力矩和剪切应力,m-i、li、EIi和Si分别为第i段梁的线密度、长度、抗弯刚度和所受轴向力(如果为拉力则为负值).

|
图 1 非均质梁 Figure 1 Non-uniform beam |
|
图 2 第i段梁的状态矢量 Figure 2 State vectors of segment i |
火箭弹轴上的每一点所受的轴向力大小不同,等于该点至火箭弹顶端部分受到的惯性力.底部所受轴向力大小等于推力,顶端所受轴向力为零.Si取第i段质心处所受的轴向力[3]为
| ${{S}_{i}}=\frac{{{F}_{T}}}{m}\left( m-\sum\limits_{j=1}^{i-1}{{{{\bar{m}}}_{j}}{{l}_{j}}-\frac{1}{2}{{{\bar{m}}}_{j}}{{l}_{j}}} \right).$ |
式中:FT为末端推力;m为整个火箭弹的质量;lj为第j段的长度;mj为第j段的线密度.
受均匀轴向压力作用的均质Euler-Bernoulli梁横向自由振动微分方程为[14]
| $EI\frac{{{\partial }^{4}}y}{\partial {{x}^{4}}}+S\frac{{{\partial }^{2}}y}{\partial {{x}^{2}}}+\bar{m}\frac{{{\partial }^{2}}y}{\partial {{t}^{2}}}=0.$ |
推导可得长度为l的Euler-Bernoulli梁的传递矩阵为
| $B\left( x \right)=\left[ \begin{matrix} cosh\left( Mx \right) & sinh\left( Mx \right) & cos\left( Nx \right) & sin\left( Nx \right) \\ Msinh\left( Mx \right) & Mcosh\left( Mx \right) & -Nsin\left( Nx \right) & Ncos\left( Nx \right) \\ EI{{M}^{2}}cosh\left( Mx \right) & EI{{M}^{2}}sinh\left( Mx \right) & -EI{{N}^{2}}cos\left( Nx \right) & -EI{{N}^{2}}sin\left( Nx \right) \\ \left( EI{{M}^{3}}-SM \right)sinh\left( Mx \right) & \left( EI{{M}^{3}}-SM \right)cosh\left( Mx \right) & \left( EI{{N}^{3}}+SN \right)sin\left( Nx \right) & -\left( EI{{N}^{3}}+SN \right)cos\left( Nx \right) \\ \end{matrix} \right],$ |
其中:
| $M=\sqrt{\frac{\frac{{{S}^{2}}}{{{\left( EI \right)}^{2}}}+\frac{4\bar{m}{{\omega }^{2}}}{EI}-\frac{S}{EI}}{2}},N=\sqrt{\frac{\frac{{{S}^{2}}}{{{\left( EI \right)}^{2}}}+\frac{4\bar{m}{{\omega }^{2}}}{EI}-\frac{S}{EI}}{2}}.$ |
对于非均质梁,连接点处在模态坐标下的状态矢量为Z0,1,Z1,2,Z2,3,…,Zi-1,i,…,Zn,n+1,每一段的传递方程为
| ${{Z}_{i,i+1}}={{U}_{i}}{{Z}_{i-1,i}},\left( i=1,2,\cdots ,n \right).$ | (1) |
因此总传递方程为
| ${{Z}_{n,n+1}}={{U}_{all}}{{Z}_{0,1}},$ |
其中,Uall为总传递矩阵Uall=UnUn-1…Ui…U2U1.
| $\Delta =\left| \begin{matrix} {{U}_{all}}_{3,1} & {{U}_{all}}_{3,2} \\ {{U}_{all}}_{4,1} & {{U}_{all}}_{4,2} \\ \end{matrix} \right|=0,$ | (2) |
式(2)即为特征方程,解此方程可得频率ω.当频率ωk(k为模态阶数)得到后,Mk、Nk、Ui-1,i和Uall都可以确定.通过边界条件可得初始端的状态矢量Z0,1=B0a,同时非均质梁任何位置的状态矢量可由式(1)得到.
1.2 气动力模型火箭弹弹身细长,翼面较小,并且翼面在弦长方向的尺寸占弹身总长很少,对于这样的柔性弹,在线性理论范围内可以将弹体沿轴向划分为若干微段,各段所受到的气动力为作用于该段压力中心的合力.在准定常理论和线性理论的假设下,不计气流的尾流影响,各段的气动力只和该段的当地攻角有关,认为变形后的弹体各段当地柔性攻角等于该段的合成速度向量与该段弦线之间的瞬时夹角,采用数值模拟方法计算出不同Ma数下的气动力系数导数的分布,可直接将气动力表述成当地柔性攻角的函数[5-6, 15-16].
弹体微段的当地柔性攻角侧滑角α(x,t)和β(x,t)分别为[15]
| $\begin{align} & \alpha x,t=\frac{w}{u}-\sum i\varphi {{\prime }_{i}}\left( x \right){{\zeta }_{i}}t+\frac{1}{u}\sum\limits_{i}{{{\varphi }_{i}}\left( x \right){{{\dot{\zeta }}}_{i}}\left( t \right)-\frac{qx}{u}}, \\ & \beta \left( x,t \right)=\frac{v}{u}-\sum\limits_{i}{\varphi {{\prime }_{i}}\left( x \right){{\eta }_{i}}t+\frac{1}{u}\sum\limits_{i}{{{\varphi }_{i}}\left( x \right){{{\dot{\eta }}}_{i}}\left( t \right)+\frac{rx}{u}}}. \\ \end{align}$ |
式中:u、v、w分别为速度在体坐标系中的分量;p、q、r分别为角速度在体坐标系中的分量;ηit、ζi(t)分别为广义坐标;φi(x)为振型函数.
基于线性理论和准定常理论,弹体所受整体的阻力、侧向力和升力分别为
| $\begin{align} & {{F}_{D}}=-{{\int }_{L}}\frac{1}{2}\rho {{V}^{2}}S{{C}^{0}}_{D}\left( x \right)+\frac{1}{2}\rho {{V}^{2}}SC{{'}_{D}}\left( x \right)({{\alpha }^{2}}\left( x,t \right)+ \\ & {{\beta }^{2}}\left( x,t \right)dx, \\ & {{F}_{S}}=-{{\int }_{L}}\frac{1}{2}\rho {{V}^{2}}SC{{'}_{S}}\left( x \right)\beta x,tdx, \\ & {{F}_{L}}=-{{\int }_{L}}12\rho {{V}^{2}}SC{{'}_{L}}\left( x \right)\alpha x,tdx. \\ \end{align}$ |
式中:C0D(x)、C′D(x)、C′S(x)、C′L(x)分别为火箭弹沿弹身轴向的单位长度零升阻力系数、阻力系数导数、侧向力系数导数、升力系数导数的分布.对于轴对称火箭弹,C′S(x)和C′L(x)相等.上述的气动力系数导数可通过气动力系数计算得到:
| ${{C}^{\prime }}_{L}={{C}^{\alpha }}_{L}\left( x \right)/\alpha ,$ | (3) |
| ${{C}^{\prime }}_{D}={{C}^{\alpha }}_{D}\left( x \right)-{{C}^{0}}_{D}\left( x \right)/{{\alpha }^{2}}.$ | (4) |
式中:CαL(x)、CαD(x)分别为刚体火箭弹在小攻角α下沿弹身的单位长度升力系数、阻力系数;C0D(x)为刚体火箭弹沿弹身轴向的单位长度零升阻力系数,通过CFD对火箭弹进行数值模拟即可计算出需要的参数值.
2 计算结果 2.1 火箭弹振动特性利用已推导的多体系统传递矩阵法公式计算某火箭弹被动段时的频率和振型,被动段时质量不变,推力为零.如图 3所示,当火箭弹所分段数超过50时1阶频率的计算结果没有明显的变化,说明将火箭弹简化为50段均质梁即可以保证计算的精度.图 4为该火箭弹前4阶振型,x/L=0为火箭弹尾部.

|
图 3 1阶频率随单元数的变化 Figure 3 Primary frequency with the number of rocket’s segments |

|
图 4 火箭弹前4阶振型 Figure 4 Rocket’s first four bending mode shapes |
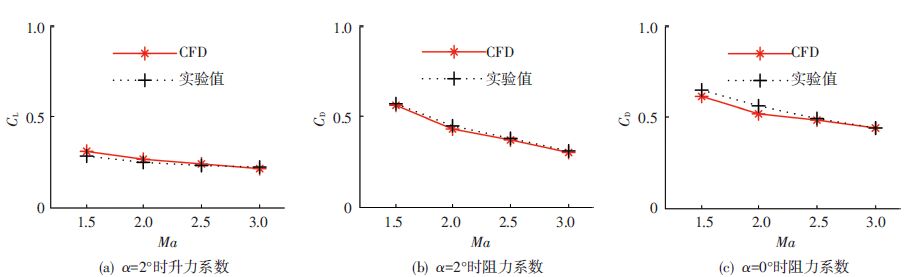
由于火箭弹为轴对称,其法向和侧向具有相同的气动特性,因此本文中对侧向气动力不予考虑.如图 5所示,火箭弹为刚体模型,沿着轴向将火箭弹切成23段,每一个小段的中间点作为气动力的作用点,采用CFD方法计算沿轴向的气动力系数分布[17-18].计算域来流条件为静压101 325 Pa,静温288 K,计算域外边界设为压力远场,即基于Rieman不变量的无反射边界条件,火箭弹物面设为无滑移壁面.采用SST k-ω湍流模型,基于密度求解器进行求解,离散格式采用AUSM格式和隐式求解格式,对流通量采用二阶迎风格式.本文采用多Block生成流场拓扑结构,外O Block生成弹体边界层的方法,生成了高质量的结构化网格,在边界层内对网格进行加密,保证y+<1,网格数为310万.如图 7所示,获得模型在α=0°和α=2°情况下的气动参数并与以往的实验数据比较,CL和CD的误差均在10%以内,验证了该数值计算方法的可行性与准确性.图 6和图 8分别是Ma=2,α=2°工况下的速度云图和火箭弹的升力、阻力系数分布.通过式(3)~(4)可得该火箭弹的气动力系数导数分布.

|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期) 图 5 火箭弹面网格 Figure 5 The mesh of the rocket’s surface |

|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期) 图 6 速度云图 Figure 6 Velocity contour of the rigid rocket |
|
图 7 某火箭弹气动力系数随Ma变化曲线及与实验数据对比 Figure 7 The rocket’s aerodynamic coefficients contrast with experimental data |

|
图 8 Ma=2,α=2°时火箭弹气动力系数分布 Figure 8 Rocket’s aerodynamic coefficient distribution with Ma=2,α=2° |
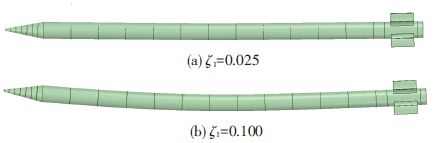
由于弹体变形基本基于1阶振型,因此本文基于1阶振型建立了弯曲的弹体模型.考虑到建模时可能存在尺寸误差及CFD计算误差,同时为了分析本文中气动力计算方法的适用范围,分别选择广义坐标ζ1=0.025和ζ1=0.100,对应的模型示意,如图 9所示.图 10为两个模型的弹体斜率,ζ1=0.025和ζ1=0.100远大于火箭弹实际正常飞行时的变形量,但是当弹体发生颤振或者弯曲发散时变形剧烈,很有可能达到这样的变形程度.
|
图 9 弯曲弹体模型 Figure 9 The model of bended rockets |

|
图 10 弯曲弹体斜率 Figure 10 The slope of bended rockets |
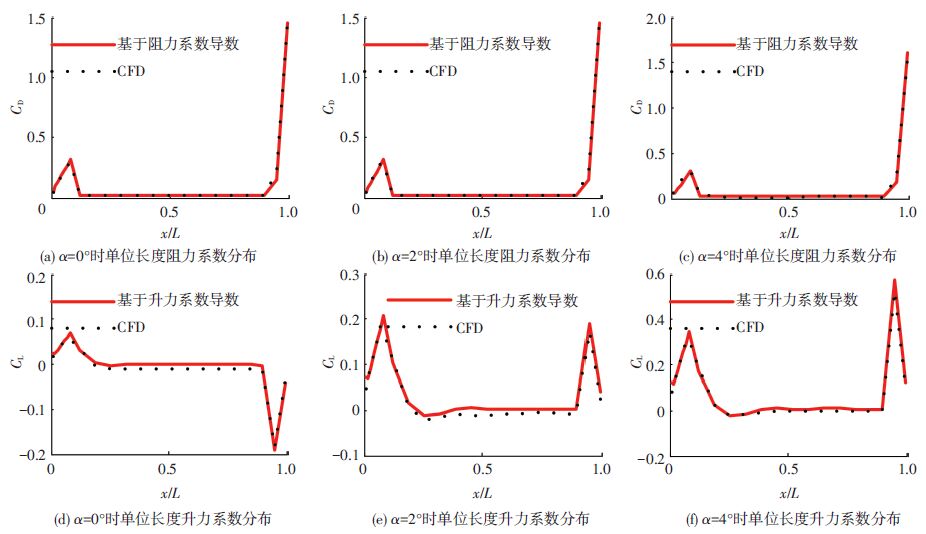
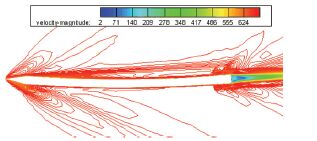
分别基于气动力系数导数和采用CFD方法计算了火箭弹在这两种弯曲变形下,Ma=2、不同攻角的气动力系数分布,并对计算结果进行对比.为了捕捉到微小变形对气流产生的影响,第1层网格高度需要足够小,此处设置y+<1,网格数为380万.对于ζ1=0.025,即变形相对较小的情况下,攻角取0°、2°、4°时的单位长度阻力系数、单位长度升力系数分布的对比结果如图 11所示,可以发现两种方法结果吻合较好,阻力系数偏差在5%以内,升力系数偏差在10%以内.对于ζ1=0.100,即变形相对较大的的情况下,攻角取0°、2°、4°时的单位长度阻力系数、单位长度升力系数分布的对比结果如图 12所示,在0°攻角时,两种方法的结果吻合较好;在2°攻角时弹的头部和尾部等局部阻力系数有一定的误差,但是误差较小;在4°攻角时,头部和尾部等局部误差增大.ζ1=0.100的变形下在4°攻角对称面速度云图如图 13所示,由于变形增大,攻角增大,头部及弹身的尾流对火箭弹尾部的流动产生了复杂影响,此时,线性理论已经不再适用.
|
图 11 ζ1=0.025的弯曲火箭弹沿弹轴单位长度气动力系数分布 Figure 11 The distribution of the aerodynamic coefficients of unit length along the bended rocket with ζ1=0.025 |

|
图 12 ζ1=0.100的弯曲火箭弹沿弹轴单位长度气动力系数分布 Figure 12 The distribution of the aerodynamic coefficients of unit length along the bended rocket with ζ1=0.100 |
|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期) 图 13 α=4°时ζ1=0.100的弯曲火箭弹速度云图 Figure 13 The velocity contour of the bended rocket wiht ζ1=0.100 at α=4° |
1) 推导了考虑轴向力作用的Euler-Bernoulli梁的传递矩阵,将某真实火箭弹简化成自由-自由的非均质Euler-Bernoulli梁,应用多体系统传递矩阵法计算了其频率和振型.
2) 采用基于SST k-ω湍流模型的CFD方法计算了该火箭弹在不同Ma数、不同攻角下的气动力系数,与实验数据相比最大误差不超过10%,证明了采用数值方法计算火箭弹气动力系数分布可以保证足够的精度以及采用数值方法验证弯曲火箭弹气动力建模的可行性.
3) 基于该火箭弹1阶振型建立了两种不同变形程度的弯曲弹体模型,在准定常理论和线性理论的假设条件下,结合气动力系数导数进行两个弯曲模型的气动力计算,得到了Ma=2,不同攻角两个模型的单位长度升力系数分布和阻力系数分布,并采用CFD方法对计算结果进行验证.通过验证发现,该火箭弹在实际飞行可能的变形范围内,基于准定常理论和线性理论的柔性弹箭气动力计算方法结果精度较好,在远超于实际的大变形时,该方法在弹头和弹身处仍具有一定精度,但尾部误差较大,计算精度降低.
| [1] |
徐明友. 弹箭飞行动力学[D]. 北京: 国防工业出版社, 2003.
XU Mingyou. Flight dynamics of missiles[D]. Beijing: National Defence of Industry Press,2003. (  0) 0)
|
| [2] |
何斌, 芮筱亭, 陆毓琪. 柔性弹箭飞行力学建模研究[J].
弹道学报,2006, 18 (1) : 22-24.
DOI: 10.3969/j.issn.1004-499X.2006.01.006 HE Bin, RUI Xiaoting, LU Yuqi. A study on flight dynamic modeling of flexible shell rocket[J]. Journal of Ballistics,2006, 18 (1) : 22-24. DOI: 10.3969/j.issn.1004-499X.2006.01.006 (  0) 0)
|
| [3] |
POURTAKDOUST S H, ASSADIAN N. Investigation of thrust effect on the vibrational characteristics of flexible guided missiles[J].
Journal of Sound and Vibration,2004, 272 (1/2) : 287-299.
DOI: 10.1016/S0022-460X(03)00779-X ( 0) 0)
|
| [4] |
JOSHI A. Free vibration characteristics of variable mass rocket having large axial thrust/acceleration[J].
Journal of Sound and Vibration,1995, 187 (4) : 727-736.
DOI: 10.1006/jsvi.1995.0559 ( 0) 0)
|
| [5] |
PLATUS D H. Aeroelastic stability of slender, spinning missiles[J].
Journal of Guidance, Control and Dynamics,1992, 15 (1) : 144-151.
DOI: 10.2514/3.20812 ( 0) 0)
|
| [6] |
黄晓鹏, 樊红祥, 蒋厚洸. 细长旋转飞行器的气动弹性研究[J].
北京理工大学学报,1998, 18 (4) : 431-435.
DOI: 10.15918/j.tbit1001-0645.1998.04.008 HUANG Xiaopeng, FAN Hongxiang, JIANG Houguang. Aeroelastic analysis of slender spinning vehicle[J]. Journal of Beijing Institute of Technology,1998, 18 (4) : 431-435. DOI: 10.15918/j.tbit1001-0645.1998.04.008 (  0) 0)
|
| [7] |
芮筱亭, 贠来峰, 陆毓琪, 等.
多体系统传递矩阵法及其应用[M]. 北京: 科学出版社, 2008 .
RUI Xiaoting, YUN Laifeng, LU Yuqi, et al. Transfer matrix method of multibody system and its applications[M]. Beijing: Science Press, 2008 . (  0) 0)
|
| [8] |
MENTER F R. Two-equation eddy-viscosity models for engineering applications[J].
AIAA Journal,1994, 32 (8) : 1598-1605.
DOI: 10.2514/3.12149 ( 0) 0)
|
| [9] |
KLEB W L, WOOD W A, GNOFFO P A, et al. Computational aeroheating predictions for X-34[J].
Journal of Spacecraft and Rockets,1999, 36 (2) : 179-188.
DOI: 10.2514/2.3448 ( 0) 0)
|
| [10] |
SAHU J, EDGE H L, HEAVEY K R, et al. Computational fluid dynamics modeling of multi-body missile aerodynamic interference[R]. U.S. Army Research Laboratory, ARL-TR-1765, Aberdeen Proving Ground, MD, 1998.
( 0) 0)
|
| [11] |
DESPIRITO J, PLOSTINS P. CFD Prediction of M910 projectile aerodynamics: unsteady wake effect on magnus moment[C]//AIAA Atmospheric Flight Mechanics Conference and Exhibit 20-23 August 2007. Hilton Head, South Carolina: AIAA-2007-6580, 2007.
( 0) 0)
|
| [12] |
臧涛成. 大长细比模拟弹模态分析与计算[J].
弹箭与制导学报,2003, 23 (2) : 40-42.
DOI: 10.3969/j.issn.1673-9728.2003.02.013 ZANG Taocheng. Great slenderness ratio imitative projectile mode analysis and theories calculation[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2003, 23 (2) : 40-42. DOI: 10.3969/j.issn.1673-9728.2003.02.013 (  0) 0)
|
| [13] |
王良明. 柔性弹丸飞行动力学研究[J].
兵工学报,1998, 19 (3) : 208-213.
WANG Liangming. Flight dynamics of flexible projectiles[J]. Acta Armamentarii,1998, 19 (3) : 208-213. (  0) 0)
|
| [14] |
ABBAS L K, LI Minjiao, RUI Xiaoting. Transfer matrix method for the determination of the natural vibration characteristics of realistic thrusting launch vehicle—Part I[J/OL]. Mathematical Problems in Engineering, 2013: 764673. http://www.hindawi.com/journals/mpe/2013/764673/ .DOI:10.1155/2013/764673.
( 0) 0)
|
| [15] |
王华毕, 黄晓鹏, 吴甲生. 大长径比旋转火箭弹气动弹性数值计算[J].
弹箭与制导学报,2006, 26 (2) : 242-245.
DOI: 10.3969/j.issn.1673-9728.2006.02.081 WANG Huabi, HUANG Xiaopeng, WU Jiasheng. The aeroelastic numerical calculation of large f ineness ratio spinning rocket[J]. Journal of Projectiles, Rockets, Missiles and Guidance,2006, 26 (2) : 242-245. DOI: 10.3969/j.issn.1673-9728.2006.02.081 (  0) 0)
|
| [16] |
JEGARKANDI M F, NOBARI A S, SABZEHPRAVAR M, et al. Aeroelastic stability consideration of supersonic flight vehicle using nonlinear aerodynamic response surfaces[J].
Journal of Fluids and Structures,2009, 25 (6) : 1079-1101.
DOI: 10.1016/j.jfluidstructs.2009.04.006 ( 0) 0)
|
| [17] |
ABBAS L K, CHEN Dongyang, Rui Xiaoting. Normal force computation for axisymmetric multistage launch vehicle[J].
Applied Mechanics and Materials,2013, 419 : 23-29.
DOI: 10.4028/www.scientific.net/AMM.419.23 ( 0) 0)
|
| [18] |
ABBAS L K, CHEN Dongyang, Rui Xiaoting. Numerical calculation of effect of elastic deformation on aerodynamic characteristics of a rocket[J/OL]. International Journal of Aerospace Engineering, 2014: 478534. http://www.hindawi.com/journals/ijae/2014/478534. DOI:10.1155/2014/478534.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


