在目标跟踪中,目标运动方程通常定义在直角坐标系(CAR)下,但目标量测通常在极/球坐标系或方向余弦坐标系(COS)下给出.这使得状态空间中量测方程呈现非线性.对于这一非线性问题,通常采用两种解决方法.一种是用特定方法近似目标状态通过非线性映射后的概率分布,从而得到目标状态的估计.扩展卡尔曼滤波器(EKF)[1]假定目标状态满足高斯分布,用目标状态估计的均值和协方差表示当前目标状态的概率分布,通过泰勒级数展开的方法获得非线性函数的线性近似表达,之后使用卡尔曼滤波器(KF)获得下一时刻目标状态的概率分布.不敏卡尔曼滤波器(UKF)[2]同样假定目标状态满足高斯分布,用目标状态空间中选取的一系列采样点来近似目标状态分布,用非线性函数作用于这些点上所得结果来近似下一时刻目标状态的概率分布.另一种方法是将量测转换到直角坐标系下,然后使用KF得到目标状态的估计.文献[3]指出带噪声量测直接转换到直角坐标系下是有偏的,并提出一种去偏转换量测(DCM)方法.文献[4]利用在极/球坐标系下可以直接通过带噪声量测得到目标状态的无偏估计,提出一种无偏转换量测(UCM)方法.文献[5]指出这种UCM方法在推导转换量测误差均值和协方差时存在兼容性问题,并在UCM方法的基础上提出一种修正无偏转换量测(MUCM)方法.文献[6-8]对现有的量测转换方法进行了总结和改进.但上述转换量测方法大都只适用于机械扫描雷达广泛使用的极/球坐标量测,并不适用于电扫描相控阵雷达的方向余弦坐标量测.
随着雷达技术的不断发展,雷达除了能够给出目标的位置信息,如距离、方位角和俯仰角,还能提供目标的径向速度信息.理论和实践已经证明[1],充分利用径向速度信息可以有效提高目标的跟踪精度.考虑多普勒量测与目标状态之间完全是非线性关系,文献[1]提出采用距离量测和多普勒量测的乘积构造伪量测来减小这种非线性,然后再用线性化方法得到转换量测误差的统计特性.但文献[9]证明了对于线性调频信号,多普勒量测误差与距离量测误差之间具有很强的相关性.文献[10]考虑这种相关性,将文献[3, 11]的方法推广到包含多普勒量测的情况.文献[12-13]针对极坐标情况,假定一个切向速度量测将多普勒量测转换为X,Y方向的速度量测再进行滤波.文献[14]设计了一个转换多普勒量测的卡尔曼滤波器(CDMKF),并将所得滤波结果与常规位置量测滤波结果融合得到最终目标状态的估计.上述方法均通过引入多普勒量测,在不同程度上改善了滤波性能.
文献[15]针对方向余弦坐标系下的位置量测给出了一种转换量测的卡尔曼滤波器(CMKFDcos).本文在此基础上引入多普勒量测,提出了一种方向余弦坐标系下带多普勒量测的去偏转换量测滤波(debiased converted position and Doppler measurements filter in the COS,DCPDMFcos)方法.通过仿真验证了此转换量测方法是一致有效的.同时将其应用于二维目标跟踪中,仿真结果证实了本文提出的方法通过引入多普勒量测确实提高了性能,并比现有EKF和UKF具有更好的跟踪效果.事实上,本文提出的方法可以直接推广应用于三维方向余弦坐标系下的目标跟踪.
1 方向余弦坐标系在阵列雷达应用中,用不随扫描角变化的余弦或余弦增量来描述波束宽度和角位置增量更方便,因此阵列雷达量测多在方向余弦坐标系下给出.假设xr-yr是与阵面固连的直角坐标系,波束指向与位于阵列平面xr轴的夹角为A,则有
| $\alpha =x/R=sin\left( 90-A \right)=cos~A.$ |
式中:α为目标与xr轴的方向余弦; x为目标在xr轴上的坐标值; R为目标至雷达的距离.阵列雷达在方向余弦坐标系下所得量测值包含与xr轴的方向余弦α,距离R和多普勒速度vR.
方向余弦坐标量测与直角坐标量测之间的关系为
| $\begin{align} & ~x=R\alpha =Rcos~A, \\ & y=R\beta =Rcos~\varepsilon . \\ \end{align}$ |
式中:
方向余弦坐标系描述电扫描阵列雷达的天线方向图和扫描特性是方便的,但是并不适合描述目标的运动状态,这就需要将阵列雷达的方向余弦坐标量测值变换到直角坐标系下.雷达同所有传感器一样,量测会受到噪声的污染.假定阵列雷达量测为Zmcos=(αm Rm vRm)T,则有
| $\left\{ \begin{matrix} {{\alpha }_{m}}=\alpha +\tilde{\alpha }, \\ {{R}_{m}}=R+\tilde{R}, \\ {{v}_{{{R}_{m}}}}={{v}_{R}}+{{{\tilde{v}}}_{R}}. \\ \end{matrix} \right.$ | (1) |
式中:α、R、vR分别为量测真值,而
| ${{R}_{cos}}=\left[ \begin{matrix} {{\sigma }^{2}}_{\alpha } & 0 & 0 \\ 0 & {{\sigma }^{2}}_{R} & \rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}} \\ 0 & \rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}} & {{\sigma }^{2}}_{{{v}_{R}}} \\ \end{matrix} \right].$ |
式中:σα、σR、σvR分别为
考虑到多普勒量测与目标状态的非线性性过强,本文用距离量测和多普勒量测的乘积构造伪量测来减轻这种非线性,则方向余弦量测转换到直角坐标系下为
| ${{Z}_{m}}={{({{x}_{m}}~{{y}_{m}}~{{\xi }_{m}})}^{T}}={{({{R}_{m}}{{\alpha }_{m}}~{{R}_{m}}{{\beta }_{m}}~{{R}_{m}}{{v}_{{{R}_{m}}}})}^{T}},$ | (2) |
由于带噪声的非线性转换是有偏的[3],所以需要估算偏差并把偏差去除.由式(1)可得:
| ${{x}_{m}}=x+\tilde{x}={{R}_{m}}{{\alpha }_{m}}=\left( R+\tilde{R} \right)\left( \alpha +\tilde{\alpha } \right),$ | (3) |
| ${{y}_{m}}=y+\tilde{y}={{R}_{m}}{{\beta }_{m}}=\left( R+\tilde{R} \right)\left( \beta +\tilde{\beta } \right),$ | (4) |
| ${{\xi }_{m}}=\xi +\tilde{\xi }={{R}_{m}}{{v}_{{{R}_{m}}}}=\left( R+\tilde{R} \right)\left( {{v}_{R}}+{{v}_{{\tilde{R}}}} \right).$ | (5) |
式中:x、y、ξ分别为直角坐标量测的真值;
| $\begin{align} & \tilde{x}=R\tilde{\alpha }+\tilde{R}\alpha +\tilde{R}\tilde{\alpha }, \\ & \tilde{y}=R\tilde{\beta }+\tilde{R}\beta +\tilde{R}\tilde{\beta }, \\ & \tilde{\xi }=R{{{\tilde{v}}}_{R}}+\tilde{R}{{v}_{R}}+\tilde{R}{{{\tilde{v}}}_{R}}. \\ \end{align}$ |
虽然
| $\beta =y/R=cos~\varepsilon =\sqrt{1-{{\alpha }^{2}}},$ |
将βm在α处泰勒展开,由于一阶泰勒展开E[
| $\begin{align} & {{\beta }_{m}}=\sqrt{1-{{\alpha }^{2}}_{m}}=\sqrt{1-{{\alpha }^{2}}}+\left( -\frac{\alpha }{\beta }\tilde{\alpha } \right)+ \\ & \left( -\frac{1}{2{{\beta }^{3}}}{{{\tilde{\alpha }}}^{2}} \right)+{{R}_{2}}\left( {\tilde{\alpha }} \right), \\ \end{align}$ |
其中R2(
| $\tilde{\beta }=-\frac{\alpha }{\beta }\tilde{\alpha }-\frac{1}{2{{\beta }^{3}}}{{{\tilde{\alpha }}}^{2}},$ | (6) |
| $E\left[ \tilde{\beta }\alpha \right]=-\frac{1}{2{{\beta }^{3}}}{{\sigma }^{2}}_{\alpha },$ | (7) |
| $E\left[ \tilde{\alpha }\tilde{\beta }\alpha \right]=-\frac{\alpha }{\beta }{{\sigma }^{2}}_{\alpha },$ | (8) |
| $E\left[ {{{\tilde{\beta }}}^{2}}\alpha \right]=\frac{{{\alpha }^{2}}}{{{\beta }^{2}}}{{\sigma }^{2}}_{\alpha }+\frac{1}{4{{\beta }^{6}}}3{{\sigma }^{4}}_{\alpha }.$ | (9) |
直角坐标量测误差的均值u为
| $\left\{ \begin{matrix} {{u}_{x}}=E\left[ \tilde{x}\alpha ,R \right]=0, \\ {{u}_{y}}=E\left[ \tilde{y}\alpha ,R \right]=RE\left[ \tilde{\beta }\alpha \right], \\ {{u}_{z}}=E\left[ \tilde{\xi }\alpha ,R,{{v}_{R}} \right]=\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}. \\ \end{matrix} \right.$ |
直角坐标量测误差的协方差RCar为
| $\begin{align} & {{R}_{Car}}\left( 1,1 \right)=cov\left( \tilde{x},\tilde{x}\alpha ,R \right)={{R}^{2}}{{\sigma }^{2}}_{\alpha }+{{\alpha }^{2}}{{\sigma }^{2}}_{R}+{{\sigma }^{2}}_{\alpha }{{\sigma }^{2}}_{R}, \\ & {{R}_{Car}}\left( 1,2 \right)={{R}_{Car}}\left( 2,1 \right)=cov\left( \tilde{x},\tilde{y}\alpha ,R \right)= \\ & ({{R}^{2}}+{{\sigma }^{2}}_{R})E\left[ \tilde{\alpha }\tilde{\beta }\alpha \right]+\alpha \beta {{\sigma }^{2}}_{R}+\alpha {{\sigma }^{2}}_{R}E\left[ \tilde{\beta }\alpha \right], \\ & {{R}_{Car}}\left( 2,2 \right)=cov\left( \tilde{y},\tilde{y}\alpha ,R \right)=\text{ }({{R}^{2}}+{{\sigma }^{2}}_{R})E[{{{\tilde{\beta }}}^{2}}\alpha ]+ \\ & {{\beta }^{2}}{{\sigma }^{2}}_{R}+2\beta {{\sigma }^{2}}_{R}E\left[ \tilde{\beta }\alpha \right]-{{R}^{2}}{{E}^{2}}\left[ \tilde{\beta }\alpha \right]. \\ \end{align}$ |
式中
| $\begin{align} & {{R}_{Car}}\left( 1,3 \right)=cov(\tilde{x},\tilde{\xi }\alpha ,R,{{v}_{R}})=\alpha R\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+\alpha {{v}_{R}}{{\sigma }^{2}}_{R}, \\ & {{R}_{Car}}\left( 2,3 \right)={{R}_{Car}}\left( 3,2 \right)=cov(\tilde{y},\tilde{\xi }\alpha ,R,{{v}_{R}})= \\ & (R\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+{{v}_{R}}{{\sigma }^{2}}_{R})E\left[ \tilde{\beta }\alpha \right]\text{ }+R\beta \rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+ \\ & \beta {{v}_{R}}{{\sigma }^{2}}_{R}, \\ & {{R}_{Car}}\left( 3,3 \right)=cov(\tilde{\xi },\tilde{\xi }R,{{v}_{R}})={{R}^{2}}{{\sigma }^{2}}_{{{v}_{R}}}+2R{{v}_{R}}\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+ \\ & {{v}^{2}}_{R}{{\sigma }^{2}}_{R}+(1+{{\rho }^{2}}){{\sigma }^{2}}_{R}{{\sigma }^{2}}_{{{v}_{R}}}. \\ \end{align}$ |
由于量测真值是未知的,可在量测已知条件下对上述真值条件下误差的均值和协方差求数学期望,分别称为平均真实偏差uE和平均真实协方差RECar,如
| $\left\{ \begin{matrix} {{u}^{E}}_{x}=E\left[ \tilde{x}{{\alpha }_{m}},{{R}_{m}} \right]=0, \\ {{u}^{E}}_{y}=E\left[ \tilde{y}{{\alpha }_{m}},{{R}_{m}} \right]={{R}_{m}}E\left[ \tilde{\beta }{{\alpha }_{m}} \right], \\ {{u}^{E}}_{\xi }=E\left[ \tilde{\xi }{{\alpha }_{m}}{{R}_{m}},{{v}_{{{R}_{m}}}} \right]=\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}. \\ \end{matrix} \right.$ | (10) |
| $\begin{align} & {{R}^{E}}_{Car}\left( 1,1 \right)=cov\left( \tilde{x},\tilde{x}{{\alpha }_{m}},{{R}_{m}} \right)= \\ & {{R}^{2}}_{m}{{\sigma }^{2}}_{\alpha }+{{\alpha }^{2}}_{m}{{\sigma }^{2}}_{R}+3{{\sigma }^{2}}_{\alpha }{{\sigma }^{2}}_{R}, \\ \end{align}$ | (11) |
| $\begin{align} & {{R}^{E}}_{Car}\left( 1,2 \right)={{R}^{E}}_{Car}(2,1)cov\left( \tilde{x},\tilde{y}{{\alpha }_{m}},{{R}_{m}} \right)= \\ & \left( {{R}^{2}}_{m}+3{{\sigma }^{2}}_{R} \right)E\left[ \tilde{\alpha }\tilde{\beta }{{\alpha }_{m}} \right]+{{\alpha }_{m}}{{\beta }_{m}}{{\sigma }^{2}}_{R}, \\ \end{align}$ | (12) |
| $\begin{align} & {{R}^{E}}_{Car}\left( 1,3 \right)={{R}^{E}}_{Car}\left( 3,1 \right)=cov\left( \tilde{x},\tilde{\xi }{{\alpha }_{m}},{{R}_{m}},{{v}_{{{R}_{m}}}} \right)= \\ & {{\alpha }_{m}}{{R}_{m}}\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+{{\alpha }_{m}}{{v}_{{{R}_{m}}}}{{\sigma }^{2}}_{R}, \\ \end{align}$ | (13) |
| $\begin{align} & {{R}^{E}}_{Car}\left( 2,2 \right)=cov\left( \tilde{y},\tilde{y}{{\alpha }_{m}},{{R}_{m}} \right)=\left( {{R}^{2}}_{m}+3{{\sigma }^{2}}_{R} \right)E\left[ {{{\tilde{\beta }}}^{2}}{{\alpha }_{m}} \right]- \\ & \left( {{R}^{2}}_{m}+3{{\sigma }^{2}}_{R} \right){{E}^{2}}\left[ \tilde{\beta }{{\alpha }_{m}} \right]+{{\beta }^{2}}_{m}{{\sigma }^{2}}_{R}, \\ \end{align}$ | (14) |
| $\begin{align} & {{R}^{E}}_{Car}\left( 2,3 \right)={{R}^{E}}_{Car}\left( 3,2 \right)=cov\left( \tilde{y},\tilde{\xi }{{\alpha }_{m}},{{R}_{m}},{{v}_{{{R}_{m}}}} \right)= \\ & {{R}_{m}}{{\beta }_{m}}\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+{{\beta }_{m}}{{v}_{{{R}_{m}}}}{{\sigma }^{2}}_{R}, \\ \end{align}$ | (15) |
| $\begin{align} & ~{{R}^{E}}_{Car}\left( 3,3 \right)=cov\left( \tilde{\xi },\tilde{\xi }{{R}_{m}},{{v}_{{{R}_{m}}}} \right){{R}^{2}}_{m}{{\sigma }^{2}}_{{{v}_{R}}}+2{{R}_{m}}{{v}_{{{R}_{m}}}}\rho {{\sigma }_{R}}{{\sigma }_{{{v}_{R}}}}+ \\ & {{v}^{2}}_{{{R}_{m}}}{{\sigma }^{2}}_{R}+3\left( 1+{{\rho }^{2}} \right){{\sigma }^{2}}_{R}{{\sigma }^{2}}_{{{v}_{R}}}. \\ \end{align}$ | (16) |
根据式(4)和式(15)并进行一定近似可得:
| $\begin{align} & E\left[ \tilde{\beta }{{\alpha }_{m}} \right]=E\left[ -\frac{1}{2{{\beta }^{3}}}{{\sigma }^{2}}_{\alpha }{{\alpha }_{m}} \right]= \\ & -\frac{1}{2E\left[ {{\left( 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}} \right)}^{\frac{3}{2}}}{{\alpha }_{m}} \right]}{{\sigma }^{2}}_{\alpha }\approx \\ & -\frac{1}{2{{E}^{32}}\left[ 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}{{\alpha }_{m}} \right]}{{\sigma }^{2}}_{\alpha }, \\ \end{align}$ | (17) |
| $\begin{align} & E\left[ \tilde{\alpha }\tilde{\beta }{{\alpha }_{m}} \right]=E\left[ -\frac{\alpha }{\beta }{{\sigma }^{2}}_{\alpha }{{\alpha }_{m}} \right]= \\ & -E\left[ \frac{{{\alpha }_{m}}-\tilde{\alpha }}{{{\left( 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}} \right)}^{\frac{1}{2}}}}{{\alpha }_{m}} \right]{{\sigma }^{2}}_{\alpha }\approx \\ & -\frac{E\left[ {{\alpha }_{m}}-\tilde{\alpha }{{\alpha }_{m}} \right]}{{{E}^{\frac{1}{2}}}\left[ 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}{{\alpha }_{m}} \right]}{{\sigma }^{2}}_{\alpha }, \\ \end{align}$ | (18) |
| $\begin{align} & E\left[ {{{\tilde{\beta }}}^{2}}\alpha \right]=E\left[ \frac{{{\alpha }^{2}}}{{{\beta }^{2}}}{{\sigma }^{2}}_{\alpha }+\frac{1}{4{{\beta }^{6}}}3{{\sigma }^{4}}_{\alpha }{{\alpha }_{m}} \right]= \\ & E\left[ \frac{{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}}{1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}}{{\alpha }_{m}} \right]{{\sigma }^{2}}_{\alpha }+ \\ & \frac{1}{4E\left[ {{\left( 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}} \right)}^{3}}{{\alpha }_{m}} \right]}3{{\sigma }^{4}}_{\alpha }\approx \\ & \frac{E\left[ {{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}{{\alpha }_{m}} \right]}{E\left[ 1-{{\left( {{\alpha }_{m}}-\tilde{\alpha } \right)}^{2}}{{\alpha }_{m}} \right]{{\sigma }^{2}}_{\alpha }}+ \\ & \frac{1}{4E\left[ {{\left( 1-{{\alpha }^{2}}_{m}-{{{\tilde{\alpha }}}^{2}}+2\alpha \tilde{\ }{{\alpha }_{m}} \right)}^{3}}{{\alpha }_{m}} \right]}3{{\sigma }^{4}}_{\alpha }, \\ \end{align}$ | (19) |
由于
| $E\left[ {{{\tilde{\alpha }}}^{n}} \right]=\left\{ \begin{matrix} 1\cdot 3\cdot 5\ldots \left( n-1 \right){{\sigma }^{n}}_{\alpha }, & n为偶数; \\ 0, & n为奇数. \\ \end{matrix} \right.$ |
式(17)~(19)可以方便求得,这里不再赘述.
3 跟踪处理流程为解决方向余弦坐标系下量测方程的强非线性,首先用多普勒量测与距离量测乘积的伪量测来减轻多普勒量测的非线性.接着将所得量测Rm,αm,ξm依据式(2)转换为直角坐标系下xm,ym,ξm,并根据式(10)~(16)得到转换之后误差的平均真实均值和平均真实协方差.最后由于转换量测中的伪量测与目标状态仍然存在非线性,但非线性已经很弱.本文利用Cholesky分解对位置量测和伪量测进行序贯处理来解决这一非线性问题[10].算法具体流程如图 1所示.

|
图 1 跟踪流程 Figure 1 Tracking logic flowchart |
为验证本文跟踪滤波器的性能,设计如下仿真场景.雷达位于(0,0)km处,采样间隔T=1 s,距离、方位和多普勒量测的标准差分别为σR=15 m,σα=0.2(°),σvR=0.1 m/s,距离量测误差与多普勒量测误差相关系数ρ=0.9[9].假定目标起始位于(10,10)km处,并以(100,100)m/s的速度匀速运动100 s.状态空间模型采用近似常加速度模型,过程噪声标准差为0.001m/s2.
由于在方向余弦坐标系下,并不能得到转换量测的无偏估计,所以UCM和MUCM方法不能被使用.为验证本文提出的算法的性能,EKF、UKF以及本文提出的DCPDMFcos在以下3个指标下被评估.同时为验证引入多普勒量测对于滤波效果的影响,文献[15]中CMKFDcos也被评估.
首先应用平均归一化转换量测误差方差(ANCMES)[3]对量测进行一致性分析:
| $ANCMES=\frac{1}{MC}\sum\limits_{i=1}^{MC}{\tilde{Z}_{i}^{T}{{P}_{\tilde{Z}\tilde{Z}}}^{-1}{{{\tilde{Z}}}_{i}}}.$ |
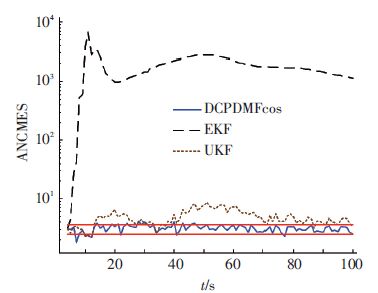
式中:${{{\tilde{Z}}}_{i}}$为被测误差向量; MC为模特卡罗次数;${{\rm{P}}_{{\rm{\tilde Z\tilde Z}}}}$为被测向量方差.由于EKF和UKF并不存在转换量测协方差,不过根据文献[3]中的定义,并不要求被测误差向量必须为转换量测.所以本文选取一步预测量测误差和一步预测量测误差协方差作为ANCMES的评估对象.如果预测量测误差与预测量测误差协方差是一致的,ANCMES将位于卡方分布置信边界内[3].500次蒙特卡洛试验所得结果如图 2所示.
|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期) 图 2 预测量测一致性检测 Figure 2 ANCMES of predicted measurements |
由于CMKFDcos并不包含多普勒量测,它的卡方分布置信边界不同与其他滤波器.所以CMKFDcos并未用此指标进行评估.图 2中红线为置信度为0.9时的卡方分布置信边界.从图 2中可以看出本文提出的转换量测方法在滤波过程中预测量测始终是一致的,而EKF在滤波全过程都不能保证预测量测的一致性,UKF仅能在滤波的某些时刻保证预测量测的一致性.
以下从滤波器估计的一致性和滤波精度两个方面对滤波器跟踪性能进行分析.滤波器的估计一致性由平均归一化估计误差方差(ANEES)[16]给出:
| $ANEES=\frac{1}{MC\cdot m}\sum\limits_{i=1}^{MC}{{{\left( {{x}_{i}}-x \right)}^{T}}{{P}^{-1}}_{i}\left( {{x}_{i}}-x \right).}$ |
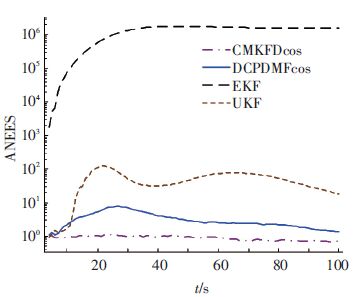
式中:(xi-x)、Pi分别为第i次蒙特卡洛仿真的估计误差和相应的误差协方差;m为量测向量的维数.如果估计误差和相应协方差匹配的话,ANEES应该接近于1,则滤波器是可信的[16].500次蒙特卡洛试验所得结果如图 3所示.从图 3中可以看出EKF完全不能保证滤波的一致性,而UKF只在滤波开始具有较好的一致性.对于DCPDMFcos,虽然由于引入多普勒量测,它的一致性相比于CMKFDcos稍有下降,但仍能在整个滤波过程中保持较好的一致性.而且从后面的仿真结果也可以看出,这一点一致性的下降并没有影响DCPDMFcos的跟踪性能.
|
图 3 滤波器状态一致性检测 Figure 3 ANESS of filter states |
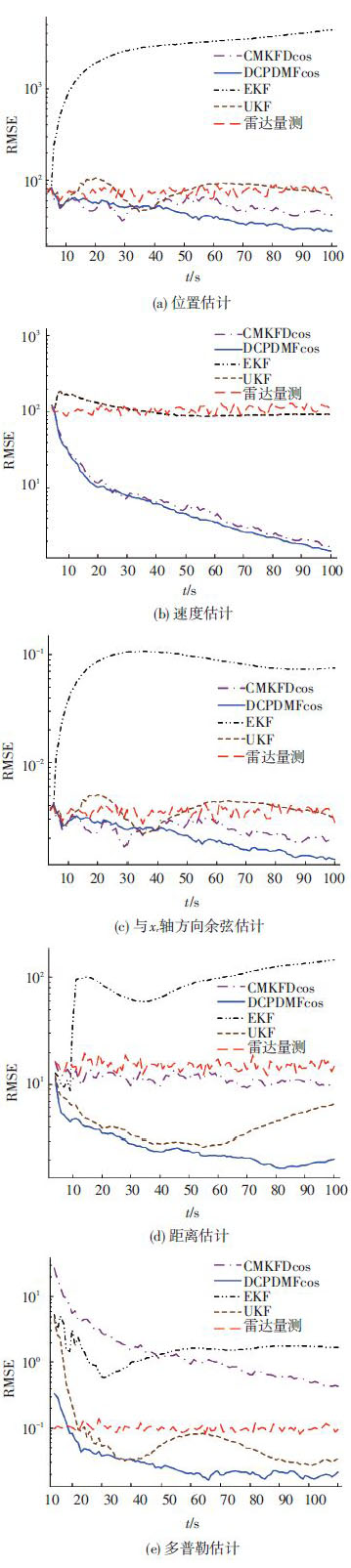
关于滤波器的估计精度,本文选取滤波器估计值与真值误差的均方根误差(RMSE)作为评价指标.同时为了更好的呈现滤波器的估计精度,各量测估计的RMSE也同样被给出.通过500次蒙特卡洛试验所得结果如图 4所示.
|
图 4 滤波精度性能比较 Figure 4 Comparison of filtering precision |
从仿真结果可以看出,通过引入多普勒量测,DCPDMFcos相比于CMKFDcos获得了更佳的滤波效果.同时由于方向余弦坐标系下量测方程的非线性过强,EKF完全不能给出目标状态的有效估计,UKF仅能在某些时刻给出目标状态的有效估计,且滤波效果较差.而DCPDMFcos在所有的指标上都具有最佳的滤波效果.
5 结 论1) 针对方向余弦坐标系下的目标跟踪问题,DCPDMFcos考虑了距离量测和多普勒量测之间的相关性,通过对量测方程中的非线性分三步进行处理,有效地降低每一步所需要处理的非线性,从而给出了目标状态的有效估计.
2) DCPDMFcos首先用距离量测与多普勒量测的乘积构造伪量测来减轻多普勒量测的非线性;然后通过对方向余弦进行二阶泰勒展开,得到了转换量测误差均值和协方差的一致性估计;最后通过对位置量测和伪量测进行序贯处理解决了伪量测的非线性问题.
3) 通过与CMKFDcos、EKF和UKF性能的比较仿真,证实了无论在滤波一致性方面,还是在滤波精度方面,DCPDMFcos都具有更佳的性能.
| [1] |
FARINA A, STUDER F A.
Radar Data Processing, Vol. I: Introduction and Tracking, Vol. II: Advanced Topics and Application[M]. Letchworth: Research Studies Press LTD, UK, 1985 : 112 -135.
( 0) 0)
|
| [2] |
JULIERS J, UHLMANN J K. Unscented filtering and nonlinear estimation[J].
Proceeding of the IEEE,2004, 92 (3) : 401-422.
DOI: 10.1109/JPROC.2003.823141 ( 0) 0)
|
| [3] |
LERRO D, BAR-SHALOM Y. Tracking with debiased consistent converted measurements versus EKF[J].
IEEE Transactions on Aerospace and Electronic Systems,1993, 29 (3) : 1015-1022.
DOI: 10.1109/7.220948 ( 0) 0)
|
| [4] |
MO Longbin, SONG Xiaoquan, ZHOU Yiyu, et al. Unbiased converted measurements for tracking[J].
IEEE Transactions on Aerospace and Electronic Systems,1998, 34 (3) : 1023-1027.
DOI: 10.1109/7.705921 ( 0) 0)
|
| [5] |
DUAN Zhansheng, HAN Chongzhao, Li X R. Comments on “Unbiased converted measurements for tracking”[J].
IEEE Transactions on Aerospace and Electronic Systems,2004, 40 (4) : 1374-1377.
DOI: 10.1109/TAES.2004.1386889 ( 0) 0)
|
| [6] |
MEI Wei, BAR-SHALOM Y. Unbiased Kalman Filter using converted measurements: Revisit[C]// Proceedings of the SPIE 7445, Signal and Data Processing of Small Targets 2009. San Diego, CA: SPIE, 2009: 7445. DOI: 10.1117/12.831218.
( 0) 0)
|
| [7] |
BORDONARO S, WILLETT P, BAR-SHALOM Y. Decorrelated unbiased converted measurement Kalman filter[J].
IEEE Transactions on Aerospace and Electronic Systems,2014, 50 (2) : 1431-1444.
DOI: 10.1109/TAES.2014.120563 ( 0) 0)
|
| [8] |
CHARLISH A, GOVAERS F, KOCH W. Distributed radar tracking using the double debiased distributed Kalman filter[C]// Proceedings of IEEE Radar Conference. Cincinnati, OH: IEEE, 2014: 1124-1129. DOI: 10.1109/RADAR.2014.6875764.
( 0) 0)
|
| [9] |
NIU Ruixin, WILLETT P, BAR-SHALOM Y. Tracking considerations in selection of radar waveform for range and range-rate measurements[J].
IEEE Transactions on Aerospace and Electronic Systems,2002, 38 (2) : 467-487.
DOI: 10.1109/TAES.2002.1008980 ( 0) 0)
|
| [10] |
DUAN Zhansheng, HAN Chongzhao, Li X R. Sequential nonlinear tracking filter with range-rate measurements in spherical coordinates[C]//Proceedings of the 7th International Conference on Information Fusion. Stockholm: IEEE, 2004: 599-605.
( 0) 0)
|
| [11] |
SUCHOMSKI P. Explicit expressions for debiased statistics of 3D converted measurements[J].
IEEE Transaction on Aerospace and Electronic Systems,1999, 35 (1) : 368-370.
DOI: 10.1109/7.745708 ( 0) 0)
|
| [12] |
BORDONARO S, WILLETT P, BAR-SHALOM Y. Consistent linear tracker with position and range rate measurements[C]// Systems and Computers (ASILOMAR), 2012 Conference Record of the Forty Sixth Asilomar Conference on Signals. Pacific Grove, CA:IEEE, 2012: 880-884.DOI: 10.1109/ACSSC.2012.6489141.
( 0) 0)
|
| [13] |
BORDONARO S, WILLETT P, BAR-SHALOM Y. Performance analysis of the converted range rate and position linear Kalman filter[C]//Systems and Computers (ASILOMAR), 2013 Conference Record of the Forty Sixth Asilomar Conference on Signals. Pacific Grove, CA: IEEE, 2013: 1751-1755. DOI: 10.1109/ACSSC.2013.6810601.
( 0) 0)
|
| [14] |
ZHOU Gongjian, PELLETIER M, KIRUBARAJAN T, et al. Statically fused converted position and doppler measurement Kalman filters[J].
IEEE Transactions on Aerospace and Electronic Systems,2014, 50 (1) : 300-318.
DOI: 10.1109/TAES.2013.120256 ( 0) 0)
|
| [15] |
ZHANG Boyan, QU Hongquan, LI Shaohong. A new method for target tracking with debiased consisitent converted measurements in direction cosines[J].
Chinese Journal of Electronics,2010, 19 (3) : 538-542.
( 0) 0)
|
| [16] |
LI X R, ZHAO Zhanlue, JILKOV V P. Estimator’s credibility and its measures[C]//Procceedings of the IFAC 15th World Congress. Barcelona:IEEE, 2002: 2779-2784.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


