群目标跟踪场景,如机群编队和地面移动车队,一系列拥有类似运动方式的空间临近目标组成跟踪对象.在群目标跟踪问题中,群目标的量测数目是时变的,传统多目标跟踪算法难以实现对群目标的稳定跟踪[1].文献[2]按照群内目标数目将群目标跟踪分成两类:大群目标跟踪和小群目标跟踪.其中大群目标主要是指:由大量目标组成,并由此导致无法跟踪全部个体目标而仅适合跟踪群整体状态的群目标类型;而小群目标主要是指:由相对较少的目标组成,在估计群整体状态的同时又可跟踪群内个体目标的群目标类型.学者针对大群目标跟踪,采用群整体跟踪方法,该方法主要有两类算法:概率密度假设(PHD)滤波算法[3-4]和贝叶斯递推算法.PHD滤波算法可用于多群目标的跟踪问题,解决群内目标数目未知和数据关联问题[5-7].它的缺点是无法内在区分假设密度传播中哪部分是由于估计不确定产生的,并且算法较为复杂,不利于实际工程应用.Koch[1]推导了群目标的贝叶斯递推算法,提出利用随机矩阵描述群的扩展状态,基于群的质心状态跟踪,实现对群整体运动的跟踪,有效地解决了单群目标的跟踪问题,但它忽略了量测误差对扩展状态的影响.文献[8]在IMM算法框架下,采用启发式近似方法,考虑量测误差情况,实现了对单群目标的有效跟踪,但它没有考虑对群目标强机动情况进行处理.文献[9]在文献[8]的基础上,利用变分贝叶斯迭代方法进行量测更新,提高了跟踪精度,但其模型转换概率需要先验设定,与复杂群目标运动模式不相符.
本文重点针对机动单群目标在高量测噪声环境中的整体跟踪问题,提出了群目标跟踪自适应IMM算法.其中,使用强跟踪算法修正群目标机动时的质心状态,基于新息计算更新量测误差协方差修正对群扩展状态的描述,利用量测数据修正quasi-Bayesian方法自适应更新后的模型转换概率.最后仿真验证本文算法的有效性.
1 基于随机矩阵的群跟踪算法将多个目标跟踪问题等效成单个群整体跟踪问题,跟踪群目标的质心状态和扩展状态,群目标的每个量测等效为群质心量测扩展状态下散射的结果[10].
1.1 量测似然函数构建随机变量xk表示群质心的运动状态[1],xk=[rkT,${\dot{r}}$kT,${\ddot{r}}$kT],其中rkT、${\dot{r}}$kT、${\ddot{r}}$kT分别表示群质心的位置、速度和加速度.对称正定(SPD)矩阵Xk代表群整体的扩展状态.zj表示量测,量测转移矩阵H=[Id,0d,0d],因此k时刻的量测方程为
| ${{z}^{j}}_{k}=H{{x}_{k}}+{{w}^{j}}_{k}.$ |
Zk={zkj}j=1nk为k时刻的量测集;nk为k时刻的量测数目.文献[11]认为量测为目标扩展范围内的近似均匀分布.因此,假设噪声wkj是均值为零,方差为εXk+Rk的高斯白噪声,其中ε是对扩展状态进行描述的比例因子,Rk是量测误差协方差.
但是和形式难以进行贝叶斯推导,故常采用如下变换形式[11]:
| $\varepsilon {{X}_{k}}+{{R}_{k}}={{B}_{k}}{{X}_{k}}B_{k}^{T}.$ |
式中,
k时刻的累积量测集为Zk={Zl,nl}kl=1,可得量测似然函数:
| $p({{Z}_{k}}|{{x}_{k}},{{X}_{k}},{{n}_{k}})=\prod\limits_{j=1}^{{{n}_{k}}}{N({{z}^{j}}_{k};H{{x}_{k}},{{B}_{k}}{{X}_{k}}B_{k}^{T})}.$ | (1) |
式中,N(x;μ,Σ)代表均值为μ,方差为Σ的正态分布.量测均值zk和对应的散射矩阵Zk为
| ${{{\bar{z}}}_{k}}=\frac{1}{{{n}_{k}}}\sum\limits_{j=1}^{{{n}_{k}}}{{{z}^{j}}_{k}},{{{\bar{Z}}}_{k}}=\sum\limits_{j=1}^{{{n}_{k}}}{({{z}^{j}}_{k}-{{{\bar{z}}}_{k}}){{({{z}^{j}}_{k}-{{{\bar{z}}}_{k}})}^{T}}}.$ |
通过数学推导,式(1)可以写为[11]
| $\begin{align} & p\left( {{Z}_{k}}|{{x}_{k}},{{X}_{k}},{{n}_{k}} \right)\propto \\ & N({{{\bar{z}}}_{k}};H{{x}_{k}},{{B}_{k}}{{X}_{k}}B_{k}^{T}/{{n}_{k}})\cdot \\ \end{align}$ | (2) |
| $W\left( X;a,A \right)\propto |A{{|}^{\frac{a}{2}}}|X{{|}^{\frac{a-d-1}{2}}}etr(-\frac{1}{2}X{{A}^{-1}}).$ | (3) |
式(3)表示均值为aA的Wishart分布函数.其中,d为SPD矩阵X的维数,a为自由度且满足a≥d,A为协方差矩阵,etr(·)为exp(tr(·))的缩写.
1.2 群状态联合先验概率密度函数构建xk和Xk的联合先验概率密度函数为
| $p\left( {{x}_{k}},{{X}_{k}}|{{Z}^{k-1}} \right)=p\left( {{x}_{k}}|{{X}_{k}},{{Z}^{k-1}} \right)p\left( {{X}_{k}}|{{Z}^{k-1}} \right).$ |
向量xk的条件概率密度函数为
| $p\left( {{x}_{k}}|{{X}_{k}},{{Z}^{k-1}} \right)=N\left( {{x}_{k}};{{x}_{k|k-1}},{{{\tilde{P}}}_{k|k-1}}\otimes {{X}_{k}} \right).$ |
式中,${\tilde{P}}$k|k-1为单维状态上的一步预测协方差矩阵,⊗为Kronecker积.
矩阵Xk的条件概率密度函数为
| $p\left( {{X}_{k}}|{{Z}^{k-1}} \right)=IW\left( {{X}_{k}};{{v}_{k|k-1}},{{{\tilde{X}}}_{k|k-1}} \right),$ | (4) |
| $IW\left( X;a,A \right)\propto {{A}^{\frac{a}{2}}}|X{{|}^{\frac{-a+d+1}{2}}}etr(-\frac{1}{2}A{{X}^{-1}}).$ | (5) |
式中:vk|k-1为k-1时刻对自由度的一步预测估计,${\tilde{X}}$k|k-1为k-1时刻对扩展状态的一步预测估计.式(5)表示均值为A/(a-d-1)的逆Wishart分布函数.其中:d为SPD矩阵X的维数;a为自由度且满足a-d-1>0;A为SPD矩阵.
因此,对应的Bayesian滤波的一步预测公式为
| ${{x}_{k|k-1}}={{F}_{k|k-1}}{{x}_{k-1|k-1}},$ | (6) |
| ${{{\tilde{P}}}_{k|k-1}}={{{\tilde{F}}}_{k|k-1}}{{{\tilde{P}}}_{k-1|k-1}}\tilde{F}_{k|k-1}^{T}+{{{\tilde{Q}}}_{k-1}}.$ | (7) |
式中,状态转移矩阵Fk|k-1=${\tilde{F}}$k|k-1⊗Id,过程噪声方差Qk-1=${\tilde{Q}}$k-1⊗Xk-1.
扩展状态的预测公式[1]为
| $\begin{align} & {{{\tilde{X}}}_{k|k-1}}=\frac{{{v}_{k|k-1}}-d-1}{{{v}_{k-1|k-1}}-d-1}{{{\tilde{X}}}_{k-1|k-1}}, \\ & {{v}_{k|k-1}}=exp\left( -T/\tau \right){{v}_{k-1|k-1}}. \\ \end{align}$ |
式中:Xk-1|k-1为k-1时刻扩展状态的量测更新值;vk-1|k-1为k-1时刻对自由度的估计值;T为传感器采样周期;τ为扩展状态的变化率,定量反映了扩展状态随时间变化的灵敏度.
1.3 群状态联合后验概率密度函数构建xk和Xk的联合后验概率密度函数为
| $p\left( {{x}_{k}},{{X}_{k}}|{{Z}^{k}} \right)=p\left( {{x}_{k}}|{{X}_{k}},{{Z}^{k}} \right)p\left( {{X}_{k}}|{{Z}^{k}} \right),$ |
其中:p(xk|Xk,Zk)=N(xk;xk|k,${\tilde{P}}$k|k⊗Xk),p(Xk|Zk)=IW(Xk;vk|k,${\tilde{X}}$k|k).
量测转移矩阵为
| $H=[{{I}_{d}},{{0}_{d}},{{0}_{d}}]=\tilde{H}\otimes {{I}_{d}},\tilde{H}=\left[ 1,0,0 \right].$ |
新息协方差为
| ${{S}_{k|k-1}}={{{\tilde{S}}}_{k|k-1}}{{X}_{k}},{{{\tilde{S}}}_{k|k-1}}=\tilde{H}{{{\tilde{P}}}_{k|k-1}}{{{\tilde{H}}}^{T}}+|{{B}_{k}}{{|}^{2/d}}/{{n}_{k}}.$ |
滤波增益为
| ${{K}_{k|k-1}}={{{\tilde{K}}}_{k|k-1}}\otimes {{I}_{d}},{{{\tilde{K}}}_{k|k-1}}={{{\tilde{P}}}_{k|k-1}}{{{\tilde{H}}}^{T}}{{{\tilde{S}}}^{-1}}_{k|k-1}.$ |
对应的Bayesian滤波的运动状态更新公式为
| $\begin{align} & {{x}_{k|k}}={{x}_{k|k-1}}+\left( {{{\tilde{K}}}_{k|k-1}}\otimes {{I}_{d}} \right)\left( {{{\bar{z}}}_{k}}-H{{x}_{k|k-1}} \right), \\ & {{{\tilde{P}}}_{k|k}}={{{\tilde{P}}}_{k|k-1}}-{{{\tilde{K}}}_{k|k-1}}{{{\tilde{S}}}_{k|k-1}}{{{\tilde{K}}}^{T}}_{k|k-1}. \\ \end{align}$ |
扩展状态量测更新公式为
| ${{{\tilde{X}}}_{k|k}}={{{\tilde{X}}}_{k|k-1}}+{{{\tilde{S}}}^{-1}}_{k|k-1}{{N}_{k|k-1}}+{{B}^{-1}}_{k}Z{{-}_{k}}{{B}^{-T}}_{k},$ | (8) |
| ${{v}_{k|k}}={{v}_{k|k-1}}+{{n}_{k}}.$ | (9) |
式中,${\tilde{X}}$k|k为k时刻扩展状态的量测更新值,Nk|k-1=(zk-Hxk|k-1)(zk-Hxk|k-1)T.
需要指明的是,群质心的条件后验概率密度p(xk|Xk,Zk)不能直接估计扩展状态Xk|k和质心的误差协方差Var(xk|Zk).
Xk|k可由pXk|Zk估计得到[9]:
| ${{X}_{k|k}}=E\left[ {{X}_{k}}|{{Z}^{k}} \right]=\frac{{{{\tilde{X}}}_{k|k}}}{{{v}_{k|k}}-d-1},$ |
而Var(xk|Zk)可由p(xk|Zk)估计得到[9]:
| $Var\left( {{x}_{k}}|{{Z}^{k}} \right)={{{\tilde{P}}}_{k|k}}\otimes {{{\tilde{X}}}_{k|k}}/\left( {{v}_{k|k}}-d-1 \right)={{{\tilde{P}}}_{k|k}}\otimes {{X}_{k|k}}.$ |
对现有的单群跟踪IMM算法进行分析,主要存在以下问题:1)群质心状态估计在目标机动时误差增大;2)量测噪声和扩展自由度的先验设定,不能实时描述目标扩展状态的变化;3)转换概率矩阵的先验设定,不能随目标运动模式的变化进行自适应调整.
基于上述问题分析,在群质心状态估计中,引入带有多重次优渐消因子的强跟踪滤波算法,提高机动阶段时对群质心状态估计精度;在扩展状态估计中,考虑量测精度对于扩展状态的影响,将量测误差协方差和扩展状态同时纳入到量测似然函数的构建中,并且基于新息计算和渐消记忆迭代过程自适应更新量测误差协方差矩阵;通过quasi-Bayesian方法自适应更新模型转换概率的算法,并且利用量测数据修正模型转换概率,抑制非匹配模型的作用,放大匹配模型的作用,优化模型与目标运动模式的实时匹配.
2.2 多重次优渐消强跟踪算法当群目标机动时,式(7)中预测误差协方差矩阵Pk|k-1不能随残差改变,因此引入带有多重次优渐消因子的强跟踪算法[12],将Cholesky分解后的多重次优渐消因子应用到预测误差协方差矩阵计算中,在线调整质心状态的预测误差协方差矩阵.假设为多重渐消因子矩阵为Ak=diag{λ1,k,λ2,k,…,λL,k},系统先验确定λ1,k:λ2,k:…:λL,k=a1:a2:…:aL.取λi,k=ai·ck,其中ai≥1,ck为待定因子.
强迫输出残差近似高斯白噪声,根据目标运动情况实时调整增益,设置的渐消因子为[13]
| ${{c}_{k}}=\left\{ \begin{matrix} \eta \left( k \right),\eta \left( k \right)>1; \\ 1,\text{ }\eta \left( k \right)\le 1. \\ \end{matrix} \right.$ |
其中:
| $\begin{align} & \eta \left( k \right)=\frac{tr\left[ G\left( k \right) \right]}{tr\left[ L\left( k \right) \right]}, \\ & G\left( k \right)={{N}_{0}}\left( k \right)-\xi R-H({{{\tilde{Q}}}_{k-1}}\otimes {{I}_{d}}){{H}^{T}}, \\ & L\left( k \right)=H{{F}_{k|k-1}}{{{\tilde{P}}}_{k-1|k-1}}{{F}^{T}}_{k|k-1}{{H}^{T}}, \\ & {{N}_{0}}\left( k \right)=E[({{{\bar{z}}}_{k}}-H{{x}_{k|k-1}}){{({{{\bar{z}}}_{k}}-H{{x}_{k|k-1}})}^{T}}]= \\ & \left\{ \begin{matrix} \gamma \left( 1 \right){{\gamma }^{T}}\left( 1 \right),k=1; \\ \frac{\rho {{N}_{0}}\left( k-1 \right)+\gamma \left( k \right){{\gamma }^{T}}\left( k \right)}{1+\rho } \\ \end{matrix} \right.,k\ge 2. \\ & \gamma \left( k \right)={{{\bar{z}}}_{k}}-H{{x}_{k|k-1}}. \\ \end{align}$ |
式中:γ(k)为新息;γ(1)为初始新息;ρ(0<ρ≤1)为遗忘因子,一般取ρ=0.95;ξ(ξ≥1)为弱化因子,可以使状态估计值更加平滑.
对多重次优渐消因子Ak进行Cholesky分解可得:
| ${{A}_{k}}={{{\bar{A}}}_{k}}\cdot {{{\bar{A}}}^{T}}_{k},{{{\bar{A}}}_{k}}=diag\left\{ \sqrt{{{\lambda }_{1,k}}},\sqrt{{{\lambda }_{2,k}}},\cdots ,\sqrt{{{\lambda }_{L,k}}} \right\}.$ |
将Cholesky分解后的多重次优渐消因子,带入Pk|k-1的计算中,得到修正后的${\tilde{P}}$k|k-1为
| ${{{\tilde{P}}}_{k|k-1}}={{{\bar{A}}}_{k}}{{F}_{k|k-1}}{{{\tilde{P}}}_{k-1|k-1}}{{F}^{T}}_{k|k-1}{{{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{A}}}^{T}}_{k}+\left( {{Q}_{k-1}}\otimes {{I}_{d}} \right).$ |
当群内目标数目较大时,传感器获得大量目标量测数据,对量测数据的处理显得尤为重要,因此必须考虑传感器的量测精度对扩展状态估计的影响.
由式(8)可知,扩展状态的量测更新中纳入了对量测噪声的考虑,其中Bk$\triangleq $(ε${\tilde{X}}$k/k-1+Rk1/2${\tilde{X}}$k/k-1-1/2是量测值对群扩展状态大小、形状和方向动态变化的描述参数.
而量测噪声协方差矩阵通常先验设定,这与复杂群目标跟踪环境不相符,因此基于渐消记忆迭代过程,充分利用新息和最近时刻的量测值,自适应更新测量误差协方差矩阵[14]:
| ${{R}_{k}}=\varphi {{R}_{k-1}}+\left( 1-\varphi \right)|{{\gamma }_{k}}||{{\gamma }_{k-1}}|.$ |
式中,φ(0<φ≤1)为遗忘因子,一般取φ=0.95.
2.4 模型转换概率自适应算法为了实时估计模型的转换概率矩阵,使用quasi-Bayesian方法能在计算量和估计精度上取得较好的平衡[15].
假设有m个子模型,未知转换概率矩阵为Π=[π1,…,πm]T,其中πi=[πi1,…,πim]T,(i=1,…,m)服从Dirichlet分布,模型的权重wk=[wk1,…,wkm]T,模型的似然值为Λk=[Λk1,…,Λkm]T.
因此,最小均方根误差下的模型转换概率矩阵估计为
| ${{{\bar{\Pi }}}_{k}}=E{{[{{\Pi }_{k}}|{{z}_{k}}]}^{T}}.$ |
初始化参数为
| $\begin{align} & {{\partial }_{i}}\left( 0 \right)={{[{{\alpha }_{i1}}\left( 0 \right),\ldots ,{{\alpha }_{im}}\left( 0 \right)]}^{T}}, \\ & {{\alpha }_{i}}\left( 0 \right)=\sum\limits_{j=1}^{m}{{{\alpha }_{ij}}\left( 0 \right)},\sum \\ & {{{\bar{\pi }}}_{i}}\left( 0 \right)=\frac{~{{\partial }_{i}}\left( 0 \right)}{{{\alpha }_{i}}\left( 0 \right)\text{ }},(i=1,\cdots ,m;{{\alpha }_{ij}}\left( 0 \right)\ge 0). \\ \end{align}$ |
递推过程为
| $\begin{align} & {{{\bar{\pi }}}_{ij}}\left( k \right)=\frac{1}{k+1}{{\alpha }_{ij}}\left( k \right), \\ & {{\alpha }_{ij}}\left( k \right)={{\alpha }_{ij}}\left( k-1 \right)+\frac{{{\alpha }_{ij}}\left( k-1 \right){{{\tilde{g}}}_{ij}}\left( k \right)}{\sum\limits_{j=1}^{m}{{{\alpha }_{ij}}\left( k-1 \right){{{\tilde{g}}}_{ij}}\left( k \right)}}, \\ & {{{\tilde{g}}}_{ij}}\left( k \right)=1+{{\eta }_{i}}\left( k \right)[{{\Lambda }^{j}}_{k}-{{({{{\bar{\pi }}}^{i}}_{k-1})}^{T}}{{\Lambda }_{k}}]. \\ \end{align}$ |
在IMM算法中,概率越大的子模型与真实的目标运动模式匹配程度越高,其他子模型向这一子模型转移的概率应越大.可以充分利用当前的量测,在线更新IMM算法中模型转移概率,使之符合实际跟踪场景.
考虑到转移概率值的非负性,取对数形式的模型[16]概率变化率为
| ${{\kappa }_{j}}\left( k \right)=exp\left( {{u}^{j}}_{k}-{{u}^{j}}_{k-1} \right).$ |
归一化后的转移概率计算公式为
| ${{{\tilde{\pi }}}_{ij}}\left( k \right)=\frac{{{\kappa }_{j}}k{{{\bar{\pi }}}_{ij}}(k)}{\sum\limits_{j=1}^{m}{{{\kappa }_{j}}k{{{\bar{\pi }}}_{ij}}\left( k \right)}}.$ |
使用m个子模型进行跟踪,群目标跟踪自适应IMM算法递推步骤如下.
Step 1 模型条件初始化.
1) 计算混合概率.计算模型Mkj的混合概率(包括群质心模型Mxkj和扩展状态模型MXkj)为
| $\begin{align} & {{\mu }^{i|j}}_{k-1|k-1}=p\left\{ {{M}^{i}}_{k-1}|{{M}^{j}}_{k},{{Z}^{k-1}} \right\}= \\ & \frac{p\left\{ {{M}^{j}}_{k}|{{M}^{i}}_{k-1},{{Z}^{k-1}} \right\}p\left\{ {{M}^{i}}_{k-1}|{{Z}^{k-1}} \right\}}{p\left\{ {{M}^{j}}_{k}|{{Z}^{k-1}} \right\}}= \\ & \frac{{{{\tilde{\pi }}}_{ij}}{{\mu }^{i}}_{k-1}}{{{{\bar{c}}}_{j}}}. \\ \end{align}$ |
式中,μk-1i为k-1时刻的模型概率,${{{\bar{c}}}_{j}}=\sum\limits_{i=1}^{m}{{{\pi }_{ij}}{{\mu }^{i}}_{k-1}}$.
2) 混合估计.
| $\hat{x}_{k-1|k-1}^{oj}=E({{x}_{k-1}}|M_{k}^{j},{{Z}^{k-1}})=\sum\limits_{i=1}^{m}{\mu _{k-1|k-1}^{i|j}}\hat{x}_{k-1|k-1}^{i},$ | (10) |
| $\begin{align} & \hat{P}_{jk-1|k-1}^{0}=\sum\limits_{i=1}^{m}{\mu _{k-1|k-1}^{i|j}\{}\hat{P}_{k-1|k-1}^{^{i}}+(\hat{x}_{k-1|k-1}^{^{i}}-\hat{x}_{jk-1|k-1}^{^{0}})\cdot \\ & {{(\hat{x}_{k-1|k-1}^{^{i}}-x_{jk-1|k-1}^{0})}^{T}}\}, \\ \end{align}$ | (11) |
| $\hat{x}_{jk-1|k-1}^{0j}=E({{X}_{k-1}}|M_{k}^{j},{{Z}^{k-1}})=\sum\limits_{i=1}^{m}{\mu _{k-1|k-1}^{i|j}}\hat{x}_{k-1|k-1}^{i}.$ | (12) |
Step 2 模型条件滤波.
1) 状态预测.参照多重次优渐消强跟踪算法进行滤波递推,使用多重次优渐消因子在线更新${\tilde{P}}$k|k-1j.
2) 计算k时刻的新息协方差阵Sk|k-1j,以及xk和Xk的联合似然值Λk|k-1j[11]为
| ${{S}^{j}}_{k|k-1}=H{{P}^{j}}_{k|k-1}{{H}^{T}}+|{{B}_{k}}{{|}^{2/d}}/{{n}_{k}}.$ |
其中:
| $\begin{align} & |{{B}_{k}}{{|}^{2/d}}=|\varepsilon {{I}_{d}}+{{R}_{k}}{{{\tilde{X}}}^{-1}}_{k/k-1}{{|}^{1/d}}, \\ & {{\Lambda }^{j}}_{k|k-1}=p\left\{ {{Z}^{k}}|{{M}^{j}}_{k},{{Z}^{k-1}} \right\}= \\ & {{\left( {{2}^{{{n}_{k}}d-1}}{{\pi }^{{{n}_{k}}d}}{{n}_{k}} \right)}^{-\frac{1}{2}}}{{\Gamma }_{d}}\left[ \frac{{{a}^{j}}_{k}+{{n}_{k}}}{2} \right]{{\Gamma }^{-1}}_{d}\left[ \frac{{{a}^{j}}_{k}}{2} \right]\times \\ & |{{B}_{k}}^{j}{{\left( B_{k}^{j} \right)}^{T}}{{|}^{\frac{1-{{n}_{k}}}{2}}}|{{S}^{j}}_{k/k-1}{{|}^{-\frac{1}{2}}}|{{X}^{j}}_{k|k-1}{{|}^{\frac{{{a}^{j}}_{k}}{2}}}|{{X}_{k|k}}{{|}^{\frac{-{{a}^{j}}_{k}-{{n}_{k}}}{2}}}. \\ \end{align}$ |
其中
| $a_{k}^{j}=v_{_{k/k-1}}^{j}-d-1.$ |
3) 滤波更新.输出单个子模型的群质心状态${\hat{x}}$k|kj,群质心状态估计协方差阵${\hat{p}}$jk|k和群扩展状态${\hat{x}}$jk|k.
Step 3 模型概率和转移概率矩阵更新.
1) 模型概率更新. 通过计算的Λk|k-1j,群质心模型和扩展模型的概率为
| ${{u}^{j}}_{k}=\frac{{{\Lambda }^{j}}_{k|k-1}{{{\bar{c}}}_{j}}}{\sum\limits_{j=1}^{m}{{{\Lambda }^{j}}_{k|k-1}{{{\bar{c}}}_{j}}}}.$ |
2) 转移概率矩阵更新. 通过计算的Λk|k-1j,再将k-1时刻的群模型概率uk-1j以及转换概率矩阵Πk-1,代入式(10)来估计出k时刻的转换概率矩阵Πk.
Step 4 估计融合.
1) 群质心的状态${\hat{x}}$k|k和${\hat{P}}$k|k的融合估计为
| $\begin{align} & {{{\hat{x}}}_{k|k}}=\sum\limits_{j=1}^{m}{u_{k}^{j}\hat{x}_{k|k}^{^{j}}}, \\ & {{{\hat{P}}}_{k|k}}=\sum\limits_{j=1}^{m}{u_{k}^{j}}\{P_{k|k}^{^{j}}+({{{\hat{x}}}_{^{k|k}}}-\hat{x}_{k|k}^{j})({{{\hat{x}}}_{k|k}}-\hat{x}_{k|k}^{^{j}})T\}. \\ \end{align}$ |
2) 群扩展的状态${\hat{X}}$k|k的融合估计为
| ${{X}^{k}}|k=\sum\limits_{j=1}^{m}{\mu _{k}^{j}\hat{X}_{k|k}^{^{j}}}.$ |
参照文献[8]的仿真实验,设置二维空间内由密集多目标构成的群目标的运动场景,为了便于比较算法性能,这里主要考虑单群目标的机动跟踪问题,不涉及群的衍生/合并情况.假设群产生的量测数目服从于量测比率为γ的泊松分布,群目标的真实扩展状态为Xk=Rkdiag([a2 b2])(Rk)T,式中:Rk为一个旋转矩阵,它与群整体运动的方向有关;a为椭圆长轴;b为椭圆短轴.假设整个观测过程持续40 s,传感器位置在原点,x轴和y轴上的量测误差的标准差分别为σx=15 m和σy=15 m,量测数据的采样间隔为T=1 s.另外,量测比率γ=20,群的初始质心运动状态为[400 m,300 m,42.4 m/s,-42.4 m/s]T,扩展状态的(ai,bi)=(20,5),其中群整体分别在9~10 s和17~20 s以Ω=$\frac{\pi }{8}$rad/s作 CT 运动,在27~34 s以Ω=$\frac{\pi }{16}$ rad/s作CT运动(径向加速度值分别近似为2、2和1 g),其他运动阶段作CV运动.
使用的跟踪模型是CV模型,过程噪声项Q按照白噪声模型来设置[17],其中质心运动状态的转移方程为
| $\begin{align} & {{x}_{k}}={{F}^{j}}_{k}{{x}_{k-1}}+{{\Gamma }^{j}}_{k}{{v}^{j}}_{k-1}. \\ & 式中:{{x}_{k}}={{\left[ {{p}_{x}},{{p}_{y}},{{v}_{x}},{{v}_{y}} \right]}^{T}},{{F}^{j}}_{k}=\tilde{F}\otimes {{I}_{d}},{{\Gamma }^{j}}_{k}=\tilde{G}\otimes {{I}_{d}}, \\ & {{v}^{j}}_{k}\tilde{\ }N\left[ 0,\tilde{Q} \right],\tilde{F}=\left[ \begin{matrix} 1 & T \\ 0 & 1 \\ \end{matrix} \right],\tilde{G}=\left[ \begin{matrix} {{T}^{2}}/2 \\ T \\ \end{matrix} \right] \\ \end{align}$ |
实验中采用3个白噪声模型,具体参数包括低过程噪声项Q=1且低扩展灵敏度τ=8T(简称为CV1),适度过程噪声项$\tilde{Q}$=10且适度扩展灵敏度τ=5T(简称为CV2),高过程噪声项$\tilde{Q}$=20且高扩展灵敏度τ=3T(简称为CV3),$\tilde{Q}$和τ的大小分别对应群质心运动状态和扩展状态变化的剧烈程度.模型初始概率设为u0=[0.8,0.1,0.1]T,模型转移概率矩阵为
| $\Pi =\left[ \begin{matrix} 0.90 & 0.05 & 0.05 \\ 0.05 & 0.90 & 0.05 \\ 0.05 & 0.05 & 0.90 \\ \end{matrix} \right].$ |
它的运动轨迹如图 1所示,其中黑色的实点表示群目标真实量测,椭圆代表群扩展状态在置信水平为0.9时的置信区域.
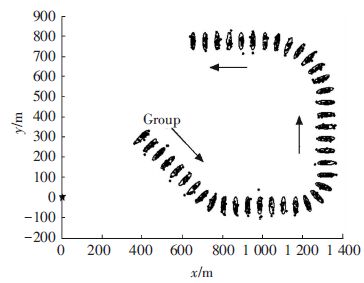
|
图 1 密集群目标的运动轨迹 Figure 1 Trajectory of group targets |
将本文改进的群目标跟踪自适应IMM算法(简称为IMM3)对比文献[8-9]中的算法(简称为IMM1和IMM2),进行100次Monte-Carlo仿真实验.图 2,3分别给出了3种算法的群质心位置和速度估计的RMSE比较结果.从图中结果可知,本文提出的IMM3算法在目标作匀速运动时期内,滤波精度与IMM1和IMM2算法相当.在群目标作机动的9~10 s、17~20 s和27~34 s 段时间内,IMM2算法通过采用变分贝叶斯迭代法,增加了对无噪量测的联合估计,滤波精度高于IMM1算法.而IMM3算法的滤波精度明显要高于IMM1算法和IMM2算法,由于本文算法在状态预测协方差中引入多重次优渐消因子,可在线实时调整增益矩阵,因而具有较强的模型失配的鲁棒性和突变状态的跟踪能力.

|
图 2 群质心位置均方根误差 Figure 2 RMSE of kinematic position |

|
图 3 群质心速度均方根误差 Figure 3 RMSE of kinematic velocity |
图 4比较了3种算法群扩展状态估计的均方根误差,计算公式为[8]
| $RMS{{E}_{X}}=\sqrt{\frac{1}{M}\sum\limits_{1}^{M}{{{\left[ tr\left[ {{({{X}_{k/k}}-{{X}_{k}})}^{2}} \right] \right]}_{i}}}}$ |
由图 2,3可知,IMM2算法由于利用变分贝叶斯推导方法,增加了对无噪量测的联合估计,将传感器量测误差合理纳入到滤波方程中,对扩展状态的估计要优于IMM1算法.而本文提出的IMM3算法,把量测误差和扩展状态同时纳入到量测似然函数的构建中,基于新息计算和渐消记忆迭代过程自适应更新量测误差协方差,提高了对扩展状态的估计精度,仿真效果最优.
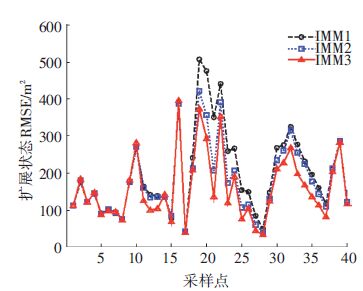
|
图 4 扩展状态均方根误差 Figure 4 RMSE of extension state |
图 5给出了3种算法的模型概率变化对比.在群目标匀速运动的阶段,过程噪声和扩展状态灵敏度都较低,目标运动状态与模型CV1更为匹配;而在机动阶段,过程噪声和扩展状态灵敏度都偏高,目标运动状态与模型CV3更为匹配.本文算法利用量测数据自适应修正模型转换概率,放大匹配模型的作用,抑制非匹配模型的作用,优化模型与目标运动模式的实时匹配.从图 5中结果可看出,本文算法在选取匹配模型时的模型概率更高.
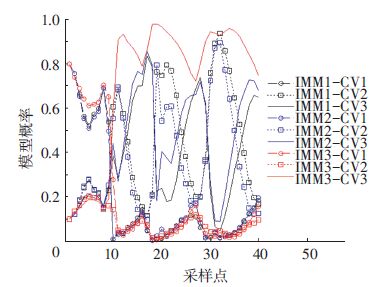
|
图 5 模型概率变化曲线 Figure 5 Curves of model transition probability |
表 1是3种方法的平均跟踪误差对比,可以看出本文所提出的群目标跟踪自适应IMM算法,滤波精度最高.
| 表 1 平均跟踪误差对比 Table 1 Comparison of average tracking error |
表 2给出了3种算法的平均单步运行时间比较,从表 2中结果可知,IMM1算法的运行时间最短,IMM2由于增加了变分贝叶斯迭代滤波环节,因此运行时间要高于IMM1算法,而本文算法自适应更新概率转换矩阵并且计算渐消因子,因而花费更对的时间,但是跟踪精度最高.
| 表 2 平均单步运行时间比较 Table 2 Comparison of average running time |
综合考虑算法的精度和时间,本文所提出的群目标跟踪自适应IMM算法,具有更好的性能.
5 结 论1) 引入带有多重次优渐消因子的强跟踪滤波算法修正群质心状态估计,基于新息计算和渐消记忆迭代过程自适应更新量测误差协方差矩阵.
2) 量测似然函数的构建纳入量测精度影响,优化扩展状态估计;通过quasi-Bayesian方法自适应更新模型转换概率,利用量测数据修正模型转换概率,优化模型与目标运动模式的实时匹配.仿真实验结果表明,与两种方法对比,本文方法具有较好的自适应跟踪能力.
| [1] |
KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices[J].
IEEE Transactions on Aerospace and Electronic Systems,2008, 44 (3) : 1042-1059.
DOI: 10.1109/TAES.2008.4655362 ( 0) 0)
|
| [2] |
MIHAYLOVA L, CARMI A Y, SEPTIER F. Overview of Bayesian sequential Monte Carlo methods for group and extended object tracking[J].
Digital Signal Processing,2014, 25 : 1-16.
DOI: 10.1016/j.dsp.2013.11.006 ( 0) 0)
|
| [3] |
MAHLER R. PHD filters of higher order in target number[J].
IEEE Transactions on Aerospace and Electronic Systems,2007, 43 (4) : 1523-1543.
DOI: 10.1109/TAES.2007.4441756 ( 0) 0)
|
| [4] |
连峰, 韩崇昭, 刘伟峰, 等. 基于SMC-PHDF的部分可分辨的群目标跟踪算法[J].
自动化学报,2010, 36 (5) : 731-741.
DOI: 10.3724/SP.J.1004.2010.00731 LIAN Feng, HAN Chongzhao, LIU Weifeng, et al. Tracking partly resolvable group targets using SMC-PHDF[J]. ACTA Automatica Sinica,2010, 36 (5) : 731-741. DOI: 10.3724/SP.J.1004.2010.00731 (  0) 0)
|
| [5] |
GRANSTRM K, LUNDQUIST C, ORGUNER U. Extended target tracking using a Gaussian mixture PHD filter[J].
IEEE Transactions on Aerospace and Electronic Systems,2012, 48 (4) : 3268-3285.
DOI: 10.1109/TAES.2012.6324703 ( 0) 0)
|
| [6] |
GRANSTRMK, ORGUNER U. A PHD filter for tracking multiple extended targets using random matrices[J].
IEEE Transactions on Signal Processing,2012, 60 (11) : 5657-5671.
DOI: 10.1109/TSP.2012.2212888 ( 0) 0)
|
| [7] |
GRANSTRM K, ORGUNER U. On spawning and combination of extended/group targets modeled with random matrices[J].
IEEE Transactions on Signal Processing,2013, 61 (3) : 678-692.
DOI: 10.1109/TSP.2012.2230171 ( 0) 0)
|
| [8] |
FELDMANN M, FRANKEN D, KOCH W. Tracking of extended objects and group targets using random matrices[J].
IEEE Transactions on Signal Processing,2011, 59 (4) : 1409-1420.
DOI: 10.1109/TSP.2010.2101064 ( 0) 0)
|
| [9] |
ORGUNER U. A variational measurement update for extended target tracking with random matrices[J].
IEEE Transactions on Signal Processing,2012, 60 (7) : 3827-3834.
DOI: 10.1109/TSP.2012.2192927 ( 0) 0)
|
| [10] |
FELDMANN M, KOCH W. Comments on "Bayesian approach to extended object and cluster tracking using random matrices"[J].
IEEE Transactions on Aerospace and Electronic Systems,2012, 48 (2) : 1687-1693.
DOI: 10.1109/TAES.2012.6178088 ( 0) 0)
|
| [11] |
LAN Jian, LI X R. Tracking of extended object or target group using random matrix-Part I: New model and approach[C]//Proceedings of the 15th Inter-national Conference on Information Fusion. Singapore: IEEE, 2012: 2177-2184.
( 0) 0)
|
| [12] |
周聪, 肖健. 改进强跟踪滤波算法及其在汽车状态估计中的应用[J].
自动化学报,2012, 38 (9) : 1520-1527.
DOI: 10.3724/SP.J.1004.2012.01520 ZHOU Cong, XIAO Jian. Improved strong track filter and its application to vehicle state estimation[J]. ACTA Automatica Sinica,2012, 38 (9) : 1520-1527. DOI: 10.3724/SP.J.1004.2012.01520 (  0) 0)
|
| [13] |
李振兴, 刘进忙, 李松, 等. 一种改进的群目标自适应跟踪算法[J].
哈尔滨工业大学学报,2014, 46 (10) : 117-123.
LI Zhenxing, LIU Jinmang, LI Song, et al. An improved adaptive tracking algorithm for group targets[J]. Journal of Harbin Institute of Technology,2014, 46 (10) : 117-123. (  0) 0)
|
| [14] |
DASHP K, HASAN S, PANIGRAHI B K. Adaptive complex unscented kalman filter for frequency estimation of time-varying signals[J].
IET Science, Measurement & Technology,2010, 4 (2) : 93-103.
DOI: 10.1049/iet-smt.2009.0003 ( 0) 0)
|
| [15] |
JILKOV V P, LI X R. Online Bayesian estimation of transition probabilities for markovian jump systems[J].
IEEE Transactions on Signal Processing,2004, 52 (6) : 1620-1630.
DOI: 10.1109/TSP.2004.827145 ( 0) 0)
|
| [16] |
郭志, 董春云, 蔡远利, 等. 时变转移概率IMM-SRCKF机动目标跟踪算法[J].
系统工程与电子技术,2015, 37 (1) : 24-30.
DOI: 10.3969/j.issn.1001-506X.2015.01.05 GUO Zhi, DONG Chunyun, CAI Yuanli, et al. Time-varying transition probability based IMM-SRCKF algorithm for maneuvering target tracking[J]. Systems Engineering and Electronics,2015, 37 (1) : 24-30. DOI: 10.3969/j.issn.1001-506X.2015.01.05 (  0) 0)
|
| [17] |
LI X R, JILKOV V P. Survey of maneuvering target tracking, part I: dynamic models[J].
IEEE Transactions on Aerospace and Electronic Systems,2003, 39 (4) : 1333-1364.
DOI: 10.1109/TAES.2003.1261132 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


