2. 哈尔滨工业大学 智能控制与系统研究所,哈尔滨150001
2. Research Institute of Intelligent Control and Systems, Harbin Institute of Technology, Harbin 150001, China
近年来针对输入受限问题出现了一系列的研究成果.文献[1-2]分别针对飞行控制中执行机构饱和的问题,采用解耦线性控制方法设计了飞控系统.文献[3]利用LMI区域法对抗饱和中D稳定问题进行了比较深入的研究.文献[4]提出了SISO系统的指令滤波反步控制方法,较好地解决系统状态与控制信号受限情况下的稳定控制问题.文献[5]利用多层神经网络逼近控制律的饱和特性,该控制策略能够有效地处理控制输入饱和受限的约束,在完成控制目标的同时,具有良好的过渡过程品质.文献[6]提出一种智能自适应滑模控制方法,利用神经网络来逼近补偿执行机构的饱和非线性.文献[7-8]利用双曲正切函数的光滑特性设计了反步控制器,并利用Nussbaum增益函数对饱和受限问题进行处理,其中系统的干扰利用神经网络或干扰观测器进行在线逼近.文献[9]利用模型预测控制自身优势,将输入饱和视为待优化目标函数的一种约束条件,在此基础上进行控制器的设计,取得了理想的效果.
以上研究成果在一定条件下均取得理想的效果,但是上述文献都是基于控制系统状态可直接测量这个假设基础之上的,对于控制系统中状态不可直接测量的情况少有研究.而在实际的控制系统中,状态不可直接测量的情况也是十分常见的,在这种情况下,需要一种基于状态观测器的控制方案.
反步法[10](backstepping)是解决非线性系统控制问题的一种行之有效的方法.其基本思想是将复杂的高阶非线性系统分解成一系列的低阶系统,通过由后至前反复为每个子系统设计Lyapunov函数和虚拟控制变量,直到完成整个控制系统的设计.传统的反步法在设计控制器的过程当中,虚拟控制变量反复求导,并且伴随着阶数的增加,计算量呈指数增长,也就是所谓的“计算膨胀”.文献[11]引入了动态面法,也即是将设计的辅助虚拟控制变量通过一阶积分滤波器,避免了求导这个复杂过程.
本文采用模糊逻辑系统(Fuzzy logic system,FLS)逼近系统中含有不确定参数和未知有界干扰的非线性函数,并由此来构建模糊状态观测器,利用具有光滑特性的双曲正切函数和Nussbaum增益函数处理系统中的输入饱和受限问题,并结合可规定跟踪误差面性能技术运用Backstepping法设计一种有效处理输入受限的输出反馈自适应控制方案.
1 问题描述考虑如下所示的一类SISO非线性系统:
| $\left\{ \begin{matrix} ~{{{\dot{x}}}_{i}}\left( t \right)={{f}_{i}}\left( {{x}_{i}}\left( t \right) \right)+{{g}_{i}}\left( {{x}_{i}}\left( t \right) \right){{x}_{i+1}}\left( t \right)+{{d}_{i}}\left( t \right), \\ ~{{{\dot{x}}}_{n}}\left( t \right)={{f}_{n}}({{x}_{n}}\left( t \right))+{{g}_{n}}({{x}_{n}}\left( t \right))u\left( v\left( t \right) \right)+{{d}_{n}}\left( t \right), \\ y\left( t \right)={{x}_{1}}\left( t \right). \\ \end{matrix} \right.$ | (1) |
式中:xi(t)=[x1(t),…,xi(t)]T∈Ri为系统的状态向量;u(v(t))∈R为系统受执行器饱和特性影响的输出;v(t)∈R为执行器的输入;y(t)∈R为系统的输出量;fi(·)、gi(·)分别为包含不确定参数的光滑非线性函数;di(t)为系统受到的外界干扰变量.为叙述方便,文中将xi(t)记为xi,其余变量作类似处理.
式(1)中的饱和受限函数具体表达形式如下:
| $~u\left( v \right)=sat\left( v \right)=sign\left( v \right)\cdot min\{|v|,{{u}_{M}}\}.$ |
式中uM为受限函数的界限值,这在一些工业控制应用中值是已知的.
考虑到双曲正切函数对饱和受限函数的近似逼近性质,上述所示的饱和受限函数等价于如下形式:
| $\begin{align} & sat\left( v \right)=h\left( v \right)+d\left( v \right), \\ & h\left( v \right)={{u}_{M}}\times tanh(\frac{v}{{{u}_{M}}})={{u}_{M}}\frac{{{e}^{v/{{u}_{M}}}}-{{e}^{-v/{{u}_{M}}}}}{{{e}^{v/{{u}_{M}}}}+{{e}^{-v/{{u}_{M}}}}}. \\ \end{align}$ |
式中:h(·)为双曲正切函数,d(v)=sat(v)-h(v)为有界函数,界限值表示为
| $~|~d\left( v \right)|=|sat\left( v \right)-h\left( v \right)|\le {{u}_{M}}(1-tanh\left( 1 \right)).$ |
则式(1)可变换为如下形式:
| $\left\{ \begin{matrix} {{{\dot{x}}}_{i}}=f_{i}^{'}\left( {{x}_{i}},{{x}_{i+1}} \right)+{{x}_{i+1}}, \\ {{{\dot{x}}}_{n}}=f_{i}^{'}\left( {{x}_{n}},u \right)+u, \\ y={{x}_{1}}. \\ \end{matrix} \right.$ |
式中:f′i(xi,xi+1)=fi(xi)+(gi(xi)-1)xi+1+di,(i=1,…,n-1);f′n(xn,u)=fn(xn)+(gn(xn)-1)u+dn;u=h(v);复合干扰dn=dn+gn(xn)d(v).
在本文中,假设只有输出y是可测量的.控制目标是设计模糊状态观测器和自适应控制方案使得系统能够稳定跟踪参考输入信号yr,闭环系统所有信号半全局一致有界且跟踪误差满足可规定的衰减动态性能.
为便于控制器的设计引入下列假设及引理.
假设1 对于含有不确定参数的非线性系统(1)外部未知干扰di有界,即di≤ω,但ω未知.
假设 2[7] 对于非线性系统(1),参考输入信号yr及其一阶导数存在且有界.
假设 3[12] 函数f′i(·)满足全局Lipschitz条件,即存在一系列的已知常数mi>0,对于X1,X2∈Ri,使得如下不等式成立:
| $|f_{i}^{'}\left( {{X}_{1}} \right)-f_{i}^{'}\left( {{X}_{2}} \right)|\le {{m}_{i}}\|{{X}_{1}}-{{X}_{2}}\|,$ |
式中‖·‖表示向量的2-norm.
定义 1 如果函数N(s)满足以下条件:
| $\underset{k\to \pm \infty }{\mathop{lim}}\,~sup\frac{1}{k}{{\int }^{k}}_{0}N\left( s \right)ds=+\infty ,\underset{k\to \pm \infty }{\mathop{lim}}\,inf\frac{1}{k}{{\int }^{k}}_{0}N\left( s \right)ds=-\infty ,$ |
则称函数N(s)为Nussbaum增益函数.
引理 1[7] 定义在[0,tf)上的光滑函数V(·)和χ(·),其中V(t)≥0,∀t∈[0,tf),N(χ)为Nussbaum函数.若满足以下不等式,则V(·)和χ(·)在[0,tf)上有界.
| $V\le V\left( 0 \right){{e}^{-Ct}}+\frac{M}{C}(1-{{e}^{-Ct}})+\frac{{{e}^{-Ct}}}{{{\gamma }_{\chi }}}{{\int }^{t}}_{0}\left( \zeta N\left( \chi \right)\dot{\chi }-\dot{\chi } \right){{e}^{-C\tau }}d\tau ,$ |
式中:C、M、γχ>0分别为常数,ζ为正变量.
2 可规定误差面性能定义误差面向量S(t)=[s1(t),…,sn(t)]T∈Rn,本文中可规定的性能是使系统误差面si(t)严格按照如下所示的范围衰减[13-14].
| $-{{\delta }_{i,1}}{{h}_{i}}\left( t \right)i\left( t \right)<{{\delta }_{i,2}}{{h}_{i}}\left( t \right),\left( \forall t\ge 0 \right).$ | (2) |
式中:设计参数δi,1,δi,2满足0<δi,1,δi,2≤1,函数hi(t)为有界且单调递减的光滑函数且具有如下特性:
| $\underset{t\to \infty }{\mathop{lim}}\,~{{h}_{i}}\left( t \right)={{h}_{i,\infty }},({{h}_{i,\infty }}>0),$ |
式中hi,∞为常数.
引入误差变换方程:
| ${{\vartheta }_{i}}\left( t \right)={{\Phi }_{i}}\left( \frac{{{s}_{i}}\left( t \right)}{{{h}_{i}}\left( t \right)} \right).$ |
式中:$\vartheta $i(t)为变换误差,Φi:(-δi,1,δi,2)→(-∞,∞)为严格递增的光滑函数.文中采用如下变换函数:
| $\begin{align} & {{\Phi }_{i}}\left( \frac{{{s}_{i}}\left( t \right)}{{{h}_{i}}\left( t \right)} \right)={{a}_{i}}ln\left( {{\delta }_{i,2}}\frac{{{s}_{i}}\left( t \right)}{{{h}_{i}}\left( t \right)}+{{\delta }_{i,1}}{{\delta }_{i,2}} \right)- \\ & {{a}_{i}}ln\left( {{\delta }_{i,1}}{{\delta }_{i,2}}-{{\delta }_{i,1}}\frac{{{s}_{i}}\left( t \right)}{{{h}_{i}}\left( t \right)} \right), \\ \end{align}$ |
式中ai>0为设计常数.
引理 2[15] 如果$\vartheta $i(t)有界,那么当t≥0时,误差面si(t)满足如式(2)所示的可规定衰减动态性能.
3 模糊状态观测器设计 3.1 模糊逻辑系统根据文献[16],带有模糊规则库(IF-THEN规则),乘积推理机,单值模糊器和中心平均解模糊器的模糊系统形式表示如下:
| $\text{ }y\left( x \right)=\frac{\sum\limits_{l=1}^{N}{{{{\bar{y}}}_{l}}}\prod\limits_{i=1}^{n}{{{\mu }_{{{F}^{l}}_{i}}}({{x}_{i}})}}{\sum\limits_{l=1}^{N}{(\prod\limits_{i=1}^{n}{{{\mu }_{{{F}^{l}}_{i}}}({{x}_{i}}))}}},$ |
式中${{{\bar{y}}}_{l}}=\underset{y\in R}{\mathop{max}}\,{{\mu }_{{{G}^{l}}}}(y).$
定义模糊基函数ξl如下:
| ${{\xi }_{l}}=\frac{\prod\limits_{i=1}^{n}{{{\mu }_{{{F}^{l}}_{i}}}\left( {{x}_{i}} \right)}}{\sum\limits_{l=1}^{N}{\left( \prod\limits_{i=1}^{n}{\left( \prod {{\mu }_{{{F}^{l}}_{i}}}\left( {{x}_{i}} \right) \right)} \right)}}.$ |
令θT=[y-1,y2,…,yN],ξT(x)=[ξ1(x),ξ2(x),…,ξN(x)],则模糊逻辑系统可以写成如下形式:
| $y\left( x \right)={{\theta }^{T}}\xi \left( x \right).$ |
定理 1 定义在紧集Ω上的连续函数y(x),对于∀ε>0,存在上述建立的模糊逻辑系统使得$\underset{x\in }{\mathop{sup}}\,|y\left( x \right)-{{\theta }^{T}}\xi \left( x \right)|\le \varepsilon $.
3.2 状态观测器由于文中只有输出y可测量,状态变量x2,…,xn不可直接测量,故需要设计一状态观测器对其进行观测.设计如下所示的模糊状态观测器[17]:
| $\left\{ \begin{matrix} {{{\dot{\hat{x}}}}_{i}}={{{\hat{x}}}_{i+1}}+{{k}_{i}}(y-{{{\hat{x}}}_{1}})+\hat{f}_{i}^{'}\left( {{{\hat{x}}}_{i+1,f}}|{{\theta }_{i}} \right), \\ {{{\dot{\hat{x}}}}_{n}}={{k}_{n}}(y-{{{\hat{x}}}_{1}})+\hat{f}_{n}^{'}({{{\hat{x}}}_{n}},{{u}_{f}}\text{ }\!\!|\!\!\text{ }{{\theta }_{n}})+u, \\ \hat{y}={{{\hat{x}}}_{1.}} \\ \end{matrix} \right.$ |
式中:${{{\dot{\hat{x}}}}_{i}}$为观测状态值;$\hat{f}_{i}^{'}\left( {{{\hat{x}}}_{i}},{{{\hat{x}}}_{i+1,f}}|{{\theta }_{i}} \right)=\theta _{i}^{T}{{\xi }_{i}}\left( {{{\hat{x}}}_{i}},{{{\hat{x}}}_{i+1,f}} \right)$为建立的模糊系统函数,${{{\hat{x}}}_{i,f}}$和uf为如下所示滤波信号值
| ${{{\hat{x}}}_{i,f}}={{H}_{L}}(s){{{\hat{x}}}_{i}},{{u}_{f}}={{H}_{L}}(s)u,$ |
式中HL(s)为Butterworth低通滤波器(Low-pass filter,LPF)[18].
令$A=\left[ \begin{array}{*{35}{l}} -{{k}_{1}} & {} & {} & {} \\ \vdots & {} & I & {} \\ -{{k}_{n}} & 0 & \cdots & 0 \\ \end{array} \right],K=\left[ \begin{matrix} {{k}_{1}} \\ \vdots \\ {{k}_{n}} \\ \end{matrix} \right],{{B}_{n}}=\left[ \begin{matrix} 0 \\ \vdots \\ 1 \\ \end{matrix} \right],{{B}_{i}}={{[0\cdots 1\cdots 0]}^{T}},C=[1\cdots 0\cdots 0]$.适当选择矩阵K,使得A为Hurwitz矩阵.则将建立的模糊状态观测器变换为
| $\left\{ \begin{matrix} {{{\dot{\hat{x}}}}_{i}}=A{{{\hat{x}}}_{^{n}}}+Ky+\sum\limits_{i+1}^{n}{{{B}_{i}}\hat{f}_{i}^{'}({{{\hat{x}}}_{i}},{{{\hat{x}}}_{i}}_{+1,f}|{{\theta }_{i}})+{{B}_{n}}u,} \\ {{{\hat{y}}}^{=}}C{{{\hat{x}}}_{n}}. \\ \end{matrix} \right.$ | (3) |
同理令${\hat{x}}$n+1,f=uf,系统(1)也可变换为如下形式:
| $\left\{ \begin{matrix} {{{\hat{x}}}_{n}}=A{{x}_{^{n}}}+Ky+\sum\limits_{i+1}^{n}{{{B}_{i}}\left[ \hat{f}_{i}^{'}({{{\hat{x}}}_{i}},{{{\hat{x}}}_{i}}_{+1,f})+\Delta {{f}_{i}} \right]+{{B}_{n}}u,} \\ {{y}^{=}}C{{x}_{n}}. \\ \end{matrix} \right.$ | (4) |
式中Δfi=f′i(xi,xi+1)-f′i(${\hat{x}}$i,${\hat{x}}$i+1,f).
3.3 观测器的稳定性分析令e=xn-${\hat{x}}$n为观测器误差,由式(3)、(4)得
| $\dot{e}=Ae+\sum\limits_{i=1}^{n}{{{B}_{i}}[{{\delta }_{i}}+\Delta {{f}_{i}}]},$ | (5) |
式中 δi=f′i(${\hat{x}}$i,${\hat{x}}$i+1,f)-${\hat{f}}$′i(${\hat{x}}$i,${\hat{x}}$i+1,fθi) 为模糊逼近误差.对于选定的Hurwitz矩阵A,给定一正定矩阵Q,存在一正定矩阵P使得如下所示的Raccati方程成立.
| $~{{A}^{T}}P+PA=-2Q.$ | (6) |
选择Lyapunov函数V0如下:
| ${{V}_{0}}=\frac{1}{2}{{e}^{T}}P\dot{e},$ |
则函数V0关于时间t的导数为
| $~{{{\dot{V}}}_{0}}=\frac{1}{2}{{{\dot{e}}}^{T}}Pe+\frac{1}{2}{{e}^{T}}P\dot{e}.$ | (7) |
将式(5)、(6)带入式(7),得
| ${{{\dot{V}}}_{0}}\le -{{\lambda }_{min}}\left( Q \right)\|e{{\|}^{2}}+{{e}^{T}}P\left( \delta +\Delta F \right),$ | (8) |
式中λmin(Q)为正定矩阵Q的最小特征值;δ=[δ1,…,δn]T,ΔF=[Δf1,…,Δfn]T.
假设 4 存在未知常数δi*,模糊系统的逼近误差δi满足不等式δi≤δi*.
假设 5 执行器具有低通特性,即使得${\hat{x}}$i,f=HL(s)${\hat{x}}$i≈${\hat{x}}$i.故存在一常数βi,0,使得不等式${\hat{x}}$i-${\hat{x}}$i,f≤βi,0成立.
根据Young不等式和假设3~5,可得:
| $\begin{align} & {{e}^{T}}P\delta \le \frac{1}{2}\|e{{\|}^{2}}+\frac{1}{2}\|P{{\|}^{2}}\|\delta {{\|}^{2}}\le \\ & \frac{1}{2}\|e{{\|}^{2}}+\frac{1}{2}\|P{{\|}^{2}}\|\delta {{\|}^{2}}, \\ \end{align}$ | (9) |
| $\begin{align} & {{e}^{T}}P\Delta F\le \frac{1}{2}\|e{{\|}^{2}}+\frac{1}{2}\|P{{\|}^{2}}\|\Delta F{{\|}^{2}}\le \\ & \frac{1}{2}\|e{{\|}^{2}}+\frac{1}{2}\|P{{\|}^{2}}\sum\limits_{i=1}^{n}{|\Delta {{f}_{i}}{{|}^{2}}\le } \\ & \frac{1}{2}\|e{{\|}^{2}}+\text{ }\|P{{\|}^{2}}\sum\limits_{i=1}^{n}{{{m}^{2}}_{i}\|e{{\|}^{2}}+} \\ & \|P{{\|}^{2}}{{\sum }^{n}}_{i=1}{{m}^{2}}_{i}{{\beta }^{2}}_{i,0}, \\ \end{align}$ | (10) |
式中δ*=[δ*1,…,δ*n]T.
联立式(8)~(10),得到:
| ${{{\dot{V}}}_{0}}\le -r\|e{{\|}^{2}}+\vartheta .$ | (11) |
式中:$\begin{align} & r={{\lambda }_{min}}\left( Q \right)-1-\|P{{\|}^{2}}\sum\limits_{i=1}^{n}{{{m}^{2}}_{i}};\wp =\frac{1}{2}\|P{{\|}^{2}}\cdot \\ & (\|{{\delta }^{*}}{{\|}^{2}}+2~\sum\limits_{i=1}^{n}{{{m}^{2}}_{i}{{\beta }^{2}}_{i,0}}). \\ \end{align}$.
选择合适的参数使得r>0,能够使得观测器稳定,即是当误差‖e‖>$\sqrt{\vartheta /r}$时,观测误差收敛.但需要注意的是观测误差只能实现实用稳定,而无法实现渐进稳定.
4 控制器设计及稳定性分析本文将结合反步法和动态面法对控制系统进行设计.
Step 1 由于系统中状态不可测量,系统中的反馈控制律不能直接利用其给出.模糊状态观测器设计中已经证明了建立的模糊状态观测器观测误差是收敛的,故观测器状态可以用于系统反馈控制律的设计,这与针对实际系统进行设计是等价的,因此定义如下:
| ${{z}_{1}}=y-{{y}_{r}},{{z}_{i}}={{{\hat{x}}}_{^{i}}}-{{a}_{i-1}},$ |
式中αi-1为虚拟控制变量,具体形式由下文给出.
为了便于控制的设计,本文中只要求系统跟踪参考信号的误差满足一定的可规定性能.
令s1=z1,则误差变换函数$\vartheta $1关于时间t的导数为
| $\begin{align} & {{{\dot{\vartheta }}}_{1}}={{p}_{1}}({{{\dot{s}}}_{1}}-({{{\dot{h}}}_{1}}/{{h}_{1}}){{s}_{1}})={{p}_{1}}(\dot{x}1-\dot{y}r-(\dot{h}1/h1)s1)= \\ & p1({{{\hat{x}}}_{^{2}}}+e2+f{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}})+\Delta {{f}_{1}}-\dot{y}r-({{{\dot{h}}}_{1}}/{{h}_{1}}){{s}_{1}})= \\ & {{p}_{1}}(z2+{{\alpha }_{1}}+{{e}_{2}}+f{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{^{2}}},f)+\Delta {{f}_{1}}-{{{\dot{y}}}_{r}}-({{{\dot{h}}}_{1}}/{{h}_{1}})s1), \\ \end{align}$ | (12) |
式中p1=a1((1/(s1+δ1,1h1))-(1/(s1-δ1,2h1))).
在上述模糊状态观测器中建立的模糊系统$\hat{f}_{i}^{'}$(${\hat{x}}$1,${\hat{x}}$2,fθ1)=θ1Tξ1(${\hat{x}}$1,${\hat{x}}$2,f),定义参数向量θ1的最优估计值为
| $\theta _{1}^{*}=arg\underset{{{\theta }_{1}}\in {{\Omega }_{1}}}{\mathop{min}}\,\{\underset{x\in R}{\mathop{sup}}\,|f{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}}){{\theta }_{1}})-f{{'}_{i}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}})\},$ |
定义模糊系统最小逼近误差ε1为
| ${{\varepsilon }_{1}}=f{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}})-\hat{f}{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}}|\theta _{1}^{*}).$ | (13) |
假设 6 存在未知常数εi*,模糊系统的逼近误差εi满足不等式εi≤εi*.
需要说明的是,根据文中所建立的Lyapunov函数导数性质和文中采用投影法确定参数的自适应律,可以保证参数有界,进而根据紧集上连续函数的性质,假设4和假设6成立是可以得到保证的.
将式(13)带入式(12),得
| ${{{\dot{\vartheta }}}_{1}}={{p}_{1}}({{z}_{2}}+{{\alpha }_{1}}+{{e}_{2}}+{{\theta }^{T}}_{1}{{\xi }_{1}}+{{{\tilde{\theta }}}^{T}}_{1}{{\xi }_{1}}+{{\varepsilon }_{1}}+\Delta f-{{{\dot{y}}}_{r}}-({{{\dot{h}}}_{1}}/{{h}_{1}}){{s}_{1}}).$ |
为防止虚拟控制变量的反复求导而引起的“计算膨胀”问题,结合动态面法,引入辅助虚拟控制变量α1,并将该变量通过如下所示的一阶滤波器为
| ${{\tau }_{1}}{{{\dot{\alpha }}}_{1}}+{{\alpha }_{1}}={{{\bar{\alpha }}}_{1}},{{\alpha }_{1}}\left( 0 \right)={{{\bar{\alpha }}}_{1}}\left( 0 \right).$ |
令κ1=α1-α-1,且对其求导可得:
| ${{{\dot{\kappa }}}_{1}}={{{\dot{\alpha }}}_{1}}-{{{\dot{\bar{\alpha }}}}_{1}}=-\frac{{{\alpha }_{1}}-{{{\bar{\alpha }}}_{1}}}{{{\tau }_{1}}}-{{{\dot{\bar{\alpha }}}}_{1}}=-\frac{{{\kappa }_{1}}}{{{\tau }_{1}}}-{{{\dot{\bar{\alpha }}}}_{1}}.$ |
由文献[11]可知,存在某一区间的连续函数N1(·)使得不等式-${\dot{\bar{\alpha }}}$1≤N1(·),并根据连续函数的性质得
| ${{{\dot{\kappa }}}_{1}}\le -({{\kappa }_{1}}/{{\tau }_{1}})+{{{\bar{N}}}_{1}},$ |
式中N1=max{N1(·)}.
选择Lyapunov函数V1为
| ${{V}_{1}}=\frac{1}{2}{{\vartheta }^{2}}_{1}+\frac{1}{2}{{\kappa }^{2}}_{1}+\frac{1}{2{{r}_{1}}}\tilde{\theta }_{1}^{T}{{{\tilde{\theta }}}_{1}}+\frac{1}{2{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}{{{\tilde{\varepsilon }}}_{1}}.$ |
式中:$\tilde{\theta }{{~}_{1}}=\theta _{1}^{*}-{{\theta }_{1}};=\varepsilon _{1}^{*}-{{{\hat{\varepsilon }}}_{^{1}}}$,其中${{{\hat{\varepsilon }}}_{^{1}}}$为ε*1的估计值.
则函数关于时间t的导数为
| $\begin{align} & {{{\dot{V}}}_{1}}={{\vartheta }_{1}}{{{\dot{\vartheta }}}_{1}}+\text{k}1\text{\dot{k}}1-\frac{1}{{{r}_{1}}}\tilde{\theta }_{1}^{T}{{\theta }_{1}}-\frac{1}{{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}{{{\dot{\hat{\varepsilon }}}}_{1}}\le \\ & {{\vartheta }_{1}}{{p}_{1}}({{z}_{2}}+{{{\bar{\alpha }}}_{1}}+\theta _{1}^{T}{{\xi }_{1}}+\tilde{\theta }_{1}^{T}{{\xi }_{1}}-{{{\dot{y}}}_{r}}-\frac{{{{\dot{h}}}_{1}}}{{{h}_{1}}}{{s}_{1}})+ \\ & {{\vartheta }_{1}}{{p}_{1}}({{k}_{1}}+{{e}_{2}}+\Delta {{f}_{1}})+\text{ }\!\!|\!\!\text{ }{{\vartheta }_{1}}{{p}_{1}}|\varepsilon _{1}^{*}+ \\ & {{k}_{1}}(-\frac{{{k}_{1}}}{{{\tau }_{1}}}+{{{\bar{N}}}_{1}})-\frac{1}{{{r}_{1}}}\tilde{\theta }_{1}^{T}-\frac{1}{{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}{{{\dot{\hat{\varepsilon }}}}_{1}}. \\ \end{align}$ | (14) |
定理 2[20] 对于∀λ>0,|x|-x tanh($\frac{x}{{\rlap{--} \lambda }}$≤0.278 5 λ-
=λ′成立.
根据定理2,式(14)可变换为
| $\begin{align} & {{{\dot{V}}}_{1}}\le {{\vartheta }_{1}}{{p}_{1}}({{z}_{2}}+{{{\bar{\alpha }}}_{1}}+{{\theta }^{T}}_{1}{{\xi }_{1}}+{{{\tilde{\theta }}}^{T}}_{1}{{\xi }_{1}}-{{{\dot{y}}}_{r}}-\frac{{{{\dot{h}}}_{1}}}{{{h}_{1}}}{{s}_{1}})+{{\vartheta }_{1}}{{p}_{1}}({{\kappa }_{1}}+ \\ & {{e}_{2}}+\Delta {{f}_{1}})+|{{\vartheta }_{1}}{{p}_{1}}|\varepsilon _{1}^{*}-{{\vartheta }_{1}}{{p}_{1}}\varepsilon _{1}^{*}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}})+ \\ & {{\vartheta }_{1}}{{p}_{1}}\varepsilon _{1}^{*}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}})+{{\text{k}}_{1}}(-\frac{{{k}_{1}}}{{{\tau }_{1}}}+{{{\bar{N}}}_{1}})-\frac{1}{{{r}_{1}}}\tilde{\theta }_{1}^{T}{{{\dot{\theta }}}_{1}}- \\ & \frac{1}{{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}{{{\dot{\hat{\varepsilon }}}}_{1}}\le {{\vartheta }_{1}}{{p}_{1}}({{z}_{2}}+{{{\bar{\alpha }}}_{1}}+{{\theta }^{T}}_{1}{{\xi }_{1}}-{{{\dot{y}}}_{r}}-\frac{{{{\dot{h}}}_{1}}}{{{h}_{1}}}{{s}_{1}}+ \\ & {{{\hat{\varepsilon }}}_{1}}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}}))+{{\vartheta }_{1}}{{p}_{1}}({{k}_{1}}+{{e}_{2}}+\Delta {{f}_{1}})+\varepsilon _{1}^{*}\text{ }\!\!'\!\!\text{ }+ \\ & {{\text{k}}_{1}}(-\frac{{{k}_{1}}}{{{\tau }_{1}}}+{{{\bar{N}}}_{1}})+\frac{1}{{{r}_{1}}}\tilde{\theta }_{1}^{T}({{r}_{1}}{{\vartheta }_{1}}{{p}_{1}}-{{{\dot{\theta }}}_{1}})+ \\ & \frac{1}{{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}({{{\bar{r}}}_{1}}{{\vartheta }_{1}}{{p}_{1}}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}})-{{{\dot{\hat{\varepsilon }}}}_{1}}) \\ \end{align}$ | (15) |
同时根据Young不等式,得
| ${{\vartheta }_{1}}{{p}_{1}}\Delta {{f}_{1}}\le \frac{1}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+\frac{1}{2}\Delta k_{1}^{2},$ | (16) |
| ${{\vartheta }_{1}}{{p}_{1}}{{e}_{2}}\le \frac{1}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+\frac{1}{2}{{e}^{2}}_{2}\le \frac{1}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+\frac{1}{2}\|e{{\|}^{2}},$ | (17) |
| $\begin{align} & {{\vartheta }_{1}}{{p}_{1}}\Delta {{f}_{1}}\le \frac{1}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+\frac{1}{2}|\Delta {{f}_{1}}{{|}^{2}}\le \\ & \frac{1}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+{{m}^{2}}_{2}\|e{{\|}^{2}}+{{m}^{2}}_{2}{{\beta }^{2}}_{2,0}. \\ \end{align}$ | (18) |
将式(16)~(18)带入式(15),得
| $\begin{align} & {{{\dot{V}}}_{1}}\le {{\vartheta }_{1}}{{p}_{1}}({{z}_{2}}+{{{\bar{\alpha }}}_{1}}+\theta _{1}^{T}{{\xi }_{1}}-{{{\dot{y}}}_{r}}-\frac{{{{\dot{h}}}_{1}}}{{{h}_{1}}}{{s}_{1}}+{{{\hat{\varepsilon }}}_{1}}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}}))+ \\ & {{M}_{1}}-(\frac{1}{\tau }-1)k_{1}^{2}+\frac{3}{2}{{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+\frac{1}{{{r}_{1}}}\tilde{\theta }_{1}^{T}({{r}_{1}}{{\vartheta }_{1}}{{p}_{1}}{{\xi }_{1}}- \\ & {{{\dot{\theta }}}_{1}})+\frac{1}{{{{\bar{r}}}_{1}}}\tilde{\varepsilon }_{1}^{T}\left( {{{\bar{r}}}_{1}}{{\vartheta }_{1}}{{p}_{1}}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}}){{{\dot{\hat{\varepsilon }}}}_{1}} \right), \\ \end{align} $ | (19) |
式中${M_1} = \frac{1}{2}{\left( {{{\bar N}_1}} \right)^2} + \left( {{m^2}_2 + \frac{1}{2}} \right){\left\| e \right\|^2} + {m^2}_2{\beta ^2}_{2,0} + \varepsilon _1^*\lambda '.$.
选取虚拟控制变量和参数的自适应律分别为
| ${{\bar \alpha }_1} = - {c_1}{\vartheta _1}{p_1} - \theta _1^T{\xi _1} + {{\dot y}_r} + \frac{{{{\dot h}_1}}}{{{h_1}}}{s_1} - {{\hat \varepsilon }_1}tanh(\frac{{{\vartheta _1}{p_1}}}{{\rlap{-} \lambda }}),$ | (20) |
| $\begin{gathered} {{\dot \theta }_1} = proj\left( {{r_1}{\vartheta _1}{p_1}{\xi _1}} \right) = \hfill \\ \left\{ {\begin{array}{*{20}{c}} \begin{gathered} {r_1}{\vartheta _1}{p_1}{\xi _1},if\left\| {{\theta _1}} \right\| < {M_1} \hfill \\ or\left( {\left\| {{\theta _1}} \right\| = {M_1}} \right) \cap \left( {{r_1}{\vartheta _1}{p_1}\theta _1^T{\xi _1} > 0} \right); \hfill \\ \end{gathered} \\ {{r_1}{\vartheta _1}{p_1}({\xi _1} - \frac{{\tilde \theta _1^T{\theta _1}\theta _1^T}}{{{{\left\| {{\theta _1}} \right\|}^2}}}{\xi _1}),else.} \end{array}} \right. \hfill \\ \end{gathered} $ | (21) |
| $\dot{\hat{\varepsilon }}={{\bar{r}}_{1}}{{\vartheta }_{1}}{{p}_{1}}tanh(\frac{{{\vartheta }_{1}}{{p}_{1}}}{{{\rlap{-} \lambda _1}}}).$ | (22) |
需要说明的是,式(21)中为采用投影法[16]确定参数的自适应律,式中M1为设定的边界值,根据文献[16]可知,参数θ1满足‖θ1‖≤M1且不等式${{\tilde \theta }^T}_1(r{\vartheta _1}{p_1}{\xi _1} - {{\dot \theta }_1}) \leqslant 0$成立.
将式(20)~(22)带入到式(19)中,得
| ${{{\dot{V}}}_{1}}\le -({{c}_{1}}-\frac{3}{2}){{\left( {{\vartheta }_{1}}{{p}_{1}} \right)}^{2}}+{{\vartheta }_{1}}{{p}_{1}}{{z}_{2}}+{{M}_{1}}-(\frac{1}{{{\tau }_{1}}}-1){{\kappa }^{2}}_{1}.$ | (23) |
Step i(2≤i<n) zi关于时间t的导数为
| $\begin{align} & {{{\dot{z}}}_{i}}=\dot{\hat{x}}i-{{{\dot{\alpha }}}_{i-1}}={{{\hat{x}}}_{i+1}}+{{k}_{i}}{{e}_{1}}+\theta _{i}^{T}{{\xi }_{i}}-{{{\dot{\alpha }}}_{i-1}}= \\ & {{z}_{i+1}}+{{\alpha }_{i}}+\theta _{i}^{T}{{\xi }_{i}}-{{{\dot{\alpha }}}_{i-1}}+\tilde{\theta }_{i}^{T}{{\xi }_{i}}+{{w}_{i}}, \\ \end{align}$ | (24) |
式中wi=εi-δi为模糊系统复合误差.
选取辅助虚拟控制变量αi,并通过如下所示的一阶滤波器为
| ${{\tau }_{i}}{{{\dot{\alpha }}}_{i}}+{{\alpha }_{i}}={{{\bar{\alpha }}}_{i}},{{\alpha }_{i}}\left( 0 \right)={{{\bar{\alpha }}}_{i}}\left( 0 \right).$ |
滤波误差κi=αi-αi,对其求导可得
| ${{{\dot{\varepsilon }}}_{i}}={{{\dot{\alpha }}}_{i}}-{{{\dot{\bar{\alpha }}}}_{i}}=\frac{{{{\bar{\alpha }}}_{i}}-{{\alpha }_{i}}}{{{\tau }_{i}}}-{{{\dot{\bar{\alpha }}}}_{i}}\le -\frac{{{\varepsilon }_{i}}}{{{\tau }_{i}}}+{{{\bar{N}}}_{i}}.$ | (25) |
选择Lyapunov函数Vi为
| $~{{V}_{i}}=\frac{1}{2}{{z}^{2}}_{i}+\frac{1}{2}{{\kappa }^{2}}_{i}+\frac{1}{2{{r}_{i}}}\tilde{\theta }_{i}^{T}{{{\tilde{\theta }}}_{i}}+\frac{1}{2{{{\bar{r}}}_{i}}}\tilde{w}_{i}^{T}{{{\tilde{w}}}_{i}},$ | (26) |
式中$\tilde{w}{{~}_{i}}=w_{i}^{*}-{{{\hat{w}}}^{i}}.$
则函数Vi关于时间t的导数,并将式(24)、(25)带入式(26)得
| $\begin{align} & {{{\dot{V}}}_{i}}={{z}_{i}}{{{\dot{z}}}_{i}}+{{k}_{i}}{{{\text{\dot{k}}}}_{i}}-\frac{1}{{{r}_{i}}}\tilde{\theta }_{i}^{T}{{{\dot{\theta }}}_{i}}\frac{1}{{{{\bar{r}}}_{i}}}\tilde{w}_{i}^{T}{{{\dot{\hat{w}}}}_{i}}\le \\ & {{z}_{i}}[{{z}_{i}}_{+1}+{{{\bar{\alpha }}}_{i}}+{{\text{k}}_{i}}+{{k}_{i}}{{e}_{1}}+\theta _{i}^{T}{{\xi }_{i}}-{{{\dot{\alpha }}}_{i-1}}+\tilde{\theta }_{i}^{T}{{\xi }_{i}}]+ \\ & |{{z}_{i}}|w_{i}^{*}-{{z}_{i}}w_{i}^{*}tanh(\frac{zi}{{{\rlap{-} \lambda _i}}})+{{z}_{i}}w_{i}^{*}tanh(\frac{zi}{{{\rlap{-} \lambda _i}}})-\frac{k_{i}^{2}}{{{\tau }_{i}}}+ \\ & {{{\bar{N}}}_{i}}{{k}_{i}}-\frac{1}{{{r}_{i}}}\theta _{i}^{T}\tilde{w}_{i}^{T}i{{{\dot{\hat{w}}}}_{i}}. \\ \end{align} $ | (27) |
根据定理2和Young不等式,式(27)可化为
| $\begin{align} & {{{\dot{V}}}_{i}}\le {{z}_{i}}[{{z}_{i+1}}+{{{\bar{\alpha }}}_{i}}+{{k}_{i}}{{e}_{1}}+\theta _{i}^{T}{{\xi }_{i}}-{{{\dot{\alpha }}}_{i-1}}+{{{\hat{w}}}^{i}}tanh(\frac{{{z}_{i}}}{{{\rlap{-} \lambda _i}}})]+ \\ & \frac{1}{2}{{z}^{2}}_{i}+\frac{1}{2}\left( {{{\bar{N}}}_{i}} \right)2+{{w}^{*}}_{i}{{'}_{i}}\left( \frac{1}{{{\tau }_{i}}}-1 \right){{\kappa }^{2}}_{i}+ \\ & \frac{1}{{{r}_{i}}}\tilde{\theta }_{i}^{T}({{r}_{i}}{{z}_{i}}{{\xi }_{i}}-{{{\dot{\theta }}}_{i}})+\frac{1}{{{{\bar{r}}}_{i}}}\bar{\varepsilon }_{i}^{T}\left( {{{\bar{r}}}_{i}}{{z}_{i}}tanh\left( \frac{{{z}_{i}}}{{{\rlap{-} \lambda _i}}} \right)-{{{\dot{\hat{w}}}}_{i}} \right). \\ \end{align}$ | (28) |
选取辅助虚拟控制变量αi和参数的自适应律如下:
| ${{\bar \alpha }_i} = - {c_i}{z_i} - {z_{i - 1}} - {k_i}{e_1} - \theta _i^T{\xi _i} + {\alpha _{i - 1}} - {{\hat w}_i}tanh(\frac{{{z_i}}}{{{{\rlap{-} \lambda }_i}}}),$ | (29) |
| ${{\dot \theta }_i} = proj({r_i}{z_i}{\xi _i}),$ | (30) |
| ${{\dot{\hat{w}}}_{i}}={{\bar{r}}_{i}}{{z}_{i}}tanh(\frac{{{z}_{i}}}{{{\rlap{-} \lambda _i}}}).$ | (31) |
将式(29)~(31)带入到式(28)中,得
| $\eqalign{ & {{\dot V}_i} \leqslant - \left( {{c_i} - \frac{1}{2}} \right){z^2}_i - {z_i}{z_{i - 1}} + {z_i}{z_{i + 1}} + \frac{1}{2}{\left( {{{\bar N}_i}} \right)^2} + \cr & {w^*}_i\rlap{--} \lambda {'_i} - \left( {\frac{1}{{{\tau _i}}} - 1} \right){\kappa ^2}_i. \cr} $ | (32) |
当i=2时,选取辅助虚拟控制变量α2如下:
| ${{\bar \alpha }_2} = - {c_2}{z_2} - {\vartheta _1}{p_1} - {k_2}{e_1} - \theta _2^T{\xi _2} + {{\dot \alpha }_1} - {{\hat w}_{^2}}tanh(z2/{{\rlap{-} \lambda }_2}).$ | (33) |
参数的自适应律如式(30)、(31)所示,并将式(33)带入式(28)中,得
| $\eqalign{ & {{\dot V}_2} \leqslant - \left( {{c_2} - \frac{1}{2}} \right){z^2}_2 - {\vartheta _1}{p_1}{z_2} + {z_2}{z_3} + \frac{1}{2}{\left( {{{\bar N}_2}} \right)^2} + \cr & {w^*}_2{{\rlap{--} \lambda }^\prime }_2 - \left( {\frac{1}{{{\tau _2}}} - 1} \right){\kappa ^2}_2. \cr} $ | (34) |
Step n 定义:
| ${z_{n + 1}} = h\left( v \right) - {\alpha _n}.$ |
zn关于时间t的导数为
| ${{\dot{z}}_{n}}={{\dot{\hat{x}}}_{n}}-{{\dot{\alpha }}_{n-1}}={{k}_{n}}{{e}_{1}}+\theta _{n}^{T}{{\xi }_{n}}+{{z}_{n+1}}+{{\alpha }_{n}}-{{\dot{\alpha }}_{n-1}}.$ | (35) |
选取辅助虚拟控制变量αn,并通过如下所示的一阶滤波器为
| ${\tau _n}{{\dot \alpha }_n} + {\alpha _n} = {{\bar \alpha }_n},{\alpha _n}\left( 0 \right) = {{\bar \alpha }_n}(0)$ |
滤波误差κn=αn-αn,并对其求导可得
| $\kappa {{\cdot }_{n}}={{\dot{\alpha }}_{n}}-{{\dot{\bar{\alpha }}}_{n}}=\frac{{{{\bar{\alpha }}}_{n}}-{{\alpha }_{n}}}{{{\tau }_{n}}}-{{\dot{\bar{\alpha }}}_{n}}\le -\frac{{{\kappa }_{n}}}{{{\tau }_{n}}}+{{\bar{N}}_{n}}.$ | (36) |
选择Lyapunov函数Vn为
| ${{V}_{n}}=\frac{1}{2}{{z}^{2}}_{n}+\frac{1}{2}{{\kappa }^{2}}_{n}+\frac{1}{2{{r}_{n}}}\tilde{\theta }_{n}^{T}{{\tilde{\theta }}_{n}}+\frac{1}{2{{{\bar{r}}}_{n}}}\tilde{w}_{n}^{T}{{\tilde{w}}_{n}},$ | (37) |
则函数Vn关于时间t的导数,并将式(35)、(36)带入式(37)得
| $\begin{align} & {{{\dot{V}}}_{n}}={{z}_{n}}{{{\dot{z}}}_{n}}+{{\text{k}}_{n}}{{{\text{\dot{k}}}}_{n}}-\frac{1}{{{r}_{n}}}\tilde{\theta }_{n}^{T}{{{\dot{\theta }}}_{n}}-\frac{1}{{{{\bar{r}}}_{n}}}\tilde{w}_{n}^{T}\dot{\hat{w}}\le {{z}_{n}}[{{k}_{n}}{{e}_{1}}+\theta _{n}^{T}{{\xi }_{n}}+ \\ & {{z}_{n+1}}+{{{\bar{\alpha }}}_{n}}-{{{\dot{\alpha }}}_{n-1}}]+{{z}_{n}}{{\text{k}}_{n}}+|{{z}_{n}}|w_{n}^{*}+{{\text{k}}_{n}}(-\frac{{{\text{k}}_{n}}}{{{\tau }_{n}}}+{{{\bar{N}}}_{n}})+\frac{1}{{{r}_{n}}}\tilde{\theta }_{n}^{T}({{r}_{n}}{{z}_{n}}{{\xi }_{n}}-{{{\dot{\theta }}}_{n}})-\frac{1}{{{{\bar{r}}}_{i}}}\tilde{w}_{i}^{T}{{{\dot{\hat{w}}}}_{i}}. \\ \end{align} $ | (38) |
根据定理2和Young不等式,式(38)可转化为
| $\begin{align} & {{{\dot{V}}}_{n}}\le {{z}_{n}}[{{k}_{n}}{{e}_{1}}+\theta _{n}^{T}{{\xi }_{n}}+{{z}_{n+1}}+\bar{\alpha }-{{{\dot{\alpha }}}_{n-1}}]+{{z}_{n}}{{\kappa }_{n}}+|\text{ }{{z}_{n}}|{{w}^{*}}_{n} \\ & -{{z}_{n}}{{w}^{*}}_{n}tanh\left( \frac{{{z}_{n}}}{{{\rlap{-} \lambda _n}}} \right)+{{z}_{n}}{{w}^{*}}_{n}tanh\left( \frac{{{z}_{n}}}{{{\rlap{-} \lambda _n}}} \right)+{{\kappa }_{n}}\left( -\frac{{{\kappa }_{n}}}{{{\tau }_{n}}}+{{{\bar{N}}}_{n}} \right)+ \\ & \frac{1}{{{r}_{n}}}\tilde{\theta }_{n}^{T}({{r}_{n}}{{z}_{n}}{{\xi }_{n}}-{{{\dot{\theta }}}_{n}})-\frac{1}{{{{\bar{r}}}_{i}}}\tilde{w}_{i}^{T}{{{\dot{\hat{w}}}}_{i}}\le {{z}_{n}}[{{k}_{n}}{{e}_{1}}+\theta _{n}^{T}{{\xi }_{n}}+ \\ & {{z}_{n+1}}+{{{\bar{\alpha }}}_{n}}-{{{\dot{\alpha }}}_{n-1}}+{{{\hat{w}}}_{n}}tanh(\frac{{{z}_{n}}}{{{\rlap{-} \lambda _n}}})]+w_{n}^{*}{{'}_{n}}+\frac{1}{2}z_{n}^{2} \\ & -\left( \frac{1}{{{\tau }_{n}}}-1 \right){{\kappa }^{2}}_{n}+\frac{1}{2}\left( {{{\bar{N}}}_{n}} \right)2+\frac{1}{{{r}_{n}}}\tilde{\theta }_{n}^{T}\left( {{r}_{n}}{{z}_{n}}{{\xi }_{n}}-{{{\dot{\theta }}}_{n}} \right)+ \\ & \frac{1}{{{{\bar{r}}}_{n}}}\tilde{w}_{n}^{T}[{{{\bar{r}}}_{n}}{{z}_{n}}tanh(\frac{{{z}_{n}}}{{{\rlap{-} \lambda _n}}})-{{{\dot{\hat{w}}}}_{n}}]. \\ \end{align}$ | (39) |
选取辅助虚拟控制变量和参数自适应律如下:
| ${{\bar \alpha }_n} = - {c_n}{z_n} - {z_{n - 1}} - {k_n}{e_1} - \theta _n^T{\xi _n} + {{\dot \alpha }_{n - 1}} - {{\dot w}_{^n}}tanh(\frac{{{z_n}}}{{{{\rlap{-} \lambda }_n}}}),$ | (40) |
| ${{\dot \theta }_n} = proj\left( {{r_n}{z_n}{\xi _n}} \right),$ | (41) |
| ${{\dot w}_n} = {{\bar r}_n}{z_n}tanh(\frac{{{z_n}}}{{{{\rlap{-} \lambda }_n}}}).$ | (42) |
将式(40)~(42)带入到式(39)中,整理合并可得
| $\eqalign{ & {{\dot V}_n} \leqslant - \left( {{c_n} - \frac{1}{2}} \right){z^2}_n - {z_n}{z_{n - 1}} + {z_n}{z_{n + 1}} + \frac{1}{2}{\left( {{{\bar N}_n}} \right)^2} + \cr & {w^*}_n{{\rlap{--} \lambda }^\prime }_n - \left( {\frac{1}{{{\tau _n} - 1}}} \right){\kappa ^2}_n. \cr} $ | (43) |
Step n+1 定义:
| $\dot v = - cv + \omega ,$ | (44) |
| $\omega = N\left( \chi \right)\bar \omega $ | (45) |
| $\bar \omega = - {c_{n + 1}}{z_{n + 1}} - {z_n} + \zeta cv + {{\dot \alpha }_n},$ | (46) |
| $\dot \chi = {\gamma _\chi }\bar \omega {z_{n + 1}}.$ | (47) |
式中:c>0,γχ>0为设计参数;N(χ)=χ2cos(χ);cn+1>0;变量$\zeta = \frac{{\partial h\left( v \right)}}{{\partial v}} = \frac{4}{{{{({e^{v/{u_M}}} + {e^{ - v/{u_M}}})}^2}}} > 0.$
中间变量zn+1关于时间t的导数为
| $\eqalign{ & {{\dot z}_{n + 1}} = \frac{{\partial h(v)}}{{\partial v}}\dot v - {{\dot \alpha }_n} = \zeta \left( { - cv + \omega } \right) - {{\dot \alpha }_n} = \cr & - \zeta cv + \left( {\zeta N\left( \chi \right) - 1} \right)\bar \omega - {{\dot \alpha }_n} + \bar \omega = \cr & - {c_{n + 1}}{z_{n + 1}} - {z_n} + \left( {\zeta N\left( \chi \right) - 1} \right)\bar \omega . \cr} $ |
选择Lyapunov函数Vn+1为
| ${V_{n + 1}} = \frac{1}{2}{z_{n + 1}}^2,$ |
则函数Vn+1关于时间t的导数为
| ${{\dot V}_{n + 1}} = {z_{n + 1}}{{\dot z}_{n + 1}} = - {c_{n + 1}}{z^2}_n - {z_n}{z_{n + 1}} + \frac{1}{{{\gamma _\chi }}}\left( {\zeta N\left( \chi \right) - 1} \right)\dot \chi .$ | (48) |
考虑到闭环系统所有信号的有界性,选择Lyapunov函数Vsum如下:
| $\eqalign{ & {V_{sum}} = {V_0} + \frac{1}{2}{\vartheta ^2}_1 + \sum\limits_{i = 2}^{n + 1} {\frac{1}{2}{z^2}_i} + \sum\limits_{i = 1}^n {({\kappa ^2}_i + \frac{1}{{2{r_i}}}\tilde \theta _i^T{{\tilde \theta }_i} + } \cr & \frac{1}{{2{{\bar r}_i}}}\tilde w_i^T{{\tilde w}_i}), \cr} $ |
式中${{\tilde w}_1} = {{\tilde \varepsilon }_1}$.
对函数Vsum求导,并结合式(11)、(23)、(32)、(34)、(43)、(48)整理合并可得
| $\begin{align} & {{{\dot{V}}}_{sum}}\le -\left( r-{{m}^{2}}_{1}-\frac{1}{2} \right){{\left\| e \right\|}^{2}}-\left( {{c}_{1}}-\frac{3}{2} \right){{\vartheta }_{1}}{{p}_{1}}^{2}- \\ & \sum\limits_{i=2}^{n}{\left( {{c}_{i}}-\frac{1}{2} \right){{z}^{2}}_{i}}-{{c}_{n+1}}{{z}^{2}}_{n+1}-\sum\limits_{i=1}^{n}{\left( \frac{1}{{{\tau }_{i}}}-1 \right){{\kappa }^{2}}_{i}+} \\ & \sum\limits_{i=1}^{n}{\frac{1}{2}{{\left( {{{\bar{N}}}_{i}} \right)}^{2}}+}\sum\limits_{i=1}^{n}{{{w}^{*}}_{i}{{{\bar{\lambda }}}^{\prime }}_{i}+\frac{1}{2}{{\left\| P \right\|}^{2}}({{\left\| {{\delta }^{*}} \right\|}^{2}}+} \\ & 2\sum\limits_{i=1}^{n}{{{m}^{2}}_{i}{{\beta }^{2}}_{i,0})+{{m}^{2}}_{2}{{\beta }^{2}}_{2,0}}. \\ \end{align}$ | (49) |
| $\begin{align} & 取C=min\{(r-{{m}^{2}}_{1}-\frac{1}{2})/{{\lambda }_{max}}\left( P \right),2{{c}_{1}}-3,(2{{c}_{i}}-1)i= \\ & 2,\ldots ,n-1\text{ },2{{c}_{n+1}},\frac{2}{{{\tau }_{i}}}-2\};M=\sum\limits_{i=1}^{n}{\frac{1}{2}{{({{{\bar{N}}}_{i}})}^{2}}}+\sum\limits_{i=1}^{n}{{{w}^{*}}_{i}{{{\bar{\lambda }}}^{\prime }}_{i}+} \\ & \frac{1}{2}{{\left\| P \right\|}^{2}}({{\left\| \delta \right\|}^{2}}+2\sum\limits_{i=1}^{n}{{{m}^{2}}_{i}{{\beta }^{2}}_{i,0})+{{m}^{2}}_{2}{{\beta }^{2}}_{2,0}}. \\ \end{align}$ |
则式(49)可转化为
| ${{{\dot{V}}}_{sum}}\le -C{{V}_{sum}}+M+\frac{1}{{{\gamma }_{\chi }}}\left( \zeta N\left( \chi \right)-1 \right)\dot{\chi },$ | (50) |
对式(50)进行积分,得
| $\begin{align} & {{{\dot{V}}}_{sum}}\le {{V}_{sum}}\left( 0 \right){{e}^{-Ct}}+\frac{M}{C}\left( 1-{{e}^{-Ct}} \right)+ \\ & \frac{{{e}^{-Ct}}}{{{\gamma }_{\chi }}}\int _{0}^{t}\left( \zeta N\left( \chi \right)\dot{\chi }-\dot{\chi } \right){{e}^{C\tau }}d\tau . \\ \end{align}$ |
根据引理1可得Vsum(·)和χ(·)有界,且跟踪误差满足如下不等式:
| $\frac{1}{2}|y-{{y}_{d}}{{|}^{2}}=\frac{1}{2}{{z}^{2}}_{1}\le {{V}_{sum}}\Rightarrow |y-{{y}_{d}}|\le \sqrt{2{{V}_{sum}}}.$ |
同时变量$\vartheta $1(t)有界,根据引理2可得,输出跟踪误差满足衰减动态性能.
故根据以上控制器的设计过程和对闭环系统稳定性分析,可得到以下定理 .
定理 3 对于满足假设1~5的输入受限非线性系统(1),设计模糊状态观测器(3),设计控制器(44)~(46),设计系统辅助虚拟控制变量(20)、(29)、(33)、(40),选取参数自适应律(21)~(22)、(30)~(31)、(41)~(42),则闭环系统所有信号半全局一致有界(SGUUB),并且输出跟踪误差满足可规定衰减动态性能.
5 仿真分析由于高超声速飞行器超高的飞行速度和特殊的飞行环境,相比于传统飞行器具有较强的参数不确定和较大的外界干扰,且飞行动力系统对姿态特别是攻角侧滑角具有非常严格的条件要求,控制系统的研究面临前所未有的挑战[21].为此需要设计鲁棒性强,跟踪误差满足一定要求的控制系统.同时由于高超声速飞行器不菲的造价,因此也要求控制系统具有一定的可靠性(如系统中状态量传感器出现故障导致状态不能直接测量的情况下,控制系统依然能够实现对指令的稳定跟踪).在飞行器进行机动飞行时由于执行器自身物理构造的限制,导致执行器出现饱和的情况.如果不考虑这种输入受限的情况,可能会导致系统动态性能变差,如调节时间增长、超调量增大、引起系统滞后和振荡加剧,严重的将导致系统不稳定[22],因此在设计控制系统时也需要考虑执行器输入受限这种情况.为验证本文所提方法的有效性,选用一类有翼锥构型的吸气式高超声速飞行器作为仿真模型.飞行高度h=110 000 ft,速度v=15 060 ft/s,其纵向动态特性表示如下[23]:
| $\left\{ \begin{matrix} ~\dot{\alpha }=q-\frac{1}{mV}\left( L+Tsin\left( \alpha \right)-mg \right), \\ \dot{q}=\frac{{{M}_{yy}}}{{{I}_{yy}}}+d. \\ \end{matrix} \right.$ | (51) |
式中:α、q分别为飞行器的攻角和俯仰角速度;m、Iyy分别为质量和转动惯量;L、T、Myy、d分别为升力、推力、俯仰力矩和俯仰轴上受到的外界干扰.上述系统中涉及的力与力矩的具体表达形式如下:
| $\begin{align} & \left\{ \begin{matrix} ~L=0.5\rho {{V}^{2}}S{{C}_{L}}, \\ T=0.5\rho {{V}^{2}}S{{C}_{T}}, \\ {{M}_{yy}}=0.5\rho {{V}^{2}}S_{-}^{c}[{{C}_{M}}\left( \alpha \right)+{{C}_{M}}({{\delta }_{e}})+{{C}_{M}}\left( q \right)]. \\ \end{matrix} \right. \\ & {{C}_{L}}=0.620\text{ }3\alpha , \\ & {{C}_{T}}=\left\{ \begin{matrix} 0.025\text{ }76\beta , & \beta <1; \\ 0.022\text{ }4+0.003\text{ }36\beta , & \beta >1. \\ \end{matrix} \right.\text{ } \\ & {{C}_{M}}\left( \alpha \right)=-0.035{{\alpha }^{2}}+0.036\text{ }617(1+\Delta {{C}_{M\alpha }})\alpha + \\ & 5.326\text{ }1\times {{10}^{-6}}, \\ & {{C}_{M}}\left( q \right)=\left( c-/2V \right)q(-6.796{{\alpha }^{2}}+0.301\text{ }5\alpha -0.228\text{ }9), \\ & {{C}_{M}}({{\delta }_{e}})={{c}_{e}}({{\delta }_{e}}-\alpha ), \\ & m={{m}_{0}}\left( 1+\Delta m\left( t \right) \right),|\Delta m\left( t \right)|\le 0.03, \\ & {{I}_{yy}}={{I}_{0}}\left( 1+\Delta I\left( t \right) \right)\times {{10}^{6}},|\Delta I\left( t \right)|\le 0.02, \\ & S={{S}_{0}}\left( 1+\Delta S\left( t \right) \right),|\Delta S\left( t \right)|\le 0.01, \\ & \bar{c}={{{\bar{c}}}_{0}}\left( 1+\Delta c-\left( t \right) \right),|\Delta c-\left( t \right)|\le 0.01, \\ & {{c}_{e}}=0.029\text{ }2\left( 1+\Delta {{c}_{e}}\left( t \right) \right),|\Delta {{c}_{e}}\left( t \right)|\le 0.03, \\ & \rho ={{\rho }_{0}}\left( 1+\Delta \rho \left( t \right) \right),|\Delta \rho \left( t \right)|\le 0.06. \\ \end{align}$ |
文中假设推力不变,攻角的跟踪控制通过舵偏角的偏转来调节.飞行器的舵偏角是在一定的范围内的,且饱和界限值(±30°)已知.采用正切函数处理饱和问题,令[x1,x2]T=[α,q]T,将式(51)等效为如下形式:
| $\left\{ \begin{matrix} {{{\dot{x}}}_{1}}=f{{'}_{1}}\left( {{x}_{1}},{{x}_{2}} \right)+{{x}_{2}}, \\ {{{\dot{x}}}_{2}}=f{{'}_{2}}\left( {{x}_{2}},v \right)+h\left( v \right)+\bar{d}. \\ \end{matrix} \right.$ |
式中:f′1(x1,x2)=-$\frac{1}{mV}$(L+Tsin(α)-mg);v为设计的控制器输入变量;h(·)为双曲正切函数; f′2(x2,v)=$\frac{{{M}_{yy}}}{{{I}_{yy}}}$-h(v);d为复合干扰.假设俯仰轴上受到的干扰力矩为谐波力矩,大小为2×106sin(2t).
假设俯仰角速度测量传感器在飞行的过程当中出现故障,无法实现精确测量,故采用本文中设计的基于模糊状态观测器的控制方法.本文中攻角的参考指令信号为yr=-22.5°cos(t)+22°.
按照本文方法设计如下所示的模糊状态观测器和反步控制器.
模糊状态观测器:
| $\left\{ \begin{matrix} {{{\dot{\hat{x}}}}_{1}}={{{\hat{x}}}^{2}}+{{k}_{1}}(y-{{{\hat{x}}}_{^{1}}})+\hat{f}{{'}_{1}}({{x}_{^{1}}},{{x}_{2,f}}|{{\theta }_{1}}), \\ {{{\dot{\hat{x}}}}_{2}}={{k}_{2}}(y-{{{\hat{x}}}_{^{1}}})+\hat{f}{{'}_{2}}({{{\hat{x}}}_{^{2}}},uf\text{ }\!\!|\!\!\text{ }{{\theta }_{2}})+u, \\ \hat{y}={{{\hat{x}}}_{^{1}}}. \\ \end{matrix} \right.$ |
式中建立的模糊系统如下: $\hat{f}{{'}_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}}\text{ }\!\!|\!\!\text{ }{{\theta }_{1}})\text{=}\theta _{1}^{T}{{\xi }_{1}}({{{\hat{x}}}_{^{1}}},{{{\hat{x}}}_{2,f}});\hat{f}{{'}_{2}}({{{\hat{x}}}_{^{2}}},{{u}_{f}}\text{ }\!\!|\!\!\text{ }\theta 2)\theta _{2}^{T}\xi 2({{{\hat{x}}}_{2,uf}});u=h(v)$.
设计的控制器如下:
| $\eqalign{ & {{\bar \alpha }_1} = - {c_1}{\vartheta _1}{p_1} - \theta _1^T({{\hat x}_{^1}},{{\hat x}_{2,f}}) + {{\dot y}_r} + \frac{{{{\dot h}_1}}}{{{h_1}}}{s_1} - {{\hat \varepsilon }_1}tanh(\frac{{{\vartheta _1}{p_1}}}{{{{\rlap{-} \lambda }_n}}}), \cr & {{\bar \alpha }_2} = - {c_2}{z_2} - {\vartheta _1}{p_1} - {k_2}{e_1} - \theta _2^T{\xi _2}\left( {{{\hat x}_2},{u_f}} \right) + {{\dot \alpha }_1} - {{\hat w}_2}tanh(\frac{{{z_2}}}{{{{\rlap{-} \lambda }_2}}}), \cr & \dot v = - cv + \omega , \cr & \omega = {\chi ^2}cos\left( \chi \right)\bar \omega , \cr & \bar \omega = - {c_3}{z_3} - {z_3} + \zeta cv + {{\dot \alpha }_2}, \cr & \dot \chi = {\gamma _\chi }\bar \omega {z_3}. \cr} $ |
设计参数分别为:k1=10,k2=18,c1=13,c2=16,c3=7,c=6,τ1=0.01,τ2=0.01,γ=0.008,χ0=0.4,r1=1,r2=2,r1=0.2,r2=0.2.
函数h1(t)=e-t+0.03,设计参数δ1,1=0.6,δ1,2=0.9,a1=0.02.
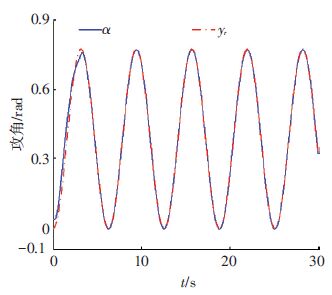
图 1为输出响应曲线,其中图 1中虚线表示为参考输入信号曲线,实线表示为跟踪响应曲线.从图 1中可以看出在系统存在不确定性参数和未知外界干扰的情况下,攻角的输出信号能够稳定地跟踪参考输入信号.
|
图 1 输出响应曲线 Figure 1 Curve of output respoN(s)e |
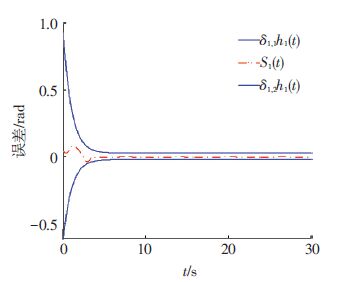
图 2为系统的控制信号曲线,虚线表示为设计的控制输入信号,实线表示为执行器信号.从图 2中可以看出虽然控制输入信号在一些情况下远远超出了界限值,但是执行器信号依然控制在饱和界限范围内.图 3,4分别为模糊状态观测器的响应曲线.虽然俯仰角在外界干扰值很大的情况下,观测效果不太理想,但是系统在输入受限的情况下,依然能够很好地跟踪参考输入信号.图 5为系统的跟踪误差曲线,虚线表示系统的跟踪误差.从图 5中可以清晰地看出,系统跟踪误差被限定在可规定性能范围内.

|
图 2 控制信号 Figure 2 Control signals |

|
图 3 攻角观测响应曲线 Figure 3 Observed respoN(s)e of the attack angle |

|
图 4 俯仰角观测响应曲线 Figure 4 Observed respoN(s)e of the pitch angle |
|
图 5 跟踪误差曲线 Figure 5 Curves of the tracking error |
1) 本文提出了一种有效处理具有不可直接测量状态的输入受限的不确定非线性系统的反步控制方法.运用Lyapunov理论对系统的稳定性进行分析,证明了闭环系统所有信号半全局一致最终有界(SGUUB).
2) 利用双曲正切函数和Nussbaum增益函数有效地处理了输入饱和约束,并采用可规定误差面性能技术对输出跟踪误差进行了有效限定.
3) 能够有效地处理控制方向未知而引起的奇异等问题,并且文中对模糊系统的逼近误差进行了自适应补偿,进一步减小了跟踪误差.
4) 仿真过程中,虽然模糊状态观测器对不可直接测量状态的估计效果不是很理想,但系统依然能够具有很好的跟踪效果和很强的鲁棒性能.
| [1] |
SIWAKOSIT W, SNELL S A, HESS R A. Robust flight control design with handling qualities constraints using scheduled linear dynamic inversion and loop-shaping[J].
IEEE Transactions on Control Systems Technology,2000, 8 (3) : 483-494.
DOI: 10.1109/87.845879 ( 0) 0)
|
| [2] |
JOHNSON E N, CALISE A J. Limitedauthority adaptive flight control for reusable launch vehicles[J].
Journal of Guidance, Control, and Dynamics,2003, 26 (6) : 906-913.
( 0) 0)
|
| [3] |
HENCEY B, ALLEYNE A. An anti-windup technique for LMI regions[J].
Automatica,2009, 45 (10) : 2344-2349.
DOI: 10.1016/j.automatica.2009.06.021 ( 0) 0)
|
| [4] |
FARRELL J A, POLYCARPOU M, SHARMA M, et al. Commandfiltered backstepping[J].
IEEE Transactions on Automatic Control,2009, 54 (6) : 1391-1395.
DOI: 10.1109/TAC.2009.2015562 ( 0) 0)
|
| [5] |
李静, 左斌, 段洣毅, 等. 输入受限的吸气式高超声速飞行器自适应Terminal滑模控制[J].
航空学报,2012, 33 (2) : 220-233.
LI Jing, ZUO Bin, DUAN Miyi, et al. Adaptive terminal sliding mode control for air-breathing hypersonic vehicles under control input constraints[J]. Acta Aeronautica ET Astronautica Sinica,2012, 33 (2) : 220-233. (  0) 0)
|
| [6] |
胡庆雷, 张爱华, 姜成平, 等. 控制受限的卫星轨道转移过程中的姿态控制[J].
哈尔滨工业大学学报,2013, 45 (5) : 1-6.
DOI: 10.11918/j.issn.0367-6234.2013.05.001 HU Qinglei, ZHANG Aihua, JIANG Chengping, et al. Attitude control of satellite in process of orbit transfer with constraint input[J]. Journal of Harbin Institute of Technology,2013, 45 (5) : 1-6. DOI: 10.11918/j.issn.0367-6234.2013.05.001 (  0) 0)
|
| [7] |
WEN Changyun, ZHOU Jing, LIU Zhitao, et al. Robust adaptive of uncertain nonlinear systems in the presence of input saturation and external disturbance[J].
IEEE Transactions on Automatic Control,2011, 56 (7) : 1672-1678.
DOI: 10.1109/TAC.2011.2122730 ( 0) 0)
|
| [8] |
周砚龙, 陈谋. 基于干扰观测器的输入受限非线性系统鲁棒控制[J].
南京理工大学学报,2011, 56 (7) : 1672-1678.
DOI: 10.3969/j.issn.1005-9830.2014.01.007 ZHOU Yanlong, CHEN Mou. Robust control of nonlinear systems with input constraint based on disturbance observer[J]. Journal of Nanjing University of Science and Technology,2011, 56 (7) : 1672-1678. DOI: 10.3969/j.issn.1005-9830.2014.01.007 (  0) 0)
|
| [9] |
孔小兵, 刘向杰. 基于输入输出线性化的连续系统非线性模型预测控制[J].
控制理论与应用,2012, 29 (2) : 217-224.
DOI: 10.7641/j.issn.1000-8152.2012.2.PCTA110510 KONG Xiaobing, LIU Xiangjie. Continuous-time nonlinear model predictive control with input/output linearization[J]. Control Theory & Applications,2012, 29 (2) : 217-224. DOI: 10.7641/j.issn.1000-8152.2012.2.PCTA110510 (  0) 0)
|
| [10] |
KANELLAKOPOULOS I, KOKOTOVI P V, MORSE A S. Systematic design of adaptive controllers for feedbacklinearizable systems[J].
IEEE Transactions on Automatic Control,1991, 36 (11) : 1241-1253.
DOI: 10.1109/9.100933 ( 0) 0)
|
| [11] |
SWAROOP D, HEDRICK J K, YIP PP, et al. Dynamic surface control for a class of nonlinear systems[J].
IEEE Transactions on Automatic Control,2000, 45 (10) : 1893-1899.
DOI: 10.1109/TAC.2000.880994 ( 0) 0)
|
| [12] |
HUA Changchun, WANG Qingguo, GUAN Xinping. Adaptive fuzzy output feedback controller design for nonlinear time-delay systems with unknown control direction[J].
IEEE Transactions on Systems, Man, and Cybernetics, Part B: Cybernetics,2009, 39 (2) : 363-374.
DOI: 10.1109/TSMCB.2008.2005204 ( 0) 0)
|
| [13] |
BECHLIOULIS C P, ROVITHAKIS G A. Prescribed performance adaptive control for multi-input multi-output affine in the control nonlinear systems[J].
IEEE Transactions on Automatic Control,2010, 55 (5) : 1220-1226.
DOI: 10.1109/TAC.2010.2042508 ( 0) 0)
|
| [14] |
XU Yinyin, TONG Shaocheng, LI Yongming. Prescribed performance fuzzy adaptive fault-tolerant control of non-linear systems with actuator faults[J].
IET Control Theory and Applications,2014, 8 (6) : 420-431.
DOI: 10.1049/iet-cta.2013.0676 ( 0) 0)
|
| [15] |
YOO S J. Fault-tolerant control of strict-feedback nonlinear time-delay systems with prescribed performance[J].
IET Control Theory and Applications,2013, 7 (11) : 1220-1226.
DOI: 10.1049/iet-cta.2013.0252 ( 0) 0)
|
| [16] |
WANG Lixin.
Adaptive fuzzy systems and control: design and stability analysis[M]. New Jersey: Prentice-Hall, 1994 .
( 0) 0)
|
| [17] |
TONG Shaocheng, LI Yongming. Observer-based adaptive fuzzy backstepping control of uncertain nonlinear pure-feedback systems[J].
Science China(Information Sciences),2014, 57 (1) : 1-14.
DOI: 10.1007/s11432-013-5043-y ( 0) 0)
|
| [18] |
ZOU Anmin, HOU Zengguang, TAN Min. Adaptive control of a class of nonlinear pure-feedback systems using fuzzy backstepping approach[J].
IEEE Transactions on Fuzzy systems,2008, 16 (4) : 886-897.
DOI: 10.1109/TFUZZ.2008.917301 ( 0) 0)
|
| [19] |
KHALIL H K.
Nonlinear systems[M]. New Jersey: Prentice Hall, 2002 .
( 0) 0)
|
| [20] |
PLOYCARPOU MM, IOANNOU P A. A robust adaptive nonlinear control design[J].
Automatica,1996, 32 (3) : 423-427.
DOI: 10.1016/0005-1098(95)00147-6 ( 0) 0)
|
| [21] |
黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J].
控制理论与应用,2011, 28 (10) : 1496-1505.
DOI: 10.7641/j.issn.1000-8152.2011.10.025 HUANG Lin, DUAN Zhisheng, YANG Jianying. Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications,2011, 28 (10) : 1496-1505. DOI: 10.7641/j.issn.1000-8152.2011.10.025 (  0) 0)
|
| [22] |
CAMPO P J, MORARI M. Robust control of processes subject to saturation nonlinearities[J].
Computers & Chemical Engineering,1990, 14 (4/5) : 343-358.
DOI: 10.1016/0098-1354(90)87011-D ( 0) 0)
|
| [23] |
XU Haojian, MIRMIRANI M D, IOANNOU P A. Adaptive sliding mode control for a hypersonic flight vehicle[J].
Journal of Guidance, Control, and Dynamics,2004, 27 (5) : 829-838.
DOI: 10.2514/1.12596 ( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


