超高速航行器凭借其独特的流体动力布局模式将大部分壳体包裹于超空泡内部,进而实现航行阻力的大幅减小,配合强大的推进装置可以实现水下200 kn以上的超高航速[1].然而,因超空泡的存在超高速航行器表现出的流体动力特性以及对控制系统的响应与常规水下航行器有很大的不同,因此控制和机动问题是超高速航行技术的研究重点和难点,同时也是当前的研究热点[2-4].在水下超高速航行条件下,常规翼型往往因空化导致舵效丧失或不可预测,为此超高速航行器多采用截面为24°锐角等腰三角形的楔形三棱柱舵片[5-7].
楔形舵片被广泛用作超高速水下航行器的控制面,具有舵效稳定、铰链力矩小、空化性能稳定等诸多优点[8-9].刘海军等[5]采用CFD的方法研究了楔形角对舵片流体动力特性的影响规律,指出较大的楔角会导致舵片阻力增加.王京华等[10]采用楔形尾舵作为控制面,通过舵片沾湿面积考虑舵效率,研究了超空泡航行体的动力学建模和控制问题.Zheng等[11]采用数值模拟的方法,研究了楔形物体的空化问题,得出了楔形物体阻力特性和空化特性与楔角的关系.Dzieiski 等[12]提出了楔形舵片在与空泡耦合时的流体动力预测方法,并基于此研究了超空泡航行器的控制技术.从国内外公开文献来看,超空泡航行技术的研究主要集中在动力学建模和运动控制等方面,楔形舵片被广泛用作超空泡航行体的控制面,关于其流体动力特性和空化特性的研究很少,对楔形舵片的失速特性等方面的研究尚未开展.
楔形舵片的失速现象将改变舵片的空化规律和流体动力特性,研究楔形舵片的失速规律和失速机理有助于建立精准的控制模型,并且改善超空泡航行器的运动特性.考虑到开展高速超空化试验的困难,本文基于低速通气工况,针对24°楔形舵片分别开展水洞试验和数值模拟研究,旨在证明楔形舵片存在失速特性,揭示舵片失速的机理,提出能够准确预测楔形舵片失速特性的数值方法,为研究楔形舵片在高速航行工况下的失速特性奠定基础.
1 数值模拟 1.1 数值模型的建立 1.1.1 控制方程超空化流动数值模型的控制方程包括气液两相的连续方程、动量方程和湍流方程.根据文献[13-14]的研究成果,本文研究内容均属于匀相流问题,可采用Mixture多相流模型;湍流控制方程采用稳定性更高的Realizable k-e湍流模型,该模型稳健性好,适用于解决复杂的流动问题;湍流模拟中近壁面处理方法可采用稳健性更好的尺度化壁面函数.
1.1.2 模型的简化以及网格的划分本文的研究对象是24°楔形三棱柱舵片,舵片的弦长D=21.5 mm,舵片的展长L=30 mm,数值模拟研究的主要目的是获得不同舵角工况下楔形舵片的流体动力特性以及附近流场的空化特性.为突出研究重点,简化数值模型,在几何建模时不考虑弹体和主体空泡对流场的影响,在尾舵完全穿刺空泡的情况下模拟器空化流场.
某型超高速航行器的楔形舵片的最大厚度约8 mm,而航行体圆柱段直径约220 mm,因此弧形壳体可以按照平壁面进行简化处理;文献[12, 15]指出在尾舵存在空泡不完全穿刺的条件下,可根据有效沾湿面积计算舵片的流体动力.因此,本文通过对合理简化的模型开展数值模拟,研究完全穿刺空泡时的楔形舵片的流体动力特性是可行的.
针对所建立的楔形空化舵片的数值计算模型,采用GAMBIT软件划分结构化网格,在近壁面添加边界层,并基于湍流模型对y+的要求优化近壁面网格,以便精确地模拟湍流;在舵片周围以及舵片后部的尾流区划分足够精细的网格,以便准确地捕捉空化泡;通过网格无关性检验,保证空泡形态和流体动力的数值模拟结果不受网格分布规律的影响.
按照上述的模型简化方法和网格划分原则,以1°为间隔建立0°~12°舵角工况下尾舵流场的几何模型并划分网格,每个模型的网格单元数为82万.以0°工况为例,楔形舵片周围的结构化网格分布情况如图 1所示.

|
图 1 楔形舵片周围的网格划分情况 Figure 1 Distribution of grids near wedge rudder |
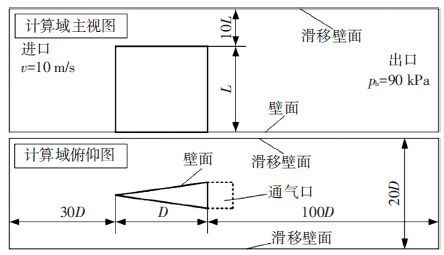
边界条件设置如下:计算域采用速度进口,流速10 m/s;计算域采用压力出口,绝对压力90 kPa;通气口采用质量流量进口,以维持舵后空泡稳定所需的最小通气量作为最终通气量,计算使用的通气量为32 g/min,不考虑气体可压缩性约合26S LPM;采用通气空化模型考虑相变,模拟超空泡的生成和发展,数值模型的计算域构建及边界条件设置情况如图 2所示.
|
图 2 计算域构建及边界条件设置 Figure 2 The structure and boundary conditions of computational domain |
根据楔形舵片在0°~12°舵角工况下的数值模拟结果,得出楔形舵片在低速通气工况下的流体动力特性.为便于分析,以尾舵纵剖面面积为参考面积、来流速度为参考速度、水的密度为参考密度对流体动力数据进行无量纲化.楔形超空化舵片在不同舵角下的升力系数和阻力系数见表 1.
表 1显示,楔形舵片在低速通气工况下,阻力系数在0°~5°舵角范围几乎保持恒定,在5°~12°范围随舵角的增加而略微增大;升力系数在0°~8°范围内与舵角正相关,超过8°以后舵片则突然变小,并且在9°~12°范围内升力系数仍与舵角正相关,但数值仅维持在5°~6°舵角时的水平.基于此,认为楔形超空化舵片在8°舵角以后,舵片的舵效突然变小,出现失速现象.因此,为保证控制效果,该类舵片的许用舵角不得超过8°.
| 表 1 楔形舵片流体动力特性的数值模拟结果 Table 1 The numerical results of hydrodynamic characteristic of wedge rudder |
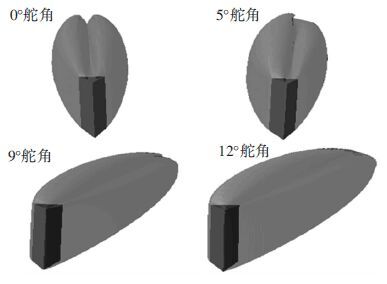
根据数值模拟结果,统计并对比不同舵角时楔形舵片周围流场的空化情况,揭示楔形舵片的失速机理.为便于观察,以舵片中截面流场的气相体积分数云图表征舵片低压面的空化情况.0°~12°舵角舵片中截面的气相分布分别如图 3所示.部分工况的三维空泡外形如图 4所示.

|
图 3 不同舵角时楔形舵片低压面的空化情况 Figure 3 The cavitation extent of the low-pressure surface of wedge rudder under different angles |
|
图 4 不同舵角时的三维空泡形态 Figure 4 The three dimensional shape of cavity under different rudder angle |
图 3显示了舵片低压面的空化情况随舵角的变化情况,可以发现舵角在0°~8°时空泡仅出现在楔形舵片之后且清晰稳定;舵角在9°~12°时楔形舵片的低压面发生空化并被空泡完全包裹.结合图 3可知,大舵角时低压面的空化是导致楔形舵片失速的主要原因.
图 4所示为0°、5°、9°和12°舵角工况时舵片后部的超空泡三维图,可知,大舵角工况下,舵片低压面发生空化并且完全被空泡包裹,空泡尺度也有所增大.
1.4 压力分布和速度矢量的数值模拟结果对比楔形舵片的低压面发生空化前后流场的压力分布和速度矢量,进而研究舵片失速的机理.舵角为8°和9°时舵片附近的压力云图和速度矢量对比如图 5所示.

|
图 5 舵面空化前、后的压力云图和速度矢量对比 Figure 5 The contrast of pressure distribution and velocity vector of flow field considering cavitation with that of flow field not considering cavitation |
图 5显示,楔形舵片在有舵角的情况下驻点位于迎流面的最前端,驻点的阻滞作用引起部分流体在舵片迎流面发生逆向流动,致使来流与楔形舵片中线的夹角大于实际舵角,进而导致9°舵角工况下低压面发生空化;低压面空化后,舵面的压力分布规律随之改变,并最终导致舵片的流体动力特性突变,发生失速现象.
2 试 验依托西北工业大学的高速水洞实验室,搭建具有自动操舵及舵角控制功能的试验系统,研究超高速水下航行器的楔形空化舵片的流体动力特性和空化特性,揭示其失速机理.
2.1 试验原理及试验条件 2.1.1 试验原理通过调节水洞的压力、水速和通气流量,生成稳定透明的超空泡.
由伺服电机、滚珠丝杠和精密位置传感器构成的伺服驱动系统精确控制主动液压缸的行程.两个完全一样的液压缸通过管路并联构成液压随动系统,主动液压缸由伺服电机驱动位于水洞外,随动液压缸通过摆杆推动舵轴转动实现操舵动作.上位机在水洞外发出舵角指令,通过液压随动系统在水洞内实现舵片在0°~12°范围内的任意角度动作.
通过三分力天平测试舵片受到的流体动力,测力信息经数据线上传至上位机并存储;测力天平的一端固定在机架上,另外一端通过连接件与楔形舵片相连接;舵轴与天平连接件之间安装深沟球轴承.
2.1.2 试验条件西北工业大学高速水洞为闭式循环水洞,工作段尺寸为Φ400 mm×2 000 mm;水速为0~18 m/s连续可调;工作压力为20~300 kPa连续可调;最小空化数为0.15.
试验所采用的水流速度10 m/s,水洞压力为90 kPa.模型通气量为54 SPLM,该通气量为维持舵后空泡稳定所需的最小通气量.舵片为24°楔形舵片,展长30 mm,弦长21.5 mm.以1°为间隔,依次给定0°~12°舵角,测试舵片受力,并拍摄流场的空化情况.
2.2 试验装置试验系统主要由空泡调节子系统、测力子系统和操舵子系统3部分构成.空泡调节子系统以6 bar的压缩空气作为气源,配合水速和压力调节,生成超空泡;测力子系统采用三分力天平测试舵片的升/阻力;操舵子系统通过伺服电机驱动液压随动系统实现舵角控制.
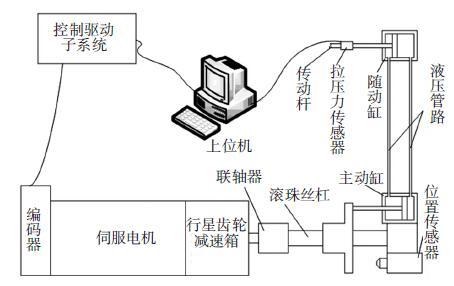
2.2.1 操舵子系统操舵子系统由伺服驱动系统和液压随动系统构成,如图 6所示.上位机发出舵角指令,伺服驱动系统控制主动缸的行程;主动液压缸与随动液压缸同步运动;伺服驱动系统和主动缸位于水洞外,随动液压缸安装于模型内部与多轴相连.
|
图 6 操舵系统工作原理 Figure 6 The operating principle of steering control system |
如图 7所示,试验模型主要由随动液压缸、测力天平、软管、舵片空化器、模型壳体以及连接装置组成,可实现超空泡生成和维持、流体动力测试与储存以及按给定舵角操舵等功能.试验模型通过支撑杆固定于水洞上盖板,如图 8所示.

|
图 7 试验装置结构图 Figure 7 The construction of experimental device |

|
图 8 试验模型在水洞的安装方式 Figure 8 The installation of experimental model in water tunnel |
以1°为间隔针对0°~12°舵角依次开展试验,分别记录测力信息和空泡形态.楔形舵片在试验工况下受到的流体动力见表 2,流体动力数据的处理方法同舵片流体动力特性数值模拟结果所述.
| 表 2 楔形舵片流体动力特性的水洞试验结果 Table 2 The experimental results of hydrodynamic characteristic of wedge rudder |
表 2显示,在0°~5°舵角范围舵片的阻力系数几乎维持稳定;在5°~12°范围内舵片的阻力系数随舵角的增加而略微增大;在0°~8°范围内,舵片升力系数随舵角的增加而显著增大;舵角为9°舵片升力系数突然下降至5°时的水平;在9°~12°范围内,舵片升力系数随舵角的增加而略微增加,然而舵效远小于小舵角工况.
2.4 舵片空化特性的试验结果采用通气空化的方法开展试验,在10 m/s的低速工况下获得足以包裹大部分模型的超空泡,试验中的模型安装以及超空泡生成情况如图 9所示.

|
图 9 试验中的超空泡 Figure 9 The supercavitaty generated in water tunnel |
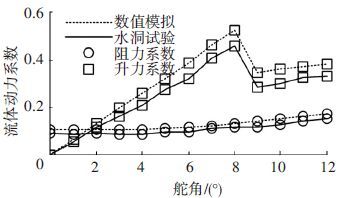
根据表 1,2中的数据,楔形舵片流体动力特性的数值模拟结果和水洞试验结果的对比如图 10所示.0°~12°不同舵角舵片低压面的绕流情况对比如图 11所示.
|
图 10 流体动力特性的数值模拟与水洞试验结果对比 Figure 10 The comparison of hydrodynamic characteristics drawn by numerical method with those drawn by experimental method |

|
图 11 不同舵角时楔形舵片低压面的空化特性对比 Figure 11 The cavitation conditions of low pressure surface of wedge rudder when angle changes from 0° to 12° |
由图 11可知,舵角超过9°时楔形舵片的低压面发生空化并被空泡覆盖.楔形舵片的流体动力特性与低压面的空化特性随舵角的变化规律吻合,均在舵角超过8°时发生突变.因此,可认为舵片低压面的空化导致了升力系数的突然减小.
结合图 10、表 1,2可知,数值模拟和试验研究所得楔形舵片的流体动力随舵角的变化规律一致;试验结果的升/阻力系数均小于数值模拟结果,相对偏差约在14%~23%之间.对比图 3和图 11可知,数值模拟和试验研究均得出在舵角超过8°时舵片低压面开始出现空化现象的结论.
图 11显示,由于受主体空泡的影响,不同舵角时楔形舵片根部均有10%左右的面积被空泡包裹,使得楔形舵片的有效沾湿面积减小,并且有可能导致试验结果偏小.此外,数值模拟模型忽略了通气工质的可压缩性,则有可能造成舵片后部空泡的压力小于试验状态,并导致数值模拟结果偏大.根据舵片流体动力特性和流场空化情况的数值模拟以及试验研究结果可以认为,在舵角超过8°以后,发生在楔形舵片低压面的空化现象导致舵片表面的压力被显著改变,进而导致舵片的流体动力特性发生突变,最终表现为楔形舵片失速.鉴于楔形舵片的流体动力特性,在失速区(9°~12°舵角)的升力系数仅与5°~6°相当,因此该类舵片的许用舵角不能超过8°.
本文分别采用数值模拟与水洞试验的方法研究了楔形舵片的失速特性,并且所得现象和结论的一致性良好.两种研究方法相互参验,表明了研究结果的可靠性和置信度,所提出的数值方法和试验方案均适用于同类问题的研究.
4 结 论1) 数值模拟和水洞试验得出的舵片流体动力特性与低压面的空化特性一致,两种研究方法相互参验,证明了本文建立的数值模型和提出的试验方案具有正确性和合理性.
2) 在低速通气工况下,楔形舵片的阻力系数在0°~5°舵角范围内基本维持不变,舵角超过5°以后阻力系数将随舵角的增大而略微增加;舵片的升力系数在0°~8°舵角范围内具有良好的线性,舵角超过8°以后楔形舵片的的升力系数下降舵角至5°水平,发生失速现象;在9°~12°舵角范围内,舵片升力系数随舵角的增大而缓慢增加,此时舵效远小于失速前.
3) 在舵角超过8°以后,楔形舵片低压面发生空化,致使该区域压力不能够进一步降低;低压面的空化是导致楔形舵片失速的根本原因;考虑楔形超空化舵片的失速特性,24°楔形舵片在低速通气工况下的许用舵角不得超过8°.
| [1] |
LUO Kai, LI Daijin, DANG Jianjun, et al. Motion control model of supercavitating vehicle considering time-delay effect of supercavitation[J].
Journal of Traffic and Transportation Engineering,2010, 10 (3) : 41-45.
( 0) 0)
|
| [2] |
LI Daijin, LUO Kai, HUANG Chuang, et al. Dynamics model and control of high-speed supercavitating vehicles incorporated with time-delay[J].
International Journal of Nonlinear Sciences and Numerical Simulation,2014, 15 (3/4) : 221-230.
DOI: 10.1515/ijnsns-2013-0063 ( 0) 0)
|
| [3] |
NGUYEN V. Dynamics and control of non-smooth systems with applications to supercavitating vehicles[D]. Maryland: University of Maryland, College Park, 2011.
( 0) 0)
|
| [4] |
HASSOUNEH M A, NGUYEN V, BALACHANDRAN B, et al. Stability analysis and control ofsupercavitating vehicles with advection delay[J].
Journal of Computational and Nonlinear Dynamics,2013, 8 (2) : 21003.
DOI: 10.1115/1.4006835 ( 0) 0)
|
| [5] |
刘海军, 邹振祝. 楔型角对尾舵的流体动力特性研究[J].
哈尔滨商业大学学报(自然科学版),2009, 25 (1) : 92-95.
LIU Haijun, ZOU Zhenzhu. Study of angles of wedge effect on hydrodynamic characteristics of rear fin[J]. Journal of Harbin University of Commerce(Natural Sciences Edition),2009, 25 (1) : 92-95. (  0) 0)
|
| [6] |
杨洪澜, 张嘉钟, 赵存宝, 等. 楔体外部超空泡形状预测[J].
哈尔滨理工大学学报,2006, 11 (4) : 106-110.
DOI: 10.3969/j.issn.1007-2683.2006.04.030 YANG Honglan, ZHANG Jiazhong, ZHAO Cunbao, et al. Prediction of wedge's supercavity shape[J]. Journal of Harbin University of Science and Technology,2006, 11 (4) : 106-110. DOI: 10.3969/j.issn.1007-2683.2006.04.030 (  0) 0)
|
| [7] |
胡影影, 朱克勤, 席葆树. 翼型空化绕流数值研究[J].
力学季刊,2003, 24 (4) : 572-576.
HU Yingying, ZHU Keqin, XI Baoshu. Numerical study of cavity flow around a hydrofoil[J]. Chinese Quarterly of Mechanics,2003, 24 (4) : 572-576. (  0) 0)
|
| [8] |
NGUYEN V, HASSOUNEH M A, BALACHANDRA B, et al. Non-steadyplaning and advection delay effects on the dynamics and control of supercavitating vehicles [C]// Amer Soc Mechanical Engineers. Denver:[s.n.], 2011: 775-781.
( 0) 0)
|
| [9] |
WANG Zou, YU Kaiping, ROGER A. Modeling and simulations of supercavitating vehicle with planing force in the longitudinal plane[J].
Applied Mathematical Modelling,2015, 39 (19) : 6008-6020.
DOI: 10.1016/j.apm.2015.01.040 ( 0) 0)
|
| [10] |
王京华, 魏英杰, 于开平, 等. 基于空泡记忆效应的水下超空泡航行体建模与控制[J].
振动与冲击,2010, 29 (8) : 160-163.
DOI: 10.3969/j.issn.1000-3835.2010.08.036 WANG Jinghua, WEI Yingjie, YU Kaiping, et al. Modeling and control of underwater supercavitating vehicle based on memory effect of cavity[J]. Journal of Vibration and Shock,2010, 29 (8) : 160-163. DOI: 10.3969/j.issn.1000-3835.2010.08.036 (  0) 0)
|
| [11] |
ZHENG Zhiying, LI Fengchen, LI Qian, et al. Numerical study on the characteristics of natural supercavitation by planar symmetric wedge-shaped cavitators for rotational supercavitating evaporator[J].
Science China Technological Sciences,2015, 58 (6) : 1072-1083.
DOI: 10.1007/s11431-015-5827-y ( 0) 0)
|
| [12] |
DZIELSKI J, KURDILA A. A benchmark control problem for supercavitating vehicles and an initial investigation of solutions[J].
Journal of Vibration and control,2003, 9 (7) : 791-804.
DOI: 10.1177/1077546303009007004 ( 0) 0)
|
| [13] |
YU Kaiping, ZHANG Guang, ZHOU Jingjun, et al. Numerical study of the pitching motions of supercavitating vehicles[J].
,2012, 24 (6) : 951-958.
DOI: 10.1016/S1001-6058(11)60323-5 ( 0) 0)
|
| [14] |
黄闯, 罗凯, 党建军, 等. 流域径向尺度对自然超空泡的影响规律[J].
西北工业大学学报,2015, 33 (6) : 936-941.
HUANG Chuang, LUO Kai, DANG Jianjun, et al. Influence of flow field’s radial dimension on natural supercavity[J]. Journal of Northwestern Polytechnical University,2015, 33 (6) : 936-941. (  0) 0)
|
| [15] |
GOEL A. Robust control ofsupercavitating vehicles in the presence of dynamic and uncertain cavity[D]. Gainesville, FL: University of Florida, 2005.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


