航天器广泛采用的大型柔性附件由于在太空中受到高温热载荷与结构变形之间的耦合作用，将导致不稳定的热振动^[1]，在此动态过程中，结构的变形导致热传导边界条件的变化，形成不均匀的温度场.反之由于温变对结构参数的影响以及温度梯度产生的热应力，则可改变结构的刚度分布，从而影响结构固有频率.这种温度场与应力场之间的相互影响即为热结构耦合效应^[2].由于固有频率的改变将影响结构的共振可靠性，为此对热载荷下的结构进行共振可靠性分析显得十分必要.文献^[3]基于ANSYS软件对齿轮结构的温度场和热应力进行了求解，并分析了热环境对结构固有频率的影响.文献^[4]采用NASTRAN软件分别研究了均匀和非均匀温度场对壁板结构模态的影响.文献^[5]基于有限元方法建立了水轮发电机组主轴系统的非线性振动可靠性模型.文献^[6]采用点估计法计算了航空输流管道的共振可靠度.

上述文献对热结构耦合以及共振可靠性的分析方法均是基于确定性结构参数和确定性数学模型，实际上由于材料特性、几何尺寸和载荷等参数等往往具有不确定性，若将这些不确定性引入分析模型中，则能更好地反映结构中各种不确定性因素对响应的影响.然而，当各参数的不确定信息量不足以用概率模型描述时，非概率可靠性理论可为工程结构安全性提供一种有效的评估方法^[7].文献^[8]基于凸模型首次提出了非概率可靠性概念，并指出凸模型包括区间模型和超椭球模型.文献^[9]利用超椭球模型变量之间相关性的优点建立了结构非概率可靠性模型.

实际工程中，对于复杂结构的极限状态函数往往不能解析表出，这将导致传统的可靠性方法无法求解.因此，近似模型的方法被提出，即利用较少的数值仿真结果，构造一个计算量小、精度高、求解速度快，并能替代结构极限状态函数的模型.目前Kriging方法作为一种新的近似模拟技术^[10]，已在机械、航空等领域得到广泛的应用，该法采用了高斯随机过程模拟，使得预测模型不仅提供了在未知点的预测值，而且还提供了不确定性的估计量.文献^[11]基于Kriging方法的优良拟合特性，高效地求解了结构的可靠性指标.

本文针对热结构耦合梁共振非概率可靠性的功能函数不能表为显性形式，且无法采用传统可靠性分析方法的弊端，为提高近似模型的拟合效率，提出了利用改进Kriging方法所建立的近似模型替代梁结构的共振可靠性功能函数的方法，并与超椭球模型相结合构建梁结构共振非概率可靠性模型，采用优化方法获得了梁结构共振非概率可靠性指标，算例表明了本文所提出方法的可行性和有效性.

1 基于Kriging近似模型的非概率可靠性 1.1 Kriging近似模型

Kriging方法是一种具有统计特征的近似技术，并有平滑效应及估计方差最小等特点，被认为是对真实计算模型最好的线性无偏估计，为复杂结构系统分析及优化提供了方便^[10].Kriging近似模型假设系统的响应是一个随机函数y(x)，由回归模型f(x)和随机误差z(x)组成形式如下:

$y\left( x \right)=\sum\limits_{i=1}^{p}{{{\beta }_{i}}}{{f}_{i}}\left( x \right)+z\left( x \right)={{f}^{T}}\left( x \right)\beta +z\left( x \right).$

式中：f(x)=[f₁(x) f₂(x) … f_p(x)]^T，β=[β₁ β₂ … β_p]^T；p为变量的训练样本容量；z(x)服从正态分布N(0,σ²)，但协方差非零，即

$~cov[z({{x}_{i}}),z({{x}_{j}})]=\sigma _{z}^{2}R({{x}_{i}},{{x}_{j}}), \left( i,j=1\ldots p \right).$

式中：x_i、x_j分别为训练样本的第i和第j个分量；R(x_i,x_j)为两样本点之间的相关函数，可表示为$R({{x}_{i}},{{x}_{j}})=\underset{k=1}{\overset{n}{\mathop{\prod }}}\,{{R}_{k}}(x_{i}^{(k)}-x_{j}^{(k)})$，其中n表示维数，R_k(x_i^(k)－x_j^(k))为^[10]

${{R}_{k}}\left( x_{i}^{(k)}-x_{j}^{(k)} \right)=exp[-\underset{{}}{\overset{n}{\mathop{\sum }}}\,k=1{{\theta }_{k}}{{\left( x_{i}^{(k)}-x_{j}^{(k)} \right)}^{2}}].$

若给定已知训练样本S=[x₁ x₂ … x_p]^T及其响应值Y=[y₁ y₂ … y_p]^T，则任意待求点x_new的线性无偏预测最优值为^[10]

$\hat{y}({{x}_{new}})={{f}^{T}}({{x}_{new}})\hat{\xi }+r{{({{x}_{new}})}^{T}}{{R}^{-1}}(Y-F\hat{\xi }).$

(1)

式中：f(x_new)为回归多项式，一般采用不高于二阶的多项式；${\hat{\xi }}$为Kriging模型多项式系数，即

$\hat{\xi }={{({{F}^{T}}{{R}^{-1}}F)}^{-1}}{{F}^{T}}{{R}^{-1}}Y.$

(2)

式中：F为由样本点处的函数f(x)所组成的列向量；R为由R(x_i,x_j)构成的对称阵；r(x_new)为待求点和训练样本之间的相关向量，其表达式为

$~r({{x}_{new}})={{[R({{x}_{new}},{{x}_{1}})\text{ }R({{x}_{new}},{{x}_{2}})\cdots R({{x}_{new}},{{x}_{p}})]}^{T}}$

方差z的估计值为

$\hat{\sigma }_{z}^{2}={{(Y-F\xi )}^{T}}{{R}^{-1}}(Y-F\xi )/p.$

(3)

式(3)中利用极大似然估计使R满足如下优化问题:

$\underset{\theta >0}{\mathop{min}}\,(m\ln (\hat{\sigma }_{z}^{2})+\ln \left| R \right|)/2.$

通过优化算法求出参数θ并代入式(2)和式(3)便可得到系数${\hat{\xi }}$以及方差估计值$\hat{\sigma }_{z}^{2}$，从而确立式(1)的Kriging模型.

1.2 非概率可靠性模型

本文基于凸模型，将参数不确定性量化在超椭球域内.首先对区间变量进行标准化转换，使变量的可行域归一化为一个等效单位超球域.给定区间变量x∈Rⁿ，满足以下关系^[9]：

${{x}_{i}}=\left( 1+{{\delta }_{i}} \right)\cdot {{{\bar{x}}}_{i}},\left( i=1,2,\ldots ,n \right).$

(4)

式中：x_i为区间参数均值，δ_i为变量x_i相对于x_i无量纲化后的离差.

将区间参数量纲一的离差向量δ的取值范围定义为超椭球集合：

$\delta \in E=\{\delta \,\!:\delta _{i}^{T}{{W}_{i}}{{\delta }_{i}}\le \varepsilon _{i}^{2}\}.$

(5)

式中，W_i为第i个超椭球模型的对称正定矩阵，其决定着超椭球的主轴方向，并与常数ε_i一起控制形状大小.

对W_i进行特征分解，有Q_i^TW_iQ_i=Λ_i，其中Q_i为W_i的特征向量，Λ_i为特征值对角矩阵，引入向量^[9]：

${{u}_{i}}=\left( 1/{{\varepsilon }_{i}} \right)\Lambda _{i}^{1/2}Q_{i}^{T}{{\delta }_{i}}.$

(6)

将式(6)代入式(5)，原凸模型集合可以转换成

${{E}_{c}}=\left\{ u:{{u}^{T}}u\le 1 \right\}.$

式中：u为区间参数x的标准化向量，E_c为标准u空间的单位超球集合.

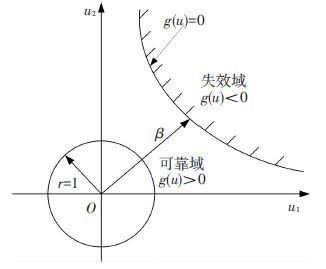
图 1所示为标准空间中的二维单位圆，为区间变量所对应的标准凸域，极限状态方程g(u)经标准化变换后，其极限状态曲线g(u)=0将标准空间划分为可靠域(g(u)>0)与失效域(g(u)<0)，记β为平面坐标原点到极限状态曲线的最短距离.由图 1中可见，当β=1，失效区相切于单位圆，结构处于临界的失效状态；当β>1时，结构变量的离差均处于可靠区内，则结构安全.显然，当β远远大于1时，结构变量的离差范围与极限状态曲线的距离越远，其安全程度就越高,因此可将β定义为结构的非概率可靠性指标^[12].对于多个结构变量的情况，可靠性指标β可采用如下最优化目标函数值形式进行求解：

$\left\{ \begin{align} & ~\underset{u}{\mathop{min}}\,~\underset{i}{\mathop{max}}\,{{\beta }_{i}}=\sqrt{u_{i}^{T}{{u}_{i}}}, \\ & s.t.~g\left( u \right)=0. \\ \end{align} \right.$

(7)

式(7)还可转化成如下等价形式：

$\left\{ \begin{align} & ~\underset{u\beta }{\mathop{min}}\,~ \\ & s.t.\text{ }g\left( u \right)=0 \\ & \sqrt{u_{i}^{T}{{u}_{i}}}\le \beta ,\left( i=1,\ldots ,n \right). \\ \end{align} \right.$

2 热结构耦合梁有限元方程的建立

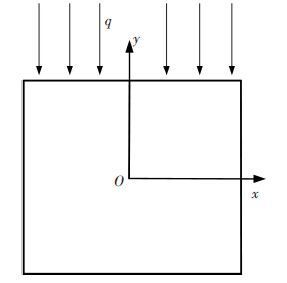
图 2为矩形截面梁结构示意图，梁左右两端固定，其y方向上表面同时受到力f₀和热流q的共同作用，下表面与外界进行对流换热，其余表面均为绝热.热流均匀加载在梁上表面(见图 3)，在梁轴线方向上无温度梯度，热流仅沿梁厚度(－y)方向热传导.对此热结构耦合梁的动力响应求解问题，须同时构建其动力学模型和热分析模型.

2.1 梁动力学有限元模型

沿梁轴向离散为单元并建立梁结构在热载荷下的无阻尼动力学有限元方程^[13]：

$M\ddot{u}+Ku={{F}_{B}}+{{F}_{T}},$

(8)

$K={{K}_{s}}+{{K}_{\sigma }}.$

(9)

式中：M为质量矩阵;u为位移向量;K为刚度矩阵;F_B为力载荷列阵;F_T为热载荷列阵^[14].式(9)中的刚度矩阵K除了结构自身的弹性刚度矩阵${{K}_{s}}={{\int }_{V}}{{B}^{T}}DBdV$外，还考虑了热应力对刚度矩阵的影响，增加了一项热应力刚度矩阵${{K}_{\sigma }}={{\int }_{V}}{{G}^{T}}\Gamma GdV$，其中:B为应变矩阵;D为弹性矩阵;G为形函数对空间坐标的微分矩阵;Γ为应力矩阵.

2.2 梁热分析有限元模型

如图 3所示，沿梁厚度方向离散为单元并建立其耦合热传导有限元方程^[15]：

$C\dot{T}+{{K}_{T}}T+H\dot{u}=P,$

(10)

其中各个矩阵和向量的表达式如下:

$\begin{align} & C=\underset{e=1}{\overset{n}{\mathop{\sum }}}\,\int_{{{V}^{e}}}{\rho }c{{N}^{T}}NdV,H=~\underset{e=1}{\overset{n}{\mathop{\sum }}}\,\frac{E\alpha {{T}_{0}}}{1-\mu }\int_{{{V}^{e}}}{{{N}^{T}}}BdV, \\ & P=\underset{e=1}{\overset{n}{\mathop{\sum }}}\,{{P}^{e}}=\underset{e=1}{\overset{n}{\mathop{\sum }}}\,\int_{{{S}^{e}}}{q}{{N}^{T}}dS, \\ & {{K}_{T}}=\underset{e=1}{\overset{n}{\mathop{\sum }}}\,\left( K_{k}^{e}+K_{h}^{e} \right)=\underset{e=1}{\overset{n}{\mathop{\sum }}}\,\int_{{{V}^{e}}}{k}{{(\frac{\partial N}{\partial x})}^{T}}(\frac{\partial N}{\partial x})dV+ \\ & \underset{e=1}{\overset{n}{\mathop{\sum }}}\,\int_{{{V}^{e}}}{h}{{N}^{T}}NdS. \\ \end{align}$

式中：C为热容矩阵；T为节点温度列阵；N为节点温度形函数；P为节点热载荷列阵；K_k、K_h分别为热传导刚度矩阵和对流换热矩阵；H为热结构耦合矩阵，它表示热载荷与结构变形的耦合作用对温度场的影响；ρ为质量密度;k为热传导系数;μ为泊松比;h为换热系数;q为热流量;c为比热容;T₀为结构初始温度;α为热膨胀系数;E为弹性模量.

联立求解式(8)和式(10)方可实现梁的热结构耦合动力响应分析.

2.3 热结构耦合作用下梁的固有频率分析

在热环境下梁结构的固有频率计算即为求解式(11)的广义特征值问题：

$(K-{{\omega }^{2}}M)\Phi =0.$

(11)

式中:ω为结构固有频率，Φ为结构振型向量.

在式(11)求解中，质量矩阵M不受温度影响，则结构固有频率ω仅与结构刚度K相关.由于在温变下所引起结构内部的热应力将导致K的改变，从而影响结构的固有频率.故在求解热环境下的结构动力特性时，需考虑热环境对结构刚度的影响.

3 热结构耦合梁共振非概率可靠性分析方法 3.1 热结构耦合梁共振非概率可靠性模型

为了防止梁结构的共振失效，结构激振力频率与固有频率应保持在一定的范围.假设结构的激振力频率为ω，固有频率为ω_i(x)，根据振动理论建立共振可靠性功能函数：

$Z={{g}_{i}}=\left| \omega -{{\omega }_{i}}\left( x \right) \right|-\gamma ,\left( i=1,2,3 \right).$

(12)

式中：x为影响结构固有频率参数向量；ω_i(x)为结构前3阶固有频率；γ为特定区间.

由热结构耦合作用下梁的固有频率分析可知，结构刚度矩阵K与物性参数以及热应力有关，因此需要联立式(8)和式(10)进行求解，由于方程式(8)和式(10)的非线性以及需要相互迭代计算，因此刚度矩阵K属于非线性隐式函数.而在式(12)中，共振可靠性功能函数中的固有频率ω_i(x)与刚度矩阵K是密切相关的，故共振可靠性功能函数Z也为非线性隐式函数.针对该问题采用传统方法来求解其可靠度将变得十分困难，特别是考虑方程的变量参数为区间不确定性变量之后，将使得计算更加复杂.为此，本文采用改进Kriging方法所建立的模型代替功能函数Z，并结合优化算法对所拟合的功能函数进行非概率可靠度指标的求解.

3.2 改进Kriging的非概率可靠度求解方法

本文进行可靠度分析的关键是如何准确的拟合功能函数Z所对应的极限状态曲面.由于抽样样本计算出来的功能函数值大多分布在极限状态曲面(Z=0)两侧，而那些在极限状态曲面附近的样本点则显得尤为重要，将直接影响到能否准确的拟合出极限状态曲面，它们具有如下两个特征^[16]：

1)这些点非常接近极限状态曲面，其拟合函数值$\left| \hat{y}\left( x \right) \right|$值接近0；2)对应的Kriging方差$\sigma _{{\hat{y}}}^{2}\left( x \right)$值较大.

考虑上述两个特征，利用学习函数L(x)构造如下方程^[16]：

$\left| \hat{y}\left( x \right) \right|-L\left( x \right)\sigma _{{\hat{y}}}^{2}\left( x \right)=0$

式中：$\hat{y}\left( x \right)$为Kriging近似模型的预测值；${{\sigma }_{{\hat{y}}}}\left( x \right)$为Kriging近似模型的标准差；L(x)用来衡量Kriging近似模型预测极限状态曲面的精度.

本文利用学习函数L(x)改进了Kriging方法选取新增训练样本的方式，使得Kriging法所拟合出来的近似模型在样本点分布的区域能更快地逼近真实极限状态方程，忽略了那些离极限状态曲线较远的样本点，从而达到提高计算精度的目的.利用改进Kriging法建立热结构耦合梁共振非概率可靠度模型的算法步骤如下：

1) 确定结构各区间参数的均值与离差.2) 初始化变量，根据参数变化区间采用拉丁超立方抽样法设计样本空间S.3) 联合迭代求解热结构耦合方程式(8)和式(10)，得到初始训练样本.基于遗传算法对Kriging近似模型参数θ进行优化并建立功能函数的近似模型$\hat{y}\left( x \right)$.4) 利用主动学习法，在总样本空间S中搜索最佳训练样本点.通过不断更新训练样本，以学习函数L(x)最小值所对应的样本点作为最佳训练样本，提高Kriging近似模型对功能函数的预测精度.5) 将新增样本点代入式(8)和(10)计算出结构响应值，重新生成新样本下的Kriging近似模型.不断重复步骤4)~5)，当满足判定条件minL(x)≥2时便停止主动学习，此时的样本已达到计算精度的要求.6) 将最优的Kriging近似模型作为功能函数替代模型，根据式(4)将变量转化成标准向量并构建凸集模型，对此建立非概率可靠性模型并采用二次规划优化算法求解非概率可靠度指标.

4 算例分析 4.1 数值小算例

假设极限状态方程f(x,y)=3+3x+3y－x²－y²+2sin 3x－sin 3y=0.以18组初始训练样本构建最初Kriging近似模型.利用遗传算法求得变量参数θ最优值为1.326 7.根据改进Kriging的非概率可靠度求解方法所述，展开主动学习，按照判定条件不断选取新的训练样本进行计算，使改进Kriging法所建立的近似模型逐渐逼近极限状态方程曲线.图 4(a)给出了近似模型第8次拟合的极限状态曲线，图 4(b)显示了在最后收敛时的拟合极限状态曲线.

对Kriging方法在改进前后所建立的近似模型精度进行对比分析见表 1，随机抽取100个样本进行方差对比($({{\sigma }^{2}}=1n\underset{i=1}{\overset{n}{\mathop{\sum }}}\,{{\left( {{y}_{i}}-y_{i}^{'} \right)}^{2}}$，其中：y为原函数值，y^'为模型预测值)，从表 1对比结果中可见改进Kriging方法在拟合精度上有了明显提高.

4.2 梁结构共振非概率可靠度分析

如图 2所示，选取航空航天领域内广泛采用的钛铝合金梁作为研究对象，尺寸为：1 000 mm×30 mm×30 mm，上表面受均匀热流q以及中部受到竖直方向激振力F=f₀sin(2πωt)作用，f₀=10 kN，初始温度T₀=20 ℃.材料及载荷的区间参数见表 2.根据共振理论建立梁结构可靠性分析功能函数为：Z=g_i=|ω－ω_i(x)|－γ，γ取相应频率均值的10%~15%.

选取20组训练样本构建初始Kriging近似模型，利用主动学习方法不断新增训练样本，达到56组时满足判定条件，然后将得到的近似模型替代原隐式极限状态方程，并将区间变量转化为超椭球模型，采用二次规划算法求解超椭球模型非概率可靠度指标.求解出梁结构的前三阶固有频率为159.25、437.29、856.79 Hz.梁结构的共振非概率可靠度指标为η=1.853，由于外激励频率360 Hz处于一阶与二阶固有频率之间，故非概率可靠度指标大于1，梁结构不会发生共振失效.本文算例还得出热应力所引起的梁结构内部应力大小为180 MPa，小于梁结构的临界应力载荷230 MPa，故梁结构不会产生屈曲现象.

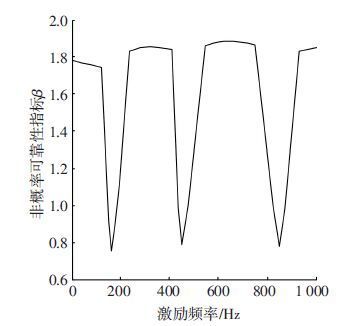
图 5给出了可靠度指标随着激励频率变化的曲线图，在共振频率的周围，结构的非概率可靠性指标(β)小于1，结构不可靠.图 6则从结构的位移响应验证了图 5的正确性，图 6中给出梁中点位置随激励频率变化的位移曲线，激励频率越远离共振频率，结构就越可靠.

在表 3中，假设变量在其区间范围内呈均匀分布，将Monte Carlo法模拟计算结果作为近似精确解.本文方法计算结果与其相对误差为1.53%，但迭代次数仅为56次，结构响应值的计算次数明显减少.而本文方法虽然比采用响应面法的迭代次数多，但本文的计算结果则更加接近精确解，表明本文方法具有较高的计算效率.表 4说明了热结构耦合的作用使得梁结构各阶固有频率值有所增大，且增加幅度基本相同.由于共振可靠性对固有频率比较敏感，因此在进行共振可靠性分析时，有必要考虑热结构耦合效应对固有频率的作用.

5 结 论

1) 将改进的Kriging模型与椭球凸集模型相结合，构建了热结构耦合梁共振非概率可靠性模型，并采用优化方法对可靠性指标进行了求解，避免了计算模型的重复调用，大大减小了计算量，数值计算结果验证了本文所提方法的准确性与高效性.

2) 热结构耦合效应对梁固有频率有增大的作用，故在热载荷下计算梁的共振可靠性时应考虑热结构耦合效应的影响.