2. 江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003 ;
3. 中国石油集团 渤海装备辽河重工有限公司,辽宁 盘锦 124010
2. School of Architecture & Ocean Engineering,Jiangsu University of Science and Technology,Zhenjiang 212003,Jiangsu,China ;
3. China Petroleum Liaohe Equipment Company,Bohai Equipment Manufacturing Co.,Ltd.,Panjin 124010,Liaoning,China
自升式平台的桩腿直接站立于海床上,它不仅承受着外界环境载荷,还承受着来自于平台的所有载荷作用,桩腿的损伤将导致整个平台无法作业甚至重大海难事故的发生,这就使得桩腿成为自升式平台强度分析中最关键的结构.国内外学者对自升式平台桩腿结构研究已取得了大量的成果,但基本集中在对桩腿结构形式对比、载荷计算方法、强度计算方法及建造精度控制方法等方面的研究[1-5],目前尚未有文献资料对桩腿节距和弦管间距变化对平台整体性能的影响来进行研究.
自升式平台设计建造向深水化、个性化和特殊海域作业方向发展趋势明显,但符合上述功能要求的平台可供参考母型资料匮乏,加之平台桩腿结构优化设计要求,因此,在设计初期,能够综合评估桩腿总强度影响因素,快速给出平台桩腿节距和弦管间距最优方案,是目前具有重要意义的研究课题.
目前桁架式桩腿的结构型式有K型、逆K型以及X型等,公认的最优型式为逆K型,因此本文直接选取逆K型桩腿结构型式进行研究.桩腿设计的通常做法是直接参考母型平台的桩腿设计,还未有文献详细描述桩腿设计的具体细节.本文首次考虑不同的桩腿节距和弦杆间距,采用参数化建模程序,实现逆K型桩腿快速建模,然后通过SESAM的GeniE软件读取模型,对平台自存工况下的桩腿结构总强度和拖航工况下的桩腿强度进行校核,得到桩腿结构部件强度校核结果、升降机构锁紧力、桩靴基底最大支反力、平台抗倾稳性等指标随桩腿节距和弦管间距变化的趋势曲线,结合不同桩腿形式的耗钢量,搜寻出各项指标最优的结构参数,对桩腿结构进行快速设计,为自升式平台的设计和建造提供参考和依据.
1 工况分析在自升式平台的整个生命周期中,主要经历拖航、安装、作业和自存等工况,对桩腿而言,拖航工况、安装工况和作业工况的环境条件相对比较温和,决定其强度的工况为自存工况.平台在拖航时,百米高度的桩腿立于甲板之上,平台较小的摇摆会在桩腿结构产生较大的惯性载荷,因此本文在研究桩腿构型选取时主要考虑拖航工况和自存工况.
1.1 拖航工况自升式平台拖航(湿拖)过程中,桩腿收回,高耸于平台之上,处于漂浮状态,受海洋风、浪、流等因素影响显著,如图 1所示.在外载荷作用下,平台产生摇荡运动,在桩腿上产生较大的惯性载荷,对桩腿强度产生了较大的影响,严重时甚至可能导致桩腿损坏,因此拖航工况下的桩腿强度分析是桩腿结构优化所必须考虑的工况.

|
图 1 拖航时平台的运动 Figure 1 Platform motion under towing condition |
规范中假设平台在拖航工况下的运动为简谐运动,平台任意时间t下的运动状态θ为[6]
| $\theta ={{\theta }_{0}}sin\frac{2\pi t}{T}$ |
式中:T为平台运动周期,s;θ0为平台运动最大幅值,(°).
平台横摇/纵摇运动的旋转轴位于水平面,并通过平台的重心,距旋转轴距离为r1的任一集中质量的垂向加速度a为
| $a=-2\pi {{T}^{2}}{{\theta }_{0}}{{r}_{1}}sin\frac{2\pi t}{T}.$ |
则垂向加速度的最大值amax为
| $~{{a}_{max}}={{\left( \frac{2\pi }{T} \right)}^{2}}{{\theta }_{0}}{{r}_{1}}.$ |
amax相对于重力加速度g的放大因子f1为
| ${{f}_{1}}={{\left( \frac{2\pi }{T} \right)}^{2}}{{\theta }_{0}}{{r}_{1}}/g.$ |
平台升沉、纵荡、横荡运动和风载荷因素对横摇/纵摇运动的耦合效应,通过给定载荷因子γ=1.2,对重力加速度放大因子进行简化考虑后,平台横摇/纵摇运动引起的距旋转轴水平距离为r2的任一集中质量的水平加速度最大值相对于重力加速度g的放大因子f2为
| ${{f}_{2}}={{\left( \frac{2\pi }{T} \right)}^{2}}{{\theta }_{0}}{{r}_{2}}/g+1.2sin~{{\theta }_{0}}.$ |
自存工况是平台所能承受的最恶劣的环境条件[7-8],需要综合考虑流体的作用、结构的动力学特性和平台的几何非线性等,对该工况下的平台进行研究分析后需要提供桩腿的强度分析、桩腿在锁紧装置处的锁紧力、桩腿的最大支反力以及平台的抗倾能力等结果,从而对平台的整体安全性能进行全面的评估,为桩腿结构形式的决定提供数据参考.
自升式平台在自存工况下,桁架式桩腿站立于海底,承受海洋风、波浪和海流的环境载荷、由外界变化载荷产生的惯性载荷以及平台发生水平位移后由自重产生的几何非线性载荷[9].
风载荷是自升式平台设计过程中的主控载荷之一,风速随时间和高度变化,通常情况下,参考结构的高度系数和形状系数,利用风载荷计算经验公式求解平台风载荷,但因其对构件间遮蔽效应等因素考虑不足,计算结果偏于保守,在缺乏母型船资料的情况下,风洞试验是研究风对结构物作用的一种常用方法,风洞试验方法可以综合考虑构件形状、高度和位置的影响因素[10-13],本文采用风洞试验方法获取风载荷数据.
波浪和海流载荷主要作用在桩腿上,可利用Morison公式进行计算,计算中考虑自存工况下大幅波浪的非线性作用以及海流对波浪的拉伸影响等.其中桩腿的弦管属于非规则圆形剖面,因此需对其做相应的等效处理来进行水动力载荷计算[14-15].
波浪的循环往复运动将对桩腿产生惯性载荷,本文选择动态系数放大法计算该惯性载荷,即假设自升式平台及其基础相当于质量-弹簧-阻尼系统[6],平台的动态响应幅值与准静态响应幅值的比值是稳定状态下频率和周期的函数,通过DAF(动态放大因子)来计算周期性的正弦激励,如
| $DAF=\frac{1}{\sqrt{{{\left[ 1-{{\left( \frac{{{T}_{N}}}{{{T}_{W}}} \right)}^{2}} \right]}^{2}}+{{\left[ 2\varepsilon \frac{{{T}_{N}}}{{{T}_{W}}} \right]}^{2}}}}.$ |
式中:TN为平台固有周期,s,通过GeniE进行模态分析获取固有周期值;TW为波浪周期,s;ε为阻尼比,取0.07.当DAF≥1.05时,需要计及惯性载荷影响,惯性载荷计算如下:
| $\begin{align} & {{F}_{in}}=\left( DAF-1 \right)B{{S}_{Amplitude}}, \\ & B{{S}_{Amplitude}}=\left( B{{S}_{\left( Q-S \right)max}}-B{{S}_{\left( Q-S \right)min}} \right)/2 \\ \end{align}$ |
式中:BSAmplitude是一个波浪周期内准静态基础剪力的幅值;BS(Q-S)max为最大准静态基剪力;BS(Q-S)min为最小准静态基剪力.
自升式平台的桩腿是相对柔性结构,在上述各种载荷的作用下平台将产生较大的水平位移,桩靴垂向支反力的作用线不再通过桩腿形心,导致桩腿的弯矩比线性分析结果大,此弯矩将引起附加变形,属于大位移非线性问题[16-17].本文采用附加弯矩法考虑几何非线性的影响,即将平台在外载荷作用下计算得到的水平位移Δ和轴力P,按线性方法计算附加弯矩ΔM=P·Δ,将它与原计算的弯矩M1叠加,通过反复迭代求得总弯矩M[18].
2 模型建立本文选取115.0、107.0、91.5 m这3种水深进行分析,假设浪向和风向一致,以0°,60°,90°,120°,180°风向和浪向进行计算,假设波浪周期不随波高和水深变化,具体参数见表 1.
| 表 1 海洋环境参数 Table 1 Ocean environmental parameter |
本文采用SESAM的GeniE软件建立自升式平台有限元模型,对主船体结构纵横舱壁采用等效截面梁的形式进行模拟,通过调整材料密度和施加质量球的形式来调整整个主船体的质量和重心.利用强度等效原则,桩腿弦管采用等效梁建模,撑管单元以实际尺寸的梁单元进行模拟.
桩腿底部边界条件依据规范取为海床下3.05 m 处铰支[6].桩腿与主船体的连接的模拟是桩腿弦管与围阱区上、下导块和锁紧结构的3点连接,上下导块只约束水平位移,锁紧位置同时约束水平和竖直位移.
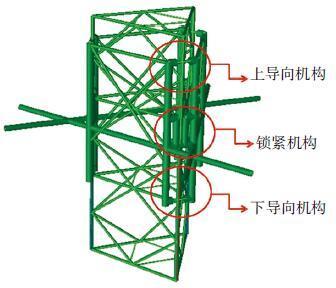
本文中风载荷采用风洞试验结果,按照力的大小和分布都相似的原则直接施加到结构上;在GeniE软件中计算波流载荷,采用Morison公式,选择Stokes五阶波理论,计算过程中软件自动加载波流载荷;考虑DAF效应和P-Δ效应,通过手工计算,采用刚性梁传递的形式,将上述附加载荷传递到结构上,如图 2所示.图 2中红色箭头表示的是附加载荷,蓝色球为质量等效单元,在保证质量重心不变的情况下施加.图 3描述了锁紧机构有限元分析模型.

|
注:彩图见电子版(http://hit.alljournals.cn)(2016年第10期) 图 2 载荷施加示意图 Figure 2 Load diagram |
|
图 3 锁紧及导向机构有限元模型 Figure 3 FEM of locking and guiding structure |
本文通过参数化建模,避免了多工况、变结构带来的重复性建模工作,分析过程如下:
1) 对各工况下的桩腿强度分析模型进行参数化编程;
2) 调用GeniE软件进行结构建模;
3) 进行环境载荷、重力载荷以及惯性载荷计算,并将载荷计算结果施加到强度分析模型中;
4) 对拖航工况下的桩腿强度进行有限元计算,得到桩腿强度分析的校核结果;
5) 改变桩腿节距,重复步骤1)~4),得到桩腿不同节距时的结构型式、结构质量、各类部件强度校核结果的变化规律;
6) 对自存工况下的桩腿总强度进行有限元计算,得到UC值、桩腿锁紧装置处的锁紧力、抗倾覆能力和桩靴基底的支反力;
7) 改变桩腿节距和弦管间距,重复步骤1)~3)、6),得到不同桩腿构型时的总强度计算结果及其变化规律.
3 结果分析本文首先研究了拖航工况下不同节距对桩腿质量和强度的影响,然后给出了自存工况下不同节距和弦管间距对桩腿质量和总强度的影响.强度校核是对桩腿的屈服和屈曲的联合校核,即考察桩腿承载外界环境载荷的能力,通常以外界影响/结构承载力的百分比表示(UC),当UC<1,则代表桩腿结构安全.
按照上述参数化建模方法进行有限元分析,可以快速地完成桩腿结构快速设计过程中涉及的工况多、分析次数多的反复性工作.
结合ABS规范[18],屈服失效准则要求,在静载工况下,轴向或弯曲应力的安全系数取值为1.67,剪切应力安全系数取值为2.50;在组合工况下,轴向或弯曲应力的安全系数取值为1.25,剪切应力安全系数取值为1.88.屈曲失效准则要求,在静载工况下,构件的屈曲强度安全系数取值为1.67,组合工况下安全系数取值为1.25.
3.1 拖航工况下的结果校核通过编程得出GeniE可以识别的命令文件,完成单桩腿参数化建模,在GeniE软件中施加载荷,进行拖航工况的桩腿强度计算,得到随节距变化的桩腿质量、通过模态分析可以得到平台的固有周期,见表 2.同时得到桩腿结构校核UC,见表 3.
| 表 2 不同节距对应的桩腿质量及平台固有周期 Table 2 Leg guality and nature periods of different pitches |
| 表 3 桩腿屈曲和屈服校核UC值表 Table 3 UC value of buckling and yield check for legs |
表 3是在0°载荷方向进行分析得到的统计数据,由结果可知,拖航工况下,桩腿斜撑管结构UC值普遍高于其他结构,当桩腿节距取值7.930 m 时,管节点UC值激增至0.95,临近失效.结合有限元分析桩腿结构应力云图可知,位于上下导向结构之间的斜撑管结构失效概率最大.因此,本文给出了不同节距下的斜撑管在不同外载荷方向下的强度校核结果,如图 4所示.

|
图 4 不同载荷方向下的斜撑管UC值 Figure 4 Brace tubes UC values under different load directions |
综合以上拖航工况下的桩腿强度分析结果,得出如下结论:
1) 桩腿质量递变趋势与节距变化趋势相反,即桩腿质量随节距增大而减小,由于桩腿为柔性构件,在外载荷作用下,平台主体结构发生相对偏离,但其偏离位移与节距变化并不呈现递变规律,此偏离值引起桩腿结构几何非线性效应,即P-Δ弯矩.
2) 由桩腿结构单元屈曲与屈服联合校核结果可知,上下导向结构之间桩腿单元的斜撑管UC值最大,极易容易受损失效.
3) 斜撑管UC值随桩腿节距增大而增大,在不同方向的外载荷作用下,0°和60°方向斜撑管承载力最大,其失效概率最大,因此,在拖航工况下,可仅考虑0°和60°方向加载.
上述分析可知,在桩腿结构满足强度和质量最轻要求的条件下,拖航工况下桩腿节距建议取值7.930 m.
3.2 自存工况下的结果校核自存工况下,外界环境载荷作用于平台,平台抗倾能力评估是总强度分析中需要考虑的问题,抗倾覆能力为抗倾力矩与载荷弯矩的比值,其中,抗倾力矩是平台固定载荷与50%可变载荷之和与抗倾力臂的乘积,载荷弯矩是风浪流引起的弯矩与考虑动态放大效应DAF和二次附加弯矩P-Δ效应的三者之和;同时平台底部所达到的最大支反力可以用来反推平台的预压能力;此时桩腿锁紧装置处的最大轴向力也为锁紧装置的能力评估提供了参考,通过有限元应力云图,在锁紧机构处,可以提取不同工况下的锁紧力,因此总强度分析中给出了平台的抗倾覆能力、最大支反力、锁紧力以及桩腿构件的强度评估结果.
3.2.1 不同弦管间距的分析结果计算中桩腿节距固定取为7.930 m ,以母型船11.75 m 为参考,0.5m 为步长,选取5组不同的弦管间距,分别为10.75、11.25 、11.75、12.25、12.75 m.以目标平台115 m作业水深为例,对平台校核结果进行分析,如图 5~8所示.

|
图 5 不同弦管间距0°载荷方向时的桩腿UC值 Figure 5 UC values for different chord spaces under 0° load direction |
|
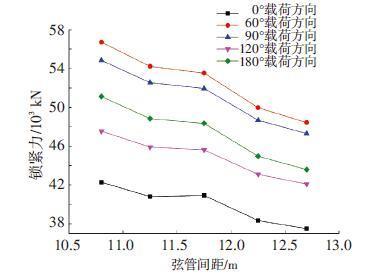
图 6 不同弦管间距时的最大锁紧力 Figure 6 Maximum locking forces for different chord spaces |

|
图 7 不同弦管间距时的基底最大支反力 Figure 7 Basal maximum support for different chord spaces |
|
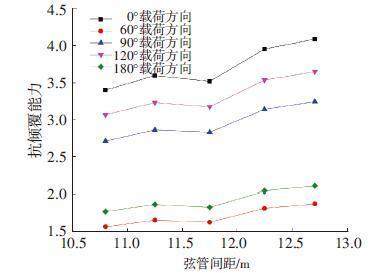
图 8 不同弦管间距时的抗倾稳性 Figure 8 Overturning stability for different chord spaces |
图 5是对0°载荷方向,不同弦管间距的桩腿结构UC值进行比较,由结果可知,弦管间距增大对弦管结构和管节点UC值递降趋势显著,撑管结构UC值对弦管间距变化敏感性较弱,在所选取的弦管间距构型条件下,桩腿所有组件结构均满足屈曲和屈服强度要求,因此,增大弦管间距有利于提升桩腿承载能力,但同时会增加桩腿结构质量,经济性能降低,应综合考虑各种因素的影响.
由图 6结果可知,5组典型载荷方向的锁紧装置处最大锁紧力对弦管间距变化具有较强的敏感性,最大锁紧力随弦管间距增大迅速降低,本文研究所参考的平台锁紧装置最大承载力达72 500 kN,在所选取的弦管间距下,锁紧力都在安全范围之内,且弦管间距越大,锁紧装置越安全;通过图 6比较,亦可知锁紧力在载荷方向60°时最大,0°方向载荷作用下锁紧力最小.
由图 7结果可知,各载荷方向下的最大支反力均出现在11.75 m弦管间距附近,最大支反力是桩靴结构设计主要参考参数,同时也直接影响平台预压载能力;通过图 7比较,亦可知120°载荷方向下的地基支反力高于其他方向载荷方向的地基支反力.
由图 8结果可知,平台抗倾稳性对弦管间距较为敏感,随弦管间距增大而增大,在本文所选取的弦管间距构型下,平台都具有较好的抗倾能力;通过图 8比较,亦可知60°载荷方向下平台抗倾能力相对低于其他载荷方向,但该载荷方向下最低的抗倾稳性系数亦在1.5以上,满足设计标准要求.
综合以上研究结果可知,各弦管间距都满足平台整体性能的要求,因此按照质量最轻的原则,并同时考虑桩靴对地承压比的要求,取弦管间距为11.75 m.
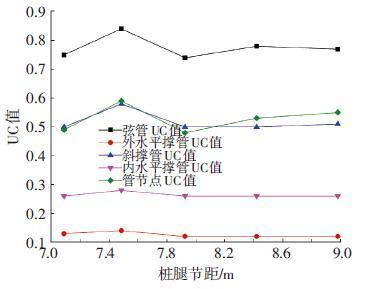
3.2.2 不同桩腿节距的分析结果本文取弦管间距11.75 m ,在保证桩腿总长不变,并满足上下段桩腿长度要求,改变定长段桩腿节数,选取5组不同的桩腿节距对自存工况下的桩腿总强度进行研究,桩腿节距分别为7.090、7.485、7.930、8.420、8.980 m,以目标平台115 m 作业水深为例,对平台进行参数化分析得出的结果如图 9~12所示.
|
图 9 不同桩腿节距0°载荷方向时的桩腿UC值 Figure 9 UC values for different pitches under 0° load direction |

|
图 10 不同桩腿节距时的最大锁紧力 Figure 10 Maximum locking forces for different pitches |
|
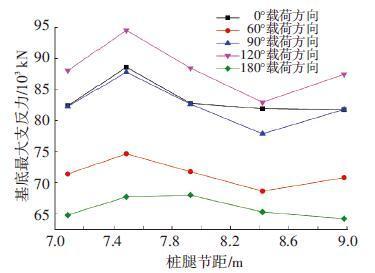
图 11 不同桩腿节距时的基底最大支反力 Figure 11 Basal maximum support for different pitches |
|
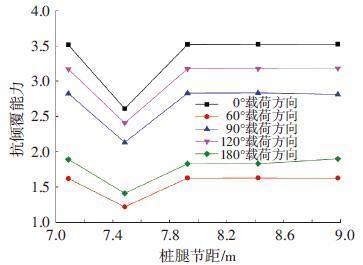
图 12 不同桩腿节距时的抗倾稳性 Figure 12 Overturning stability for different pitches |
由图 9~12的分析结果可知,当桩腿节距取值7.485 m时,桩腿结构强度校核的UC值、锁紧力和支反力均达最大,平台的抗倾能力亦为最差,其他节距取值时分析结果变化平缓.究其原因,当节距取值7.485 m时,平台固有周期与计算的波浪周期接近,进而产生共振,导致平台各项性能指标降低,因此,在平台设计中,应避免平台固有周期与外界环境载荷作用周期接近的情况.
综合以上研究结果可知,除了7.485 m 的桩腿节距,其他桩腿节距都满足平台整体性能的要求,因此按照质量最轻的原则,针对自存工况分析,可取最大的桩腿节距8.98 m.
3.2.3 不同弦管间距和桩腿节距的桩腿质量结果桩腿结构形式的优化应在保证平台整体性能的同时,还应使其质量达到最轻,图 13,14给出了随弦管间距和桩腿节距变化的桩腿质量结果.

|
图 13 桩腿质量随弦管间距的变化趋势 Figure 13 The variation trend of leg weights with chord space |

|
图 14 桩腿质量随桩腿节距的变化趋势 Figure 14 The variation trend of leg weights with leg pitches |
根据图 13,14可知,弦管间距从12.75 m减小到10.75 m,桩腿质量降幅达到137 t ;桩腿节距从7.090 m增加到8.980 m,桩腿质量降幅达到169 t ,综合考虑弦管间距和桩腿节距因素,可实现减重300 t左右.
结合拖航工况及自存工况联合分析,如果选取自存工况下推荐的8.980 m 桩腿节距,在拖航工况下,桩腿斜撑管和管节点将失效,因此,可以快速的确定最优桩腿节距7.930 m 和弦管间距11.75 m 的桩腿构型.
本文参考平台桩腿节距由8.540 m 降至7.930 m,弦管间距由13.10 m降至11.75 m ,桩腿质量降低达20%左右,经济性显著.
4 结 论1) 拖航工况下,桩腿斜撑管和管节点强度对桩腿节距变化敏感性较强,随节距增大,UC值增大,在节距7.930 m时UC值激增至0.95,临近失效,因此,7.930 m 为桩腿节距极限值.
2) 拖航工况下,斜撑管UC值普遍高于其他桩腿组件,结合不同载荷方向下的斜撑管UC值分析,可知0°和60°载荷方向下的斜撑管失效概率最大.
3) 自存工况下,桩腿撑管UC值对弦管间距变化敏感性较弱,但弦管间距UC值和锁紧力随弦管间距增大而降低,平台抗倾能力随弦管间距增大而增强.
4) 自存工况下,桩腿节距取值7.485 m时,因其构型下的平台固有周期接近波浪周期,水动力动态放大效应显著,导致桩腿结构强度校核的UC值、锁紧力和支反力均达最大,平台的抗倾稳性亦为最差,因此需要考虑桩腿构型变化对平台固有周期的影响.
| [1] |
KARUNAKARAN D, SPIDSOE N. Verification of methods for simulation of nonlinear dynamic response of jack-up platforms[J].
Marine Structures,1997, 10 (2-4) : 181-219.
DOI: 10.1016/S0951-8339(96)00023-8 ( 0) 0)
|
| [2] |
CASSIDY M J. Non-linear analysis of Jack-up structures subjected to random waves [D]. Oxford: University of Oxford, 1999.
( 0) 0)
|
| [3] |
任宪刚.深浅海自升式平台结构非线性分析方法研究[D].哈尔滨:哈尔滨工程大学,2012.
REN Xiangang. Research on non-linear analysis method of jack-up unit’s structure in deeper sea[D]. Harbin: Harbin Engineering University,2012. (  0) 0)
|
| [4] |
张建, 唐文献, 苏世杰, 等. 环境载荷对自升式钻井平台动力响应的影响[J].
中国造船,2013, 54 (1) : 93-100.
ZHANG Jian, TANG Wenxian, SU Shijie, et al. Effect of environmental loads on dynamical responses of jack-up[J]. Shipbuilding of China,2013, 54 (1) : 93-100. (  0) 0)
|
| [5] |
陆浩华.自升式海洋平台结构动力响应分析[D].武汉:武汉理工大学,2005.
LU Haohua. The dynamic response of offshore jack-up platform[D]. Wuhan: Wuhan University of Technology,2005. (  0) 0)
|
| [6] |
Technical and research bulletin 5-5A site specific assessment of jack-up units[S]. New Jersey: Society of Naval Architects and Marine Engineers, 2012.
( 0) 0)
|
| [7] |
沈恺.海洋自升式平台结构安全评估及寿命预报[D].上海:上海交通大学,2002.
SHEN Kai.Structural safety assessment and life prediction of offshore jack-up platform[D]. Shanghai: Shanghai Jiao Tong University,2002. (  0) 0)
|
| [8] |
郭东杰.在役自升式平台风暴自存状态强度评估[D].天津:天津大学,2009.
GUO Dongjie. The strength evaluation in survival condition for Jack-up in service[D].Tianjin: Tianjin University,2009. (  0) 0)
|
| [9] |
吴小平, 陆晟. 自升式钻井平台环境载荷及结构强度[J].
上海造船,2010 (3) : 36-40.
DOI: 10.3969/j.issn.1005-9962.2010.03.009 WU Xiaoping, LU Sheng. Environmental loading and structure strength of self-elevating drilling units[J]. Shanghai Shipbuilding,2010 (3) : 36-40. DOI: 10.3969/j.issn.1005-9962.2010.03.009 (  0) 0)
|
| [10] |
林一, 胡安康, 孙建. 自升式平台风载荷的空气动力学干扰研究[J].
船舶与海洋工程,2013 (2) : 5-10.
DOI: 10.3969/j.issn.2095-4069.2013.02.002 ( 0) 0)
|
| [11] |
林长刚.自升式海洋平台风载荷及风暴环境图谱研究[D].大连:大连理工大学,2013.
LIN Changgang.Research on wind loads and environmental charts for storm of Jack-up platform[D]. Dalian: Dalian University of Technology,2013. (  0) 0)
|
| [12] |
谭美, 冯军, 熊飞. 自升式钻井平台风载荷研究[J].
船舶与海洋工程,2014 (1) : 18-23.
DOI: 10.3969/j.issn.2095-4069.2014.01.004 ( 0) 0)
|
| [13] |
林一, 胡安康, 熊飞. 自升式平台风载荷数值模拟与试验研究[J].
水动力学研究与进展,2012, 27 (2) : 208-215.
DOI: 10.3969/j.issn1000-4874.2012.02.013 LIN Yi, HU Ankang, XIONG Fei. Numerical simulation and experiment study on wind load of Jack-Up platform[J]. Journal of Hydrodynamics,2012, 27 (2) : 208-215. DOI: 10.3969/j.issn1000-4874.2012.02.013 (  0) 0)
|
| [14] |
黄祥鹿, 陆鑫森.
海洋工程流体力学及结构动力响应[M]. 上海: 上海交通大学出版社, 1992 .
( 0) 0)
|
| [15] |
钱昆.浮体在大幅波浪中的运动和荷载计算研究[D].大连:大连理工大学,2004.
QIAN Kun. Study on calculation of motions and loads on floating bodys in large amplitude waves[D].Dalian: Dalian University of Technology,2004. (  0) 0)
|
| [16] |
徐长航, 陈国明, 谢静, 等. 风暴状态下自升式平台非线性动力分析模型[J].
石油大学学报(自然科学版),2003, 27 (4) : 80-86.
DOI: 10.3321/j.issn:1000-5870.2003.04.021 XU Changhang, CHEN Guoming, XIE Jing, et al. Nonlinear dynamic analysis model for jack-ups under extreme storm condition[J]. Journal of the University of Petroleum,China(Edition of Natural Science),2003, 27 (4) : 80-86. DOI: 10.3321/j.issn:1000-5870.2003.04.021 (  0) 0)
|
| [17] |
施丽娟, 李东升, 潘斌. 自升式钻井平台结构自振特性分析[J].
中国海上油气(工程),2001, 13 (5) : 6-8.
DOI: 10.3969/j.issn.1673-1506.2001.05.002 SHI Lijuan, LI Dongsheng, PAN Bin. Analysis of bibration characteristics for jack-up rigs[J]. China Offshore Oil And Gas(Engineering),2001, 13 (5) : 6-8. DOI: 10.3969/j.issn.1673-1506.2001.05.002 (  0) 0)
|
| [18] |
Rules for building and classing mobile offshore drilling units[S]. Houston: American Bureau of Shipping, 2014.
( 0) 0)
|
 2016, Vol. 48
2016, Vol. 48


