2. 中国科学院大学,北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
近年来,有效载荷传感器的精度不断提高,如高分辨率的光学载荷[1]、SAR载荷等,这些应用对卫星数据传输效能提出了更高的要求.同时,随着微小卫星的发展,遥感系统星座化已成为一种发展趋势[2].由于体积、质量的约束,小卫星往往具有更加严格的能源设计限制[3].如何在有限的数传时间内,以尽可能小的能耗完成将大量数据下传给地面站的任务,已成为卫星数传工程领域亟待解决的问题.虽然具有更高带宽的Ka频段已被广泛认为未来对地探测卫星下行数据链路的发展方向[4],但是,目前我国存在大量技术成熟的X波段地面站设备,改造成为Ka波段需要投入大量的经费和时间成本.因此,研究通过新型数传体制以提高X波段数传链路效能仍然非常必要.
可变编码调制(variable coding modulation,VCM)是在通信过程中快速切换信道编码和调制方式的方法.VCM要求预先设计好编码调制方式选用的流程.遥感卫星的动态信道条件是可以预测的,无须设计信息反馈结构,因此其数传系统满足使用VCM的条件.例如,随着卫星轨道位置的变化,链路余量会形成规律性的动态变化.传统的卫星数传系统设计采用固定编码调制体制(constant coding modulation,CCM),为保证误码率要求,须根据最小的链路余量设计编码调制方式.那么,在整个数传过程中随着链路余量增大,必然存在较大的链路资源浪费.通过VCM技术可以降低这种浪费,从而更加充分地利用链路资源.
VCM的研究依托于信道编码和信号调制的设计.空间数据咨询委员会(the consultative committee for space data systems,CCSDS)针对于星地链路提出了两种支持VCM的通信协议:一种是蓝皮书[5]中给出的串联级联卷积码(serially concatenated convolutional codes,SCCC);另一种是基于欧洲电信标准化协会(European telecommunication standards institute,ETSI)于2003年制定的Digital Video Broadcasting by satellites (DVB-S2)协议[6],使用Bose-Chaudhuri-Hochquenghem (BCH) 为外码,Low Density Parity Check (LDPC)为内码的级联编码方式.2013年美国喷气动力实验室(jet propulsion laboratory,JPL)在CCSDS会议上提议制定关于VCM帧结构的标准化协议,从而推动并规范VCM在工程中的使用.2014年11月,VCM协议紫皮书[7]进入修订阶段.
JPL的Hamkins等[8-10]在DVB-S2协议的基础上,阐述了基于AR4JA LDPC的编码调制子系统,并在不同调制阶数和编码率下详细地仿真分析了系统性能,为设计基于LDPC的VCM系统奠定基础.MAPSK高阶调制技术针对卫星数传应用的研究和实现[11-13],为卫星数传VCM系统提供了关于高阶调制的技术基础.Cossu等[14]提出将VCM思想应用到低轨地球观测卫星数据传输体制设计中,给出VCM系统软件设计体系结构框图,并基于SCCC的VCM技术评估了某K波段遥感卫星的链路效率;张旭[15]设计了VCM的系统设计框图,使用DVB-S2中推荐的4种调制方式和LDPC编码,结合低轨卫星过境时间内的链路预算,使用一种简单的 VCM流程,使卫星下行数据的传输量提高35.5%.可见,VCM在卫星数传领域的应用价值已经得到较为全面的分析和认识.在现有研究的基础上,本文从通信有效性的原理角度出发,通过分析链路预算,设计出一套针对卫星数传链路环境和给定编码调制方式的最佳VCM流程设计算法.该算法能够保证在有效数传时间内获得最大的信息吞吐量.
1 可变编码调制原理与体系模型 1.1 VCM概念与应用模型在卫星数传应用中,信道条件具有一定的规律性变化.例如一颗在高度为600 km的太阳同步轨道上的卫星(简称“例星1”).当它经过地面站时,向地面站传输数据.卫星在仰角大于5°时建立数传链路.例星1的链路设计参数见表 1.
| 表 1 某遥感卫星的X波段数传链路设计参数 Table 1 Design parameter for a X-band remote sensing satellite data transmission link |
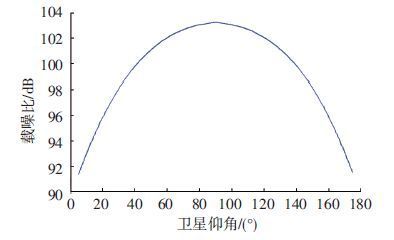
卫星与地面站之间的距离,即数传链路长度R随仰角而变化,从而带来了动态的链路预算结果,如图 1所示.
|
图 1 例星1对地面站的动态数传链路预算 Figure 1 Dynamic data transmission link budget of E_Sat1 to its ground station |
图 1中横坐标为地面站对卫星仰角,纵坐标为链路预算的S/N0.从图 1中可以看出,随着仰角的增大,链路预算充裕度增加.在本例中,卫星过境期间存在着11.8 dB的余量波动.
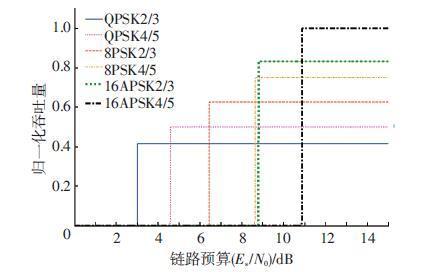
图 2为6种编码调制方案下的系统归一化吞吐量的仿真示意图.仿真中认为误码率大于10-5时,数据有效传输.从图 2中可以看出,低阶调制编码方案在信噪比较低时其系统吞吐量比高阶调制编码方案高,但是随着信噪比的增大,吞吐量稳定在一个较低的水平;而高阶调制编码方案在信噪比较低时由于信道噪声的影响,误码率较高,不能实现有效传输.但是随着信道状况的改善,采用高阶调制编码方式,可获得更高的系统吞吐量.
|
图 2 不同编码调制方案之下的归一化吞吐量 Figure 2 Normalized throughput with different modulation and code rate |
因此VCM思想应运而生,即根据某一预定的流程采用不同的编码调制传输模式,以适应不同的信道条件(例如,传输距离),最大限度地利用链路增益余量,降低链路资源浪费,从而在不增加能量消耗和设备成本的条件下,提高数据传输系统的总吞吐量.
1.2 VCM体系数学模型对于本文所讨论的低轨遥感卫星,其信道可以近似视为加性高斯白噪声(additive white Gaussian noise,AWGN)信道.在这种近似假设下,暂不讨论多普勒、衰落等因素的影响,以便于独立地分析可变编码调制子系统的性能.同时,假设模型中接收设备有理想的载波和同步性能,无相位噪声.
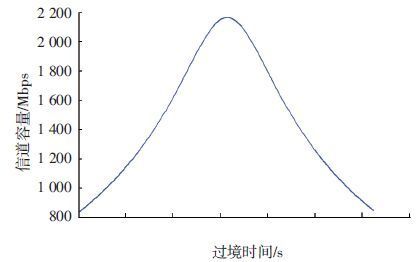
在AWGN信道中,根据香农公式,例星1在数传时间内,信道容量表现为图 3的变化规律.
|
图 3 例星1数传链路容量的变化规律 Figure 3 Variation of E_Sat1’s transmission link capacity |
根据上述分析,VCM流程设计的原则就是:有效的数传时间内,在带宽限制的条件下,满足传输误码率要求的同时使有效比特率尽可能地靠近链路容量曲线,从而获得尽可能大的数据吞吐量.这个问题,用数学表示为优化问题:
| $\begin{align} & \max imize T \\ & s.t. \\ & B\leqq {{B}_{\lim it}}, \\ & {{P}_{e}}\leqq {{P}_{e,t\operatorname{arget}}}. \\ \end{align}$ |
式中:B为系统所用的实际带宽;Blimit为可用的最大带宽;Pe为系统的误比特率;Pe,target是设计要求得目标误比特率;T为数据吞吐量(bits),即卫星在数传时间内,向地面传输的总信息量为
| $T=\int_{{{T}_{p}}}{{{R}_{b}}}\left( t \right)dt.$ |
式中:Rb(t)为有效信息比特速率,其取值可随时间变化,因此表示为时间t的函数;Tp为卫星过境时数传链路保持的时间.
设信道编码方式集合为C,其元素个数为nC;调制方式集合为M,其中包含nM种不同的调制方式.为了方便表达,本文只讨论PSK、APSK调制方式和LDPC编码.定义εM为调制阶数,εC为编码码率.对于M中的元素,εM取1、2、3、4、5分别表示BPSK、QPSK、8PSK、16APSK和32APSK.
对于PSK、APSK,符号速率
| ${{R}_{s}}=\frac{1}{2}{{B}_{\lim it}}.$ | (1) |
VCM的目标是:在限制条件内选用合适的调制编码,使得有效信息比特速率Rb尽可能大.
| ${{R}_{b}}={{R}_{s}}\cdot {{\varepsilon }_{M}}\cdot {{\varepsilon }_{C}},$ |
式中η为频谱利用率.因此,对于单载波系统有
| $\eta =\frac{{{R}_{b}}}{B}=\frac{1}{2}{{\varepsilon }_{M}}{{\varepsilon }_{C}},$ |
由此可见,VCM体系的核心内容是对数传过程中编码调制方式变化流程的设计(即选择合适的εM和εC),从而求解对T的优化问题.
2 VCM流程设计方法以Δ为编码调制方式变化的最小时间单位,将卫星的过境时间Tp(一般设定仰角5°以上为可见)量化为
对所有的 tk∈{Tp\tN},通过链路预算得出S(tk)/N0.设Es表示经过调制映射后的平均符号能量,则由式(1)有
| ${{E}_{s}}({{t}_{k}})/{{N}_{0}}=\frac{S({{t}_{k}})/{{N}_{0}}}{{{R}_{s}}}=\frac{2\cdot S({{t}_{k}})/{{N}_{0}}}{{{B}_{limit}}}.$ |
设某种编码调制方式在AWGN信道中的解调门限为γ([εM,εC],Pe,target).它表示使用M中阶数为εM的调制方式和C中码率为εC的编码方式组,使系统在AWGN信道中达到目标误比特率Pe,target时所需的最小Es/N0.
定义1 有效编码调制组合.
设[εM,εC]i是C
否则,存在一种组合[εM,εC]j具有更低的解调门限,同时又能够得到更高(或相等)的频谱利用率,那么[εM,εC]i在VCM系统设计中就不存在使用价值了,便称其为无效组合.
定义Γ为C和M构建的全部有效编码调制组合的解调门限集合.将Γ中的元素按数值从小到大排序,得到:
| $~\Gamma =\{{{\gamma }_{i}}({{\left[ {{\varepsilon }_{M}},{{\varepsilon }_{C}} \right]}^{i}},{{P}_{e,}}target)|i=1,2,\ldots ,K;{{\gamma }_{i}}<{{\gamma }_{i+1}}\},$ |
由定义1可知,ηi<ηj.
比较Es(tk)/N0和Es(tk+1)/N0,若
| ${{E}_{s}}({{t}_{k}})/{{N}_{0}}\le {{E}_{s+1}}({{t}_{k}})/{{N}_{0}},$ | (2) |
寻找γi∈Γ∪{γ0=0,γK+1=∞},使其满足:
| $~{{\gamma }_{i}}\le {{E}_{s}}\left( {{t}_{k}} \right)/{{N}_{0}}<{{\gamma }_{i+1}}.$ | (3) |
如果只有γ0满足式(3),则表示:在tk~tk+1的时间段内,无法建立有效数传链路,暂不传递信息.否则,有γi([εMm,εCc]i,Pe,target)满足式(3),那么,在tk~tk+1的时间段内安排εMm阶调制和εCc码率编码建立数传链路.因为根据定义1,可以断定,组合[εMm,εCc]i给出满足误码率要求条件下的最大频谱利用率,η(k)=εMmεCc.
同理,若Es(tk)/N0≤Es+1(tk)/N0,视为链路余量在tk~tk+1的时间段内减性变化.为了保证误码率要求,以较小的Es(tk+1)/N0为判断依据,寻找γi∈Γ∪{γ0=0,γK+1=∞},满足:
| ${{\gamma }_{i}}\le {{E}_{s}}\left( {{t}_{k+1}} \right)/{{N}_{0}}<{{\gamma }_{i+1}},$ | (4) |
并按照其对应的组合建立数传链路,或者暂停数传.
最终,根据上述的流程规划,得到卫星过境时间内的信息吞吐量为Es/N0.
| $T=\sum\limits_{k=1}^{N-1}{\Delta \cdot R_{b}^{(k)}}=\sum\limits_{k=1}^{N-1}{\Delta \cdot {{\eta }^{(k)}}}\cdot {{B}_{limit}},$ |
其中,η(k)为tk~tk+1时间段内的频谱利用率.
3 仿真与结果分析针对例星1的数传链路,设计VCM数传体系,并讨论其对链路效率的影响.
M中的元素为QPSK、8PSK、16APSK和32APSK,即εM的可能取值为2、3、4、5.C中为各码率的AR4JA LDPC编码,εC的可能取值为2/3、3/4、4/5、5/6.
表 2中总结了通过计算机仿真得到的编码调制子系统解调门限,满足Pe,target =10-5.
| 表 2 编码调制子系统满足Pe=10-5的解调门限 Table 2 Demodulation threshold for Pe=10-5 of the coding modulation sub-system |
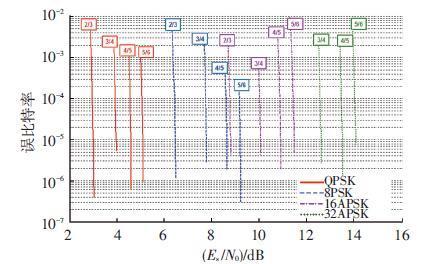
图 4中所示为通过仿真所得的表 2中各编码调制方式的误码率曲线.为了得出满足Pe,target=10-5的解调门限,仿真中关注的目标误码率范围在10-7≤Pe,target≤10-2之内,并确保误码率曲线经过Pe,target=10-5刻线.参与仿真的数据量在108量级,因此针对于Pe,target=10-5的解调门限仿真结果精确到小数点后两位.
解映射时通过计算接收符号的对数似然比(log-likelihood ratio,LLR)得到解调的软判决,以此作为LDPC解码器的输入.通过LDPC解码获取硬判决信息.仿真中,LDPC解码采用迭代解码方式,迭代最高次数为50次.
根据定义1可以判断,表 2中8PSK 5/6,即[3,5/6]组合为无效组合.除此之外的14个组合的解调门限构成有效编码调制组合的解调门限集合Γ.
算例 星1的过境时间Tp= 630 s,取VCM最小变化周期Δ=5 s,将Tp量化为126段.在轨道的上行阶段,链路余量变化满足式(2),按式(3)原则选取最优编码调制组合;在轨道下行阶段,组合选择遵循式(4).如此所得的VCM流程见表 3.
| 表 3 VCM流程设计 Table 3 VCM schedule design |
由于算例中星1轨道对称的特点,VCM流程变化也呈现上下行对称.
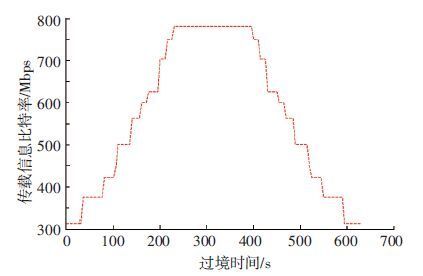
图 5中给出根据表 3中VCM流程所获得的信息比特率随卫星过境时间变化的规律.可以看出,与CCM相比,VCM设计下的比特率曲线呈现与图 2中理论信道容量曲线相似的变化趋势.该VCM设计和几种传统的CCM设计性能对比见表 4 .
|
图 5 VCM有效信息比特率 Figure 5 VCM effective information bit rate |
可见,相比于传统的CCM数传体系,表 3中的VCM数传体系将吞吐量提高了70%以上.这种VCM流程设计方法,在保证系统误码率要求的前提下,最佳地安排了给定编码调制组合的使用时间和顺序,使链路效率得到了明显的优化.
| 表 4 数传链路效率对比 Table 4 Comparison of data transmission link efficiency |
1) 本文针对低轨道探测卫星的应用模型提出卫星对地数传体制的优化问题.给出一种基于可变编码调制的低轨卫星对地数传体制设计方法,以降低链路资源浪费、提高星-地数据传输的吞吐量,从而达到优化链路传输效率的目的.
2) 通过数学描述、定义及推导,重点阐述VCM流程的设计方法,通过最佳安排给定的编码调制组合,求解链路效率优化问题.最后,针对某太阳同步轨道遥感卫星的X波段数传链路,应用所述流程算法设计其VCM流程.通过仿真计算对比,证明所设计的VCM体系明显地提高了过境时间内的吞吐量,优化了链路效率,更加充分地利用了数传链路能力.
| [1] |
DI ROBERTO R, NASCETTI A, PAOLOZZI A,et al. Optical payloads for high-resolution earth imaging suitable for microsatellites[C]//Proceeding of the 15th International Conference on Environment and Electrical Engineering (EEEIC). Rome, Italy: IEEE, 2015. DOI:10.1109/EEEIC.2015.7165456.
( 0) 0)
|
| [2] |
吴国强, 孙兆伟, 赵丹, 等. 编队小卫星星间通信系统的发展和趋势[J].
哈尔滨工业大学学报,2007, 39 (11) : 1699-1703.
DOI: 10.3321/j.issn:0367-6234.2007.11.005 WU Guoqiang, SUN Zhaowei, ZHAO Dan, et al. Development and trend research of inter-satellite communication system on formation small satellites[J]. Journal of Harbin Institute of Technology,2007, 39 (11) : 1699-1703. DOI: 10.3321/j.issn:0367-6234.2007.11.005 (  0) 0)
|
| [3] |
LAN Shengchang, CHEN Qing, ZHANG Jinxiu, et al. A taxonomy of energy efficiency strategies for cubesat cluster formation networks[C]//Proceeding of the 64th International Astronautical Congress (IAC), Beijing: International Astronautical Federation, 2013: 11486-11493.
( 0) 0)
|
| [4] |
MCCARTHY K P, STOCKLIN F J, GELDZAHLER B J, et al. NASA’s evolution to Ka-band space communications for near-earth spacecraft[C]//Proceedings of the Space Ops Conference. Huntsville, AL: American Institute of Aeronautics and Astronautics Inc., 2010.
( 0) 0)
|
| [5] |
Consultative Committee for Space Data Systems (CCSDS). Blue Book: TM Synchronization and Channel Coding: CCSDS 131.0-B-2[S]. Washington DC: CCSDS, 2011,8.
( 0) 0)
|
| [6] |
European Telecommunications Standards Institute (ETSI).European Standard: Digital Video Broadcasting (DVB); Second Generation Framing Structure, Channel Coding and Modulation Systems for Broadcasting, Interactive Services, News Gathering and other Broadband Satellite Applications: ETSI EN 302 307 V1.2.1 (2009-08)[S]. Sophia-Antipolis: ETSI, 2014,3.
( 0) 0)
|
| [7] |
Consultative Committee for Space Data Systems (CCSDS). Magenta Book: Variable Coded Modulation Protocol: CCSDS 131.5-M-1.1[S]. Washington DC: CCSDS, 2014,3.
( 0) 0)
|
| [8] |
HAMKINS J. Performance of Low-Density Parity-Check Coded Modulation[C]//Proceeding of 2010 IEEE Aerospace Conference. Big Sky, U.S.: IEEE, 2010.
( 0) 0)
|
| [9] |
MITCHELL D G M, LENTMAIER M, COSTELLO D J. New families of LDPC block codes formed by terminating irregular photograph-based LDPC convolutional codes[C]//Proceeding of the International Symposium on Information Theory (ISIT). Austin: IEEE, 2010. DOI:10.1109/ISIT.2010.5513633.
( 0) 0)
|
| [10] |
王秀妮. 基于LDPC码的编码调制技术研究[D].广州:中山大学,2013.
( 0) 0)
|
| [11] |
雷菁, 黄英, 刘志新. 非线性卫星信道中APSK信号星座优化设计研究[J].
武汉理工大学学报,2006, 28 (8) : 117-121.
DOI: 10.3321/j.issn.1671-4431.2006.08.032 LEI Jing, HUANG Ying, LIU Zhixin. Optimization of APSK signal constellation for nonlinear satellite channels[J]. Journal of Wuhan University of Technology,2006, 28 (8) : 117-121. DOI: 10.3321/j.issn.1671-4431.2006.08.032 (  0) 0)
|
| [12] |
GUO Shuxiao, HUANG Guodong, LIU Bing, et al. Research of MAPSK modulation based on the no-linear satellite channel[C]//Proceeding of the 3rd Broadband Network and Multimedia Technology. Beijing, China: IEEE, 2010.DOI:10.1109/ICBNMT.2010.5705279.
( 0) 0)
|
| [13] |
DENG Yuance, WANG Zhugang. Modulation recognition of MAPSK signals using template matching[J].
Electronics Letters,2014, 50 (25) : 1986-1988.
DOI: 10.1049/el.2014.2700 ( 0) 0)
|
| [14] |
COSSU M, ROSCIGNO R,GIANCRISTOFARO M, et al. Effects of link availability on the achievable performance with variable coding modulation earth observation satellites[C]//Proceedings of the 1st AESS European Conference on Satellite Telecommunications (ESTEL). Rome, Italy: IEEE Computer Society,2012.DOI:10.1109/ESTEL.2012.6400108.
( 0) 0)
|
| [15] |
张旭. 基于VCM的对地探测卫星数据传输体制分析[J].
电讯技术,2014, 54 (1) : 15-16.
DOI: 10.3969/j.issn.1001-893x.2014.01.003 ZHANG Xu. Analysis of VCM data transmission method for earth exploration satellite system[J]. Telecommunication Engineering,2014, 54 (1) : 15-16. DOI: 10.3969/j.issn.1001-893x.2014.01.003 (  0) 0)
|
 2016, Vol. 48
2016, Vol. 48